Keywords

1 Introduction

High-resolution computational simulations of blood flow have been employed to study biomedical problems such as malaria [7], thrombosis [28], and sickle-cell anemia [16]. However, as simulations are scaled from microvasculature to mesovasculature, the problem size demands efficient and scalable parallel fluid-structure interaction algorithms. As reviewed by [12], one of the most popular fluid-structure interaction algorithms in this space is the immersed boundary (IB) method. The IB method is often implemented as a partitioned fluid-structure interaction scheme, with separate solvers for the fluid and cells. Characterized by a time-invariant Eulerian fluid lattice and body-fitted Lagrangian meshes for the cells, the IB method transfers data between the fluid and cell grids using smoothed discrete delta functions [17, 20]. While maintaining separate Eulerian and Lagrangian grids provides distinct advatanges (e.g., avoiding remeshing), it also complicates parallelization in a distributed-memory environment. In this study, we introduce a scalable IB framework for a hemodynamics application and explore how model parameters influence the cost of halo exchange and recomputation in the IB method.

Parallelization of the IB method for blood flow has several components. Depending on the method, the fluid solver requires at least a halo exchange. Likewise, the movement of blood cells across MPI domains must also be accounted for. Additionally, due to the diffusivity of the IB interface, the IB method interaction of the cell and fluid grids must also be parallelized. This halo exchange for the IB method is particularly interesting: because the IB method can transfer data between the fluid and cell grids, these Lagrangian and Eulerian data are effectively equivalent. Consequently, in principle, either could be communicated on the halo. For notational simplicity, we will denote as Lagrangian and Eulerian communication the transfer of the eponymous types of data.

Implementations of the IB method with distributed-memory parallelism originate with the work of [25] and [8]. While differences necessarily exist between continuous and direct forcing immersed boundary methods, the general challenges related to Lagrangian and Eulerian grids remain similar. In these and subsequent frameworks, the domain decomposition and requisite communication of IB-related data take various forms. To reduce or eliminate the movement of IB structures between tasks, [8] and [26] use separate domain decompositions for Eulerian and Lagrangian data and perform Eulerian communication of IB-related data. In contrast, the majority of implementations have used coincident domain decompositions for the fluid and structure. These schemes typically employ Lagrangian communication on a halo region (e.g., [18, 24, 25, 27, 29]). Eulerian communication over a halo region was judged prohibitively expensive for coincident domain decompositions [6]. More recently, a hybrid parallelization approach has improved load balance of the IB-related workload [19].

Intuitively, the optimal communication arrangement is expected to depend on particular details of the physical system being modeled. For instance, in the implementations discussed above, the IB structures being considered range from a suspension of point particles to a set of small cells to a single large membrane. Algorithmic choices would also seem to play a role: dynamic Lagrangian communication is inherently more complex than static Eulerian communication, but this could be offset by smaller message sizes. Further, other aspects of the simulations may already demand at least a basic level of Lagrangian or Eulerian communication. Moreover, choices about communicating Eulerian or Lagrangian data have implications for which aspects of the algorithm are fully parallelized versus involving some re-computation on overlap regions.

In this study, we investigate the relative parallel efficiency and scaling of Eulerian and Lagrangian communication frameworks applied to blood flow with coincident fluid and structural domain decompositions. Simulations are conducted with HARVEY, a parallel hemodynamics solver for flows in complex vascular geometries [22]. We describe an MPI+OpenMP implementation of the lattice Boltzmann and immersed boundary methods, coupled with finite element models for the cell mechanics. We explore the relative costs of Eulerian and Lagrangian communication for the force which is generated by the cell and spread onto the surrounding fluid. We investigate the dependence of the communication and recomputation costs on three factors: the support of the immersed boundary delta function, the density of the cell suspension, and the relative cost of the finite element method.

2 Methods

HARVEY performs the fluid-structure interaction with the immersed boundary method, coupling the lattice Boltzmann method for the fluid flow with a finite element method representing blood cells. An early version of this framework was presented in [9]. The present section extends that work by generalizing the IB method implementation and by discussing the parallelization schemes in depth. In the subsequent equations, we employ the convention of using lower- and upper-case letters for Eulerian and Lagrangian quantities, respectively.

2.1 Lattice Boltzmann Method for Fluid Flow

The Navier-Stokes equations governing continuum-level fluid flow are solved with the lattice Boltzmann method (LBM), which represents the fluid with a distribution function f of fictitious particles moving about a fixed Cartesian lattice [4]. The quantity \(f_i\) represents the component of the distribution with discrete velocity \(\mathbf {c}_i\). For the D3Q19 velocity discretization used here, 18 of the 19 velocity vectors \(\mathbf {c}_i\) point to nearest-neighbor lattice positions and remaining stationary velocity points to the same lattice position. The lattice Boltzmann equation for a fluid subject to an external force takes the form

$$\begin{aligned} f_{i}(\mathbf {x}+\mathbf {c}_i, t + 1) = (1 - \frac{1}{\tau }) f_{i}(\mathbf {x}, t) + \frac{1}{\tau } f_{i}^{eq}(\mathbf {x}, t) + h_i(\mathbf {x}, t) \end{aligned}$$
(1)

for lattice position \(\mathbf {x}\), timestep t, external force distribution \(h_i\), equilibrium distribution \(f_i^{eq}\), and relaxation time \(\tau \). Without loss of generality, we assume the LBM spatial (dx) and temporal (dt) steps equal to unity.

The external force field \(\mathbf {g}(\mathbf {x}, t)\) is incorporated into the collision kernel – the right-hand side of Eq. 1 – in two steps [10]. First, the moments of the distribution function, density \(\rho \) and momentum \(\rho \mathbf {v}\), are computed by the sums:

$$\begin{aligned} \rho = \sum _{i=1}^{19} f_i \qquad \rho \mathbf {v} = \sum _{i=1}^{19} \mathbf {c}_i f_i + \frac{1}{2}\mathbf {g}. \end{aligned}$$
(2)

From these moments, the equilibrium Maxwell-Boltzmann distribution is approximated as

$$\begin{aligned} f_i^{eq}(\mathbf {x},t) = \omega _i \rho \Bigl ( 1 + \frac{\mathbf {c}_i \cdot \mathbf {v}}{c_s^2} + \frac{\mathbf {v} \mathbf {v} : (\mathbf {c}_i \mathbf {c}_i - c_s^2\mathbf {I})}{2c_s^4} \Bigr ) \end{aligned}$$
(3)

for the standard D3Q19 lattice weights \(\omega _i\) and lattice speed of sound \(c_s^2 = \frac{1}{3}\). Second, the external force \(\mathbf {g}\) is converted into the force distribution \(h_i\),

$$\begin{aligned} h_i = \Bigl ( 1-\frac{1}{2\tau } \Bigr ) \omega _i \Bigl [\frac{\mathbf {c}_i-\mathbf {v}}{c_s^2}+\frac{\mathbf {c}_i \cdot \mathbf {v}}{c_s^4}\mathbf {c}_i \Bigr ] \cdot \mathbf {g}. \end{aligned}$$
(4)

The lattice Boltzmann implementation in HARVEY is targeted at performing highly parallel simulations in sparse vascular geometries. To deal efficiently with this sparsity, the fluid points are indirectly addressed and an adjacency list for the LBM streaming operation is computed during setup. While the reference implementation of LBM stores two copies of the distribution function, we implement the AA scheme in HARVEY, which stores a single copy of the distribution function [1]. Other aspects of the lattice Boltzmann implementation, including grid generation and boundary conditions, may be found in previous work [9, 21].

2.2 Finite Element Methods for Deformable Cells

Each cell is described by a fluid-filled triangulated mesh, derived from successive refinements of an icosahedron. Red blood cell membrane models include physical properties such as elasticity, bending stiffness, and surface viscosity [11]. For the sake of simplicity in this study, we model the cell surface as a hyperelastic membrane using a Skalak constitutive law. The elastic energy W is computed as

$$\begin{aligned} W = \frac{G}{4} \Bigl ( I_1^2 + 2I_1 - 2I_2 \Bigr ) + \frac{C}{4} I_2^2 \end{aligned}$$
(5)

for strain invariants \(I_1\), \(I_2\), and for shear and dilational elastic modul G and C, respectively [14]. We consider two common continuum-level finite element methods for the structural mechanics of deformable cells in blood flow. First, by assuming the displacement gradient tensor is constant over a given triangular element, the forces arising from the deformation of the triangular element can be computed using only the three vertices of the triangle [23]. This method is simple, efficient, and widely implemented but may be limited with respect to stability and extensibility. Second, subdivision elements have been used to develop more stable and extensible models, but require using a ‘one-ring’ of 12 vertices to compute the strain on a triangular element [3, 5, 15]. Compared with the simple model, the subdivision model is much more computationally expensive.

2.3 Immersed Boundary Method for Fluid-Structure Interaction

The Eulerian fluid lattice is coupled with the Lagrangian cell meshes by the immersed boundary method (IB) using a standard continuous forcing approach. Developed to model blood flow in the heart, the IB method uses discrete delta functions \(\delta \) to transfer simulation data between the two grids [20]. Three computational kernels are involved in each timestep of the IB method: interpolation, updating, and spreading. At a given timestep t, the velocity \(\mathbf {V}\) of the cell vertex located at \(\mathbf {X}\) is interpolated from the surrounding fluid lattice positions \(\mathbf {x}\):

$$\begin{aligned} \mathbf {V}(\mathbf {X}, t) = \sum _{\mathbf {x}} \, \mathbf {v}(\mathbf {x}, t) \, \delta (\mathbf {x}-\mathbf {X}(t)). \end{aligned}$$
(6)

The position \(\mathbf {X}\) of the cell vertices is updated using a forward Euler method

$$\begin{aligned} \mathbf {X}(t+1) = \mathbf {X}(t) + \mathbf {V}(t), \end{aligned}$$
(7)

by the no-slip condition. With the cell having been translated and deformed by the fluid, the elastic response to cell deformation is computed according to either method discussed in the previous section. The Lagrangian force \(\mathbf {G}\) is ‘spread’ from cell vertices onto the surrounding fluid lattice positions,

$$\begin{aligned} \mathbf {g}(\mathbf {x}, t) = \sum _{\mathbf {x}} \, \mathbf {G}(\mathbf {X}, t) \, \delta (\mathbf {x}-\mathbf {X}(t)) \end{aligned}$$
(8)

which defines the external force \(\mathbf {g}(\mathbf {x}, t)\) acting on the fluid.

The support of the delta function, which we denoted by the symbol \(\phi \), determines the interaction distance between the Eulerian and Lagrangian grids. Support is measured by the number of Eulerian grid points in a given physical dimension which may influence or be influenced by a given IB point. For a given vertex, the delta function is computed for each dimension at each fluid point within the finite support, using the single-dimension distance \(r \ge 0\) from the fluid point to the IB vertex. This corresponds to 8, 27, and 64 fluid points per IB vertex for delta functions with 2, 3, and 4 point support, respectively. The support of the delta function influences on simulation stability and accuracy, with certain supports being favorable for particular applications [14, 20]. We consider three delta functions, where the index i indicates whether the distance \(r \ge 0\) is taken in the x, y, or z direction.

Delta function support \(\phi = 2\):

$$\begin{aligned} \delta _i (r) = {\left\{ \begin{array}{ll} 1 - r &{}\mathrm {if} \, r\le 1 \\ 0 &{}\mathrm {if} \, r>1 \end{array}\right. } \end{aligned}$$
(9)

Delta function support \(\phi = 3\):

$$\begin{aligned} \delta _i (r) = {\left\{ \begin{array}{ll} \frac{1}{3} \Bigl ( 1 + \root \of {1-3r^2}\Bigr ) &{}\mathrm {if} \, r \le \frac{1}{2} \\ \frac{1}{6} \Bigl ( 5 - 3r - \root \of {-2+6r-3r^2}\Bigr )&{}\mathrm {if} \, \frac{1}{2} < r \le \frac{3}{2} \\ 0 &{}\mathrm {if} \, r>\frac{3}{2} \end{array}\right. } \end{aligned}$$
(10)

Delta function support \(\phi = 4\):

$$\begin{aligned} \delta _i (r) = {\left\{ \begin{array}{ll} \frac{1}{4} \Bigl ( 1 + \cos (\frac{\pi }{2}r)\Bigr ) &{}\mathrm {if} \, r\le 2 \\ 0 &{}\mathrm {if} \, r>2 \end{array}\right. } \end{aligned}$$
(11)

We note that computational expense of the interpolation and spreading operations varies with the number of vertices, the complexity of the delta function and the number of fluid point within the support. The latter factor is exacerbated when the fluid points are not directly addressed, such as the indirect addressing in this study. Unlike the static adjacency list for LBM streaming, the dynamic set of fluid points falling within the support of a given IB vertex varies in time. Consequently, a lookup operation must be performed for each fluid point in the support to identify the memory location for the Eulerian velocity or force data with which it is associated. As the indirect addressing scheme is not random but has limited local patterns, it can be advantageous for larger \(\phi \) to guess-and-check a subset of lookups and, if successful, interpolate between them.

Fig. 1.
figure 1

Example of domain decomposition, with cells coloured by the bounding box to which they below. Dotted lines indicate halo for the green task.

Full size image

2.4 General Parallelization Framework

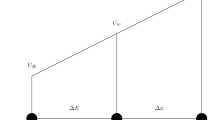
The simulation domain is spatially decomposed among tasks into rectangular cuboid bounding boxes. Forming a partition of the vascular geometry, the bounding boxes for the Eulerian fluid domain and Lagrangian cell domain are coincident. The boundary between two bounding boxes is located exactly halfway between the last fluid point belonging to each bounding box. Based on [18], communication between tasks is governed by a hierarchy of overlapping halos on which Lagrangian or Eulerian communication is performed. When the halo of a task overlaps with the bounding box of another task, the latter task is considered a ‘neighbor’ of the former task with respect to this halo and vice versa. For linguistic convenience, fluid points and IB vertices which are and are not located within the task bounding box will be denoted as ‘owned’ and ‘shared’, respectively, from the task’s perspective. Analogously, a cell is considered to be owned or shared based on the position of the unweighted average of its vertices. An example of the bounding box decomposition in shown in Fig. 1.

Fluid Halo: A halo of fluid points is placed around the task bounding box, with a two-fold purpose. First, a single point-wide halo may be used to communicate LBM distribution components which will stream into the bounding box in the subsequent timestep. Second, by setting the halo width to \(\lfloor \frac{\phi }{2}\rceil \), the IB interpolation operation may be computed locally for all owned vertices. As \(\delta _i(\frac{3}{2})=0\) in Eq. 10, we have a single point-wide fluid halo for \(\phi =2\) and 3, but a two point-wide fluid halo for \(\phi =4\).

Cell Halo: A halo for cells is placed about the task bounding box in order to facilitate IB-related computation. In contrast to [18], a shared cell in a halo is a complete and fully updated copy of the cell. The width of this halo is set to \(\lfloor \frac{\phi }{2}\rceil +r\), in which r is the largest cell radius expected in the simulation. This width ensures that all vertices which may spread a force onto a fluid point owned by the task are shared with the task. That is, if forces were known on cells within the halo, spreading may be computed locally for all owned fluid points.

2.5 Lagrangian and Eulerian Communication for IB Spreading

Algorithm 1 shows the basic coupling of fluid solver and finite element solver with the immersed boundary method for a serial code. To explore the options of communicating Eulerian or Lagrangian data, we focus on the parallelization of the last two steps: the finite element method (FEM) to compute forces at vertices of the cells and the IB spreading operation, in which forces defined at cell vertices are spread onto the fluid lattice. Two general approaches are possible for handling the communication at task boundaries.

figure a
Fig. 2.
figure 2

Lagrangian communication for the IB spreading operation for \(\phi =2\). First (left), the Lagrangian force is computed on the owned IB vertex (black circle) by the upper task and communicated to the same vertex (yellow circle) on the lower task. Second (right), the IB spreading operation (red box) is performed for this vertex by both tasks. Solid blue lines indicate fluid grid points owned by the task, dash blue line denotes fluid points on the halo, and the dotted line represents the boundary between tasks. (Color figure online)

Full size image

First, Lagrangian data – the forces defined at cell vertices – can be communicated, as depicted in Fig. 2. This allows for the finite element method to be computed in a conservative manner. In our implementation, tasks run the finite element method over cells which they own. Forces defined at vertices within another task’s halo are then communicated, which allows each task to perform the spreading operation locally. However, recomputation occurs when multiple tasks perform the spreading operation for vertices located near task boundaries.

Fig. 3.
figure 3

Eulerian communication for the IB spreading operation for \(\phi =2\). First (left), the upper task computes the Lagrangian force on the owned vertex (black circle) and perform the IB spreading operation (red box). Second (right), the upper task communicates the Eulerian forces to the same fluid grid points (yellow box) on the lower task. Solid blue lines indicate fluid grid points owned by the task, dash blue line denotes fluid points on the halo, and the dotted line represents the boundary between tasks. (Color figure online)

Full size image

Second, Eulerian data – the forces defined on the fluid grid – can be communicated instead, as depicted in Fig. 3. We compute the forces at all owned vertices, which leads to recomputation for finite elements which include vertices owned by two tasks. The forces of a task’s owned vertices are spread onto owned and halo fluid points, which is a conservative operation. Finally, a halo exchange is performed for forces on fluid points adjacent to and located on the halo.

3 Results

3.1 Simulation Setup

The fluid domain is assumed to be cylindrical, representing an idealized blood vessel. A variety of approaches exist for generating dense suspensions of red blood cells or other suspended bodies. In the context of blood flow, the density of the suspension – the volume percentage of red blood cells in blood – is referred to as the hematocrit (Hct) level. Iterative schemes for packing rigid [30] and deformable [13] red blood cells have been demonstrated to achieve physiological hematocrit levels. To avoid the additional startup and parallelization cost of such a scheme, we perform dense packing of minimally enclosing ellipsoids in a cubic geometry using an external library [2]. The cubic arrangement is used to periodically ‘tile’ the vascular geometry during preprocessing and red blood cells meshes are initialized within ellipsoids. A warmup period is necessarily required before a well-developed flow is realized but other schemes incur similar costs [30]. In subsequent simulations, we completely tile the geometry with a dense red blood cell suspension and, if necessary, randomly remove cells until the desired hematocrit is achieved. A small example of a dense cell suspension in a vascular geometry is shown in Fig. 4.

Fig. 4.
figure 4

Example image of red blood cells at a bifurcation in a vascular geometry. Cells are colored by vertex velocity. (Color figure online)

Full size image

Runs are conducted on two different architectures, Intel Broadwell and IBM Blue Gene/Q. Part of the Duke Computer Cluster (DCC), the Broadwell system is a cluster with two Intel Xeon E5-2699 v4 processors per node and 56Gb/s Mellanox Infiniband interconnect, using 32 MPI ranks per node and 2 OpenMP threads per rank. The LLNL Blue Gene/Q system Vulcan has a Power BQC 16C on each node and custom interconnect, and is used with 16 MPI ranks and 4 OpenMP threads per rank. In the subsequent sections, we investigate single node performance and scaling across multiple nodes. For single node performance on Intel, we study a cylindrical geometry with a radius of 197 \(\upmu \)m, which includes approximately 900,000 red blood cells when packed at 43% hematocrit. Due to the limited memory available on a Blue Gene/Q node, we use a scaled cylinder with a radius of 99 \(\upmu \)m and approximately 100,000 red blood cells. For weak scaling across nodes, we consider progressively larger cylinders which maintain the same number of red blood cells per node when densely packed.

3.2 Comparing Lagrangian and Eulerian Communication On-Node

In this section, we compare the efficiency of Lagrangian and Eulerian communication methods from Sect. 2.5 for performing the IB spreading operation. Accordingly, we focus on the three components of the simulation related to this task (the finite element model, IB spreading itself, and pertinent communication) and consider the runtime of these three components, rather than the runtime of the entire simulation.

An important difference between the two communication schemes is the amount of data to be transferred. For the Lagrangian scheme, communication size will be dependent by the number of cells located near to task boundaries. Assuming a non-pathological distribution of cells, this will vary with the density of cells in the flow or Hct. In contrast, the Eulerian scheme will have a uniform communication size independent of Hct. Further, the communication pattern for the Eulerian scheme is time-independent, while bookkeeping may be necessary to update the Lagrangian scheme as cells move and deform. In Fig. 5, we observe the intuitive result: runtime for Eulerian communication time is constant while the Lagrangian communication time varies directly with hematocrit.

Fig. 5.
figure 5

Communication time for Lagrangian and Eulerian schemes for a DCC (Broadwell) node at left and a Vulcan (Blue Gene/Q) node at right. Communication times are measured in seconds and are normalized by the value of the Lagrangian scheme for \(\phi =2\) and Hct=5.

Full size image

The size of the data to be transferred will also depend on the support of the delta function. For \(\phi =4\), the fluid halo increases to two grid points. This effectively doubles the amount of communicated data for the Eulerian scheme relative to the single grid point halo for \(\phi = 2\) or 3. While the amount of Lagrangian data to be communicated is somewhat higher for \(\phi = 4\), we observe in Fig. 5 that this increase is considerably more modest. Additionally, while hematocrit value at which Eulerian scheme begins to outperform is roughly similar between the two architectures, this cross-over value is consistently approximately 5% higher on Vulcan (Blue Gene/Q).

Fig. 6.
figure 6

For \(\phi =2\), we compare runtime on a DCC (Broadwell) node as a function of Hct for Lagrangian (left bar) and Eulerian (right bar) communication. Runtimes are measured in seconds and, for a given Hct, are normalized by the Lagrangian runtime. Left and right images show simple and subdivision finite element models, respectively.

Full size image

However, the merits of the two communication schemes also have to be judged in the context of the recomputation required and its impact on overall runtime. Figure 6 shows how the significance of recomputation varies not only with the communication scheme but also with the finite element model. As discussed above, the IB spreading operation performs expensive lookup operations when used with an indirectly addressed fluid grid. When paired with an inexpensive finite element model, we observe that the IB spreading recomputation performed by the Lagrangian scheme in the spreading operation becomes expensive relative to the finite element recomputation of the Eulerian scheme. As a result, the Eulerian scheme outperfoms in this framework, even at the low hematocrit values for which the communication cost exceeds than of the Lagrangian scheme.

Conversely, this situation is reversed for the subdivision finite element model. Due to the high computational expense of this model, the recomputation when computing forces on the cells exceeds that of the IB spreading operation. The Lagrangian scheme consequently proves more efficient for higher hematocrit values, with communication costs for either scheme being relatively inconsequential. This result is also relevant to other approaches for modeling cell mechanics, such as discrete element methods, which have reported that the force computation kernel is responsible for the majority of their runtime [18].

In summary, we observe that both communication and recomputation are associated with the relative performance of Lagrangian and Eulerian communication schemes. Looking solely at communication time, the Eulerian communication scheme clearly outperform its Lagrangian counterpart at the hematocrit values typical of blood flow. This advantage is most significant for smaller immersed boundary supports but remains even for \(\phi = 4\). This result for a high density of immersed boundary vertices serves as a complement for the experience of [6], who found performing Eulerian communication was inefficient for a simulation with \(\phi = 4\) and a density of immersed boundary vertices comparable to 10% Hct. However, we also find that the disparity between the cost of the finite element and spreading operations may render recomputation a more important factor than communication cost in determining the more efficient scheme, especially at higher cell densities.

3.3 Weak Scaling

As the purpose of a distributed memory parallelization scheme is to enable large simulations which require multiple nodes, the scalability of a communication scheme is also important. In contrast to the previous section, we now consider the scalabity of the full simulation, rather than the kernels and communication which differed in the Lagrangian and Eulerian communication schemes. Figure 7 shows weak scaling at 43% hematocrit for \(\phi = 2\), 3, and 4 and using the simple finite element model. For weak scaling, we increase the problem size proportionately with the number of tasks, maintaining the same amount of work per task over successively larger task counts. To measure weak scalability, we normalize all runtimes by the runtime at the lowest task count.

Fig. 7.
figure 7

Weak scaling for \(\phi = 2\), 3, and 4 for DCC (Broadwell) in the top row and Vulcan (Blue Gene/Q) in bottom row

Full size image

We observe broadly similar performance with the two architectures, although DCC (Broadwell) benefits from the much larger problem size per node. On both architectures, we observe a drop in performance between 32 and 64 tasks due to the maximum number of neighboring tasks being first encountered on the latter task count. A similarly marginal gain occurs with the Eulerian communication scheme for the IB spreading operation, which outperformed for this parameter set on a single node and maintains this modest advantage when the problem is weakly scaled across nodes. However, the primary influence on scalability comes from the delta function support, as performance with \(\phi =4\) is limited by larger communication and recomputation times due to the larger halo. In contrast, weak scaling remains around 89% parallel efficiency for \(\phi =2\) and 3.

3.4 Discussion

In this study, we investigate the factors influencing the performance of halo exchange for the immersed boundary method in the context of the hemodynamics application HARVEY. Focusing on the on-node performance of the IB spreading operation, we compare Lagrangian and Eulerian communication frameworks. In this comparison, the purpose is not to propose an optimal configuration based on our application, but to provide a starting point for evaluating IB method parallelization options for a given physical problem and model.

With respect to purely communication-related costs, we find that the intuitive cross-over for more efficient Eulerian than Lagrangian communication for the IB spreading operation occurred for a density of IB vertices relevant to many applications including blood flow. For physiological values of red blood cell hematocrit, Eulerian communication may provide an improvement, regardless of the delta function support. Conversely, for lower IB vertex densities and \(\phi =4\), we agree with the assertion of [6] that Eulerian communication may not be an efficient scheme. However, the exact cross-over point will nonetheless be variable: on systems with limited memory per node, like the Vulcan Blue Gene/Q, we see the hematocrit cross-over point, at which Eulerian scheme outperforms the Lagrangian, to be about 5% higher than the larger Broadwell nodes on the DCC cluster.

However, we find that communication costs must also be assessed in the context of the required recomputation. The support of the delta function and relative cost of the IB spreading and finite element model will influence the relative costs of communication and recomputation. We observe that while larger delta function support sizes necessarily increase compute costs, the additional communication costs may be modest relative to factors like recomputation. In future work, we plan to extend this study of immersed boundary halo exchange to simulations on heterogeneous CPU-GPU compute nodes, where the differences in recomputation and data motion cost are expected to become more significant.