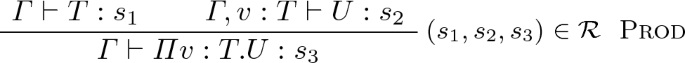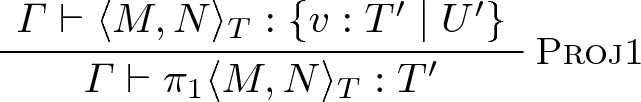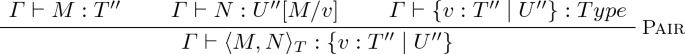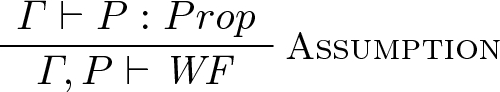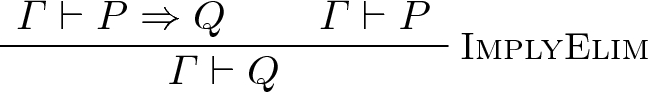Abstract
Adding predicate subtyping to higher-order logic yields a very expressive language in which type-checking is undecidable, making the definition of a system of verifiable certificates challenging. This work presents a solution to this issue with a minimal formalization of predicate subtyping, named PVS-Core, together with a system of verifiable certificates for PVS-Core, named PVS-Cert. PVS-Cert is based on the introduction of proof terms and explicit coercions. Its design is similar to that of PTSs with dependent pairs, with the exception of the definition of conversion, which is based on a specific notion of reduction \(\rightarrow _{\beta *}\), corresponding to \(\beta \)-reduction combined with the erasure of coercions. The use of this reduction instead of the more standard reduction \(\rightarrow _{\beta \sigma }\) allows to establish a simple correspondence between PVS-Core and PVS-Cert. On the other hand, a type-checking algorithm is designed for PVS-Cert, built on proofs of type preservation of \(\rightarrow _{\beta \sigma }\) and strong normalization of both \(\rightarrow _{\beta \sigma }\) and \(\rightarrow _{\beta *}\). Combining these results, PVS-Cert judgements are used as verifiable certificates for predicate subtyping. In addition, the reduction \(\rightarrow _{\beta \sigma }\) is used to define a cut elimination procedure for predicate subtyping. This definition provides a new tool to study the properties of predicate subtyping, as illustrated with a proof of consistency.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Extending higher-order logic with predicate subtyping yields a very expressive type system, used notably at the core of the proof system PVS [17]. However, proof judgements and typing judgements become entangled in the presence of predicate subtyping, making type-checking undecidable. As a consequence, defining a language of verifiable proofs for predicate subtyping becomes challenging. In pure higher-order logic, complete judgement derivations are too heavy to be used in practice as certificates, but lighter certificates can be produced by removing typing rules, recording deduction rules only: as this approach requires the decidability of type-checking, it doesn’t apply directly to predicate subtyping.
This paper presents a new formal language, PVS-Cert, designed to be used as a language of verifiable certificates for predicate subtyping. PVS-Cert is built starting from a minimal formalization of predicate subtyping named PVS-Core, by adding explicit proofs and coercions. PVS-Cert is also equipped with a notion of cut elimination, which can be used directly to study both PVS-Cert and PVS-Core meta-theoretical properties.
1.1 Extending Higher-Order Logic with Predicate Subtyping
Higher-order logic is characterized by the coexistence of types and predicates as two radically different kinds of attributes to mathematical expressions. For instance, the mathematical expression \(1\,+\,1\) can be assigned a type \( Nat \) expressing that it is a natural number, or a predicate \( Even \) expressing that it is divisible by two. The assignment of types remains very simple: in particular, type-checking is decidable in higher-order logic. In return, most attributes of mathematical expressions formulated as predicates cannot be formulated as types: for instance, being a natural number different from 0 is expressible as a predicate, but not as a type.
Predicate subtyping allows to recover a symmetrical situation between the expressivity of types and predicates. It is defined as the addition of new types, referred to as predicate subtypes. Given a predicate P defined on a domain A (e.g. \( Even \), defined on the domain \( Nat \)), the predicate subtype \(\{x : A \mid P(x)\}\) is defined. An expression t can be assigned this type if and only if it can be assigned the type A and P(t) is provable. For instance, if \( Nonzero \) is a predicate of domain \( Nat \) expressing the difference of a natural number from 0, proving \( Nonzero (1)\) allows to conclude that 1 admits the type \(\{x : Nat \mid Nonzero (x)\}\).
This augmented expressivity of the language of types permits to exclude many unwanted expressions from reasoning. For instance, defining the denominators domain of Euclidean division as \(\{x : Nat \mid Nonzero (x)\}\), all divisions in which the denominator is not provably different from zero become ill-typed.
As expressions may have several types, predicate subtyping induces a form of subtyping: for instance, as any expression of type \(\{x : Nat | Nonzero (x)\}\) also admits the type \( Nat \), the former can be considered as a subtype of the latter.
As previously mentioned, a major counterpart of this extension of higher-order logic is the fact that typing judgements and proof judgements become entangled. For instance, proving the equality \((1/1) = 1\) requires that 1 can be assigned the type \(\{x : Nat | Nonzero (x)\}\), which, in turn, requires to prove \( Nonzero (1)\). As a direct consequence, type-checking is not decidable in the presence of predicate subtyping.
1.2 Contributions
PVS-Core. Higher-order logic, as well as its extension with predicate subtyping, can be defined in various ways. The first contribution of this paper is the formalization, in Sect. 2, of a minimal system for predicate subtyping, denoted PVS-Core. Besides its minimality, the main design choice for this system is the use of \(\beta \)-equivalence as a conversion relation (or definitional equality).
PVS-Cert and Its Basic Properties. Starting from PVS-Core, the second contribution of this work is the formalization, in Sect. 3, of a language of verifiable proofs for PVS-Core. This new language, denoted PVS-Cert, is designed from PVS-Core with the addition of explicit proof terms, formalized as \(\lambda \)-terms, as well as the addition, at the level of expressions, of explicit coercions based on these proof terms. The addition of explicit proof terms follows the Curry-Howard isomorphism in the sense that PVS-Cert proofs terms are typed by their corresponding formulas.
PVS-Cert is an extension of the Pure Type System (PTS) \(\lambda \)-HOL (see for instance [4], where \(\lambda \)-HOL as well as the general notion of PTS are defined). More precisely, PVS-Cert is designed to extend \(\lambda \)-HOL in the same way that PVS-Core extends higher-order logic (denoted HOL in the following). This situation is illustrated in this diagram, where vertical arrows represent extensions and horizontal arrows represent the introduction of explicit proofs (and, in the case of PVS-Core and PVS-Cert, of explicit coercions).

This choice of a PTS-like system is well-suited to describe reasoning modulo \(\beta \): all steps of \(\beta \)-reduction or \(\beta \)-expansion are kept implicit in proof terms, which allows to keep them compact. As detailed in Sect. 3.3, PVS-Cert is comparable to the formalism of PTSs with dependent pairs. However, conversion in PVS-Cert is neither defined as \(\equiv _{\beta }\) nor as its extension \(\equiv _{\beta \sigma }\) (see for instance [16]) used in PTSs with dependent pairs: instead, it uses a new conversion relation \(\equiv _{\beta *}\) corresponding to syntactical equality modulo \(\beta \)-reduction and coercion erasure (defined in Sect. 3.1). This distinctive definition allows to define a simple correspondence between PVS-Core and PVS-Cert – presented later in Sect. 9.
Basic properties of PVS-Cert are presented in Sect. 4, containing notably the Church-Rosser property for the reduction \(\rightarrow _{\beta *}\) underlying the conversion \(\equiv _{\beta *}\), as well as the uniqueness of types: contrary to the case of PVS-Core, a well-typed term admits a unique type up to \(\equiv _{\beta *}\).
As in \(\lambda \)-HOL, well-typed terms are organized according to a stratification, presented in Sect. 5, which includes a class of types, a class of expressions (containing notably propositions), and a class of proof terms. This stratification is at the core of the correspondence between PVS-Cert and PVS-Core.
Type Preservation and Strong Normalization. In contrast to the case of the reduction \(\rightarrow _{\beta \sigma }\) in PTSs with dependent pairs, \(\rightarrow _{\beta *}\) is not a type preserving reduction in PVS-Cert. We prove however in Sect. 6 that \(\rightarrow _{\beta \sigma }\) is a type preserving reduction in PVS-Cert (Theorem 6).
In Sect. 7, we present the main ideas leading to a proof of strong normalization for both \(\rightarrow _{\beta *}\) and \(\rightarrow _{\beta \sigma }\) (Theorem 7) – the details of the proof can be found in the author’s PhD dissertation [1]. Moreover, the strong normalization of the type preserving reduction \(\rightarrow _{\beta \sigma }\) defines a cut elimination theorem (Theorem 8). This theorem is used in the remainder of this section to prove the consistency of PVS-Cert. This result is used in turn at the very end of this work to conclude the consistency of PVS-Core, illustrating how cut elimination in PVS-Cert can be used to study the meta-theoretical properties of predicate subtyping.
Type-Checking in PVS-Cert. We present in Sect. 8 the design of a type-checking algorithm for PVS-Cert, showing that, contrary to the case of PVS-Core, type-checking is decidable in PVS-Cert. This algorithm is based on the type preservation of \(\rightarrow _{\beta \sigma }\) as well as the strong normalization of \(\rightarrow _{\beta *}\) and \(\rightarrow _{\beta \sigma }\).
Using PVS-Cert as a System of Verifiable Certificates for PVS-Core. The connection between PVS-Core and PVS-Cert is formalized in Sect. 9. On the one hand, a translation from PVS-Cert to PVS-Core is defined through the erasure of coercions. On the other hand, the choice of conversion \(\equiv _{\beta *}\) in PVS-Cert allows to define a very simple translation from PVS-Core derivations to PVS-Cert derivable judgements (Definition 7 and Theorem 11).
These translations are used in Sect. 10 together with the PVS-Cert type-checking algorithm to define how to use PVS-Cert judgements as verifiable certificates for PVS-Core, reaching the first purpose of this paper. Such certificates are much lighter than the PVS-Core derivations represented through them, as they only require to record one single judgement.
Last, the translations between PVS-Core and PVS-Cert are exploited to transpose the consistency property, established in PVS-Cert using cut elimination, to PVS-Core. This illustrates how the PVS-Cert cut elimination theorem can be used to study both PVS-Cert and PVS-Core meta-theoretical properties.
1.3 Related Works
The most important related work is the author’s PhD dissertation [1], which contains detailed versions of all proofs presented in this paper.
The introduction of predicate subtyping can be traced back to the first-order language OBJ2 [9] and its sort constraints, allowing to restrict some typing relations to the satisfaction of a predicate. This idea was later refined and combined with higher-order logic in the proof system PVS, which is one of the most important systems based on predicate subtyping. Overviews of the PVS specification language and its use of predicate subtyping are given for instance in [17] and [20].
In the present work, the issue of the undecidability of predicate subtyping is handled with the introduction of an alternative system, PVS-Cert. An alternative approach to this issue is to weaken the definition of predicate subtyping sufficiently to obtain systems in which type-checking remains decidable. This approach has been followed in [13, 19]. A intermediary situation is followed in [15], in which predicate subtyping is weakened sufficiently to allow for run-time type-checking verifications. However, contrary to the case of PVS, predicate subtyping is not fully represented in these different systems.
As mentioned in the previous section, PVS-Cert is an adaptation of the formalism of Pure Type Systems (PTSs) – sometimes also referred to as Generalized Type Systems (GTSs) –, presented for instance in [4]. The definition of PTSs is itself the result of several successive works, including notably [3, 7, 11, 24,25,26]. More specifically, PVS-Cert is derived from the notion of PTSs with dependent pairs, which has its roots in the system ECC [16]. A subsystem of PVS-Cert, named PVS-Cert\(^-\) and presented in Sect. 3, corresponds directly to a fragment of ECC (PVS-Cert\(^-\) is the system obtained from PVS-Cert by replacing \(\equiv _{\beta *}\) by the standard conversion \(\equiv _{\beta \sigma }\) of PTSs with dependent pairs). PVS-Cert\(^-\) is also comparable to the notion of subset types in Coq [5]. However, contrary to PVS-Cert, PVS-Cert\(^-\) and subset types are not well-suited to reflect predicate subtyping, as conversion in these systems does not reflect conversion in PVS-Core – more precisely, Proposition 5 doesn’t hold with \(\equiv _{\beta \sigma }\).
Another important related work is [8], in which two systems are presented: ICC\(_\varSigma \), a type system with implicit type constructions, and AICC\(_\varSigma \), a system obtained from ICC\(_\varSigma \) by adding explicit coercions. ICC\(_\varSigma \) contains several advanced features, including a generalization of predicate subtypes. The construction of PVS-Cert from PVS-Core follows the same idea as the construction of AICC\(_\varSigma \) from ICC\(_\varSigma \): adding the missing information explicitly in the terms of the language to recover the decidability of type-checking. The main difference between the two approaches lies in the complexity of the respective languages. ICC\(_\varSigma \) is a very rich and complex language, making its analysis difficult – in particular, strong normalization in ICC\(_\varSigma \) is kept as a conjecture, on which the decidability of type-checking itself relies. Conversely, PVS-Core is designed as a minimal language including predicate subtyping, making its analysis simpler.
A variant of predicate subtyping was also formalized as an extension of the calculus of constructions in [22]. As in the present work, this presentation contains two systems connected with each other. On the one hand, it includes one system, named Russell, which is comparable to a weakened version of PVS-Core in which a term t of type A admits the type \(\{x : A \mid P\}\) even when P[t / x] is not provable. In this variant of predicate subtyping named subset equivalence, type-checking is decidable. On the other hand, this work includes a system with explicit coercions which is comparable to PVS-Cert. Contrary to PVS-Core, Russell derivations are not intended to contain all information necessary to build complete terms with explicit coercions: instead, a translation producing incomplete terms in the system with explicit coercions is presented. This system allows to write programs and specifications together in Russell, and to prove their correctness in a second step by filling all proof holes produced through the translation, in a way which is similar to the functioning of PVS.
Contrary to the case of PVS-Core and Russell, PVS-Cert and the counterpart of Russell with explicit coercions have similar characteristics. Although its theoretical properties are not formalized, this latter system is presented as a simple extension of the proof-irrelevant type theory presented in [27]. There exists indeed a tight connection between proof irrelevance and PVS-Cert: if one considers for instance the usual predicate \( Even \) on natural numbers expressing divisibility by two, the predicate subtype \( even = \{x : Nat \mid Even (x)\}\), and two expressions with explicit coercions \(\langle 2, p \rangle _{ even }\) and \(\langle 2, q \rangle _{ even }\) of this type with p and q two proofs of \( Even (2)\), then the hypothesis of proof irrelevance ensures that the expressions \(\langle 2, p \rangle _{ even }\) and \(\langle 2, q \rangle _{ even }\) are convertible, as does the choice of conversion relation \(\equiv _{\beta *}\) in PVS-Cert.
This relation between proof irrelevance and predicate subtyping is explored further in [27]. Besides the fact that this work is based on the calculus of constructions and besides some technical differences in the precise definition of conversion between the system presented in this paper and PVS-Cert, analyzing the strong relation between these two systems appears as a very interesting future work. In particular, it would provide a possible strategy for building a proof of strong normalization for this system from the proof of strong normalization presented in Sect. 7. Also following the relation between proof irrelevance and predicate subtyping, the system IITT presented in [2], which is equipped with explicit occurrences of irrelevant terms, also admits some similarities with PVS-Cert. However, it is restricted to predicative type theory, in which higher-order reasoning cannot be expressed.
Another important work carried out on predicate subtyping is the presentation of a formal semantics for PVS in [18]. This work defines, for some fragment of the PVS language including predicate subtyping but also other features such as parametric theories, set-theoretical interpretations of types and expressions. These interpretations are limited to standard interpretations: the interpretation of a function type is the set of all functions from the interpretation of the domain to the interpretation of the co-domain, and the interpretation of the type of propositions is a set containing exactly two elements, distinguishing true propositions from false ones. Such an approach is complementary to the presented paper, which is only focused on the distinction between provable propositions and unprovable ones. As a possible future work, it would be interesting to adapt the work presented in [18] to obtain a notion of standard model for PVS-Core.
2 PVS-Core: A Minimal Extension of HOL with Predicate Subtyping
This section is dedicated to the first contribution of this work: the formalization of a minimal system for predicate subtyping. This system is named PVS-Core, in reference to PVS [17]. The main distinctive design choice for PVS-Core is the introduction of a conversion relation (or definitional equality), corresponding to \(\beta \)-equivalence.
2.1 Definitions
Variables and Terms. We first define a set of variables \(\mathcal {V}\) as the disjoint union of two infinite countable sets of symbols \(\mathcal {V}_{expressions}\) and \(\mathcal {V}_{types}\). We introduce the generic notation v or w to refer to a variable in general, as well as the following specific notations:
-
The notation X or Y refers to variables in \(\mathcal {V}_{types}\).
-
The notation x or y refers to variables in \(\mathcal {V}_{expressions}\).
Then, we define a set of terms as the disjoint union of the three following sets. The last two are defined together recursively.
-
The first set contains a unique symbol: Type.
-
The second set is the set of types. It is given with the following grammar:
\(A, B := X \mid Prop \mid \varPi x : A . B \mid \{x : A \mid P\} \)
-
The last set is the set of expressions. It is given with the following grammar:
\(t, u, P, Q := x \mid \forall x : A . P \mid P \Rightarrow Q \mid \lambda x : A . t \mid t u\)
Remark 1
There is no formal distinction between the expressions denoted t or u and the expressions denoted P or Q, as all of them refer to expressions in general. Yet, in the following, the notations P and Q will be often used to refer to expressions admitting the type Prop, also referred to as formulas or propositions.
Declarations, Contexts, Judgements. We define:
-
Three kinds of declarations:
\(X : Type \mid x : A \mid P\)
-
Contexts, denoted \(\varGamma \), as lists of declarations:
\(\varGamma := \varnothing \mid \varGamma , X : Type \mid \varGamma , x : A \mid \varGamma , P\)
-
Four kinds of judgements:
\(\varGamma \vdash WF \mid \varGamma \vdash A : Type \mid \varGamma \vdash t : A \mid \varGamma \vdash P\)
We use the notation \(DV(\varGamma )\) to refer to the set of variables declared in a context \(\varGamma \): for instance, \(DV(P, x : A, X : Type) = \{x, X\}\).
Reduction. We equip PVS-Core terms with the usual \(\beta \)-reduction. In the following, we use the notation \(\triangleright _\beta \) for the reduction of a \(\beta \)-redex, \(\rightarrow _\beta \) for the context closure of \(\triangleright _\beta \), \(\twoheadrightarrow _\beta \) for the reflexive transitive closure of \(\rightarrow _\beta \), and \(\equiv _\beta \) for the symmetric closure of \(\twoheadrightarrow _\beta \), i.e. \(\beta \)-conversion.
Derivation Rules.The rules of PVS-Core are the following:
Well-formed contexts

2.2 A Minimal System Expressing Predicate Subtyping
Predicate subtyping is expressed in PVS-Core with the term construction \(\{x : A \mid P\}\) and the following rules:
-
Subtype, the rule of formation of predicate subtypes.
-
SubtypeIntro, which is a rule of introduction.
-
SubtypeElim1 and SubtypeElim2, which are rules of elimination.
The system obtained from PVS-Core by removing the construction \(\{x : A \mid P\}\) and these four rules is a formulation of constructive higher-order logic. In particular, the types of this subsystem correspond to the expected simple types: for any type of the form \(\varPi x : A . B\) in this subsystem, x cannot appear free in B, hence this type is a non-dependent function type. As a consequence, the rule TypeConversion can be safely removed from this subsystem to obtain a simpler but equivalent formulation of higher-order logic.
PVS-Core is a minimal constructive system, which can be extended with classical reasoning or extensionality principles through the addition of axioms.
The rule PropConversion allows to consider reasoning modulo \(\beta \), which will be useful in the definition of PVS-Core to keep proof terms compact. The rule TypeConversion is its counterpart at the level of types, allowing to consider typing modulo \(\beta \) as well.
3 PVS-Cert: Verifiable Certificates for PVS-Core
This section is dedicated to the presentation of an alternative system, PVS-Cert, which will be used to achieve the purpose of the work: defining a language of verifiable certificates for predicate subtyping.
At first glance, there is no need to introduce any new system to design PVS-Core certificates: the language of PVS-Core derivations itself is a language of verifiable proofs for PVS-Core. However, this language is heavy as many parts of PVS-Core derivations contain unnecessary or redundant information. As a comparison, in higher-order logic, as type-checking is decidable, only the deduction rules need to be recorded.
The main idea in the definition of PVS-Cert as a language of certificates for predicate subtyping is to formalize proofs as new kinds of terms, in addition to the types and expressions which are already present in PVS-Core, and to introduce explicit coercions based on these proof terms in order to ensure the decidability of type-checking. As a consequence, a complete certificate is simply the typing judgement of some proof term with its corresponding theorem. Such certificates are much lighter than PVS-core derivations, as only one single judgement is recorded.
Moreover, PVS-Cert will be equipped (in Sect. 7) with a definition of cut elimination, defined as a computation rule on proof terms.
3.1 Definitions
As detailed further in Sect. 3.2, the definition of PVS-Cert is strongly related to the formalism of PTSs, presented for instance in [4].
Terms. We define:
-
Sorts \(\mathcal {S} = \{Prop, Type, Kind\}\)
We use the notation s to refer to a sort.
-
Axioms \(\mathcal {A} = \{(Prop, Type), (Type, Kind)\}\)
-
Rules \(\mathcal {R} = \{(Prop, Prop, Prop), (Type, Type, Type), (Type, Prop, Prop)\}\)
-
Variables The set of variables \(\mathcal {V}\) is the disjoint union of three infinite countable sets of symbols \(\mathcal {V}_{proofs}\), \(\mathcal {V}_{expressions}\), and \(\mathcal {V}_{types}\). The sets \(\mathcal {V}_{expressions}\) and \(\mathcal {V}_{types}\) refer to their respective definitions in PVS-Core, while the set \(\mathcal {V}_{proofs}\) is new. We use the notation v to refer to a variable and s(v) to refer to the unique sort s such that \(v \in \mathcal {V}_s\).
-
Terms \(\mathcal {T}\) is given by the following grammar:
\(M, N, T, U := s \mid v \mid \lambda v : T . M \mid M N \mid \varPi v : T . U \mid \{v : T \mid U\}\mid \langle M, N \rangle _T \mid \pi _1(M) \mid \pi _2(M)\)
Contexts, Judgements. We define:
-
Contexts \(\varGamma := \varnothing \mid \varGamma , v : T\)
-
Judgements \(\varGamma \vdash WF \mid \varGamma \vdash M : T\)
As in PVS-Core, set of variables declared in a context \(\varGamma \) is denoted \(DV(\varGamma )\).
Reduction. The main specificity of PVS-Cert is the use of a distinctive notion of reduction and conversion. In addition to the usual \(\beta \)-redex reduction \((\lambda v : T . M) N \triangleright _\beta M[N/v]\), we introduce a new reduction relation \(\triangleright _*\), defined with the following rules:
-
\(\langle M_1, M_2 \rangle _T \triangleright _* M_1\)
-
\(\pi _1 (M) \triangleright _* M\)
We denote the union of \(\triangleright _\beta \) and \(\triangleright _*\) as \(\triangleright _{\beta *}\). As in the definition of PVS-Core, we use the notation \(\rightarrow _{\beta *}\) for the context closure of \(\triangleright _{\beta *}\), \(\twoheadrightarrow _{\beta *}\) for the reflexive transitive closure of \(\rightarrow _{\beta *}\), and \(\equiv _{\beta *}\) for the symmetric closure of \(\twoheadrightarrow _{\beta *}\).
The new relation \(\triangleright _*\), which can be interpreted as the elimination of a coercion at the head of a term, allows the expression of predicate subtyping in PVS-Cert. More detailed motivations and justifications for this definition are given in Sect. 3.3.
Derivation Rules. The rules of PVS-Cert are defined as follows:

3.2 An Extension of \(\lambda \)-HOL
PVS-Cert is an extension of the PTS \(\lambda \)-HOL (see for instance [4]). More precisely, \(\lambda \)-HOL can be obtained from PVS-Cert by removing the term constructions \(\{v : T \mid U\}\), \(\pi _i(M)\), and \(\langle M, N \rangle _T\), removing the rules Subtype, Pair, Proj1, and Proj2, and replacing \(\equiv _{\beta *}\) by \(\equiv _\beta \) in the Conversion rule.
As PTS-like systems, the formalism of PVS-Cert allows to describe reasoning modulo \(\beta \): all steps of \(\beta \)-reduction or \(\beta \)-expansion in reasoning are kept implicit, which allows to keep proof terms compact, making PVS-Cert more scalable. Moreover, the choice of formalization of PVS-Cert as a PTS-like system allows to transpose some PTS properties to PVS-Cert, such as the thinning property and the substitution property mentioned in the next section. It also allows to describe this system using a small number of rules in comparison with PVS-Core, making the proof of certain expected properties of PVS-Cert lighter.
The well-typed terms of PVS-Cert are classified into the same classes as in the case of \(\lambda \)-HOL, involving a class of types, a class of expressions, and a class of proof terms. This property is presented in Sect. 5, and referred to as stratification.
3.3 Expressing Predicate Subtyping
The expression of predicate subtyping in PVS-Cert is enlightened through the stratification: indeed, in any derivable judgement,
-
terms of the form \(\{v : T \mid U\}\) are types, expressing predicate subtypes
-
terms of the form \(\langle M, N \rangle _T\) or \(\pi _1(M)\) are expressions, and correspond respectively to explicit coercions going from a type to one of its predicate subtypes and back
-
terms of the form \(\pi _2(M)\) are proofs, expressing the PVS-Core deduction rule SubtypeElim2.
As mentioned in the introduction, this formalism used to express predicate subtyping is very similar to the formalism of dependent pairs, used for instance in the type system ECC [16]. More precisely, the terms \(\{v : T \mid U\}\) are comparable with types of dependent pairs (usually denoted \(\varSigma v : T . U\)), the terms \(\langle M, N \rangle _T\) are comparable with dependent pairs, and the terms \(\pi _i(M)\) are comparable with projections.
The only difference between PVS-Cert and the formalism of dependent pairs lies in the choice of conversion \(\equiv _{\beta *}\): in the case of a system with dependent pairs, \(\equiv _{\beta *}\) is replaced by the more standard conversion \(\equiv _{\beta \sigma }\). This conversion is defined from the usual reduction \(\pi _i \langle M_1, M_2 \rangle _T \triangleright _\sigma M_i\). We define the relations \(\triangleright _{\beta \sigma }\), \(\rightarrow _{\beta \sigma }\), \(\twoheadrightarrow _{\beta \sigma }\), and \(\equiv _{\beta \sigma }\) in a similar way to the definitions of \(\triangleright _{\beta *}\), \(\rightarrow _{\beta *}\), \(\twoheadrightarrow _{\beta *}\), and \(\equiv _{\beta *}\).
Applied to types or expressions, the conversion \(\equiv _{\beta *}\) includes the more standard conversion \(\equiv _{\beta \sigma }\) (this property is a direct consequence of Theorem 5 together with the Church-Rosser property of \(\rightarrow _{\beta \sigma }\)). However, this inclusion is strict: for instance, it is not difficult to find two well-typed terms \(\langle M, N_1 \rangle _T\) and \(\langle M, N_2 \rangle _T\) which are not convertible using \(\equiv _{\beta \sigma }\), although they are convertible using \(\equiv _{\beta *}\).
As a direct consequence of this property, PVS-Cert is an extension of the system obtained from it by replacing \(\equiv _{\beta *}\) by \(\equiv _{\beta \sigma }\), and this extension is strict. In this paper, this subsystem will be referred to as PVS-Cert\(^-\). It is a PTS with dependent pairs, and corresponds more precisely to the system obtained from the PTS \(\lambda \)-HOL by adding the single dependent pair rule (Type, Prop, Type). It is strictly included in the type system ECC presented in [16].
An mentioned in the introduction, this choice of a strictly more flexible conversion allows to define a very simple translation from PVS-Core derivations to PVS-Cert derivable judgements. Indeed, using \(\equiv _{\beta *}\) ensures that two PVS-Cert types (resp. expressions) are convertible as long as the corresponding types (resp. expressions) in PVS-Core are also convertible, which allows to define a very simple translation from PVS-Core derivations to PVS-Cert derivable judgements (Definition 7 and Theorem 11).
The reduction \(\rightarrow _{\beta *}\) underlying conversion does not preserve typing: for instance, the judgement \(x : Prop, h : x \vdash \langle x, h \rangle _T : T\) with \(T = \{y : Prop \mid y\}\) is derivable, and \(\langle x, h \rangle _T \rightarrow _{\beta *} x\), but \(x : Prop, h : x \vdash x : T\) is not derivable. However, as presented in Sect. 6, the reduction \(\rightarrow _{\beta \sigma }\) is type preserving, and will be used both as a definition of cut elimination for PVS-Cert proofs (Sect. 7) and in the definition of a type checking-algorithm (Sect. 8).
4 Properties of PVS-Cert
One of the most important properties satisfied by PVS-Cert is the Church-Rosser property.
Theorem 1
(Church-Rosser for \(\rightarrow _{\beta *}\)). Whenever \(M_1 \equiv _{\beta *} M_2\), there exists N such that \(M_1 \twoheadrightarrow _{\beta *} N\) and \(M_2 \twoheadrightarrow _{\beta *} N\).
Proof
\(\mathcal {T}\) equipped with \(\rightarrow _{\beta *}\) is an orthogonal combinatory reduction system (as defined in [14]), as rules are left-linear and non-overlapping. As proved in [14], such a system admits the Church-Rosser property.
In the case of PTSs, the Church-Rosser property of \(\rightarrow _\beta \) is at the core of the type preservation of \(\rightarrow _\beta \). In the case of PVS-Cert, the situation is different, as \(\rightarrow _{\beta *}\) is not a type preserving reduction. However, in a first step, the Church-Rosser property of \(\rightarrow _{\beta *}\) will be used to establish the expected stratification theorem, presented in Sect. 5. In a second step, the Church-Rosser property of \(\rightarrow _{\beta *}\) will be used again together with the stratification theorem to establish the type preservation of an alternative reduction, \(\rightarrow _{\beta \sigma }\), used both as a definition of cut elimination (Sect. 7) and at the core of the definition of a type-checking algorithm (Sect. 8).
Another important property of PVS-Cert used to design a type-checking algorithm is the uniqueness of types modulo conversion. As presented in Sect. 8, this property allows – together with the decidability of \(\equiv _{\beta *}\) on well-typed terms – to reduce the problem of type-checking to a problem of type inference. This property also underlines the fact that, even though PVS-Cert is designed to reflect predicate subtyping, it doesn’t admit any subtyping itself. The proof of type uniqueness is standard, and does not involve any specific difficulty.
Theorem 2
(Uniqueness of types). If two judgements \(\varGamma \vdash M : T_0\) and \(\varGamma \vdash M : T_1\) are derivable, then \(T_0 \equiv _{\beta *} T_1\).
PVS-Cert also satisfies several other standard properties expected from PTSs and PTSs extended with dependent pairs, among which thinning and substitution, described for instance in [4], as well as context conversion, described for instance in [21], which is based on the extension of conversion to contexts. In these three cases, the corresponding proofs are straightforwardly adapted from the case of PTS.
We end this section with the following important theorem, which also holds in \(\lambda \)-HOL. The proof is adapted from the case of \(\lambda \)-HOL and does not involve any specific difficulty.
Theorem 3
If \(\varGamma \vdash M : T\) is derivable and \(T \ne Kind\), there exists a sort s such that \(\varGamma \vdash T : s\).
5 Stratification in PVS-Cert
The stratification of terms in PVS-Cert reveals a strong link between PVS-Cert and PVS-Core (defined in Sect. 9), in the same way that the stratification of terms in \(\lambda \)-HOL reveals its link with higher-order logic. The property of stratification holds for several other systems, such as the injective PTSs presented in [11] – in this paper, PTSs are referred to as GTSs, and this result is referred to as classification.
The main lemma used to establish such a result is the fact that, whenever the rule of conversion is used in some derivation, the two terms involved in the conversion belong to the same class of terms. The simplest way to prove this result is to choose classes of terms that are stable under reduction and to conclude using the Church-Rosser theorem. In the case of injective PTSs, these classes are specific classes of well-typed terms, and the stability under reduction follows from the type preservation of \(\rightarrow _\beta \).
However, as mentioned in Sect. 3.3, type preservation does not hold for \(\rightarrow _{\beta *}\) in PVS-Cert. For this reason, we will choose a relaxed definition of stratified terms, where the different classes are not restricted to well-typed terms. Using this relaxed definition, it will be possible to prove, even in the absence of type preservation for \(\rightarrow _{\beta *}\), that most classes of stratified terms are stable by reduction with \(\rightarrow _{\beta *}\).
We first present three classes of terms: types, expressions, and proofs. The expected property of stability by reduction will only be proved for types and expressions (Proposition 1), which is not problematic as the conversion rules are never directly applied to proofs in valid derivations.
Definition 1
(Variables stratification). We introduce the notations:
-
X, Y, Z for variables in \(\mathcal {V}_{types}\)
-
x, y, z for variables in \(\mathcal {V}_{expressions}\)
-
h for variables in \(\mathcal {V}_{proofs}\)
Definition 2
(Stratified terms). We define stratified terms as follows.
-
Types \(A, B := X \mid Prop \mid \varPi x : A . B \mid \{x : A \mid P\} \)
-
Expressions
\(t, u, P, Q := x \mid \varPi x : A . P \mid \varPi h : P . Q \mid \lambda x : A . t \mid t \; u \mid \langle t, M \rangle _A \mid \pi _1(t)\)
-
Proofs \(p, q := h \mid \lambda h : P . p \mid \lambda x : A . p \mid p \; q \mid p \; t \mid \pi _2(t)\)
Remark 2
As in the case of PVS-Core (Remark 1), there is no formal distinction between the notations t, u, P, and Q although, in the following, the notations of expressions P, Q will be preferred for expressions of type Prop.
The most important remark on the definition of stratified terms is the fact that any pair \(\langle t, M \rangle _A\) (where t is an expression and A is a type) is accepted as a correct expression: the term M used in it can be arbitrary, and in particular it is not required to be a proof term. This choice is due to the fact that proofs are not stable by \(\rightarrow _{\beta *}\): for instance, \((\lambda h : x . h) y\) is a proof, but y is not. Hence, compared to the alternative of restricting pairs to terms of the form \(\langle t, p \rangle _A\), the present relaxed definition is necessary to ensure the stability of types and expressions under \(\rightarrow _{\beta *}\), which is formalized in the following proposition – the proof does not involve any specific difficulty, as the definitions of types and expressions are designed to satisfy this property.
Proposition 1
Whenever \(M \rightarrow _{\beta *} N\) and M is a type (resp. an expression), so is N.
Beyond its use in the proof of the stratification theorem (Theorem 4), this stability property is also directly useful in the proof of the strong normalization theorem for \(\rightarrow _{\beta *}\) and \(\rightarrow _{\beta \sigma }\), as briefly mentioned in Sect. 7.
Finally, we present the expected stratification theorem, based on the following definitions.
Definition 3
(Stratified contexts, stratified judgements). We define
-
stratified contexts as contexts in which all declarations have the form X : Type, x : A (for some type A), or h : P (for some expression P).
-
stratified judgements as judgements of one of the following forms, in which \(\varGamma \) is a stratified context:
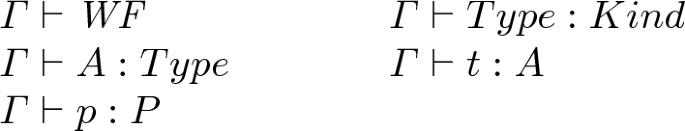
Theorem 4
(Stratification). Any derivable judgement is stratified.
Proof
The proof is straightforward by induction on the derivation. In the case of Conversion, Proposition 1 and the Church-Rosser property of \(\rightarrow _{\beta *}\) are used together to conclude that the two convertible terms are either both expressions, both types, both Type, or both Kind. Basic stability properties of types and expressions under substitution are also involved in the cases Proj2 and App. They are proved directly by induction.
6 A Type Preserving Reduction
Contrary to the case of PTSs (resp. PTSs with dependent pairs), in which \(\rightarrow _\beta \) (resp. \(\rightarrow _{\beta \sigma }\)) is a type preserving reduction, \(\rightarrow _{\beta *}\) is not a type preserving reduction in PVS-Cert. Instead, we present in this section the type preservation of the reduction \(\rightarrow _{\beta \sigma }\) in PVS-Cert. This reduction will be used both as a definition of cut elimination for PVS-Cert proofs (Sect. 7) and in the type-checking algorithm (Sect. 8).
The specificity of this proof of type preservation compared to similar results for PTSs lies in the fact that \(M \rightarrow _{\beta \sigma } N\) does not imply \(M \equiv _{\beta *} N\) in general. However, this implication always holds if M is either a type or an expression – the corresponding proof involves no particular difficulty.
Theorem 5
Whenever \(M \rightarrow _{\beta \sigma } N\) and M is a type (resp. an expression), so is N, and \(M \equiv _{\beta *} N\).
Finally, the type preservation theorem for \(\rightarrow _{\beta \sigma }\) is the following.
Theorem 6
Given a derivable judgement \(\varGamma \vdash M : T\), and N such that \(M \rightarrow _{\beta \sigma } N\), the judgement \(\varGamma \vdash N : T\) is derivable.
Proof
The proof is done by induction on the derivation. The situations where  and the cases where \(M \triangleright _{\beta \sigma } N\) are separated. We present here one case for each situation – the full proof can be found in the author’s PhD dissertation [1].
and the cases where \(M \triangleright _{\beta \sigma } N\) are separated. We present here one case for each situation – the full proof can be found in the author’s PhD dissertation [1].
-
We illustrate the situation where
 with the case of the rule Prod, which involves Theorem 5. Discarding the notations of the original statement, we describe the last inference step with the following new notations:
with the case of the rule Prod, which involves Theorem 5. Discarding the notations of the original statement, we describe the last inference step with the following new notations: 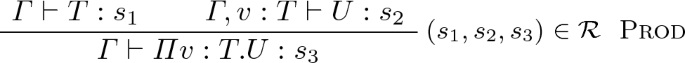
If the reduction occurs in U, we conclude directly by induction hypothesis. If the reduction occurs in T, we write \(T \rightarrow _{\beta \sigma } T'\). By induction hypothesis, \(\varGamma \vdash T' : s_1\) is derivable. By the stratification theorem, \(v \in \mathcal {V}_{s_1}\), hence \(\varGamma , v : T' \vdash WF \) is derivable using the Decl rule. By the stratification theorem and Theorem 5, \(T \equiv _{\beta *} T'\). Hence, using the second premise and context conversion (mentioned in Sect. 4), \(\varGamma , v : T' \vdash U : s_2\) is derivable. Finally, using Prod, \(\varGamma \vdash \varPi v : T' . U : s_3\) is derivable.
-
We illustrate the situation where \(M \triangleright _{\beta \sigma } N\) with the case of the rule Proj1. As M is a first projection and \(M \triangleright _{\beta \sigma } N\), M is a \(\sigma \)-redex. We replace the notation M and T of the original statement by \(\pi _1 \langle M, N \rangle _{T} \triangleright _{\beta \sigma } M\) and \(T'\). In this setting, the last inference step has the following form:
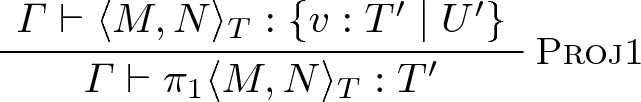
Analyzing the derivation of the premise (and more precisely the last rule different from Conversion used in it, which is necessarily Pair), we conclude that T has the form \(\{ v : T'' \mid U''\}\) where \(\{ v : T' \mid U'\} \equiv _{\beta *} \{ v : T'' \mid U''\}\) and \(\varGamma \vdash \langle M, N \rangle _T : \{ v : T'' \mid U''\}\) admits a derivation ending with an inference step of the form
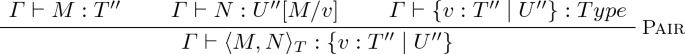
We derive the expected judgement \(\varGamma \vdash M : T'\) from the first premise of this latter derivation using conversion. For this, we need to prove \(T'' \equiv _{\beta *} T'\) and to derive \(\varGamma \vdash T' : s\) for some s. These two requirements are proved as follows. On the one hand, we establish \(T'' \equiv _{\beta *} T'\) from \(\{ v : T'' \mid U''\} \equiv _{\beta *} \{ v : T' \mid U'\}\) using the Church-Rosser property (Theorem 1). On the other hand, by the stratification theorem, \(T' \ne Kind\), hence we can use Theorem 3 on the original conclusion to establish that \(\varGamma \vdash T' : s\) is derivable for some sort s, as expected.
7 Strong Normalization and Cut Elimination
This section is dedicated to the strong normalization of both \(\rightarrow _{\beta \sigma }\) and \(\rightarrow _{\beta *}\) on well-typed PVS-Cert terms. These two reductions will be used separately in Sect. 8 to define a type-checking algorithm for PVS-Cert: more precisely, the reduction \(\rightarrow _{\beta *}\) is used to decide whether two well-typed terms are convertible with \(\equiv _{\beta *}\), while the type preserving reduction \(\rightarrow _{\beta \sigma }\) will be used in the type-checking of applications. Moreover, the strong normalization of \(\rightarrow _{\beta \sigma }\) combined with its type preservation property provides a cut elimination theorem, which is a powerful tool to study properties of both PVS-Cert and PVS-Core. Its use is illustrated in a proof of consistency of PVS-Cert (Theorem 9), used in turn to establish the consistency of PVS-Core (Theorem 12) at the end of this paper.
7.1 Strong Normalization
A direct approach to prove the strong normalization of \(\rightarrow _{\beta \sigma }\) and \(\rightarrow _{\beta *}\) for well-typed terms would be to prove the strong normalization for well-typed terms of their union, referred to as \(\rightarrow _{\beta \sigma *}\). Unfortunately, this reduction is not strongly terminating on well-typed terms, as shown in the following proposition.
Proposition 2
There exists a well-typed term admitting an infinite reduction using \(\rightarrow _{\beta \sigma *}\).
Proof
We first define two well-typed terms M and N such that MN admits an infinite reduction. It is simple to find two such terms, using the fact that PVS-Cert is an extension of System F [12]. For instance:
-
We take \(\top = \varPi P : Prop . \varPi h : P . P\) together with \(M = \lambda h : \top . h \;\top \;h\) and \(N = \lambda h' : \top . \lambda h : \top . h \;\top \;h\)
-
M admits the type \(\varPi h : \top . \top \) and N admits the type \(\varPi h' : \top . \varPi h : \top . \top \).
-
MN admits an infinite reduction \(M N \rightarrow _{\beta \sigma *} N \; \top \; N \rightarrow _{\beta \sigma *} M N \rightarrow _{\beta \sigma *} ...\)
Using these terms, we build the expected counter-example of normalization of \(\rightarrow _{\beta \sigma *}\) as follows:
-
We define \(N' = \lambda P : Prop . \lambda h : P . h\), \(T = \{x : Prop \mid \varPi h' : \top . \varPi h : \top . \top \}\), and \(U = \{y : T \mid \top \}\).
-
It is straightforward to show that \(M \; \pi _2 \langle \langle \top , N \rangle _T, N' \rangle _U\) admits the type \(\top \).
-
\(M \; \pi _2 \langle \langle \top , N \rangle _T, N' \rangle _U \twoheadrightarrow _{\beta \sigma *} M N\), hence it admits an infinite reduction.
Because of Proposition 2, we keep the expected strong normalization theorem in PVS-Cert formulated as follows.
Theorem 7
(Strong normalization). For any derivable judgement \(\varGamma \vdash M : T\), M is strongly normalizing under both \(\rightarrow _{\beta \sigma }\) and \(\rightarrow _{\beta *}\):
-
any reduction sequence starting from M and using \(\rightarrow _{\beta *}\) terminates
-
any reduction sequence starting from M and using \(\rightarrow _{\beta \sigma }\) terminates
The proof of this theorem is left out of the scope of this paper. It is detailed in the author’s PhD dissertation [1]. We simply highlight here some of its specificities, which illustrate the consequences of the choice, in PVS-Cert, of a conversion relation which is not based on a type-preserving reduction.
-
The proof uses Tait’s approach based on saturated sets (see for instance [23]). However, only one single notion of saturated set is used: saturated sets are defined here as specific subsets of the set of terms which are both strongly normalizing under \(\rightarrow _{\beta \sigma }\) and strongly normalizing under \(\rightarrow _{\beta *}\). As a consequence, compatibility properties for such saturated sets must be proved with respect to both reductions.
-
Following Tait’s approach, an interpretation function is defined in order to prove that, whenever term M admits a type T, it belongs to the interpretation of T, which is the main theorem established to conclude strong normalization. The definition of this function is inspired from the definitions of Girard in [12] for the strong normalization of \(F^\omega \) – which corresponds to \(\lambda \)-HOL without type declarations –, but several ideas are also taken from [10], which presents, among other things, a proof of strong normalization of an extension of the calculus of constructions with dependent pairs.
-
As the interpretation function is expected to be stable under \(\rightarrow _{\beta *}\), its domain cannot be restricted to well-typed terms only, as well-typed terms are not stable under \(\rightarrow _{\beta *}\). For this reason, it is chosen to define this interpretation function on the classes of types and expressions, as presented in the definition of stratified terms (Definition 3): indeed, this specific definition, which uses arbitrary terms instead of proof terms in the construction \(\langle t, M \rangle _A\), is designed to ensure the stability of types and expressions under \(\rightarrow _{\beta *}\).
7.2 Cut Elimination in PVS-Cert
The following cut elimination theorem is a direct corollary of the strong normalization theorem and the type preservation of \(\rightarrow _{\beta \sigma }\).
Theorem 8
(Cut elimination). Whenever some PVS-Cert judgement of the form \(\varGamma \vdash p : P\) is derivable for some proposition P and some proof p, p can be reduced using the reduction \(\rightarrow _{\beta \sigma }\) to a normal form q such that the judgement \(\varGamma \vdash q : P\) is derivable.
Proof
By the strong normalization theorem, p can be reduced to a normal form q using the reduction \(\rightarrow _{\beta \sigma }\). By the type preservation theorem (Theorem 6), the judgement \(\varGamma \vdash q : P\) is derivable.
We conclude this section showing how the cut elimination theorem can be used together with the properties of terms in normal form with respect to \(\rightarrow _{\beta \sigma }\) as a tool to analyze some meta-theoretical properties of PVS-Cert. As presented at the end of this work, this approach will also allow to use cut elimination in PVS-Cert to analyze some meta-theoretical properties of PVS-Core. This use of cut elimination is illustrated with the following proof of consistency.
Theorem 9
PVS-Cert is consistent: there exists no proof term p such that \(\vdash p : \varPi x : Prop . x\) is derivable.
We use the following notion of elimination context in the proof:
Definition 4
(Elimination contexts). We define the set of elimination contexts \(\mathcal {E}\) with the grammar \(e := {\scriptstyle \bullet } \mid \pi _i(e) \mid e \; M\).
For any term N we define the instantiation e[N] by

Proof
(Theorem 9 ). We suppose that there exists a proof p such that the judgement \(\vdash p : \varPi x : Prop . x\) admits some derivation, and find a contradiction in the following way. Using the thinning property (mentioned in Sect. 4), \(x : Prop \vdash p : \varPi x : Prop . x\) is also derivable. Hence, applying the rule Lam followed by the rule App, \(\vdash \lambda x : Prop . (p x) : \varPi x : Prop . x\) is derivable.
By the cut elimination Theorem 8, \(\lambda x : Prop . (p x)\) admits a normal form \(\lambda x : Prop . q\) with respect to \(\twoheadrightarrow _{\beta \sigma }\), which is such that the judgement \(\vdash \lambda x : Prop . q : \varPi x : Prop . x\) is derivable.
Considering the last rule different from Conversion used in such a derivation (which is necessarily Lam), and using the stratification theorem, there exists a derivable judgement \(x : Prop \vdash q : t\) for some expression \(t \equiv _{\beta *} x\). Hence, using Conversion, \(x : Prop \vdash q : x\) is also derivable. We consider D a possible derivation of this judgement.
As q is a proof and is in normal form with respect to \(\twoheadrightarrow _{\beta \sigma }\), we conclude from a careful case analysis that q has one of the following forms: \(\lambda v : T . M\) or e[v]. We discard the first possibility as follows. If \(q = \lambda v : T . M\), considering the last rule different from Conversion used in D (which is necessarily Lam), there exists some term of the form \(\varPi v' : T' . U'\) such that \(\varPi v' : T' . U' \equiv _{\beta *} x\). By the Church-Rosser property (Theorem 1), this conversion cannot hold. As a consequence, q has the form e[v] for some elimination context e and some variable v.
Considering the last rule different from Conversion, Proj1, Proj2, or App used in D (which is necessarily Var), some judgement of the form \(x : Prop \vdash v : T\) is derivable, and \(v = x\). As q is a proof, \(e[x] = q \ne x\). Hence, D admits some subderivation of a judgement of the form \(x : Prop \vdash x t' : T'\) or \(x : Prop \vdash \pi _i(x) : T'\). Considering the last rule different from Conversion in such a derivation, and using the uniqueness of types (Theorem 2), this implies that there exists a term U of the form \(\varPi v' : T_1 . T_2\) or \(\{ v' : T_1 \mid T_2 \}\) such that \(U \equiv _{\beta *} Prop\). By the Church-Rosser property (Theorem 1), this conversion cannot hold. As a consequence, there exists no proof term p such that the judgement \(\vdash p : \varPi x : Prop . x\) is derivable.
8 Type-Checking in PVS-Cert
The purpose of this section is to present the main ideas leading to the definition of a type-checking algorithm for PVS-Cert. The decidability of type-checking is one of the most important results expected for PVS-Cert. In particular, it will be used in Sect. 10 together with the translation from PVS-Core derivations to PVS-Cert established in Sect. 9 to show that PVS-Cert judgements can be used as verifiable certificates for PVS-Core.
This algorithm is mainly based on the type preservation Theorem 6 and the strong normalization Theorem 7 presented in the previous sections. In this section, we will only focus on the main specificities of the algorithm. Its precise definition, as well as the proofs of its soundness, termination, and completeness can be found in the author’s PhD dissertation [1].
The algorithm is comparable to the algorithm presented in [6] for the general case of injective PTSs (which applies to \(\lambda \)-HOL). Besides the fact that our algorithm is extended to handle predicate subtypes, coercions \(\langle M, N \rangle _T\) and projections \(\pi _i(M)\), the main difference between the two is the use of both reductions \(\rightarrow _{\beta *}\) and \(\rightarrow _{\beta \sigma }\) in the case of PVS-Cert, while only \(\rightarrow _\beta \) is used for injective PTSs.
On the one hand, \(\rightarrow _{\beta *}\)-normalization is used to check \(\equiv _{\beta *}\)-conversion on well-typed terms: by the Church-Rosser property and strong normalization, two well-typed terms are \(\equiv _{\beta *}\)-equivalent if and only if they admit the same normal form, which is unique. As in [6], this decision procedure for conversion on well-typed terms is used in turn together with the uniqueness of types (Theorem 2) to define type-checking from type inference, which is itself defined recursively.
Remark 3
In order to avoid redundant context well-formedness verifications in the multiple recursive calls of the type inference algorithm, we choose here to check the well-formedness of a context \(\varGamma \) beforehand when inferring a type for some term M in \(\varGamma \). For this reason, type inference and type-checking are defined in two steps. First, we define auxiliary type inference and type-checking algorithms which are only ensured to operate soundly with well-formed contexts. Then, we use these auxiliary functions to define context well-formedness verification as well as complete type inference and type-checking algorithms, which operate soundly with any context.
On the other hand, \(\rightarrow _{\beta \sigma }\) is used in type inference to handle applications:

In this situation, the recursive call on the first premise may produce a term U such that \(\varGamma \vdash M : U\) is derivable, but U is not ensured to have the form \(\varPi v : U_1 . U_2\) – counterexamples can be easily found when M is a proof and U is a proposition. The usual solution to this issue, used e.g. in [6], is to reduce U using the reduction underlying conversion (or more specifically its restriction to weak head reduction, which is more economic): indeed, using the uniqueness of types as well as strong normalization, type preservation, and the Church-Rosser property, it can be proved that a term \(U'\) will be obtained, that M admits the type \(U'\), and that \(U'\) has the form \(\varPi v : U_1 . U_2\) if M admits a type of this form.
However, in the case of PVS-Cert, this approach cannot be followed directly, as the reduction underlying conversion, which is \(\rightarrow _{\beta *}\), is not type preserving: \(U'\) is not necessary a valid type for M. For this reason, we use instead the type preserving reduction \(\rightarrow _{\beta \sigma }\) (again, we use more specifically its restriction to weak head reduction, which is more economic). Using the strong normalization theorem, this operation terminates and yields some term \(U''\). As a direct corollary of type preservation (based on Theorems 3 and 5), M admits the type \(U''\). What is left is to prove that \(U''\) has the form \(\varPi v : U_1 . U_2\) if M admits a type of this form, which is done as follows. If M admits a type of the form \(\varPi v : T_1 . T_2\), then \(U'' \equiv _{\beta *} \varPi v : T_1 . T_2\) by the uniqueness of types. Hence, analyzing the possible forms of the weak head normal form \(U''\) and using the Church-Rosser property, we conclude that \(U''\) has the form \(\varPi v : U_1 . U_2\), as expected.
Compared to [6], new cases must be added for predicate subtypes, coercions \(\langle M, N \rangle _T\), and projections \(\pi _i(M)\). These cases are handled in a similar way as in the case of PTSs with dependent pairs (see for instance ECC [16]), and don’t involve any specific difficulty. Instead, a more distinctive specificity of the algorithm lies in the case of \(\lambda \)-abstraction:

As in the case of injective PTSs studied in [6], applying a recursive call on this second premise would be problematic. On the one hand, it would make the algorithm slower. On the other hand, it would break the simplicity of the proof of termination, based on the fact that recursive calls of type inference are done on subterms exclusively.
A general solution for this issue, applicable to any injective PTSs, is presented in [6] using some classification of terms to avoid this unwanted recursive call. The solution selected for PVS-Cert follows the same approach, adapted to the stratified terms of PVS-Cert. It relies on a classifying algorithm \(\textsc {Level}(\cdot )\), which ensures that whenever M is either an expression, a type, Type, or Kind, then \(\textsc {Level}(M)\) is either 1, 2, 3, or 4 respectively. As it is specifically suited to PVS-Cert, this definition is simpler than the classification presented in [6], which is intended to be applicable to a wide family of type systems. The algorithm is defined as follows:
Definition 5
We define the algorithm \(\textsc {Level}(\cdot )\) by recursion on its argument. The possible cases are the following.
-
\(\textsc {Level}(Kind) = 4\), \(\textsc {Level}(Type) = 3\), \(\textsc {Level}(Prop) = 2\)
-
\(\textsc {Level}(\varPi v : T . U) = \textsc {Level}(U)\), \(\textsc {Level}(\{v : T \mid U\}) = 2\), \(\textsc {Level}(X) = 2\)
-
In all other cases, \(\textsc {Level}(M) = 1\)
9 Expressing PVS-Core in PVS-Cert
The final purpose of PVS-Cert is to encode PVS-Core derivations as PVS-Cert judgements, and to use the type-checking algorithm presented in Sect. 8 to use these judgements as verifiable certificates. In this perspective, we define a correspondence between PVS-Core and PVS-Cert. This correspondence reflects the fact that, even though these two systems are very different at the level of terms and judgements, they are almost identical at the level of derivations.
9.1 An Erasing Function from PVS-Cert to PVS-Core
We begin the description of this correspondence with a translation from PVS-Cert to PVS-Core, referred to as erasing. This translation mainly consists in the erasure of PVS-Cert explicit coercions \(\langle \cdot , M \rangle _A\) and \(\pi _1(\cdot )\).
Definition 6
We define an erasure function \(\llbracket \cdot \rrbracket \) from PVS-Cert expressions, types, and Type to PVS-Core terms recursively as follows.

Then, we extend straightforwardly \(\llbracket \cdot \rrbracket \) from PVS-Cert stratified contexts to PVS-Core contexts: for instance, \(\llbracket P, x : A, X : Type \rrbracket = \llbracket P \rrbracket , x : \llbracket A \rrbracket , X : Type\).
Last, we extend straightforwardly \(\llbracket \cdot \rrbracket \) from all PVS-Cert stratified judgements except those of the form \(\varGamma \vdash Type : Kind\) to PVS-Core judgements. For instance, \(\llbracket x : A, X : Type \vdash p : P \rrbracket = x : \llbracket A \rrbracket , X : Type \vdash \llbracket P \rrbracket \). The PVS-Cert judgements of the form \(\varGamma \vdash Type : Kind\) are not translated.
By the stratification theorem in PVS-Cert, all PVS-Cert derivable judgements are stratified judgements. Hence, unless they have the form \(\varGamma \vdash Type : Kind\), their erasure in PVS-Core is well-defined. We will prove in Theorem 10 that they are derivable in PVS-Core. This theorem relies in particular on the fact that conversion in PVS-Cert and PVS-Core are related through the erasure function \(\llbracket \cdot \rrbracket \), established in the following proposition. The corresponding proof does not involve any specific difficulty.
Proposition 3
For all terms M and N which are either expressions, types, or Type, whenever \(M \equiv _{\beta *} N\), then \(\llbracket M \rrbracket \equiv _\beta \llbracket N \rrbracket \).
Using the two previous propositions and the stratification theorem in PVS-Cert, we conclude the following theorem, which allows to map PVS-Cert derivations to PVS-Core derivations.
Theorem 10
Every derivable PVS-Cert judgement either has the form \(\varGamma \vdash Type : Kind\) or admits an image through \(\llbracket \cdot \rrbracket \). In the latter case, this image is derivable in PVS-Core.
Proof
The first part of the proof is a direct consequence of the stratification theorem. The second part is proved by induction on the height of PVS-Cert derivations. All cases are straightforward, using the stratification theorem when necessary to establish a correspondence between stratified versions of PVS-Cert rules and PVS-Core rules. For instance:
-
Decl corresponds either to TypeDecl, EltDecl, or Assumption
-
Sort corresponds to Prop only (judgements of the form \(\varGamma \vdash Type : Kind\) are not translated)
-
Prod corresponds either to Pi, Forall, or Imply
9.2 Expressing PVS-Core Derivations as PVS-Cert Judgements
Theorem 10 shows that a PVS-Cert derivable judgement can testify to the PVS-Core derivability of another judgement: its erasure. In this section, we show conversely that, given any PVS-Core derivation, we can build such a PVS-Cert judgement. For this purpose, we first present an algorithm \(\textsc {Certificate}\), which translates a PVS-Core derivation into a PVS-Cert judgement. In a second step, we will prove that such PVS-Cert judgements are always derivable in PVS-Cert.
Definition 7
For any PVS-Core derivation D, we define recursively the PVS-Cert stratified judgement \(\textsc {Certificate}(D)\) such that \(\llbracket \textsc {Certificate}(D) \rrbracket \) corresponds to the conclusion of D.
In this definition, we use an injective function \(h(\cdot )\) mapping natural numbers to PVS-Cert proof variables, which can be chosen arbitrarily. We present two cases: Assumption, which shows how \(h(\cdot )\) is used, and ImplyElim. This latter case (as well as ForallElim) is more complex than others as it involves the computation of a normal form with respect to \(\triangleright _*\), i.e. the erasure of coercions at the head of a term. The other cases are detailed in the author’s PhD dissertation [1].
-
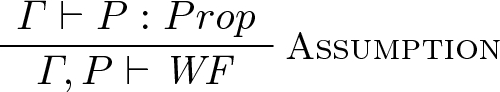
We consider \(D_1\) the derivation of \(\varGamma \vdash P : Prop\). \(\textsc {Certificate}(D_1)\) has the form \(\varGamma _1 \vdash P_1 : Prop\). We consider n the number of declarations of the form (h : Q) in \(\varGamma _1\), and we define \(\textsc {Certificate}(D) = \varGamma _1, h(n) : P_1 \vdash WF \).
-
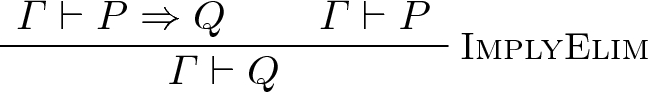
We consider \(D_1\) and \(D_2\) the respective derivations of \(\varGamma \vdash P \Rightarrow Q\) and \(\varGamma \vdash P\). \(\textsc {Certificate}(D_2)\) has the form \(\varGamma _2 \vdash p_2 : P_2\) and \(\textsc {Certificate}(D_1)\) has the form \(\varGamma _1 \vdash p_1 : Q'_1\). As \(\llbracket Q'_1 \rrbracket = (P \Rightarrow Q)\), its normal form with respect to \(\triangleright _*\) has the form \(\varPi h : P_1 . Q_1\). We define \(\textsc {Certificate}(D) = \varGamma _1 \vdash p_1 p_2 : Q_1[p_2/h]\). As all proof terms are deleted through the erasure function, \(\llbracket Q_1 [p_2/h] \rrbracket = \llbracket Q_1 \rrbracket \). On the other hand, by induction hypothesis, \(\llbracket Q_1 \rrbracket = Q\), hence the erasure of this judgement is \(\varGamma \vdash Q\), as expected.
9.3 Relating Conversion in PVS-Core and PVS-Cert
In order to prove that the outputs of the algorithm \(\textsc {Certificate}\) are derivable in PVS-Cert (presented in Theorem 11), the main required lemma is the fact that is the converse of Proposition 3: for any terms M and N which are either expressions, types, or Type and which verify \(\llbracket M \rrbracket \equiv _\beta \llbracket N \rrbracket \), then \(M \equiv _{\beta *} N\). More precisely, this property will be used in the proof of Theorem 11 to handle the cases of conversion rules TypeConversion and PropConversion.
We first establish a modified version of this expected result, using equality and \(\equiv _*\) instead of \(\equiv _\beta \) and \(\equiv _{\beta *}\) respectively. The proof is straightforward by induction on the two involved terms.
Proposition 4
For all terms M and N which are either expressions, types, or Type, whenever \(\llbracket M \rrbracket = \llbracket N \rrbracket \), then \(M \equiv _* N\).
Then, we establish the expected converse of Proposition 3 as follows.
Proposition 5
For all terms M and N which are either expressions, types, or Type, whenever \(\llbracket M \rrbracket \equiv _\beta \llbracket N \rrbracket \), then \(M \equiv _{\beta *} N\).
Proof
We present a proof based on the definition of a simple translation of PVS-Core terms as PVS-Cert expressions, types, or Type, which does not introduce any explicit coercion: for instance,
-
\([ \varPi x : A . B ] = \varPi x : [ A ] . [ B ]\)
-
\([ P \Rightarrow Q ] = \varPi h : [ P ] . [ Q ]\) for an arbitrary proof variable h
We first show straightforwardly that the respective images through \([\cdot ]\) of two terms related by \(\equiv _\beta \) are also related by \(\equiv _\beta \). As a consequence,  .
.
On the other hand, it is straightforward to show that \([\cdot ]\) is a right inverse of the erasure function  . Hence,
. Hence,  . By Proposition 4, we conclude that
. By Proposition 4, we conclude that  . Following the same reasoning,
. Following the same reasoning,  .
.
As a consequence,  .
.
9.4 Soundness of the Synthesis of Certificates
The last proposition needed to prove the soundness of the algorithm \(\textsc {Certificate}\) is the following. It shows that the operation of normalization through \(\triangleright _*\) (which erases the coercions \(\pi _1(\cdot )\) and \(\langle \cdot , M \rangle _T\) at the head of a term) is safely used in the definition of \(\textsc {Certificate}\).
Proposition 6
For any derivable PVS-Cert judgement of the form \(\varGamma \vdash t : \{x_n ...\{x_1 : Prop \mid Q_1 \} ... \mid Q_n \}\), if t admits a normal form with respect to \(\triangleright _*\) which has the form \(\varPi v : M . T\), then \(\varGamma \vdash \varPi v : M . T : Prop\) is derivable.
In fact, only the specific case \(n = 0\) is used in the proof of soundness of \(\textsc {Certificate}\), but this generalization is preferred as it admits a direct proof by induction on t, which does not involve any specific difficulty.
Last, we present the expected soundness property for \(\textsc {Certificate}\):
Theorem 11
For any PVS-Core derivation D, \(\textsc {Certificate}(D)\) is derivable in PVS-Cert.
Proof
The proof is done by induction on D. Most cases are proved without any specific difficulty. In particular, the cases of conversion rules TypeConversion and PropConversion are straightforward using Proposition 5.
The most complex cases correspond to the rules ImplyElim and ForallElim which involve, by definition of \(\textsc {Certificate}\), some normalization with respect to \(\triangleright _*\). In such cases, Proposition 6 is used to handle the specific difficulties related to this normalization. We present the case ImplyElim:

We consider \(D_1\) and \(D_2\) the respective derivations of \(\varGamma \vdash P \Rightarrow Q\) and \(\varGamma \vdash P\). \(\textsc {Certificate}(D_2)\) has the form \(\varGamma _2 \vdash p_2 : P_2\) and \(\textsc {Certificate}(D_1)\) has the form \(\varGamma _1 \vdash p_1 : Q'_1\). As \(\llbracket Q'_1 \rrbracket = (P \Rightarrow Q)\), its normal form with respect to \(\triangleright _*\) has the form \(\varPi h : P_1 . Q_1\). In this setting, \(\textsc {Certificate}(D) = \varGamma _1 \vdash p_1 p_2 : Q_1[p_2/h]\). By induction hypothesis, \(\varGamma _1 \vdash p_1 : Q'_1\) and \(\varGamma _2 \vdash p_2 : P_2\) are derivable in PVS-Cert. By Proposition 3 and the stratification theorem, \(\varGamma _1 \vdash Q'_1 : Prop\) is derivable in PVS-Cert. Hence, by Proposition 6, \(\varGamma _1 \vdash \varPi h : P_1 . Q_1 : Prop\) is derivable as well. As \(Q'_1 \equiv _{\beta *} \varPi h : P_1 . Q_1\), we conclude applying the Conversion rule that \(\varGamma _1 \vdash p_1 : \varPi h : P_1 . Q_1\) is derivable.
On the other hand, using Proposition 4, we can conclude from \(\llbracket \varGamma _1 \rrbracket = \varGamma = \llbracket \varGamma _2 \rrbracket \) that \(\varGamma _1 \equiv _* \varGamma _2\) as long as both contexts admit the list of declared proof variables, in the same order. This is the case as, by straightforward induction on PVS-Core derivations, this list is h(1), h(2), ..., h(n), where \(h(\cdot )\) is the injective function used in the definition of \(\textsc {Certificate}\) and n is the number of proof variable declarations in \(\varGamma _1\) and \(\varGamma _2\). Hence, \(\varGamma _1 \equiv _* \varGamma _2\).
As \(\varGamma _1 \vdash p_1 : \varPi h : P_1 . Q_1\) is derivable, by Theorem 3 and the stratification theorem, \(\varGamma _1 \vdash \varPi h : P_1 . Q_1 : Prop\) is derivable. Hence, considering the last rule different from Conversion used in such a derivation (which is necessarily Prod), and using the stratification theorem, \(\varGamma _1 \vdash P_1 : Prop\) is derivable as well. As a consequence, using context conversion (mentioned in Sect. 4), \(\varGamma _1 \vdash p_2 : P_1\) is derivable in PVS-Cert. Hence, applying the rule App, \(\varGamma _1 \vdash p_1 p_2 : Q_1 [p_2/h]\) is derivable, as expected.
10 Using PVS-Cert as a System of Verifiable Certificates for PVS-Core
This final section shows how to use the different results presented in this paper to answer to the main question addressed in the current work: defining a system of verifiable certificates for PVS-Core.
A PVS-Cert judgement \(\varGamma \vdash p : P\) can be used as a certificate for its PVS-Core erasure \(\llbracket \varGamma \rrbracket \vdash \llbracket P \rrbracket \) (Definition 6), which is verifiable using the type-checking algorithm presented in Sect. 8. On the one hand, this approach is sound: whenever the type-checking algorithm succeeds, \(\varGamma \vdash p : P\) is derivable in PVS-Cert, hence \(\llbracket \varGamma \rrbracket \vdash \llbracket P \rrbracket \) is derivable in PVS-Core by Theorem 10.
On the other hand, valid certificates can be generated for arbitrary PVS-Core theorems in the following way. Given some PVS-Core judgement \(\varDelta \vdash Q\) derivable through some derivation D, the PVS-Cert judgement \(\textsc {Certificate}(D)\) can be used as a certificate of \(\varDelta \vdash Q\). Indeed, using the notations \(\varGamma \vdash p : P\) for \(\textsc {Certificate}(D)\), the following statements hold.
-
By definition of \(\textsc {Certificate}\), \(\llbracket \varGamma \rrbracket = \varDelta \) and \(\llbracket P \rrbracket = Q\), hence this judgement is a certificate for \(\varDelta \vdash Q\).
-
By Theorem 11, \(\varGamma \vdash p : P\) is derivable, hence the execution of the type-checking algorithm on this judgement succeeds: this certificate is valid.
These PVS-Cert certificates represent PVS-Core derivations in a very compact way. As each of the different constructions of types, expressions, and proofs in PVS-Cert corresponds to some PVS-Core derivation rule, the size of a PVS-Cert certificate is comparable, as a rough estimation, with the size of a corresponding PVS-Core derivation in which all PVS-Core judgements are deleted.
We finally show that, through the construction of certificates, the PVS-Cert cut elimination theorem can be used to study meta-theoretical properties of PVS-Core. This possible use is illustrated with the case of consistency, proved in PVS-Cert in Theorem 9 using cut elimination.
Theorem 12
The system PVS-Core is consistent: the judgement \(\vdash \forall x : Prop . x\) is not derivable.
Proof
If the judgement \(\vdash \forall x : Prop . x\) admits a PVS-Core derivation D, we consider \(\vdash p : P = \textsc {Certificate}(D)\). By definition, \(\llbracket P \rrbracket = \forall x : Prop . x = \llbracket \varPi x : Prop . x \rrbracket \). Hence, by Proposition 5, \(P \equiv _{\beta *} \varPi x : Prop . x\). As \(\vdash \varPi x : Prop . x : Prop\) is derivable in PVS-Cert, we can apply the conversion rule to conclude that \(\vdash p : \varPi x : Prop . x\) is derivable in PVS-Cert, which is impossible by Theorem 9.
References
Gilbert, F.: Extending higher-order logic with predicate subtyping: application to PVS. Ph.D. dissertation, Sorbonne Paris Cité, Inria, CEA LIST (2018)
Abel, A., Scherer, G.: On irrelevance and algorithmic equality in predicative type theory. arXiv preprint arXiv:1203.4716 (2012)
Barendregt, H.: Introduction to generalized type systems. J. Funct. Program. 1(2), 125–154 (1991)
Barendregt, H.: Lambda calculi with types. In: Abramsky, S., Gabbay, D.M., Maibaum, T.S.E. (eds.) Handbook of Logic in Computer Science, vol. ii. Oxford University Press, Oxford (1992)
Barras, B., et al.: The Coq proof assistant reference manual: Version 6.1 (1997)
Barthe, G.: Type-checking injective pure type systems. J. Funct. Program. 9(06), 675–698 (1999)
Berardi, S.: Towards a mathematical analysis of the Coquand-Huet calculus of constructions and the other systems in Barendregt’s cube. Technical report, Carnegie-Mellon University, USA and Universita di Torino, Italy (1988)
Bernardo, B.: An implicit calculus of constructions with dependent sums and decidable type inference. Ph.D. thesis, École polytechnique, October 2015
Futatsugi, K., Goguen, J.A., Jouannaud, J.-P., Meseguer, J.: Principles of OBJ2. In: Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, pp. 52–66. ACM (1985)
Geuvers, H.: A short and flexible proof of strong normalization for the calculus of constructions. In: Dybjer, P., Nordström, B., Smith, J. (eds.) TYPES 1994. LNCS, vol. 996, pp. 14–38. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60579-7_2
Geuvers, H., Nederhof, M.-J.: Modular proof of strong normalization for the calculus of constructions. J. Funct. Program. 1(02), 155–189 (1991)
Girard, J.-Y.: Interprétation fonctionelle et élimination des coupures de l’arithmétique d’ordre supérieur. Ph.D. thesis, Université Paris VII (1972)
Kent, A.M., Kempe, D., Tobin-Hochstadt, S.: Occurrence typing modulo theories. In: Proceedings of the 37th ACM SIGPLAN Conference on Programming Language Design and Implementation, vol. 51, pp. 296–309. ACM (2016)
Klop, J.W., van Oostrom, V., van Raamsdonk, F.: Combinatory reduction systems: introduction and survey. Theoret. Comput. Sci. 121(1), 279–308 (1993)
Knowles, K., Flanagan, C.: Hybrid type checking. ACM Trans. Program. Lang. Syst. (TOPLAS) 32(2), 6 (2010)
Luo, Z.: ECC, an extended calculus of constructions. In: Proceedings of Fourth Annual Symposium on Logic in Computer Science. LICS 1989, pp. 386–395. IEEE (1989)
Owre, S., Rushby, J.M., Shankar, N.: PVS: a prototype verification system. In: Kapur, D. (ed.) CADE 1992. LNCS, vol. 607, pp. 748–752. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55602-8_217
Owre, S., Shankar, N.: The formal semantics of PVS (1999)
Rondon, P.M., Kawaguci, M., Jhala, R.: Liquid types. In: ACM SIGPLAN Notices, vol. 43, pp. 159–169. ACM (2008)
Rushby, J., Owre, S., Shankar, N.: Subtypes for specifications: predicate subtyping in PVS. IEEE Trans. Softw. Eng. 24(9), 709–720 (1998)
Siles, V., Herbelin, H.: Pure type system conversion is always typable. J. Funct. Program. 22(2), 153–180 (2012)
Sozeau, M.: Subset coercions in Coq. In: Altenkirch, T., McBride, C. (eds.) TYPES 2006. LNCS, vol. 4502, pp. 237–252. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74464-1_16
Tait, W.W.: A realizability interpretation of the theory of species. In: Parikh, R. (ed.) Logic Colloquium, vol. 453, pp. 240–251. Springer, Heidelberg (1975). https://doi.org/10.1007/BFb0064875
Terlouw, J.: Een nadere bewijstheoretische analyse van GSTT’s. Manuscript (in Dutch) (1989)
Terlouw, J.: Sterke normalisatie in C a la Tait. In: Notes of a Talk Held at the Intercity Seminar on Typed Lambda Calculus, Nijmegen, Netherlands (1989)
Terlouw, J.: Strong normalization in type systems: a model theoretical approach. Ann. Pure Appl. Logic 73(1), 53–78 (1995)
Werner, B.: On the strength of proof-irrelevant type theories. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 604–618. Springer, Heidelberg (2006). https://doi.org/10.1007/11814771_49
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Gilbert, F. (2019). Verifiable Certificates for Predicate Subtyping. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)





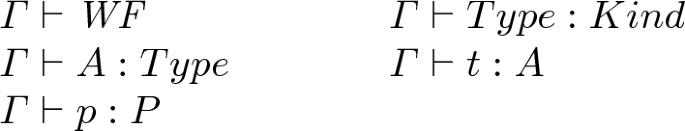
 with the case of the rule
with the case of the rule