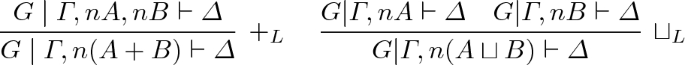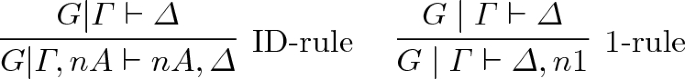Abstract
We present a structural proof system, based on the machinery of hypersequent calculi, for a simple probabilistic modal logic underlying very expressive probabilistic \(\mu \)-calculi. We prove the soundness and completeness of the proof system with respect to an equational axiomatisation and the fundamental cut-elimination theorem.
The authors were supported by the French project ANR-16-CE25-0011 REPAS.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Modal and temporal logics are formalisms designed to express properties of mathematical structures representing the behaviour of computing systems, such as, e.g., Kripke frames, trees and labeled transition systems. A fundamental problem regarding such logics is the equivalence problem: given two formulas \(\phi \) and \(\psi \), establish whether \(\phi \) and \(\psi \) are semantically equivalent. For many temporal logics, including the basic modal logic K (see, e.g., [BdRV02]) and its many extensions such as the modal \(\mu \)-calculus [Koz83], the equivalence problem is decidable and can be answered automatically. This is, of course, a very desirable fact. However, a fully automatic approach is not always viable due to the high complexity of the algorithms involved. An alternative and complementary approach is to use human-aided proof systems for constructing formal proofs of the desired equalities. As a concrete example, the well-known equational axioms of Boolean algebras together with two axioms for the \(\Diamond \) modality:

can be used to construct formal proofs of all valid equalities between formulas of modal logic using the familiar deductive rules of equational logic (see Definition 3). The simplicity of equational logic is a great feature of this kind of system but sometimes comes at a cost because even seemingly trivial equalities often require significant human ingenuity to be proved.Footnote 1 The problem lies in the transitivity rule \( (a = b\ \& \ b = c \Rightarrow a=c)\) which requires to guess, among infinitely many possibilities, an interpolant formula b to prove the equality \(a=c\).
The field of structural proof theory (see [Bus98]), originated with the seminal work of Gentzen on his sequent calculus proof system LK for classical propositional (first-order) logic [Gen34], investigates proof systems which, roughly speaking, require less human ingenuity. The key technical result regarding the sequent calculus, the cut-elimination theorem, implies that when searching for a proof of a statement, only certain formulas need to be considered: the so-called sub-formula property. This simplifies significantly, in practice, the proof search endeavour. The original system LK of Gentzen has been extensively investigated and generalised and, for example, it can be extended with rules for the \(\Diamond \) modality and becomes a convenient proof system for modal logic [Wan96]. Furthermore, it is possible to extend it with rules for dealing with (co)inductive definitions and it becomes a proof system for the modal \(\mu \)-calculus (see, e.g., [Stu07]). Research on the structural proof theory of the modal \(\mu \)-calculus is an active area of research (see, e.g., recent [Dou17]).
Probabilistic Logics and the Riesz Modal Logic. Probabilistic logics are temporal logics specifically designed to express properties of mathematical structures (e.g., Markov chains and Markov decision processes) representing the behaviour of computing systems using probabilistic features such as random bit generation. Unlike the non-probabilistic case, the equivalence problem for most expressive probabilistic logics (e.g., pCTL [LS82, HJ94], see also [BK08, BBLM17]) is not known to be decidable. Hence, human-aided proof systems are currently the only viable approach to establish equalities of formulas of expressive probabilistic logics. To the best of our knowledge, however, all the proof systems proposed in the literature (see, e.g., [DFHM16] for the logic pCTL, [BGZB09, Hsu17] for pRHL and [Koz85] for pPDL) are not entirely satisfactory because they include rules, such as the transitivity rule discussed above, violating the sub-formula property.
Another line of work on probabilistic logics has focused on probabilistic \(\mu \)-calculi ([MM07, HK97, DGJP00, dA03, MS17, Mio11, Mio12a, Mio14]). These logical formalisms are, similarly to Kozen’s modal \(\mu \)-calculus, obtained by extending a base real-valued modal logic with (co)inductively defined operators. Recently, in [MFM17], a base real-valued modal logic called Riesz modal logic (\(\mathcal {R}\)) has been defined and a sound and complete equational axiomatisation has been obtained (see Definition 2). Importantly, the logic \(\mathcal {R}\) extended with (co)inductively defined operators is sufficiently expressive to interpret most other probabilistic logics, including pCTL [Mio12b, Mio18, MS13a]. Hence, the Riesz modal logic appears to be a convenient base for developing the theory of probabilistic \(\mu \)-calculi and, more generally, probabilistic logics.
Contributions of This Work. This work is a first step towards the development of the structural proof theory of probabilistic \(\mu \)-calculi. We introduce a hypersequent calculus called MGA (read modal GA) for a version of the Riesz modal logic (the scalar-free fragment, see Sect. 2 for details) and by proving the cut-elimination theorem. Formally we prove:
Theorem 1
The hypersequent calculus MGA is sound and complete with respect to the equational axioms of Fig. 1 and the CUT rule is eliminable.
The machinery of hypersequent calculi has been introduced by Avron in [Avr87] and, independently, by Pottinger in [Pot83]. Our calculus extends the hypersequent calculus GA of Metcalfe, Olivetti and Gabbay [MOG05] (see also the book [MOG09] and the related [CM03] and [DMS18]) which is a sound and complete structural proof system for the equational theory of lattice-ordered abelian groups (axioms (1) in Fig. 1, see [Vul67] for an overview). The main contributions of this work are:
-
1.
The careful extension of the system GA of [MOG05] with appropriate proof rules for the modality (\(\Diamond \)) and the proof of soundness and completeness.
-
2.
The non-trivial adaptation of the proof-technique used in [MOG09, §5.2] to prove the cut-elimination theorem for GA.
-
3.
The formalisation using the theorem prover Agda of our key technical results: Theorems 4 and 9. The code is freely available at [Agd].
In particular, the last point above guarantees the correctness of the proofs of all our novel technical results which, as it is often the case in proof theory, involve complex and long induction arguments. Given the availability of formalised proofs, in this work we focus on illustrating the main ideas behind our arguments rather than spelling out all technical details.
Organisation of the Paper. In Sect. 2 we provide the necessary definitions about the Riesz modal logic from [MFM17, Mio18] and about the hypersequent calculus GA of [MOG05, MOG09]. In Sect. 3 we present our hypersequent calculus MGA and state the main theorems. In Sect. 4 we sketch the main ideas behind our proof of cut-elimination. Lastly, in Sect. 5 we discuss some directions for future work.
2 Technical Background
2.1 The Riesz Modal Logic and Its Scalar-free Fragment
The Riesz modal logic \(\mathcal {R}\) introduced in [MFM17] is a probabilistic logic for expressing properties of discrete or continuous Markov chains. We refer to [MFM17] for a detailed introduction. Here we just restrict ourselves to the purely syntactical aspects of this logic: its syntax and its axiomatisation.
Definition 1
(Syntax). The set of formulas of the Riesz modal logic is generated by the following grammar:  where r, called a scalar, ranges over the set \(\mathbb {R}\) of real numbers. We just write \(-\phi \) in place of \((-1)\phi \).
where r, called a scalar, ranges over the set \(\mathbb {R}\) of real numbers. We just write \(-\phi \) in place of \((-1)\phi \).
A main result of [MFM17] is that two formulas \(\phi \) and \(\psi \) are semantically equivalent if and only if the identity \(\phi =\psi \) holds in all modal Riesz spaces.
Definition 2
A modal Riesz space is an algebraic structure R over the signature \(\varSigma = \{ 0,1, +, r, \sqcup , \sqcap , \Diamond \}_{r\in \mathbb {R}}\) such that the following set \(\mathcal {R}\) of axioms hold:
-
1.
\(\{R, 0,+, r, \sqcup , \sqcap \}_{r\in \mathbb {R}}\) is a Riesz space (see, e.g., [LZ71]), i.e.,
-
\((R, 0, +, r)_{r\in \mathbb {R}}\) is an \(\mathbb {R}\)-vector space,
-
\((R, \sqcup , \sqcap )\) is a lattice,
-
the lattice order (\(x \le y \Leftrightarrow x\sqcap y = x)\) is compatible with addition, i.e.:
-
(a)
\(x\le y\) implies \(x + z \le y +z\) (i.e., \((x \sqcap y) + z = ((x\sqcap y) + z) \sqcap (y + z) \)),
-
(b)
\(x\ge 0\) implies \(r x \ge 0\) (i.e., \( 0= 0 \sqcap r(x\sqcup 0) \)) for every \(r\in \mathbb {R}_{\ge 0}\),
-
(a)
-
-
2.
\(0\le 1\) (i.e., \(0 = 0 \sqcap 1\)),
-
3.
the \(\Diamond \) operation is linear, positive and 1-decreasing, i.e.:
-
\(\Diamond (x + y ) = \Diamond (x) + \Diamond (y)\) and \(\Diamond (r x) = r\Diamond (x)\),
-
if \(x\ge 0\) then \(\Diamond (x)\ge 0\) (i.e., \(0 = 0 \sqcap \Diamond (x\sqcup 0) \)),
-
\(\Diamond (1) \le 1\) (i.e., \(\Diamond 1 = \Diamond 1 \sqcap 1\)).
-
Note that the definition of modal Riesz spaces is purely equational: all axioms of Riesz spaces (1) can be expressed equationally and so can the axioms (2) and (3). This means, by Birkoff completeness theorem, that two formulas are semantically equivalent if and only if the identity \(\phi =\psi \) can be derived using the familiar deductive rules of equational logic, written as \(\mathcal {R}\vdash \phi =\psi \).
Definition 3
(Deductive Rules of Equational Logic). Rules for deriving identities from a set \(\mathcal {A}\) of equational axioms:

where \(C[\cdot ]\) is a context and f, g are function symbols of the fixed signature.
In what follows we denote with \(\mathcal {R}\vdash \phi \le \psi \) the judgment \(\mathcal {R}\vdash \phi = \phi \sqcap \psi \). The following elementary facts from the theory of Riesz spaces (see, e.g., [LZ71, §2.12]) will be useful.
Proposition 1
The following assertions hold:
-
\(\mathcal {R} \vdash \phi = \psi \) iff \(\mathcal {R} \vdash \phi - \psi = 0\),
-
\(\mathcal {R} \vdash \phi = \psi \) iff \(\big ( \mathcal {R} \vdash \phi \le \psi \,\,\text { and} \,\,\mathcal {R} \vdash \psi \le \phi \big )\).
-
\(\mathcal {R} \vdash r(x\sqcup y) = rx \sqcup ry\), \(\mathcal {R} \vdash r(x\sqcap y) = rx \sqcap ry\).
The first point says that an equality \(\phi =\psi \) can always be expressed as an identity with 0. The second point says that we can express equalities with inequalities and vice versa. The third point, together will the other axioms, implies that scalar multiplication distributes over all other operations \(\{+,\sqcup ,\sqcap ,\Diamond \}\).
For most practical purposes (when expressing properties of probabilistic models) the scalars in the Riesz modal logic can be restricted to be rational numbers.
Definition 4
(Rational and Scalar-free formulas). A formula \(\phi \) is rational if all its scalars are rational numbers. Similarly, \(\phi \) is scalar-free if its scalars are all equal to \((-1)\). Equivalently, the set of scalar-free formulas is generated by the following grammar:  .
.
Note how we have switched to the letters A and B to range over scalar-free formulas to highlight this distinction.
Proposition 2
Let \(\phi \) be a rational formula. Then there exists a scalar-free formula A such that \(\mathcal {R} \vdash \phi = 0\) iff \(\mathcal {R} \vdash A = 0\).
Proof
Let \(\{r_i\}_{i\in I}\) be the list of rational scalars in \(\phi \), with \(r_i = \frac{n_i}{m_i}\) and let \(d= \prod _i m_i\) be the product of all denominators. Since scalar multiplication distributes with all operations it is easy to show that \(\mathcal {R} \vdash d\phi = \psi \), for a formula \(\psi \) whose scalars are all integers. We can then obtain A from \(\psi \) by inductively replacing any sub-formula of \(\psi \) the form nB with \((B+ B +\dots + B)\) (n times) if n is positive, with \(-(B+ B +\dots + B)\) if n is negative and with 0 if \(n=0\). \(\square \)
For this reason in this work we restrict attention to scalar-free formulas and we consider the restricted set of axioms \(\mathbbm {T}\) of Fig. 1. The axioms of Riesz spaces, when scalar multiplication is omitted, reduce to the axioms of lattice ordered abelian groups (see, e.g., [Vul67]). The axiom \(0\le 1\) is unaltered and the axioms for the \(\Diamond \) modality are naturally adapted. For these reasons we refer to these axioms as of those of lattice-ordered modal abelian groups.
Remark 1
Note that from the previous discussion it does not follow directly that \(\mathcal {R}\vdash A=B\) implies \(\mathbbm {T}\vdash A=B\). We indeed conjecture that \(\mathcal {R}\) is a conservative extension of \(\mathbbm {T}\) but we have not proved this fact so far. In any case, this is not required for results of this work.
The main contribution of this work is the design of a sound and complete hypersequent calculus for the theory \(\mathbbm {T}\) and the proof of cut-elimination.
2.2 The Hypersequent Calculus GA
Our starting point is the hypersequent calculus GA of [MOG05, MOG09] for the theory of lattice-ordered abelian groups (set of axioms (1) in Fig. 1).
Definition 5
(Formulas, Sequents and hypersequents). A formula A is a term built from a set of variables (ranged over by x, y, z) over the signature \(\{0, +, -,\sqcap , \sqcup \}\). A sequent S is a pair of two (possibly empty) multisets of formulas \(\varGamma =A_0,\dots , A_n\) and \(\varDelta =B_0,\dots , B_m\), denoted as \(\varGamma \vdash \varDelta \). A hypersequent G is a nonempty multiset \(S_1,\dots , S_n\) of sequents, denoted as \(S_1|\dots | S_n\).
Following [MOG05, MOG09], with some abuse of notation, we denote with S both the sequent and the hypersequent consisting of only the sequent S. The system GA is a deductive system for deriving hypersequents consisting of the rules of Fig. 2. The system GA without the CUT rule is denoted by \(\text {GA}^*\).
Another convention we adopt from [MOG05, MOG09] is to write \(d\vDash _{\text {GA}}G\) to express the fact that d is a valid GA-derivation of the hypersequent G. We write \(\vDash _{\text {GA}}G\) to express the existence of a GA-derivation d such that \(d\vDash _{\text {GA}}G\). Similarly, we write \(d\vDash _{\text {GA}^*}G\) and \(\vDash _{\text {GA}^*}G\) when referring to the subsystem \(\text {GA}^*\).
Inference rules of the hypersequent system GA of [MOG05].
Multisets of formulas, sequents and hypersequents are interpreted as a single formula as follows:
Definition 6
(Interpretation). A multiset of formulas \(\varGamma = \phi _1,\dots , \phi _n\) is interpreted as the formula \( \llbracket \varGamma \rrbracket =\phi _1 + \phi _1 +\dots +\phi _n\) if \(n\ge 1\) and as \( \llbracket \varGamma \rrbracket =0\) if \(\varGamma =\emptyset \). A sequent \(S = \varGamma \vdash \varDelta \) is interpreted as the formula \( \llbracket S \rrbracket = \llbracket \varDelta \rrbracket - \llbracket \varGamma \rrbracket \). Finally, a hypersequent \(G = S_0 \mid \dots \mid S_n\) is interpreted as the formula \( \llbracket G \rrbracket = \llbracket S_0 \rrbracket \sqcup \dots \sqcup \llbracket S_n \rrbracket \).
Example 1
Consider the hypersequent \(G= \big (0\sqcup x, y \vdash y \big ) \ \mid \ \big (-y \vdash \big ) \) consisting of two sequents. Then \( \llbracket G \rrbracket = \big ( y - \big ( (0\sqcup x) + y \big ) \big ) \sqcup \big ( 0 - (-y) \big ). \)
The soundness and completeness of the hypersequent system GA with respect to the theory of lattice-ordered abelian groups (axioms (1) of Fig. 1, written as \(\mathbbm {T}_{(1)}\)) is expressed by the following theorem.
Theorem 2
([MOG05]). For all formulas A and hypersequents G:
-
Soundness: if \(\vDash _{\text {GA}}G\) then \(\mathbbm {T}_{(1)} \vdash \llbracket G \rrbracket \ge 0\).
-
Completeness: if \(\mathbbm {T}_{(1)} \vdash A \ge 0\) then \(\vDash _{\text {GA}} (\vdash A)\)
Proof
The proofs presented in [MOG05] exploit the following well-known fact (see, e.g., [Vul67]): the equality \(A=B\) holds in all lattice-ordered abelian groups if and only if it holds in \((\mathbb {R}, 0, +, -, \max , \min )\) under any interpretation of the variables as real numbers. In other words, \(\mathbb {R}\) generates the variety of lattice-ordered abelian groups. \(\square \)
The main result of [MOG05] regarding GA is that the CUT rule is eliminable.
Theorem 3
(Cut-elimination [MOG05]). Any GA-derivation of a hypersequent G can be effectively transformed into a \(\text {GA}^*\)-derivation of G.
3 The Hypersequent System MGA
In this section we introduce our hypersequent calculus system MGA, a modal extension of the GA system of [MOG05]. The system MGA deals with formulas over the signature of modal lattice-ordered abelian groups (see Fig. 1) thus including the constant 1 and the unary modality \(\Diamond \).
Definition 7
(Formulas of MGA). A formula A is a term built from a set of variables (ranged over by x, y, z) over the signature \(\{0, 1, +, -,\sqcap , \sqcup ,\Diamond \}\).
The definitions of sequents and hypersequents are given exactly as for the system GA in Definition 5 of Sect. 2.2. Similarly, multisets of formulas, sequents and hypersequents are interpreted as formulas exactly as already specified in Definition 6 of Sect. 2.2 for the system GA. Before presenting the deduction rules of MGA, it is useful to introduce the following abbreviations.
-
For \(n\in \mathbb {N}_{\ge 0}\), we denote with nF the multiset of formulas \(F,F, \dots , F\).
So for example we write \(2A,1B\vdash 0C,D\) to denote the sequent \(A,A,B \vdash D \).
-
Given a multiset of formulas \(\varGamma = F_0, \dots , F_k\) and \(n\in \mathbb {N}_{\ge 0}\) we denote with \(n \varGamma \) the multiset of formulas \(n F_0, \dots , n F_k\). If \(\varGamma =\emptyset \) then also \(n\varGamma =\emptyset \).
-
Given a multiset of formulas \(\varGamma = F_0,\dots , F_n\) we denote with \(\Diamond \varGamma \) the multiset of formulas \(\Diamond F_0,\dots , \Diamond F_n\). Consistently, if \(\varGamma =\emptyset \) then also \(\Diamond \varGamma =\emptyset \).
The rules of the system MGA consist of all rules of GA (see Fig. 2) together with the additional rules of Fig. 3.
The axiom  for the constant 1 is straightforward and it simply expresses the axiom \(0\le 1\) from Fig. 1 (i.e., \(\mathbbm {T}\vdash \llbracket \vdash 1 \rrbracket \ge 0\)).
for the constant 1 is straightforward and it simply expresses the axiom \(0\le 1\) from Fig. 1 (i.e., \(\mathbbm {T}\vdash \llbracket \vdash 1 \rrbracket \ge 0\)).
The rule (\(\Diamond \)-rule) for the modality is more subtle as it imposes strong constraints on the shape of its premise and conclusion. First, both the conclusion and the premise are required to be hypersequents consisting of exactly one sequent. Furthermore, in the conclusion, all formulas, except those of the form 1 on the right side, need to be of the form \(\Diamond C\) for some C.
The following is an illustrative example of derivation in the system MGA:

Our first theorem regarding MGA states its soundness and completeness with respect to the theory of modal lattice-ordered abelian groups (see Fig. 1). The proof of [MOG05] of Theorem 2 cannot be directly adapted here because, unlike the case for lattice-ordered abelian groups and \(\mathbb {R}\), we are not aware of any simple modal lattice-order abelian group which generates the whole variety.
Theorem 4
For all formulas A and hypersequents G:
-
Soundness: if \(\vDash _{\text {MGA}}G\) then \(\mathbbm {T}\vdash \llbracket G \rrbracket \ge 0\).
-
Completeness: if \(\mathbbm {T}\vdash A \ge 0\) then \(\vDash _{\text {MGA}} (\vdash A)\).
Proof
Soundness is proven by translating every MGA derivation d of G to a derivation in equational logic \(\pi \) of \( \llbracket G \rrbracket \ge 0\). This is done by induction on the complexity of d. The difficult cases correspond to when d ends by applications of either the S-rule, the M-rule or the \(\sqcup _L\) rule. The formalised proof is implemented in the agda file Syntax/Agda/MGA-Cut/Soundness.agda in [Agd] and the type of the function is:

Conversely, completeness is proven by translating every equational logic derivation \(\pi \) of \(A=B\) to the MGA derivations \(d_1\) and \(d_2\) of the (hyper)sequents \(A \vdash B\) and \(B \vdash A\) respectively. The proof goes by induction on \(\pi \). First, MGA derivations are obtained for all axioms of Fig. 1. For example, for the axiom \(\Diamond (x+y) = \Diamond (x) + \Diamond (y)\) we can derive the (hyper)sequent \(\Diamond ( x + y) \vdash \Diamond ( x) + \Diamond (y) \) as showed below (left-side). Translating applications of the rules refl and sym is simple. Translating applications of the trans rules is immediate using the CUT rule of MGA. To translate applications of the ctxt rule, it is sufficient to prove (by induction) a simple context-lemma that states that if \(A\vdash B\) is MGA derivable then also \(C[A]\vdash C[B]\) is MGA derivable. Similarly, to translate applications of the subst rule, it is sufficient to prove (by induction) a simple substitution-lemma stating that if G is MGA derivable then G[A/x] is also derivable, where G[A/x] is the hypersequent where every occurrence of x is replaced by A.
Note that \(\mathbbm {T}\vdash A \ge 0\) means that \(\mathbbm {T}\vdash 0 = 0 \sqcap A\). By the translation method outlined above, the (hyper)sequent \(0\vdash 0\sqcap A\) is MGA derivable. We can then get a MGA derivation of \(\vdash A\) as follows (right-side):

The file Syntax/Agda/MGA-Cut/Completeness.agda in [Agd] contains the formalised proof and the type of the function is:
 \(\square \)
\(\square \)
Remark 2
The following natural looking variant of the (\(\Diamond \)-rule), allowing hypersequents with more than one component, is unsound:

Our main theorem regarding the system MGA is the cut-elimination theorem. We denote with \( MGA ^*\) the system without the CUT rule.
Theorem 5
(Cut-elimination). Any MGA-derivation of a hypersequent G can be effectively transformed into a \( MGA ^*\)-derivation of G.
Theorems 4 and 5 imply the statement of Theorem 1 in the Introduction.
4 Overview of the Proof of the Cut-Elimination Theorem
In this section we illustrate the structure of our proof of the cut-elimination theorem. We first explain the main ideas behind the proof of cut-elimination for GA of [MOG09, §5.2]. We then explain why these idea are not directly applicable to the system MGA. Lastly, we discuss our key technical contribution which makes it possible to adapt the proof method of [MOG09, §5.2] to prove the cut-elimination theorem for the MGA system.
4.1 The CAN-Elimination Theorem for the System GA
A key idea of [MOG09, §5.2] is to replace the CUT rule with an easier to handle rule called cancellation (CAN) rule. The CAN rule can derive the CUT rule in the basic cut-free system \( GA ^*\) as follows (right-side):

The cut-elimination theorem is obtained in [MOG09, §5.2] by proving a CAN-elimination theorem expressed as: if \(\vDash _{\text {GA}^*} G | \varGamma , A \vdash A , \varDelta \) then \(\vDash _{\text {GA}^*}G | \varGamma \vdash \varDelta \).
The CAN-elimination theorem for the system GA is proved in three steps: Step A: proving the invertibility of all the logical rules ([MOG09, Lemma 5.18]). The invertibility states that if the conclusion of a logical rule (for instance, \(G | \varGamma , A + B \vdash \varDelta \) for the \(+_L\) rule) is derivable without the CAN-rule, then all the premises (in this case \(G | \varGamma , A , B \vdash \varDelta \)) are derivable too without the CAN-rule.
Step B: proving the atomic CAN-elimination theorem ([MOG09, Lemma 5.17]). This theorem deals with the special case of A being a variable and states that if \(d \vDash _{\text {GA}^*} G | \varGamma , x \vdash x , \varDelta \) then \(\vDash _{\text {GA}^*}G | \varGamma \vdash \varDelta \). This theorem is proven by induction on d and is mostly straightforward: the only difficult case is when d finishes with an application of the M-rule. A separate technical result ([MOG09, Lemma 5.16]) is used to take care of this difficult case.
Step C: proving the CAN-elimination theorem ([MOG09, Theorem 5.19]). The CAN-elimination theorem states that if \(\vDash _{\text {GA}^*} G | \varGamma , A \vdash A , \varDelta \) then \(\vDash _{\text {GA}^*}G | \varGamma \vdash \varDelta \). This proof is by induction on A:
-
If A is a variable, we can conclude with the atomic CAN-elimination theorem.
-
Otherwise we use the invertibility of the logical rules and we can conclude with the induction hypothesis. For instance, if \(A=B + C\), then by invertibility of the \(+_L\) and \(+_R\) rules we have a \( GA ^*\)-derivation of \( \vDash _{\text {GA}^*}G | \varGamma , B , C \vdash \varDelta , B , C\) and, from it, we can obtain a \( GA ^*\)-derivation of \(G | \varGamma \vdash \varDelta \) by using twice the induction hypothesis, first on B then on C.
4.2 Issues in Adapting the Proof for the System MGA
The proofs of [MOG09] can be adapted to the context of MGA without much difficulty to perform the first two steps:
Theorem 6
(Invertibility of the logical rules). All logical rules (including the \(\Diamond \)-rule) are invertible in the system MGA\(^*\).
Proof
The same proof technique used in [MOG09] works. The main idea is, in order to deal easily with the (S) and the (C) rules, to prove a slightly stronger statement about the invertibility of more general rules. For instance, the generalisation of the rule \(+_L\) is:

\(\square \)
Theorem 7
(Atomic CAN-elimination theorem). If \(\vDash _{\text {MGA}^*} \varGamma , x \vdash x, \varDelta \) then \(\vDash _{\text {MGA}^*} \varGamma \vdash \varDelta \).
The complication comes from the third and last Step C. We want to prove that if \(\vDash _{\text {MGA}^*} G | \varGamma , A \vdash A , \varDelta \) then \(\vDash _{\text {MGA}^*}G | \varGamma \vdash \varDelta \). An ordinary proof by induction on A could get stuck when \(A=\Diamond B\). For instance, if the hypersequent is \(x, \Diamond B \vdash \Diamond B,x\), the invertibility of the \(\Diamond \)-rule can not be used because of the syntactic constraints the \(\Diamond \)-rule imposes on its conclusion. Indeed the invertibility of the \(\Diamond \)-rule states that if \(\vDash _{\text {MGA}^*} \Diamond \varGamma \vdash \Diamond \varDelta \) then \(\vDash _{\text {MGA}^*} \varGamma \vdash \varDelta \), but \(x, \Diamond A \vdash \Diamond A,x\) is not of this form because it contains the variable x.
For this reason, we deal with the case \(A=\Diamond B\) in a different way, using an induction argument on the derivation of \(G | \varGamma , A \vdash A , \varDelta \). In this argument, however, the M-rule is hard to deal with (as already remarked it is a main source of complications also on the proof of atomic CAN-elimination of [MOG09, §5.2]).
Our main technical result is that the M-rule can be eliminated from a simple variant of the system MGA called MGA-SR (which stands MGA with scalar rules). The system MGA-SR is obtained by modifying MGA as follows:
-
The logical left-rules and right-rules for the connectives \(\{0,-,+,\sqcup ,\sqcap \}\) are generalised to deal with scalar coefficients (syntactic sugaring introduced in Sect. 3). For instance, the rules \(+_L\) and \(\sqcup _L\) become:
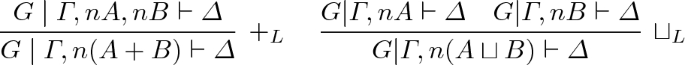
-
The axioms ID-ax and 1-ax are replaced by the rules
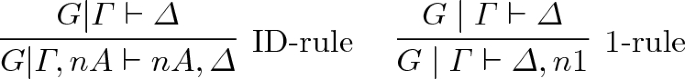
-
All structural rules (C, W, S, M), the \(\Diamond \)-rule and the CAN rule remain exactly as in MGA (see Fig. 2).
It is possible to verify that MGR and MGR-SR are equivalent, i.e., they can derive exactly the same hypersequents (Theorem 8 below). The first modification (scalar rules) is technically motivated because it simplifies several proofs: in fact scalar rules are also implicitly considered in several of the proofs of [MOG09] for the system GA. The second modification (ID-rule and 1-rule) is essential. Indeed in the system MGA (and also in GA) the (hyper)sequent \(x ,y\vdash x,y\) is not derivable without applying the M-rule. Hence M-elimination in MGA is impossible. On the other hand the (hyper)sequent \(x,y\vdash x,y\) is easily derivable in MGA-SR without requiring applications of the M rule

and, as we will prove (Theorem 12), it is indeed possible to eliminate all applications of the M-rule from MGA-SR.
As outlined above, the presence of the M-rule was the main source of complications in adapting Step C. Once the equivalence between MGA-SR and \( MGA-SR \) without the M-rule is established, most complications disappear and the CAN-elimination proof can be obtained by performing Steps A–B–C for the system MGA-SR.
4.3 The System MGA-SR and the M-Elimination Theorem
In this subsection we introduce the system MGA-SR (MGA with scalar rules) for which we will prove the M-elimination theorem.
Definition 8
(MGA-SR). The inference rules of MGA-SR are the rules of MGA modified as discussed previously. We denote by MGA-SR\(^*\), MGA-SR\(^\dag \) and MGA-SR\(^{\dag *} \) the systems without the CUT rule, the M-rule and both the CUT and M-rules, respectively.
Theorem 8
The two systems MGA and MGA-SR are equivalent: \(\vDash _{\text {MGA}} G\) if and only if  .
.
The two systems MGA\(^*\) and MGA-SR\(^*\) are equivalent: \(\vDash _{\text {MGA}^*} G\) if and only if  .
.
Proof
Translating MGA proofs to MGA-SR proofs is straightforward. All rules of MGA are specific instances of the scalar rules of MGA-SR (taking the scalar \(n=1\)) and the the axioms 1-Axiom and ID-axioms are easily derivable in MGA-SR (without the need of the CAN rule) by using the id-rule and 1-rule (again, using the scalar \(n=1\)). Translating MGA-SR to MGA is also mostly straightforward. Some care is needed to translate instances of the scalar-rules \(\sqcup _L\) and \(\sqcap _R\) from MGA-SR to MGA. This can be done by induction on the scalar n using the fact that the two premises \(G | \varGamma , n A , B \vdash \varDelta \) and \(G | \varGamma , n B , A \vdash \varDelta \) are derivable from \(G | \varGamma , (n+1) A \vdash \varDelta \) and \(G | \varGamma , (n+1) B \vdash \varDelta \). We remark that this derivation may require the usage of the M rule. \(\square \)
We now state our main technical contribution: the M-elimination theorem for the system MGA-SR.
Theorem 9
(M-elimination). If \(d_1\vDash _{\text {MGA-SR}^\dag } G_1 \mid \varGamma \vdash \varDelta \) and \(d_2\vDash _{\text {MGA-SR}^\dag } G_2 \mid \varSigma \vdash \varPi \) then \(\vDash _{\text {MGA-SR}^\dag } G_1 \mid G_2 \mid \varGamma , \varSigma \vdash \varDelta , \varPi \).
If \(d_1\vDash _{\text {MGA-SR}^{\dag *}} G_1 \mid \varGamma \vdash \varDelta \) and \(d_2\vDash _{\text {MGA-SR}^{\dag *}} G_2 \mid \varSigma \vdash \varPi \) then \(\vDash _{\text {MGA-SR}^{\dag *}} G_1 \mid G_2 \mid \varGamma , \varSigma \vdash \varDelta , \varPi \).
We now give a sketch of our proof argument. A formalised proof in Agda is available in [Agd] and is contained in the files Syntax/MGA-SR/M-Elim.agda and Syntax/MGA-SR-CAN/M-Elim-CAN.agda.
The general idea is to combine the derivations \(d_1\) and \(d_2\) in a sequential way. We first consider the case when no applications of the \(\Diamond \)-rule appear in \(d_1\) nor \(d_2\). First the proof \(d_1\) is transformed into a pre-proof (i.e., where the derivation is left incomplete at some leaves) \(d_1^\prime \) of \(G_1\mid G_2 \mid \varGamma , \varSigma \vdash \varDelta , \varPi \). The pre-proof \(d_1^\prime \) is structurally identically to \(d_1\) and it essentially just ignores the \(G_2\), \(\varSigma \) and \(\varPi \) components of the hypersequent. While the leaves of \(d_1\) are all of the form \((\vdash )\) because \(\varDelta \)-ax is the only axiom of MGA-SR, the leaves of the pre-proof \(d_1^\prime \) are of the form \(G_2\mid n \varSigma \vdash n\varPi \) (the ignored part carried out until the end, which can get multiplied by applications of the C and S rules). We can now proceed with the second step and provide derivations for these leaves using (easily modified versions of) the proof \(d_2\).
When occurrences of the \(\Diamond \)-rule appear in \(d_1\) or \(d_2\) the argument requires more care. Indeed an application of the \(\Diamond \)-rule on \(d_1\) acting on some hypersequent (necessarily) of the form:
cannot turned into an application of \(\Diamond \)-rule on:
because this hypersequent violates the structural constraints of the \(\Diamond \)-rule. For this reason, we stop the construction of \(d_1^\prime \) at these points and, as a results, the leaves of the pre-proof \(d_1^\prime \) are generally of the form: \(G_2 \mid n\varSigma , \Diamond \varGamma _1 \vdash \Diamond \varDelta _1, k1, n\varPi \), for some \(\varGamma _1, \varDelta _1\) and scalars n, k.
The idea now is, following the same kind of procedure, to modify the proof \(d_2\) and turn it to a pre-proof \(d_2^\prime \) of \(G_2 \mid n\varSigma , \Diamond \varGamma _1 \vdash \Diamond \varDelta _1, k1, n\varPi \). Crucially, the previous issue disappears. Indeed proof steps in \(d_2\) acting on hypersequents of the form:
using the \(\Diamond \)-rule, can be turned into valid \(\Diamond \)-rule steps for the extended hypersequent:
because the shape of the sequent is compatible with the constraint of the \(\Diamond \) rule. Note that the hypersequent resulting from the application of the \(\Diamond \)-rule is \( \varSigma _1, \varGamma _1 \vdash \varGamma _1, k_1 1, \varPi _1, m_1 1\) and has a lower modal-depth than the starting one. Hence an inductive argument on modal-complexity can be arranged to recursively reduce the general M-elimination procedure to the simpler case where \(d_1\) and \(d_2\) do not have occurrences of the \(\Diamond \)-rule (Fig. 4).
The following is a direct consequence Theorems 8 and 9.
Corollary 1
The two systems MGA and MGA-SR\(^\dag \) are equivalent: \(\vDash _{\text {MGA}} G\) if and only if  .
.
The two systems MGA\(^*\) and MGA-SR\(^{\dag *}\) are equivalent:  if and only if
if and only if  .
.
4.4 Cut-Elimination Theorem for the System MGA
We have already remarked that the cut-elimination theorem for the system MGA follows from the CAN-elimination theorem. By Corollary 1, the CAN-elimination theorem for the system MGA-SR\(^\dag \) implies the CAN-elimination for MGA. Since there is no M-rule in MGA-SR\(^\dag \), the proof of CAN-elimination can follow the three Steps A–B–C outlined in Subsect. 4.1. As for Step A, we need to prove the invertibility of the logical rules in the system MGA-SR\(^{\dag *}\).
Theorem 10
(Invertibility of the logical rules). The logical rules of the system MGA-SR\(^{\dag *}\), \(\{ 0_L, 0_R, +_L, +_R, \sqcup _L, \sqcup _R, \sqcap _L, \sqcup _R \}\), are invertible.
Remark 3
We note that, just as in [MOG09, §5.2], it is in fact possible and indeed technically useful to prove the invertibility of generalised scalar rules dealing with scalar rules, as in the proof of Theorem 6.
As for Step B we prove the atomic CAN-elimination theorem. Following the previous remark, we prove the following stronger version of the statement.
Theorem 11
(Atomic CAN-elimination). If \(\vDash _{\text {MGA-SR}^{\dag *}} \left[ \varGamma _i , k_ix \vdash k_ix,\right. \left. \varDelta _i \right] _{i=1}^n\) then \(\vDash _{\text {MGA-SR}^{\dag *}} \left[ \varGamma _i \vdash \varDelta _i \right] _{i=1}^n\).
Since we removed the M-rule, there are no significant difficulties in the induction arguments, and the proof is quite straightforward.
We also need a technical lemma regarding the constant formula 1 which is provable by a simple induction on the length of derivations.
Lemma 1
If \(\vDash _{\text {MGA-SR}^{\dag *}} \left[ \varGamma _i , n_i 1 \vdash n_i 1, \varDelta _i \right] _{i=1}^n\) then \(\vdash _{\text {MGA-SR}^{\dag *}} \left[ \varGamma _i \vdash \varDelta _i \right] _{i=1}^n\).
We can now prove the CAN-elimination theorem for \(\text {MGA-SR}^{\dag }\). This, together with Corollary 1 implies the cut-elimination (Theorem 5) for MGA.
Theorem 12
(CAN-elimination). If \(d \vDash _{\text {MGA-SR}^{\dag *}} G\mid \varGamma , A \vdash A ,\varDelta \) then \(\vDash _{\text {MGA-SR}^{\dag *}} G\mid \varGamma \vdash \varDelta \).
Proof
Again, it is convenient to prove the stronger statement: If \(d \vDash _{\text {MGA-SR}^{\dag *}} \left[ \varGamma _i , k_iA \vdash , k_iA ,\varDelta _i \right] _{i=1}^n\) then \(\vDash _{\text {MGA-SR}^{\dag *}} \left[ \varGamma _i \vdash \varDelta _i \right] _{i=1}^n\). This is done by induction on the (lexicographical) complexity of the pair (A, d):
-
If A is a variable, we can conclude with Theorem 11.
-
If \(A=1\), we can conclude with Lemma 1.
-
If \(A=\Diamond B\), we look at d.
-
If d finished with the \(\Diamond \)-rule, then the end hypersequent is necessarily of the form: \( \left[ \varGamma _i , k_iA \vdash , k_iA ,\varDelta _i \right] _{i=1}^n = \Diamond \varGamma _1 , n_1 \Diamond B \vdash n_1\Diamond B , \Diamond \varDelta _1, k1 \), and is derived from the hypersequent \(\vDash _{\text {MGA-SR}^{\dag *}}\varGamma _1 , n_1 B \vdash n_1 B, \varDelta _1, k 1\). By induction hypotheses (B has smaller complexity than A), we have that \(\vDash _{\text {MGA-SR}^{\dag *}}\varGamma _1 \vdash \varDelta _1 , k 1\). Hence we can derive \(\vDash _{\text {MGA-SR}^{\dag *}}\Diamond \varGamma _1 \vdash \Diamond \varDelta _1, k 1\) by application of the \(\Diamond \)-rule.
-
Otherwise, the hypersequent is derived by application of some other rule (not active on \(A=\Diamond B\)) from some premises. In this case, we simply apply the inductive hypothesis on the premises (the formula A is unchanged but the complexity of the premise derivation has decreased) and use the same rule to construct a derivation of the desired hypersequent.
-
-
Otherwise, using the same argument of [MOG09, §5.2] discussed in Sect. 4.1, we make progress in the inductive proof (reducing the complexity of A) by using the invertibility of the logical rules (Theorem 10). \(\square \)
5 Conclusions and Future Work
We have presented a structural proof system called MGA for the scalar-free fragment of the Riesz modal logic. A natural direction of research is to extend the system MGA to deal with the full Riesz modal logic, thus handling arbitrary scalars \(r\in \mathbb {R}\). The (integer-)scalar rules of the system MGA-SR could be naturally generalised to handle real-scalars but it is not clear, at the present moment, if the resulting system would satisfy a reasonable formulation of the sub-formula property. Another interesting topic of research is to consider extensions of MGA for fixed-point extensions of the Riesz modal logic (e.g., [MS17, Mio18]). In this direction, the machinery of cyclic proofs (see, e.g., [Stu07, MS13b, BS11, Dou17]) appears to be particularly promising.
Notes
- 1.
Example: the law of idempotence \(x\vee x=x\) can be derived from the standard axioms of Boolean algebras (i.e., complemented distributive lattices) as: \(x \vee x = (x\vee x) \wedge \top = (x\vee x) \wedge (x \vee \lnot x) = x \vee (x \wedge \lnot x) = x \vee \bot =x\).
References
Repository containing the proofs formalised in Agda. https://github.com/clucas26e4/M-elimination
Avron, A.: A constructive analysis of RM. J. Symbolic Logic 52(4), 939–951 (1987)
Bacci, G., Bacci, G., Larsen, K.G., Mardare, R.: On the metric-based approximate minimization of Markov chains. In: Proceedings of 44th ICALP. LIPIcs, vol. 80, pp. 104:1–104:14. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2017)
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge (2002)
Barthe, G., Grégoire, B., Zanella-Beguelin, S.: Formal certification of code-based cryptographic proofs. In: Proceedings of POPL, pp. 90–101 (2009)
Baier, C., Katoen, J.P.: Principles of Model Checking. The MIT Press, Cambridge (2008)
Brotherston, J., Simpson, A.: Sequent calculi for induction and infinite descent. J. Log. Comput. 21(6), 1177–1216 (2011)
Buss, S.R.: An introduction to proof theory. In: Handbook of Proof Theory, pp. 1–78. Elsevier (1998)
Ciabattoni, A., Metcalfe, G.: Bounded Łukasiewicz logics. In: Cialdea Mayer, M., Pirri, F. (eds.) TABLEAUX 2003. LNCS (LNAI), vol. 2796, pp. 32–47. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45206-5_6
Alfaro, L.: Quantitative verification and control via the \(\mu \)-calculus. In: Amadio, R., Lugiez, D. (eds.) CONCUR 2003. LNCS, vol. 2761, pp. 103–127. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45187-7_7
Dimitrova, R., Ferrer Fioriti, L.M., Hermanns, H., Majumdar, R.: Probabilistic CTL\(^{*}\): the deductive way. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 280–296. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_16
Desharnais, J., Gupta, V., Jagadeesan, R., Panangaden, P.: Approximating labelled Markov processes. In: Proceedings of LICS (2000)
Diaconescu, D., Metcalfe, G., Schnüriger, L.: A real-valued modal logic. Log. Methods Comput. Sci. 14(1), 1–27 (2018)
Doumane, A.: On the infinitary proof theory of logics with fixed points. Ph.D. thesis, University Paris Diderot (2017)
Gentzen, G.: Untersuchungen über das logische schließen. Math. Z. 39, 405–431 (1934)
Hansson, H., Jonsson, B.: A logic for reasoning about time and reliability. Form. Asp. Comput. 6, 512–535 (1994)
Huth, M., Kwiatkowska, M.: Quantitative analysis and model checking. In: Proceedings of LICS (1997)
Hsu, J.: Probabilistic couplings for probabilistic reasoning. Ph.D. thesis, University of Pennsylvania (2017)
Kozen, D.: Results on the propositional \(\mu \)-calculus. Theor. Comput. Sci. 27, 333–354 (1983)
Kozen, D.: A probabilistic PDL. J. Comput. Syst. Sci. 30(2), 162–178 (1985)
Lehmann, D., Shelah, S.: Reasoning with time and chance. Inf. Control 53(3), 165–1983 (1982)
Luxemburg, W.A.J., Zaanen, A.C.: Riesz Spaces. North-Holland Mathematical Library, vol. 1. Elsevier, Amsterdam (1971)
Mio, M., Furber, R., Mardare, R.: Riesz modal logic for Markov processes. In: 32nd ACM/IEEE Symposium on Logic in Computer Science (LICS), pp. 1–12. IEEE (2017). https://doi.org/10.1109/LICS.2017.8005091
Mio, M.: Probabilistic modal \(\mu \)-calculus with independent product. In: Hofmann, M. (ed.) FoSSaCS 2011. LNCS, vol. 6604, pp. 290–304. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19805-2_20
Mio, M.: On the equivalence of denotational and game semantics for the probabilistic \(\mu \)-calculus. Log. Methods Comput. Sci. 8(2) (2012). https://lmcs.episciences.org/787, https://doi.org/10.2168/LMCS-8(2:7)2012
Mio, M.: Probabilistic modal \(\mu \)-calculus with independent product. Log. Methods Comput. Sci. 8(4) (2012). https://lmcs.episciences.org/789, https://doi.org/10.2168/LMCS-8(4:18)2012
Mio, M.: Upper-expectation bisimilarity and Łukasiewicz \(\mu \)-calculus. In: Muscholl, A. (ed.) FoSSaCS 2014. LNCS, vol. 8412, pp. 335–350. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54830-7_22
Mio, M.: Riesz modal logic with threshold operators. In: 33rd ACM/IEEE Symposium on Logic in Computer Science (LICS), pp. 710–719. ACM (2018). https://doi.org/10.1145/3209108.3209118
McIver, A., Morgan, C.: Results on the quantitative \(\mu \)-calculus qM\(\mu \). ACM Trans. Comput. Log. 8(1) (2007). https://dl.acm.org/citation.cfm?doid=1182613.1182616
Metcalfe, G., Olivetti, N., Gabbay, D.M.: Sequent and hypersequent calculi for Abelian and Łukasiewicz logics. ACM Trans. Comput. Log. 6(3), 578–613 (2005)
Metcalfe, G., Olivetti, N., Gabbay, D.M.: Proof Theory for Fuzzy Logics. Applied Logic Series, vol. 36. Springer, Dordrecht (2009). https://doi.org/10.1007/978-1-4020-9409-5
Mio, M., Simpson, A.: Łukasiewicz \(\mu \)-calculus. In: Proceedings Workshop on Fixed Points in Computer Science, FICS. EPTCS, vol. 126, pp. 87–104 (2013). https://doi.org/10.4204/EPTCS.126.7
Mio, M., Simpson, A.: A proof system for compositional verification of probabilistic concurrent processes. In: Pfenning, F. (ed.) FoSSaCS 2013. LNCS, vol. 7794, pp. 161–176. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37075-5_11
Mio, M., Simpson, A.: Łukasiewicz \(\mu \)-calculus. Fundam. Informaticae 150(3–4), 317–346 (2017). https://doi.org/10.3233/FI-2017-1472
Pottinger, G.: Uniform, cut-free formulations of T, S4 and S5 (abstract). J. Symbolic Logic 48(3), 898–910 (1983)
Studer, T.: On the proof theory of the modal \(\mu \)-calculus. Stud. Logica. 89(3), 343–363 (2007)
Vulikh, B.Z.: Introduction to the Theory of Partially Ordered Spaces. Wolters-Noordhoff Scientific Publications LTD., Groningen (1967)
Wansing, H. (ed.): Proof Theory of Modal Logic. Applied Logic Series, vol. 2. Springer, Dordrecht (1996). https://doi.org/10.1007/978-94-017-2798-3
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Lucas, C., Mio, M. (2019). Towards a Structural Proof Theory of Probabilistic \(\mu \)-Calculi. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)