Abstract
Increased deposition of reactive nitrogen (N) since pre-industrial times has dramatically altered the conditions for forest growth and decomposition of organic material in Germany. The second National Forest Soil Inventory (NFSI II, 2006–2008) shows the status of N accumulation in forest soils. A median N stock of 6.3 t ha–1 has been found in the soil profile down to a depth of maximum 90 cm, whereof 50% is stored in the upper 30 cm of the mineral soil. The high regional variability of N stocks is explained by forest type, parent material, soil acidity, annual mean temperature, and adjacent agricultural land use. C/N ratios of the top soil were on average higher (24.0) than those during NFSI I (22.4, 1989–1992), which may be seen as a first effect of slowly decreasing deposition rates. Observations on limed plots suggest that acidification inhibits soil biological activity and thereby reduces N-storage in the mineral soil. The median annual N balance for German forest soils between NFSI I and II varies between +2.9 and +7 kg ha–1, depending on the harvest regime assumed. Negative N balances occurred mainly in mountain ranges like the Black Forest or the Rhenish Slate Mountains. N stocks in the upper 30 cm of the soil generally increased, while there are indications for losses of N from deeper soil layers, potentially linked to progressing acidification in these layers. Irrespective of existing measurement uncertainties, the findings indicate the vulnerability of forest N stocks under changing conditions. Further reductions of N deposition should be strived for to reduce the risk of nitrate leaching from forest soils.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
5.1 Introduction
Nitrogen (N) in forest soils is a key variable to assess the state of forest ecosystems due to the large effects it has on forest growth, ecosystem integrity, and human health. High amounts of N are needed for biomass production in forests as N is one of the four elements that are structural components of most organic molecules forming biomass. In contrast to the other main elements essential for biomass production (carbon (C), oxygen (O), and hydrogen (H)), forest trees could over the longest part of their evolution not get these amounts of N directly by using ubiquitous media like water or gases from the atmosphere. Since atmospheric nitrogen (N2) is a very stable molecule, requiring high amounts of energy for the transformation into reactive N species that may contribute to plant-available N, forest trees always depended on the recycling of organic N from the decomposition of dead organic matter in the soil, where organic molecules are with 95% the prevailing form of N (Rohmann and Sontheimer 1985). Their mineralization and the subsequent nitrification by microbes are exergonic and provide the inorganic molecules ammonium (NH4 +) and nitrate (NO3 –) that may both be taken up by plant roots. NO3 – and NH4 + assimilation in the roots and leaves of trees require energy from photosynthesis, which provides the energy source keeping this forest internal N recycling running. In terms of ecosystem services, nutrient recycling is considered the economically most valuable ecosystem service of forests (Costanza et al. 1997).
Without consideration of human activities, there is only limited exchange of this ecosystem-internal cycle with the environment (Larcher 2001): The natural sources for additional plant-available N (lightnings and N2 fixing microbes, redistribution of N by moving water or animals) are scarce; thus tree species show mechanisms for minimizing N losses from the forest ecosystem due to leaching or gaseous emission. These include to build up dense fine root and mycorrhizal networks close to the origin of newly mineralized N compounds or immediate uptake of any plant-available N, preferentially NH4 + (Ek et al. 1994; Posch et al. 2015). In this sense, forest ecosystems have evolved towards increased capability for N storage, with the upper parts of the soil as major N stock in temperate forests, as a response to the low reliability of N supply in nature.
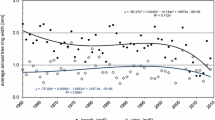
In modern times, these conditions have dramatically changed due to N deposition from industrial processes with high energy consumption that lead deliberately (fertilizer production) or as a by-product (combustion processes) to the transformation of atmospheric N2 to reactive N species. Atmospheric N deposition to forests in Germany had continuously risen since pre-industrial times until a maximum was reached between 1980 and 1995, when NFSI I took place. Partly due to the introduction of catalytic converters for Otto engines (in Germany since 1989), N deposition started to decrease and was already much lower during NFSI II (see Sect. 2.2), though historically still on a high level (Fagerli et al. 2007; Fagerli and Aas 2008). The temporal course of the calculated N deposition (Fig. 5.1) agrees well with other models of deposition history in Europe (cf. Engardt et al. 2017).
The high additional amount of NO3 – and NH4 + currently reaching forest ecosystems through atmospheric deposition strongly affects the recycling of N: Forest growth is no longer limited by N availability such that other minimum factors gain importance for controlling growth (Spiecker et al. 1996; Talkner et al. 2015). The increased amounts of plant-available N in the soil lead to changes in the species composition of ground vegetation , favouring nitrophilous species (Förster et al. 2017; Strengbom and Nordin 2008). If N is deposited over longer time periods, the N retention capacity of forest soils may be exceeded (N saturation, Aber et al. 1989, 1998; Lovett and Goodale 2011; Meesenburg et al. 2016), and excess N is leached in the form of NO3 –, which leads to increased NO3 – concentrations in the groundwater commonly used as drinking water and in lakes, where algal bloom and fish-poisonous conditions may be the consequence (Erisman et al. 2015; Oulehle et al. 2015). Lakes and brooks are also affected by acidity that is generated by plant uptake of NH4 + or its nitrification and may among other effects cause fish- and root-toxic aluminium ions (Al3+) to dissolve, which can be leached together with NO3 – (Vitousek et al. 1997). Due to electroneutrality, NO3 – leaching also leads to a loss of base cations from the soil (de Vries et al. 2014). Also gaseous emissions of N2O and other N compounds may increase with increasing N input (Eickenscheidt et al. 2011; Eickenscheidt and Brumme 2012; Krupa 2003), thereby contributing to the rising concentrations of the greenhouse gas N2O in the atmosphere.
Since forests are typically much less affected by fertilizer application compared to agricultural areas, the groundwater under forested areas is often used for drinking water supply. Therefore, the quality of groundwater under forests is of direct relevance for human health. While a maximum of 50 mg NO3 – per litre is tolerated according to the water framework directive of the EU (EU Directive 2006/118/EC), it is known that even much lower concentrations over longer periods may induce health risks like bowel cancer (Ward et al. 2005).
The NFSI, as the only spatially representative inventory of forest soils in Germany, may provide evidence for the effects of decreasing, but still high N deposition on N availability and N retention in the soil. It may show whether there are yet signs of recovery from the most extreme deposition rates and help to find out the time scale for such recovery. However, the soils were not only affected by changes in deposition of NO3 – and NH4 +: Between NFSI I and NFSI II, a strong reduction in sulphur deposition (Engardt et al. 2017), a climate change induced rise in temperatures , higher availability of carbon dioxide (CO2), and changed availability of water may have altered the relationship between N transformation processes in the soil (Fleck et al. 2017). For example, during the vegetation periods, days with extremely low soil water availability (<40% of plant available water capacity ) were much less frequent in the 10 years before NFSI I (21.6 days) than in the 10 years before NFSI II (30.4 days, Fig. 3.11), while annual precipitation remained unchanged, thereby potentially increasing the amount of wetting and drying cycles that increase the availability of soil organic matter to decay processes (Borken and Matzner 2009). Management effects of liming and conversion of tree species composition provide additional influencing factors. The measurement results must, therefore, be interpreted with care, since they are the result of several interacting environmental and management factors.
The following sub-chapters show first the status of N stocks and C/N ratios and highlight some of the most important impact factors for these patterns. The status results rely on NFSI II measurements (complete sample including peatland plots). Results from NFSI I and Intensive Forest Monitoring plots (IFM plots, i.e. Level II plots and beyond them other plots sampled according to the same methodology) are occasionally given for comparison. Nitrogen stock changes from NFSI I to NFSI II are then derived with two alternative approaches: (1) differential measurement of N stocks at two points in time (NFSI I and NFSI II), based on the paired sample without peatland plots or on IFM plot measurements, and (2) N balance of the modelled input and output rates for the period between NFSI I and NFSI II. These trend calculations are followed by the discussion of methods and a final discussion of the results.
5.2 Nitrogen Stocks in Forest Soils
Nitrogen stocks in the soil profile were assessed from the organic layer to a maximum depth of 90 cm. Because the soil depth was lower than 90 cm at a considerable proportion of sites and because of lower data availability at deeper depth, soil profile data are in most cases only shown for organic layer—60 cm. The typical gradient of N stocks with soil depth is, however, best visible for organic layer—90 cm. Considering the skewness of N stock distributions from NFSI I (see Sect. 5.5.3), medians are presented for each layer instead of means wherever distributions are not normal. All medians and means are area-weighted (see Sect. 1.17).
5.2.1 Gradient of Nitrogen Stocks with Depth in the Soil Profile
In NFSI II , 11% of N were kept in the organic layer, 52% in the uppermost 30 cm of the mineral soil, 21% in 30–60 cm depth, and 12% in 60–90 cm depth (layer medians as percentages of the organic layer—90 cm median). This gradient was similarly observed in NFSI I (12%, 50%, 21%, and 13%, respectively) and did not significantly change (Figs. 5.2 and 5.12a). Even the results from the much lower number of IFM plots with available inventory data show a very similar gradient (see Sect. 5.4.2). The observed gradient reflects the flow of organic material and its descendants through the ecosystem: Dead biomass is predominantly integrated via the organic layer, where the fresh litter is in the prevailing case of aerobic conditions not stored, but subject to high turnover rates and bioturbation, leading to its integration into soil organic matter . Total soil N stocks are, therefore, typically several times higher than those of only the organic layer and depend mainly on the quality and amount of litter entering the soil at its upper border or from fine roots in the upper mineral soil. Other important determinants of soil N stock are the climatic and soil-chemical conditions for litter decomposition . The sharpest decrease in N stocks occurs between the uppermost 30 cm and the next 30 cm of soil, since the aboveground organic material mainly adds to the uppermost part of the mineral soil. The decrease between 30–60 cm depth and 60–90 cm depth is rather moderate and apparently reflects the decreasing fine root density, which is mostly considered irrelevant in even deeper layers, where N concentrations often fall below the detection limit.
Depth gradient of nitrogen stocks in t ha–1 for NFSI I (left, dark columns) and NFSI II (right, dark columns) related to the total sample of each inventory. Results from the first and second inventory on Intensive Forest Monitoring plots (IFM , light columns) measured within a time shift of maximum 5 years to each of the NFSIs (see “Results from Intensive Forest Monitoring Plots” under Sect. 5.4.2) are given for comparison. All values are medians with interquartile ranges as error bars and sample sizes given at the horizontal axis. As representative result for German forest soils, medians and interquartile ranges of NFSIs are area-weighted (see Sect. 1.17 and Fig. 5.11)
5.2.2 Nitrogen Stocks in the Organic Layer
Nitrogen stock in the organic layer was with 0.67 t ha–1 and an interquartile range (iqr) of {0.24; 1.22} t ha–1 (n = 1794) smaller than the amount of N stored in the upper 5 cm of the mineral soil (1.09 t ha–1, iqr{0.76; 1.43}, n = 1846). Since the delineation between both compartments is to a certain extent subjective (Jansen et al. 2005), the joint N stock in organic layer—5 cm (1.81 t ha–1, iqr {1.43; 2.37}, n = 1784) is a more robust estimate.
5.2.3 Nitrogen Stocks in the Soil Profile: Organic Layer—Maximum 90 cm
While the whole rooting zone may—especially on sandy soils—often go deeper than 90 cm of the mineral soil (cf. Czajkowski et al. 2009), about 6% of NFSI II plots had soil profiles shallower than 90 cm. As a representative number for German forest soils, the area-weighted median of N stocks for all soil profiles from the organic layer down to maximum depth of 90 cm of the mineral soil was 6.3 t ha–1 (iqr {4.5; 8.6}, n = 1647). The empirical national rating for N stocks in the rooting zone of forests (AK Standortskartierung 2016) was confirmed to some extent by the scatter of these results, since high (>10 t ha–1) and very high (>20 t ha–1) N stocks in the soil profile were observed on only 14% and 1% of the plots, respectively. These highest values were mainly reached in organic soils on actual or former peatland area. Very low nitrogen stocks (≤2.5 t ha–1) were found on only 3% of the plots.
Nitrogen stocks of the soil profile (Fig. 5.3) were highest on peatland plots and organic soils in the western part of the North-German Lowland, the Alps and their foothills, and the Bavarian Forest. Other regions with very high N stocks are the Rhine Rift Valley (here the N redistribution on alluvial plains may play a role), and mountain ranges surrounding the Thuringian Basin, Upper Franconia, large parts of the Rhenish Slate Mountains, the Southern Swabian Alb, Harz and nearby mountain ranges in Lower Saxony, and the Saarland. Out of these regions, the western part of the North-German Lowland, the Bavarian Forest, Upper Franconia, Harz, and the Rhenish Slate Mountains received comparatively high amounts of N deposition between 1990 and 2007. Plots in the Alps, the Bavarian Forest, and plots on high altitude in other mountain ranges have low annual mean temperature, which hampers decomposition in all stages and leads to an accumulation of N (see Sect. 5.3.3). Upper Franconia, the southern Swabian Alb, the Alps and their foothills, and a part of the Saarland provide soils from carbonate bedrock .
The lowest N stocks of the soil profile are found in the Eastern part of the North-German Lowland with a focus on Brandenburg and adjacent areas in Saxony, Saxony-Anhalt, Lower Saxony, and Mecklenburg-West-Pomerania, where nutrient-poor, sandy soils in a dryer climate prevail and pine is the most abundant forest tree species (compare Sect. 5.3). Other regions with very low N stocks are parts of the mountain ranges Black Forest, Palatinate Forest, the Northern part of the Swabian Alb, as well as Odenwald and the lower mountain ranges of North-Hesse, which are (except Odenwald) among the mountain ranges with relatively low N deposition . Black Forest and Odenwald possess mostly soils from acidic bedrock .
5.2.4 C/N Ratios in the Top Soil
C/N ratios as indicators of soil fertility and degradability of organic material in the upper horizons are traditionally calculated for the Ah horizon of the mineral soil when the humus form is mull or mull-like moder, while the Oa horizon of the organic layer is used in all other cases (AK Standortskartierung 2003). In accordance with Cools et al. (2014), we separated between forest floor (organic layer) and top soil (here: 0–5 cm).
The significance of C/N ratios for soil fertility gets visible when they are related to the nutrient indicator values of the ground vegetation present at each plot. The nutrient indicator values (from nutrient poor (1) to nutrient rich (9), Ellenberg et al. 2003) of plants in the herb layer show a decrease with increasing C/N ratio class (Fig. 5.4) and thereby confirm earlier findings on plant species adaptation.
Nutrient indicator values of the herb layer (mN(KS)) after Ellenberg et al. (2003) as dependent on the C/N ratio of the upper mineral soil (0–5 cm depth, sample sizes at the horizontal axis)
C/N ratios in the organic layer reached a mean value of 25.2 ± 0.1 (iqr {22.5; 27.3}, n = 1792). C/N ratios below 20.7 (10%-quantile, q10) would be considered very low values, and C/N ratios above 30.4 (90%-quantile, q90) are very high in the NFSI II dataset for the organic layer, which includes undecomposed as well as partly decomposed litter and humus. In the upper 5 cm of the mineral soil, the mean of C/N ratios was 20.6 ± 0.14 (iqr {16.5; 23.7}, n = 1850). Here, very low C/N ratios were the ones below 14.2 (q10), and very high C/N ratios start from 27.9 (q90). Due to the operator-dependent separation between both layers, it may sometimes be interesting to also know these values for the continuum from the organic layer to 5 cm: The mean was 24.3 ± 0.09 (iqr {21.8; 29.3}, n = 1787), and very low values would be smaller than 20 (q10), while values above 29.3 (q90) would be considered very high.
The mean values for the organic layer and 0–5 cm, respectively, were similar to the previously reported mean values for the forest floor and the mineral topsoil for the whole of Europe (Cools et al. 2014).
C/N ratios in the organic layer were similar among humus forms (Table 5.1); in this layer mull and mull-like moder are factually represented by merely the Oi-layer, such that C/N ratios are strongly influenced by the C/N ratios of fresh litter. In layer 0–5 cm, where the different velocities of decomposition and the bioturbation play a role, C/N ratios varied between 16.5 for mull and 26.6 for mor.
As will be discussed in Sect. 5.3, the main determinant for the pattern of C/N ratios in Germany is the occurrence of tree species, with pine as the species with highest C/N ratios and all other coniferous forest trees on the second rank (compare Sect. 5.3 and Cools et al. 2014). On the level of forest growth regions, there is also an influence of land use proportions: The average C/N ratios (0–5 cm) of NFSI plots are significantly lower in growth regions with more than 50% agricultural land use , compared to growth regions with less than 50% agricultural area ( p < 0.001). Geographically (Fig. 5.5), the highest C/N ratios in the uppermost 5 cm of the mineral soil of forests occurred mainly in the pine-dominated North-German Lowland. Coniferous tree species are also the determining factor for high C/N ratios in Thuringian Forest, Palatinate Forest, and Erzgebirge, as well as Northern Bavaria, while the lowest C/N ratios are mainly found in beech-dominated landscapes like the Rhenish Slate Mountains and in regions with soils from carbonate bedrock , such as the Swabian-Franconian Alb and the foothills of the Alps .
5.2.5 Comparison to C/N Ratios of NFSI I
For C/N ratios , comparisons to NFSI I are more adequate for organic layer—5 cm than for the both sub-layers separately, since humus forms with their different reference horizons may have changed between NFSI I and NFSI II. The C/N ratios were on average lower in NFSI I (22.4, n = 1155) than those from NFSI II (24.0). Also, the few organic soils not included in the paired sample had lower C/N ratios in NFSI I (16.6, n = 9) than in NFSI II (19.2). Considering that N stocks in the organic layer down to 5 cm of the mineral soil increased between NFSI I and NFSI II, the results show that the accumulation of N in this layer was accompanied by an even stronger and disproportionately high accumulation of C that led to a marked increase of C/N ratios. The resulting change rate of C/N ratios was +0.09 year–1. While an increase of C/N ratios would generally fit to the decrease of N deposition or an increase of nitrogen uptake by the growing stand, some studies indicate that N deposition as a growth-triggering condition contributes to the variability of C stocks in organic and mineral soil layers of forests—in combination with other growth conditions, e.g. climatic factors (Bedison and Johnson 2009). Nitrogen stocks have already been proposed as an indicator for the C sequestration potential of soils (Vesterdal et al. 2008). A time shift between N deposition and the subsequently increased C input to the soil could well explain the observed increase of C/N ratios during a phase of decreasing N-deposition rates (Fig. 5.1).
5.3 Impact Factors
5.3.1 Forest Type
The different amounts and qualities of litter from the stand forming tree species have a strong influence on C/N ratios and N stocks not only of the organic layer. Due to the preferred use of certain tree species for certain soil substrates , the effect of tree species may not fully be disentangled from the one of soil substrates .
Stands dominated by pine had with 27.6 and 25.3, respectively, the highest organic layer and 0–5 cm C/N ratios of all forest types (Fig. 5.6). This rank is occupied by pine in all individual soil substrate groups. High C/N ratios generally indicate both: poor decomposability in the initial stage of decomposition , where mainly cellulose is degraded, and good decomposability in the later stages, where lignified litter components are degraded over much longer time intervals and where the presence of too high amounts of N would hamper decomposition through the suppression of lignolytic enzyme production and the creation of recalcitrant compounds (Berg 2014). Corresponding to both, N stocks of pine (Fig. 5.7) were the highest of all forest types in the organic layer (1.14 ± 0.03 t ha–1), where the initial stage of decomposition takes place, while they were lowest for organic layer—60 cm (4.47 ± 0.12 t ha–1), where the decomposition of lignin is included, which agrees well with the decomposition model of Berg (2014). On the other end of the scale, the lowest C/N ratio (which means highest initial, but lowest total decomposability) in the organic layer or in 0–5 cm of the mineral soil (C/N = 24 or 15.8, respectively) is found under the canopy of broadleaved forests that are not dominated by beech or oak , and this rank is also valid across soil substrate groups. Accordingly, the organic layer N stocks of broadleaved forests are very low (0.4 ± 0.03 t ha–1), while they have the highest N stocks of all forest types in organic layer—60 cm (8.82 ± 0.37 t ha–1).
C/N ratios of the forest types beech-dominated broadleaved forest (B), oak -dominated broadleaved forest (O), spruce-dominated coniferous forest (S), pine-dominated coniferous forest (P), other broadleaved forest (oB), mixed coniferous and broadleaved forest (M), and other coniferous forest (oC) in the organic layer (a) and in 0–5 cm of the mineral soil (b). Sample sizes are given at the horizontal axis. The other broadleaved forests are mainly forests with high proportions (>70%) of specialty hardwood trees like ash and sycamore but also hornbeam, alder, and birch. Other coniferous forests predominantly comprise silver fir, Douglas fir, and larch forests. The mixed forests are typically mixtures of beech with spruce, pine, larch, and silver fir or forest stands with pine or spruce and high proportions of birch or oak
Nitrogen stocks of the different forest types (see caption of Fig. 5.6) in the organic layer (a), in 0–10 cm of the mineral soil (b), and in the soil profile from organic layer to 60 cm of the mineral soil (c). Significant differences are indicated by minor case letters and sample sizes at the horizontal axis
Beech and oak stands were similar to the other broadleaved forests in terms of relatively low C/N ratios and lowest N stocks in the organic layer, whereof the latter is confirmed across soil substrate groups. Their N stocks in organic layer—60 cm were intermediate, comparable to those of other forest types (mixed forests, other coniferous forests).
The C/N ratios of spruce stands were the second highest of all forest types and similar to those of pine stands. The low initial decomposability of their litter agrees well with the rank as the second highest of all N stocks in the organic layer. Complying with Berg (2014), N stocks of spruce stands in organic layer—60 cm were higher than those of pine, but they were even higher than those of beech and oak stands. The effect of tree species-specific litter quality may be less clear in this case due to other factors like the permanently high leaf area index of spruce stands and, consequently, reduced exposition of their soils to sun, rain, snow, wind, and temperature changes. Spruce litter is also better protected by its acidity against decomposition . The higher productivity of spruce compared to pine is generally due to the selection of sites with better nutrient and water availability.
5.3.2 Parent Material and Soil Acidity
Soil parent material mainly affects N stocks through its influence on soil acidity: Soils from weathered carbonate bedrock or from basic-intermediate bedrock provide the least acidic conditions for nutrient uptake , decomposition by microbes, and redistribution of organic material by bioturbation. They have the lowest C/N ratio (16.3 or 17.7, respectively) in 0–5 cm of the mineral soil (Fig. 5.8). As an effect of a soil property , the C/N ratio differences between soil substrates are more pronounced in the uppermost part of the mineral soil than in the organic layer. In accordance with the effect of C/N ratios postulated by Berg (2014), both parent material groups have significantly lower N stocks (Fig. 5.9) in the organic layer than all other parent material groups and the highest N stocks in 0–10 cm of the mineral soil (2.64 t ha–1 and 2.17 t ha–1, respectively) and in the soil profile from organic layer to 60 cm (7.51 t ha–1 and 6.71 t ha–1, respectively).
C/N ratios of the different soil substrate groups in organic layer (a) and 0–5 cm depth of the mineral soil (b). (1) Soils from base-poor unconsolidated sediments, (2) soils of alluvial plains, (3) loamy soils of the lowlands, (4) soils from weathered carbonate bedrock , (5) soils from basic-intermediate bedrock , (6) soils from base-poor consolidated bedrock , (7) soils of the Alps, (8) organic soils from peatland. Sample sizes are given at the horizontal axis
Nitrogen stocks of the eight soil substrate groups (compare caption of Fig. 4.8) in the organic layer (a), 0–10 cm of the mineral soil (b), and the soil profile from organic layer to 60 cm of the mineral soil (c). Sample sizes are given at the horizontal axis
Additional features that protect organic material in the mineral soil from decomposition are relevant in the three smaller substrate groups: Organic soils from peatland (15.7 t ha–1 in organic layer—60 cm, n = 38) and the partly submerged soils of alluvial plains (7.35 t ha–1, n = 63) provide anaerobic zones through the influence of water and may be supplied with organic material from moving water, while soils from the Alps (10.97 t ha–1, n = 27) may provide organic matter protecting enclosures between rocks (compare Sabatini et al. 2015). Organic soils from peatland are the parent material group with the highest variability in N stocks but also the highest average N stocks in all layers. This is due to the fact that the most diverse peatland types like fens and bogs are summarized in one material group.
Apart from organic soils , soils from base-poor consolidated bedrock or base-poor unconsolidated sediments have the highest C/N ratios in 0–5 cm of the mineral soil and also the highest N stocks in the organic layer. Consistent with highest C/N ratios, their total N stocks in organic layer—60 cm are lower than in all other parent material groups (4.77 and 5.67 t ha–1, respectively).
Soil acidity may also be influenced by liming, which is only a relevant management option on acid-sensitive plots (see Chap. 4), and only this subsample of plots is considered in the liming evaluation. Liming did show no direct effect on C/N ratios in NFSI II. But similar to the pattern observed in soils from carbonate bedrock , limed plots showed a decrease of N stocks between NFSI I and NFSI II in the organic layer (−7.8 kg ha–1 year–1 ± 2.4), but an increase of N stocks by +11.8 kg ha–1 year–1 ± 4.2 in the upper mineral soil (0–30 cm). The not limed plots of the acid-sensitive subsample showed instead more or less constant N stocks in the organic layer (−0.7 kg ha–1 year–1 ± 3.2) and a decrease of −11.6 kg ha–1 year–1 ± 4.5 in the upper 30 cm of the mineral soil. Both trends can be explained by the acidifying effect of N-deposition: Acidity inhibits (micro-)biological activity such that particulate organic matter accumulates in the organic layer, while the formation of mineral-associated organic matter and N-storage in the mineral soil is reduced, thereby reversing the usually opposite effect of N-addition on microbial growth and decomposition occurring when acidification is counteracted with liming (Averill and Waring 2018). Supporting this explanation, a multifactorial covariance analysis (ANCOVA ) on the factors liming, forest type, and clay content reveals that only the combined effect of clay content and liming had a significant influence on N accumulation rates in 0–30 cm of the mineral soil. This points to a potentially enhanced formation of N containing clay-organic matter complexes in limed soil, which contributes to the recalcitrant fraction of N compounds (Preston et al. 2009) in the mineral soil. Soil biological activity is vulnerable to acidification: Earthworm activity generally increases under the changed chemical conditions in limed soils (Homan et al. 2016), and also microbial activity increases with increases of soil pH (Anderson and Domsch 1993).
5.3.3 Annual Mean Temperature
Low temperatures are an additional condition that may slow down the process of decomposition of soil organic matter . Concordantly, N stocks in the organic layer and the upper mineral soil up to 10 cm are highest on the plots with the lowest annual mean temperatures (Fig. 5.10) and increase stepwise to the higher temperature classes. The highest temperature classes above 9 °C, however, have again somewhat higher N stocks than the neighbouring class, which may be due to the relevance of dry conditions on these plots that have a prohibitive effect on decomposition of soil organic matter .
5.3.4 Agricultural Land Use
The influence of the regional distribution of agricultural land use was identified based on CORINE land cover data for the forest growth districts in Germany (Gauer and Kroiher 2012). The NHx/NOy ratio of total N deposition generally increases with the proportion of agricultural land use in growth districts (r 2 = 0.42, p < 0.05), but total N deposition to forests in the same district is not generally increased (here meteorological conditions like precipitation , wind speed, and fog rate are also important factors). However, dividing the German forest growth districts into classes of agricultural land use reveals that C/N ratios in 0–5 cm of the mineral soil are lower in growth districts with high or very high proportion of agricultural area, while they are highest in districts with less agriculture (Fig. 5.11a). This apparent effect of agricultural land use is directly due to higher N stocks in 0–5 cm of the mineral soil. In accordance with this finding, also N stocks in agricultural districts are higher than in those with less agriculture (Fig. 5.11b).
As a summary, forest type, parent material , soil acidity, annual mean temperature, and agricultural land use all contribute to the variability of N stocks (Fig. 5.3) and C/N ratios (Fig. 5.5) of German forests and may explain much of the geographical pattern observed. From these factors, parent material and annual mean temperature are naturally given factors that have affected stand and soil condition for centuries, while forest type, soil acidification and agricultural land use are comparatively younger and mainly man-made factors with a shorter, but apparently long enough impact period to affect the N status of forest soils. In the case of agricultural land use , it is probable that the duration of the impact period is linked to N emissions from agriculture that started with the production of N containing mineral fertilizer since about 1910 and the increased imports of forage for more intensive livestock production. Due to multiple interactions in the processes leading to N accumulation or release, the relative contribution of these and other factors may not directly be derived and will need a more complete multivariate model where also other variables (e.g. local exposition, soil wetness, soil texture, podzolation, rooting depth, forest growth, and harvest practice) are expected to play a role .
5.4 Nitrogen Stock Changes
The result of N stock changes over more than a decade is visible in the N stock difference between NFSI I and NFSI II as differential measurement of a state variable at two points in time (Sect. 5.4.1). Apart from NFSI plots, an N stock difference was similarly also detected on IFM plots (Sect. 5.4.2). Due to the integration over several years, this approach does not directly investigate the actually occurring change rates on specific plots. It may, however, indicate the average annual change rate as a trend that would explain the difference between both points in time, thereby integrating over change rate variability between years as well as seasonal and spatial variability of the processes contributing to the observed difference. A more directed approach investigating the processes leading to N stock changes is provided by N balance estimations, describing the flow of nitrogen in and out of an ecosystem with sub-models based on the known course of meteorological variables between NFSI I and NFSI II (Sect. 5.4.3).
5.4.1 Nitrogen Stock Difference on NFSI Plots
Actual status (Sect. 5.2) and trend of N stocks between both NFSIs rely on different sampling approaches: While the presented status results are always based on measurements of the complete NFSI II sample, the calculated trends may only be based on those plots that were investigated two times (paired sample). In the case of N, the paired sample lacks data from Saarland and Bavaria. Organic soils were not included in the paired sample. In all cases, area-weighted medians are reported for N stocks of NFSI instead of means due to the skewness of distributions, and trends are only integrated down to a depth of 60 cm due to the increased uncertainty of low concentration N measurements relevant in deeper layers (see Sect. 5.5.3 and Table 1.2). An overview of the main results is given in Table 5.2.
Trends in Organic Layer: 5 cm
The comparison with NFSI I values yields a non-significant trend: While N stocks in the organic layer showed a slight decrease relative to NFSI I values (−2.4 kg ha–1 year–1), they increased by +6.5 kg ha–1 year–1 in the uppermost 5 cm of the mineral soil, leading to a total accumulation of +5.3 kg ha–1 year–1 in organic layer—5 cm.
The apparent N stock accumulation between NFSI I and NFSI II in organic layer—5 cm tends to even higher values, when a statewise comparison of the complete sample of NFSI I and NFSI II is performed (weighted medians of federal states: +0.2 kg ha–1 year–1 in the organic layer and +12.2 kg ha–1 year–1 in 0–5 cm). Since the measured concentrations in these layers are high, they are less affected by potential analytical errors, which underpins the reliability of this result. The N stock accumulation in the organic and uppermost soil layer coincides with the measured increase of N concentrations in tree leaves and needles between both points in time (see Chap. 9), which might indicate higher N availability for trees as well as higher input to the organic layer. It is questionable, however, whether this increase in leaf N concentrations reflects a general trend or just interannual variability (Riek et al. 2016). It has to be considered, though, that the accumulation of dead organic matter on the forest floor over several years is less sensitive to such interannual variability and might thereby help to recognize longer-term trends in nutrient input and turnover. Under conditions of rising N concentrations in leaves and in the upper mineral soil, the apparent slight decrease of N stocks in the organic layer could be interpreted as a hint towards increased turnover rates of organic material (see Chap. 6).
Trend in Organic Layer: 60 cm
The median of N stock changes in organic layer—60 cm equals −8.2 kg ha–1 year–1 (Table 5.2, Fig. 5.12c). The tendency given by this number for the whole country is mainly due to very high differences between NFSI I and NFSI II in the layer 30–60 cm, while the other layers remained nearly unchanged or showed the opposite tendency (Fig. 5.12c). The tendency is regionally very diverse and may not be seen as typical for the whole country, since large parts of Germany show only negligible changes and others are not included in the paired sample. In contrast, the median for organic layer—30 cm was +6.2 kg ha–1 year–1. This contrasting trend between upper and lower soil compartments comes along with a slight recovery from acidification in the upper soil compartments, while still increasing acidity is observed in the subsoil (see Chap. 4), which could explain higher N losses from deeper soil layers.
Depth gradient of nitrogen stocks in NFSI I and NFSI II related to the total sample of each inventory (a) and respective sums of nitrogen stocks for the soil profile from organic layer up to 60 cm of the mineral soil (b). The annual change rates of nitrogen stocks (c and d) were calculated based on the paired sample of both inventories except peatland. The shown statistical significance of differences between medians (indicated as stars) does not reflect the influence of measurement uncertainties (see Sect. 5.5.2). Outliers are not shown
5.4.2 Nitrogen Stock Difference on IFM Plots
Alternative insight into the status and dynamics of N stocks in German forest soils between NFSI I and NFSI II may only be derived from Intensive Forest Monitoring plots (IFM plots) of the ICP Forests Level II network and additional plots operated according to the same methodology (UNECE ICP Forests Programme Co-ordinating Centre 2016), as the only available independent dataset from approximately the same area and within nearly the same time frame. The soil surveys conducted at these densely instrumented plots are combined with numerous other surveys (Fleck et al. 2017) and aim to provide the basis for the analysis of cause-effect relationships in forest ecosystems.
Intensive Forest Monitoring plots are located in forest stands covering regionally typical combinations of soil type , tree species, climate, and pollution levels (e.g. deposition rates of N and S). Due to their relatively small number and irregular spatial arrangement (Fig. 5.13), results from IFM plots are considered indicative for their respective forest ecosystem types but are not suited to derive spatially representative results (medians reported are, thus, not area-weighted). Nevertheless, ranges of measured N stocks, N deposition , and calculated N leaching rates (see Sect. 5.4.3) from these plots yield an independent source of information for the time span between NFSI I and NFSI II. Only IFM plots with a maximum temporal shift of ±5 years compared to the two NFSIs have been selected for analysis.
The depth gradient of N stocks on the intensive monitoring sites shows a similar pattern compared to NFSI plots for both the first and second inventory (Fig. 5.2). In terms of trends, N stocks of IFM plots (Fig. 5.14) show a marked increase between the first and second inventory (median: +28.0 kg N ha–1 year–1, iqr{−23.9; +79.4}, n = 36). The direction of this overall trend is opposite to the findings from NFSI plots, but the variability of all results from IFM plots is higher than on NFSI plots. However, the NFSI pattern of decreasing N stocks in the organic layer and increasing N stocks in the upper layers of the mineral soil is also reflected in the results from IFM plots (−4.5 kg ha–1 year–1, iqr{−24.7; +8.8}, n = 37 in the organic layer and +43.1 kg ha–1 year–1, iqr{−6.6; +71.3}, n = 47 in 0–30 cm).
Depth gradient of nitrogen stocks in the first and second inventory on the Intensive Forest Monitoring (IFM ) plots (a) and respective sums of nitrogen stocks for the soil profile from the organic layer down to 60 cm of the mineral soil (b). The annual change rates of nitrogen stocks (c and d) were calculated based on the paired sample of both inventories. Since layers 0–5 cm and 5–10 cm were not separately sampled on many plots, the sample size of these layers is lower than, e.g. of organic layer—60 cm
In contrast to NFSI findings, the N stocks in the lower layers of the mineral soil did only slightly change on IFM plots (+1.9 kg ha–1 year–1, iqr {−23.7; +40.9}, n = 46 in 30–60 cm and −1.2 kg N ha–1 year–1, iqr {−30.9; +24.9}, n = 21 in 60–90 cm).
Thus, while the two monitoring networks show different trends in total for organic layer—60 cm, they both indicate a marked difference between the increasing trend in the soil compartments above 30 cm and the negative or constant trend in the layers deeper than 30 cm of the mineral soil. The relevance and interpretation of this finding are further discussed in Sects. 5.5 and 5.6.
5.4.3 Nitrogen Balance Estimation
The additional measurement of nitrate concentration from soil water extracts within NFSI II allows for N balance estimations as an alternative approach to derive N stock change rates.
N budgets of forest ecosystems have been used to evaluate and quantify the effects of deposition and other impacts on forest soil dynamics (Korhonen et al. 2013; Meesenburg et al. 2016; Palviainen et al. 2017). Under the assumption that N fixation in most forest ecosystems is negligible (Posch et al. 2015), the calculation of N pool changes in the soil was simplified to:
with change of N pools in the soil (ΔS ) being based on N D (total N input by atmospheric deposition —wet + dry + occult), N E (gaseous emission of N2, N2O, and NO), N L (leaching of N below the rooting zone), and net N uptake of the vegetation (N nU, the balance of N gains due to root uptake from the soil and N losses due to litter fall and harvest residues remaining on the floor): The assumptions regarding the calculation of each term of the N balance are given in the following sections since they are not measured but modelled values.
5.4.3.1 Atmospheric Nitrogen Deposition
Long-term trends of N deposition were calculated following Thiele et al. (2017) with the model MAKEDEP (Alveteg et al. 1998). The model was run with grid -based estimates for Germany for the year 2009 (Schaap et al. 2015). We reconstructed N deposition before 2009 using the regional trend from the EMEP database (Tarrasón and Nyiri 2008) and standard time series from Alveteg et al. (1998) as published in Ahrends et al. (2010), Fleck et al. (2017), and Hauck et al. (2012). Reconstructed deposition was evaluated with measurements from Level II plots (Fig. 5.15).
Evaluation of reconstructed nitrogen deposition (open circle) against values calculated with a canopy budget model (Ulrich 4) from deposition measurement (filled square) of three ICP Forests Intensive Forest Monitoring plots in Germany: Augustendorf/Lower Saxony (left), Klötze/Saxony-Anhalt (centre), and Klingenthal/Saxony (right)
5.4.3.2 Gaseous Nitrogen Emissions
The gaseous emissions N E were considered as linearly related to net N input (de Vries et al. 1994):
with N nU for net removal of N in harvested trees, N I for long-term net immobilization of N in soil organic matter , and f E for the site-specific emission fraction (0 ≤ f E < 1). N E is thus considered a second-order process after immobilization and uptake needs are fulfilled. f E as a fraction based on soil drainage (Reinds et al. 2001) was approximated using clay content (C) (Ahrends et al. 2010; Murray et al. 2017) in an exponential function between the minimum for sandy soil (0.05; C = 0%) and the maximum for clay soils (0.7; C = 45%) (Rihm and Achermann 2016).
This approximation gets very close to published texture-specific classes (Park and Shim 2001; Reinds and De Vries 2010; Nagel and Gregor 1999). The basic function was supplemented by rules taking into account peat soils ( f E = 0.8; Rihm and Achermann 2016), depth to groundwater level, and stagnic soil conditions. N I was quantified after Nagel and Gregor (1999) being 1 kg ha–1 year–1 for most plots (Posch et al. 2015).
5.4.3.3 Nitrogen Leaching
Nitrogen leaching rates were estimated by multiplying the amount of annual seepage water with the mean nitrate concentration of the lowest soil layer. Plot-specific soil water fluxes were estimated with the physically based hydrological model LWF-BROOK90 (Version 3.4, Hammel and Kennel 2001). Nitrate concentration in seepage water (NO3seepage) was estimated from soil water extracts, assuming that leaching of ammonium (NH4 +) can be neglected in forest ecosystems due to its preferential uptake and complete nitrification within the root zone (Posch et al. 2015). Several authors confirm the possibility to empirically derive NO3seepage from soil water extracts, using regression approaches (Schlotter et al. 2012; Kohlpaintner et al. 2012; Evers et al. 2002; Ludwig et al. 1999). The applied methodologies, however, differ with respect to (1) the ratio between soil and water, (2) utilization of fresh or dried soil, (3) the facultative correction of nitrate concentrations measured in the soil water extract (NO3extract) to either the actual water content (m3 m–3) at the time of soil sampling (Θ) or the calculated water content at field capacity (ΘFC), and (4) the assumed functional relationship in the regression between NO3seepage and NO3extract. In the following, we describe the methods used to derive estimates of NO3seepage for the data presented here.
The method applied during NFSI II to measure NO3extract is to mix one mass part of dry soil with two mass parts of deionized water. The suspension is left for 24 h at room temperature and stirred frequently. After filtration NO3extract is analysed (GAFA 2009).
The statistical model used is based on water extracts from soil samples and direct measurements of NO3seepage in tight spatial and temporal proximity. The data was taken from Evers et al. (2002) comprising 10 plots from five federal states with 4 investigation points each and from 21 plots with 5 investigation points in Bavaria (Lutz 2015). Due to an elimination of extreme values, problems with seepage water sampling in dry soils, and lack of data, a total of 95 (85 with additional soil properties ) pairs of values was available for statistical modelling. The linear regression between NO3extract and NO3seepage yielded R 2 values between 0.39 and 0.51 (Table 5.3). Best results were obtained when NO3extract was corrected to Θ, closely followed by the correction to ΘFC, where field capacity was estimated from soil texture according to Ad-HocAG_Boden (2005). Model performance was enhanced by the consideration of additional soil properties . Significant impacts of soil bulk density , gravel content, and the content of sand, silt, and clay in the fine earth were identified using generalized additive models (GAM ) (Table 5.4).
The best performing GAM (Corr. ΘFC) was selected and replaced by a multilinear function to facilitate calculation (Equation 5.4), including the variables in their linear or quadratic form only in the case of significance (p < 0.001) and forcing the results through zero if negative:
with NO3extract for nitrate concentration in soil water extract corrected to water content at field capacity [mmolc l–1] and variables S, SI, and C for sand, silt, and clay content in fine earth [% mass]. The coefficients are a = 0.5911, b = 0.03252, c = −0.0001516, d = 0.000366, e = 0.000317, f = −1.702, and g = 0.3144.
The resulting model was applied to a set of validation data from Level II plots in Germany and two smaller studies in Baden Württemberg and Bavaria. As expected, due to the high spatial and temporal variability of nitrate concentrations in soil solution, the 85 pairs of values could not compete with the dataset used for model building. As a consequence the quality of statistical properties for validation was low (Table 5.5). However, the modelled values corresponded well to measurements with respect to magnitude and value distribution, especially if compared to the direct relationship between NO3extract and NO3seepage (Fig. 5.16). This correspondence was even preserved in double logarithmic display applied due to low nitrate concentrations in a large part of the seepage water samples.
Dispersion of measured values taken for model building (filled square) and for validation (open circle) around the 1:1-line in the relationships between NO3extract and NO3seepage (left), modelled (Eq. 5.4) and measured NO3seepage (centre), and modelled and measured NO3seepage in logarithmic display (right), NO3extract and NO3seepage in mmolc l–1
5.4.3.4 Net Nitrogen Uptake for Different Harvest Scenarios
For managed forest, the long-term average net N uptake of vegetation (NnU) is equal to the amount of N exported with harvested tree compartments and can be calculated by multiplying the average annual growth rate of the respective compartments with their element concentrations (Posch et al. 2015):
with k gr for the average annual growth rate (m3 ha–1 year–1), p for density (kg m–3), and ctN (kg kg–1) for N concentration in the compartments solid volume under bark, bark, and branches (subscripts sv, ba, and br, respectively). Dependent on the harvesting practice, the contribution of branches has to be included (whole-tree harvest) or not (stem only). Forest growth for each NFSI plot was estimated from a forest inventory in 2011–2012 using yield tables (Schober 1995) for the reconstruction up to 1990. Correction factors were applied to consider the higher growth rates due to environmental factors and mixed forests (Pretzsch 2016). The results were evaluated with growth data from the Third National Forest Inventory (BMEL 2016) for about 50,000 plots in Germany (Fig. 5.17).
Yearly increment of solid volume at the NFI3 plots (https://bwi.info; 77Z1Jl_L101of_2012) in the different federal states of Germany and the estimated yearly increment for the NFSI plots with modified yield tables for the period 2002–2012. Filled circle, values from the federal states of Germany; open circle, area weighed mean for Germany
The parameters for the biomass expansion factors, the density of the compartments, and the nitrogen concentration in biomass were taken from Ahner et al. (2013) and Jacobsen et al. (2002). As there is a great uncertainty regarding harvesting practice on NFSI plots and the representativeness of the long-term average for the shorter timescales relevant between NFSI I and II, we calculated N exports for both whole-tree and stem-only harvest, to consider and represent the high uncertainty in uptake estimations. It should be noted that tree stumps as harvest residues (Pretzsch 2009) were not included so that net N uptake of the vegetation may be slightly overestimated. As an approximation for realistic harvest exports, we used the averages between the two variants in the N balance .
5.4.3.5 Discussion of Estimated Balances
Figure 5.18 shows the nitrogen balance and the different components for the NFSI plots in Germany. The balance was calculated for three different harvesting practice scenarios: stem only (B min), whole tree without needles and leaves (B max), and the average of both (B).
Composition and fluxes from the nitrogen balance for forest ecosystems at German NFSI plots. D, deposition; E, emission; L, leaching ; U, net uptake of the vegetation ; B, balance; min, minimum harvest scenario (solid volume over bark); and max, maximum harvest scenario (whole tree harvesting without leaves and needles)
Between 1990 and 2007, the average annual N input for the NFSI plots by atmospheric deposition ranged from 10.6 to 40.7 kg ha–1 year–1 (median 19.7 kg ha–1 year–1), which is in good accordance to measured deposition rates for 57 Level II plots in Germany (Borken and Matzner 2004). The generally decreasing trend for nitrogen deposition during the investigated period (Fig. 5.1) is supported by other investigations (Waldner et al. 2014). One should note that the accurate quantification of total nitrogen deposition , especially for dry deposition, for forest ecosystems is very difficult and uncertain, because of the lack of measurements, species variability, and the different deposition processes and fluxes that need to be simplified on a landscape scale (compare Harrison et al. (2000)). Simpson et al. (2011) estimated an error of 30% for the different regional models and methods in Europe. The choice of a certain deposition method depends on the purpose of the study and the availability of throughfall measurements. Because the latter are not available for NFSI plots, we used the state-of-the-art modelling approach for critical load calculations in Germany (see also Schaap et al. 2017) in combination with a reconstruction procedure. The evaluation of the estimated trend in the calculated deposition data was done by throughfall measurement in combination with a canopy budget model.
The quantified gaseous N flux to the atmosphere ranged between 0 and 16.8 kg ha–1 year–1 (median 1.4 kg ha–1 year–1). The results are in good agreement with the range (0.2–2 kg ha–1 year–1 NO-N) given by Molina-Herrera et al. (2017). Upper values are mostly found for groundwater-affected plots or clear-cut stands (Dutch and Ineson 1990; Gundersen 1991; Tietema et al. 1991). For upland forest soils, typical rates are between 1 and 3 kg ha–1 year–1 (Dutch and Ineson 1990).
Sixty-one percent of all NFSI plots leached less than 5 kg ha–1 year–1 N with seepage water . The resulting median of 2.6 kg ha–1 year–1 matches with an earlier study covering 57 Level II plots in Germany (Borken and Matzner 2004). There, the leaching rates ranged between 0 and 26.5 kg ha–1 year–1 (median 1.4 kg ha–1 year–1). About 71% of all plots released less than 5 kg ha–1 year–1. Additional more recently evaluated data of the federal forest authorities using published reports on IFM plots (Barth et al. 2016; FAWF n.d.; Hammel and Kennel 2001; Hannemann et al. 2016; Karl et al. 2012; Klinck et al. 2012; Morgenstern 2015; Russ et al. 2017; Steinert and Feger 2010) confirm this range and median. Mellert et al. (2005) classified nitrate leaching rates for Bavarian forests with 66% showing values of 0–5 kg ha–1 year–1, 20% of 5–15 kg ha–1 year–1, and 14% higher than 15 kg ha–1 year–1. In comparison, our estimates for Bavaria were 79.3% (0–5 kg ha–1 year–1), 15.4% (5–15 kg N ha–1 year–1), and 5.3% (>15 kg ha–1 year–1). Kiese et al. (2011) estimated the nitrate leaching from German forest ecosystems by coupling Forest-DNDC to a GIS. Their results varied between 0 and 85 kg NO3-N ha–1 year–1 with an area-averaged mean of 5.5 kg ha–1 year–1. The higher N output is probably explained by the higher deposition rates used as input for the DNDC model based on values from Gauger et al. (2002) where problems with the nitrogen mass balance occurred in the applied version of the LOTOS-EUROS deposition model (Schaap et al. 2015).
The medians of net N uptake were between 6.6 kg ha–1 year–1 (scenario stem only) and 11.9 kg ha–1 year–1 (scenario whole tree without needles/leaves). Averaging both scenarios resulted in 8.7 kg ha–1 year–1 and thus on a similar scale as in other studies (Ahner et al. 2013; Korhonen et al. 2013; Meesenburg et al. 2005; Nagel and Gregor 1999; Rademacher et al. 2009).
Because of the high atmospheric N input, the median of the N balance was always positive for all harvest scenarios (B min: +7.0 kg ha–1 year–1, B: +4.8 kg ha–1 year–1, B max: +2.9 kg ha–1 year–1). Figure 5.19 shows the geographical distribution of the nitrogen balance for NFSI plots in Germany. Positive N balances are mainly found in the Bavarian Danube Plain, Upper Palatinate and Upper Franconia, the Ore Mountains, and nearly the whole North-German Lowland except Schleswig-Holstein. An accumulation of negative N balances is visible in the Black Forest and nearby mountain ranges, the Rhenish Slate Mountains, lower mountain ranges of North-Hesse, the Saarland, and Schleswig-Holstein.
In many regions, N stock decreases of the differential measurement approach are confirmed by the balance approach, and the federal statewise geographical distribution of change rates from differential N stock measurements on NFSI plots is rank correlated to the calculated balances (Spearman’s Rho = 0.8, n = 13, p < 0.005). A plotwise comparison of modelled (balances) and measured (N stock difference) changes in N stocks showed lower rank correlation (Spearman’s Rho = 0.21, n = 979, p < 10–10).
5.5 Discussion of Methods
Nitrogen measurements are a special case in NFSI, since their repeatability in ring tests was much lower than for most other parameters, especially when concentrations were low (compare Table 1.2). It is the goal of this discussion to better understand the sources of uncertainty for these data and to highlight their special properties in order to improve the conclusions that can be drawn on their basis.
5.5.1 Spatial Variability
Nitrogen stock is one of the parameters with highest small-scale spatial variability . Next to the distribution of fine roots and earthworm activity (Meier and Leuschner 2010; Andriuzzi et al. 2016), the spatial variability of litterfall , parent material , pH, and microclimate (Sabatini et al. 2015), the distribution of stagnant conditions on the plot (Bekele et al. 2013), and the presence of N fixing bacteria in the root system of a few tree species (Rodriguez et al. 2011) were identified as causes for this variability. Mellert et al. (2008) systematically investigated the variability of NFSI soil parameters on 33 Bavarian plots along a sampling grid of 3 m distance and discovered the least spatial autocorrelation in N stocks , while other parameters like pH or C/N ratio showed lower spatial variability on small scales. While Kirwan et al. (2005) recommend to sample N at least at 36 locations per plot, Mellert et al. (2008) require total N stock changes of 37% or more as precondition for a proof of N stock changes between NFSI I and NFSI II. This degree of change was by far not reached in the presented trend results.
The representativeness of the soil subsamples (see Sect. 1.17.3) put into analysis from the bulk samples is very important under high small-scaled variability, since also the bulk samples could be more spatially variable in this parameter than in others. This is especially valid for NFSI I, where only 0.01–0.07 g of soil material were used in C/N analysers to derive N concentration of the whole sample, while the newer devices during NFSI II could analyse 1 or 2 g at once .
5.5.2 Uncertainty from Analytical Errors
In the following, we compile the magnitude of potential errors in laboratory analyses in order to estimate the uncertainty of N stocks as the sum of uncertainties of the quantities participating in N stock calculation (JCGM 2008). Since N stocks are calculated as the product of N concentration and fine-earth stock , the uncertainty (Var) of both measurands was estimated as (IPCC 2013):
The uncertainty of bulk density estimates was not considered separately since they are included in the observed uncertainty of fine-earth stocks . Uncertainty of depth delineations and the partial derivatives of quantities measured to each other were assumed to be negligible in a first approximation.
For chemical analysis of N concentration, Var (repeatability) was estimated from the pooled intra-laboratory standard deviation of N analyses within the labs (ring-test results, compare Sect. 1.8), and Var (all means) was based on the inter-laboratory standard deviation.
The uncertainty of N concentrations of the NFSI I ring tests (König and Wolff 1993) summed to 0.033 mg g–1 or 12% of sample means. For NFSI II, the inter-laboratory ring tests (König et al. 2013) revealed an uncertainty of 0.027 mg g–1, equaling ca. 4% of the sample means.
Var (fine-earth stock ) was estimated based on Grüneberg et al. (2014). In their study, data from NFSI plots was used where fine-earth stocks were measured during both inventories. The fine-earth stock of NFSI I was on average 193 ± 35 t ha–1 higher than that of NFSI II. It was assumed that fine-earth stocks are constant between both inventories. Therefore the mean deviation plus the deviation (standard error) of the fine-earth stocks represents a certain degree of measurement inaccuracy of fine-earth stocks . This uncertainty amounted to 8% of the fine-earth stocks.
The reported relative uncertainties (percentage values) were used to calculate the uncertainties of the fine-earth stocks of each depth layer. The variance of the annual N stock changes was then summed up with inaccuracies of the measurement technique to obtain an estimate of the total uncertainty . The comparison of observed N stock differences in each layer with the total uncertainty of each layer resulted in all cases to non-significance, such that the observed N stock changes from differential measurements on NFSI plots must be considered scientifically non-significant tendencies, though statistical significance was shown (compare Wasserstein and Lazar 2016; Lemoine et al. 2016).
5.5.3 Treatment of Very Low Concentrations
Apart from the relative uncertainties given as percentages, absolute uncertainties were taken into account when judging the accuracy of N concentrations in the lowest soil layer (interquartile range 0.2–0.5 mg g–1, 60–90 cm). As the given limits of quantification for the different devices used during NFSI I were in a range up to 0.24 mg g–1, the 44% of measured values which were below or equal to this threshold were considered potentially inaccurate, especially with regard to the fact that potential measurement errors would always occur in positive direction under these circumstances, since negative values are not possible. The whole layer was excluded from trend calculation since the potential influence of measurement errors on the calculated stock differences was not negligible due to high fine-earth stocks (interquartile range 2–4.5 Gg ha–1) that could easily lead to distortions when calculating stock differences.
The relevance of such a distortion is difficult to verify in the final dataset of calculated N stocks ; however, there was a noticeable high proportion of exceptionally high N stocks observed especially in the data from deeper layers of NFSI I, which is reflected in the very high coefficients of skewness for these datasets (Table 5.6). While the high levels of N deposition preceding and during the NFSI I period might have caused elevated N concentrations also in deeper layers, such high coefficients of skewness have neither been observed in NFSI II nor in the inventories on IFM plots at both points in time. Coefficients of skewness were also regionally very diverse.
The numerous exceptionally high N stocks from deeper layers of NFSI I are the main cause for a number of plots with extreme changes in N stocks. As usual in other long-term investigations (Johnson et al. 2007; Kiser et al. 2009), some of these stored samples were subsampled with a sample divider and reanalysed with a C/N analyser in 2017. First analyses show that a part of the high N concentrations from NFSI I may be reproduced; however, it is unclear to what extent the re-analyses are influenced by storage conditions.
In NFSI I, also the layer 30–60 cm of the mineral soil shows a high relative proportion of exceptionally high N stocks (coefficient of skewness = 28.1). The measured N concentrations were higher than in 60–90 cm (interquartile range 0.3–0.9 mg g–1) and were, thus, in their majority expected to be less affected by the laboratory limit of quantification. However, since their influence is high in stock calculations (fine-earth stocks interquartile range: 2.2–4.3 Gg ha–1) and also other error sources may have contributed to the skewed distribution, only weighted median values of trends derived from this layer in NFSI I are presented, thereby reducing the influence of very high or low absolute numbers on the results. For better comparability, all results of the paired and the complete sample are presented as weighted medians.
5.5.4 Plot Selection Effects
Most methodological problems complicating the evaluation of temporal changes between the two NFSIs equally apply for NFSI plots and IFM plots and are not likely to be the cause for the apparently opposite direction of the trends derived from both networks and from balance calculations. Of course the number of IFM plots with two N stock inventories is much smaller than the number of NFSI plots, such that outliers have the potential to affect the overall pattern of temporal changes. While NFSI plots are systematically selected along a spatial grid , IFM plots were selected in order to represent the regionally typical forest types. May sample size and plot selection be the causes for an opposite direction of trends derived for the time between both NFSIs?
A bootstrap analysis was performed to investigate the plot selection effect. 100 million subsamples of NFSI plots (paired sample) were randomly chosen for each layer with a sample size identical to the corresponding number of IFM plots available. If IFM plots were just another selection of plots from the same population, there would probably also be plot combinations from the NFSI plots generating the same deviation to the whole NFSI result or an even larger deviation. The results are given in Table 5.7: For example, for the organic layer, the analysis revealed that an N stock decrease ≤ −4.5 kg ha–1 year–1 (the value measured on IFM plots) would also have been the outcome of 37.7% of all samples with the same sample size (n = 37) drawn from NFSI plots, showing that IFM plot results are not generally different from the results of NFSI in the organic layer. On the other hand, for the mineral soil between 0 and 30 cm depth, only 0.02% of the equal-sized subsamples of the NFSI plots would lead to an N stock increase ≥ +43.1 kg ha–1 year–1—here NFSI plots and IFM plots are generally different.
The bootstrap analysis shows that the IFM plot results of the first inventory could also have been derived from a reasonable number of combinations from NFSI plots. Especially in the upper part of the mineral soil and to a lesser extent in the other layers, IFM plots had in the first inventory N stocks typical for NFSI plots. In the second inventory, N stocks of layers deeper than 30 cm of the mineral soil and of the organic layer of IFM plots were again quite typical results for subsamples of the NFSI, but the upper 30 cm of the mineral soil had results that could hardly be generated based on NFSI plots: Only 1.1% of the random NFSI plot subsamples would produce such a result. Also the trends derived from the difference between first and second inventory may not be generated based on subsamples of the NFSI in 0–30 cm and in 30–60 cm of the mineral soil.
It may be concluded from this analysis that it is not just the low number of IFM plots that is responsible for the apparently opposite direction of their trend results: Some IFM plot results especially of the second inventory appear to be not from the same population as the results of NFSI plots. It may also be concluded that the initial plot selection is not the primary cause for the diverging results in terms of absolute N stocks , since the first inventory after plots were selected could reasonably be reproduced by subsamples of NFSI plots. Only with respect to the occurring change rates, the selected IFM plots are not comparable to the NFSI dataset.
Several alternative explanations for the different trend results from both networks are possible: (1) Since the inventories were not all performed in exactly the main year of NFSI I or NFSI II, it could be that N stock changes are more variable in time than expected, such that the results of both networks represent different stages of N stock development. Other long-term monitoring programmes on N stocks in forests also found subsequent N stock changes with reversed direction that were difficult to explain as a long-term development (Johnson et al. 2007; Johnson and Turner 2014; Kiser et al. 2009; Binkley et al. 2000). (2) The originally more typical state of N stocks on IFM plots may have changed after the first inventory due to their use as IFM plots. Most IFM plots are highly instrumented plots with less regular thinning, with the consequence that the stands are on average older than the mean age of NFSI plots and, thus, could accumulate more N in the soil during their lifetime. Many of the plots are fenced, which lowers bioturbation, browsing, and predation by larger mammals. (3) The small methodological differences between both networks may have contributed to the deviation in trend results. Differences exist, e.g. with regard to the number of soil samples taken in the forest, such that the high spatial variability of N stocks may better be accounted for by IFM plots. (4) No IFM plots with sufficient data are located in those areas in the southwest of Germany where predominantly negative change rates of soil N stocks have been observed. Thus, a systematic underrepresentation of geographic areas with negative change rates within the set of IFM plots contributes to the results from the bootstrapping approach.
Summarizing the methods discussion, it may not be excluded that the results of differential N stock measurements are subject to relevant over- or underestimations. Namely the measurements in deeper layers are influenced by the mentioned error sources, since the employed techniques especially in NFSI I operated close to their limit of quantification. However, they are the only representative benchmark values we can relate to from the 1990s, and there is no proof that would justify to discard them. It is of course important to take the uncertainties mentioned into account when drawing conclusions especially on long-term trends.
5.6 Summary and Conclusions
Nitrogen stocks in German forest soils are with 6.3 t ha–1 on the most frequently observed level in European forest soils (5–10 t ha–1, Fleck et al. 2016), which is considered a medium level according to the empirical rating for German forest soils (AK Standortskartierung 2016). This result was similarly observed in NFSI I and NFSI II and agrees in general terms with the measurements on IFM plots (Fig. 5.2).
More than 50% of N in forest soils is generally stored in the uppermost 30 cm of the mineral soil. The next 30 cm contains more than 20%, and roughly another 15% is stored in 60–90 cm depth of the mineral soil. The organic layer contains usually the remaining 10–15% of N in the whole soil profile up to 90 cm. This result is confirmed by NFSI I and NFSI II measurements as a representative result for Germany, and it is in the same order of magnitude also observed on the selected IFM plots.
A general property of N stocks in German forest soils is their high regional variability, which is visible in all evaluations (Figs. 5.3, 5.5, and 5.19). The observed pattern may largely be explained as the long-term impact of factors like tree species, parent material , soil acidification, annual mean temperature, and agricultural land use with the related N deposition . The depth gradient of N stocks observed on plots from the different tree species and parent materials is well explained by the decomposability approach of Berg (2014), whereby high C/N ratios in organic layer—5 cm indicate organic material with low initial decomposability (decomposition of cellulose), but high total decomposability (including the decomposition of lignin ), leading to high N stocks in the organic layer, but low N stocks in total for organic layer—60 cm. Low C/N ratios in turn were nearly always associated with low N stocks in the organic layer and high N stocks in organic layer—60 cm. These results demonstrate the central relevance of C/N ratios of the organic material provided for its decomposability in the soil.
A potential explanation for the relationship between C/N ratio and the depth gradient of N stocks may be found in the observation that C/N ratios initially decrease during decomposition due to N immobilization taking place in the first 9 months of decomposition (Hasegawa and Takeda 1996). Parton et al. (2007) also showed that immobilization during the first phases of decomposition is highest in litter with high C/N ratios (when microbial biomass growth is N limited) and very low when C/N ratios are small and microbial biomass growth is C limited. The effect of C/N ratios on microbial biomass growth and subsequent decomposition is, however, twofold: While an increase of microbial biomass reduces the amount of easily accessible particulate organic matter, it increases the amount of mineral-associated organic matter, which mainly originates from microbial necromass and exudates (Averill and Waring 2018).
The effect of soil pH on decomposition processes is visible from the liming effect on acid-sensitive plots, where N stocks in the organic layer decreased in the years between NFSI I and NFSI II, while N stocks increased in the mineral soil (0–30 cm): Apparently, this effect is independent from C/N ratios , since there was no direct effect on C/N ratios, while the directly stimulating effect of increased soil pH on microbial activity is known (Anderson and Domsch 1993). Increased decomposition of particulate organic matter by microbes in the organic layer may here again be associated with an increase of mineral-associated organic matter in the mineral soil, eventually enhanced by the decreasing influence of liming on soil pH with depth.
In the years between NFSI I and NFSI II, an N accumulation took place in organic layer—5 cm. More precisely, the N accumulation was concentrated in the uppermost 5 cm of the mineral soil, while there appeared to be a slight decrease of N stocks in the organic layer. This result is derived from differential N stock measurements on NFSI plots as well as on IFM plots. C/N ratios in organic layer—5 cm increased in the same time from a moderate level in NFSI I to a somewhat higher level in NFSI II. Such an increase of C/N ratios could be the first visible effect of the slowly decreasing N deposition rates, since uptake of N compounds into the organic layer is reduced with decreasing deposition. This interpretation is consistent with the fact that the formerly observed decrease of C/N ratios in the years around NFSI I had been attributed to the increasing N deposition rates at that time (Geissen and Brümmer 1999). The expected inhibitory effect of increasing C/N ratios on microbial biomass growth in the organic layer (low initial decomposability) did not occur and may have been overridden in this case by the increase of pH values in the organic layer (compare Chap. 4) associated with decreasing N deposition . Also the climatic changes in the period before each of the NFSIs may have contributed to higher organic matter decomposition by microbes in the organic layer: Increasing temperatures and the potentially increasing frequency of drought-rewetting cycles in the 10 years before sampling (compare Chap. 3) may yet in these years have led to accelerated decomposition and increased microbial activity, thereby decreasing the amount of particulate organic matter N in the organic layer and increasing the N stocks in mineral-associated organic matter in the upper mineral soil. A direct link between N deposition and C/N ratios appears to be likely also from the observed impact of agricultural land use .
While N accumulation in organic layer—5 cm may be derived from NFSI as well as IFM plots, increasing N stocks in the mineral soil above 30 cm depth and decreasing N stocks below this depth were only found on NFSI plots. IFM plots confirm the increase in the mineral soil above 30 cm, but yield constant N stocks in the layers below. However, a discrepancy in the change rates between mineral soil layers above and below 30 cm depth seems to be a common feature of both networks’ results on N stock change rates from differential N stock measurements. Regardless of the uncertainties associated with low concentration measurements in deeper layers, a potential explanation for such a discrepancy would most likely be connected to the acidifying effect of N deposition , which has been found to be independent of the effect of C/N ratios . After N (and S) deposition had slowly decreased, an increase of soil pH and base saturation was only observed in the uppermost layers (compare Chap. 4). This reduction of acidity together with climatic changes induced an increase of (micro-) biological activity, reducing the amount of stored N in the organic layer by decomposition, but increasing the amount of mineral-associated organic matter in the upper mineral soil, while the ongoing acidification in the deeper mineral soil of acid-sensitive plots would be expected to reduce microbial activity and potentially even the amount of N stored in this compartment.
The approaches to derive N stock changes between NFSI I and NFSI II show a diverse picture. While the modelled N balances lead to the expectation of on average increasing N stocks (+2.8 to +7.0 kg ha–1 year–1, depending on harvest scenario ), they also estimate N stock decreases for a substantial proportion of the sites, even if only a minimum amount of harvesting is assumed. The differential N stock measurement results from IFM plots, which partly follow the scenario of no harvest, indeed show a clear increase of N stocks , which is with +28.0 kg ha–1 year–1 even higher than the range given from modelled N balances. While N stocks on NFSI plots in organic layer—30 cm slightly increased (+6.2 kg ha–1 year–1), N stock decreases are reported for the deeper layers with their generally low N concentrations that turn the result for organic layer—60 cm to a median decrease of −8.2 kg ha–1 year–1. Since both NFSI and IFM plot results are outside the range given by N balance estimations, it may not be excluded that they are over- or underestimations. The representativeness of modelled N balances from NFSI plots is considered higher than their differential N stock measurements, since N stock differences of the latter, coined by the extremely high spatial and temporal variability of N concentrations in soil samples and resulting measurement uncertainties , were scientifically not significant.
Summarizing, the effect of decreasing N deposition rates yet appears to be visible as increasing C/N ratios and pH values (Chap. 4) in the organic layer, whereof the latter is partly achieved by liming and the reduction of S deposition and contributes to decreasing N stocks in the organic layer. Changes in climate , litter quality, and soil pH appear to be responsible for the observed shift of N stocks towards the upper mineral soil. The forest soils contain still a medium high amount of N stocks and further accumulate N, preferentially in the uppermost 30 cm of the mineral soil, while there are indications for large N stock decreases in the deeper layers of the mineral soil that are potentially influenced by continuing acidification in these layers. While no general increase of N in groundwater from forest catchments has been reported for Germany in the years between NFSI I and NFSI II (Sucker et al. 2011), the risk of such a development requires more intensive monitoring of processes in the deeper mineral soil. Modelling studies are needed especially on acid-sensitive forest sites to better predict the development of N-leaching under forest soils recovering from acidification. The data show, how vulnerable biological activity and N-storage in forest soils may be under changing conditions, and losses of N by leaching from forests need to be considered as a serious possibility. Further reductions of N deposition are, thus, still needed as a preventive measure for environmental protection.
References
Aber JD, Nadelhoffer KJ, Steudler P, Melillo JM (1989) Nitrogen saturation in northern forest ecosystems. BioScience 39(6):378–386
Aber JD, McDowell W, Nadelhoffer K, Magill A, Berntson G, Kamakea M, McNulty S, Currie W, Rustad L, Fernandez I (1998) Nitrogen saturation in temperate forest ecosystems—hypotheses revisited. BioScience 48(11):921–934. https://doi.org/10.2307/1313296
Ad-HocAG_Boden (ed) (2005) Bodenkundliche Kartieranleitung (KA 5), vol 5. Schweizerbart’sche Verlagsbuchhandlung, Stuttgart, Germany
Ahner J, Ahrends B, Engel F, Hansen J, Hentschel S, Hurling R, Meesenburg H, Mestermacher U, Meyer P, Möhring B, Nagel J, Nagel R, Pape B, Rohde M, Rumpf H, Schmidt M, Schmidt M, Spellmann H, Sutmöller J (2013) Waldentwicklungsszenarien für das Hessische Ried. Entscheidungsunterstützung vor dem Hintergrund sich beschleunigt ändernder Wasserhaushalts-und Klimabedingungen und den Anforderungen aus dem europäischen Schutzgebietssystem Natura 2000. Beiträge aus der Nordwestdeutschen Forstlichen Versuchsanstalt, vol 10. Nordwestdeutsche Forstliche Versuchsanstalt, Göttingen, Germany
Ahrends B, Meesenburg H, Döring C, Jansen M (2010) A spatio-temporal modelling approach for assessment of management effects in forest catchments. In: Status and perspectives of hydrology in small basins, IAHS Publ. 336, pp 32–37
AK Standortskartierung (2003) Forstliche Standortsaufnahme: Begriffe, Definitionen, Einteilungen, Kennzeichnungen, Erläuterungen, 6th edn. IHW-Verlag, Eiching near Munich, Germany
AK Standortskartierung (2016) Forstliche Standortsaufnahme: Begriffe, Definitionen, Einteilungen, Kennzeichnungen, Erläuterungen, 7th edn. IHW-Verlag, Eiching near Munich, Germany
Alveteg M, Walse C, Warfvinge P (1998) Reconstructing historic atmospheric deposition and nutrient uptake from present day values using MAKEDEP. Water Air Soil Pollut 104(3–4):269–283. https://doi.org/10.1023/a:1004958027188
Anderson T, Domsch K (1993) The metabolic quotient for CO2 (qCO2) as a specific activity parameter to assess the effects of environmental conditions, such as pH, on the microbial biomass of forest soils. Soil Biol Biochem 25:393–395
Andriuzzi WS, Ngo PT, Geisen S, Keith AM, Dumack K, Bolger T, Bonkowski M, Brussaard L, Faber JH, Chabbi A, Rumpel C, Schmidt O (2016) Organic matter composition and the protist and nematode communities around anecic earthworm burrows. Biol Fertil Soils 52(1):91–100. https://doi.org/10.1007/s00374-015-1056-6
Averill C, Waring B (2018) Nitrogen limitation of decomposition and decay: how can it occur? Global Change Biol 24:1417–1427
Barth N, Tannert R, Kurzer H-J, Kolber H, Andreae H, Haferkorn U, Rust M, Grunert M (2016) Stickstoffmonitoring sächsicher Böden. Landesamt für Umwelt, Landwirtschaft und Geologie, Dresden, Germany
Bedison JE, Johnson AH (2009) Controls on the spatial patterns of carbon and nitrogen in Adirondack forest soils along a gradient of nitrogen deposition. Soil Sci Soc Am J 73(6):2105–2117. https://doi.org/10.2136/sssaj2008.0336
Bekele A, Kellman L, Beltrami H (2013) Plot level spatial variability of soil organic carbon, nitrogen, and their stable isotopic compositions in temperate managed forest soils of Atlantic Canada. Soil Sci 178(8):400–416. https://doi.org/10.1097/ss.0000000000000003
Berg B (2014) Decomposition patterns for foliar litter—a theory for influencing factors. Soil Biol Biochem 78:222–232. https://doi.org/10.1016/j.soilbio.2014.08.005
Binkley D, Son Y, Valentine DW (2000) Do forests receive occult inputs of nitrogen? Ecosystems 3:321–331
BMEL (2016) Der Wald in Deutschland—Ausgewählte Ergebnisse der dritten Bundeswaldinventur, 2nd edn. Bundesministerium für Ernährung und Landwirtschaft (BMEL), Berlin, Germany
Borken W, Matzner E (2004) Nitrate leaching in forest soils: an analysis of long-term monitoring sites in Germany. J Plant Nutr Soil Sci 167(3):277–283. https://doi.org/10.1002/jpln.200421354
Borken W, Matzner E (2009) Reappraisal of drying and wetting effects on C and N mineralization and fluxes in soils. Global Change Biol 15(4):808–824. https://doi.org/10.1111/j.1365-2486.2008.01681.x
Cools N, Vesterdal L, de Vos B, Vanguelova E, Hansen K (2014) Tree species is the major factor explaining C:N ratios in European forest soils. Forest Ecol Manag 311:3–16. https://doi.org/10.1016/j.foreco.2013.06.047
Costanza R, d’Arge R, de Groot R, Farber S, Grasso M, Hannon B, Limburg K, Naeem S, O’Neill RV, Paruelo J, Raskin RG, Sutton P, van den Belt M (1997) The value of the world’s ecosystem services and natural capital. Nature 387(6630):253–260. https://doi.org/10.1038/387253a0
Czajkowski T, Ahrends B, Bolte A (2009) Critical limits of soil water availability (CL-SWA) for forest trees—an approach based on plant water status. Landbauforschung Volkenrode 59(2):87–93
de Vries W, Kros J, van der Salm C (1994) Long-term impacts of various emission deposition scenarios on Dutch forest soils. Water Air Soil Pollut 75:1–35
de Vries W, Dobbertin MH, Solberg S, Van Dobben HF, Schaub M (2014) Impacts of acid deposition, ozone exposure and weather conditions on forest ecosystems in Europe: an overview. Plant Soil 380(1–2):1–45
Dutch J, Ineson P (1990) Denitrification of an upland forest site. Forestry 63(4):363–377. https://doi.org/10.1093/forestry/63.4.363
Eickenscheidt N, Brumme R (2012) NOx and N2O fluxes in a nitrogen-enriched European spruce forest soil under experimental long-term reduction of nitrogen depositions. Atmos Environ 60:51–58
Eickenscheidt N, Brumme R, Veldkamp E (2011) Direct contribution of nitrogen deposition to nitrous oxide emissions in a temperate beech and spruce forest—a 15N tracer study. Biogeosciences 8:621–635
Ek H, Andersson S, Arnebrant K, Söderström B (1994) Growth and assimilation of NH4+ and NO3- by Paxillus involutus in association with Betula pendula and Picea abies as affected by substrate pH. New Phytol 128:629–637
Ellenberg H, Weber HE, Düll R, Wirth V, Werner W (2003) Zeigerwerte von Pflanzen in Mitteleuropa. Scripta Geobotanica XVIII, Datenbank. Erich Goltze Göttingen, Germany
Engardt M, Simpson D, Schwikowski M, Granat L (2017) Deposition of sulphur and nitrogen in Europe 1900-2050. Model calculations and comparison to historical observations. Tellus Ser B Chem Phys Meteorol 69(1):1328945. https://doi.org/10.1080/16000889.2017.1328945
Erisman J, Dammers E, van Damme M, Soudzilovskaia N, Schaap M (2015) Trends in EU nitrogen deposition and effects on ecosystems. Air Waste Manag Assoc Mag 65:31–35
Evers J, König N, Wolff B, Meiwes KJ (2002) Vorbereitung der Zweiten Bodenzustandserhebung im Wald (BZE II): Untersuchungen zur Laboranalytik, Stickstoffbestimmung und zeitlichen Variabilität bodenchemischer Parameter. Federal Ministry of Food, Agriculture and Consumer Protection, Northwest German Forest Research Institute, Bonn, Germany
Fagerli H, Aas W (2008) Trends of nitrogen in air and precipitation: model results and observations at EMEP sites in Europe, 1980-2003. Environ Pollut 154(3):448–461. https://doi.org/10.1016/j.envpol.2008.01.024
Fagerli H, Legrand M, Preunkert S, Vestreng V, Simpson D, Cerqueira M (2007) Modeling historical long-term trends of sulfate, ammonium, and elemental carbon over Europe: a comparison with ice core records in the Alps. J Geophys Res Atmos 112:D23. https://doi.org/10.1029/2006jd008044
FAWF (n.d.) Forschung an Dauerbeobachtungsflächen. http://www.fawf.wald-rlp.de/fileadmin/website/fawfseiten/fawf/FUM/index.htm?umweltmonitoring/DBFL/forschung.html. Accessed 12/15/2017
Fleck S, Cools N, Vos BD, Meesenburg H, Fischer R (2016) The Level II aggregated forest soil condition database links soil physicochemical and hydraulic properties with long-term observations of forest condition in Europe. Ann Forest Sci 73(4):945–957. https://doi.org/10.1007/s13595-016-0571-4
Fleck S, Ahrends B, Sutmöller J, Albert M, Evers J, Meesenburg H (2017) Is biomass accumulation in forests an option to prevent climate change induced increases in nitrate concentrations in the North German Lowland? Forests 8(6):219
Förster A, Becker T, Gerlach A, Meesenburg H, Leuschner C (2017) Long-term change in understorey plant communities of conventionally managed temperate deciduous forests: effects of nitrogen deposition and forest management. J Veg Sci 28(4):747–761. https://doi.org/10.1111/jvs.12537
GAFA (ed) (2009) Handbuch Forstliche Analytik (HFA). Grundwerk und 1. - 4. Ergänzung des Gutachterausschuss Forstliche Analytik (GAFA). Bundesministerium für Verbraucherschutz, Ernährung und Landwirtschaft, Bonn, Germany
Gauer J, Kroiher F (2012) Waldökologische Naturräume Deutschlands—Forstliche Wuchsgebiete und Wuchsbezirke—Digitale Topographische Grundlagen—Neubearbeitung Stand 2011. Landbauforschung vTI Agriculture and Forestry Research, Braunschweig, Germany
Gauger T, Anshelm F, Schuster H, Draaijers GPJ, Bleeker A, Erisman JW, Vermeulen AT, Nagel H-D (2002) Kartierung ökosystembezogener Langzeittrends atmosphärischer Stoffeinträge und Luftschadstoffkonzentrationen in Deutschland und deren Vergleich mit Critical Loads und Critical Levels. Forschungsvorhaben im Auftrag des BMU/UBA. Institut für Navigation, Universität Stuttgart, Stuttgart
Geissen V, Brümmer GW (1999) Decomposition rates and feeding activities of soil fauna in deciduous forest soils in relation to soil chemical parameters following liming and fertilization. Biol Fertil Soils 29:335–342
Grüneberg E, Ziche D, Wellbrock N (2014) Organic carbon stocks and sequestration rates of forest soils in Germany. Global Change Biol 20(8):2644–2662. https://doi.org/10.1111/gcb.12558
Gundersen P (1991) Nitrogen deposition and the forest nitrogen cycle—role of denitrification. Forest Ecol Manag 44(1):15–28. https://doi.org/10.1016/0378-1127(91)90194-z
Hammel K, Kennel M (2001) Charakterisierung und Analyse der Wasserverfügbarkeit und des Wasserhaushalts von Waldstandorten in Bayern mit dem Simulationsmodell BROOK90. Forstliche Forschungsberichte München, vol 185. Technische Uni München Wissenschaftszentrum Weihenstephan, Munich, Germany
Hannemann J, Russ A, Kallweit R, Riek W (2016) Betrachtungen zu den Stoffbilanzen von Level II-Flächen in Brandenburg. In: Ministerium für Ländliche Entwicklung Umwelt und Landwirtschaft des Landes Brandenburg (ed) 30 Jahre Forstliches Umweltmonitoring in Brandenburg. Eberswalder Forstliche Schriftenreihe. LFE, Eberswalde, Germany
Harrison A, Schulze E-D, Gebauer G, Bruckner G (2000) Canopy uptake and utilization of atmospheric pollutant nitrogen. In: Carbon and nitrogen cycling in European forest ecosystems. Springer, Berlin, pp 171–188
Hasegawa M, Takeda H (1996) Carbon and nutrient dynamics in decomposing pine-needle litter in relation to fungal and faunal abundances. Pedobiologia 40:171–184
Hauck M, Zimmermann J, Jacob M, Dulamsuren C, Bade C, Ahrends B, Leuschner C (2012) Rapid recovery of stem increment in Norway spruce at reduced SO2 levels in the Harz Mountains, Germany. Environ Pollut 164:132–141. https://doi.org/10.1016/j.envpol.2012.01.026
Homan C, Beier C, McCay T, Lawrence G (2016) Application of lime (CaCO3) to promote forest recovery from severe acidification increases potential for earthworm invasion. Forest Ecol Manag 368:39–44. https://doi.org/10.1016/j.foreco.2016.03.002
IPCC (2013) Good practice guidance for land use, land-use change and forestry. Institute for Global Environmental Strategies for the Intergovernmental Panel on Climate Change (IPCC), Hayama, Japan
Jacobsen C, Rademacher P, Meesenburg H, Meiwes K (2002) Gehalte chemischer Elemente in Baumkompartimenten—Literaturstudie und Datensammlung. Berichte des Forschungszentrums Waldökosysteme. Niedersächsische Forstliche Versuchsanstalt Göttingen, Göttingen, Germany
Jansen M, Chodak M, Saborowski J, Beese F (2005) Determination of humus stocks and qualities of forest floors in pure and mixed stands of spruce and beech (Erfassung von Humusmengen und -qualitaten in organischen Auflagen in Rein- und Mischbestanden von Buchen und Fichten unterschiedlichen Alters). Allgemeine Forst- und Jagdzeitung 176(9/10):176–186
JCGM (2008) Evaluation of measurement data—guide to the expression of uncertainty in measurement
Johnson DW, Turner J (2014) Nitrogen budgets of forest ecosystems: a review. Forest Ecol Manag 318:370–379
Johnson DW, Todd DE Jr, Trettin CF, Sedinger JS (2007) Soil carbon and nitrogen changes in forests of walker branch watershed, 1972 to 2004. Soil Sci Soc Am J 71(5):1639–1646. https://doi.org/10.2136/sssaj2006.0365
Karl S, Block J, Schüler G, Schultze B, Scherzer J (2012) Wasserhaushaltsuntersuchungen im Rahmen des forstlichen Umweltmonitorings und bei waldbaulichen Versuchen in Rheinland-Pfalz. Mitteilungen aus der Forschungsanstalt für Waldökologie und Forstwirtschaft Rheinland-Pfalz (FAWF), vol 71/12. Trippstadt, Germany
Kiese R, Heinzeller C, Werner C, Wochele S, Grote R, Butterbach-Bahl K (2011) Quantification of nitrate leaching from German forest ecosystems by use of a process oriented biogeochemical model. Environ Pollut 159(11):3204–3214. https://doi.org/10.1016/j.envpol.2011.05.004
Kirwan N, Oliver MA, Moffat AJ, Morgan GW (2005) Sampling the soil in long-term forest plots: the implications of spatial variation. Environ Monit Assess 111(1–3):149–172. https://doi.org/10.1007/s10661-005-8219-0
Kiser LC, Kelly JM, Mays PA (2009) Changes in forest soil carbon and nitrogen after a thirty-year interval. Soil Sci Soc Am J 73(2):647–653. https://doi.org/10.2136/sssaj2008.0102
Klinck U, Rademacher P, Scheler B, Wagner M, Fleck S, Ahrends B, Meesenburg H (2012) Ökosystembilanzen auf forstwirtschaftlich genutzten Flächen. In: Höper H, Meesenburg H (eds) GeoBerichte 23—Tagungsband 20 Jahre Bodendauerbeobachtung in Niedersachsen. Landesamt für Bergbau, Energie und Geologie, Hannover, Germany, pp 163–174
Kohlpaintner M, Huber C, Göttlein A (2012) Improving the precision of estimating nitrate (NO3 -) concentration in seepage water of forests by prestratification with soil samples. Eur J Forest Res 131(5):1399–1409. https://doi.org/10.1007/s10342-012-0606-9
König N, Wolff B (1993) Abschlussbericht über die Ergebnisse und Konsequenzen der im Rahmen der bundesweiten Bodenzustandserhebung im Wald (BZE) durchgeführten Ringanalysen. Reports of the Research Centre for Forest Ecosystems/Forest Decline—Series B. Göttingen University, Göttingen, Germany
König N, Schönfelder E, Blum U (2013) Auswertung der Standardmessungen und der Ringversuche im Rahmen der BZE II. Federal Ministry of Food, Agriculture and Consumer Protection, Berlin, Germany
Korhonen JFJ, Pihlatie M, Pumpanen J, Aaltonen H, Hari P, Levula J, Kieloaho AJ, Nikinmaa E, Vesala T, Ilvesniemi H (2013) Nitrogen balance of a boreal Scots pine forest. Biogeosciences 10(2):1083–1095. https://doi.org/10.5194/bg-10-1083-2013
Krupa SV (2003) Effects of atmospheric ammonia (NH3) on terrestrial vegetation: a review. Environ Pollut 124(2):179–221. https://doi.org/10.1016/s0269-7491(02)00434-7
Larcher W (2001) Ökophysiologie der Pflanzen, 6th edn. Ulmer, Stuttgart
Lemoine NP, Hoffman A, Felton AJ, Baur L, Chaves F, Gray J, Yu Q, Smith MD (2016) Underappreciated problems of low replication in ecological field studies. Ecology 97(10):2554–2561
Lovett GM, Goodale CL (2011) A new conceptual model of nitrogen saturation based on experimental nitrogen addition to an oak forest. Ecosystems 14(4):615–631. https://doi.org/10.1007/s10021-011-9432-z
Ludwig B, Meiwes KJ, Khanna P, Gehlen R, Fortmann H, Hildebrand EE (1999) Comparison of different laboratory methods with lysimetry for soil solution composition—experimental and model results. J Plant Nutr Soil Sci 162(3):343–351. https://doi.org/10.1002/(sici)1522-2624(199906)162:3<343::aid-jpln343>3.0.co;2-e
Lutz F (2015) Methodenvergleich zur Ableitung der Ionenkonzentrationen im Sickerwasser aus Analysen der Bodenfestphase. Technische Universität München, München
Meesenburg H, Mohr K, Dämmgen U, Schaaf S, Meiwes KJ, Horváth B (2005) Stickstoff-Einträge und -Bilanzen in den Wäldern des ANSWER-Projektes—Eine Synthese. Landbauforschung Völkenrode 279:95–108
Meesenburg H, Ahrends B, Fleck S, Wagner M, Fortmann H, Scheler B, Klinck U, Dammann I, Eichhorn J, Mindrup M (2016) Long-term changes of ecosystem services at Solling, Germany: recovery from acidification, but increasing nitrogen saturation? Ecol Indicat 65:103–112
Meier IC, Leuschner C (2010) Variation of soil and biomass carbon pools in beech forests across a precipitation gradient. Global Change Biol 16(3):1035–1045. https://doi.org/10.1111/j.1365-2486.2009.02074.x
Mellert KH, Gensior A, Kolling C (2005) Nitrogen saturation in Bavarian forests—results of the nitrate inventory (Stickstoffsättigung in den Wäldern Bayerns—Ergebnisse der Nitratinventur.). Forstarchiv 76(2):35–43
Mellert KH, Kölling C, Rücker G, Schubert A (2008) Kleinräumige Variabilität von Waldboden-Dauerbeobachtungsflächen in Bayern—Ein Beitrag zur Unsicherheitsabschätzung der BZE II. Waldökologie, Landschaftsforschung und Naturschutz 6:43–61
Molina-Herrera S, Haas E, Grote R, Kiese R, Klatt S, Kraus D, Kampffmeyer T, Friedrich R, Andreae H, Loubet B, Ammann C, Horvath L, Larsen K, Gruening C, Frumau A, Butterbach-Bahl K (2017) Importance of soil NO emissions for the total atmospheric NOX budget of Saxony, Germany. Atmos Environ 152:61–76. https://doi.org/10.1016/j.atmosenv.2016.12.022
Morgenstern Y (2015) Wasserhaushaltsmodellierung der Intensivmessstellen Level-II unter Buche und Fichte mit dem 1D-Standortsmodell LWF-Brook90. FVA Freiburg, Freiburg
Murray CA, Whitfield CJ, Watmough SA (2017) Uncertainty-based terrestrial critical loads of nutrient nitrogen in northern Saskatchewan, Canada. Boreal Environ Res 22:231–244
Nagel H-D, Gregor H-D (1999) Ökologische Belastungsgrenzen—Critical Loads & Levels. Ein internationales Konzept für die Luftreinhaltepolitik. Springer, Berlin
Oulehle F, Cosby BJ, Austnes K, Evans CD, Hruska J, Kopacek J, Moldan F, Wright RF (2015) Modelling inorganic nitrogen in runoff: seasonal dynamics at four European catchments as simulated by the MAGIC model. Sci Total Environ 536:1019–1028. https://doi.org/10.1016/j.scitotenv.2015.05.047
Palviainen M, Pumpanen J, Berninger F, Ritala K, Duan B, Heinonsalo J, Sun H, Koster E, Koster K (2017) Nitrogen balance along a northern boreal forest fire chronosequence. PLoS One 12(3):e0174720. https://doi.org/10.1371/journal.pone.0174720
Park S-U, Shim JM (2001) Estimation of critical loads of sulfur and nitrogen for the Korean ecosystem. Int J Soc Mater Eng Resour 10(2):121–129
Parton W, Silver WL, Burke IC, Grassens L, Harmon ME, Currie WS, King JY, Adair EC, Brandt LA, Hart SC, Fasth B (2007) Global-scale similarities in nitrogen release patterns during long-term decomposition. Science 315(5810):361–364
Posch M, de Vries W, Sverdrup HU (2015) Mass balance models to derive critical loads of nitrogen and acidity for terrestrial and aquatic ecosystems. In: de Vries W, Hettelingh JP, Posch M (eds) Critical loads and dynamic risk assessments: nitrogen, acidity and metals in terrestrial and aquatic ecosystems. Environmental pollution, vol 25. Springer, Dordrecht, pp 171–205. https://doi.org/10.1007/978-94-017-9508-1_6
Preston CM, Nault JR, Trofymow JA, Smyth C, Cidet Working Group (2009) Chemical changes during 6 years of decomposition of 11 litters in some Canadian forest sites. Part 1. Elemental composition, tannins, phenolics, and proximate fractions. Ecosystems 12(7):1053–1077. https://doi.org/10.1007/s10021-009-9266-0
Pretzsch H (2009) Forest dynamics, growth and yield: from measurement to model. Springer, Berlin
Pretzsch H (2016) Ertragstafel-Korrekturfaktoren für Umwelt- und Mischungseffekte. AFZ-Der Wald 14:47–50
Rademacher P, Khanna PK, Eichhorn J, Guericke M (2009) Tree growth, biomass, and elements in tree components of three beech sites. In: Brumme R, Khanna PK (eds) Functioning and management of European beech ecosystems. Ecological studies, vol 208. Springer, Berlin, pp 105–136
Reinds GJ, De Vries W (2010) Uncertainties in critical loads and target loads of sulphur and nitrogen for European forests: analysis and quantification. Sci Total Environ 408(8):1960–1970. https://doi.org/10.1016/j.scitotenv.2009.12.001
Reinds GJ, Posch M, de Vries W (2001) A semi-empirical dynamic soil acidification model for use in spatially explicit integrated assessment models for Europe. Alterra Report. Alterra Green World Research, Wageningen, Netherlands
Riek W, Russ A, Hannemann J, Kallweit R (2016) Bodenzustand und Baumernährung: Kennwerte aus BZE und Level II-Programm. In: 30 Jahre forstliches Umweltmonitoring in Brandenburg. Eberswalder Forstliche Schriftenreihe, vol 63. Ministerium für Ländliche Entwicklung Umwelt und Landwirtschaft des Landes Brandenburg, Eberswalde, Germany, pp 40–60
Rihm B, Achermann B (2016) Critical loads of nitrogen and their exceedances. Swiss contribution to the effects-oriented work under the Convention on Long-range Transboundary Air Pollution (UNECE). Environmental Studies. Federal Office for the Environment, Bern, Switzerland
Rodriguez A, Duran J, Covelo F, Fernandez-Palacios JM, Gallardo A (2011) Spatial pattern and variability in soil N and P availability under the influence of two dominant species in a pine forest. Plant Soil 345(1–2):211–221. https://doi.org/10.1007/s11104-011-0772-4
Rohmann U, Sontheimer H (1985) Nitrat im Grundwasser. Ursachen - Bedeutung - Lösungswege. DVGW-Forschungsstelle am Engler-Bunte-Institut der Universität Karlsruhe, Karlsruhe, Germany
Russ A, Riek W, Martin J (2017) Forstliches Umweltmonitoring Mecklenburg-Vorpommern—Ergebnisse der Untersuchungen auf den Intensivmonitoringflächen (Level II). Mitteilungen aus dem Forstlichen Versuchswesen Mecklenburg-Vorpommern. Landesforst Mecklenburg-Vorpommern (AöR), Schwerin, Germany
Sabatini FM, Zanini M, Dowgiallo G, Burrascano S (2015) Multiscale heterogeneity of topsoil properties in southern European old-growth forests. Eur J Forest Res 134(5):911–925. https://doi.org/10.1007/s10342-015-0899-6
Schaap M, Wichink Kruit R, Hendriks C, Kranenburg R, Segers A, Builtjes P, Banzhaf S, Scheuschner T (2015) Atmospheric deposition to German natural and semi-natural ecosystems during 2009. Interim Report to UFOPLAN Project 3712 63 240-1—1st PINETI Federal Environment Agency (UBA), Dessau-Roßlau, Germany
Schaap M, Banzhaf S, Scheuschner T, Geupel M, Hendriks C, Kranenburg R, Nagel H-D, Segers AJ, von Schlutow A, Wichink Kruit R, Builtjes PJH (2017) Atmospheric nitrogen deposition to terrestrial ecosystems across Germany, Biogeosciences Discuss. Dessau-Roßlau, Germany. https://doi.org/10.5194/bg-2017-491
Schlotter D, Schack-Kirchner H, Hildebrand EE, von Wilpert K (2012) Equivalence or complementarity of soil-solution extraction methods. J Plant Nutr Soil Sci 175(2):236–244. https://doi.org/10.1002/jpln.201000399
Schober R (1995) Ertragstafeln wichtiger Baumarten bei verschiedener Durchforstung. 4th edn. Sauerländer, Frankfurt a. M.
Simpson D, Aas W, Bartnicki J, Berge H, Bleeker A, Cuvelier K, Dentener F, Dore T, Erisman JW, Fagerli H (2011) Atmospheric transport and deposition of reactive nitrogen in Europe
Spiecker H, Mielikäinen K, Köhl M, Skovsgaard JP (1996) Growth trends in European forests: studies from 12 countries. Springer, Berlin
Steinert M, Feger KH (2010) Modellierung und Interpretation des Wasser- und Stoffhaushaltes für die Thüringer Hauptmessstationen Großer Eisenberg, Holzland, Possen und Lehesten. Dresden Technical University, Department for Soil Science and Site Ecology, Dresden, Germany
Strengbom J, Nordin A (2008) Commercial forest fertilization causes long-term residual effects in ground vegetation of boreal forests. Forest Ecol Manag 256(12):2175–2181. https://doi.org/10.1016/j.foreco.2008.08.009
Sucker C, von Wilpert K, Puhlmann H (2011) Acidification reversal in low mountain range streams of Germany. Environ Monit Assess 174(1–4):65–89. https://doi.org/10.1007/s10661-010-1758-z
Talkner U, Meiwes KJ, Potocic N, Seletkovic I, Cools N, De Vos B, Rautio P (2015) Phosphorus nutrition of beech (Fagus sylvatica L.) is decreasing in Europe. Ann Forest Sci 72(7):919–928. https://doi.org/10.1007/s13595-015-0459-8
Tarrasón L, Nyiri Á (2008) Transboundary acidification, eutrophication and ground level ozone in Europe in 2006. EMEP status report. The Meteorological Institute, Oslo, Norway
Thiele JC, Nuske RS, Ahrends B, Panferov O, Albert M, Staupendahl K, Junghans U, Jansen M, Saborowski J (2017) Climate change impact assessment—a simulation experiment with Norway spruce for a forest district in Central Europe. Ecol Model 346(2017):30–47
Tietema A, Bouten W, Wartenbergh PE (1991) Nitrous oxide dynamics in an oak beech forest ecosystem in the Netherlands. Forest Ecol Manag 44(1):53–61. https://doi.org/10.1016/0378-1127(91)90197-4
Ulrich B (1994) Nutrient and acid-base budget of central european forest ecosystems. In: Godbold D, Hüttermann A (eds) Effects of acid rain on forest processes. Wiley-Liss, New York, pp 1–50
UNECE ICP Forests Programme Co-ordinating Centre (2016) Manual on methods and criteria for harmonized sampling, assessment, monitoring and analysis of the effects of air pollution on forests. Eberswalde, Germany
Vesterdal L, Schmidt IK, Callesen I, Nilsson LO, Gundersen P (2008) Carbon and nitrogen in forest floor and mineral soil under six common European tree species. Forest Ecol Manag 255(1):35–48. https://doi.org/10.1016/j.foreco.2007.08.015
Vitousek PM, Aber JD, Howarth RW, Likens GE, Matson PA, Schindler DW, Schlesinger WH, Tilman D (1997) Human alteration of the global nitrogen cycle: sources and consequences. Ecol Appl 7(3):737–750. https://doi.org/10.2307/2269431
Waldner P, Marchetto A, Thimonier A, Schmitt M, Rogora M, Granke O, Mues V, Hansen K, Karlsson GP, Zlindra D, Clarke N, Verstraeten A, Lazdins A, Schimming C, Iacoban C, Lindroos AJ, Vanguelova E, Benham S, Meesenburg H, Nicolas M, Kowalska A, Apuhtin V, Napa U, Lachmanova Z, Kristoefel F, Bleeker A, Ingerslev M, Vesterdal L, Molina J, Fischer U, Seidling W, Jonard M, O’Dea P, Johnson J, Fischer R, Lorenz M (2014) Detection of temporal trends in atmospheric deposition of inorganic nitrogen and sulphate to forests in Europe. Atmos Environ 95:363–374. https://doi.org/10.1016/j.atmosenv.2014.06.054
Ward MH, deKok TM, Levallois P, Brender J, Gulis G, Nolan BT, VanDerslice J (2005) Workgroup report: drinking-water nitrate and health - recent findings and research needs. Environ Health Perspect 113(11):1607–1614. https://doi.org/10.1289/ehp.8043
Wasserstein RL, Lazar N (2016) The ASA’s statement on p-values: context, process, and purpose. Am Statistician 70(2):129–133
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Fleck, S. et al. (2019). Nitrogen Status and Dynamics in German Forest Soils. In: Wellbrock, N., Bolte, A. (eds) Status and Dynamics of Forests in Germany . Ecological Studies, vol 237. Springer, Cham. https://doi.org/10.1007/978-3-030-15734-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-15734-0_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-15732-6
Online ISBN: 978-3-030-15734-0
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)