Abstract
Combining hierarchical watersheds has proven to be a good alternative method to outperform individual hierarchical watersheds. Consequently, this raises the question of whether the resulting combinations are hierarchical watersheds themselves. Since the naive algorithm to answer this question has a factorial time complexity, we propose a new characterization of hierarchical watersheds which leads to a quasi-linear time algorithm to determine if a hierarchy is a hierarchical watershed.
This research is partly funded by the Bézout Labex, funded by ANR, reference ANR-10-LABX-58.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Hierarchical watersheds [2, 5, 10, 13] are hierarchies of partitions obtained from an initial watershed segmentation [3, 4]. They can be represented thanks to their saliency maps [1, 6, 13]. Departing from the watershed segmentation of an image, hierarchical watersheds are constructed by merging the regions of this initial segmentation according to regional attributes. As shown in [14], the performance of hierarchical watersheds is competitive compared to other hierarchical segmentation methods while being fast to compute.
Despite their good global performance, hierarchical watersheds based on a single regional attribute can fail at merging the adequate regions at all levels of the hierarchy. This problem is illustrated in Fig. 1, where we present the saliency maps of two hierarchical watersheds based on area [11] and dynamics [13], and two segmentation levels extracted from each hierarchy. In this representation of saliency maps, the darkest contours are the ones that persist at the highest levels of the hierarchies. From the saliency map of the hierarchical watershed based on area shown in Fig. 1, we can see that the sky region is oversegmented at high levels of this hierarchy. On the other hand, the beach is oversegmented at high levels of the hierarchy based on dynamics. To counter this problem, a method to combine hierarchical watersheds has been proposed and evaluated in [6, 9]. As illustrated in Fig. 1, the combination of hierarchical watersheds can provide better segmentations than their individual counterparts.
Combining hierarchical watersheds raises the question whether the hierarchies resulting from combinations are hierarchical watersheds themselves. If so, then there might be an attribute A such that the combinations of hierarchical watersheds are precisely the hierarchical watersheds based on A. Therefore, we could simply compute hierarchical watersheds based on A, which is more efficient than combining hierarchies. Otherwise, it follows that the range of combinations of hierarchical watersheds is larger than the domain of hierarchical watersheds, which is an invitation for studying this new category of hierarchies. More generally, combining hierarchical watersheds raises the problem of recognizing hierarchical watersheds: given a hierarchy \(\mathcal {H}\), decide if \(\mathcal {H}\) is a hierarchical watershed.
The contributions of this article are twofold: (1) a new characterization of hierarchical watersheds; and (2) a quasi-linear time algorithm for solving the problem of recognizing hierarchical watersheds. Therefore, we have an efficient algorithm to determine if a given combination of hierarchical watersheds is a hierarchical watershed. It is noteworthy that the naive approach to recognize hierarchical watersheds has a factorial time complexity, which is explained later.
This article is organized as follows. In Sect. 2, we review basic notions on graphs, hierarchies and saliency maps. In Sect. 3, we formally state the problem of recognizing hierarchical watersheds, we introduce a characterization of hierarchical watersheds, and we present our quasi-linear time algorithm to recognize hierarchical watersheds.
2 Background Notions
In this section, we first introduce hierarchies of partitions. Then, we review the definition of graphs, connected hierarchies and saliency maps. Subsequently, we define hierarchical watersheds.
2.1 Hierarchies of Partitions
Let V be a set. A partition of V is a set \(\mathbf P \) of non empty disjoint subsets of V whose union is V. If \(\mathbf P \) is a partition of V, any element of \(\mathbf P \) is called a region of \(\mathbf P \). Let V be a set and let \(\mathbf P _1\) and \(\mathbf P _2\) be two partitions of V. We say that \(\mathbf P _1\) is a refinement of \(\mathbf P _2\) if every element of \(\mathbf P _1\) is included in an element of \(\mathbf P _2\). A hierarchy (of partitions on V) is a sequence \(\mathcal {H}=(\mathbf P _0, \dots , \mathbf P _n)\) of partitions of V such that \(\mathbf P _{i-1}\) is a refinement of \(\mathbf P _{i}\), for any \(i \in \{1, \dots , n\}\) and such that \(\mathbf P _n = \{V\}\). For any i in \(\{0, \dots , n\}\), any region of the partition \(\varvec{P}_i\) is called a region of \(\mathcal {H}\). The set of all regions of \(\mathcal {H}\) is denoted by \(\mathscr {R}(\mathcal {H})\).
Hierarchies of partitions can be represented as trees whose nodes correspond to regions, as shown in Fig. 2(a). Given a hierarchy \(\mathcal {H}\) and two regions X and Y of \(\mathcal {H}\), we say that X is a parent of Y (or that Y is a child of X) if \(Y \subset X\) and X is minimal for this property. In other words, if X is a parent of Y and if there is a region Z such that \(Y \subseteq Z \subset X\), then \(Y=Z\).
In Fig. 2(a), the regions of the hierarchy \(\mathcal {H}\) are linked to their parents (and to their children) by straight lines. It can be seen that any region X of \(\mathcal {H}\) such that \(X \ne V\) has exactly one parent. Thus, for any region X such that \(X \ne V\), we write \(parent(X)=Y\) where Y is the unique parent of X. For any region R of \(\mathcal {H}\), if R is not the parent of any region of \(\mathcal {H}\), we say that R is a leaf region of \(\mathcal {H}\). Otherwise, we say that R is a non-leaf region of \(\mathcal {H}\). The set of all non-leaf regions of \(\mathcal {H}\) is denoted by \(\mathscr {R}^*(\mathcal {H})\).
In the hierarchy of Fig. 2(a), we have \(parent(M_{1})=parent(M_{2})=X_{5}\). The set of non-leaf regions of \(\mathcal {H}\) is \(\mathscr {R}^*=\{X_1, X_2, X_3, X_4, X_{5}, X_{6}, X_{7}\}\).
2.2 Graphs, Connected Hierarchies and Saliency Maps
A graph is a pair \(G=(V, E)\), where V is a finite set and E is a set of pairs of distinct elements of V, i.e., \(E \subseteq \{\{x,y\} \subseteq V | x \ne y\}\). Each element of V is called a vertex (of G), and each element of E is called an edge (of G). To simplify the notations, the set of vertices and edges of a graph G will be also denoted by V(G) and E(G), respectively.
Let \(G= (V,E)\) be a graph and let X be a subset of V. A sequence \(\pi =( x_0, \dots , x_n)\) of elements of X is a path (in X) from \(x_0\) to \(x_n\) if \(\{x_{i-1},x_i\}\) is an edge of G for any i in \(\{1, \dots , n\}\). The subset X of V is said to be connected if, for any x and y in X, there exists a path from x to y. The subset X is a connected component of G if X is connected and if, for any connected subset Y of V, if \(X \subseteq Y\), then we have \(X = Y\). In the following, we denote by CC(G) the set of all connected components of G. It is well known that this set CC(G) of all connected components of G is a partition of the set V.
Let \(G = (V,E)\) be a graph. A partition of V is connected for G if each of its regions is connected and a hierarchy on V is connected (for G) if every one of its partitions is connected. For example, the hierarchy of Fig. 2(a) is connected for the graph of Fig. 2(b).
Let G be a graph. If w is a map from the edge set of G to the set \(\mathbb {R}^+\) of positive real numbers, then the pair (G, w) is called an (edge) weighted graph. If (G, w) is a weighted graph, for any edge u of G, the value w(u) is called the weight of u (for w).
As established in [6], a connected hierarchy can be equivalently treated by means of a weighted graph through the notion of a saliency map. Given a weighted graph (G, w) and a hierarchy \(\mathcal {H} = (\mathbf P _0, \ldots , \mathbf P _n)\) connected for G, the saliency map of \(\mathcal {H}\) is the map from E(G) to \(\{0, \dots , n\}\), denoted by \(\varPhi (\mathcal {H})\), such that, for any edge \(u=\{x, y\}\) in E(G), the value \(\varPhi (\mathcal {H})(u)\) is the smallest value i in \(\{0, \dots , n\}\) such that x and y belong to a same region of \(\mathbf P _{i}\). It follows that any connected hierarchy has a unique saliency map. Moreover, from any saliency map, we can recover the departing connected hierarchy. Consequently, the bijection between connected hierarchies and saliency maps allows us to work indifferently with any of those notions during our study. For instance, the map depicted in Fig. 2(b) is the saliency map of the hierarchy of Fig. 2(a).
2.3 Hierarchical Minimum Spanning Forests and Watersheds
The watershed segmentation [3, 4] derives from the topographic definition of watersheds lines and catchment basins. A catchment basin is a region whose collected precipitation drains to the same body of water, as a sea, and the watershed lines are the separating lines between neighbouring catchment basins. In [4], the authors formalize watersheds in the framework of weighted graphs and show the optimality of watersheds in the sense of minimum spanning forests. In this section, we present hierarchical watersheds following the definition of hierarchical minimum spanning forests (see efficient algorithm in [5, 12]).
Let G be a graph. We say that G is a forest if, for any edge u in E(G), the number of connected components of \((V(G), E(G)\setminus \{u\})\) is larger than the number of connected components of G. Given another graph \(G'\), we say that \(G'\) is a subgraph of G, denoted by \(G' \sqsubseteq G\), if \(V(G') \subseteq V(G)\) and \(E(G') \subseteq E(G)\). Let (G, w) be a weighted graph and let \(G'\) be a subgraph of G. A graph \(G''\) is a Minimum Spanning Forest (MSF) of G rooted in \(G'\) if:
-
1.
the graphs G and \(G''\) have the same set of vertices, i.e., \(V(G'') = V(G)\); and
-
2.
the graph \(G'\) is a subgraph of \(G''\); and
-
3.
each connected component of \(G''\) includes exactly one connected component of \(G'\); and
-
4.
the sum of the weight of the edges of \(G''\) is minimal among all graphs for which the above conditions 1, 2 and 3 hold true.
Intuitively, a drop of water on a topographic surface drains in the direction of a local minimum. Indeed, there is a bijection between the catchment basins of a surface and its local minima. As established in [4], in the framework of weighted graphs, watershed-cuts can be induced by the minimum spanning forest rooted in the minima of this graph. Let (G, w) be a weighted graph and let k be a value in \(\mathbb {R}^+\). A subgraph \(G'\) of G is a minimum (of w) at level k if:
-
1.
\(V(G')\) is connected for G; and
-
2.
for any edge u in \(E(G')\), the weight of u is equal to k; and
-
3.
for any edge \(\{x,y\}\) in \(E(G)\setminus E(G')\) such that \(| \{x,y\} \cap V(G') | \ge 1\), the weight of \(\{x,y\}\) is strictly greater than k.
In the following, we define hierarchical watersheds which are optimal in the sense of minimum spanning forests [5].
Definition 1
(hierarchical watershed). Let (G, w) be a weighted graph and let \(\mathcal {S} = (M_1, \dots , M_n)\) be a sequence of pairwise distinct minima of w such that \(\{M_1, \dots , M_n\}\) is the set of all minima of w. Let \((G_0, \dots , G_{n-1})\) be a sequence of subgraphs of G such that:
-
1.
for any \(i \in \{0, \dots , n-1\}\), the graph \(G_i\) is a MSF of G rooted in \(( \cup \{V(M_j) \mid j \in \{i+1, \dots , n\}\}, \cup \{E(M_j) \mid j \in \{i+1, \dots , n\}\})\); and
-
2.
for any \(i \in \{1, \dots , n-1\}\), we have \(G_{i-1} \sqsubseteq G_i\).
The sequence \(\mathcal {T} = (CC(G_0), \dots , CC(G_{n-1}))\) is called a hierarchical watershed of (G, w) for \(\mathcal {S}\). Given a hierarchy \(\mathcal {H}\), we say that \(\mathcal {H}\) is a hierarchical watershed of (G, w) if there exists a sequence \(\mathcal {S} = (M_1, \dots , M_{n})\) of pairwise distinct minima of w such that \(\{M_1, \dots , M_{n}\}\) is the set of all minima of w and such that \(\mathcal {H}\) is a hierarchical watershed for \(\mathcal {S}\).
A weighted graph (G, w) and a hierarchical watershed \(\mathcal {H}\) of (G, w) are illustrated in Fig. 3(a) and (b), respectively. We can see that \(\mathcal {H}\) is the hierarchical watershed of (G, w) for the sequence \(\mathcal {S}=(M_1, M_2, M_3, M_4)\).
Important Notations and Notions: In the sequel of this article, the symbol G denotes a tree, i.e., a forest with a unique connected component. To shorten the notation, the vertex set of G is denoted by V and its edge set is denoted by E. The symbol w denotes a map from E into \(\mathbb {R}^+\) such that, for any pair of distinct edges u and v in E, we have \(w(u) \ne w(v)\). Thus, the pair (G, w) is a weighted graph. The number of minima of w is denoted by n. Every hierarchy considered in this article is connected for G. Therefore, for the sake of simplicity, we use the term hierarchy instead of hierarchy which is connected for G.
3 Recognition of Hierarchical Watersheds
In this study, we tackle the following recognition problem:
-
(P) given a weighted graph (G, w) and a hierarchy of partitions \(\mathcal {H}\), determine if \(\mathcal {H}\) is a hierarchical watershed of (G, w).
Problem (P) can be related to the problem studied in [8]. In [8], the authors search for a minimum set of markers which lead to a given watershed segmentation. In our case, we are interested in ordering a predefined set of markers (the set of all minima of w) that allows to solve the minimum set of markers problem for the series of all watershed segmentations (partitions) of a given hierarchy.
A naive approach to solve Problem (P) is to verify if there is a sequence \(\mathcal {S}=(M_1, \dots , M_n)\) of pairwise distinct minima of w such that \(\mathcal {H}\) is the hierarchical watershed of (G, w) for \(\mathcal {S}\). However, there exist n! sequences of n pairwise minima of w, which leads to an algorithm of factorial time complexity.
To solve Problem (P) more efficiently, we propose in Sect. 3.2 a characterization of hierarchical watersheds based on the binary partition hierarchy by altitude ordering (Sect. 3.1) which, as stated in [7], is known to be closely related to hierarchical watersheds. This characterization leads to a quasi-linear time algorithm to recognize hierarchical watersheds (Sect. 3.3).
3.1 Binary Partition Hierarchies by Altitude Ordering
Given any set X, we denote by |X| the cardinality of X. Let k be any element in \(\{1,\dots ,|E|\}\). We denote by \(u_k\) the edge in E such that there are \(k-1\) edges in E whose weights are strictly smaller than \(w(u_k)\). We set \(\mathbf B _{0} = \{\{x\} \mid x \in V\}\). The k-partition of V (by the map w) is defined by \(\mathbf{B }_{k} = \{ \mathbf{B }_{k-1}^{y} \cup \mathbf{B }_{k-1}^x \} \cup \mathbf{B }_{k-1} \setminus \{\mathbf{B }_{k-1}^{x}, \mathbf{B }_{k-1}^{y}\}\) where \(u_k = \{x,y\}\) and \(\mathbf B _{k-1}^x\) and \(\mathbf B _{k-1}^y\) are the regions of \(\mathbf B _{k-1}\) that contain x and y, respectively. The edge \(u_k\) is called a building edge of the region \(\{ \mathbf B _{k-1}^y \cup \mathbf B _{k-1}^x \}\). The binary partition hierarchy by altitude ordering (of (G, w)), denoted by \(\mathcal {B}\), is the hierarchy \((\mathbf B _0, \dots , \mathbf B _{|E|})\). Since G is a tree, we have \(\mathbf B _i \ne \mathbf B _{i-1}\) for any i in \(\{1, \dots , |E|\}\), so each region of \(\mathcal {B}\) has a unique building edge and each edge of G is the building edge of a region of \(\mathcal {B}\). Given an edge u in E, we denote by \(R_u\) the region of \(\mathcal {B}\) whose building edge is u.
In Fig. 3(c), we present the binary partition hierarchy \(\mathcal {B}\) of the graph (G, w) (shown in Fig. 3(a)). The building edges are shown above the regions in \(\mathscr {R}^*(\mathcal {B})\).
Important Notation: In the sequel of this article, the binary partition hierarchy by altitude ordering of (G, w) is denoted by \(\mathcal {B}\).
Let X and Y be two distinct regions of \(\mathcal {B} \setminus \{V\}\). If the parents of X and of Y are the same, we say that X is a sibling of Y, that Y is a sibling of X or that X and Y are siblings. It can be seen that X has exactly one sibling and we denote this unique sibling of X by sibling(X).
3.2 Characterization of Hierarchical Watersheds
In this section, we first introduce one-side increasing maps, which, as shown later, are closely related to hierarchical watersheds. Then, we state the main result of this article (Theorem 3), which characterizes the hierarchical watersheds as the hierarchies whose saliency maps are one-side increasing maps. Finally, we present a sketch of the proof of Theorem 3.Footnote 1
To define one-side increasing maps, we first introduce watershed-cut edges for a map. In a topographic surface, the watershed lines are the set of separating lines between neighbouring catchment basins. In the framework of weighted graphs, the catchment basins of the map w are the connected components of the minimum spanning forest rooted in the minima of w. In other words, the catchment basins of w are the leaf regions of any hierarchical watershed of (G, w). Thus, given any edge \(u=\{x,y\}\) in E, we say that u is a watershed-cut edge for w if x and y are in distinct catchment basins of w.
Important Notation: In the sequel of this article, we denote by \( WS (w)\) the set of watershed-cut edges of w.
Definition 2
(one-side increasing map). We say that a map f from E into \(\mathbb {R}^+\) is a one-side increasing map for \(\mathcal {B}\) if:
-
1.
\(range(f) = \{0, \dots , n-1\}\);
-
2.
for any u in E, \(f(u) > 0\) if and only if \(u \in WS (w)\); and
-
3.
for any u in E, there exists a child R of \(R_u\) such that \(f(u) \ge \vee \{ f(v)\) such that \(R_v\) is included in \(R\}\), where \(\vee \{\} = 0\).
where \(range(f) = \{f(u) \mid u \in E\}\)
The next theorem establishes that hierarchical watersheds can be characterized as the hierarchies whose saliency maps are one-side increasing maps.
Theorem 3
(characterization of hierarchical watersheds). Let \(\mathcal {H}\) be a hierarchy and let \(\varPhi (\mathcal {H})\) be the saliency map of \(\mathcal {H}\). The hierarchy \(\mathcal {H}\) is a hierarchical watershed of (G, w) if and only if \(\varPhi (\mathcal {H})\) is a one-side increasing map for \(\mathcal {B}\).
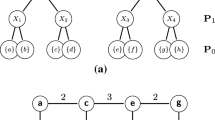
Let us consider the hierarchy \(\mathcal {H}\), the saliency map \(\varPhi (\mathcal {H})\) of \(\mathcal {H}\) and the binary partition hierarchy by altitude ordering \(\mathcal {B}\) (of (G, w) of Fig. 3(a)) shown in Fig. 4(a), (b) and (c), respectively. It can be verified that \(\varPhi (\mathcal {H})\) is one-side increasing for \(\mathcal {B}\). Thus, by Theorem 3, we may affirm that \(\varPhi (\mathcal {H})\) is the saliency map of a hierarchical watershed of (G, w) and that \(\mathcal {H}\) is a hierarchical watershed of (G, w). On the other hand, the saliency map \(\varPhi (\mathcal {H}')\) shown in Fig. 4(e), is not one-side increasing for \(\mathcal {B}\). Indeed, the weight \(\varPhi (\mathcal {H}')(\{c,e\})\) of the building edge of the region \(Y_7\) is 1, which is smaller than both \(\vee \{\varPhi (\mathcal {H}')(v) \mid R_v \subseteq Y_5\}=2\) and \(\vee \{\varPhi (\mathcal {H}')(v) \mid R_v \subseteq Y_6\}=3\). Hence, the condition 3 of Definition 2 is not satisfied by \(\varPhi (\mathcal {H}')\). Thus, by Theorem 3, we may deduce that \(\varPhi (\mathcal {H}')\) is not the saliency map of a hierarchical watershed of (G, w) and that \(\mathcal {H}'\) is not a hierarchical watershed of (G, w).
(a) and (d) The hierarchies \(\mathcal {H}\) and \(\mathcal {H}'\), respectively. (b) and (e) the weighted graphs \((G,\varPhi (\mathcal {H}))\) and \((G,\varPhi (\mathcal {H}'))\), respectively. (c) and (f) The maps \(\varPhi (\mathcal {H})\) and \(\varPhi (\mathcal {H}')\) represented on the hierarchy \(\mathcal {B}\) of Fig. 3(c). For any edge u, the values \(\varPhi (\mathcal {H})(u)\) and \(\varPhi (\mathcal {H}')(u)\) are shown above the region \(R_u\) of \(\mathcal {B}\).
In the remaining of this section, we present a sketch of the proof of Theorem 3. To prove the forward implication of Theorem 3, we first present the definition of extinction values and extinction maps.
Let \(S=(M_1, \dots , M_n)\) be a sequence of n pairwise distinct minima of w. Let R be a region of \(\mathcal {B}\). As defined in [7], the extinction value of R for \(\mathcal {S}\) is zero if there is no minimum of w included in R and, otherwise, it is the maximum value i in \(\{1, \dots , n\}\) such that the minimum \(M_i\) is included in R. Given a map P from the regions of \(\mathcal {B}\) to \(\mathbb {R}^+\), we say that P is an extinction map of w if there exists a sequence S of n pairwise distinct minima of w such that, for any region R of \(\mathcal {B}\), the value P(R) is the extinction value of R for \(\mathcal {S}\).
We provide an example of an extinction map in Fig. 5(a). We can see that the map P is the extinction map of w for the sequence \(\mathcal {S} = (M_2, M_1, M_4, M_3)\).
The next property clarifies the relation between hierarchical watersheds and extinction maps. It can be deduced from the results of [7], which makes a correspondence between extinction values for a given sequence of minima of w and the hierarchical watershed for this sequence of minima.
Property 4
Let f be a map from E into \(\mathbb {R}^+\). The map f is the saliency map of a hierarchical watershed of (G, w) if and only if there exists an extinction map P of w such that, for any u in E, we have
The forward implication of Theorem 3 can be obtained from Property 4. Given a hierarchy \(\mathcal {H}\), if \(\mathcal {H}\) is a hierarchical watershed, then there exists an extinction map P of w such that, for any u in E, we have \(\varPhi (\mathcal {H})(u) = \min \{P(R)\) such that R is a child of \(R_u\}\), which can be proven to be a one-side increasing map. In order to establish the backward implication of Theorem 3, we introduce the notion of estimated extinction maps. Given the saliency map \(\varPhi (\mathcal {H})\) of a hierarchy \(\mathcal {H}\), an estimated extinction map of \(\varPhi (\mathcal {H})\) is a map P such that, for any u in E, we have \(\varPhi (\mathcal {H})(u) = \min \{P(R)\) such that R is a child of \(R_u\}\). Indeed, if P is an extinction map, then \(\varPhi (\mathcal {H})\) is a one-side increasing map.
Important Notation: In the sequel, we consider a total ordering \(\prec \) on the regions of \(\mathcal {B}\) such that, given any two edges u and v in E, if \(w(u) < w(v)\) then \(R_u \prec R_v\). Since the leaf regions of \(\mathcal {B}\) do not have building edges, there are several orderings on the regions of \(\mathcal {B}\) with this property. However, the lemmas stated here hold for any arbitrary choice of \(\prec \).
Definition 5
(estimated extinction map). Let f be a one-side increasing map. The estimated extinction map of f is the map \(\xi _f\) from \(\mathscr {R}(\mathcal {B})\) into \(\mathbb {R}^+\) such that:
-
1.
\(\xi _f(R) = n\) if \(R = V\);
-
2.
\(\xi _f(R) = 0\) if there is no minimum M of w such that \(M \subseteq R\);
-
3.
\(\xi _f(R) = f(u)\), where \(R_u\) is the parent of R, if there is a minimum M of w such that \(M \subseteq R\) and \(sibling(R) \in \mathscr {R}^*(\mathcal {B})\) and
-
if \(\vee ^{f}(R) < \vee ^{f}(sibling(R))\)
-
or if \(\vee ^{f}(R) = \vee ^{f}(sibling(R))\) and \(R \prec sibling(R)\); and
-
-
4.
\(\xi _f(R) = \xi _f(S)\), where S is the parent of R otherwise.
where \(\vee ^{f}(R) = \vee \{f(v)\ |\ v \in E, R_v \subseteq R\}\)
The next lemma establishes that the estimated extinction map of any one-side increasing map is indeed an extinction map.
Lemma 6
Let f be a one-side increasing map for \(\mathcal {B}\). The estimated extinction map \(\xi _f\) of f is an extinction map of w.
For instance, let \(\prec \) be a total ordering on the regions of the hierarchy \(\mathcal {B}\) of Fig. 3(c) such that \(\{a\} \prec \{b\} \prec \{c\} \prec \{d\} \prec \{e\} \prec \{f\} \prec \{g\} \prec \{h\} \prec M_2 \prec M_1 \prec M_4 \prec M_3 \prec Y_5 \prec Y_6 \prec Y_7\). Then, the extinction map P of Fig. 5(a) is precisely the estimated extinction map \(\xi _{\varPhi (\mathcal {H})}\) of the map \(\varPhi (\mathcal {H})\) of Fig. 5(b).
The next lemma is the key result for establishing the backward implication of Theorem 3.
Lemma 7
Let f be a one-side increasing map. Then, for any u in E, we have
The backward implication of Theorem 3 is a consequence of Lemmas 6 and 7 and the backward implication of Property 4. Let \(\mathcal {H}\) be a hierarchy. If \(\varPhi (\mathcal {H})\) is a one-side increasing map, then the estimated extinction map \(\xi _{\varPhi (\mathcal {H})}\) of \(\varPhi (\mathcal {H})\) is an extinction map of w by Lemma 6. Thus, for any u in E, we have \(\varPhi (\mathcal {H})(u) = min\{\xi _{\varPhi (\mathcal {H})}(R)\) such that R is a child of \(R_u\}\) by Lemma 7. Then, by the backward implication of Property 4, we conclude that \(\varPhi (\mathcal {H})\) is the saliency map of a hierarchical watershed of (G, w) and that \(\mathcal {H}\) is a hierarchical watershed of (G, w).
To illustrate Lemma 7, in Fig. 5, we can verify that \(\varPhi (\mathcal {H})(u) = \min \{P(R)\) such that R is a child of \(R_u\}\) for any edge u in E(G) where P (shown in Fig. 5(a)) is precisely the estimated extinction map of \(\varPhi (\mathcal {H})\).
3.3 Recognition Algorithm for Hierarchical Watersheds
In this section, we present a quasi-linear time algorithm to recognize hierarchical watersheds based on Theorem 3. Given any hierarchy \(\mathcal {H}\), to test if \(\mathcal {H}\) is a hierarchical watershed of (G, w), it is sufficient to verify that the saliency map of \(\mathcal {H}\) is a one-side increasing map for \(\mathcal {B}\).
Algorithm 1 provides a description of our algorithm to recognize hierarchical watersheds. The inputs are a weighted graph ((V, E), w) whose edge weights are already sorted and the saliency map f of a hierarchy \(\mathcal {H}\). In this implementation, the edges in E are represented by unique indexes ranging from 1 to |E|.

The first step of Algorithm 1 is to compute the binary partition hierarchy by altitude ordering \(\mathcal {B}\) of ((V, E), w). As established in [12], any binary partition hierarchy can be computed in quasi-linear time with respect to |E| provided that the edges in E are already sorted or can be sorted in linear time. Subsequently, the computation of the watershed edges of w and the number of watershed edges at lines \(2{-}7\) is based on the quasi-linear time algorithm proposed in [12]. At lines \(8{-}14\), for each edge u in E, we compute Max[u], which is the maximal value f(v) such that \(R_v \subseteq R_u\). Since each region of \(\mathcal {B}\) has at most two children, the time complexity to compute the array Max is also linear with respect to |E|. The last for loop (lines \(15{-}24\)) verifies that the three conditions of Definition 2 for f to be a one-side increasing map hold true. Each instruction between lines 17 and 24 can be performed in constant time. Therefore, the overall time complexity of Algorithm 1 is quasi-linear with respect to |E|.
We illustrate Algorithm 1 in Fig. 6. The inputs are a weighted graph (G, w) and a saliency map f. First, we obtain the binary partition hierarchy by altitude ordering \(\mathcal {B}\) of (G, w) and the four watershed-cut edges of w (underlined). Then, we compute the array Max. For each edge u of G, the value Max[u] is the greatest value in the set \(\{f(v) \mid R_v \subseteq R_u\}\). We can verify that the range of f is \(\{0, 1, 2, 3, 4\}\) and that only the watershed-cut edges of w have non-zero weights for f. Therefore, the conditions 1 and 2 of Definition 2 for f to be a one-side increasing map for \(\mathcal {B}\) hold true. Finally, we test the condition 3 of Definition 2. For each watershed-cut edge u of G, we test if \(f(u) > Max[v]\) for an edge v such that \(R_v\) is a child of \(R_u\). For the building edges of the regions \(Y_6\), \(Y_7\) and \(Y_8\) the condition 3 hold true, but this is not the case for \(Y_9\). Thus, f is not a one-side increasing map for \(\mathcal {B}\) and Algorithm 1 returns false.
4 Conclusion
We introduced a new characterization of hierarchical watersheds based on binary partition hierarchies by altitude ordering. Based on this characterization, we designed a quasi-linear time algorithm to determine if a hierarchy is a hierarchical watershed.
In future work, we will extend the recognition of hierarchical watersheds to arbitrary graphs, i.e., graphs which are not trees and whose edge weights are not pairwise distinct. We are also interested in the frequency study of hierarchical watersheds, namely investigating which hierarchies are more likely to be the hierarchical watersheds of a weighted graph (G, w) for arbitrary sequences of minima of w.
Notes
- 1.
The proofs of the lemmas, properties and theorem presented in this article can be found in https://perso.esiee.fr/~santanad/proofs.pdf.
References
Arbelaez, P., Maire, M., Fowlkes, C., Malik, J.: Contour detection and hierarchical image segmentation. IEEE PAMI 33(5), 898–916 (2011)
Beucher, S.: Watershed, hierarchical segmentation and waterfall algorithm. In: Serra, J., Soille, P. (eds.) ISMM, pp. 69–76. Kluwer, Dordrecht (1994)
Beucher, S., Meyer, F.: The morphological approach to segmentation: the watershed transformation. Opt. Eng. 34, 433 (1992). Marcel Dekker Incorporated, New York
Cousty, J., Bertrand, G., Najman, L., Couprie, M.: Watershed cuts: minimum spanning forests and the drop of water principle. IEEE PAMI 31(8), 1362–1374 (2009)
Cousty, J., Najman, L.: Incremental algorithm for hierarchical minimum spanning forests and saliency of watershed cuts. In: Soille, P., Pesaresi, M., Ouzounis, G.K. (eds.) ISMM 2011. LNCS, vol. 6671, pp. 272–283. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21569-8_24
Cousty, J., Najman, L., Kenmochi, Y., Guimarães, S.: Hierarchical segmentations with graphs: quasi-flat zones, minimum spanning trees, and saliency maps. JMIV 60(4), 479–502 (2018)
Cousty, J., Najman, L., Perret, B.: Constructive links between some morphological hierarchies on edge-weighted graphs. In: Hendriks, C.L.L., Borgefors, G., Strand, R. (eds.) ISMM 2013. LNCS, vol. 7883, pp. 86–97. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38294-9_8
Lotufo, R., Silva, W.: Minimal set of markers for the watershed transform. In: Proceedings of ISMM 2002, pp. 359–368 (2002)
Santana Maia, D., de Albuquerque Araujo, A., Cousty, J., Najman, L., Perret, B., Talbot, H.: Evaluation of combinations of watershed hierarchies. In: Angulo, J., Velasco-Forero, S., Meyer, F. (eds.) ISMM 2017. LNCS, vol. 10225, pp. 133–145. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57240-6_11
Meyer, F.: The dynamics of minima and contours. In: Maragos, P., Schafer, R., Butt, M. (eds.) ISMM, pp. 329–336. Kluwer, Dordrecht (1996)
Meyer, F., Vachier, C., Oliveras, A., Salembier, P.: Morphological tools for segmentation: connected filters and watersheds. Ann. Télécommun. 52, 367–379 (1997)
Najman, L., Cousty, J., Perret, B.: Playing with Kruskal: algorithms for morphological trees in edge-weighted graphs. In: Hendriks, C.L.L., Borgefors, G., Strand, R. (eds.) ISMM 2013. LNCS, vol. 7883, pp. 135–146. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38294-9_12
Najman, L., Schmitt, M.: Geodesic saliency of watershed contours and hierarchical segmentation. IEEE PAMI 18(12), 1163–1173 (1996)
Perret, B., Cousty, J., Guimaraes, S.J.F., Maia, D.S.: Evaluation of hierarchical watersheds. IEEE TIP 27(4), 1676–1688 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Maia, D.S., Cousty, J., Najman, L., Perret, B. (2019). Recognizing Hierarchical Watersheds. In: Couprie, M., Cousty, J., Kenmochi, Y., Mustafa, N. (eds) Discrete Geometry for Computer Imagery. DGCI 2019. Lecture Notes in Computer Science(), vol 11414. Springer, Cham. https://doi.org/10.1007/978-3-030-14085-4_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-14085-4_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-14084-7
Online ISBN: 978-3-030-14085-4
eBook Packages: Computer ScienceComputer Science (R0)