Life Expectancy Convergence Among Nations Since 1820: Separating the Effects of Technology and Income

Abstract

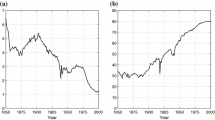
Figure 16.1 shows some details of the probable trajectories of limits and convergence for average life expectancy over the past four centuries. The curved line is an attempt to define the upper bound, or “best practice”, average life expectancy that could be achieved at any one time. We can think of this as an evolving upper bound to the “technophysio” evolution of the human population, in the sense proposed by Fogel and Costa (1997). The bottom limit of the graph is drawn at an average life expectancy of 22.5 years, to approximate the lowest level that a population could experience and still be viable in the long term. Today, even a country like Sierra Leone, with one of the lowest life expectancies recorded by the U.N., is close to the upper limit for a pre-1800 population.

I should like to gratefully acknowledge the enormous help I have received, from a large number of kind individuals and institutions, in building the demographic data-series for this paper. A full list of their names and the sources used will appear in the longer version of this paper. It is also clear that this topic could not have been addressed at all without the economic data published by Angus Maddison.

1 Limits and Convergence in Life Expectancy

Figure 16.1 shows some details of the probable trajectories of limits and convergence for average life expectancy over the past four centuries. The curved line is an attempt to define the upper bound, or “best practice”, average life expectancy that could be achieved at any one time.¹ We can think of this as an evolving upper bound to the “technophysio” evolution of the human population, in the sense proposed by Fogel and Costa (1997). The bottom limit of the graph is drawn at an average life expectancy of 22.5 years, to approximate the lowest level that a population could experience and still be viable in the long term.² Today, even a country like Sierra Leone, with one of the lowest life expectancies recorded by the U.N., is close to the upper limit for a pre-1800 population.

Fig. 16.1

Limits and convergence for national average female life expectancy at birth

If these two limits are plausible, then the history of average life expectancy over the last four centuries must lie between them. It is immediately apparent that the scope for absolute divergence after 1850 is much greater than before. Since the middle of the twentieth century, data on life expectancy or U.N. estimates are available for most countries and convergence has been generally apparent, although there has been recent concern about sub-Saharan Africa and the former communist bloc. A particularly effective way of depicting this convergence was published by Wilson (2001).³ He weighted national averages by populations to estimate the concentration of life expectancy for the World population at three dates. The vertical bars show the inter-quartile range of life expectancy for countries containing half the World’s population.

The bars emphasise three massive changes: rapid improvement in life expectancy, greater symmetry in the distribution, and the globalisation, or compression, of mortality experience. It also becomes clear that the years from 1850 to 1950 were probably the period of maximum diversity in the history of human mortality. After 1950 cross-sectional, or sigma, convergence is apparent, with compression from below, but the gap between the 75th percentile and the national “best-practice” limit seems to be growing.⁴ This might be interpreted as evidence of a new period of divergence. Today’s highest levels of life expectancy can only be achieved by reducing the mortality of the elderly and it may be that some countries will find this harder to achieve than the gains they made at younger ages.

So how do we explain these broad patterns of rising and converging life expectancy, bounded by one fixed and one evolving limit? Many economists have assumed that survival improvements follow automatically from economic development. This is supported by the observation that the rank ordering of countries across both variables is broadly similar and persistent over time, although the ratio of highest to lowest in income is massively bigger than that for mortality, suggesting a non-linear relationship.⁵ Thus rising world life expectancy could be a simple function of rising real incomes, but what role should be assigned to technology transfers?

A second problem is that while the mortality range is compressing across nations over time, the consensus seems to be that the same is not true for income, although this is a subject of debate among economists. One might seek to explain it as the approach to a fixed biological upper bound to average life expectancy, resulting in diminishing returns to wealth, but this common idea of a fixed and imminent limit receives no support in two recent investigations (Oeppen and Vaupel 2002; White 2002). We have also seen that the World population does not seem to be converging on the evolving upper bound.

For insights into the roles of wealth and technology in determining the levels and convergence of life expectancy we turn to the classic article in the field.

2 The Classic Article: Preston (1975)

Slightly longer versions detailing cause-of-death effects are contained in Preston (1976) and (1985).

Speculation and assumption regarding the link between income and health persist. The first concrete, macro-level, study seems to have been undertaken by Preston (1975). In this article, Preston partitioned an historic fall in mortality into two factors: modern economic growth, and improvements in health technology. The first step was to find a function linking national income per head and life expectancy. Figure 16.2 is an updated version of Preston’s graph – the original included cross-sections for the 1900s, 1930s, and 1960s, with logistic functions fitted to the latter two.⁶ The idea is that there is a level of technology, or universal production function, that links input (National Income per capita) to output (average life expectancy) at any one moment in time, but that these functions are subject to temporal shifts. For example, an input of 5000 dollars per head “produced” an average lifetime of 50 years with the technology prevailing in the 1900s, but the same amount of money realised about 70 years in the 1960s. The addition of data for the 1990s does not alter the basic finding and shows that the curve is still shifting upwards in the wealthier countries.

Fig. 16.2

Female life-expectancy at birth and GDP per capita

Easterlin (1996) has pointed out the similarities between Preston’s approach and a pioneering study of modern economic growth by Solow, who divided growth in output into two components: (1) input growth with fixed technology, and (2) shifts in the production function due to technological change. In between technological shifts, countries could still make gains by increasing inputs. Easterlin describes Preston’s study as “done independently of Solow’s work and no less deserving of classic status” (1996, p. 75).

Preston calculated the rise in life expectancy that would have occurred if health technology had been fixed at the 1930s curve, but real incomes per head had risen as observed. Subtracting the hypothetical gain due to income change from the total gain led to the conclusion that about 80% of the rise in life expectancy from 1930 to 1960 could not be attributed to increases in income. This model of mortality treated changes in health technology as an unidentified, exogenous component expressed as a function of time. In subsequent papers, Preston (1980) included variables measuring literacy and nutrition, showing that 70% of the mortality decline in LDCs (excluding China) between 1940 and 1970 could not be accounted for by changes in income. For the period 1965 to 1979, again for LDCs, he has estimated that the technology share has fallen to 30% (Preston 1985).

3 Extending the Analysis

Preston’s model of the linkage between health and national income offered a new way of looking at an old problem, but it still leaves some questions unanswered. The two cross-sections enclose a period of rapid technological change in health, including the introduction of antibiotics, so we have to question whether the dominance of technological change over income change is a long-term phenomenon. The “best-practice” line in Fig. 16.1 suggests that these cross-sections enclosed the only marked “step” in survival over the last century. The rest of the period suggests stable change at the top level. For countries lower down the list, some authors have suggested that the period of inter-war retrenchment in international trade may have deferred demographic innovations, accentuating “catch-up” in the immediate post-war period (see e.g. Bloom and Williamson 1998).

Another important question is whether the dynamics of the model are well specified. Is health technology simply scalable with income? The “sectoral” changes in the age-distribution of deaths required to move from a life expectancy of 50 to one of 80 have been associated with major shifts of emphasis; changes in the importance of infectious versus chronic diseases, public health measures versus medicine, and the changing share of responsibility between the individual and the state. It seems unlikely that every country will experience these changes in the same way. We should expect persistent, “national” effects within the overall relationship.

For this paper on convergence, Preston’s major result is that if we assume a fixed and universal health technology function then the curves show that rising real incomes will lead to convergence in life expectancy, without the requirement that the real income distribution should itself converge. But since Preston argues that technological change dominated between the 1930s and the 1970s, a mechanism based only on income offers little insight into the full mechanisms of long-run convergence. Today there is a considerable literature on economic convergence, but almost no formal analyses of demographic convergence (Wilson 2001). Demographers have concentrated on transition models, with time-scale compression for the late-entrants. The discussion favours technology transfer rather than economic growth, and emphasises the countries that have achieved high life expectancy with relatively low incomes. As with economic growth, late-entrants are recognised to have experienced rates of life expectancy increase never seen in the pioneering countries, but this is not framed in an analysis of the lower costs of imitation compared with innovation.⁷

This paper tries to expand the wealth of results that Preston’s article generated into three new areas. Firstly, the temporal range of the data can be extended. Secondly, new statistical methods may allow us to learn more about the precise roles of time/technology and income. Finally, these same methods may provide more insights into country-level patterns, treated as residuals in the Preston model.

4 New Data

The desire to look at change in life expectancy over the long course of the health transition is severely restricted by the available data, and thus the resulting model will be unsatisfactory in many ways.⁸ Time and GDP per capita are poor proxies for the things we would really like to know.

This paper takes advantage of the collection of national time-series for 56 countries published by Maddison (1995).⁹ GDP per capita is used here, expressed in 1990 Geary-Khamis dollars to remove the effects of inflation and currency. The series were made comparable using a Purchasing Power Parity (PPP) approach rather than relying on exchange rates, which are often distorting.¹⁰ For most advanced capitalist countries, there are estimates for 1820, 1850, and then annually from 1870 to 1994. For other countries, the starting dates and continuity are variable.

Despite the recent increase in the number of countries with annual life-table series, much of the life expectancy data is sporadic and covers varying periods.¹¹ The GDP data has been averaged to match the time spans of the life expectancy estimates, which are shown for females in Fig. 16.3. The nineteenth century has few low-survival countries and is largely confined to countries in Europe, or of European origin. Some Asian and Latin American estimates start in the first half of the twentieth century, but the U.N. estimates for African countries only begin in 1950. This results in a very unbalanced design with discontinuous data, and places a limitation on the kinds of models that can be used. Initial experiments in modelling showed that the 1918 flu epidemic created problems with the residuals, as did wars. An attempt has been made to identify the years when countries were subject to the direct and indirect effects of war and these, together with data for 1918, have been omitted.

Fig. 16.3

Female life-expectancy at birth

The income data used in the model is log GDP per capita in real dollars, and the life expectancy data is expressed as the log-odds of survival assuming an upper limit on life expectancy of 100 years.¹²

Equation 16.1: Log Odds of Life Expectancy at Birth

$$ \ln\;odds\;\left({e}_0\right)=\ln \left({e}_0/\left(100-{e}_0\right)\right) $$

The average number of years lived is divided by the average number of years “lost” assuming an upper limit on average life expectancy of 100 years. Taking the natural log means that the measure is unbounded on the positive and negative sides. This has the advantage of linearising the life expectancy data and removing any ceiling effect – something that Preston did with a logistic transform.

5 National Effects: A Shopping Analogy

Although economists would be quick to point out that there is no real market, Preston introduced us to the idea of an international price/technology/quantity relationship for life expectancy. We can hold any one constant and think about the other pair. Five thousand dollars in 1960 “bought” 70 years of life expectancy, but the same money in 1900 could only buy 50 years. Most people are familiar with this from buying personal computers and other electrical goods. A thousand dollars today buys a greater quantity of computing power than it did 5 years ago because technology has shifted the supply curve upwards.

Is a model based on an international relationship sufficient to reproduce the data? Preston considered that there were also national relationships hidden within the international model, but he didn’t integrate them and treated them as residuals. He observed, for example, that Japan seemed to have very high life expectancy in the 1900s, relative to its income per head, and cites Taeuber’s explanation of “personal cleanliness and the assumption of health responsibility by government organizations as important factors in counteracting the adverse effects of poverty”(Preston 1975, n. 22, p. 236).

To extend the shopping analogy, suppose that technology is always a year ahead in Japan compared to the U.S. – as a result you get a better PC at any given price in Japan, because the technology/price relationship is higher.

Similarly, if delivery costs are high in a country, then the quantity/price ratio is pulled down for any given technology. Thus there may be persistent technological leads and lags, and pricing discounts and surcharges at the national level.

This viewpoint prompts new questions. For example, Norway seems to have always been close to the top of the life expectancy rankings, yet it was relatively poor by European standards at the start of the nineteenth century. Has it always been able to “buy” its life expectancy at a discount, perhaps because an egalitarian society gives a real meaning to “per capita” income, and more easily translates this into health for all the population? Or have they always had a technological lead, perhaps because literacy was so high, not gender specific, and created a tradition of investment in human capital? (Graff 1987, p. 375; Houston 1988, p. 135). Maybe both factors were at work and they were lucky? When they were poor, they knew how to control infant mortality at little cost. By the time mortality reduction required expensive items, like advanced health care for all and State support for the elderly, they had become rich.

Preston’s analysis was for the sexes combined, but we can also consider who is doing the “shopping” – a man or a woman? Why, in the modern era, do women seem to be able to buy more? Each discipline that addresses this question – from evolutionary biology to sociology – has its own explanation.

6 Multilevel Models

For information on multi-level models, in increasing order of complexity, see Kreft and de Leeuw (1998), Snijders and Bosker (1999), and Goldstein (1995).

In Preston’s original paper, the model was fitted to cross-sectional data. This raises a number of familiar estimation problems. We can illustrate this in an intuitive way by examining the points in Fig. 16.1. It is likely that had lines been plotted for countries rather than cross-sections, a very different impression of the data would have been gained. Each country’s data can be thought of as a number of repeated measures on a single unit or group. Preston’s plot shows us the between-groups picture at three points in time, but we also need to understand the within-group change.

This paper uses a multilevel model to go beyond Preston’s “series of cross-sections” approach. Multilevel models are designed to respect the hierarchical nature of both data and explanations. The textbook examples often use school data. Pupils may be tested several times; they are grouped within classes and by teachers, which are grouped within schools, districts, and so on. Historical demographers are used to seeing nested data on regions, villages, families, parents, siblings, and individuals. Treating the hierarchy explicitly solves a number of problems. Factors may be significant at one level and not at another, or they may work differently at two levels. For example, the income of a family may have one effect on infant mortality and the average income of the village may have another. One may reflect familial access to resources, and the other may affect community provision of health infrastructure. Many studies ignore the hierarchy and force all the variables to one level. Thus we might see person-level regressions of infant mortality, with population density, a higher level measure, as an explanatory variable.

Equation 16.2 shows a naïve regression model that we can use as a means of introducing the concepts of multilevel models.

Equation 16.2: Regression Model

$$ \ln\;{oddsf}_{j,t}={\beta}_0+{\beta}_1\times t+{\beta}_2\times \ln\;{GDP}_{j,t}+{\varepsilon}_{j,t} $$

This equation models the log odds of female life expectancy in all countries, indexed by j, and for all time periods t, as the sum of a constant, a function of time, a function of log GDP per capita in the country at time t, and an error term. This is a “one size fits all” model, and it probably wouldn’t work very well, judging by the plots of the data. A standard method of extending such a model is to fit a separate intercept term, or constant, for each country. In bivariate regression, this results in a series of parallel lines, one for each country. In this regression, it leads to a family of parallel planes. The model is usually referred to as Analysis of Covariance, or ANCOVA. The intercepts are really weighted means of the extent to which a particular country differs from the international model. A similar model is RANCOVA, or Random ANCOVA, shown in Eq. 16.3. In this model, we have a global intercept β_{0, 0} and an additive term, β_{0, j}, for each country j. The additive terms are estimated as a sample from a normal distribution with mean zero. They sum to zero, so they can also be regarded as a “national” residual that doesn’t vary with time.

Equation 16.3: RANCOVA Model

$$ \ln\;{oddsf}_{j,t}=\left({\beta}_{0,0}+{\beta}_{0,j}\right)+{\beta}_1\times t+{\beta}_2\times \ln {GDP}_{j,t}+{\varepsilon}_{j,t} $$

This idea of national offsets, or residuals, about an international model can be extended to the other parameters. Equation 16.4a shows a multilevel model with country-specific offsets for all parameters – β_{1, j} for time, and β_{2, j} for income.

Equation 16.4a: Multilevel Model

$$ {\displaystyle \begin{array}{l}\ln\;{oddsf}_{j,t}=\left({\beta}_{0,0}+{\beta}_{0,j}\right)\\ {}+\left({\beta}_{1,0}+{\beta}_{1,j}\right)\times t+\left({\beta}_{2,0}+{\beta}_{2,j}\right)\times \ln\;{GDP}_{j,t}+{\varepsilon}_{j,t}\end{array}} $$

Rearranging the terms to Eq. 16.4b reveals another view of the model and exposes its levels. The first line is an international model (or fixed part in mutilevel model terminology); line two is a country-specific level expressed as offsets or residuals from the higher level (level 2); and finally there is a lowest level residual term (level 1). We now have a model that is interpretable at the international and national levels. It can also be forecast, in both the international and national components.¹³

Equation 16.4b: Multilevel Model Separated into a Fixed Part and Two Residual Levels

$$ {\displaystyle \begin{array}{l}\ln\;{oddsf}_{j,t}={\beta}_{0,0}+{\beta}_{1,0}\times t+{\beta}_{2,0}\times \ln\;{GDP}_{j,t}\\ {}+{\beta}_{0,j}+{\beta}_{1,j}\times t+{\beta}_{2,j}\times \ln\;{GDP}_{j,t}+{\varepsilon}_{j,t}\end{array}} $$

To make the interpretation easier, Eq. 16.5 illustrates such a model, which we will pretend is for Finland, country number 6 in this dataset. The international intercept for the log odds is .45, but ceteris paribus, Finland always seems to lag behind by a factor of −0.01. Overall, the measure of survival rises 0.15 for each additional unit of time, but Finland lags a little behind by −0.07, with a combined effect giving a rise of +0.08 per year. On the other hand, Finland seems to be “buying” its survival at a discount of 0.26. Instead of the international gain of 0.19 per additional unit of income, it gets 0.45 for each extra income unit.

Equation 16.5: Illustrative Multilevel Equation for Country Number 6

$$ {\displaystyle \begin{array}{l}\ln\;{oddsf}_{6,t}=0.45+0.15\times t+0.19\times \ln\;{GDP}_{6,t}\\ {}-0.01-0.07\times t+0.26\times \ln\;{GDP}_{6,t}+{\varepsilon}_{6,t}\end{array}} $$

Turning back to Eq. 16.4a, we can interpret the combined effects on the explanatory variables. 1,j results in a growing lead when it is positive, and a growing lag when it is negative. Similarly, β_{2, j}is a discount when it is positive, and a surcharge when it is negative. As with the intercept in the regression model, we don’t really know how to interpret a particular β_{0, j} parameter. It could represent a fixed lead (lag), independent of time. Or if it were associated with income, then it is a stable rebate (cost). In practice, these two fixed possibilities cannot be logically differentiated.

This is a very simplified introduction to the use of the model in this context. It would take too long to recount the full properties of multi-level models here, but a number are particularly relevant. Firstly, the model recognises that the structure of the data is hierarchical. Each country’s data is a set of repeated measures over time which share certain implicit factors that cannot be ignored. Secondly, the model does not require that the time points are evenly spaced, or that the data are known for all countries. This allows us to use unbalanced data.

7 Model Results

As expected, the model represented in Eq. 16.4 does not work very well. Examination of the residuals shows that they have significant patterns. The strategy adopted for this paper, which concentrates on the national effects, is to make the fixed or international part of the model as flexible as possible. This is an attempt to avoid having the failures of the fixed part interpreted as national effects. Conversely, the national component of the model has been kept as simple as simple as possible, and the form used in that part of Eq. 16.4 is retained.

The final form of the international model uses a polynomial in time because the log transforms do not fully linearise the data. It is also clear that there are epochs in the data. For this reason, the data has been partitioned into pre-World War I, Inter-War, and post World-War II epochs for both time and income. Even then, the post-World War II reconstruction decade presents significant problems. This is an extremely important period in the diffusion of antibiotics and other health technologies, and a time of rapid economic change, so rather than delete the data points, affected countries have been identified and a special component fitted in the model. Finally, even with this expanded model, it was clear that the variance in the level 1 residuals seemed to be a negative function of income, so the model was expanded to allow complex level 1 variation to remove this heteroscedasticity (Goldstein 1995).

The parameter estimates for the fixed, or international, part of the model are shown in Table 16.1.¹⁴

Table 16.1 Multilevel model for log odds of life expectancy

This model suggests that the long-term upward trend in survival was depressed in the inter-war period, but jumped up after 1945. In both periods men seem to be in a worse position. Income terms for females are positive, particularly so in the inter-war period, but there is evidence for a post-war diminution in the effect of income, and this contrasts with Preston’s conclusions for combined male and female life expectancy in LDCs. The inter-war period does seem to show a period of retrenchment – temporal gains slowed and wealth became more important. For men, income seems to be less important than for women and is not statistically significant after 1945. Broadly speaking, the parameters for females and males show similar patterns, although the model is less successful in explaining the male data.

8 National Patterns

The nation-specific component of the model for country j is

The Nation-Specific Component of the Multi-level Model

$$ {\beta}_{0,j}+{\beta}_{1,j}\times t+{\beta}_{2,j}\times \ln\;{GDP}_{j,t} $$

and this can be interpreted as the national “offset” that can be added to the international prediction to get the full prediction for any country.¹⁵ It tells us how one country is performing after controlling for the functions of income and time common to all countries. Figure 16.4 plots the three elements that sum to the national component for the USA and Japan. Because it is controlled out, the international level can be thought of as the horizontal line at zero years. The first panel shows the country-specific constants. Multilevel models are usually fitted to grand-mean centred data so that the variance of the intercept has meaning. The second panel shows the temporal components. Japan’s offset relative to overall temporal change seems to be fixed and approximately zero. The USA has a broadly similar “health technology”, if we can interpret it this way, which is not surprising. The real difference in their contemporary position is shown in the third panel. The US has become progressively unable to translate log dollars into health. It is now about 10 years behind the position we would expect based on income alone, a figure slightly offset by a small advantage of about 2 years in technology. The American pattern is typical of the countries of Northwest European origin, but only the southern European countries come close to Japan’s position of combining a high income with a good conversion rate. The sums of the three components that make up the national offset from the international model are shown in the fourth panel. The USA has regressed to the mean, but Japan shows some strengthening of a long-term advantage.

Fig. 16.4

Components of national level life-expectancy estimates

Figure 16.5 shows the raw data for Japan and the USA, together with dashed lines showing the life expectancy we would expect if they had zero offsets from the international model. As we might expect from the previous graph, this model fits quite well for Japan but overestimates US life expectancy for women today by about 5 years. The full model fits the US data quite well by setting diminishing returns to log GDP per capita. Figure 16.6 shows the same data plotted against income. The slope of the US response to log GDP seems to have changed around 1950, but it could be argued that both Japan and the US may now be back on the long-term path.

Fig. 16.5

Female life expectancy – model and data against time

Fig. 16.6

Female life-expectancy: model and data against per capita income

Figure 16.7 shows these offsets for all the countries, plotted against time. It is immediately apparent that the model is estimating convergence. The fixed part of the model predicts an overall life expectancy in the low twenties for 1820. This is both viable and plausible, and suggests that countries like Norway had a female life expectancy about 25 years above the international prediction. Over time they have progressively lost this advantage, until today it is less than 5 years. It also seems clear that some of the low life expectancy countries are also converging, although perhaps not at the same temporal pace when the disadvantage is greater than 10 years. It should also be noted that these data stop in 1994 and do not show the recent effects of the AIDS epidemic.

Fig. 16.7

National level female life-expectancy estimates against time

Plotting the same data against GDP in Fig. 16.8 is even more striking. Now it seems much clearer that there is overall convergence in life expectancy as income increases. There doesn’t seem to be much evidence that there are different points of convergence for some countries, although the poorest ones are not well represented in Maddison’s data.

Fig. 16.8

National female life-expectancy estimates against GDP per capita

In general, examination of the level 1 residuals shows that the fits for each country are very good, but there is temporal autocorrelation that has not been removed.¹⁶ An exception to the encouraging results concerns the former communist countries of central and Eastern Europe. Paradoxically, the model gives better fits in the 1990s during and after the transition problems than it does in the 1960s. There is a consistent pattern of under-estimation in that period. One plausible possibility is that the economies were difficult to quantify and the GDP estimates are too low. The alternative explanation is that command economies really could deliver good health at lower cost when the challenge was to keep infants, children, and adults alive. Perhaps it was the shift of focus to the elderly population that created difficulties.

9 Convergence

Many researchers have commented on the apparent convergence in life expectancy over time, and also identified a significant number of countries where the progress in health easily outruns their economic performance (Caldwell 1986). Despite this, there seems to have been no attempt to address convergence in a formal way, although there is an extensive literature in Economics on estimating convergence across countries (Jones 1998; Barro and Sala-I-Martin 1995). Among the many insights this provides for demographic studies is the distinction made between “sigma” and “beta” convergence. The former, as the name suggests, is assessed by calculating cross-sectional standard deviations (sigmas). Their evolution over time is then examined. If the trend is towards lower dispersion, it may be interpreted as convergence.¹⁷ Sigma convergence is a measure of what actually happened, but calculating it is difficult with the demographic data before 1950 because they are unbalanced and sporadic.

Beta convergence exists if the slope of a regression line over time is negatively related to the intercept. For example, if a country has a high starting position, or intercept, and a negative slope over time relative to the average, then it is an indication that this country may eventually converge towards the mean. Beta convergence is really a measure of the propensity to converge, holding other effects constant. While it may lead to sigma convergence, it may also be overtaken by changes in other variables or random shocks.

The multilevel model facilitates the estimation of beta convergence, because of the explicit national-level intercepts and slope parameters, but two departures from the conventional intercept-slope regression approach should be borne in mind when interpreting the results. Firstly, all the “national” parameters are estimated from zero-mean normal distributions, so they can be thought of as offsets from the fixed or international model. Secondly, the intercepts in this paper are estimated at the grand means of the data. This is not a requirement of the method, although conventional in multi-level modelling, but it means that the variance of the intercept distribution has meaning within the scales of the data. This allows one to compare the variances across parameters and convert the parameter estimates into z-scores for comparative purposes.

Returning to a consideration of Eq. 16.4b, the national parameter estimates β_{0, j}, β_{1, j}, and β_{2, j} may reveal correlation. Suppose that the intercept terms, the β_{0, j} are negatively correlated with the lead/lag parameters, the β_{1, j}. In this case a high (low) intercept will be associated with a falling (rising) national offset over time, and the country will tend to converge on the international model. The same applies to the β_{0, j} and β_{2, j} parameters. Negative (positive) correlation means that a country with a good starting discount will have a falling (rising) response with respect to income. Finally, if β_{1, j}, and β_{2, j} are negatively (positively) correlated, then relative gains with respect to one variable may be offset (reinforced) by the other.

Before examining convergence in the life expectancy data, we need to consider whether the income data are converging, although the Preston model reveals that this is not a necessary condition for convergence. If there were a simple linkage between income and survival, then economic convergence might be driving mortality convergence directly. Economic convergence is a subject of great debate and the general opinion seems to be that there is no unconditional convergence (Jones 1998). Some groups of countries seem to be converging within their own “club”, but it has been argued that this is conditional on the structures of their economies.¹⁸ My own very simple attempts to look at convergence in the full Maddison GDP dataset, using a multilevel model without covariates, also indicate that there is no evidence of global convergence. In fact, divergence is suggested.

Figure 16.9 plots the national intercepts, β_{0, j} against the parameters on Time, β_{1, j}, after they have been converted to z-scores. There is a negative correlation of −0.38, which indicates a slight but statistically significant tendency for countries with high intercepts to decline against time, and vice versa, leading to convergence.¹⁹ There is some evidence of clustering by geographic areas and economic types. On this time scale, advanced economies with high life expectancies seem to be progressing faster. These correspond to the economies that Sachs and Warner identified as “open” to international trade in 1960 (Sachs and Warner 1995). By 1992, the few remaining “closed” economies are confined to a peripheral arc running from China to Egypt. The former communist countries are making slower progress.

Fig. 16.9

National level parameters for female life expenctancy

Table 16.2 56 countries

Figure 16.10, with a correlation of −0.63 shows that income is the major factor driving beta convergence. As incomes rise, laggard countries are adding years faster than the leaders. Countries of north-west Europe, and their wealthier former colonies, seem to be doing badly, with Britain, the Netherlands, and New Zealand in the worst position. Figure 16.11 shows that the correlation between the time and income parameters, β_{1, j} and β_{2, j} is also negative and significant at −0.39, indicating that the effects are offsetting to some degree. Two countries are worth highlighting across all three graphs. Japan is the only wealthy country that is close to the origin on all three scales. Ireland seems to be associated with the countries of the former communist bloc!

Fig. 16.10

National level parameters for female life-expectancy

Fig. 16.11

National level parameters for female life-expectancy

The full possibilities of this model are not covered here, but some work has been done. For exploratory purposes one can treat the parameter estimates as data. The intercept for females is strongly related to educational attainment as measured in 1985, so the broad ranking may be a long-run feature. There is some evidence that countries with mid-range average education of between 5 and 9 years have the positive time-parameters that indicate “catch-up”. The GDP parameter is strongly and negatively associated with education. It seems that the educated countries are in a phase when additional years of life expectancy are “expensive”.

The effect of income inequality on life expectancy has been a subject of debate (Wilkinson 1998). It could be that, with the international parameter controlling for the broad effect of GDP, the national parameter might be associated with the income distribution of the country. Countries where there is high inequality may have below par conversion of income into health. Using contemporary data from the World Bank on the share of income held by the lowest 20%, there seems to be no relationship with the GDP parameters. However, the more egalitarian countries do seem to have higher intercepts, but they also have lower rates of change over time. No relationships are significant when the data are restricted to the 17 countries described by Maddison as “advanced capitalist”, although the hypothesis is only expected to apply to richer countries.

Because the model is parameterised at the “national” level it would be possible to use country-specific GDP forecasts to forecast life expectancy. Another experiment is to enter the US GDP time-series into each country’s equation. I expected that this would lead to impossible values, but they looked plausible. For example, the model suggests that in the post-Independence era, Indian women would have had US life expectancy if they had had US incomes. The only forecast that exceeded the “best practice” line in Fig. 16.1 was for Russian women. In general, there seemed to be little evidence that there were “structural” limits in the fitted equations that would prevent life expectancy approaching the best levels if incomes grow. One of the insights from this exercise was that some countries have trajectories that are independent of GDP. Chile and China, for example, have national parameters that are approximately equal to the international parameter on GDP, but with a negative sign, so that changing GDP has no effect at all.

10 Conclusion

Multilevel models offer considerable scope for disentangling effects in collections of unbalanced, repeated-measures data. These results are preliminary and designed to explore what can be done, rather than suggesting final interpretations. Preston’s finding that time seems to be becoming less important in LDCs is contradicted in the international component of this model, where it is the income effects that seem to have diminished in the post-war era, particularly for men. On the other hand, changes in income seem to be more important than health technology in explaining survival convergence. Breaking down the national level effects into their constituent components suggests that countries of Northwest European origin have translated a diminishing proportion of their gains in income into gains in health. Combined with the “catch-up” opportunities for the laggard countries, this has led to rapid convergence. Japan and the Southern European countries seem to be the exceptions to this diminishing return to log income.²⁰ They seem to have emerged from the “pack” by maintaining a small long run advantage over the international position. The story of why women’s patterns are different from men’s will have to wait for another day.