Keywords

1 Introduction

A consistent global height reference system is essential for monitoring change processes on Earth in the vertical direction, such as sea level rise, crustal motion, continental water storage variation and so on. Today, over 100 regional/national height systems are practically used. These height systems have their own datums relative to various local mean sea levels which exhibit discrepancies from dm to m (Sánchez and Sideris 2017). Other systematic errors like slopes appear along the levelling lines of a local height system (Gruber et al. 2014). They are inevitably introduced by spirit leveling where the error accumulates over long distances. In addition, different conventions lead to different types of local height systems, like the normal, orthometric, or dynamic height system (Jekeli 2000). It is therefore a challenging task to realize a height system with high precision and homogeneous consistency worldwide.

During the IUGG General Assembly in 2015, IAG released a resolution on the definition of an International Height Reference System (IHRS). The IHRS is defined with conventions on W0 (the reference gravity potential value of an equipotential surface of the Earth’s gravity field), the tide system for data reduction, the terrestrial coordinates of the reference stations and so on. More details are given in Ihde et al. (2017). We would like to underline the convention that the geopotential number (gravity potential difference w.r.t. to W0) rather than the height has been adopted as the vertical coordinate. This will certainly avoid some inconsistencies between different types of height systems. The resolution also includes conventions on the realization of IHRS or the establishment of IHRF. The reference network of the IHRF shall follow the same hierarchy as the ITRF (International Terrestrial Reference Frame), i.e., a global network with regional/national densifications. The challenge is the precise determination of the geopotential numbers and their changes over time for all reference stations.

Classical geodetic methods have been widely used in past decades for the determination of geopotential numbers or gravity potential differences between distant points. One combines spirit levelling and terrestrial gravimetry, which is however time consuming and labour demanding and poses challenges in areas with a complex terrain, like mountain areas (Rummel and Teunissen 1988). Another method is geoid modelling. It estimates the potential value by solving a geodetic boundary value problem (Pavlis 1991). This method can achieve a precise and high-spatial-resolution geoid model in regions with high-quality data available. But the performance of the geoid model might be severely degraded in areas where no or sparse observations are available or data is in a poor quality. One can also use a global gravity field model to calculate the potential value through the procedure of spherical harmonic synthesis. Although there might be some smoothing effects due to a limited spatial resolution or omission errors due to a truncated degree (Gruber et al. 2014). Moreover, oceanographic modelling can potentially be used to estimate the potential differences between points separated by the sea (Woodworth et al. 2012).

Meanwhile, new measurement tools like clock networks have emerged and rapidly developed. The latest generation of optical clocks reaches the level of 10−18 (fractional frequency) and even beyond, which is expected to enable relativistic geodesy with cm-level accuracy. Under the theoretical framework of relativistic geodesy, gravity potential differences (resp. geopotential numbers or height differences) between distant sites can be obtained through measuring the gravitational redshift effect by comparing the clocks’ frequencies (Bjerhammar 1985). The clock-based method shows advantages in several aspects: (1) delivering the potential values directly, well-fitting the definition of the IHRS; (2) precise measurements over long distances without an accumulated error as in spirit levelling; (3) point-wise measurements, without a smoothing effect due to the spatial resolution of gravity field models; (4) continuous observation, while a gravity field model represents an average signal within a time period. These points make clock networks a perfect candidate to realize a consistent and accurate global height system.

In this context, we propose to use a hybrid clock network for the establishment of the IHRF following some specified hierarchy. This clock network is composed of different types of clocks, where stationary clocks are used to build the global reference network of IHRF and transportable clocks are responsible for the regional densification. The vertical coordinates of reference clock stations can be obtained with respect to the unique datum of IHRF through the precise comparison of distant clocks by various frequency transfer techniques. Another way to achieve an IHRF is to unify all existing regional/local height systems. The challenges are the estimation of discrepancies between different height datums and the adjustment of systematic errors along levelling lines in each local height system. We propose to use an inter-connected clock network where a few clocks were assumed in each local region for the unification. The idea is verified through closed-loop simulations.

The paper is structured as follows. In Sect. 2, we review the theory of relativistic geodesy with clocks. Next, we focus on the realization of the IHRS using a hybrid clock network. Then, we run dedicated simulations to verify the idea by using clock networks for height system unification. In the last section, we address our conclusions and some future perspectives.

2 Relativistic Geodesy with Clocks

2.1 Relativistic Geodesy

Einstein’s theory of general relativity predicts that clocks tick at different rates if they are transported with different speed or they are under the influence of different gravitational potential. Considering the case that two motionless clocks are operated at different points on the Earth’s surface, the change of the clocks’ frequencies is proportional to the difference of the gravity potential (sum of the gravitational potential and the centrifugal potential) at both points (Bjerhammar 1985). It reads

$$\displaystyle \begin{aligned} \frac{\varDelta f_{21}}{f_1} = \frac{f_2 - f_1}{f_1} = \frac{W_2 - W_1}{c^2} + O(c^{-4}) , {} \end{aligned} $$
(1)

where f1 and f2 are the proper frequencies at points 1 and 2 on the Earth’s surface, while W1 and W2 are the corresponding gravity potentials, c is the speed of light, and higher order terms are neglected. Supposing that point 1 is on the equipotential surface of Earth’s gravity field with W0, i.e., the geoid, we obtain

$$\displaystyle \begin{aligned} \frac{\varDelta f_{21}}{f_1} = \frac{W_2 - W_0}{c^2} = - \frac{C_2}{c^2} , {} \end{aligned} $$
(2)

where C2 is the geopotential number (the vertical coordinate of IHRS) of point 2. For any two arbitrary points, we can further write

$$\displaystyle \begin{aligned} \frac{\varDelta f_{21}}{f_1} = \frac{(W_2 - W_0) - (W_1 - W_0)}{c^2} = -\frac{C_2 - C_1}{c^2} . {} \end{aligned} $$
(3)

The difference of the clocks’ frequencies is proportional to the difference of the geopotential numbers for two different points. When the geopotential number (difference) is obtained, it can be converted to the physical height (difference). For example, the difference of the orthometric height ΔH21 can be written as (Müller et al. 2018)

$$\displaystyle \begin{aligned} \varDelta H_{21} = \frac{C_2 - C_1} {\overline{g}} = - \frac{\varDelta f_{21}}{f_1} \times \frac{c^2}{\overline{g}}. {} \end{aligned} $$
(4)

Or the normal height difference \(\varDelta H_{21}^{N}\) is written as

$$\displaystyle \begin{aligned} \varDelta H_{21}^{N} = \frac{C_2 - C_1} {\overline{\gamma}} = - \frac{\varDelta f_{21}}{f_1} \times \frac{c^2}{\overline{\gamma}}, {} \end{aligned} $$
(5)

where \(\overline {g}\) is the mean gravity value along the plumb line between the Earth’s surface and the equipotential surface of W0, while \(\overline {\gamma }\) is the mean normal gravity value.

The method to observe height or geopotential differences between two points through the comparison of proper frequencies is called relativistic geodesy or chronometric levelling (Vermeer 1983). The measurement scheme is illustrated in Fig. 1. For an approximate estimation, a fractional frequency inaccuracy of 1.0 × 10−18 corresponds to an uncertainty of about 1.0 cm in height or 0.1 mˆ2/sˆ2 in geopotential. This method is ideal for the establishment of the IHRF, since it can directly obtain the vertical coordinates as geopotential numbers and shows advantages in connecting distant points without being affected by accumulated errors as in spirit levelling. It delivers measurements point-wise so that it can get rid of the smoothing effect of a global gravity field model with limited spatial resolution. Besides, this method is powerful to determine height differences between points that are separated by the sea or a big mountain. Therefore, high-performance clocks that can provide the proper frequency at a high accuracy level, e.g., 1.0 × 10−18, will be a novel tool for height measurements.

Fig. 1
figure 1

The measurement scheme of chronometric levelling with connected clocks

Full size image

2.2 Clock Networks

Clock networks are expected to realize relativistic geodesy in practice. When the theory of relativistic geodesy was presented by Bjerhammar in the 1980s, the most accurate clock was probably the atomic hydrogen maser, with a 10−13 level of frequency uncertainty. Atomic clocks were rapidly developed in the past decades and their performance has significantly improved. An atomic clock that uses electron transition in the microwave range as the frequency standard reaches the level of 10−16 (Heavner et al. 2014). One best representative for this kind of clock is the cesium clock, which is used for the definition of the second. Another type of atomic clocks that received much attention in recent years is the optical clock, using electron transition in the optical range. The latest generation of optical clocks that were built in laboratories achieved the level of 10−18 and even beyond (Brewer et al. 2019; McGrew et al. 2018; Huntemann et al. 2016). The evolvement of the frequency uncertainty for both types of atomic clocks is displayed in Fig. 2. Moreover, efforts were directed to make clocks more compact so that they can be operated in transportable vehicles like a car trailer and used for field measurement campaigns. Such a transportable optical clock was reported with an uncertainty of 7.0 × 10−17 (Koller et al. 2017). Optical clocks were also developed for the application in space (Origlia et al. 2018).

Fig. 2
figure 2

The evolvement of the frequency uncertainty for optical clocks and Cs clocks

Full size image

For the comparison of distant clocks, frequency transfer techniques that use ultra-high frequency (UHF) microwaves, free-space laser links and optical fibers have been greatly developed. The TWSTFT (Two-Way Satellite Time and Frequency Transfer) method exchanges the signals of two distant clocks through a UHF microwave via a relay satellite like a navigation satellite or a geostationary satellite. This method can cancel or reduce some common error sources since the signals are transmitted along the same path. The frequency transfer instability can reach the level of 10−17 at several days averaging (Petit et al. 2014). By using free-space laser beams to replace the microwaves, the two-way link can principally reduce the instability of frequency transfer much faster. An experiment with two ground clocks linked by a 4-km laser beam shows that the instability for frequency transfer reaches 1.2 × 10−17 at 1 s and drops to 6 × 10−20 at 850 s (Sinclair et al. 2018). The frequency transfer based on optical fibers is also extensively experimented. The link between clocks in Paris (France) and in Braunschweig (Germany) by 1,415 km of optical fibers reached the level of 10−19 at 1 day (Lisdat et al. 2016). With these various frequency transfer techniques, high-performance clocks can be combined in networks and applied for geodetic applications (Müller et al. 2018).

3 A Hybrid Clock Network for the Establishment of IHRF

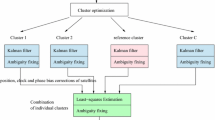
According to the IAG convention, the reference network of IHRF should follow the same hierarchy as ITRF, i.e., a global reference network with regional/national densifications. Here, we propose to apply a hybrid clock network for the realization of the global network of IHRF. Different types of clocks are included in this network, and they are linked via different means of frequency transfer. The assumed clock network is illustrated in Fig. 3. We classify the used clocks into different groups based on their functionality, which are

Fig. 3
figure 3

Different types of clocks that linked with various frequency transfer techniques are proposed to realize the global reference network of IHRF

Full size image

  • Datum clock: The IHRF global network has a unique datum. The datum station is in principle located on the equipotential surface of the global gravity field with W0, or its potential difference w.r.t. W0 is precisely known. It should also have a good accessibility to other reference stations. We assume the most accurate and stable clock at the unique datum station.

  • Core clocks: The global network includes some high-level core stations which are benchmarks for regional and national networks. We assume ultra-high performance clocks at these core stations. These clocks should be referenced to the datum clock so that their vertical coordinates, i.e., geopotential numbers, can be determined through the precise comparison of frequencies. The link between core clocks might be across continents, where the free-space frequency transfer via relay satellites is necessary.

  • Regional/national clocks: For a local area, high-performance clocks are assumed on some permanent, continuous observatories to realize a regional or national network. These regional and national clocks are linked to the core clocks or directly referenced to the datum clock. The free-space frequency transfer and the optical fibers can be used for their link. Since clock-based levelling shows advantages in long-distance height measuring, a few permanent clocks might be sufficient for a regional network. This is not like the classic geodetic levelling network, where more nodal points are required. Also, considering the size, cost and operationality, clock-based levelling might not be superior to the classic geodetic levelling in a relatively small area or in some practical engineer construction. Nevertheless, the existing local levelling networks can be connected to those regional and national clock stations.

  • Transportable clocks: The above mentioned clocks are more likely stationary and permanent. We still need transportable clocks for field measurement campaigns. Transportable clocks might also be useful for the connection of existing local levelling networks to regional and national clock networks.

  • Relay satellites: The free-space link between distant clocks needs some high-orbit relay satellites, like the navigation satellites or geostationary satellites. These satellites can enable the comparison of distant clocks at any time.

4 Clock Networks for Height System Unification

Another way to achieve a global height system is to unify all practically-used local height systems around the world. Generally, a local height system has its own datum related to a local mean sea level which might however be biased to the global reference equipotential surface, i.e., the geoid. The discrepancies can result in offsets from dm to m between different local height datums (Sánchez and Sideris 2017). Within a local height system, reference networks are also suspectable to systematic errors that are introduced by spirit levelling. Levelling errors accumulate over long distances and can reach 1.0–3.0 cm every 100 km. These systematic errors might cause slopes in a local height system, see examples in Spain, France and Germany where linear slopes in the latitudinal and longitudinal directions were found (Gruber et al. 2014). More complex systematic errors, like distortions within a local height system, might also exist.

We propose to use clock networks for local height system unification and verify the idea through closed-loop simulations (Wu et al. 2019). We take the a-priori unified height system EUVN/2000 (European United Vertical Network) (Ihde et al. 2000), which contains 202 reference stations covering most countries in Europe. These stations are manually divided into four groups, with each own datum related to a historic tide gauge station, see Fig. 4. For each local group, we introduced artificial errors to the levelling heights to generate a realistic scenario. The introduced errors are listed in Table 1, including random noise, biases (corresponding to offsets between datums) and slopes along the longitudinal and latitudinal directions (accounting for the accumulated errors for local levelling networks). The values of these errors are assumed based on the a-priori knowledge of realistic cases. Afterwards, a few clocks are assumed for every local system and all clocks are inter-connected to obtain the height differences between the corresponding levelling stations. The clock measurements and the levelling heights in the local systems are then jointly processed by a least-squares adjustment to re-unify all levelling heights to a unique datum. Here, the datum of the local height system G3 was chosen as the unique one for the re-unified system. Finally, the differences between the levelling heights in the re-unified system and the a-priori system are taken for the result evaluation.

Fig. 4
figure 4

The reference stations of EUVN/2000 are divided into four groups G1, G2, G3 and G4, which are marked in different colors

Full size image
Table 1 Introduced errors for each local height system
Full size table

Four clocks in quadrangular distributions are employed in each local system. They are assimilated to levelling stations and marked with different types of symbols, cf. Fig. 5b. The clock measurement accuracy is assumed at the level of 1.0 × 10−18, about 1.0 cm in terms of height. As shown in Fig. 5, the boundary between different local systems (due to the offsets) and the trends for the regional levelling networks (due to the slopes) disappeared after unification. The comparison between the re-unified system and the a-priori system shows that the height differences for all levelling points behave randomly and deviate around zero. The RMSs (Root Mean Square) of the height differences for each group are 0.84, 1.19, 1.29, 1.58 cm. That manifests that the systematic offsets and slopes are precisely estimated and adjusted. The result demonstrates that clock networks are a powerful tool to unify local height systems to achieve the IHRF. Furthermore, we ran simulations to optimize the number and the distribution of clocks, and evaluated the performance by using clocks with different magnitudes of accuracy. These results are published in Wu et al. (2019).

Fig. 5
figure 5

The left figure shows the introduced errors (height differences between the local height systems and the a-priori system) for each levelling point of EUVN/2000, while the right shows the adjusted errors (height differences between the re-unified system and the a-priori system). The magenta symbols shown in the right figure represent clocks, where each of the four types of symbols indicates clocks employed for one local height system. (a) Before unification. (b) After unification

Full size image

5 Conclusions and Future Perspectives

We investigated the potential of using clock networks for the realization of the International Height Reference System under its latest definition. Clock networks, with high-performance clocks (at the level of 1.0 × 10−18 or even beyond) linked by relevant frequency transfer techniques, are a powerful tool to directly observe the gravity potential differences or height differences between distant points. This fact makes clock networks a perfect candidate for the establishment of the IHRF. We proposed a hybrid clock reference network following the hierarchy of the ITRF, which contains high-performance stationary clocks as the backbone of the frame and transportable clocks for regional densifications. The vertical coordinates of the clock stations can be precisely referenced to a unique datum through frequency comparison by free-space links via relay satellites or by optical fibers. Because of the high performance in transmitting heights over long distances, clock networks are also suitable for the unification of local height systems. They can be used to estimate the offsets between different height datums and the systematic slopes within a local height system. We verified this idea through closed-loop simulations and found that measurements acquired by a few clocks, e.g., three or four in triangular or quadrangular distributions for each local system, can precisely remove those systematic discrepancies to achieve a unified system.

Today, extensive efforts are still ongoing to improve the performance of optical clocks and the frequency transfer techniques. Clocks developed in various laboratories worldwide will achieve the level of 10−19 in the next decade, and transportable clocks are promising to achieve the 10−18 level. More fibre links will facilitate the realization of an operational clock network in Europe. In addition, free-space links via satellites will be demonstrated soon by the upcoming ACES (Atomic Clock Ensemble in Space) mission. This makes us believe that clock networks will become a common geodetic measurement tool in the near future.