Abstract
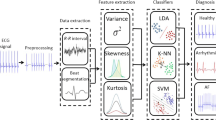
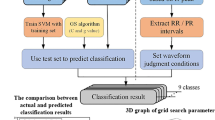
We propose a novel hybrid Hölder-SVM detection algorithm for arrhythmia classification. The Hölder exponents are computed efficiently using the wavelet transform modulus maxima (WTMM) method.
The hybrid system performance is evaluated using the benchmark MIT-BIH arrhythmia database. The implemented model classifies 160 of Normal sinus rhythm, 25 of Ventricular bigeminy, 155 of Atrial fibrillation and 146 of Nodal (A-V junctional) rhythm with 96.94% accuracy. The distinct scaling properties of different types of heart rhythms may be of clinical importance.
Chapter PDF
Similar content being viewed by others
Keywords
- Support Vector Machine
- Wavelet Transformation
- Normal Sinus Rhythm
- Multifractal Formalism
- Multiclass Support Vector Machine
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Morchen, F.: Time series feature extraction for data mining using DWT and DFT. Technical Report 33, Dept. of Mathematics and Computer Science, Philipps-University Marburg., Germany (2003)
Owis, M., Abou-Zied, A., Youssef, A.B., Kadah, Y.: Robust feature extraction from ECG signals based on nonlinear dynamical modeling. In: 23rd Annual Int. Conf. IEEE Eng. Med. Biol. Soc. (EMBC 2001), vol. 2, pp. 1585–1588 (2001)
Scafetta, N., Griffin, L., West, B.J.: Hölder exponent spectra for human gait. Physica A: Statistical Mechanics and its Applications 328, 561–583 (2003)
Struzik, Z.R., Siebes, A.P.J.M.: Outlier detection and localisation with wavelet based multifractal formalism. Technical Report INS-R0008, CWI (2000)
Struzik, Z.R.: Revealing local variability properties of human heartbeat intervals with the local effective Hö lder exponent. Fractals 9, 77–93 (2001)
Muzy, J., Bacry, E., Arneodo, A.: The multifractal formalism revisited with wavelets. International Journal of Bifurcation and Chaos 4, 245–302 (1994)
Hwang, W.L., Mallat, S.: Characterization of self-similar multifractals with wavelet maxima. Applied and Computational Harmonic Analysis 1, 316–328 (1994)
Arneodo, A., Bacry, E., Muzy, J.: The thermodynamics of fractals revisited with wavelets. Physica A: Statistical and Theoretical Physics 213, 232–275 (1995)
Struzik, Z.R.: Removing divergences in the negative moments of the multi-fractal partition function with the wavelet transform. Technical Report INS-R9803, CWI (1998)
Struzik, Z.R.: Determining local singularity strengths and their spectra with the wavelet transform. Fractals 8 (2000)
Vapnik, V.: The nature of statistical learning theory. Springer, New York (1995)
Kulkarni, A., Jayaraman, V.K., Kulkarni, B.D.: Support vector classification with parameter tuning assisted by agent based techniques. Computers and Chemical Engineering 28, 311–318 (2004)
Mitra, P., Uma Shankar, B., Sankar, K.P.: Segmentation of multispectral remote sensing images using active support vector machines. Pattern recognition letters 25, 1067–1074 (2004)
Hsu, C.W., Lin, C.J.: A comparison of methods for multiclass support vector machines. IEEE Transactions on Neural Networks 13, 415–425 (2002)
Novak, D., Cuesta-Frau, D., Eck, V., Perez-Cortes, J., Andreu-Garcia, G.: Denoising electrocardiographic signals using adaptive wavelets. Biosignal, 18–20 (2000)
Chang, C.C., Lin, C.J.: LIBSVM: a library for support vector machines (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Joshi, A., Rajshekhar, Chandran, S., Phadke, S., Jayaraman, V.K., Kulkarni, B.D. (2005). Arrhythmia Classification Using Local Hölder Exponents and Support Vector Machine. In: Pal, S.K., Bandyopadhyay, S., Biswas, S. (eds) Pattern Recognition and Machine Intelligence. PReMI 2005. Lecture Notes in Computer Science, vol 3776. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11590316_33
Download citation
DOI: https://doi.org/10.1007/11590316_33
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-30506-4
Online ISBN: 978-3-540-32420-1
eBook Packages: Computer ScienceComputer Science (R0)