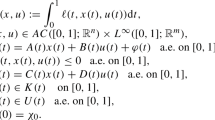Abstract
Second order necessary and sufficient optimality conditions for bang-bang control problems in a very general form have been obtained by the first author. These conditions require the positive (semi)-definiteness of a certain quadratic form on the finite-dimensional critical cone. In the present paper we formulate a generalization of these results to optimal control problems where the control variable has two components: a continuous unconstrained control appearing nonlinearly and a bang-bang control appearing linearly and belonging to a convex polyhedron. Many examples of control of this kind may be found in the literature.
Paper partially supported by NSh-304.2003.1 and RFBR 04-01-00482.
Chapter PDF
Similar content being viewed by others
keywords
References
A.A. Agrachev, G. Stefani, R.L. Zezza Strong optimality for a bang-bang trajectory. SIAM J. Control and Optimization 41:991–1014, 2002.
H. Maurer, N.R. Osmolovskii. Second order sufficient conditions for time optimal bang-bang control problems. SIAM J. Control and Optimization 42:2239–2263, 2004.
H. Maurer, N.R. Osmolovskii. Second order optimality conditions for bang-bang control problems. Control & Cybernetics 32:555–584, 2003.
A.A. Milyutin, N.P. Osmolovskii. Calculus of Variations and Optimal Control. Translations of Mathematical Monographs, Vol. 180, American Mathematical Society, Providence, 1998.
N.R Osmolovskii. High-order necessary and sufficient conditions for Pontryagin and bounded-strong minima in the optimal control problems. Dokl Akad. Nauk SSSR, Ser. Cybernetics and Control Theory 303: 1052–1056, 1988; English transl., Sov. Phys. Dokl. 33, N. 12:883–885, 1988.
N.R Osmolovskii. Quadratic conditions for nonsingular extremals in optimal control (A theoretical treatment). Russian J. of Mathematical Physics 2:487–516, 1995.
N.R Osmolovskii. Second order conditions for broken extremal. In: Calculus of variations and optimal control. (Technion 1998), A. Ioffe, S. Reich and I. Shafir, eds., Chapman and Hall/CRC, Boca Raton, Florida, 198–216, 2000.
N.P. Osmolovskii. Second-order sufficient conditions for an extremum in optimal control. Control and Cybernetics 31 803–831, 2002.
N.P. Osmolovskii. Quadratic optimality conditions for broken extremals in the general problem of calculus of variations. Journal of Math. Science 123: 3987–4122, 2004.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 International Federation for Information Processing
About this paper
Cite this paper
Osmolovskii, N.P., Maurer, H. (2006). Second Order Optimality Conditions for Controls with Continuous and Bang-Bang Components. In: Ceragioli, F., Dontchev, A., Furuta, H., Marti, K., Pandolfi, L. (eds) Systems, Control, Modeling and Optimization. CSMO 2005. IFIP International Federation for Information Processing, vol 202. Springer, Boston, MA . https://doi.org/10.1007/0-387-33882-9_28
Download citation
DOI: https://doi.org/10.1007/0-387-33882-9_28
Publisher Name: Springer, Boston, MA
Print ISBN: 978-0-387-33881-1
Online ISBN: 978-0-387-33882-8
eBook Packages: Computer ScienceComputer Science (R0)