Abstract
The paper studies continuous-time Markov chains (CTMCs) as transformers of real-valued functions on their state space, considered as generalised predicates and called observables. Markov chains are assumed to take values in a countable state space \(\mathbf {S}\); observables \(f: \mathbf {S} \rightarrow {\mathbb {R}}\) may be unbounded. The interpretation of CTMCs as transformers of observables is via their transition function \( P_{t} \): each observable \(f\) is mapped to the observable \( P_{t} f\) that, in turn, maps each state \(x\) to the mean value of \(f\) at time \(t\) conditioned on being in state \(x\) at time \(0\).
The first result is computability of the time evolution of observables, i.e., maps of the form \((t,f)\,{\mapsto }\, P_{t} f\), under conditions that imply existence of a Banach sequence space of observables on which the transition function \( P_{t} \) of a fixed CTMC induces a family of bounded linear operators that vary continuously in time (w.r.t. the usual topology on bounded operators). The second result is PTIME-computability of the projections \(t\,{\mapsto }\,( P_{t} f)(x)\), for each state \(x\), provided that the rate matrix of the CTMC \(X_t\) is locally algebraic on a subspace containing the observable \(f\).
The results are flexible enough to accommodate unbounded observables; explicit examples feature the token counts in stochastic Petri nets and sub-string occurrences of stochastic string rewriting systems. The results provide a functional analytic alternative to Monte Carlo simulation as test bed for mean-field approximations, moment closure, and similar techniques that are fast, but lack absolute error guarantees.
T. Heindel gratefully acknowledges support from RUBYX (project ID 628877 funded by FP7-PEOPLE).
I. Garnier is supported by the ERC project RULE (grant number 320823).
J.G. Simonsen is partially supported by the Danish Council for Independent Research Sapere Aude grant Complexity via Logic and Algebra (COLA).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Stochastic processes are currently a very active research topic in computer science and they have been studied avidly in mathematics, even prior to Kolmogorov’s axiomatic approach to probability. For the special case of continuous-time Markov chains (CTMCs), we shall study how they act on functions from their state space to the reals, which we call observables, alluding to measurement of observable quantities of states. In analogy to predicate transformer semantics [Koz83], observables are considered as generalised predicates that Markov chains transform over time, thus leading to observations that evolve continuously in time. The principal question is how to compute the time evolution of observables.
On computability of time-dependent observations. The following scenario introduces the basic concepts and leads to the core questions of computability. Suppose, we want to compute the mean \( \mathsf {E} [f(X_t)] \) of an observable \(f\) on a CTMC \(X_t\) with denumerable state space. However, initially, we are given only a specification of its dynamics, say, by a finite model that determines the transition function \( P_{t} \), i.e., the matrix of probabilities \(p_{t,xy}\) to jump from state \(x\) to state \(y\) during a time interval of length \(t\); the initial distribution, i.e., the distribution \(\pi \) of \(X_0\), will be available only much later.
As we do not know the initial distribution in advance, we want to split the computation of the mean \( \mathsf {E} [f(X_t)] = \sum _{x,y}\pi (x)p_{t,xy}f(y)\) into a first phase in which we compute conditional means \( \mathsf {E} _{x}(f(X_t)) = \mathsf {E} [f(X_t) \mid X_0 =x] = \sum _{y}p_{t,xy}f(y)\) for a sufficiently large, but finite set of possible initial states \(x\) and a second phase for integration w.r.t. the initial distribution \(\pi \). The two core questions for an approximation of the mean \( \mathsf {E} [f(X_t)] \) to desired precision \(\epsilon >0\) using the described two phase approach are: Is it actually possible to restrict to a finite set of initial states \(x\) that we need to consider? If so, can we compute the conditional means \({ \mathsf {E} _{x}(f(X_t)) = \sum _{y}p_{t,xy}f(y)}\) w.r.t. these states to sufficient precision?
We want to condense these two questions into a single computability question. For this, we first congregate the conditional means \( \mathsf {E} _{x}(f(X_t)) \) into a single observable \( P_{t} f\) with \( P_{t} f (x) = \mathsf {E} _{x}(f(X_t)) \); then, fixing a suitable Banach space of observables, it makes sense to ask for an approximation of \( P_{t} f\) to precision \(\epsilon \). Finally, employing the framework of type 2 theory of effectivity, we can simply ask if the observable \( P_{t} f\) is computable. We go one step further and study computability of the time evolution of these observables.
Examples. For motivation, we give two paradigmatic examples of transient means of the form \( \mathsf {E} [f(X_t)] \). The first example of a stochastic process of the form \(f(X_t)\), i.e., a pair of a CTMC \(X_t\) and an observable \(f\), is the classic CTMC model of a set of chemical reactions where states are multisets over a finite set of species with the count of a certain chemical species as observable; thus, we are interested in the time evolution of the mean count of a certain species.
An example native to computer science is the stochastic interpretation of any string rewriting system as a CTMC \(X_t\). An obvious class of observables for string rewriting are functions that count the occurrence of a certain word as sub-string in each state of the CTMC \(X_t\); note that this is different from counting “molecules” as there is always only a single word! For example, consider the string rewriting system with the single rule  and initial state \(a\): the mean occurrence count of the letter \(a\) grows as the exponential function \(e^t\) while the mean occurrence count of the word \(aa\) is zero at all times; adding the rule
and initial state \(a\): the mean occurrence count of the letter \(a\) grows as the exponential function \(e^t\) while the mean occurrence count of the word \(aa\) is zero at all times; adding the rule  does not change the mean \(a\)-count but renders the mean count of the word \(aa\) non-trivial.
does not change the mean \(a\)-count but renders the mean count of the word \(aa\) non-trivial.
Note that these two classes of models are only the most basic types of rule-based models, besides more powerful examples such as Kappa models [DFF+10] and stochastic graph transformation [HLM06].Footnote 1 The results of this paper are independent of any particular modelling language for CTMCs.
Finite state case. For the sake of clarity, let us describe explicitly the objects that we would manipulate and compute in the basic case where the CTMC has a finite state space. The dynamics of a continuous-time Markov chain on a finite state space \( \mathbf {S} \) is entirely captured by its \(q\)-matrix, which is an \(\mathbf S \times \mathbf S \)-indexed real matrix in which every row sums to zero and all negative entries lie on the diagonal. Every \(q\)-matrix \(Q\) induces a matrix semigroup \(t\,{\mapsto }\,P_t = e^{t Q}\) which is exactly the transition function of the CTMC where \(e^{t Q}\) is the matrix exponential of \(tQ\). Viewing a distribution \(\pi \) on \( \mathbf {S} \) as a row vector, the map \(t\,{\mapsto }\,\pi P_t\) describes the time evolution of the distribution over states at time \(t\) starting from the initial distribution \(\pi \) at time \(0\). In particular, if \(X_0\) is distributed according to \(\pi \), the associated CTMC \(X_t\) is distributed according to \(\pi P_t\). Dually, for any function \(f : \mathbf {S} \rightarrow {\mathbb {R}}\) (seen as a column vector), \(P_t f\) is the vector of conditional means \( \mathsf {E} _{x}(f(X_t)) \) of \(f\) at time \(t\) as a function of the initial state \(x\). As said before, the time evolution of observables in the CTMC with \(q\)-matrix \(Q\), i.e., the map \(t\,{\mapsto }\, P_{t} f\), is the main object of interest for the present paper; the principal question is whether it is computable.
For the finite state case, computability of \(t\,{\mapsto }\,P_t f\) is trivial, assuming \(f\) is computable and the \(q\)-matrix consists of rational entries. Here, computability is in the sense of type 2 theory of effectivity (TTE), which for the function \(t\,{\mapsto }\,P_t f\) means that there are approximation schemes for all coordinates \(P_t f(x)\) to arbitrary desired precision. Even the whole matrix \( P_{t} \) is computable, as it is finite dimensional in the finite state case; finally, observe that all observables on a finite state space are necessarily bounded functions.
The general case. The characterisation of the function \(t\,{\mapsto }\,P_tf\) as the unique solution to the initial value problem (IVP)
will turn out to be very useful as it generalises rather naturally to arbitrary Banach spaces [Ein52]. However, there are two points to note. While the \(q\)-matrix \(Q\) is a bounded linear operator on the finite-dimensional vector space of all observables when we have a finite state space, this does not hold true for the general case. Moreover, the observable \(f\) itself might be unbounded, which poses an additional difficulty for solving an IVP like (1) as described in Sect. 3.3.
The first contribution of the paper consists in setting up a suitable generalisation of the initial value problem (1) in a Banach space space of observables such that the time-dependent observable \( P_{t} f\), mapping a state \(x\) to the conditional mean \( \mathsf {E} _{x}(f(X_t)) \), is its unique solution; for this, we heavily use the functional analytic techniques recently developed in Refs. [Spi12, Spi15]. The main contribution is Theorem 2 on computability of the function \((t,f)\,{\mapsto }\, P_{t} f\) under mild additional assumptions on the \(q\)-matrix of the Markov chain, putting to use recent results by Weihrauch and Zhong [WZ07] on computability of solutions of initial value problems in Banach spaces. The sufficient conditions are general enough to encompass many interesting unbounded observables. Finally, we show that, for a fixed state \(x\) and observable \(f\), the time evolution of the conditional mean \( \mathsf {E} _{x}(f(X_t)) \) is PTIME computable (Theorem 3) under conditions that are strict enough to re-use results on linear ODEs [PG16], yet general enough to capture mean word counts in context-free stochastic string rewriting (Corollary 2).
Related work. Computability of continuous-time Markov chains as transformers of unbounded observables is related to computation of transient means \( \mathsf {E} [f(X_t)] \) of an observable \(f\) on a CTMC \(X_t\) with countable state space. Computability of transient means, in turn, is related to first passage probabilities of a decidable set of states \(U\) (cf. [GM84, Sect. 6.2]): the latter problem can be reduced to computing transient means by use of an indicator function that checks for states in \(U\) and a modified dynamics of the Markov chain, disabling jumps out of \(U\).
Adaptive uniformisation (AU) [VMS93, VMS94] allows one to compute transient means of bounded observables without further complications. However, AU requires the initial distribution to be finite and known from the start. Our results are not subject to these two restrictions, though we need that for each desired precision \(\epsilon \), there is a finite number of states to which we can restrict possible initial distributions, which is a restriction on the dynamics of the CTMC.Footnote 2 The main novelties are the focus on the observable and its time evolution, answering the question of how the dynamics a Markov chain acts on an observable, in general and independent of the initial distribution, and its computability to arbitrary desired precision. We even treat the case of unbounded observables, relying on recent mathematical results [Spi12, Spi15].
Model-checking of continuous-time Markov chains typically concern properties of sample paths of CTMCs relative to a labeling function on states [BHHK03]. In the present paper we neither have a labeling function nor do we rely on sample paths, explicitly. However, it may be that the methods of the present paper can be adapted to the labeled case.
Structure of the paper. The paper starts out with the detailed description of the motivating examples, namely string rewriting and stochastic Petri nets. Then we review the mathematical preliminaries, in particular continuous-time Markov chains on a countable state space and the basic concepts of transition functions and \(q\)-matrices. The generalisation of the initial value problem (1) and the characterisation of the continuous-time observation transformation \(t\,{\mapsto }\, P_{t} f\) of an observable \(f\) by the transition function \( P_{t} \) of a CTMC (Theorem 1) are given in Sect. 4. The main result (Theorem 2) on computability of the continuous-time transformation of observables by CTMCs is presented in Sect. 5. In Sect. 6, we show PTIME-computability of the time evolution of the conditional mean \( \mathsf {E} _{x}(f(X_t)) \), for all states \(x\), under assumptions that allow to restrict to a finite-dimensional space (Theorem 3) and its direct consequence for string rewriting (Corollary 2). Finally, we conclude with a summary of results and directions for future work.
2 Two Motivating Examples of CTMCs with Observables
We illustrate our constructions with: (i) chemical reaction networks (CRN), aka stochastic Petri nets, and (ii) stochastic string rewriting as a simple example of (rule-based) modelling. In both cases, the construction of the \(q\)-matrix implied by a model is readily done, and so is the definition of a natural set of unbounded observables with clear relevance to the dynamics of a model: word occurrence counts for stochastic string rewriting (Definition 2) and multiset inclusions for Petri nets (Definition 3).
2.1 Stochastic String Rewriting and Word Occurrences
Stochastic string rewriting can be thought of as never ending, fair competition between all redexes of rules, “racing” for reduction; the formal definition is as follows, in perfect analogy to Ref. [HLM06] which covers the case of graphs.
Definition 1 (Stochastic string rewriting)
Let  be a rule. The q-matrix of \( \rho \), denoted by \( Q_{{\rho }} \), is the \(q\)-matrix
be a rule. The q-matrix of \( \rho \), denoted by \( Q_{{\rho }} \), is the \(q\)-matrix  on the state space of words \(\varSigma {}^{+}\) with off-diagonal entries
on the state space of words \(\varSigma {}^{+}\) with off-diagonal entries
for each pair of words \(u,v \in \varSigma {}^{+}\) such that \(u\ne v\), and diagonal entries \( q_{{u}{u}}^{\rho } = -\sum _{v\ne u } q_{{u}{v}}^{\rho } \) for all \(u \in \varSigma {}^{+}\). For a finite set of rules \( \mathcal {R} \subseteq \varSigma ^+ \times \varSigma ^+\), we define \( Q_{ \mathcal {R} } = \sum _{\rho \in \mathcal {R} } Q_{\rho } \), and with additional choices of rate constants  , we define \( Q_{ \mathcal {R} , \mathsf{k} } = \sum _{\rho \in \mathcal {R} } \mathsf{k}_{\rho } Q_{\rho } \).
, we define \( Q_{ \mathcal {R} , \mathsf{k} } = \sum _{\rho \in \mathcal {R} } \mathsf{k}_{\rho } Q_{\rho } \).
For a given rule set \( \mathcal {R} \), each entry \( q_{{u}{v}}^{ \mathcal {R} } \) of the \(q\)-matrix corresponds to the propensity to rewrite: it is just the number of ways in which \(u\) can be rewritten to \(v\). We shall usually work without rate constants for the sake of readability. Note that the use of \(\varSigma ^+\) for the left and right hand side of rules is convenient to get string rewriting as a special case of graph transformation in a straightforward manner.
The occurrence counting function of a word as sub-string in the state of the CTMC of \( \mathcal {R} \) is as follows.
Definition 2 (Word counting functions)
Let \({ w }\in \varSigma {}^{+}\) be a word. The w-counting function, denoted by \(\sharp _w :\varSigma {}^{+}\rightarrow \mathbb {R}_{\ge 0}\), maps each word \(x\in \varSigma {}^{+}\) to \(\sharp _{w}(x) = |\{ (u,v)\in \varSigma {}^*\times \varSigma {}^* \mid x = u{ w }v\}| \).
2.2 Stochastic Petri Nets and Sub-multiset Occurrences
We recall the definition of stochastic Petri nets and occurrence counting of a multisets. Note that for the purposes of the present paper, places and species are synonymous.
Definition 3 (Multisets and multiset occurrences)
A multiset over a finite set \(\mathcal {P}\) of places is a function \(x:\mathcal {P}\rightarrow \mathbb {N} \) that maps each place to the number of tokens in that place. Given a multiset, \(x \in \mathbb {N} ^{\mathcal {P}}\), the x-occurrence counting function \(\sharp _{x} : \mathbb {N} ^{\mathcal {P}} \rightarrow \mathbb {N} \) is defined by
where \(z! = \prod _{p\in \mathcal {P}} z(p)!\) is the multiset factorial for all \(z\in \mathbb {N} ^{\mathcal {P}}\).
Definition 4 (Stochastic Petri net)
Let \(\mathcal {P}\) be a finite set of places. A stochastic Petri net over \(\mathcal {P}\) is a set
where \( \mathbb {N} ^{\mathcal {P}}\) is the set of multisets over \(\mathcal {P}\), which are called markings of the net; elements of the set \(\mathcal {T}\) are called transitions. The \(q\)-matrix \( Q_{l,k,r} \) on the set of markings for a transition \((l,k,r) \equiv l \rightarrow ^k r \in \mathcal {T}\) has off-diagonal entries
where addition and subtraction is extended pointwise to \( \mathbb {N} ^{\mathcal {P}}\). The \(q\)-matrix of \(\mathcal {T}\) is \( Q_{\mathcal {T}} = \sum _{(l,k,r)\in \mathcal {T}} Q_{l,k,r} \).
3 Preliminaries
For the remainder of the paper, we fix an at most countable set \( \mathbf {S} \) as state space.
3.1 Transition Functions and q-Matrices
We first recall the basic definitions of transition functions and \(q\)-matrices. We make the usual assumptions [And91] one needs to work comfortably: namely that \(q\)-matrices are stable and conservative and that transition functions are standard and also minimal as described at the end of Sect. 3.1.
With these assumptions in place, transition functions and \(q\)-matrices determine each other, and one can freely work with one or the other as is most convenient.
Definition 5
(Standard transition function [And91, p. 5f]). A transition function on \( \mathbf {S} \) is a family \( \{P_{t}\}_{t \in \mathbb {R}_{\ge 0}} \) of \( \mathbf {S} \times \mathbf {S} \)-matrices  with non-negative, real entries \( {p_{t,xy}} \) such that
with non-negative, real entries \( {p_{t,xy}} \) such that
-
1.
\(\lim _{t\searrow 0} p_{t,xx} = 1\) for all \(x\in \mathbf {S} \);
-
2.
\(\lim _{t\searrow 0} p_{t,xy} = 0\) for all \(x,y\in \mathbf {S} \) such that \(y\ne x\);
-
3.
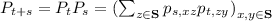 for all \(s,t\in \mathbb {R}_{\ge 0}\); and
for all \(s,t\in \mathbb {R}_{\ge 0}\); and -
4.
\(\sum _{z\in \mathbf {S} } p_{t,xz} \le 1\) for all \(x\in \mathbf {S} \) and \(t\in \mathbb {R}_{\ge 0}\).
Thus, each row of a transition function corresponds to a sub-probability measure, and transition functions converge entry-wise to the identity matrix at time zero.
Taking entry-wise derivatives of a transition function at time \(0\) is possible [Kol51, Aus55] and gives a \(q\)-matrix.
Definition 6
\(\mathbf ( \varvec{q}\)
-matrix). A q-matrix on \( \mathbf {S} \) is an \( \mathbf {S} \times \mathbf {S} \)-matrix  with real entries \( q_{{x}{y}} \) such that \( q_{{x}{y}} \ge 0 \text { (if } x\ne y),\, q_{{x}{x}} \le 0, \text { and } \textstyle \sum _{z\in \mathbf {S} } q_{{x}{z}} = 0 \) for all \(x,y\in \mathbf {S} \).
with real entries \( q_{{x}{y}} \) such that \( q_{{x}{y}} \ge 0 \text { (if } x\ne y),\, q_{{x}{x}} \le 0, \text { and } \textstyle \sum _{z\in \mathbf {S} } q_{{x}{z}} = 0 \) for all \(x,y\in \mathbf {S} \).
Conversely, for each \(q\)-matrix, there exists a unique entry-wise minimal transition function that solves Eq. (2) [And91, Theorem 2.2],
which is called the transition function of \(Q\). From now on, we assume that all transition functions are minimal solutions to Eq. (2) for some \(q\)-matrix \(Q\) (see [Nor98, p. 69]).
3.2 The Abstract Cauchy Problem for \(P_tf\)
Abstract Cauchy problems (ACPs) in Banach spaces [Ein52] are the classic generalisation of finite-dimensional initial value problems (see also Refs. [ABHN11, EN00]). Specifically, we want to obtain \(P_t f\) as unique solution \(u_t\) of the following generalisation of our earlier IVP (1):
where \(f\) is an observable and \( \mathcal {Q} \) is a linear operator which plays the role of the \(q\)-matrix. ACPs that allow for unique differentiable solutions are intimately related to strongly continuous semigroups (SCSGs) and their generators (see, e.g., [EN00, Proposition II.6.2]).
Definition 7
Let \(\mathcal {B}_{}\) be a real Banach space with norm \(\Vert \_\Vert \). A strongly continuous semigroup on \(\mathcal {B}_{}\) is a family \( \{P_{t}\}_{t \in \mathbb {R}_{\ge 0}} \) of bounded linear operators \(P_t\) on \(\mathcal {B}_{}\) satisfying (i) \(P_0 = {I}_{\mathcal {B}_{}} \) (the identity on \(\mathcal {B}_{}\)); (ii) \(P_{t+s} = P_{t}P_{s}\), for all \(s,t\in \mathbb {R}_{\ge 0}\); and (iii) \( \lim _{h\searrow 0}\Vert P_hf - f\Vert =0 \), for all \(f\in \mathcal {B}_{}\). The infinitesimal generator \( \mathcal {Q} \) of a strongly continuous semigroup \(P_t\) on \(\mathcal {B}_{}\) is the linear operator defined by  for all \(f \in \mathcal {B}_{}\) that belong to the domain of definition
for all \(f \in \mathcal {B}_{}\) that belong to the domain of definition 
There are a few points worth noting on how to pass from the IVP (1) to a corresponding ACP. First, the topological vector space of all observables \({\mathbb {R}}^{ \mathbf {S} }\) cannot be equipped with a suitable complete norm to turn it into a Banach space. Therefore, one has to look for a subspace \(\mathcal {B}_{}\subset {\mathbb {R}}^{ \mathbf {S} }\) wherein to interpret the above equation. Second, as \(P_t f = u_t\) is the desired solution, and \(P_0=I\), it follows that \( \frac{\mathrm {d}}{\mathrm {d}t} P_t f|_{t=0} = \mathcal {Q} f\). If this derivative does not exist, \( \mathcal {Q} f\) is simply not defined. In fact, as is clear from the examples in Sect. 2, we can only expect \( \mathcal {Q} \) to be partially defined as it is not a bounded operator, in general.Footnote 3
On the positive side, if we know that \( P_{t} \) is an SCSG on \(\mathcal {B}_{}\), meaning \(\lim _{h\searrow 0} P_h f = f\) for all \(f\in \mathcal {B}_{}\), we can take \( \mathcal {Q} \) to be its generator, i.e., the linear operator defined on \(g\in \mathcal {B}_{}\) by \( \mathcal {Q} g := \frac{\mathrm {d}}{\mathrm {d}t} P_t g|_{t=0}\) whenever this limit exists, and obtain \(P_t f\) as unique solution of (ACP) [EN00, Proposition II.6.2]. Even better, in this case, not only does (ACP) have \(P_tf\) as unique solution, but we get an explicit approximation scheme:
where \(\theta \) is a constant of the SCSG such that \(n {I}_{} - \mathcal {Q} \) is invertible for \(n>\theta \) and the operators \(A_n = n \mathcal {Q} (n {I}_{} - \mathcal {Q} )^{-1}\), known as Yosida approximants, are bounded.
Yosida approximants are the cornerstone of the generation theorems for SCSGs [EN00, Corollary 3.6] that allow one to pass from the generator \( \mathcal {Q} \) to the corresponding SCSG. The constant \(\theta \) also bounds the growth of the SCSG in norm, namely \(\Vert P_t\Vert \le M e^{\theta t}\) for some \(M\). This should already make clear that Eq. (3) is crucial to obtain error bounds for results on the computability of SCSGs. In fact, it is the starting point of the proof of the main result on the computability of SCSGs [WZ07, Theorem 5.4.2, p. 521].
It remains to see whether we can exhibit Banach spaces to build ACPs that accomodate interesting (specifically unbounded) observables.
3.3 Banach Space Wanted!
Table 1 gives an overview of initial value problems for transient distributions (first row) and transient conditional means (second row). Transient distributions are summable sequences, and transition functions form SCSGs [Reu57] and therefore allow for a well-posed corresponding ACP. But the classic example of a Banach space to reason about conditional means [RR72] is the space \(C_0( \mathbf {S} )\) of functions vanishing at infinity, i.e., functions \(f: \mathbf {S} \rightarrow {\mathbb {R}}\) such that for all \(\epsilon >0\), the set \(\{ x \in \mathbf {S} \mid f(x) \ge \epsilon \}\) is finite, equipped with the supremum norm. The corresponding processes are called Feller transition functions [And91, Sect. 1.5] and verify a principle of finite velocity of information flow (for all t, y, the function \(x\,{\mapsto }\,p_{t,xy}\) vanishes as x goes to infinity).
4 Spieksma’s Theorem
A solution is provided by a result of Spieksma [Spi12, Theorem 6.3], giving a class of candidate Banach spaces \(\mathcal {B}_{}\) for a given \(q\)-matrix \(Q\) and an observable \(f\) of interest such that \( P_{t} \) forms an SCSG on \(\mathcal {B}_{}\) (Theorem 1.1). As a consequence, we are led to ACPs generalising the IVP (1) in which the operator \( \mathcal {Q} \) is the generator of the transition function \( P_{t} \) (seen as an SCSG on \(\mathcal {B}_{}\)) and is a restriction of the \(q\)-matrix \(Q\), i.e., \( \mathcal {Q} f = Qf\) for all \(f\in \mathrm {dom}( \mathcal {Q} )\). Moreover, we obtain a characterization of part of the the domain \(\mathrm {dom}( \mathcal {Q} )\) (Proposition 1). The results of this section set the mathematical stage for the main results.
4.1 Weighted \(C_0\)-Spaces and Drift Functions
The Banach spaces that we shall work with are weighted variants of \(C_0( \mathbf {S} )\) such that functions vanish at infinity relative to a chosen weight function on states.
Definition 8
(Weighted \(\varvec{C_0( \mathbf {S} )}\)
-spaces). Let \( \mathbf {S} \) be a set and let \(W: \mathbf {S} \rightarrow \mathbb {R}_{>0}\) be a positive real-valued function, referred to as a weight. The Banach space \( C_0( \mathbf {S} ,W) \) consists of functions \(f: \mathbf {S} \rightarrow {\mathbb {R}}\) such that  vanishes at infinity, where
vanishes at infinity, where  . The norm \(\Vert \_\Vert _W\) on such functions \(f\) is
. The norm \(\Vert \_\Vert _W\) on such functions \(f\) is  .
.
As \(C_0( \mathbf {S} ,W)\) is isometric to \(C_0( \mathbf {S} )\) it is indeed a Banach space. It is also a closed subspace of \({L^\infty }( \mathbf {S} ,W)\), the set of functions such that  is bounded. We shall use later the fact that:
is bounded. We shall use later the fact that:
Lemma 1
Finite linear combinations of indicator functions,Footnote 4 form a dense subset of \(C_0( \mathbf {S} )\).
Spieksma’s theorem [Spi12, Theorem 6.3] will be in terms of so-called drift functions, which intuitively are functions whose mean w.r.t. a given CTMC grows with at most constant rate.
Definition 9 (Drift function)
Let \(Q\) be a \(q\)-matrix on \( \mathbf {S} \), and let \(c\in {\mathbb {R}}\). A function \(W: \mathbf {S} \rightarrow \mathbb {R}_{>0}\) is called a c-drift function for \(Q\) if for all \(x\in \mathbf {S} \) \((Q W)(x) := \sum _{y\in \mathbf {S} } q_{{x}{y}} W(y) \le cW(x)\).
We shall say that W is a drift function for \(Q\) if there exists \(c\in {\mathbb {R}}\) such that it is a \(c\)-drift function for \(Q\). One can show that \(P_t W \le e^{ct}W\) in this case. Thus, drift functions control their own growth under the transition function.
4.2 Transition Functions as Stronlgy Continuous Semigroups
The crux of Spieksma’s theorem [Spi12, Theorem 6.3] is a pair of positive drift functions \(V,W\) for \(Q\) such that \(V\in C_0( \mathbf {S} ,W) \), i.e., such that the quotient  vanishes at infinity. Intuitively, qua drift function, their growth is at most exponential in mean; moreover \(V\) is negligible compared to \(W\) at infinity, and thus functions on the order of \(V\) are as good as functions vanishing at infinity, in analogy to the case of Feller processes [RR72], which is exactly the class of CTMCs whose transition functions induce SCSGs on \(C_0( \mathbf {S} )\). Hence, the following result is a first step towards a theory of weighted Feller processes.
vanishes at infinity. Intuitively, qua drift function, their growth is at most exponential in mean; moreover \(V\) is negligible compared to \(W\) at infinity, and thus functions on the order of \(V\) are as good as functions vanishing at infinity, in analogy to the case of Feller processes [RR72], which is exactly the class of CTMCs whose transition functions induce SCSGs on \(C_0( \mathbf {S} )\). Hence, the following result is a first step towards a theory of weighted Feller processes.
Theorem 1
Let \(P_t\) be a transition function on the state space \( \mathbf {S} \) with \(q\)-matrix \(Q\) and let \({V,W : \mathbf {S} \rightarrow \mathbb {R}_{>0}}\) be drift functions for \(Q\). Then the following hold.
-
1.
The transition function \(P_t\) induces an SCSG on \( C_0( \mathbf {S} ,W) \) iff \(V\in C_0( \mathbf {S} ,W) \).
-
2.
If \(V\in C_0( \mathbf {S} ,W) \), for all \(f\in C_0( \mathbf {S} ,W) \) and \(t\in \mathbb {R}_{\ge 0}\), \( P_{t} f\) is given by Eq. (3) in the Banach space \( C_0( \mathbf {S} ,W) \) where \( \mathcal {Q} \) is the generator of \( P_{t} \).
The first part of the theorem is proved in [Spi12, Theorem 6.3]; the second part follows from the general theory of ACPs. Note that \(f\) does not need to be in the domain of \( \mathcal {Q} \), in which case we only obtain a mild solution to the ACP [EN00, Definition II.6.3], i.e., a solution to its integral form which is not everywhere differentiable. In fact, the solution is differentiable if and only if \(f\) belongs to the domain of the generator [EN00, Proposition II.6.2].
4.3 On the Domain of the Generator
One difficulty in working with SCSGs is to find a useful description of the domain of their generator. However, the graph of the infinitesimal generator of an SCSG is completely determined by the restriction to any dense subset. The following characterisation of subsets of the domains of generators of SCSGs that are obtained via Theorem 1 is a corrected weakening [Spi16] of the second part of Theorem 6.3 of Ref. [Spi12], naturally generalising the classic result for Feller processes [RR72, Theorem 5].
Proposition 1
Let \(P_t\) be a transition function on \( \mathbf {S} \) with \(q\)-matrix \(Q\) and let \(V,W : \mathbf {S} \rightarrow \mathbb {R}_{>0}\) be positive drift functions for \(Q\) such that \(V\in C_0( \mathbf {S} ,W) \). Let \( \mathcal {Q} \) be the generator of the SCSG \( P_{t} \) on \( C_0( \mathbf {S} ,W) \) (cf. Theorem 1).
For all \(f \in C_0( \mathbf {S} ,W) \) that satisfy \( \Vert f\Vert _V < \infty \) and \(Qf \in \mathrm {dom}(Q)\), we have

i.e., the latter limit exists in \( C_0( \mathbf {S} ,W) \) and in particular \(f\in \mathrm {dom}( \mathcal {Q} )\).
We have now covered the mathematical ground needed to characterise the transformation of observations by transition functions of CTMCs as solutions of an ACP, generalising the finite state case of IVP (1). This, however, does not immediately yield an algorithm for computing transient means. Even transient conditional distributions can fail to be computable [AFR11]! Before we proceed to the question of computability, let us return to our two classes of examples.
4.4 Applications: String Rewriting and Petri Nets
We now give examples of drift functions for stochastic string rewriting and Petri nets. The former case is well-behaved since the mean letter count grows at most exponentially. The case of Petri nets will be more subtle and we shall give an example of an explosive Petri net such that we can nevertheless reason about conditional means of unbounded observables.
For string rewriting, we have canonical drift functions.
Lemma 2 (Powers of length are drift functions)
Let \( \mathcal {R} \subseteq \varSigma ^+\times \varSigma ^+\) be a finite string rewriting system and let \(n\in \mathbb {N}^{+} \) be a positive natural number. There exists a constant \(c_n\in \mathbb {R}_{>0}\) such that \(|{\_}|^n:\varSigma ^+\rightarrow \mathbb {R}_{\ge 0}\) is a \(c_n\)-drift function.
Now, we can apply Spieksma’s method to get a Banach space for reasoning about conditional means and moments of word counting functions.
Corollary 1 (Stochastic string rewriting)
Let \( \mathcal {R} \) be a finite string rewriting system, let \(n\in \mathbb {N} {\setminus }\{0\}\), and let  be the word length function. The transition function \(P_t\) of \(q\)-matrix \( Q_{ \mathcal {R} } \) is an SCSG on \( C_0(\varSigma ^+,|\_|^n) \).
be the word length function. The transition function \(P_t\) of \(q\)-matrix \( Q_{ \mathcal {R} } \) is an SCSG on \( C_0(\varSigma ^+,|\_|^n) \).
Thus, all higher conditional moments of word counting functions can be accommodated in a suitable Banach space. The case of Petri nets is more subtle, since, in general, the (weighted) token count is not a drift function.
Example 1
Consider the Petri net with single transition \(2A \rightarrow ^{1} 3A\) and with one place \(A\). The token count \(\sharp _A\) is not a drift function. In fact, the corresponding CTMC is explosive (by Theorem 2.1 of Ref. [Spi15]).
Our final example is an extension of the previous explosive CTMC with a new species whose count can nevertheless be treated using Theorem 1.
Example 2
(Unobserved explosion). Consider the Petri net with transitions
The underlying CTMC is explosive, and we cannot apply Theorem 1 to compute the transient conditional mean of the \(A\)-count for the exact same reason as in Example 1. However, we can do so for the \(B\)-count, using the weight function \(W=\sharp _{B}{}^2\) and observable \(f=\sharp _{B}\). Putting \(V=f\) allows one to apply Spieksma’s recipe (ruling out states with \(B\)-count \(0\) for convenience). The conditional mean \( \mathsf {E} _{2A+B}(\sharp _{B}(X_t)) \) can be best understood by adding a coffin state, on which both the \(A\)- and \(B\)-count are zero and in which the Markov chain resides after (the first and only) explosion.
5 Computability
We follow the school of type-2 theory of effectivity. A real number \(x\) is computable iff there is a Turing machine that on input \(d \in \mathbb {N} \) (the desired precision), outputs a rational number \(r\) with \(\vert r - x \vert < 2^{-d}\). Next, a function \(g :{\mathbb {R}}\rightarrow {\mathbb {R}}\) is computable if there is a Turing machine that, for each \(x \in {\mathbb {R}}\), takes an arbitrary Cauchy sequence with limit \(x\) as input and generates a Cauchy sequence that converges to \(g(x)\)—where convergence has to be sufficiently rapid, e.g., by using the dyadic representation of the reals.
Computability extends naturally to any Banach space \(\mathcal {B}_{}\) other than \({\mathbb {R}}\). We only need a recursively enumerable dense subset on which the norm, addition and scalar multiplication are computable, thus making \(\mathcal {B}_{}\) a computable Banach space; usually, the dense subset is induced by a basis of a dense subspace. For weighted \(C_0\)-spaces (with computable weight functions) and their duals \(( C_0( \mathbf {S} ,W) )^*\), we fix an arbitrary enumeration of all rational linear combinations of indicator functions \( \mathbbm {1}_{x} \); for the Banach space of bounded linear operators on weighted \(C_0\)-spaces we use the standard construction for continuous function spaces [WZ07, Lemma 3.1]. A SCSG \( P_{t} \) is computable if the function \(t\mapsto P_{t} \) from the reals to the Banach space of bounded linear operators is computable. The computable SCSGs correspond to those obtained from CTMCs through Theorem 1.
We restrict to row- and column-finite \(q\)-matrices with rational entries in our main result, motivated by the observation that we do not lose any of the intended applications to rule-based modelling.
Theorem 2 (Computability of CTMCs as observation transformers)
Let \(Q\) be a \(q\)-matrix on \( \mathbf {S} \), let \(W: \mathbf {S} \rightarrow \mathbb {R}_{\ge 0}\) be a positive drift function for \(Q\) such that there exists \(V\in C_0( \mathbf {S} ,W) \) that is a drift function for \(Q\). If
-
the \(q\)-matrix \(Q\) is row- and column-finite, consists of rational entries, and is computable as a function \(Q : \mathbf {S} ^2 \rightarrow \mathbb {Q}^{} \) and the function \(y\,{\mapsto }\,\{x \in \mathbf {S} \mid q_{xy} \ne 0\}\) is computable, and
-
\(W : \mathbf {S} \rightarrow \mathbb {Q}^{} \) is computable,
the following hold.
-
1.
The SCSG \( P_{t} \) is computable.
-
2.
The evolution of conditional means \((t,f)\,{\mapsto }\,P_t f\) is computable as partial function from \({\mathbb {R}}\times C_0( \mathbf {S} ,W) \) to \( C_0( \mathbf {S} ,W) \) defined on \(\mathbb {R}_{\ge 0}\times C_0( \mathbf {S} ,W) \).
-
3.
The evolution of means \((\pi ,t,f)\,{\mapsto }\,\pi P_t f \) is computable as partial function from \( C_0( \mathbf {S} ,W) ^*\times {\mathbb {R}}\times C_0( \mathbf {S} ,W) \) to \({\mathbb {R}}\) defined on \( C_0( \mathbf {S} ,W) ^*\times \mathbb {R}_{\ge 0}\times C_0( \mathbf {S} ,W) \).
Proof
We shall apply a result by Weihrauch and Zhong on the computability of SCSGs [WZ07, Theorem 5.4]. Applying this result requires some extra information:
-
1.
the SCSG \( P_{t} \) must be bounded in norm by \(e^{\theta t}\) for some positive constant \(\theta \);
-
2.
we must have a recursive enumeration of a dense subset of the graph of the infinitesimal generator of the SCSG \( P_{t} \).
We first show that the constant \(\theta \), featuring in Theorem 1, i.e., the witness that \(W\) is a \(\theta \)-drift function for \(Q\), satisfies \(\Vert P_{t} \Vert \le e^{\theta t}\) (using the first part of the proof of Theorem 6.3 of Ref. [Spi12]). Next, we obtain a recursive enumeration of a dense subset \(A\subseteq \mathrm {dom} \mathcal {Q} \) of the domain of the generator \( \mathcal {Q} \) by applying \(Q\) to all rational linear combinations of indicator functions \( \mathbbm {1}_{x} \). Note that for the latter, we use that indicator functions belong to the domain of the generator and \( \mathcal {Q} \mathbbm {1}_{x} = Q \mathbbm {1}_{x} \) by Proposition 1.
Now, by Theorem 5.4.2 of Ref. [WZ07], we obtain the first two computability results, as \((\theta , A,1)\) is a so-called piece of type IG-information [WZ07, p. 513]. Finally, the third point amounts to showing computability of the duality pairing
This theorem immediately gives computability of the CTMCs and (conditional) means for stochastic string rewriting and Petri nets discussed in Sect. 4. Note that the theorem does not assume that \(V\) itself is computable; its role is to establish that the transition functions is an SCSG, but \(V\) plays no role in the actual computation of the solution. Note also that the algorithms that compute the functions \(t\,{\mapsto }\, P_{t} \), \((t,f)\,{\mapsto }\,P_t f\), and \((\pi ,t,f)\,{\mapsto }\,\pi P_t f \) push the responsibility to give arbitrarily good approximations of the respective input parameters \(\pi , t \) and \(f\) to the user. This however is no problem for any of our examples or rule-based models in general: \(t\) is typically rational, \(f\) is computable and even to the natural numbers, and \(\pi \) is often finitely supported or a Gaussian.
Computability ensures existence of algorithms computing transient means, but yields no guarantees of the efficiency of such algorithms. We now proceed to a special case that (i) encompasses a number of well-known examples, including context-free string rewriting, and (ii) leads to PTIME computability, by reducing the problem of transient conditional means to solving finite linear ODEs.
6 The Finite Dimensional Case and PTIME via ODEs
We now turn to the special case where we can restrict to finite dimensional subspaces \(\mathcal {B}_{}\subseteq {\mathbb {R}}^{ \mathbf {S} }\). The prime example will be word counting functions and context-free string rewriting systems. Hyperedge replacement systems [DKH97], the context-free systems of graph transformation, can be handled mutatis mutandis. The main result is PTIME computability of conditional means. For convenience, we extend the usage of the term locally algebraic as follows.
Definition 10 (Locally algebraic)
We call a \(q\)-matrix \(Q\) on \( \mathbf {S} \) locally algebraic for an observable \(f\in {\mathbb {R}}^{ \mathbf {S} }\) if the set \(\{Q^n f\mid n\in \mathbb {N} \}\), containing all multiple applications of the \(q\)-matrix \(Q\) to the observable \(f\), is linearly dependent, i.e., if there exists a number \(N\in \mathbb {N} \) such that the application \(Q^N f\) of the \(N\)-th power is a linear combination \(\sum _{i=0}^{N-1} \alpha _i Q^i f\) of lower powers of \(Q\) applied to \(f\).
Using local algebraicity of a \(q\)-matrix \(Q\) for an observable \(f\), one can generate a finite ODE with one variable for each conditional mean \( \mathsf {E} [Q^nf(X_t)\mid X_0=x] \) (as detailed in the proof of Theorem 3); then, recent results from computable analysis [PG16] entail PTIME complexity.
Theorem 3 (PTIME complexity of conditional means)
Let \(Q\) be a \(q\)-matrix on \( \mathbf {S} \), let \(x\in \mathbf {S} \), let \(f: \mathbf {S} \rightarrow {\mathbb {R}}\) be a function such that \(f(x)\) is a PTIME computable real and \(Q^N f =\sum _{i=0}^{N-1} \alpha _i Q^i f\) for some \(N\in \mathbb {N} \) and PTIME computable coefficients \(\alpha _i\).
The time evolution of the conditional mean \(P_t f(x)\), i.e., the function \(t\,{\mapsto }\,P_t f(x)\), is computable in polynomial time.
Proof
Consider the \(N\)-dimensional ODE with one variable \(E_n\) for each \(n \in \{0,\cdots ,N-1\}\) with time derivative
and initial condition \(E_n(0) = Q^nf(x)\). Solving this ODE is in PTIME [PG16] (even over all of \(\mathbb {R}_{\ge 0}\), using the “length” of the solution curve as implicit input). Finally, \(E_i(t)= P_t Q^if(x)\) is the unique solution.
Note that the linear ODE that we construct has a companion matrix as evolution operator, which allows one to use special techniques for matrix exponentiation [TR03, BCO+07].
Proposition 2 (Local algebraicity of context-free string rewriting)
Let \( \mathcal {R} \) be a string rewriting system, let \( w \in \varSigma ^+\), let \(m\in \mathbb {N} \). The \(q\)-matrix \( Q_{ \mathcal {R} } \) of the string rewriting system \( \mathcal {R} \) is locally algebraic for the \(m\)-th power of \( w \)-occurrence counting \(\sharp _{w}{}^{m}\) if \( \mathcal {R} \subseteq \varSigma \times \varSigma ^+\).
Proof
For every product of word counting functions \(\prod _{i=1}^{m} \sharp _{wi}\), applying the \(q\)-matrix \( Q_{ \mathcal {R} } \) to this product yields the observable \( Q_{ \mathcal {R} } \prod _{i=1}^{m}\sharp _{wi}\). Using previous work on graph transformation [DHHZS14, DHHZS15], restricted to acyclic, finite, edge labelled graphs that have a unique maximal path (with at least one edge), the observable \( Q_{ \mathcal {R} } \prod _{i=1}^{m}\sharp _{wi}\) is a linear combination \(\sum _{j=1}^k \alpha _{j} \prod _{l=1}^{k_j}\sharp _{wj,l}\) of word counting functions \(\sharp _{wj,l}\) (with all \(k_j \le m\)). Moreover, if \( \mathcal {R} \) is context-free (\( \mathcal {R} \subseteq \varSigma \times \varSigma ^+\)), we have \(\sum _{l=1}^{k_j}| w_{j,l} |\le \sum _{i=1}^m| w_{i} |\) for all \(j\in \{1,\cdots ,k\}\). Thus, we stay in a subspace that is spanned by a finite number of products of word counting functions.
Corollary 2
For context-free string rewriting, conditional means and moments of word occurrence counts are computable in polynomial time.
We conclude with a remark on lower bounds for the complexity.
Remark 1
The complexity of computing transient means, even for context-free string rewriting, is at least as hard as computing the exponential function. This becomes clear if we consider the rule \(a\rightarrow aa\), and the observable of \(a\)-counts \(\sharp _{a}\). Now, the time evolution of the \(\sharp _a\)-mean conditioned on the initial state to be \(a\), i.e., the function \(t\mapsto \mathsf {E} _{a}(\sharp _{a}(X_t)) \), is exactly the exponential function \(e^t\). Tight lower complexity bounds for the exponential function are a longstanding open problem [Ahr99].
7 Conclusion
The main result is computability of transient (conditional) means of Markov chains \(X_t\) “observed” by a function \(f\), i.e., stochastic processes of the form \(f(X_t)\). For this, we have described conditions under which a CTMC, specified by its \(q\)-matrix, induces a continuous-time transformer \( P_{t} \) that acts on observation functions. In analogy to predicate transformer semantics for programs, this could be called observation transformer semantics for CTMCs; formally, \( P_{t} \) is a strongly continuous semigroup on a suitable function space. Finally, motivated by important examples of context-free systems – be it the well-known class from Chomsky’s hierarchy or the popular preferential attachment process (covered in previous work [DHHZS15]) – we have considered the special case of locally finite \(q\)-matrices. For this special case, we obtain a first complexity result, namely PTIME computability of transient conditional means.
The obvious next step is to implement our theoretical results since one cannot expect that the general algorithms of Weihrauch and Zhong [WZ07] perform well for every SCSG on a computable Banach space. For example, the Gauss-Jordan algorithm for infinite Matrices [Par12] should already be more practicable for inverting the operator \(nI- \mathcal {Q} \) from Eq. (3) compared to the brute force approach used by Weihrauch and Zhong [WZ07]. Computability ensures existence of algorithms for computing transient means, but yields no guarantees of the efficiency of such algorithms.
Even if it should turn out that efficient algorithms are a pipe dream – after all, transient probabilities \(p_{t,xy}\) are a special case of transient conditional means – we expect that already implementations that are slow but to arbitrary desired precision will be useful for gauging the quality of approximations of the “mean-field” of a Markov process, especially in the area of social networks [Gle13], but possibly also for chemical systems [SSG15]. Theoretically, they are a valid alternative to Monte Carlo simulation, or even preferable.
Notes
- 1.
In fact, stochastic string rewriting is the restriction of stochastic graph transformation [HLM06] to directed, connected, acyclic, edge labelled graphs with in and out degree of nodes bounded by one, i.e., to graphs consisting of a unique maximal path.
- 2.
Specifically, all CTMCs that fail to be Feller processes [RR72] are problematic.
- 3.
Even when \( \mathcal {Q} f\) is defined, one has to check \( \mathcal {Q} f = Q f\), that is to say:
 converges to \(Qf\) in the Banach space norm. But this will turn out to be easy compared to finding sufficient conditions for \( \mathcal {Q} f\) to be defined.
converges to \(Qf\) in the Banach space norm. But this will turn out to be easy compared to finding sufficient conditions for \( \mathcal {Q} f\) to be defined. - 4.
The indicator function \( \mathbbm {1}_{x} \) is defined as usual as \( \mathbbm {1}_{x} (y) = \delta _{xy}\).
References
Arendt, W., Batty, C.J.K., Hieber, M., Neubrander, F.: Vector-Valued Laplace Transforms and Cauchy Problems, vol. 96. Springer, Basel (2011)
Ackerman, N.L., Freer, C.E., Roy, D.M.: Noncomputable conditional distributions. In: Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science, LICS 2011, Ontario, Canada, pp. 107–116, 21–24 June 2011
Ahrendt, T.: Fast computations of the exponential function. In: Meinel, C., Tison, S. (eds.) STACS 1999. LNCS, vol. 1563, pp. 302–312. Springer, Heidelberg (1999). doi:10.1007/3-540-49116-3_28
Anderson, W.J.: Continuous-Time Markov Chains. Springer, New York (1991)
Austin, D.G.: On the existence of the derivative of Markoff transition probability functions. Proc. Natl. Acad. Sci. USA 41(4), 224–226 (1955)
Bostan, A., Chyzak, F., Ollivier, F., Salvy, B., Schost, É, Sedoglavic, A.: Fast computation of power series solutions of systems of differential equations. In: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2007, Philadelphia, PA, USA, pp. 1012–1021. Society for Industrial and Applied Mathematics (2007)
Baier, C., Haverkort, B., Hermanns, H., Katoen, J.-P.: Model-checking algorithms for continuous-time Markov chains. IEEE Trans. Softw. Eng. 29(6), 524–541 (2003)
Danos, V., Feret, J., Fontana, W., Harmer, R., Krivine, J.: Abstracting the differential semantics of rule-based models: exact and automated model reduction. In: Proceedings of the 25th Annual IEEE Symposium on Logic in Computer Science, LICS 2010, Edinburgh, United Kingdom, pp. 362–381, 11–14 July 2010
Danos, V., Heindel, T., Honorato-Zimmer, R., Stucki, S.: Approximations for stochastic graph rewriting. In: Merz, S., Pang, J. (eds.) ICFEM 2014. LNCS, vol. 8829, pp. 1–10. Springer, Cham (2014). doi:10.1007/978-3-319-11737-9_1
Danos, V., Heindel, T., Honorato-Zimmer, R., Stucki, S.: Moment semantics for reversible rule-based systems. In: Krivine, J., Stefani, J.-B. (eds.) RC 2015. LNCS, vol. 9138, pp. 3–26. Springer, Cham (2015). doi:10.1007/978-3-319-20860-2_1
Drewes, F., Kreowski, H.-J., Habel, A.: Hyperedge: replacement, graph grammars. In: Rozenberg, G. (ed.) Handbook of Graph Grammars and Computing by Graph Transformation, pp. 95–162. World Scientific, Singapore (1997)
Einar, H.: A note on Cauchy’s problem. Annales de la Société Polonaise de Mathématique 25, 56–68 (1952)
Engel, K.-J., Nagel, R.: One-Parameter Semigroups for Linear Evolution Equations. Springer, New York (2000)
Gleeson, J.P.: Binary-state dynamics on complex networks: pair approximation and beyond. Phys. Rev. X 3, 021004 (2013)
Gross, D., Miller, D.R.: The randomization technique as a modeling tool and solution procedure for transient Markov processes. Oper. Res. 32(2), 343–361 (1984)
Heckel, R., Lajios, G., Menge, S.: Stochastic graph transformation systems. Fundamenta Informaticae 74(1), 63–84 (2006)
Andrey Nikolaevich Kolmogorov: On the differentiability of the transition probabilities in stationary Markov processes with a denumberable number of states. Moskovskogo Gosudarstvennogo Universiteta Učenye Zapiski Matematika 148, 53–59 (1951)
Kozen, D.: A probabilistic PDL. In: Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing, STOC 1983, pp. 291–297. ACM, New York (1983)
Norris, J.R.: Markov Chains. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge (1998)
Paraskevopoulos, A.G.: The infinite Gauss-Jordan elimination on row-finite \(\omega \times \omega \) matrices. arXiv preprint math (2012)
Pouly, A., Graça, D.S.: Computational complexity of solving polynomial differential equations over unbounded domains. Theor. Comput. Sci. 626, 67–82 (2016)
Reuter, G.E.H.: Denumerable Markov processes and the associated contraction semigroups on l. Acta Mathematica 97(1), 1–46 (1957)
Reuter, G.E.H., Riley, P.W.: The Feller property for Markov semigroups on a countable state space. J. Lond. Math. Soc. s2–5(2), 267–275 (1972)
Spieksma, F.M.: Kolmogorov forward equation and explosiveness in countable state Markov processes. Ann. Oper. Res. 241, 3–22 (2012)
Spieksma, F.M.: Countable state Markov processes: non-explosiveness and moment function. Probab. Eng. Inf. Sci. 29, 623–637 (2015)
Spieksma, F.M.: Personal communication, October 2016
David Schnoerr, Guido Sanguinetti, Ramon Grima: Comparison of different moment-closure approximations for stochastic chemical kinetics. J. Chem. Phys. 143(18) (2015)
Rajae Ben Taher and Mustapha Rachidi: On the matrix powers and exponential by the r-generalized fibonacci sequences methods: the companion matrix case. Linear Algebra Appl. 370, 341–353 (2003)
Van Moorsel, A.P., Sanders, W.H.: Adaptive uniformization: technical details. Technical report, Department of Computer Science and Department of Electrical Engineering, University of Twente (1993)
Van Moorsel, A.P., Sanders, W.H.: Adaptive uniformization. Commun. Stat. Stoch. Models 10, 619–647 (1994)
Weihrauch, K., Zhong, N.: Computable analysis of the abstract Cauchy problem in a Banach space and its applications I. Math. Logic Q. 53(4–5), 511–531 (2007)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Danos, V., Heindel, T., Garnier, I., Simonsen, J.G. (2017). Computing Continuous-Time Markov Chains as Transformers of Unbounded Observables. In: Esparza, J., Murawski, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2017. Lecture Notes in Computer Science(), vol 10203. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54458-7_20
Download citation
DOI: https://doi.org/10.1007/978-3-662-54458-7_20
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54457-0
Online ISBN: 978-3-662-54458-7
eBook Packages: Computer ScienceComputer Science (R0)





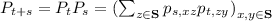 for all
for all  converges to
converges to 