Can PPAD Hardness be Based on Standard Cryptographic Assumptions?

Abstract

We consider the question of whether PPAD hardness can be based on standard cryptographic assumptions, such as the existence of one-way functions or public-key encryption. This question is particularly well-motivated in light of new devastating attacks on obfuscation candidates and their underlying building blocks, which are currently the only known source for PPAD hardness.

Central in the study of obfuscation-based PPAD hardness is the sink-of-verifiable-line (SVL) problem, an intermediate step in constructing instances of the PPAD-complete problem source-or-sink. Within the framework of black-box reductions we prove the following results:

• Average-case PPAD hardness (and even SVL hardness) does not imply any form of cryptographic hardness (not even one-way functions). Moreover, even when assuming the existence of one-way functions, average-case PPAD hardness (and, again, even SVL hardness) does not imply any public-key primitive. Thus, strong cryptographic assumptions (such as obfuscation-related ones) are not essential for average-case PPAD hardness.

• Average-case SVL hardness cannot be based either on standard cryptographic assumptions or on average-case PPAD hardness. In particular, average-case SVL hardness is not essential for average-case PPAD hardness.

• Any attempt for basing the average-case hardness of the PPAD-complete problem source-or-sink on standard cryptographic assumptions must result in instances with a nearly-exponential number of solutions. This stands in striking contrast to the obfuscation-based approach, which results in instances having a unique solution.

Taken together, our results imply that it may still be possible to base PPAD hardness on standard cryptographic assumptions, but any such black-box attempt must significantly deviate from the obfuscation-based approach: It cannot go through the SVL problem, and it must result in source-or-sink instances with a nearly-exponential number of solutions.

1 Introduction

In recent years there has been increased interest in the computational complexity of finding a Nash equilibrium. Towards this end, Papadimitriou defined the complexity class PPAD, which consists of all TFNP problems that are polynomial-time reducible to the source-or-sink problem [31].¹ Papadimitriou showed that the problem of finding a Nash equilibrium is reducible to source-or-sink, and thus belongs to PPAD. He also conjectured that there exists a reduction in the opposite direction, and this was proved by Daskalakis, Goldberg and Papadimitriou [18], and by Chen, Deng and Teng [11]. Thus, to support the belief that finding a Nash equilibrium may indeed be computationally hard, it became sufficient to place a conjectured computationally-hard problem within the class PPAD.

Currently, no PPAD-complete problem is known to admit a sub-exponential-time algorithm. At the same time, however, we do not know how to generate instances that defeat known heuristics for these problems (see [24] for oracle-based worst-case hard instances of computing Brouwer fixed points and [36] for finding a Nash equilibrium). This leaves us in an intriguing state of affairs, in which we know of no efficient algorithms with provable worst-case guarantees, but we are yet to systematically rule out the possibility that known heuristic algorithms perform well on the average.

“Post-obfuscation” PPAD hardness. A natural approach for arguing hardness on the average would be to reduce from problems that originate from cryptography. Working in the realm of cryptography has at least two advantages. First of all, it enables us to rely on well-studied problems that are widely conjectured to be average-case hard. Secondly, and no less importantly, cryptography supplies us with frameworks for reasoning about average-case hardness. On the positive direction, such frameworks are highly suited for designing and analyzing reductions between average-case problems. On the negative direction, in some cases it is possible to argue that such “natural” reductions do not exist [27, 34].

Up until recently not much progress has been made in relating between cryptography and PPAD hardness. This has changed as a result of developments in the study of obfuscation [4, 19], a strong cryptographic notion with connections to the hardness of source-or-sink. As shown by Bitansky, Paneth and Rosen [8] the task of breaking sub-exponentially secure indistinguishability obfuscation can be reduced to solving source-or-sink. Beyond giving the first extrinsic evidence of PPAD hardness, the result of Bitansky et al. also provided the first method to sample potentially hard-on-average source-or-sink instances. Their result was subsequently strengthened by Garg, Pandey and Srinivasan, who based it on indistinguishability obfuscation with standard (i.e., polynomial) hardness [20].

“Pre-obfuscation” PPAD hardness? Indistinguishability obfuscation has revealed to be an exceptionally powerful primitive, with numerous far reaching applications. However, its existence is far from being a well-established cryptographic assumption, certainly not nearly as well-established as the existence of one-way functions or public-key encryption. Recently, our confidence in existing indistinguishability obfuscation candidates has somewhat been shaken, following a sequence of devastating attacks on both candidate obfuscators and on their underlying building blocks (see, for example, [10, 12,13,14,15, 17, 25, 29, 30]). It thus became natural to ask:

By standard cryptographic assumptions we are in general referring to “pre-obfuscation” type of primitives, such as the existence of one-way functions or public-key cryptography. As mentioned above, such assumptions are currently by far more well-established than indistinguishability obfuscation, and basing average-case PPAD hardness on them would make a much stronger case.

For all we know PPAD hardness may be based on the existence of one-way functions. However, if it turned out that average-case PPAD hardness implies public-key encryption, then this would indicate that basing average-case PPAD hardness on one-way functions may be extremely challenging since we currently do not know how to base public-key encryption on one-way functions (and in fact cannot do so using black-box techniques [27]). Similarly, if it turned out that average-case PPAD hardness implies indistinguishability obfuscation, this would indicate that basing average-case PPAD average on any standard cryptographic assumption would require developing radically new techniques. More generally, the stronger the implication of PPAD hardness is, the more difficult it may be to base PPAD hardness on standard assumptions. This leads us to the following second question:

As discussed above, a negative answer to the above question would actually be an encouraging sign. It would suggest, in particular, that program obfuscation is not essential for PPAD hardness, and that there may be hope to base PPAD hardness on standard cryptographic assumptions.

1.1 Our Contributions

Motivated by the above questions, we investigate the interplay between average-case PPAD hardness and standard cryptographic assumptions. We consider this interplay from the perspective of black-box reductions, the fundamental approach for capturing natural relations both among cryptographic primitives (e.g., [27, 28, 34]) and among complexity classes (e.g., [7, 16]).

Average-case PPAD hardness does not imply cryptographic hardness. Our first result shows that average-case PPAD hardness does not imply any form of cryptographic hardness in a black-box manner (not even a one-way function). In addition, our second result shows that, even when assuming the existence of one-way functions, average-case PPAD hardness does not imply any public-key primitive (not even key agreement).² In fact, we prove the following more general theorems by considering the sink-of-verifiable-line (SVL) problem, introduced by Abbot et al. [1] and further studied by Bitansky et al. [8] and Garg et al. [20]:

Theorem 1.1

There is no black-box construction of a one-way function from a hard-on-average distribution of SVL instances.

Theorem 1.2

There is no black-box construction of a key-agreement protocol from a one-way function and a hard-on-average distribution of SVL instances.

Abbot et al. [1] and Bitansky et al. [8] showed that any hard-on-average distribution of SVL instances can be used in a black-box manner for constructing a hard-on-average distribution of instances to a PPAD-complete problem (specifically, instances of the source-or-sink problem). Thus, Theorem 1.1 implies, in particular, that there is no black-box construction of a one-way function from a hard-on-average distribution of instances to a PPAD-complete problem. Similarly, Theorem 1.2 implies, in particular, that there is no black-box construction of a key-agreement protocol from a one-way function and a hard-on-average distribution of instances to a PPAD-complete problem.

As discussed in the previous section, the fact that average-case PPAD hardness does not naturally imply any form of cryptographic hardness is an encouraging sign in the pursuit of basing average-case PPAD hardness on standard cryptographic assumptions. For example, if average-case PPAD hardness would have implied program obfuscation, this would have indicated that extremely strong cryptographic assumptions are likely to be essential for average-case PPAD hardness. Similarly, if average-case PPAD hardness would have implied public-key cryptography, this would have indicated that well-structured cryptographic assumptions are essential for average-case PPAD hardness. The fact that average-case PPAD hardness does not naturally imply any form of cryptographic hardness hints that it may be possible to base average-case PPAD hardness even on the minimal (and unstructured) assumption that one-way functions exist.

PPAD hardness vs. SVL hardness. The SVL problem played a central role in the recent breakthrough of Bitansky et al. [8] and Garg et al. [20] in constructing a hard-on-average distribution of instances to a PPAD-complete problem based on indistinguishability obfuscation. Specifically, they constructed a hard-on-average distribution of SVL instances, and then reduced it to a hard-on-average distribution of source-or-sink instances [1, 8].

We show, however, that the SVL problem is in fact far from representing PPAD hardness: Whereas Abbot et al. [1] and Bitansky et al. [8] showed that the SVL problem can be efficiently reduced to the source-or-sink problem (even in the worst case), we show that there is no such reduction in the opposite direction (not even an average-case one). We prove the following theorem:

Theorem 1.3

There is no black-box construction of a hard-on-average distribution of SVL instances from a hard-on-average distribution of source-or-sink instances. Moreover, this holds even if the underlying source-or-sink instances always have a unique solution.

On basing average-case PPAD hardness on standard assumptions. Theorem 1.1 encouragingly shows that it may still be possible to base average-case PPAD hardness on standard cryptographic assumptions, but Theorem 1.3 shows that the obfuscation-based approach (which goes through the SVL problem) may not be the most effective one. Now, we show that in fact any attempt for basing average-case PPAD hardness on standard cryptographic assumptions (e.g., on one-way functions, public-key encryption, and even on injective trapdoor functions) in a black-box manner must significantly deviate from the obfuscation-based approach. Specifically, the source-or-sink instances resulting from that approach have exactly one solution³, and we show that when relying on injective trapdoor functions in a black-box manner it is essential to have a nearly-exponential number of solutions. We prove the following theorem:

Theorem 1.4

There is no black-box construction of a hard-on-average distribution of source-or-sink instances over $\{0,1\}^n$ with $2^{n^{o(1)}}$ solutions from injective trapdoor functions.

In particular, since Abbot et al. [1] and Bitansky et al. [8] showed that hard-on-average SVL instances lead to hard-on-average source-or-sink instances having a unique solution, Theorem 1.4 implies the following corollary which, when combined with Theorem 1.1, shows that average-case SVL hardness is essentially incomparable to standard cryptographic assumptions.

Corollary 1.5

There is no black-box construction of hard-on-average distribution of SVL instances from injective trapdoor functions.

More generally, although Theorem 1.4 and Corollary 1.5 focus on injective trapdoor functions, our impossibility result holds for a richer and larger class of building blocks. Specifically, it holds for any primitive that exists relative to a random injective trapdoor function oracle. Thus, Theorem 1.4 and Corollary 1.5 hold, for example, also for collision-resistant hash functions (which are not implied by one-way functions or injective trapdoor functions in a black-box manner [23, 37]).

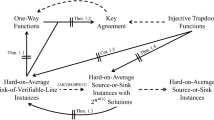
Taken together, our results imply that it may be possible to base average-case PPAD hardness on standard cryptographic assumptions, but any black-box attempt must significantly deviate from the obfuscation-based approach: It cannot go through the SVL problem, and it must result in source-or-sink instances with a nearly-exponential number of solutions. See Fig. 1 for an illustration of our results.

A wider perspective: From Rudich’s impossibility to structured building blocks and bounded-TFNP hardness. Our results apply to a wide class of search problems, and not only to the specific source-or-sink and SVL problems. We consider the notion of TFNP instances with a guaranteed (non-trivial) upper bound on their number of existing solutions, to which we refer as bounded-TFNP instances. This captures, in particular, source-or-sink instances and (valid) SVL instances, and provides a more general and useful perspective for studying cryptographic limitations in constructing hard instances of search problems.

Equipped with such a wide perspective, our approach and proof techniques build upon, and significantly extend, Rudich’s classic proof for ruling out black-box constructions of one-way permutations based on one-way functions [34]. We extend Rudich’s approach from its somewhat restricted context of one-way functions (as building blocks) and one-way permutations (as target objects) to provide a richer framework that considers: (1) significantly more structured building blocks, and (2) significantly less restricted target objects. Specifically, we bound the limitations of hard-on-average source-or-sink and SVL instances as building blocks (instead of one-way functions), and we rule out bounded-TFNP instances as target objects (instead of one-way permutations).

Fig. 1.

An illustration of our results. Dashed arrows correspond to known implications, and solid arrows correspond to our separations.

1.2 Open Problems

Several interesting open problems arise directly from our results, and here we point out some of them.

• The strong structural barrier put forward in Theorem 1.4 stands in stark contrast to the approach of Bitansky et al. [8] and Garg et al. [20]. Thus, an intriguing open problem is either to extend our impossibility result to rule out constructions with any number of solutions, or to circumvent our impossibility result by designing instances with an nearly-exponential number of solutions based on standard cryptographic assumptions.

• More generally, the question of circumventing black-box impossibility results by utilizing non-black-box techniques is always fascinating. In our specific context, already the obfuscation-based constructions of Bitansky et al. [8] and Garg et al. [20] involve non-black-box techniques (e.g., they apply an indistinguishability obfuscator to a circuit that uses a pseudorandom function). However, as recently shown by Asharov and Segev [2, 3], as long as the indistinguishability obfuscator itself is used in a black-box manner, such techniques can in fact be captured by refining the existing frameworks for black-box separations (specifically, the framework of Asharov and Segev captures the obfuscation-based constructions of Bitansky et al. [8] and Garg et al. [20]). Thus, an exciting open problem is to circumvent our results by utilizing non-black-box techniques while relying on standard cryptographic assumptions.

• Our impossibility results in Theorem 1.4 and Corollary 1.5 apply to any building block that exists relative to a random injective trapdoor function oracle (e.g., a collision-resistent hash function). It is not clear, however, whether similar impossibility results may apply to one-way permutations. Thus, an intriguing open problem is either to extend our impossibility results to rule out constructions based on one-way permutations, or to circumvent our impossibility results by designing hard-on-average instances based on one-way permutations. We note that by relying on one-way permutations it is rather trivial to construct some arbitrary hard-on-average TFNP distribution (even one with unique solutions), but it is not known how to construct less arbitrary forms of hardness, such as average-case PPAD or SVL hardness.

• The recent work of Hubácek, Naor, and Yogev [26] proposes two elegant approaches for constructing hard-on-average TFNP instances. Their first approach is based on any hard-on-average NP relation (the existence of which is implied, for example, by any one-way function) in a black-box manner, and results in TFNP instances with a possibly exponential number of solutions. Their second approach is based on any injective one-way function and a non-interactive witness-indistinguishable proof system for $\mathsf{NP}$ (which can be constructed based on trapdoor permutations), and results in TFNP instances having at most two solutions. An interesting question is whether their approaches imply not only average-case TFNP hardness for the particular problems defined by their underlying one-way function and proof system, but also more specific forms of TFNP hardness, such as average-case PPAD or SVL hardness.

1.3 Overview of Our Approach

In this section we provide a high-level overview of the main ideas underlying our results. Each of our results is of the form “the existence of P does not imply the existence of Q in a black-box manner”, where each of P and Q is either a cryptographic primitive (e.g., a one-way function) or a hard-on-average search problem (e.g., the source-or-sink problem). Intuitively, such a statement is proved by constructing a distribution over oracles relative to which there exists an implementation of P, but any implementation of Q can be “efficiently broken”. Our formal proofs properly formalize this intuition via the standard framework of black-box reductions (e.g., [21, 27, 28, 32]).

Average-case SVL hardness does not imply OWFs. Theorem 1.1 is proved by presenting a distribution of oracles relative to which there exists a hard-on-average distribution of SVL instances, but there are no one-way functions. An SVL instance is of the form $\{(\mathsf{S}_n, \mathsf{V}_n, L(n))\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ it holds that $\mathsf{S}_n : \{0,1\}^n \rightarrow \{0,1\}^n$, $\mathsf{V}_n : \{0,1\}^n \times [2^n] \rightarrow \{0,1\}$, and $L(n) \in [2^n]$. Such an instance is valid if for every $n \in \mathbb {N}$, $x \in \{0,1\}^n$, and $i \in [2^n]$, it holds that $\mathsf{V}_n(x,i) = 1$ if and only if $x = \mathsf{S}_n^i(0^n)$. Intuitively, the circuit $\mathsf{S}_n$ can be viewed as implementing the successor function of a directed graph over $\{0,1\}^n$ that consists of a single line starting at $0^n$, and the circuit $\mathsf{V}_n$ enables to efficiently test whether a given node x is of distance i from $0^n$ on the line. The goal is to find the node of distance L(n) from $0^n$ (see Sect. 2.1 for the formal definition of the SVL problem).

We consider an oracle that is a valid SVL instance $\mathcal {O}_\mathsf{SVL}$ corresponding to a graph with a single line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ of length $L(n) = 2^{n/2}$. The line is chosen uniformly among all lines in $\{0,1\}^n$ of length L(n) starting at $0^n$ (and all nodes outside the line have self loops and are essentially irrelevant). First, we show that the oracle $\mathcal {O}_\mathsf{SVL}$ is indeed a hard-on-average SVL instance. This is based on the following, rather intuitive, observation: Since the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ is sparse and uniformly sampled, then any algorithm performing $q = q(n)$ oracle queries should not be able to query $\mathcal {O}_\mathsf{SVL}$ with any element on the line beyond the first q elements $0^n, x_1, \ldots , x_{q-1}$. In particular, for our choice of parameters, any algorithm performing at most, say, $2^{n/4}$ queries, has only an exponentially-small probability of reaching $x_{L(n)}$ (where the probability is taken over the choice of the oracle $\mathcal {O}_\mathsf{SVL}$).

Then, we show that any oracle-aided function $F^{\mathcal {O}_\mathsf{SVL}}(\cdot )$ can be inverted (with high probability over the choice of the oracle $\mathcal {O}_\mathsf{SVL}$) by an algorithm whose query complexity is polynomially-related to that of the function $F^{\mathcal {O}_\mathsf{SVL}}(\cdot )$. The proof is based on the following approach. Consider a value $y = F^{\mathcal {O}_\mathsf{SVL}}(x)$ that we would like to invert. If F performs at most $q = q(n)$ oracle queries, the above-mentioned observation implies that the computation $F^{\mathcal {O}_\mathsf{SVL}}(x)$ should not query $\mathcal {O}_\mathsf{SVL}$ with any elements on the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ except for the first q elements $x_0, x_1, \ldots , x_{q-1}$. This observation gives rise to the following inverter $\mathcal {A}$: First perform q queries to $\mathcal {O}_\mathsf{SVL}$ for discovering $x_1, \ldots , x_q$, and then invert $y = F^{\mathcal {O}_\mathsf{SVL}}(x)$ relative to the oracle $\widetilde{\mathcal {O}_\mathsf{SVL}}$ defined via the following successor function $\widetilde{\mathsf{S}}$:

$$\begin{aligned} \widetilde{\mathsf{S}}(\alpha ) = \left\{ \begin{array}{cl} x_{i+1} &{} \text{ if } \alpha =x_i \text{ for } \text{ some } i \in \{0, \ldots , q - 1\} \\ \alpha &{} \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

The formal proof is in fact more subtle, and requires a significant amount of caution when inverting $y = F^{\mathcal {O}_\mathsf{SVL}}(x)$ relative to the oracle $\widetilde{\mathcal {O}_\mathsf{SVL}}$. Specifically, the inverter $\mathcal {A}$ should find an input $\widetilde{x}$ such that the computations $F^{\widetilde{\mathcal {O}_\mathsf{SVL}}}(\widetilde{x})$ and $F^{\mathcal {O}_\mathsf{SVL}}(\widetilde{x})$ do not query the oracles $\widetilde{\mathcal {O}_\mathsf{SVL}}$ and $\mathcal {O}_\mathsf{SVL}$, respectively, with any of $x_q, \ldots , x_{L(n)}$. In this case, we show that indeed $F^{\mathcal {O}_\mathsf{SVL}}(\widetilde{x}) = y$ and the inverter is successful. We refer the reader to Sect. 3 for more details and for the formal proof.

Average-case SVL hardness and OWFs do not imply key agreement. Theorem 1.2 is proved by showing that in any black-box construction of a key-agreement protocol based on a one-way function and a hard-on-average distribution of SVL instances, we can eliminate the protocol’s need for using the SVL instances. This leads to a black-box construction of key-agreement protocol based on a one-way function, which we can then rule out by invoking the classic result of Impagliazzo and Rudich [27] and its refinement by Barak and Mahmoody-Ghidary [6].

Specifically, consider a key-agreement protocol $(\mathcal {A}^{f,\mathcal {O}_\mathsf{SVL}},\mathcal {B}^{f,\mathcal {O}_\mathsf{SVL}})$ in which the parties have oracle access to a random function f and to the oracle $\mathcal {O}_\mathsf{SVL}$ used for proving Theorem 1.1. Then, if $\mathcal {A}$ and $\mathcal {B}$ perform at most $q = q(n)$ oracle queries, the observation underlying the proof of Theorem 1.1 implies that, during an execution $(\mathcal {A}^{f,\mathcal {O}_\mathsf{SVL}}, \mathcal {B}^{f,\mathcal {O}_\mathsf{SVL}})$ of the protocol, the parties should not query $\mathcal {O}_\mathsf{SVL}$ with any elements on the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ except for the first q elements $x_0, x_1, \ldots , x_{q-1}$. This observation gives rise to a key-agreement protocol $(\widetilde{\mathcal {A}}^f, \widetilde{\mathcal {B}}^f)$ that does not require access to the oracle $\mathcal {O}_\mathsf{SVL}$: First, $\widetilde{A}$ samples a sequence $x_1, \ldots , x_q$ of q values, and sends these values to $\widetilde{B}$. Then, $\widetilde{\mathcal {A}}$ and $\widetilde{\mathcal {B}}$ run the protocol $(\mathcal {A}^{f,\mathcal {O}_\mathsf{SVL}},\mathcal {B}^{f,\mathcal {O}_\mathsf{SVL}})$ by using the values $x_1, \ldots , x_q$ instead of accessing $\mathcal {O}_\mathsf{SVL}$. That is, $\widetilde{A}$ and $\widetilde{B}$ run the underlying protocol relative to the given oracle f and to the oracle $\widetilde{\mathcal {O}_\mathsf{SVL}}$ defined via the following successor function $\widetilde{\mathsf{S}}$ (which each party can compute on its own):

$$\begin{aligned} \widetilde{\mathsf{S}}(\alpha ) = \left\{ \begin{array}{cl} x_{i+1} &{} \text{ if } \alpha =x_i \text{ for } \text{ some } i \in \{0, \ldots , q - 1\} \\ \alpha &{} \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

The formal proof is again rather subtle, and we refer the reader to the full version of this paper [33] for the formal proof.

Average-case PPAD hardness does not imply unique-TFNP hardness. Theorem 1.3 is proved by presenting a distribution of oracles relative to which there exists a hard-on-average distribution of instances of a PPAD-complete problem (specifically, we consider the source-or-sink problem), but there are no hard TFNP instances having unique solutions.

A TFNP instance with a unique solution, denoted a unique-TFNP instance, is of the form $\{C_n\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ it holds that $C_n : \{0,1\}^n \rightarrow \{0,1\}$ and there is a unique $x^* \in \{0,1\}^n$ such that $C(x) = 1$. Note that any valid SVL instance yields a TFNP instance that has a unique solution. Therefore, relative to our distribution over oracles any valid SVL instance can be efficiently solved.

A source-or-sink instance is of the form $\{(\mathsf{S}_n, \mathsf{P}_n)\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ it holds that $\mathsf{S}_n : \{0,1\}^n \rightarrow \{0,1\}^n$ and $\mathsf{P}_n : \{0,1\}^n \rightarrow \{0,1\}^n$. Intuitively, the circuits $\mathsf{S}_n$ and $\mathsf{P}_n$ can be viewed as implementing the successor and predecessor functions of a directed graph over $\{0,1\}^n$, where the in-degree and out-degree of every node is at most one, and the in-degree of $0^n$ is 0 (i.e., it is a source). The goal is to find any node, other than $0^n$, with either no incoming edge and no outgoing edge. We again refer the reader to Sect. 2.1 for the formal definitions.

We consider an oracle that is a source-or-sink instance $\mathcal {O}_\mathsf{PPAD}$ which is based on the same sparse structure used to define the oracle $\mathcal {O}_\mathsf{SVL}$: It corresponds to a graph with a single line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ of length $L(n) = 2^{n/2}$. The line is chosen uniformly among all lines in $\{0,1\}^n$ of length L(n) starting at $0^n$ (and all nodes outside the line have self loops). The fact that the oracle $\mathcal {O}_\mathsf{PPAD}$ is a hard-on-average source-or-sink instance follows quite easily from the above-mentioned observation on its sparse and uniform structure: Any algorithm performing $q=q(n)$ oracle queries should not be able to query $\mathcal {O}_\mathsf{PPAD}$ with any element on the line beyond the first q elements $x_0, x_1, \ldots , x_{q-1}$. In particular, for our choice of parameters, any such algorithm should have only an exponentially-small probability of reaching $x_{L(n)}$.

Solving any oracle-aided unique-TFNP instance relative to $\mathcal {O}_\mathsf{PPAD}$, however, turns out to be a completely different challenge. One might be tempted to follow a same approach based on the oracle’s sparse and uniform structure. Specifically, let $C_n$ be a unique-TFNP instance, and consider the unique value $x^* \in \{0,1\}^n$ for which $C^{\mathcal {O}_\mathsf{PPAD}}_n(x^*)=1$. Then, if $C_n$ issues at most $q=q(n)$ oracle queries, the computation $C^{\mathcal {O}_\mathsf{PPAD}}_n(x^*)$ should essentially not be able to query $\mathcal {O}_\mathsf{PPAD}$ with any elements on the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ except for the first q elements $0^n, x_1, \ldots , x_{q-1}$. Therefore, one can define a “fake” oracle $\widetilde{\mathcal {O}_\mathsf{PPAD}}$ whose successor and predecessor functions agree with $\mathcal {O}_\mathsf{PPAD}$ on $0^n, x_1, \ldots , x_q$ (and are defined as the identity functions for all other inputs), and then find the unique $\widetilde{x}$ such that $C^{\widetilde{\mathcal {O}_\mathsf{PPAD}}}_n(\widetilde{x}) = 1$. This approach, however, completely fails since the solution $x^*$ itself may depend on $\mathcal {O}_\mathsf{PPAD}$ in an arbitrary manner, providing the computation $C^{\mathcal {O}_\mathsf{PPAD}}_n(x^*)$ with sufficient information for querying $\mathcal {O}_\mathsf{PPAD}$ with an input $x_i$ that is located further along the line (i.e., $q\le i \le L(n)$).

As discussed in Sect. 1.1, our proof is obtained by significantly extending Rudich’s classic proof for ruling out black-box constructions of one-way permutations based on one-way functions [34]. Here, we show that his approach provides a rich framework that allows to bound not only the limitations of one-way functions as a building block, but even the limitations of significantly more structured primitives as building blocks. Specifically, our proof of Theorem 1.3 generalizes Rudich’s technique for bounding the limitations of hard-on-average source-or-sink instances. We refer the reader to Sect. 4 for more details and for the formal proof.

Injective trapdoor functions do not imply bounded-TFNP hardness. Theorem 1.4 and Corollary 1.5 are proved by presenting a distribution of oracles relative to which there exists a collection of injective trapdoor functions, but there are no hard TFNP instances having a bounded number of solutions (specifically, our result will apply to a sub-exponential number of solutions).

A TFNP instance with bounded number $k(\cdot )$ of solutions, denoted a k-bounded TFNP instance, is of the form $\{C_n\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ it holds that $C : \{0,1\}^n \rightarrow \{0,1\}$, and there is at least one and at most k(n) distinct inputs $x \in \{0,1\}^n$ such that $C(x) = 1$ (any one of these x’s is a solution). In particular, as discussed above, any valid SVL instance yields a 1-bounded TFNP instance (i.e., a unique-TFNP instance), and therefore our result rules out black-box constructions of a hard-on-average distribution of SVL instances from injective trapdoor functions. Similarly, any source-or-sink instance which consists of at most $(k+1)/2$ disjoint lines yields a k-bounded TFNP instance, and therefore our result rules out black-box constructions of a hard-on-average distribution of source-or-sink instances with a bounded number of disjoint lines from injective trapdoor functions.

For emphasizing the main ideas underlying our proof, in Sect. 5 we first prove our result for constructions that are based on one-way functions, and then in Sect. 6 we generalize the proof to constructions that are based on injective trapdoor functions. Each of these two parts requires introducing new ideas and techniques, and such a level of modularity is useful in pointing them out.

When considering constructions that are based on one-way functions, our proof is obtained via an additional generalization of Rudich’s proof technique [34]. As discussed above, we first observe that Rudich’s approach can be generalized from ruling out constructions of one-way permutations based on one-way functions to ruling out constructions of any hard-on-average distribution of unique-TFNP instances based on one-way functions. Then, by extending and refining Rudich’s proof technique once again, we show that we can rule out not only constructions of unique-TFNP instances, but even constructions of bounded-TFNP instances. This require a substantial generalization of Rudich’s attacker, and we refer reader to Sect. 5 for more details and for the formal proof.

Then, when considering constructions that are based on injective trapdoor functions, we show that our proof from Sect. 5 can be generalized from constructions of bounded-TFNP instances based on one-way functions to constructions of bounded-TFNP instances based on injective trapdoor functions. Combined with our the proof of Theorem 1.3, this extends Rudich’s approach from its somewhat restricted context of one-way functions (as building blocks) and one-way permutations (as target objects) to provide a richer framework that considers: (1) significantly more structured building blocks, and (2) significantly less restricted target objects. We refer reader to Sect. 6 for more details and for the formal proof.

1.4 Paper Organization

The remainder of this paper is organized as follows. In Sect. 2 we introduce our notation as well as the search problems and the cryptographic primitives that we consider in this paper. In Sect. 3 we show that average-case SVL hardness does not imply one-way functions in a black-box manner (proving Theorem 1.1). In Sect. 4 we show that average-case PPAD hardness does not imply unique-TFNP hardness in a black-box manner (proving Theorem 1.3). In Sect. 5 we show that one-way functions do not imply bounded-TFNP hardness in a black-box manner, and in Sect. 6 we generalize this result, showing that even injective trapdoor functions do not imply bounded-TFNP hardness in a black-box manner (proving Theorem 1.4 and Corollary 1.5). In the full version of this paper [33] we extend our approach from Sect. 3 and show that average-case SVL hardness does not imply key agreement even when assuming the existence of one-way functions.

2 Preliminaries

In this section we present the notation and basic definitions that are used in this work. For a distribution X we denote by $x \leftarrow X$ the process of sampling a value x from the distribution X. Similarly, for a set $\mathcal {X}$ we denote by $x \leftarrow \mathcal {X}$ the process of sampling a value x from the uniform distribution over $\mathcal {X}$. For an integer $n \in \mathbb {N}$ we denote by [n] the set $\{1,\ldots , n\}$. A q-query algorithm is an oracle-aided algorithm A such that for any oracle $\mathcal {O}$ and input $x \in \{0,1\}^*$, the computation $A^{\mathcal {O}}(x)$ consists of at most q(|x|) oracle calls to $\mathcal {O}$.

2.1 Complexity Classes and Total Search Problems

An efficiently-verifiable search problem is described via a pair $(I,R)$, where $I\subseteq \{0,1\}^*$ is an efficiently-recognizable set of instances, and $R$ is an efficiently-computable binary relation. Such a search problem is total if for every instance $z\in I$ there exists a witness w of length polynomial in the length $z$ such that $R(z,w) = 1$.

The class TFNP consists of all efficiently-verifiable search problem that are total, and its sub-class PPAD consists of all such problems that are polynomial-time reducible to the source-or-sink problem [31], defined as follows.

Definition 2.1

(The source-or-sink problem). A source-or-sink instance consists of a pair of circuits $\mathsf{S},\mathsf{P}: \{0,1\}^n \rightarrow \{0,1\}^n$ such that $\mathsf{P}(0^n)=0^n \ne \mathsf{S}(0^n)$. The goal is to find an element $w \in \{0,1\}^n$ such that $\mathsf{P}(\mathsf{S}(w))\ne w$ or $\mathsf{S}(\mathsf{P}(w)) \ne w\ne 0^n$.

Intuitively, the circuits $\mathsf{S}$ and $\mathsf{P}$ can be viewed as implementing the successor and predecessor functions of a directed graph over $\{0,1\}^n$, where for each pair of nodes x and y there exists an edge from x to y if and only if $\mathsf{S}(x) = y$ and $\mathsf{P}(y) = x$ (note that the in-degree and out-degree of every node in this graph is at most one, and the in-degree of $0^n$ is 0). The goal is to find any node, other than $0^n$, with either no incoming edge or no outgoing edge. Such a node must always exist by a parity argument.

The sink-of-verifiable-line (SVL) problem is a search problem introduced by Abbot et al. [1] and further studied by Bitansky et al. [8] and Garg et al. [20]. It is defined as follows:

Definition 2.2

(The sink-of-verifiable-line (SVL) problem). An SVL instance consists of a triplet $(\mathsf{S},\mathsf{V},T)$, where $T \in [2^n]$, and $\mathsf{S}:\{0,1\}^n \rightarrow \{0,1\}^n$ and $\mathsf{V}: \{0,1\}^n \times [2^n] \rightarrow \{0,1\}$ are two circuits with the guarantee that for every $x \in \{0,1\}^n$ and $i \in [2^n]$ it holds that $\mathsf{V}(x,i) = 1$ if and only if $x = \mathsf{S}^i(0^n)$. The goal is to find an element $w \in \{0,1\}^n$ such that $\mathsf{V}(w,T)= 1$.

Intuitively, the circuit $\mathsf{S}$ can be viewed as implementing the successor function of a directed graph over $\{0,1\}^n$ that consists of a single line starting at $0^n$. The circuit $\mathsf{V}$ enables to efficiently test whether a given node x is of distance i from $0^n$ on the line, and the goal is to find the node of distance T from $0^n$. Note that not any triplet $(\mathsf{S},\mathsf{V},T)$ is a valid SVL instance (moreover, there may not be an efficient algorithm for verifying whether a triplet $(\mathsf{S},\mathsf{V},T)$ is a valid instance).

Oracle-aided instances with private randomness. We consider source-or-sink and SVL instances that are described by oracle-aided circuits, and we would like to allow these circuits to share an oracle-dependent state that may be generated via private randomness (this clearly strengthens the class of problems that we consider, and in particular, capture those constructed by [8, 20] using indistinguishability obfuscation). For this purpose, we equip the instances with an oracle-aided randomized index-generation algorithm, denoted $\mathsf{Gen}$, that produces a public index $\sigma$ which is then provided to all circuits of the instance (and to any algorithm that attempts to solve the instance).

Specifically, we consider source-or-sink instances of the form $\{(\mathsf{Gen}_n, \mathsf{S}_n, \mathsf{P}_n)\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $\mathsf{S}_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^n$ and $\mathsf{P}_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^n$. Similarly, we consider SVL instances of the form $\{(\mathsf{Gen}_n, \mathsf{S}_n, \mathsf{V}_n, T(n))\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $\mathsf{S}_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^n$, $\mathsf{V}_n(\sigma ,\cdot ,\cdot ) : \{0,1\}^n \times [2^n] \rightarrow \{0,1\}$, and $T(n) \in [2^n]$. We say that an SVL instance is valid if for every $n \in \mathbb {N}$, $\sigma$ produced by $\mathsf{Gen}_n$, $x \in \{0,1\}^n$, and $i \in [2^n]$, it holds that $\mathsf{V}_n(\sigma ,x,i) = 1$ if and only if $x = \mathsf{S}_n^i(\sigma ,0^n)$.

Bounded TFNP instances. As discussed in Sect. 1.1, we prove our results using the notion of bounded-TFNP instances, naturally generalizing source-or-sink instances (and valid SVL instances) by considering TFNP instances with a guaranteed upper bound on the number of solutions.

Definition 2.3

A k-bounded TFNP instance is of the form $\{\mathsf{Gen}_n, C_n\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $C_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}$, and there is at least one and at most k(n) distinct inputs $x \in \{0,1\}^n$ such that $C_n(\sigma ,x) = 1$ (any one of these x’s is a solution).

Note that any valid SVL instance yields a 1-bounded TFNP instance (to which we refer as a unique-TFNP instance), and any source-or-sink instance which consists of at most $(k+1)/2$ disjoint lines yields a k-bounded TFNP instance.

Average-case PPAD hardness and bound-TFNP hardness. The following two definitions formalize the standard notion of average-case hardness in the specific context of source-or-sink instances and k-bounded TFNP instances. These notions then serve as the basis of our definitions of black-box constructions.

Definition 2.4

Let $t = t(n)$ and $\epsilon = \epsilon (n)$ be functions of the security parameter $n \in \mathbb {N}$. A source-or-sink instance $\{(\mathsf{Gen}_n, \mathsf{S}_n, \mathsf{P}_n)\}_{n \in \mathbb {N}}$ is $(t,\epsilon )$-hard if for any algorithm $\mathcal {A}$ that runs in time t(n) it holds that

$$\begin{aligned} \Pr \left[ \mathcal {A}\left( 1^n,\sigma \right) = w \text{ s.t. } \mathsf{P}_n(\sigma ,\mathsf{S}_n(\sigma ,w))\ne w \text{ or } \mathsf{S}_n(\sigma ,\mathsf{P}_n(\sigma ,w)) \ne w\ne 0^n \right] \le \epsilon (n) \end{aligned}$$

for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma \leftarrow \mathsf{Gen}_n()$ and over the internal randomness of $\mathcal {A}$.

Definition 2.5

Let $k = k(n)$, $t = t(n)$ and $\epsilon = \epsilon (n)$ be functions of the security parameter $n \in \mathbb {N}$. A k-bounded TFNP instance $\{\mathsf{Gen}_n, C_n\}_{n \in \mathbb {N}}$ is $(t,\epsilon )$-hard if for any algorithm $\mathcal {A}$ that runs in time t(n) it holds that

$$\begin{aligned} \Pr \left[ \mathcal {A}\left( 1^n,\sigma \right) = x \text{ s.t. } C_n(\sigma ,x)=1 \right] \le \epsilon (n) \end{aligned}$$

for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma \leftarrow \mathsf{Gen}_n()$ and over the internal randomness of $\mathcal {A}$.

2.2 One-Way Functions and Injective Trapdoor Functions

We rely on the standard (parameterized) notions of a one-way function and injective trapdoor functions [22].

Definition 2.6

An efficiently-computable function $f : \{0,1\}^* \rightarrow \{0,1\}^*$ is $(t(\cdot ), \epsilon (\cdot ))$-one-way if for any probabilistic algorithm A that runs in time t(n) it holds that

$$\begin{aligned} \Pr \left[ A\left( f(x) \right) \in f^{-1}\left( f(x) \right) \right] \le \epsilon (n) \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$, where the probability is taken over the choice of $x \leftarrow \{0,1\}^n$ and over the internal randomness of A.

A collection of injective trapdoor functions is a triplet $(\mathsf {KG}, \mathsf{F}, \mathsf{F}^{-1})$ of polynomial-time algorithms. The key-generation algorithm $\mathsf {KG}$ is a probabilistic algorithm that on input the security parameter $1^n$ outputs a pair $(\mathsf{pk},\mathsf{td})$, where $\mathsf{pk}$ is a public key and $\mathsf{td}$ is a corresponding trapdoor. For any $n \in \mathbb {N}$ and for any pair $(\mathsf{pk},\mathsf{td})$ that is produced by $\mathsf {KG}(1^n)$, the evaluation algorithm $\mathsf{F}$ computes an injective function $\mathsf{F}(\mathsf{pk},\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^{\ell (n)}$, and the inversion algorithm $F^{-1}(\mathsf{td},\cdot ) : \{0,1\}^{\ell (n)} \rightarrow \{0,1\}^n \cup \{ \bot \}$ computes its inverse whenever an inverse exists (i.e., it outputs $\bot$ on all values y that are not in the image of the function $\mathsf{F}(\mathsf{pk},\cdot )$). The security requirement of injective trapdoor functions is formalized as follows:

Definition 2.7

A collection of injective trapdoor functions $(\mathsf {KG}, \mathsf{F}, \mathsf{F}^{-1})$ is $(t(\cdot ), \epsilon (\cdot ))$-secure if for any probabilistic algorithm A that runs in time t(n) it holds that

$$\begin{aligned} \Pr \left[ A\left( \mathsf{pk}, \mathsf{F}(\mathsf{pk},x) \right) = x \right] \le \epsilon (n) \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$, where the probability is taken over the choice of $(\mathsf{pk},\mathsf{td}) \leftarrow \mathsf {KG}(1^n)$, $x \leftarrow \{0,1\}^n$, and over the internal randomness of A.

3 Average-Case SVL Hardness Does Not Imply One-Way Functions

In this section we prove that there is no fully black-box construction of a one-way function from a hard-on-average distribution of SVL instances⁴ (proving Theorem 1.1). Our result is obtained by presenting a distribution of oracles relative to which the following two properties hold:

• 1. There exists a hard-on-average distribution of SVL instances.

• 2. There are no one-way functions.

Recall that an SVL instance is of the form $\{(\mathsf{Gen}_n, \mathsf{S}_n, \mathsf{V}_n, L(n))\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $\mathsf{S}_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^n$, $\mathsf{V}_n(\sigma ,\cdot ,\cdot ) : \{0,1\}^n \times [2^n] \rightarrow \{0,1\}$, and $L(n) \in [2^n]$. We say that an SVL instance is valid if for every $n \in \mathbb {N}$, $\sigma$ produced by $\mathsf{Gen}_n$, $x \in \{0,1\}^n$, and $i \in [2^n]$, it holds that $\mathsf{V}_n(\sigma ,x,i) = 1$ if and only if $x = \mathsf{S}_n^i(\sigma ,0^n)$. The following definition tailors the standard notion of a fully black-box construction (based, for example, on [21, 28, 32]) to the specific primitives under consideration.

Definition 3.1

A fully black-box construction of a one-way function from a hard-on-average distribution of SVL instances consists of an oracle-aided polynomial-time algorithm F, an oracle-aided algorithm M that runs in time $T_M(\cdot )$, and functions $\epsilon _{M,1}(\cdot )$ and $\epsilon _{M,2}(\cdot )$, such that the following conditions hold:

• Correctness: There exists a polynomial $\ell (\cdot )$ such that for any valid SVL instance $\mathcal {O}_\mathsf{SVL}$ and for any $x \in \{0,1\}^*$ it holds that $F^{\mathcal {O}_\mathsf{SVL}}(x) \in \{0,1\}^{\ell (|x|)}$.

• Black-box proof of security: For any valid SVL instance $\mathcal {O}_\mathsf{SVL}= \{(\mathsf{Gen}_n,\mathsf{S}_n, \mathsf{V}_n, L(n))\}_{n \in \mathbb {N}}$, for any oracle-aided algorithm $\mathcal {A}$ that runs in time $T_\mathcal {A}=T_\mathcal {A}(n)$, and for any function $\epsilon _\mathcal {A}(\cdot )$, if

  $$\begin{aligned} \Pr \left[ \mathcal {A}^{\mathcal {O}_\mathsf{SVL}}\left( F^{\mathcal {O}_\mathsf{SVL}}(x)\right) \in \left( F^{\mathcal {O}_\mathsf{SVL}}\right) ^{-1} \left( F^{\mathcal {O}_\mathsf{SVL}}(x)\right) \right] \ge \epsilon _\mathcal {A}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $x \leftarrow \{0,1\}^n$ and over the internal randomness of $\mathcal {A}$, then

  $$\begin{aligned}&\Pr \left[ M^{\mathcal {A},\mathcal {O}_\mathsf{SVL}}\left( 1^n, \sigma \right) \text{ solves } \left( \mathsf{S}_n(\sigma ,\cdot ), \mathsf{V}_n(\sigma ,\cdot ), L(n) \right) \right] \\&\qquad \qquad \ge \epsilon _{M,1}\left( T_\mathcal {A}(n) / \epsilon _\mathcal {A}(n)\right) \cdot \epsilon _{M,2}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma \leftarrow \mathsf{Gen}_n()$ and over the internal randomness of M.

Following Asharov and Segev [2, 3], we split the security loss in the above definition to an adversary-dependent security loss and an adversary-independent security loss, as this allows us to capture constructions where one of these losses is super-polynomial whereas the other is polynomial (e.g., [8, 9]). In addition, we note that the correctness requirement in the above definition may seem somewhat trivial since the fact that the output length of $F^{\mathcal {O}_\mathsf{SVL}}(\cdot )$ is polynomial follows directly from the requirement that F runs in polynomial time. However, for avoiding rather trivial technical complications in the proofs of this section, for simplicity (and without loss of generality) we nevertheless ask explicitly that the output length is some fixed polynomial $\ell (n)$ for any input length n (clearly, $\ell (n)$ may depend on the running time of F, and shorter outputs can always be padded). Equipped with the above definition we prove the following theorem in the full version of this paper [33]:

Theorem 3.2

Let $(F,M,T_M,\epsilon _{M,1}, \epsilon _{M,2})$ be a fully black-box construction of a one-way function from a hard-on-average SVL instance. Then, at least one of the following properties holds:

• 1. $T_M(n)\ge 2^{\zeta n}$ for some constant $\zeta > 0$ (i.e., the reduction runs in exponential time).

• 2. $\epsilon _{M,1}(n^c) \cdot \epsilon _{M,2}(n) \le 2^{- n/10}$ for some constant $c > 1$ (i.e., the security loss is exponential).

In particular, Theorem 3.2 rules out standard “polynomial-time polynomial-loss” reductions. More generally, the theorem implies that if the running time $T_M(\cdot )$ of the reduction is sub-exponential and the adversary-dependent security loss $\epsilon _{M,1}(\cdot )$ is polynomial (as expected), then the adversary-independent security loss $\epsilon _{M,2}(\cdot )$ must be exponential (thus even ruling out constructions based on SVL instances with sub-exponential average-case hardness).

In what follows we first describe the oracle, denoted $\mathcal {O}_\mathsf{SVL}$, on which we rely for proving Theorem 3.2. Then, we describe the structure of the proof, showing that relative to the oracle $\mathcal {O}_\mathsf{SVL}$ there exists a hard-on-average distribution of SVL instances, but there are no one-way functions. For the remainder of this section we remind the reader that a q-query algorithm is an oracle-aided algorithm A such that for any oracle $\mathcal {O}$ and input $x \in \{0,1\}^*$, the computation $A^{\mathcal {O}}(x)$ consists of at most q(|x|) oracle calls to $\mathcal {O}$.

The oracle $\varvec{\mathcal {O}_\mathsf{SVL}}$ . The oracle $\mathcal {O}_\mathsf{SVL}$ is a valid SVL instance $\{ \left( \mathsf{S}_n, \mathsf{V}_n, L(n) \right) \}_{n \in \mathbb {N}}$ that is sampled via the following process for every $n \in \mathbb {N}$:

• Let $L(n) = 2^{n/2}$, $x_0 = 0^n$, and uniformly sample distinct elements $x_1, \ldots , x_{L(n)} \leftarrow \{0,1\}^n \setminus \{ 0^n \}$.

• The successor function $\mathsf{S}_n : \{0,1\}^n \rightarrow \{0,1\}^n$ is defined as

  $$\begin{aligned} \mathsf{S}_n(x) = \left\{ \begin{array}{cl} x_{i+1} &{} \text{ if } x=x_i \text{ for } \text{ some } i \in \{0, \ldots , L(n) - 1\} \\ x &{} \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

• The verification function $\mathsf{V}_n : \{0,1\}^n \times [2^n] \rightarrow \{0,1\}$ is defined in a manner that is consistent with $\mathsf{S}_n$ (i.e., $\mathsf{V}_n$ is defined such that the instance is valid).

Part I: $\varvec{\mathcal {O}_\mathsf{SVL}}$ is a hard-on-average SVL instance. We show that the oracle $\mathcal {O}_\mathsf{SVL}$ itself is a hard-on-average SVL instance, which implies in particular that relative to the oracle $\mathcal {O}_\mathsf{SVL}$ there exists a hard-on-average distribution of SVL instances. We prove the following claim stating that, in fact, the oracle $\mathcal {O}_\mathsf{SVL}$ is an exponentially hard-on-average SVL instance (even without an index-generation algorithm):

Claim 3.3

For every q(n)-query algorithm M, where $q(n)\le L(n)-1$, it holds that

$$\begin{aligned} \Pr \left[ M^{\mathcal {O}_\mathsf{SVL}}\left( 1^n\right) \text{ solves } \left( \mathsf{S}_n, \mathsf{V}_n, L(n) \right) \right] \le \frac{(q(n)+1) \cdot L(n)}{2^n - q(n) - 1} \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$, where the probability is taken over the choice of the oracle $\mathcal {O}_\mathsf{SVL}= \{ \left( \mathsf{S}_n, \mathsf{V}_n, L(n) \right) \}_{n \in \mathbb {N}}$ as described above.

The proof of the above claim is based on the following, rather intuitive, observation: Since the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ is sparse and uniformly sampled, then any algorithm performing $q=q(n)$ oracle queries should not be able to query $\mathcal {O}_\mathsf{SVL}$ with any element on the line beyond the first q elements $0^n, x_1, \ldots , x_{q-1}$. In particular, for our choice of parameters, any such algorithm should have only an exponentially-small probability of reaching $x_{L(n)}$.

Part II: Inverting oracle-aided functions relative to $\varvec{\mathcal {O}_\mathsf{SVL}}$ . We show that any oracle-aided function $F^{\mathcal {O}_\mathsf{SVL}}(\cdot )$ computable in time t(n) can be inverted with high probability by an inverter that issues roughly $t(n)^4$ oracle queries. We prove the following claim:

Claim 3.4

For every deterministic oracle-aided function F that is computable in time t(n) there exists a q(n)-query algorithm $\mathcal {A}$, where $q(n) = O(t(n)^4)$, such that

$$\begin{aligned} \Pr \left[ \mathcal {A}^{\mathcal {O}_\mathsf{SVL}}\left( F^{\mathcal {O}_\mathsf{SVL}}(x)\right) \in \left( F^{\mathcal {O}_\mathsf{SVL}}\right) ^{-1} \left( F^{\mathcal {O}_\mathsf{SVL}}(x)\right) \right] \ge \frac{1}{2} \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$ and for every $x\in \{0,1\}^n$, where the probability is taken over the choice of the oracle $\mathcal {O}_\mathsf{SVL}= \{ \left( \mathsf{S}_n, \mathsf{V}_n, L(n) \right) \}_{n \in \mathbb {N}}$ as described above. Moreover, the algorithm $\mathcal {A}$ can be implemented in time polynomial in q(n) given access to a $\mathsf{PSPACE}$-complete oracle.

The proof of the above claim is based on the following approach. Consider the value $y = F^{\mathcal {O}_\mathsf{SVL}}(x)$ that is given as input to the inverter $\mathcal {A}$. Since F is computable in time $t = t(n)$, it can issue at most t oracle queries and therefore the observation used for proving Claim 3.3 implies that the computation $F^{\mathcal {O}_\mathsf{SVL}}(x)$ should not query $\mathcal {O}_\mathsf{SVL}$ with any elements on the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ except for the first t elements $x_0, x_1, \ldots , x_{t-1}$. In this case, any $\mathsf{S}_n$-query $\alpha$ in the computation $F^{\mathcal {O}_\mathsf{SVL}}(x)$ can be answered as follows: If $\alpha =x_i$ for some $i \in \{ 0, \ldots , t-1\}$ then the answer is $x_{i+1}$, and otherwise the answer is $\alpha$. Similarly, any $\mathsf{V}_n$-query $(\alpha ,j)$ in the computation $F^{\mathcal {O}_\mathsf{SVL}}(x)$ can be answered as follows: If $(\alpha ,j) = (x_i,i)$ for some $i \in \{ 0, \ldots , t-1\}$ then the answer is 1, and otherwise the answer is 0.

This observation gives rise to the following inverter $\mathcal {A}$: First perform t queries to $\mathsf{S}_n$ for discovering $x_1, \ldots , x_t$, and then invert $y = F^{\mathcal {O}_\mathsf{SVL}}(x)$ relative to the oracle $\widetilde{\mathcal {O}_\mathsf{SVL}}$ defined via the following successor function $\widetilde{\mathsf{S}}_n$:

$$\begin{aligned} \widetilde{\mathsf{S}}_n(\alpha ) = \left\{ \begin{array}{cl} x_{i+1} &{} \text{ if } \alpha =x_i \text{ for } \text{ some } i \in \{0, \ldots , t - 1\} \\ \alpha &{} \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

The formal proof is in fact more subtle, and requires a significant amount of caution when inverting $y = F^{\mathcal {O}_\mathsf{SVL}}(x)$ relative to the oracle $\widetilde{\mathcal {O}_\mathsf{SVL}}$. Specifically, the inverter $\mathcal {A}$ should find an input $\widetilde{x}$ such that the computations $F^{\widetilde{\mathcal {O}_\mathsf{SVL}}}(\widetilde{x})$ and $F^{\mathcal {O}_\mathsf{SVL}}(\widetilde{x})$ do not query the oracles $\widetilde{\mathcal {O}_\mathsf{SVL}}$ and $\mathcal {O}_\mathsf{SVL}$, respectively, with any of $x_t, \ldots , x_{L(n)}$. In this case, we show that indeed $F^{\mathcal {O}_\mathsf{SVL}}(\widetilde{x}) = y$ and the inverter is successful.

4 Average-Case PPAD Hardness Does Not Imply Unique-TFNP Hardness

In this section we prove that there is no fully black-box construction of a hard-on-average distribution of TFNP instances having a unique solution from a hard-on-average distribution of instances of a PPAD-complete problem (proving, in particular, Theorem 1.3). Our result is obtained by presenting a distribution of oracles relative to which the following two properties hold:

• 1. There exists a hard-on-average distribution of instances of a PPAD-complete problem (specifically, we consider the source-or-sink problem).

• 2. There are no hard-on-average distributions over TFNP instances having a unique solution.

Recall that a TFNP instance with a unique solution, denoted a unique-TFNP instance (see Definitions 2.3 and 2.5), is of the form $\{\mathsf{Gen}_n, C_n\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $C_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}$ and there is a unique $x^* \in \{0,1\}^n$ such that $C_n(\sigma ,x) = 1$. In particular, for any valid SVL instance $(\mathsf{Gen}, \mathsf{S}, \mathsf{V}, T)$ it holds that $(\mathsf{Gen}, \mathsf{V}(\cdot ,\cdot ,T))$ is a TFNP instance that has a unique solution since for every $\sigma$ produced by $\mathsf{Gen}$ there is exactly one value $x^*$ for which $\mathsf{V}(\sigma ,x^*,T)=1$. Therefore, our result shows, in particular, that there is no fully black-box construction of a hard-on-average distribution of SVL instances from a hard-on-average distribution of instances of a PPAD-complete problem⁵.

Recall that a source-or-sink instance is of the form $\{(\mathsf{Gen}_n, \mathsf{S}_n, \mathsf{P}_n)\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $\mathsf{S}_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^n$ and $\mathsf{P}_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^n$. The following definition tailors the standard notion of a fully black-box construction to the specific primitives under consideration.

Definition 4.1

A fully black-box construction of a hard-on-average distribution of unique-TFNP instances from a hard-on-average distribution of source-or-sink instances consists of a sequence of polynomial-size oracle-aided circuits $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$, an oracle-aided algorithm M that runs in time $T_M(\cdot )$, and functions $\epsilon _{M,1}(\cdot )$ and $\epsilon _{M,2}(\cdot )$, such that the following conditions hold:

• Correctness: For any source-or-sink instance $\mathcal {O}_\mathsf{PPAD}$, for any $n \in \mathbb {N}$, and for any index $\sigma$ produced by $\mathsf{Gen}^{\mathcal {O}_\mathsf{PPAD}}_n$, there exists a unique $x^* \in \{0,1\}^n$ such that $C^{\mathcal {O}_\mathsf{PPAD}}_n(\sigma ,x^*) = 1$.

• Black-box proof of security: For any source-or-sink instance $\mathcal {O}_\mathsf{PPAD}= \{(\mathsf{Gen}'_n, \mathsf{S}_n, \mathsf{P}_n)\}_{n \in \mathbb {N}}$, for any oracle-aided algorithm $\mathcal {A}$ that runs in time $T_\mathcal {A}=T_\mathcal {A}(n)$, and for any function $\epsilon _\mathcal {A}(\cdot )$, if

  $$\begin{aligned} \Pr \left[ \mathcal {A}^{\mathcal {O}_\mathsf{PPAD}}\left( 1^n,\sigma \right) = x^* \text{ s.t. } C^{\mathcal {O}_\mathsf{PPAD}}_n(\sigma ,x^*)=1 \right] \ge \epsilon _\mathcal {A}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma \leftarrow \mathsf{Gen}_n()$ and over the internal randomness of $\mathcal {A}$, then

  $$\begin{aligned}&\Pr \left[ M^{\mathcal {A},\mathcal {O}_\mathsf{PPAD}}\left( 1^n,\sigma '\right) \text{ solves } \left( \mathsf{S}_n(\sigma ',\cdot ), \mathsf{P}_n(\sigma ',\cdot ) \right) \right] \\&\qquad \qquad \ge \epsilon _{M,1}\left( T_\mathcal {A}(n) / \epsilon _\mathcal {A}(n)\right) \cdot \epsilon _{M,2}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma ' \leftarrow \mathsf{Gen}'_n()$ and over the internal randomness of M.

We note that, as in Definition 3.1, we split the security loss in the above definition to an adversary-dependent security loss and an adversary-independent security loss, as this allows us to capture constructions where one of these losses is super-polynomial whereas the other is polynomial. Equipped with the above definition we prove the following theorem in the full version of this paper [33]:

Theorem 4.2

Let $(C,M,T_M,\epsilon _{M,1}, \epsilon _{M,2})$ be a fully black-box construction of a hard-on-average distribution of unique-TFNP instances from a hard-on-average distribution of source-or-sink instances. Then, at least one of the following properties holds:

• 1. $T_M(n)\ge 2^{\zeta n}$ for some constant $\zeta > 0$ (i.e., the reduction runs in exponential time).

• 2. $\epsilon _{M,1}(n^c) \cdot \epsilon _{M,2}(n) \le 2^{- n/10}$ for some constant $c > 1$ (i.e., the security loss is exponential).

In particular, Theorem 4.2 rules out standard “polynomial-time polynomial-loss” reductions. More generally, the theorem implies that if the running time $T_M(\cdot )$ of the reduction is sub-exponential and the adversary-dependent security loss $\epsilon _{M,1}(\cdot )$ is polynomial (as expected), then the adversary-independent security loss $\epsilon _{M,2}(\cdot )$ must be exponential (thus even ruling out constructions based on SVL instances with sub-exponential average-case hardness).

In what follows we first describe the oracle, denoted $\mathcal {O}_\mathsf{PPAD}$, on which we rely for proving Theorem 4.2. Then, we describe the structure of the proof, showing that relative to the oracle $\mathcal {O}_\mathsf{PPAD}$ there exists a hard-on-average distribution of source-or-sink instances, but there are no hard-on-average unique-TFNP instances. For the remainder of this section we remind the reader that a q-query algorithm is an oracle-aided algorithm A such that for any oracle $\mathcal {O}$ and input $x \in \{0,1\}^*$, the computation $A^{\mathcal {O}}(x)$ consists of at most q(|x|) oracle calls to $\mathcal {O}$.

The oracle $\varvec{\mathcal {O}_\mathsf{PPAD}}$ . The oracle $\mathcal {O}_\mathsf{PPAD}$ is a source-or-sink instance $\{ \left( \mathsf{S}_n, \mathsf{P}_n \right) \}_{n \in \mathbb {N}}$ that is based on the same sparse structure used to define the oracle $\mathcal {O}_\mathsf{SVL}$ in Sect. 3. The oracle $\mathcal {O}_\mathsf{PPAD}$ is sampled via the following process for every $n \in \mathbb {N}$:

• Let $L(n) = 2^{n/2}$, $x_0 = 0^n$, and uniformly sample distinct elements $x_1, \ldots ,x_{L(n)}\leftarrow \{0,1\}^n \setminus \{ 0^n \}$.

• The successor function $\mathsf{S}_n : \{0,1\}^n \rightarrow \{0,1\}^n$ is defined as

  $$\begin{aligned} \mathsf{S}_n(x) = \left\{ \begin{array}{cl} x_{i+1} &{} \text{ if } x=x_i \text{ for } \text{ some } i \in \{0, \ldots , L(n) - 1\} \\ x &{} \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

• The predecessor function $\mathsf{P}_n : \{0,1\}^n \rightarrow \{0,1\}^n$ is defined in a manner that is consistent with the successor function $\mathsf{S}_n$:

  $$\begin{aligned} \mathsf{P}_n(x) = \left\{ \begin{array}{cl} x_{i-1} &{} \text{ if } x=x_i \text{ for } \text{ some } i \in \{1, \ldots , L(n)\} \\ x &{} \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

Note that the oracle $\mathcal {O}_\mathsf{PPAD}$ corresponds to a source-or-sink instance that consists of the single line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$, and therefore the only solution to this instance is the element $x_{L(n)}$.

Part I: $\varvec{\mathcal {O}_\mathsf{PPAD}}$ is a hard-on-average source-or-sink instance. We show that the oracle $\mathcal {O}_\mathsf{PPAD}$ itself is a hard-on-average source-or-sink instance, which implies in particular that relative to the oracle $\mathcal {O}_\mathsf{PPAD}$ there exists a hard-on-average distribution of instances to the source-or-sink problem. We prove the following claim stating that, in fact, the oracle $\mathcal {O}_\mathsf{PPAD}$ is an exponentially hard-on-average source-or-sink instance (even without an index-generation algorithm):

Claim 4.3

For every q(n)-query algorithm M, where $q(n) \le L(n)-1$, it holds that

$$\begin{aligned} \Pr \left[ M^{\mathcal {O}_\mathsf{PPAD}}\left( 1^n\right) \text{ solves } \left( \mathsf{S}_n, \mathsf{P}_n \right) \right] \le \frac{(q(n)+1) \cdot L(n)}{2^n - q(n) - 1} \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$, where the probability is taken over the choice of the oracle $\mathcal {O}_\mathsf{PPAD}= \{ \left( \mathsf{S}_n, \mathsf{P}_n \right) \}_{n \in \mathbb {N}}$ as described above.

The proof of the claim, which is provided in the full version of this paper [33], is based on an observation similar to the one used for proving Claim 3.3: Since the line $0^n \rightarrow x_1 \rightarrow \cdots \rightarrow x_{L(n)}$ is sparse and uniformly sampled, then any algorithm performing $q=q(n)$ oracle queries should not be able to query $\mathcal {O}_\mathsf{PPAD}$ with any element on the line beyond the first q elements $x_0, x_1, \ldots , x_{q-1}$. In particular, for our choice of parameters, any such algorithm should have only an exponentially-small probability of reaching $x_{L(n)}$.

Part II: Solving oracle-aided unique-TFNP instances relative to $\varvec{\mathcal {O}_\mathsf{PPAD}}$ . We show that any oracle-aided unique-TFNP instance $\{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$, where $\mathsf{Gen}_n$ and $C_n$ are circuits that contain at most q(n) oracle gates, can always be solved by an algorithm that issues roughly $q(n)^2$ oracle queries. We prove the following claim:

Claim 4.4

Let $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$ be an oracle-aided unique-TFNP instance, where $\mathsf{Gen}_n$ and $C_n$ are circuits that contain at most q(n) oracle gates each for every $n \in \mathbb {N}$. If C satisfies the correctness requirement stated in Definition 4.1, then there exists an $O(q(n)^2)$-query algorithm $\mathcal {A}$ such that

$$\begin{aligned} \Pr \left[ \mathcal {A}^{\mathcal {O}_\mathsf{PPAD}}\left( 1^n,\sigma \right) = x^* \text{ s.t. } C^{\mathcal {O}_\mathsf{PPAD}}_n(\sigma ,x^*)=1 \right] = 1 \end{aligned}$$

for every $n \in \mathbb {N}$, where the probability is taken over the choice of the oracle $\mathcal {O}_\mathsf{PPAD}= \{ \left( \mathsf{S}_n, \mathsf{P}_n \right) \}_{n \in \mathbb {N}}$ as described above and over the choice of $\sigma \leftarrow \mathsf{Gen}^{\mathcal {O}_\mathsf{PPAD}}_n()$. Moreover, the algorithm $\mathcal {A}$ can be implemented in time $q(n)^2 \cdot \mathsf{poly}(n)$ given access to a $\mathsf{PSPACE}$-complete oracle.

For proving Claim 4.4, one might be tempted to follow the same approach used for proving Claim 3.4, based on the sparse and uniform structure of the oracle. However, as discussed in Sect. 1.3, this approach seems to completely fail.

Our proof of Claim 4.4, which is provided in the full version of this paper [33], is obtained by building upon Rudich’s classic proof for ruling out black-box constructions of one-way permutations based on one-way functions [34]. We show, by extending and refining Rudich’s proof technique, that his approach provides a rich framework that allows to bound not only the limitations of one-way functions as a building block, but even the limitations of significantly more structured primitives as building blocks. Specifically, our proof of Claim 4.4 extends Rudich’s technique for bounding the limitations of hard-on-average source-or-sink instances.

5 One-Way Functions Do Not Imply Bounded-TFNP Hardness

In this section we prove that there is no fully black-box construction of a hard-on-average distribution of TFNP instances having a bounded number of solutions from a one-way function. Our result is obtained by presenting a distribution of oracles relative to which the following two properties hold:

• 1. There exists a one-way function.

• 2. There are no hard-on-average distributions of TFNP instances having a bounded number of solutions. Specifically, our result will apply to any sub-exponential number of solutions.

Recall that a TFNP instance with bounded number $k(\cdot )$ of solutions, denoted a k-bounded TFNP instance (see Definitions 2.3 and 2.5), is of the form $\{\mathsf{Gen}_n, C_n\}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ and for every index $\sigma$ produced by $\mathsf{Gen}_n$ it holds that $C_n(\sigma ,\cdot ) : \{0,1\}^n \rightarrow \{0,1\}$, and there is at least one and at most k(n) distinct inputs $x \in \{0,1\}^n$ such that $C_n(\sigma ,x) = 1$ (any one of these x’s is a solution). In particular, as discussed in Sect. 4, any valid SVL instance yields a 1-bounded TFNP instance (i.e., a unique-TFNP instance as defined in Sect. 4), and therefore our result rules out fully black-box constructions of a hard-on-average distribution of SVL instances from a one-way function. Similarly, any source-or-sink instance which consists of at most $(k+1)/2$ disjoint lines yields a k-bounded TFNP instance, and therefore our result rules out fully black-box constructions of a hard-on-average distribution of source-or-sink instances with a bounded number of disjoint lines from a one-way function.

In this section we model a one-way function as a sequence $f = \{ f_n \}_{n \in \mathbb {N}}$, where for every $n \in \mathbb {N}$ it holds that $f_n : \{0,1\}^n \rightarrow \{0,1\}^n$. The following definition tailors the standard notion of a fully black-box construction to the specific primitives under consideration.

Definition 5.1

A fully black-box construction of a hard-on-average distribution of k-bounded TFNP instances from a one-way function consists of a sequence of polynomial-size oracle-aided circuits $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$, an oracle-aided algorithm M that runs in time $T_M(\cdot )$, and functions $\epsilon _{M,1}(\cdot )$ and $\epsilon _{M,2}(\cdot )$, such that the following conditions hold:

• Correctness: For any function $f = \{ f_n \}_{n \in \mathbb {N}}$, for any $n \in \mathbb {N}$, and for any index $\sigma$ produced by $\mathsf{Gen}^{f}_n$, there exists at least one and at most k(n) distinct inputs $x \in \{0,1\}^n$ such that $C^{f}_n(\sigma ,x) = 1$.

• Black-box proof of security: For any function $f = \{ f_n \}_{n \in \mathbb {N}}$, for any oracle-aided algorithm $\mathcal {A}$ that runs in time $T_\mathcal {A}=T_\mathcal {A}(n)$, and for any function $\epsilon _\mathcal {A}(\cdot )$, if

  $$\begin{aligned} \Pr \left[ \mathcal {A}^{f}\left( 1^n,\sigma \right) = x \text{ s.t. } C^{f}_n(\sigma ,x)=1 \right] \ge \epsilon _\mathcal {A}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma \leftarrow \mathsf{Gen}^f_n()$ and over the internal randomness of $\mathcal {A}$, then

  $$\begin{aligned} \Pr \left[ M^{\mathcal {A},f}\left( f_n(x) \right) \in f^{-1}_n \left( f_n(x)\right) \right] \ge \epsilon _{M,1}\left( T_\mathcal {A}(n) / \epsilon _\mathcal {A}(n)\right) \cdot \epsilon _{M,2}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $x \leftarrow \{0,1\}^n$ and over the internal randomness of M.

We note that, as in Definitions 3.1 and 4.1, we split the security loss in the above definition to an adversary-dependent security loss and an adversary-independent security loss, as this allows us to capture constructions where one of these losses is super-polynomial whereas the other is polynomial. Equipped with the above definition we prove the following theorem in the full version of this paper [33]:

Theorem 5.2

Let $(C,M,T_M,\epsilon _{M,1}, \epsilon _{M,2})$ be a fully black-box construction of a hard-on-average distribution of k-bounded TFNP instances from a one-way function. Then, at least one of the following properties holds:

• 1. $T_M(n)\ge 2^{\zeta n}$ for some constant $\zeta > 0$ (i.e., the reduction runs in exponential time).

• 2. $k(T_M(n))\ge 2^{n/8}$ (i.e., the number of solutions, as a function of the reduction’s running time, is exponential).

• 3. $\epsilon _{M,1}(k(n) \cdot n^c) \cdot \epsilon _{M,2}(n) \le 2^{- n/2}$ for some constant $c > 1$ (i.e., the security loss is exponential).

In particular, Theorem 5.2 rules out standard “polynomial-time polynomial-loss” reductions resulting in at most $2^{n^{o(1)}}$ solutions. That is, if $T_M(n)$, $\epsilon _{M,1}(n)$ and $\epsilon _{M,2}(n)$ are all polynomials in n, then the number k(n) of solutions must be at least sub-exponential in n (i.e., $k(n) \ge 2^{n^{\Theta (1)}}$). In addition, if the number k(n) of solutions is constant, the running time $T_M(\cdot )$ of the reduction is sub-exponential, and the adversary-dependent security loss $\epsilon _{M,1}(\cdot )$ is polynomial (all as in [8]), then the adversary-independent security loss $\epsilon _{M,2}(\cdot )$ must be exponential (thus even ruling out constructions based on one-way functions with sub-exponential hardness).

In what follows we first describe the oracle, denoted f, on which we rely for proving Theorem 5.2. Then, we describe the structure of the proof, showing that relative to the oracle f there exists a one-way function, but there are no hard-on-average bounded-TFNP instances. For the remainder of this section we remind the reader that a q-query algorithm is an oracle-aided algorithm A such that for any oracle $\mathcal {O}$ and input $x \in \{0,1\}^*$, the computation $A^{\mathcal {O}}(x)$ consists of at most q(|x|) oracle calls to $\mathcal {O}$.

The oracle $\varvec{f}$ . The oracle f is a sequence $\{ f_n \}_{n \in \mathbb {N}}$ where for every $n \in \mathbb {N}$ the function $f_n : \{0,1\}^n \rightarrow \{0,1\}^n$ is sampled uniformly from the set of all functions mapping n-bit inputs to n-bit outputs.

Part I: $\varvec{f}$ is a one-way function. We prove the following standard claim stating that the oracle f is an exponentially-hard one-way function.

Claim 5.3

For every q(n)-query algorithm M it holds that

$$\begin{aligned} \Pr \left[ M^{f}\left( f_n(x) \right) \in f^{-1}_n \left( f_n(x)\right) \right] \le \frac{2(q(n)+1)}{2^n - q(n)} \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$, where the probability is taken over the choice of $x \leftarrow \{0,1\}^n$, and over the choice of the oracle $f = \{ f_n \}_{n \in \mathbb {N}}$ as described above.

Part II: Solving oracle-aided bounded-TFNP instances relative to $\varvec{f}$ . We show that any oracle-aided k-bounded TFNP instance $C = \{ C_n \}_{n \in \mathbb {N}}$, where each $C_n$ is a circuit that contains at most q(n) oracle gates, can always be solved by an algorithm that issues roughly $k(n) \cdot q(n)^2$ oracle queries. We prove the following claim:

Claim 5.4

Let $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$ be an oracle-aided k(n)-bounded TFNP instance, where $\mathsf{Gen}_n$ and $C_n$ are circuits that contain at most q(n) oracle gates each for every $n \in \mathbb {N}$. If C satisfies the correctness requirement stated in Definition 5.1, then there exists an $O(k(n)\cdot q(n)^2)$-query algorithm $\mathcal {A}$ such that

$$\begin{aligned} \Pr \left[ \mathcal {A}^{f}\left( 1^n,\sigma \right) = x \text{ s.t. } C^{f}_n(\sigma ,x)=1 \right] = 1 \end{aligned}$$

for all $n \in \mathbb {N}$, where the probability is taken over the choice of the oracle $f = \{ f_n \}_{n \in \mathbb {N}}$ as described above and over the choice of $\sigma \leftarrow \mathsf{Gen}^f_n()$. Moreover, the algorithm $\mathcal {A}$ can be implemented in time $k(n) \cdot q(n)^2 \cdot \mathsf{poly}(n)$ given access to a $\mathsf{PSPACE}$-complete oracle.

Our proof of Claim 5.4, which is provided in the full version of this paper [33], is obtained by further generalizing our extension of Rudich’s classic proof technique [34]. As discussed in Sect. 4, by extending and refining Rudich’s proof technique once again, we show that his approach allows to rule out even constructions of bounded-TFNP instances.

6 Public-Key Cryptography Does Not Imply Bounded-TFNP Hardness

In this section we generalize the result proved in Sect. 5 from considering a one-way function as the underlying building block to considering a collection of injective trapdoor functions as the underlying building block (thus proving, in particular, Theorem 1.4 and Corollary 1.5). Specifically, we prove that there is no fully black-box construction of a hard-on-average distribution of TFNP instances having a bounded number of solutions from a collection of injective trapdoor functions. Our result is obtained by presenting a distribution of oracles relative to which the following two properties hold:

• 1. There exists a collection of injective trapdoor functions.

• 2. There are no hard-on-average distributions of TFNP instances having a bounded number of solutions. Specifically, our result will apply to any sub-exponential number of solutions, exactly as in Sect. 5.

From the technical perspective, instead of considering an oracle $f = \{ f_n \}_{n \in \mathbb {N}}$ where for every $n \in \mathbb {N}$ the function $f_n : \{0,1\}^n \rightarrow \{0,1\}^n$ is sampled uniformly, we consider a more structured oracle, $\mathcal {O}_\mathsf{TDF}$, corresponding to a collection of injective trapdoor functions. Proving that the oracle $\mathcal {O}_\mathsf{TDF}$ is indeed hard to invert is quite standard (based, for example, on the approach of Haitner et al. [23]). However, showing that relative to the oracle $\mathcal {O}_\mathsf{TDF}$ we can solve bounded-TFNP instances is significantly more challenging than the corresponding proof relative to the oracle f.

We say that $\tau = \left\{ \left( \mathsf {KG}_n, \mathsf{F}_n, \mathsf{F}_n^{-1} \right) \right\} _{n \in \mathbb {N}}$ is a collection of injective trapdoor functions if for every $n \in \mathbb {N}$ and for every pair $(\mathsf{td},\mathsf{pk})$ produced by $\mathsf {KG}_n()$, the function $\mathsf{F}_n(\mathsf{pk},\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^m$ is injective (for some $m \ge n$) and the function $\mathsf{F}_n^{-1}(\mathsf{td},\cdot )$ computes it inverse whenever an inverse exists (i.e., it outputs $\bot$ on all values y that are not in the image of the function $\mathsf{F}_n(\mathsf{pk},\cdot )$) – see Sect. 2.2 for more details. The following definition tailors the standard notion of a fully black-box construction to the specific primitives under consideration.

Definition 6.1

A fully black-box construction of a hard-on-average distribution of k-bounded TFNP instances from a collection of injective trapdoor functions consists of a sequence of polynomial-size oracle-aided circuits $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$, an oracle-aided algorithm M that runs in time $T_M(\cdot )$, and functions $\epsilon _{M,1}(\cdot )$ and $\epsilon _{M,2}(\cdot )$, such that the following conditions hold:

• Correctness: For any collection $\tau$ of injective trapdoor functions, for any $n \in \mathbb {N}$, and for any index $\sigma$ produced by $\mathsf{Gen}^{\tau }_n$, there exists at least one and at most k(n) distinct inputs $x \in \{0,1\}^n$ such that $C^{\tau }_n(\sigma ,x) = 1$.

• Black-box proof of security: For any collection $\tau = \left\{ \left( \mathsf {KG}_n, \mathsf{F}_n, \mathsf{F}_n^{-1} \right) \right\} _{n \in \mathbb {N}}$ of injective trapdoor functions, for any oracle-aided algorithm $\mathcal {A}$ that runs in time $T_\mathcal {A}=T_\mathcal {A}(n)$, and for any function $\epsilon _\mathcal {A}(\cdot )$, if

  $$\begin{aligned} \Pr \left[ \mathcal {A}^{\tau }\left( 1^n,\sigma \right) = x \text{ s.t. } C^{\tau }_n(\sigma ,x)=1 \right] \ge \epsilon _\mathcal {A}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $\sigma \leftarrow \mathsf{Gen}^{\tau }_n()$ and $x \leftarrow \{0,1\}^n$, and over the internal randomness of $\mathcal {A}$, then

  $$\begin{aligned} \Pr \left[ M^{\mathcal {A},\tau }\left( \mathsf{pk}, \mathsf{F}_n(\mathsf{pk}, x) \right) =x \right] \ge \epsilon _{M,1}\left( T_\mathcal {A}(n) / \epsilon _\mathcal {A}(n)\right) \cdot \epsilon _{M,2}(n) \end{aligned}$$

  for infinitely many values of $n \in \mathbb {N}$, where the probability is taken over the choice of $(\mathsf{td},\mathsf{pk}) \leftarrow \mathsf {KG}_n()$, $x \leftarrow \{0,1\}^n$, and over the internal randomness of M.

We note that, as in Definitions 3.1, 4.1 and 5.1, we split the security loss in the above definition to an adversary-dependent security loss and an adversary-independent security loss, as this allows us to capture constructions where one of these losses is super-polynomial whereas the other is polynomial. Equipped with the above definition we prove the following theorem in the full version of this paper [33] (generalizing Theorem 5.2):

Theorem 6.2

Let $(C,M,T_M,\epsilon _{M,1}, \epsilon _{M,2})$ be a fully black-box construction of a hard-on-average distribution of k-bounded TFNP instances from a collection of injective trapdoor functions. Then, at least one of the following properties holds:

• 1. $T_M(n)\ge 2^{\zeta n}$ for some constant $\zeta > 0$ (i.e., the reduction runs in exponential time).

• 2. $k(T_M(n))\ge 2^{n/8}$ (i.e., the number of solutions, as a function of the reduction’s running time, is exponential).

• 3. $\epsilon _{M,1}(k(n) \cdot n^c) \cdot \epsilon _{M,2}(n) \le 2^{- n/2}$ for some constant $c > 1$ (i.e., the security loss is exponential).

In particular, and similarly to Theorem 5.2, Theorem 6.2 rules out standard “polynomial-time polynomial-loss” reductions resulting in at most $2^{n^{o(1)}}$ solutions. That is, if $T_M(n)$, $\epsilon _{M,1}(n)$ and $\epsilon _{M,2}(n)$ are all polynomials in n, then the number k(n) of solutions must be at least sub-exponential in n (i.e., $k(n) \ge 2^{n^{\Theta (1)}}$). In addition, if the number k(n) of solutions is constant, the running time $T_M(\cdot )$ of the reduction is sub-exponential, and the adversary-dependent security loss $\epsilon _{M,1}(\cdot )$ is polynomial (all as in [8]), then the adversary-independent security loss $\epsilon _{M,2}(\cdot )$ must be exponential (thus even ruling out constructions based on one-way functions with sub-exponential hardness). Given our claims in the remainder of this section, the proof of Theorem 6.2 is derived in a nearly identical to proof of 5.2, and is therefore omitted.

In what follows we first describe the oracle, denoted $\mathcal {O}_\mathsf{TDF}$, on which we rely for proving Theorem 6.2. Then, we describe the structure of the proof, and explain the main challenges in generalizing our proof from Sect. 5.

The oracle $\varvec{\mathcal {O}_\mathsf{TDF}}$ . The oracle $\mathcal {O}_\mathsf{TDF}$ is a sequence of the form $\{ \left( \mathsf {G}_n, \mathsf{F}_n, \mathsf{F}^{-1}_n \right) \}_{n \in \mathbb {N}}$ that is sampled via the following process for every $n \in \mathbb {N}$:

• The function $\mathsf {G}_n : \{0,1\}^n \rightarrow \{0,1\}^{2n}$ is sampled uniformly from the set of all functions mapping n-bit inputs to n-bit outputs.

• For every $\mathsf{pk}\in \{0,1\}^{2n}$ the function $\mathsf{F}_n(\mathsf{pk},\cdot ) : \{0,1\}^n \rightarrow \{0,1\}^{2n}$ is sampled uniformly from the set of all injective functions mapping n-bit inputs to 2n-bit outputs.

• For every $\mathsf{td}\in \{0,1\}^n$ and $y\in \{0,1\}^{2n}$ we set

  $$\begin{aligned} \mathsf{F}^{-1}_n(\mathsf{td},y) = \left\{ \begin{array}{cl} x &{} \text{ if } \mathsf{F}_n(\mathsf {G}_n(\mathsf{td}),x)=y \\ \bot &{} \text{ if } \text{ no } \text{ such } x \text{ exists }\\ \end{array} \right. . \end{aligned}$$

Part I: $\varvec{\mathcal {O}_\mathsf{TDF}}$ is a hard-to-invert collection of injective trapdoor functions. We show that the oracle $\mathcal {O}_\mathsf{TDF}$ naturally defines a hard-on-average collection of injective trapdoor functions. Specifically, the key-generation algorithm on input $1^n$ samples $\mathsf{td}\leftarrow \{0,1\}^n$ uniformly at random, and computes $\mathsf{pk}= \mathsf {G}_n(\mathsf{td})$ (where $\mathsf{F}_n$ and $\mathsf{F}_n^{-1}$ are used as the evaluation and inversion algorithms). We prove the following claim stating that collection of injective trapdoor functions is exponentially secure.

Claim 6.3

For every q(n)-query algorithm M it holds that

$$\begin{aligned} \Pr \left[ M^{\mathcal {O}_\mathsf{TDF}}\left( \mathsf {G}_n(\mathsf{td}), \mathsf{F}_n(\mathsf {G}_n(\mathsf{td}),x) \right) = x \right] \le \frac{4(q(n)+1)}{2^n-q(n)} \end{aligned}$$

for all sufficiently large $n \in \mathbb {N}$, where the probability is taken over the choice of $\mathsf{td}\leftarrow \{0,1\}^n$, $x \leftarrow \{0,1\}^n$, and the oracle $\mathcal {O}_\mathsf{TDF}= \{(\mathsf {G}_n,\mathsf{F}_n,\mathsf{F}_n^{-1})\}_{n \in \mathbb {N}}$.

The proof of Claim 6.3, which is provided in the full version of this paper [33], is based on the observation that the inversion oracle $F_n^{-1}$ is not quite useful. Specifically, the function $\mathsf {G}_n$ itself is uniformly chosen and thus hard to invert, and therefore any algorithm M that is given as input $(\mathsf{pk}, \mathsf{F}_n(\mathsf{pk},x))$ should not be able to find the trapdoor $\mathsf{td}$ corresponding to $\mathsf{pk}= \mathsf {G}_n(\mathsf{td})$. Combining this with the fact that the function $\mathsf{F}_n(\mathsf{pk},\cdot )$ is uniformly chosen and length doubling, such an algorithm M should not be able to find any y in its image, unless y was obtained as the result of a previous query (and, in this case, its inverse is already known). Therefore, the task of computing x given $(\mathsf{pk}, \mathsf{F}_n(\mathsf{pk},x))$ essentially reduces to that of inverting a uniformly-sampled injective function.

Part II: Solving oracle-aided bounded-TFNP instances relative to $\varvec{\mathcal {O}_\mathsf{TDF}}$ . We show that any oracle-aided k-bounded TFNP instance $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$, where $\mathsf{Gen}_n$ and $C_n$ contain at most q(n) oracle gates, and the input to each such gate is of length at most q(n) bits, can always be solved with constant probability by an algorithm that issues roughly $k(n)^3 \cdot q(n)^9$ oracle queries. We prove the following claim:

Claim 6.4

Let $C = \{ \mathsf{Gen}_n, C_n \}_{n \in \mathbb {N}}$ be an oracle-aided k-bounded TFNP instance, where for every $n \in \mathbb {N}$ it holds that $\mathsf{Gen}_n$ and $C_n$ are circuits that contain at most q(n) oracle gates, and the input to each such gate is of length at most q(n) bits. If C satisfies the correctness requirement stated in Definition 6.1, then there exists a $O(q(n)^9\cdot k(n)^3)$-query algorithm $\mathcal {A}$ such that

$$\begin{aligned} \Pr \left[ \mathcal {A}^{\mathcal {O}_\mathsf{TDF}}\left( 1^n,\sigma \right) = x \text{ s.t. } C^{\mathcal {O}_\mathsf{TDF}}_n(\sigma ,x)=1 \right] \ge \frac{1}{2} \end{aligned}$$

for all $n \in \mathbb {N}$, where the probability is taken over the choice of the oracle $\mathcal {O}_\mathsf{TDF}= \{(\mathsf {G}_n,\mathsf{F}_n,\mathsf{F}_n^{-1})\}_{n \in \mathbb {N}}$ as described above and over the choice of $\sigma \leftarrow \mathsf{Gen}^{\mathcal {O}_\mathsf{TDF}}_n()$. Moreover, the algorithm $\mathcal {A}$ can be implemented in time $q(n)^9\cdot k(n)^3 \cdot \mathsf{poly}(n)$ given access to a $\mathsf{PSPACE}$-complete oracle.

The proof of Claim 6.4, which is provided in the full version of this paper [33], generalizes the proof of Claim 5.4 (which holds relative to the oracle f defined in Sect. 5). Recall that for the proof of Claim 5.4 we introduced an adversary that runs for $q+1$ iterations, with the goal of discovering a new oracle query from the computation $C^f_n(\sigma ,x^*)$ in each iteration where $x^*$ is any fixed solution of the instance $C^f_n(\sigma ,\cdot )$. This approach is based on the observation if no progress is made then there exists an oracle $g'$ for which the instance $C^{g'}_n(\sigma ,\cdot )$ has too many solutions. The oracle oracle $g'$ can be constructed by “pasting together” partial information on the actual oracle f with full information on an additional oracle g that is partially-consistent with f.

When dealing with the oracle $\mathcal {O}_\mathsf{TDF}$, which is clearly more structured than just a single random function f, this argument becomes much more subtle. One may hope to follow a similar iteration-based approach and argue that if no progress is made then there exists an oracle $\mathcal {O}_\mathsf{TDF}'$ for which the instance $C^{\mathcal {O}_\mathsf{TDF}'}_n(\sigma ,\cdot )$ has too many solutions. However, “pasting together” partial information on the actual oracle $\mathcal {O}_\mathsf{TDF}$ with full information on an additional injective trapdoor function oracle that is partially-consistent with $\mathcal {O}_\mathsf{TDF}$ may completely fail, as the resulting oracle may not turn out injective at all.

Our main observation is that although pasting together the two oracles may not always work (as in Sect. 5), it does work with high probability over the choice of the oracle $\mathcal {O}_\mathsf{TDF}$. By closely examining the way the two oracles are combined, we show that if the resulting oracle is not a valid collection of injective trapdoor functions, then one of the following “bad” events must have occurred:

• The adversary was able to “guess” an element $\mathsf{pk}$ for which there exists $\mathsf{td}$ such that $\mathsf{pk}= \mathsf {G}_n(\mathsf{td})$ without previously querying $\mathsf {G}_n$ with $\mathsf{td}$.

• The adversary was able to “guess” a public key $\mathsf{pk}$ and an element y for which there exists an input x such that $y = \mathsf{F}_n(\mathsf{pk},x)$ without previously querying $\mathsf{F}_n$ with $(\mathsf{pk},x)$.

We show that the probability of each of these two events is small, as we choose both $\mathsf {G}_n$ and all functions $\mathsf{F}_n(\mathsf{pk},\cdot )$ to be length increasing and uniformly distributed.