Abstract
The interactive theorem prover Isabelle/HOL is based on the well understood Higher-Order Logic (HOL), which is widely believed to be consistent (and provably consistent in set theory by a standard semantic argument). However, Isabelle/HOL brings its own personal touch to HOL: overloaded constant definitions, used to achieve Haskell-like type classes in the user space. These features are a delight for the users, but unfortunately are not easy to get right as an extension of HOL—they have a history of inconsistent behavior. It has been an open question under which criteria overloaded constant definitions and type definitions can be combined together while still guaranteeing consistency. This paper presents a solution to this problem: non-overlapping definitions and termination of the definition-dependency relation (tracked not only through constants but also through types) ensures relative consistency of Isabelle/HOL.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In Isabelle/HOL, as in any HOL-based prover, the “datatype” command is not primitive, but is compiled into “typedef.”
- 2.
- 3.
Namely, Coq 8.4pl5; the inconsistency is fixed in Coq 8.5 beta.
- 4.
The deduction in polymorphic HOL takes place using open formulas in contexts. In addition, Isabelle/HOL distinguishes between theory contexts and proof contexts. We ignore these aspects in our presentation here, since they do not affect our consistency argument.
- 5.
Any infinite (not necessarily countable) set would do here; we only choose \(\mathbb {N}\) for simplicity.
- 6.
Composability reduces the search space when we are looking for the cycle—it tells us that there exist three cases on how to extend a path (to possibly close a cycle): in two cases we can still (easily) extend the path (\(v \le u'\) or \(u' \le v\)) and in one case we cannot (\(v \, {\#}\, u'\)). The fourth case (v and \(u'\) have a non-trivial common instance; formally \(u' \not \le v\) and \(v \not \le u'\) and there exists w such that \(w\le u'\), \(w\le v\)), which complicates the extension of the path, is ruled out by composability. More about composability can be found in the original paper.
- 7.
The correctness proof is relatively general and works for any
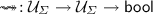
on a set \(\mathcal {U}_\varSigma \) endowed with a certain structure—namely, three functions \(= \,: \mathcal {U}_\varSigma \rightarrow \mathcal {U}_\varSigma \rightarrow \mathsf{bool}\), \(\mathsf {App}: (\mathsf {{Type}}\rightarrow \mathsf {{Type}}) \rightarrow \mathcal {U}_\varSigma \rightarrow \mathcal {U}_\varSigma \) and \({\mathsf {size}}: \mathcal {U}_\varSigma \rightarrow \mathbb {N}\), indicating how to compare for equality, type-substitute and measure the elements of \(\mathcal {U}_\varSigma \). In this paper, we set \(\varSigma = (K,\mathsf {arOf},C,{{\mathsf {tpOf}}})\) and \(\mathcal {U}_\varSigma = {{\mathsf {Type}^{\bullet }}}\cup {{\mathsf {CInst}}}^\bullet \). The definition of \(=, \mathsf {App}\) and \({\mathsf {size}}\) is then straightforward: two elements of \({{\mathsf {Type}^{\bullet }}}\cup {{\mathsf {CInst}}}^\bullet \) are equal iff they are both constant instances and they are equal or they are both types and they are equal; \(\mathsf {App}\,\rho \,\tau = \rho (\tau )\) and \(\mathsf {App}\,\rho \,c_{\tau } = c_{\rho (\tau )}\); finally, \({\mathsf {size}}(\tau )\) counts the number of type constructors in \(\tau \) and \({\mathsf {size}}(c_\tau ) = {\mathsf {size}}(\tau )\).
References
The HOL4 Theorem Prover. http://hol.sourceforge.net/
Adams, M.: Introducing HOL Zero. In: Fukuda, K., Hoeven, J., Joswig, M., Takayama, N. (eds.) ICMS 2010. LNCS, vol. 6327, pp. 142–143. Springer, Heidelberg (2010)
Anand, A., Rahli, V.: Towards a formally verified proof assistant. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 27–44. Springer, Heidelberg (2014)
Arthan, R.D.: Some mathematical case studies in ProofPower-HOL. In: TPHOLs 2004 (2004)
Barras, B.: Coq en Coq. Technical report 3026, INRIA (1996)
Barras, B.: Sets in Coq, Coq in Sets. J. Formalized Reasoning 3(1), 29–48 (2010)
Bertot, Y., Casteran, P.: Interactive Theorem Proving and Program Development: Coq’Art: The Calculus of Inductive Constructions. Springer, Heidelberg (2004)
Blanchette, J.C., Popescu, A., Traytel, D.: Foundational extensible corecursion. In: ICFP 2015. ACM (2015)
Bove, A., Dybjer, P., Norell, U.: A brief overview of Agda – a functional language with dependent types. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 73–78. Springer, Heidelberg (2009)
Dénès, M.: [Coq-Club] Propositional extensionality is inconsistent in Coq, archived at https://sympa.inria.fr/sympa/arc/coq-club/2013-12/msg00119.html
Gordon, M.J.C., Melham, T.F. (eds.): Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge University Press, New York (1993)
Haftmann, F., Wenzel, M.: Constructive type classes in Isabelle. In: Altenkirch, T., McBride, C. (eds.) TYPES 2006. LNCS, vol. 4502, pp. 160–174. Springer, Heidelberg (2007)
Harrison, J.: HOL Light: a tutorial introduction. In: Srivas, M., Camilleri, A. (eds.) FMCAD 1996. LNCS, vol. 1166, pp. 265–269. Springer, Heidelberg (1996)
Harrison, J.: Towards self-verification of HOL Light. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 177–191. Springer, Heidelberg (2006)
Hölzl, J., Immler, F., Huffman, B.: Type classes and filters for mathematical analysis in Isabelle/HOL. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 279–294. Springer, Heidelberg (2013)
Huffman, B., Urban, C.: Proof pearl: a new foundation for Nominal Isabelle. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 35–50. Springer, Heidelberg (2010)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: HOL with definitions: semantics, soundness, and a verified implementation. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 308–324. Springer, Heidelberg (2014)
Kunčar, O.: Correctness of Isabelle’s cyclicity checker: implementability of overloading in proof assistants. In: CPP 2015. ACM (2015)
Kunčar, O., Popescu, A.: A consistent foundation for Isabelle/HOL. Technical report (2015). www.eis.mdx.ac.uk/staffpages/andreipopescu/pdf/IsabelleHOL.pdf
Leino, K.R.M., Moskal, M.: Co-induction simply–automatic co-inductive proofs in a program verifier. In: FM 2014 (2014)
Lochbihler, A.: Light-Weight Containers for Isabelle: Efficient, Extensible, Nestable. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 116–132. Springer, Heidelberg (2013)
McBride, C., et al.: [HoTT] Newbie questions about homotopy theory and advantage of UF/Coq, archived at http://article.gmane.org/gmane.comp.lang.agda/6106
Müller, O., Nipkow, T., von Oheimb, D., Slotosch, O.: HOLCF = HOL + LCF. J. Funct. Program. 9, 191–223 (1999)
Myreen, M.O., Davis, J.: The reflective Milawa theorem prover is sound. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 421–436. Springer, Heidelberg (2014)
Nipkow, T., Klein, G.: Concrete Semantics - With Isabelle/HOL. Springer, New York (2014)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002)
Kang, J., Adibi, S.: Type classes and overloading resolution via order-sorted unification. In: Doss, R., Piramuthu, S., ZHOU, W. (eds.) Functional Programming Languages and Computer Architecture. LNCS, vol. 523, pp. 1–14. Springer, Heidelberg (1991)
Obua, S.: Checking conservativity of overloaded definitions in higher-order logic. In: Pfenning, F. (ed.) RTA 2006. LNCS, vol. 4098, pp. 212–226. Springer, Heidelberg (2006)
Pitts, A.: Introduction to HOL: a theorem proving environment for higher order logic. Chapter The HOL Logic, pp. 191–232. In: Gordon and Melham [12] (1993)
Shankar, N., Owre, S., Rushby, J.M.: PVS Tutorial. Computer Science Laboratory, SRI International (1993)
Sozeau, M., Oury, N.: First-class type classes. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 278–293. Springer, Heidelberg (2008)
Urban, C.: Nominal techniques in Isabelle/HOL. J. Autom. Reason. 40(4), 327–356 (2008)
Wadler, P., Blott, S.: How to make ad-hoc polymorphism less ad-hoc. In: POPL (1989)
Wenzel, M.: Type classes and overloading in higher-order logic. In: Gunter, E.L., Felty, A.P. (eds.) TPHOLs 1997. LNCS, vol. 1275, pp. 307–322. Springer, Heidelberg (1997)
Acknowledgments
We thank Tobias Nipkow, Larry Paulson and Makarius Wenzel for inspiring discussions and the anonymous referees for many useful comments. This paper was partially supported by the DFG project Security Type Systems and Deduction (grant Ni 491/13-3) as part of the program Reliably Secure Software Systems (RS3, priority program 1496).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Kunčar, O., Popescu, A. (2015). A Consistent Foundation for Isabelle/HOL. In: Urban, C., Zhang, X. (eds) Interactive Theorem Proving. ITP 2015. Lecture Notes in Computer Science(), vol 9236. Springer, Cham. https://doi.org/10.1007/978-3-319-22102-1_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-22102-1_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22101-4
Online ISBN: 978-3-319-22102-1
eBook Packages: Computer ScienceComputer Science (R0)