Abstract
The list segment predicate \(\mathtt {ls}\) used in separation logic for verifying programs with pointers is well-suited to express properties on singly-linked lists. We study the effects of adding \(\mathtt {ls}\) to the full propositional separation logic with the separating conjunction and implication, which is motivated by the recent design of new fragments in which all these ingredients are used indifferently and verification tools start to handle the magic wand connective. This is a very natural extension that has not been studied so far. We show that the restriction without the separating implication can be solved in polynomial space by using an appropriate abstraction for memory states whereas the full extension is shown undecidable by reduction from first-order separation logic. Many variants of the logic and fragments are also investigated from the computational point of view when \(\mathtt {ls}\) is added, providing numerous results about adding reachability predicates to propositional separation logic.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Separation logic [20, 25, 28] is a well-known assertion logic for reasoning about programs with dynamic data structures. Since the implementation of Smallfoot and the evidence that the method is scalable [3, 33], many tools supporting separation logic as an assertion language have been developed [3, 8, 9, 16, 17, 33]. Even though the first tools could handle relatively limited fragments of separation logic, like symbolic heaps, there is a growing interest and demand to consider extensions with richer expressive power. We can point out three particular extensions of symbolic heaps (without list predicates) that have been proved decidable.
-
Symbolic heaps with generalised inductive predicates, adding a fixpoint combinator to the language, is a convenient logic for specifying data structures that are more advanced than lists or trees. The entailment problem is known to be decidable by means of tree automata techniques for the bounded tree-width fragment [1, 19], whereas satisfiability is ExpTime-complete [6]. Other related results can be found in [21].
-
List-free symbolic heaps with all classical Boolean connectives \(\wedge \) and \(\lnot \) (and with the separating conjunction \(*\)), called herein \(\mathrm {SL}(*)\), is a convenient extension when combinations of results of various analysis need to be expressed, or when the analysis requires a complementation. This extension already is PSpace-complete [11].
-
Propositional separation logic with separating implication, a.k.a. magic wand
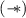 , is a convenient fragment (called herein
, is a convenient fragment (called herein 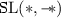 ) in which can be solved two problems of frame inference and abduction, that play an important role in static analysers and provers built on top of separation logic.
) in which can be solved two problems of frame inference and abduction, that play an important role in static analysers and provers built on top of separation logic.  can be decided in PSpace thanks to a small model property [32].
can be decided in PSpace thanks to a small model property [32].
A natural question is how to combine these extensions, and which separation logic fragment that allows Boolean connectives, magic wand and generalised recursive predicates can be decided with some adequate restrictions. As already advocated in [7, 18, 24, 29, 31], dealing with the separating implication  is a desirable feature for program verification and several semi-automated or automated verification tools support it in some way, see e.g. [18, 24, 29, 31].
is a desirable feature for program verification and several semi-automated or automated verification tools support it in some way, see e.g. [18, 24, 29, 31].
Our Contribution. In this paper, we address the question of combining magic wand and inductive predicates in the extremely limited case where the only inductive predicate is the gentle list segment predicate \(\mathtt {ls}\). So the starting point of this work is this puzzling question: what is the complexity/decidability status of propositional separation logic  enriched with the list segment predicate \(\mathtt {ls}\) (herein called
enriched with the list segment predicate \(\mathtt {ls}\) (herein called  )? More precisely, we study the decidability/complexity status of extensions of propositional separation logic
)? More precisely, we study the decidability/complexity status of extensions of propositional separation logic  by adding one of the reachability predicates among \(\mathtt {ls}\) (precise predicate as usual in separation logic), \(\mathtt {reach}\) (existence of a path, possibly empty) and \(\mathtt {reach}^{\scriptscriptstyle {+}}\) (existence of a non-empty path).
by adding one of the reachability predicates among \(\mathtt {ls}\) (precise predicate as usual in separation logic), \(\mathtt {reach}\) (existence of a path, possibly empty) and \(\mathtt {reach}^{\scriptscriptstyle {+}}\) (existence of a non-empty path).
First, we establish that the satisfiability problem for the propositional separation logic  is undecidable. Our proof is by reduction from the undecidability of first-order separation logic [5, 14], using an encoding of the variables as heap cells (see Theorem 1). As a consequence, we also establish that
is undecidable. Our proof is by reduction from the undecidability of first-order separation logic [5, 14], using an encoding of the variables as heap cells (see Theorem 1). As a consequence, we also establish that  is not finitely axiomatisable. Moreover, our reduction requires a rather limited expressive power of the list segment predicate, and we can strengthen our undecidability results to some fragments of
is not finitely axiomatisable. Moreover, our reduction requires a rather limited expressive power of the list segment predicate, and we can strengthen our undecidability results to some fragments of  . For instance, surprisingly, the extension of
. For instance, surprisingly, the extension of  with the atomic formulae of the form \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\) (existence of a path between \(\mathtt {x}\) and \(\mathtt {y}\) of respective length 2 or 3) is already undecidable, whereas the satisfiability problem for
with the atomic formulae of the form \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\) (existence of a path between \(\mathtt {x}\) and \(\mathtt {y}\) of respective length 2 or 3) is already undecidable, whereas the satisfiability problem for  is known to be in PSpace [15].
is known to be in PSpace [15].
Second, we show that the satisfiability problem for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) is PSpace-complete, extending the well-known result on \(\mathrm {SL}(*)\). The PSpace upper bound relies on a small heap property based on the techniques of test formulae, see e.g. [4, 15, 22, 23], and the PSpace-hardness of \(\mathrm {SL}(*)\) is inherited from [11]. The PSpace upper bound can be extended to the fragment of  made of Boolean combinations of formulae from
made of Boolean combinations of formulae from  (see the developments in Sect. 4). Even better, we show that the fragment of
(see the developments in Sect. 4). Even better, we show that the fragment of  in which \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is not in the scope of
in which \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is not in the scope of  is decidable. As far as we know, this is the largest fragment including full Boolean expressivity,
is decidable. As far as we know, this is the largest fragment including full Boolean expressivity,  and \(\mathtt {ls}\) for which decidability is established.
and \(\mathtt {ls}\) for which decidability is established.
2 Preliminaries
Let \(\mathrm PVAR= \{ \mathtt {x}, \mathtt {y}, \ldots \}\) be a countably infinite set of program variables and \(\mathrm{LOC}= \{ \ell _0,\ell _1, \ell _2, \ldots \}\) be a countable infinite set of locations. A memory state is a pair \((s,h)\) such that \(s: \mathrm PVAR\rightarrow \mathrm{LOC}\) is a variable valuation (known as the store) and \(h: \mathrm{LOC}\rightarrow _{\text {fin}} \mathrm{LOC}\) is a partial function with finite domain, known as the heap. We write \(\mathrm{dom}(h)\) to denote its domain and \(\mathrm{ran}(h)\) to denote its range. Given a heap \(h\) with \(\mathrm{dom}(h) = \{ \ell _1, \ldots , \ell _n \}\), we also write \(\{ \ell _1 \mapsto h(\ell _1), \ldots ,\ell _n \mapsto h(\ell _n) \}\) to denote \(h\). Each \(\ell _i \mapsto h(\ell _i)\) is understood as a memory cell of \(h\).
As usual, the heaps \(h_1\) and \(h_2\) are said to be disjoint, written \(h_1 \perp h_2\), if \(\mathrm{dom}(h_1) \cap \mathrm{dom}(h_2) = \emptyset \); when this holds, we write \(h_1 + h_2\) to denote the heap corresponding to the disjoint union of the graphs of \(h_1\) and \(h_2\), hence \(\mathrm{dom}(h_1 + h_2) = \mathrm{dom}(h_1) \uplus \mathrm{dom}(h_2)\). When the domains of \(h_1\) and \(h_2\) are not disjoint, the composition \(h_1 + h_2\) is not defined. Moreover, we write \(h' \sqsubseteq h\) to denote that \(\mathrm{dom}(h') \subseteq \mathrm{dom}(h)\) and for all locations \(\ell \in \mathrm{dom}(h')\), we have \(h'(\ell ) = h(\ell )\). The formulae \(\varphi \) of the separation logic  and its atomic formulae \(\pi \) are built from \( \pi \,{:}{:}\!\!= \mathtt {x}= \mathtt {y}\ \mid \ \mathtt {x}\hookrightarrow \mathtt {y}\ \mid \ \mathtt {ls}(\mathtt {x}, \mathtt {y}) \ \mid \ \mathtt {emp}\ \mid \ \top \) and
and its atomic formulae \(\pi \) are built from \( \pi \,{:}{:}\!\!= \mathtt {x}= \mathtt {y}\ \mid \ \mathtt {x}\hookrightarrow \mathtt {y}\ \mid \ \mathtt {ls}(\mathtt {x}, \mathtt {y}) \ \mid \ \mathtt {emp}\ \mid \ \top \) and  , where \(\mathtt {x}, \mathtt {y}\in \mathrm PVAR\) (\(\Rightarrow \), \(\Leftrightarrow \) and \(\vee \) are defined as usually). Models of the logic
, where \(\mathtt {x}, \mathtt {y}\in \mathrm PVAR\) (\(\Rightarrow \), \(\Leftrightarrow \) and \(\vee \) are defined as usually). Models of the logic  are memory states and the satisfaction relation \(\models \) is defined as follows (omitting standard clauses for \(\lnot , \wedge \)):
are memory states and the satisfaction relation \(\models \) is defined as follows (omitting standard clauses for \(\lnot , \wedge \)):

Note that the semantics for \(*\),  , \(\hookrightarrow \), \(\mathtt {ls}\) and for all other ingredients is the usual one in separation logic and \(\mathtt {ls}\) is the precise list segment predicate. In the sequel, we use the following abbreviations:
, \(\hookrightarrow \), \(\mathtt {ls}\) and for all other ingredients is the usual one in separation logic and \(\mathtt {ls}\) is the precise list segment predicate. In the sequel, we use the following abbreviations:  and for all \(\beta \ge 0\),
and for all \(\beta \ge 0\),  ,
,  and
and  . Moreover,
. Moreover,  (septraction connective),
(septraction connective),  and
and  . W.l.o.g., we can assume that \(\mathrm{LOC}= \mathbb {N}\) since none of the developments depend on the elements of \(\mathrm{LOC}\) as the only predicate involving locations is the equality. We write
. W.l.o.g., we can assume that \(\mathrm{LOC}= \mathbb {N}\) since none of the developments depend on the elements of \(\mathrm{LOC}\) as the only predicate involving locations is the equality. We write  to denote the restriction of
to denote the restriction of  without \(\mathtt {ls}\). Similarly, we write \(\mathrm {SL}(*)\) to denote the restriction of
without \(\mathtt {ls}\). Similarly, we write \(\mathrm {SL}(*)\) to denote the restriction of  without
without  . Given two formulae \(\varphi , \varphi '\) (possibly from different logical languages), we write
. Given two formulae \(\varphi , \varphi '\) (possibly from different logical languages), we write  whenever for all \((s,h)\), we have \((s,h) \models \varphi \) iff \((s,h) \models \varphi '\). When
whenever for all \((s,h)\), we have \((s,h) \models \varphi \) iff \((s,h) \models \varphi '\). When  , the formulae \(\varphi \) and \(\varphi '\) are said to be equivalent.
, the formulae \(\varphi \) and \(\varphi '\) are said to be equivalent.
Variants with Other Reachability Predicates. We use two additional reachability predicates \(\mathtt {reach}(\mathtt {x},\mathtt {y})\) and \(\mathtt {reach}^{\scriptscriptstyle {+}}(\mathtt {x},\mathtt {y})\) and we write  (resp.
(resp.  ) to denote the variant of
) to denote the variant of  in which \(\mathtt {ls}\) is replaced by \(\mathtt {reach}\) (resp. by \(\mathtt {reach}^{\scriptscriptstyle {+}}\)). The relation \(\models \) is extended as follows: \((s,h) \models \mathtt {reach}(\mathtt {x},\mathtt {y})\) holds when there is \(i \ge 0\) such that \(h^i(s(\mathtt {x})) = s(\mathtt {y})\) (i functional composition(s) of \(h\) is denoted by \(h^i\)) and \((s,h) \models \mathtt {reach}^{\scriptscriptstyle {+}}(\mathtt {x},\mathtt {y})\) holds when there is \(i \ge 1\) such that \(h^i(s(\mathtt {x})) = s(\mathtt {y})\). As
in which \(\mathtt {ls}\) is replaced by \(\mathtt {reach}\) (resp. by \(\mathtt {reach}^{\scriptscriptstyle {+}}\)). The relation \(\models \) is extended as follows: \((s,h) \models \mathtt {reach}(\mathtt {x},\mathtt {y})\) holds when there is \(i \ge 0\) such that \(h^i(s(\mathtt {x})) = s(\mathtt {y})\) (i functional composition(s) of \(h\) is denoted by \(h^i\)) and \((s,h) \models \mathtt {reach}^{\scriptscriptstyle {+}}(\mathtt {x},\mathtt {y})\) holds when there is \(i \ge 1\) such that \(h^i(s(\mathtt {x})) = s(\mathtt {y})\). As  and
and  , the logics
, the logics  and
and  have identical decidability status. As far as computational complexity is concerned, a similar analysis can be done as soon as \(*\), \(\lnot \), \(\wedge \) and \(\mathtt {emp}\) are parts of the fragments (the details are omitted here). Similarly, we have the equivalences:
have identical decidability status. As far as computational complexity is concerned, a similar analysis can be done as soon as \(*\), \(\lnot \), \(\wedge \) and \(\mathtt {emp}\) are parts of the fragments (the details are omitted here). Similarly, we have the equivalences:  and
and  . So clearly, \(\mathrm {SL}(*, \mathtt {reach})\) and \(\mathrm {SL}(*, \mathtt {ls})\) can be viewed as fragments of \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and,
. So clearly, \(\mathrm {SL}(*, \mathtt {reach})\) and \(\mathrm {SL}(*, \mathtt {ls})\) can be viewed as fragments of \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and,  as a fragment of
as a fragment of  . It is therefore stronger to establish decidability or complexity upper bounds with \(\mathtt {reach}^{\scriptscriptstyle {+}}\) and to show undecidability or complexity lower bounds with \(\mathtt {ls}\) or \(\mathtt {reach}\). Herein, we provide the optimal results.
. It is therefore stronger to establish decidability or complexity upper bounds with \(\mathtt {reach}^{\scriptscriptstyle {+}}\) and to show undecidability or complexity lower bounds with \(\mathtt {ls}\) or \(\mathtt {reach}\). Herein, we provide the optimal results.
Decision Problems. Let \(\mathfrak {L}\) be a logic defined above. As usual, the satisfiability problem for \(\mathfrak {L}\) takes as input a formula \(\varphi \) from \(\mathfrak {L}\) and asks whether there is \((s,h)\) such that \((s,h) \models \varphi \). The validity problem is also defined as usual. The model-checking problem for \(\mathfrak {L}\) takes as input a formula \(\varphi \) from \(\mathfrak {L}\), \((s,h)\) and asks whether \((s,h) \models \varphi \) (\(s\) is restricted to the variables occurring in \(\varphi \) and \(h\) is encoded as a finite and functional graph). Unless otherwise specified, the size of a formula \(\varphi \) is understood as its tree size, i.e. approximately its number of symbols.
The main purpose of this paper is to study the decidability/complexity status of  and its fragments.
and its fragments.
3 Undecidability of 
In this section, we show that  has an undecidable satisfiability problem even though it does not admit first-order quantification.
has an undecidable satisfiability problem even though it does not admit first-order quantification.
Let  be the first-order extension of
be the first-order extension of  obtained by adding the universal quantifier \(\forall \). The formulae \(\varphi \) of
obtained by adding the universal quantifier \(\forall \). The formulae \(\varphi \) of  are built from \( \pi \,{:}{:}\!\!= \mathtt {x}= \mathtt {y}\ \mid \ \mathtt {x}\hookrightarrow \mathtt {y}\) and
are built from \( \pi \,{:}{:}\!\!= \mathtt {x}= \mathtt {y}\ \mid \ \mathtt {x}\hookrightarrow \mathtt {y}\) and  , where \(\mathtt {x}, \mathtt {y}\in \mathrm PVAR\). Note that \(\mathtt {emp}\) can be easily defined by \(\forall \ \mathtt {x}, \mathtt {x}' \ \lnot (\mathtt {x}\hookrightarrow \mathtt {x}')\). Models of the logic
, where \(\mathtt {x}, \mathtt {y}\in \mathrm PVAR\). Note that \(\mathtt {emp}\) can be easily defined by \(\forall \ \mathtt {x}, \mathtt {x}' \ \lnot (\mathtt {x}\hookrightarrow \mathtt {x}')\). Models of the logic  are memory states and the satisfaction relation \(\models \) is defined as for
are memory states and the satisfaction relation \(\models \) is defined as for  with the additional clause:
with the additional clause:
Without any loss of generality, we can assume that the satisfiability [resp. validity] problem for  is defined by taking as inputs closed formulae (i.e. without free occurrences of the variables).
is defined by taking as inputs closed formulae (i.e. without free occurrences of the variables).
Proposition 1
[5, 14] The satisfiability problem for  is undecidable and the set of valid formulae for
is undecidable and the set of valid formulae for  is not recursively enumerable.
is not recursively enumerable.
In a nutshell, we establish the undecidability of  by reduction from the satisfiability problem for
by reduction from the satisfiability problem for  . The reduction is nicely decomposed in two intermediate steps: (1) the undecidability of
. The reduction is nicely decomposed in two intermediate steps: (1) the undecidability of  extended with a few atomic predicates, to be defined soon, and (2) a tour de force resulting in the encoding of these atomic predicates in
extended with a few atomic predicates, to be defined soon, and (2) a tour de force resulting in the encoding of these atomic predicates in  .
.
3.1 Encoding Quantified Variables as Cells in the Heap
In this section, we assume for a moment that we can express three atomic predicates \(\mathtt {alloc}^{-1}(\mathtt {x})\), \(n(\mathtt {x}) = n(\mathtt {y})\) and \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\), that will be used in the translation and have the following semantics:
-
\((s,h)\!\models \mathtt {alloc}^{-1}(\mathtt {x})\) holds whenever \(s(\mathtt {x}) \in \mathrm{ran}(h)\),
-
\((s,h)\!\models n(\mathtt {x})=n(\mathtt {y})\) holds iff \(\{s(\mathtt {x}),s(\mathtt {y})\} \subseteq \mathrm{dom}(h)\) and \(h(s(\mathtt {x}))=h(s(\mathtt {y}))\),
-
\((s,h)\!\models n(\mathtt {x})\!\hookrightarrow \!n(\mathtt {y})\) holds iff \(\{s(\mathtt {x}),s(\mathtt {y})\} \subseteq \mathrm{dom}(h)\) and \({h^2(s(\mathtt {x}))=h(s(\mathtt {y}))}\).
Let us first intuitively explain how the two last predicates will help encoding  . By definition, the satisfaction of the quantified formula \(\forall \mathtt {x}\ \psi \) from
. By definition, the satisfaction of the quantified formula \(\forall \mathtt {x}\ \psi \) from  requires the satisfaction of the formula \(\psi \) for all the values in \(\mathrm{LOC}\) assigned to \(\mathtt {x}\). The principle of the encoding is to use a set L of locations initially not in the domain or range of the heap to mimic the store by modifying how they are allocated. In this way, a variable will be interpreted by a location in the heap and, instead of checking whenever \(\mathtt {x}\hookrightarrow \mathtt {y}\) (or \(\mathtt {x}= \mathtt {y}\)) holds, we will check if \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) (or \(n(\mathtt {x}) = n(\mathtt {y})\)) holds, where \(\mathtt {x}\) and \(\mathtt {y}\) correspond, after the translation, to the locations in L that mimic the store for those variables. Let X be the set of variables needed for the translation. In order to properly encode the store, each location in L only mimics exactly one variable, i.e. there is a bijection between X and L, and cannot be reached by any location. As such, the formula \(\forall \mathtt {x}\ \psi \) will be encoded by the formula
requires the satisfaction of the formula \(\psi \) for all the values in \(\mathrm{LOC}\) assigned to \(\mathtt {x}\). The principle of the encoding is to use a set L of locations initially not in the domain or range of the heap to mimic the store by modifying how they are allocated. In this way, a variable will be interpreted by a location in the heap and, instead of checking whenever \(\mathtt {x}\hookrightarrow \mathtt {y}\) (or \(\mathtt {x}= \mathtt {y}\)) holds, we will check if \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) (or \(n(\mathtt {x}) = n(\mathtt {y})\)) holds, where \(\mathtt {x}\) and \(\mathtt {y}\) correspond, after the translation, to the locations in L that mimic the store for those variables. Let X be the set of variables needed for the translation. In order to properly encode the store, each location in L only mimics exactly one variable, i.e. there is a bijection between X and L, and cannot be reached by any location. As such, the formula \(\forall \mathtt {x}\ \psi \) will be encoded by the formula  , where \(\text {OK}(X)\) (formally defined below) checks whenever the locations in L still satisfy the auxiliary conditions just described, whereas \(\mathrm {T}(\psi )\) is the translation of \(\psi \).
, where \(\text {OK}(X)\) (formally defined below) checks whenever the locations in L still satisfy the auxiliary conditions just described, whereas \(\mathrm {T}(\psi )\) is the translation of \(\psi \).
Unfortunately, the formula  cannot simply be translated into
cannot simply be translated into  because the evaluation of \(\mathrm {T}(\psi _1)\) in a disjoint heap may need the values of free variables occurring in \(\psi _1\) but our encoding of the variable valuations via the heap does not allow to preserve these values through disjoint heaps. In order to solve this problem, for each variable \(\mathtt {x}\) in the formula, X will contain an auxiliary variable \(\overline{\mathtt {x}}\), or alternatively we define on X an involution \(\overline{(.)}\). If the translated formula has q variables then the set X of variables needed for the translation will have cardinality 2q. In the translation of a formula whose outermost connective is the magic wand, the locations corresponding to variables of the form \(\overline{\mathtt {x}}\) will be allocated on the left side of the magic wand, and checked to be equal to their non-bar versions on the right side of the magic wand. As such, the left side of the magic wand will be translated into
because the evaluation of \(\mathrm {T}(\psi _1)\) in a disjoint heap may need the values of free variables occurring in \(\psi _1\) but our encoding of the variable valuations via the heap does not allow to preserve these values through disjoint heaps. In order to solve this problem, for each variable \(\mathtt {x}\) in the formula, X will contain an auxiliary variable \(\overline{\mathtt {x}}\), or alternatively we define on X an involution \(\overline{(.)}\). If the translated formula has q variables then the set X of variables needed for the translation will have cardinality 2q. In the translation of a formula whose outermost connective is the magic wand, the locations corresponding to variables of the form \(\overline{\mathtt {x}}\) will be allocated on the left side of the magic wand, and checked to be equal to their non-bar versions on the right side of the magic wand. As such, the left side of the magic wand will be translated into

where \(Z\) is the set of free variables in \(\psi _1\), whereas the right side will be

The use of the separating conjunction before the formula \(\mathrm {T}(\psi _2)\) separates the memory cells corresponding to \(\overline{\mathtt {x}}\) from the rest of the heap. By doing this, we can reuse \(\overline{\mathtt {x}}\) whenever a magic wand appears in \(\mathrm {T}(\psi _2)\).
For technical convenience, we consider a slight alternative for the semantics of the logics  and
and  , which does not modify the notion of satisfiability/validity and such that the set of formulae and the definition of the satisfaction relation \(\models \) remain unchanged. So far, the memory states are pairs of the form \((s,h)\) with \(s: \mathrm PVAR\rightarrow \mathrm{LOC}\) and \(h: \mathrm{LOC}\rightarrow _{\text {fin}} \mathrm{LOC}\) for a fixed countably infinite set of locations \(\mathrm{LOC}\), say \(\mathrm{LOC}= \mathbb {N}\). Alternatively, the models for
, which does not modify the notion of satisfiability/validity and such that the set of formulae and the definition of the satisfaction relation \(\models \) remain unchanged. So far, the memory states are pairs of the form \((s,h)\) with \(s: \mathrm PVAR\rightarrow \mathrm{LOC}\) and \(h: \mathrm{LOC}\rightarrow _{\text {fin}} \mathrm{LOC}\) for a fixed countably infinite set of locations \(\mathrm{LOC}\), say \(\mathrm{LOC}= \mathbb {N}\). Alternatively, the models for  and
and  can be defined as triples \((\mathrm{LOC}_1,s_1,h_1)\) such that \(\mathrm{LOC}_1\) is a countable infinite set, \(s_1: \mathrm PVAR\rightarrow \mathrm{LOC}_1\) and \(h_1: \mathrm{LOC}_1 \rightarrow _{\text {fin}} \mathrm{LOC}_1\). As shown below, this does not change the notion of satisfiability and validity, but this generalisation will be handy in a few places. Most of the time, a generalised memory state \((\mathrm{LOC}_1,s_1,h_1)\) shall be written \((s_1,h_1)\) when no confusion is possible.
can be defined as triples \((\mathrm{LOC}_1,s_1,h_1)\) such that \(\mathrm{LOC}_1\) is a countable infinite set, \(s_1: \mathrm PVAR\rightarrow \mathrm{LOC}_1\) and \(h_1: \mathrm{LOC}_1 \rightarrow _{\text {fin}} \mathrm{LOC}_1\). As shown below, this does not change the notion of satisfiability and validity, but this generalisation will be handy in a few places. Most of the time, a generalised memory state \((\mathrm{LOC}_1,s_1,h_1)\) shall be written \((s_1,h_1)\) when no confusion is possible.
Given a bijection \(\mathfrak {f}: \mathrm{LOC}_1 \rightarrow \mathrm{LOC}_2\) and a heap \(h_1: \mathrm{LOC}_1 \rightarrow _{\text {fin}} \mathrm{LOC}_1\) equal to \(\{ \ell _1 \mapsto h_1(\ell _1), \ldots ,\ell _n \mapsto h_1(\ell _n) \}\), we write \(\mathfrak {f}(h_1)\) to denote the heap \(h_2: \mathrm{LOC}_2 \rightarrow _{\text {fin}} \mathrm{LOC}_2\) with \(h_2 = \{ \mathfrak {f}(\ell _1) \mapsto \mathfrak {f}(h_1(\ell _1)), \ldots , \mathfrak {f}(\ell _n) \mapsto \mathfrak {f}(h_1(\ell _n)) \}\).
Definition 1
Let \((\mathrm{LOC}_1,s_1,h_1)\) and \((\mathrm{LOC}_2,s_2,h_2)\) be generalised memory states and \(X\subseteq \mathrm PVAR\). A partial isomorphism with respect to \(X\) from \((\mathrm{LOC}_1,s_1,h_1)\) to \((\mathrm{LOC}_2,s_2,h_2)\) is a bijection \(\mathfrak {f}: \mathrm{LOC}_1 \rightarrow \mathrm{LOC}_2\) such that \(h_2 = \mathfrak {f}(h_1)\) and for all \(\mathtt {x}\in X\), \(\mathfrak {f}(s_1(\mathtt {x})) = s_2(\mathtt {x})\) (we write \((\mathrm{LOC}_1,s_1,h_1) \approx _{X} (\mathrm{LOC}_2,s_2,h_2)\)).
A folklore result states that isomorphic memory states satisfy the same formulae since the logics  ,
,  can only perform equality tests.
can only perform equality tests.
Lemma 1
Let \((\mathrm{LOC}_1,s_1,h_1)\) and \((\mathrm{LOC}_2,s_2,h_2)\) be two generalised memory states such that \((\mathrm{LOC}_1,s_1,h_1) \approx _{X} (\mathrm{LOC}_2,s_2,h_2)\), for some \(X\subseteq \mathrm PVAR\). (I) For all formulae \(\varphi \) in  whose free variables are among \(X\), we have \((\mathrm{LOC}_1,s_1,h_1) \models \varphi \) iff \((\mathrm{LOC}_2,s_2,h_2) \models \varphi \). (II) For all formulae \(\varphi \) in
whose free variables are among \(X\), we have \((\mathrm{LOC}_1,s_1,h_1) \models \varphi \) iff \((\mathrm{LOC}_2,s_2,h_2) \models \varphi \). (II) For all formulae \(\varphi \) in  built on variables among \(X\), we have \((\mathrm{LOC}_1,s_1,h_1)\models \varphi \) iff \({(\mathrm{LOC}_2,s_2,h_2) \models \varphi }\).
built on variables among \(X\), we have \((\mathrm{LOC}_1,s_1,h_1)\models \varphi \) iff \({(\mathrm{LOC}_2,s_2,h_2) \models \varphi }\).
As a direct consequence, satisfiability in  as defined in Sect. 2, is equivalent to satisfiability with generalised memory states, the same holds for
as defined in Sect. 2, is equivalent to satisfiability with generalised memory states, the same holds for  . Next, we define the encoding of a generalised memory state. This can be seen as the semantical counterpart of the syntactical translation process and, as such, formalise the intuition of using part of a heap to mimic the store.
. Next, we define the encoding of a generalised memory state. This can be seen as the semantical counterpart of the syntactical translation process and, as such, formalise the intuition of using part of a heap to mimic the store.
Definition 2
Let \(X=\{\mathtt {x}_1,\dots ,\mathtt {x}_{2q}\}\), \(Y\subseteq \{ \mathtt {x}_1, \dots , \mathtt {x}_q \}\) and, \((\mathrm{LOC}_1,s_1,h_1)\) and \((\mathrm{LOC}_2,s_2,h_2)\) be two (generalised) memory states. We say that \((\mathrm{LOC}_1,s_1,h_1)\) is encoded by \((\mathrm{LOC}_2,s_2,h_2)\) w.r.t. \(X,Y\), written \({(\mathrm{LOC}_1,s_1,h_1) \rhd ^{Y}_{q}(\mathrm{LOC}_2,s_2,h_2)}\), if the following conditions hold:
-
\(\mathrm{LOC}_1=\mathrm{LOC}_2\setminus \{ s_2(\mathtt {x})\mid \mathtt {x}\in X \}\),
-
for all \(\mathtt {x}\ne \mathtt {y}\in X\), \(s_2(\mathtt {x})\ne s_2(\mathtt {y})\),
-
\(h_2=h_1 + \{ s_2(\mathtt {x})\mapsto s_1(\mathtt {x})\mid \mathtt {x}\in Y \}\).
Notice that \(h_2\) is equal to \(h_1\) plus the heap \(\{ s_2(\mathtt {x})\mapsto s_1(\mathtt {x})\mid \mathtt {x}\in Y \}\) that encodes the store \(s_1\). The picture below presents a memory state (left) and its encoding (right), where \(Y= \{\mathtt {x}_i,\mathtt {x}_j,\mathtt {x}_k\}\). From the encoding, we can retrieve the initial heap by removing the memory cells corresponding to \(\mathtt {x}_i\), \(\mathtt {x}_j\) and \(\mathtt {x}_k\). By way of example, the memory state on the left satisfies the formulae \(\mathtt {x}_i = \mathtt {x}_j\), \(\mathtt {x}_i \hookrightarrow \mathtt {x}_k\) and \(\mathtt {x}_k \hookrightarrow \mathtt {x}_k\) whereas its encoding satisfies the formulae \(n(\mathtt {x}_i) = n(\mathtt {x}_j)\), \({n(\mathtt {x}_i) \hookrightarrow n(\mathtt {x}_k)}\) and \({n(\mathtt {x}_k) \hookrightarrow n(\mathtt {x}_k)}\).

3.2 The Translation
We are now ready to define the translation of a first-order formula in propositional separation logic extended with the three predicates introduced at the beginning of the section. Let \(\varphi \) be a closed formula of  with quantified variables \(\{\mathtt {x}_1,\dots ,\mathtt {x}_q\}\). W.l.o.g., we can assume that distinct quantifications involve distinct variables. Moreover, let \(X= \{\mathtt {x}_1,\dots ,\mathtt {x}_{2q}\}\) and \(\overline{(.)}\) be the involution on \(X\) such that for all \(i \in [1,q]\)
with quantified variables \(\{\mathtt {x}_1,\dots ,\mathtt {x}_q\}\). W.l.o.g., we can assume that distinct quantifications involve distinct variables. Moreover, let \(X= \{\mathtt {x}_1,\dots ,\mathtt {x}_{2q}\}\) and \(\overline{(.)}\) be the involution on \(X\) such that for all \(i \in [1,q]\)  .
.
We write \(\mathrm{OK}(X)\) to denote the formula \( (\bigwedge _{i \ne j} \mathtt {x}_i \ne \mathtt {x}_j) \wedge (\bigwedge _{i} \lnot \mathtt {alloc}^{-1}(\mathtt {x}_i)) \). The translation function \(\mathrm {T}\) has two arguments: the formula in  to be recursively translated and the total set of variables potentially appearing in the target formula (useful to check that \(\mathrm{OK}(X)\) holds on every heap involved in the satisfaction of the translated formula). Let us come back to the definition of \(\mathrm {T}(\psi , X)\) (homomorphic for Boolean connectives) with the assumption that the variables in \(\psi \) are among \(\mathtt {x}_1\), ..., \(\mathtt {x}_q\).
to be recursively translated and the total set of variables potentially appearing in the target formula (useful to check that \(\mathrm{OK}(X)\) holds on every heap involved in the satisfaction of the translated formula). Let us come back to the definition of \(\mathrm {T}(\psi , X)\) (homomorphic for Boolean connectives) with the assumption that the variables in \(\psi \) are among \(\mathtt {x}_1\), ..., \(\mathtt {x}_q\).

Lastly, the translation  is defined as
is defined as


where \(Z\subseteq \{ \mathtt {x}_1, \ldots , \mathtt {x}_q \}\) is the set of free variables in \(\psi _1\).
Here is the main result of this section, which is essential for the correctness of \(\mathcal {T}_\mathrm{SAT}(\varphi )\), defined below.
Lemma 2
Let \(X= \{ \mathtt {x}_1, \ldots , \mathtt {x}_{2q} \}\), \(Y\subseteq \{\mathtt {x}_1, \ldots , \mathtt {x}_q\}\), \(\psi \) be a formula in  with free variables among \(Y\) that does not contain any bound variable of \(\psi \) and \((\mathrm{LOC}_1,s_1,h_1) \rhd _q^{Y} \ (\mathrm{LOC}_2,s_2,h_2)\). We have \((s_1,h_1) \models \psi \) iff \((s_2,h_2) \models \mathrm {T}(\psi ,X)\).
with free variables among \(Y\) that does not contain any bound variable of \(\psi \) and \((\mathrm{LOC}_1,s_1,h_1) \rhd _q^{Y} \ (\mathrm{LOC}_2,s_2,h_2)\). We have \((s_1,h_1) \models \psi \) iff \((s_2,h_2) \models \mathrm {T}(\psi ,X)\).
We define the translation \(\mathcal {T}_\mathrm{SAT}(\varphi )\) in  where \(\mathrm {T}(\varphi , X)\) is defined recursively.
where \(\mathrm {T}(\varphi , X)\) is defined recursively.

The first two conjuncts specify initial conditions, namely each variable \(\mathtt {y}\) in \(X\) is interpreted by a location that is unallocated, it is not in the heap range and it is distinct from the interpretation of all other variables; in other words, the value for \(\mathtt {y}\) is isolated. Similarly, let \(\mathcal {T}_\mathrm{VAL}(\varphi )\) be the formula in  defined by \(((\bigwedge _{i \in [1,2q]} \lnot \mathtt {alloc}(\mathtt {x}_i)) \wedge \mathrm{OK}(X)) \Rightarrow \mathrm {T}(\varphi , X)\). As a consequence of Lemma 2, \(\varphi \) and \(\mathcal {T}_\mathrm{SAT}(\varphi )\) are shown equisatisfiable, whereas \(\varphi \) and \(\mathcal {T}_\mathrm{VAL}(\varphi )\) are shown equivalid.
defined by \(((\bigwedge _{i \in [1,2q]} \lnot \mathtt {alloc}(\mathtt {x}_i)) \wedge \mathrm{OK}(X)) \Rightarrow \mathrm {T}(\varphi , X)\). As a consequence of Lemma 2, \(\varphi \) and \(\mathcal {T}_\mathrm{SAT}(\varphi )\) are shown equisatisfiable, whereas \(\varphi \) and \(\mathcal {T}_\mathrm{VAL}(\varphi )\) are shown equivalid.
Corollary 1
Let \(\varphi \) be a closed formula in  using quantified variables among \(\{ \mathtt {x}_1, \ldots , \mathtt {x}_q \}\). (I) \(\varphi \) and \(\mathcal {T}_\mathrm{SAT}(\varphi )\) are equisatisfiable. (II) \(\varphi \) and \(\mathcal {T}_\mathrm{VAL}(\varphi )\) are equivalid.
using quantified variables among \(\{ \mathtt {x}_1, \ldots , \mathtt {x}_q \}\). (I) \(\varphi \) and \(\mathcal {T}_\mathrm{SAT}(\varphi )\) are equisatisfiable. (II) \(\varphi \) and \(\mathcal {T}_\mathrm{VAL}(\varphi )\) are equivalid.
3.3 Expressing the Auxiliary Atomic Predicates
To complete the reduction, we briefly explain how to express the formulae \(\mathtt {alloc}^{-1}(\mathtt {x})\), \(n(\mathtt {x}) = n(\mathtt {y})\) and \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) within  . Let us introduce a few macros that shall be helpful.
. Let us introduce a few macros that shall be helpful.
-
Given \(\varphi \) in
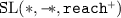 and \(\gamma \ge 0\), we write \([\varphi ]_{\gamma }\) to denote the formula \({(\mathtt {size}= \gamma \wedge \varphi ) *\top }\). It is easy to show that for any memory state \((s,h)\), \((s,h) \models [\varphi ]_{\gamma }\) iff there is \(h' \sqsubseteq h\) such that \(\mathrm{card}(\mathrm{dom}(h')) = \gamma \) and \((s,h') \models \varphi \).
and \(\gamma \ge 0\), we write \([\varphi ]_{\gamma }\) to denote the formula \({(\mathtt {size}= \gamma \wedge \varphi ) *\top }\). It is easy to show that for any memory state \((s,h)\), \((s,h) \models [\varphi ]_{\gamma }\) iff there is \(h' \sqsubseteq h\) such that \(\mathrm{card}(\mathrm{dom}(h')) = \gamma \) and \((s,h') \models \varphi \). -
We write \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = \gamma \) to denote the formula \([\mathtt {ls}(\mathtt {x},\mathtt {y})]_{\gamma }\), which is satisfied in any memory state \((s,h)\) where \(h^\gamma (s(\mathtt {x})) = s(\mathtt {y})\). Lastly, we write \(\mathtt {reach}(\mathtt {x},\mathtt {y}) \le \gamma \) to denote the formula \(\bigvee _{0 \le \gamma ' \le \gamma } \mathtt {reach}(\mathtt {x},\mathtt {y}) = \gamma '\).
In order to define the existence of a predecessor (i.e. \(\mathtt {alloc}^{-1}(\mathtt {x})\)) in  , we need to take advantage of an auxiliary variable \(\mathtt {y}\) whose value is different from the one for \(\mathtt {x}\). Let \(\mathtt {alloc}_{\mathtt {y}}^{-1}(\mathtt {x})\) be the formula
, we need to take advantage of an auxiliary variable \(\mathtt {y}\) whose value is different from the one for \(\mathtt {x}\). Let \(\mathtt {alloc}_{\mathtt {y}}^{-1}(\mathtt {x})\) be the formula

Lemma 3
Let \(\mathtt {x},\mathtt {y}\in \mathrm PVAR\). (I) For all memory states \((s,h)\) such that \(s(\mathtt {x}) \ne s(\mathtt {y})\), we have \((s,h) \models \mathtt {alloc}_{\mathtt {y}}^{-1}(\mathtt {x})\) iff \(s(\mathtt {x}) \in \mathrm{ran}(h)\). (II) In the translation, \(\mathtt {alloc}^{-1}(\mathtt {x})\) can be replaced with \(\mathtt {alloc}_{\overline{\mathtt {x}}}^{-1}(\mathtt {x})\).
As stated in Lemma 3(II), we can exploit the fact that in the translation of a formula with variables in \(\{ \mathtt {x}_1,\dots ,\mathtt {x}_q \}\), we use 2q variables that correspond to 2q distinguished locations in the heap in order to retain the soundness of the translation while using \(\mathtt {alloc}_{\overline{\mathtt {x}}}^{-1}(\mathtt {x})\) as \(\mathtt {alloc}^{-1}(\mathtt {x})\). Moreover, \(\mathtt {alloc}_{\mathtt {y}}^{-1}(\mathtt {x})\) allows to express in  whenever a location corresponding to a program variable reaches itself in exactly two steps (we use this property in the definition of \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\)). We write \(\mathtt {x}\hookrightarrow _\mathtt {y}^2 \mathtt {x}\) to denote the formula
whenever a location corresponding to a program variable reaches itself in exactly two steps (we use this property in the definition of \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\)). We write \(\mathtt {x}\hookrightarrow _\mathtt {y}^2 \mathtt {x}\) to denote the formula  . For any memory state \((s,h)\) such that \(s(\mathtt {x}) \ne s(\mathtt {y})\), we have \((s,h) \models \mathtt {x}\hookrightarrow _\mathtt {y}^2 \mathtt {x}\) if and only if \(h^2(s(\mathtt {x})) = s(\mathtt {x})\) and \(h(s(\mathtt {x})) \ne s(\mathtt {x})\).
. For any memory state \((s,h)\) such that \(s(\mathtt {x}) \ne s(\mathtt {y})\), we have \((s,h) \models \mathtt {x}\hookrightarrow _\mathtt {y}^2 \mathtt {x}\) if and only if \(h^2(s(\mathtt {x})) = s(\mathtt {x})\) and \(h(s(\mathtt {x})) \ne s(\mathtt {x})\).
The predicate \(n(\mathtt {x}) = n(\mathtt {y})\) can be defined in  as
as

Lemma 4
Let \(\mathtt {x},\mathtt {y}\in \mathrm PVAR\). For all memory states \((s,h)\), we have \((s,h) \models n(\mathtt {x}) = n(\mathtt {y})\) iff \(h(s(\mathtt {x})) = h(s(\mathtt {y}))\).
Similarly to \(\mathtt {alloc}^{-1}(\mathtt {x})\), we can show that \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) is definable in  by using one additional variable \(\mathtt {z}\) whose value is different from both \(\mathtt {x}\) and \(\mathtt {y}\). Let \(\varphi _{\hookrightarrow }(\mathtt {x},\mathtt {y}, \mathtt {z})\) be \((n(\mathtt {x}) = n(\mathtt {y}) \wedge \varphi ^{=}_{\hookrightarrow }(\mathtt {x},\mathtt {y},\mathtt {z})) \vee (n(\mathtt {x}) \ne n(\mathtt {y}) \wedge \varphi ^{\ne }_{\hookrightarrow }(\mathtt {x},\mathtt {y}))\) where \(\varphi ^{=}_{\hookrightarrow }(\mathtt {x},\mathtt {y},\mathtt {z})\) is defined as
by using one additional variable \(\mathtt {z}\) whose value is different from both \(\mathtt {x}\) and \(\mathtt {y}\). Let \(\varphi _{\hookrightarrow }(\mathtt {x},\mathtt {y}, \mathtt {z})\) be \((n(\mathtt {x}) = n(\mathtt {y}) \wedge \varphi ^{=}_{\hookrightarrow }(\mathtt {x},\mathtt {y},\mathtt {z})) \vee (n(\mathtt {x}) \ne n(\mathtt {y}) \wedge \varphi ^{\ne }_{\hookrightarrow }(\mathtt {x},\mathtt {y}))\) where \(\varphi ^{=}_{\hookrightarrow }(\mathtt {x},\mathtt {y},\mathtt {z})\) is defined as

whereas \(\varphi ^{\ne }_{\hookrightarrow }(\mathtt {x},\mathtt {y})\) is defined as

Lemma 5
Let \(\mathtt {x}, \mathtt {y}, \mathtt {z}\in \mathrm PVAR\). (I) For all memory states \((s,h)\) such that \({s(\mathtt {x}) \ne s(\mathtt {z})}\) and \(s(\mathtt {y}) \ne s(\mathtt {z})\), we have \((s,h) \models \varphi _{\hookrightarrow }(\mathtt {x},\mathtt {y}, \mathtt {z})\) iff \(\{s(\mathtt {x}),s(\mathtt {y})\} \subseteq \mathrm{dom}(h)\) and \(h(h(s(\mathtt {x}))) = h(s(\mathtt {y}))\); (II) In the translation, \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) can be replaced by \(\varphi _{\hookrightarrow }(\mathtt {x},\mathtt {y},\overline{\mathtt {x}})\).
As for \(\mathtt {alloc}_{\mathtt {y}}^{-1}(\mathtt {x})\), the properties of the translation imply the equivalence between \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\varphi _{\hookrightarrow }(\mathtt {x},\mathtt {y},\overline{\mathtt {x}})\) (as stated in Lemma 5(II)). By looking at the formulae herein defined, the predicate \(\mathtt {reach}\) only appears bounded, i.e. in the form of \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y})=3\). The three new predicates can therefore be defined in  enriched with \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\).
enriched with \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\).
3.4 Undecidability Results and Non-finite Axiomatization
It is time to collect the fruits of all our efforts and to conclude this part about undecidability. As a direct consequence of Corollary 1 and the undecidability of  , here is one of the main results of the paper.
, here is one of the main results of the paper.
Theorem 1
The satisfiability problem for  is undecidable.
is undecidable.
As a by-product, the set of valid formulae for  is not recursively enumerable. Indeed, suppose that the set of valid formulae for
is not recursively enumerable. Indeed, suppose that the set of valid formulae for  were r.e., then one can enumerate the valid formulae of the form \(\mathcal {T}_\mathrm{VAL}(\varphi )\) as it is decidable in PTime whether \(\psi \) in
were r.e., then one can enumerate the valid formulae of the form \(\mathcal {T}_\mathrm{VAL}(\varphi )\) as it is decidable in PTime whether \(\psi \) in  is syntactically equal to \(\mathcal {T}_\mathrm{VAL}(\varphi )\) for some
is syntactically equal to \(\mathcal {T}_\mathrm{VAL}(\varphi )\) for some  formula \(\varphi \). This leads to a contradiction since this would allow the enumeration of valid formulae in
formula \(\varphi \). This leads to a contradiction since this would allow the enumeration of valid formulae in  .
.
The essential ingredients to establish the undecidability of  are the fact that the following properties \(n(\mathtt {x}) = n(\mathtt {y})\), \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\) are expressible in the logic.
are the fact that the following properties \(n(\mathtt {x}) = n(\mathtt {y})\), \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\) are expressible in the logic.
Corollary 2
 augmented with built-in formulae of the form \(n(\mathtt {x}) = n(\mathtt {y})\), \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\) (resp. of the form \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\)) admits an undecidable satisfiability problem.
augmented with built-in formulae of the form \(n(\mathtt {x}) = n(\mathtt {y})\), \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\) (resp. of the form \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\)) admits an undecidable satisfiability problem.
This is the addition of \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\) that is crucial for undecidability since the satisfiability problem for  is in PSpace [15]. Following a similar analysis, let SL1(
is in PSpace [15]. Following a similar analysis, let SL1( ) be the restriction of
) be the restriction of  (i.e.
(i.e.  plus \(*\)) to formulae of the form \( \exists \mathtt {x}_1 \ \cdots \ \exists \mathtt {x}_q \ \varphi \), where \(q \ge 1\), the variables in \(\varphi \) are among \(\{ \mathtt {x}_1, \ldots , \mathtt {x}_{q+1} \}\) and the only quantified variable in \(\varphi \) is \(\mathtt {x}_{q+1}\). The satisfiability problem for SL1(
plus \(*\)) to formulae of the form \( \exists \mathtt {x}_1 \ \cdots \ \exists \mathtt {x}_q \ \varphi \), where \(q \ge 1\), the variables in \(\varphi \) are among \(\{ \mathtt {x}_1, \ldots , \mathtt {x}_{q+1} \}\) and the only quantified variable in \(\varphi \) is \(\mathtt {x}_{q+1}\). The satisfiability problem for SL1( ) is PSpace-complete [15]. Note that SL1(
) is PSpace-complete [15]. Note that SL1( ) can easily express \(n(\mathtt {x}) = n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\). The distance between the decidability for SL1(
) can easily express \(n(\mathtt {x}) = n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\). The distance between the decidability for SL1( ) and the undecidability for
) and the undecidability for  , is best witnessed by the corollary below, which solves an open problem [15, Sect. 6].
, is best witnessed by the corollary below, which solves an open problem [15, Sect. 6].
Corollary 3
SL1( ) augmented with \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) (resp. SL1(
) augmented with \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) (resp. SL1( ) augmented with \(\mathtt {ls}\)) admits an undecidable satisfiability problem.
) augmented with \(\mathtt {ls}\)) admits an undecidable satisfiability problem.
4 \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and Other PSpace Variants
As already seen in Sect. 2, \(\mathrm {SL}(*, \mathtt {ls})\) can be understood as a fragment of \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\). Below, we show that the satisfiability problem for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) can be solved in polynomial space. Refining the arguments used in our proof, we also show the decidability of the fragment of  where \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is constrained not to occur in the scope of
where \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is constrained not to occur in the scope of  , i.e. \(\varphi \) belongs to that fragment iff for any subformula \(\psi \) of \(\varphi \) of the form
, i.e. \(\varphi \) belongs to that fragment iff for any subformula \(\psi \) of \(\varphi \) of the form  , \(\mathtt {reach}^{\scriptscriptstyle {+}}\) does not occur in \(\psi _1\) and in \(\psi _2\).
, \(\mathtt {reach}^{\scriptscriptstyle {+}}\) does not occur in \(\psi _1\) and in \(\psi _2\).
The proof relies on a small heap property: a formula \(\varphi \) is satisfiable if and only if it admits a model with a polynomial amount of memory cells. The PSpace upper bound then follows by establishing that the model-checking problem for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) is in PSpace too. To establish the small heap property, an equivalence relation on memory states with finite index is designed, following the standard approach in [10, 32] and using test formulae as in [4, 15, 22, 23].
4.1 Introduction to Test Formulae
Before presenting the test formulae for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\), let us recall the standard result for  (that will be also used at some point later on).
(that will be also used at some point later on).
Proposition 2
[22, 32] Any formula \(\varphi \) in  built over variables in \(\mathtt {x}_1\), ...,\(\mathtt {x}_q\) is logically equivalent to a Boolean combination of formulae among \({\mathtt {x}_i\! =\!\mathtt {x}_j}\), \(\mathtt {alloc}(\mathtt {x}_i)\),
built over variables in \(\mathtt {x}_1\), ...,\(\mathtt {x}_q\) is logically equivalent to a Boolean combination of formulae among \({\mathtt {x}_i\! =\!\mathtt {x}_j}\), \(\mathtt {alloc}(\mathtt {x}_i)\),  and \({\mathtt {size}\ge \beta }\) (\(i,j \in \{ 1,\ldots ,q \}\), \(\beta \in \mathbb {N}\)).
and \({\mathtt {size}\ge \beta }\) (\(i,j \in \{ 1,\ldots ,q \}\), \(\beta \in \mathbb {N}\)).
By way of example,  is equivalent to \({\mathtt {size}\ge 2} \wedge \mathtt {alloc}(\mathtt {x}_1)\). As a corollary of the proof of Proposition 2, in \(\mathtt {size}\ge \beta \) we can enforce that \(\beta \le 2 \times |\varphi |\) (rough upper bound) where \(|\varphi |\) is the size of \(\varphi \). Similar results will be shown for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and for some of its extensions.
is equivalent to \({\mathtt {size}\ge 2} \wedge \mathtt {alloc}(\mathtt {x}_1)\). As a corollary of the proof of Proposition 2, in \(\mathtt {size}\ge \beta \) we can enforce that \(\beta \le 2 \times |\varphi |\) (rough upper bound) where \(|\varphi |\) is the size of \(\varphi \). Similar results will be shown for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and for some of its extensions.
In order to define a set of test formulae that captures the expressive power of \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\), we need to study which basic properties on memory states can be expressed by \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) formulae. For example, consider the memory states from Fig. 1.
The fragment memory states \((s_1,h_1)\) and \((s_2,h_2)\) can be distinguished by the formula \(\top *(\mathtt {reach}(\mathtt {x}_i,\mathtt {x}_j) \wedge \mathtt {reach}(\mathtt {x}_j,\mathtt {x}_k) \wedge \lnot \mathtt {reach}(\mathtt {x}_k,\mathtt {x}_i))\). Indeed, \((s_1,h_1)\) satisfies this formula by considering a subheap that does not contain a path from \(s(\mathtt {x}_k)\) to \(s(\mathtt {x}_i)\), whereas it is impossible to find a subheap for \((s_2,h_2)\) that retains the path from \(s(\mathtt {x}_i)\) to \(s(\mathtt {x}_j)\), the one from \(s(\mathtt {x}_j)\) to \(s(\mathtt {x}_k)\) but where the path from \(s(\mathtt {x}_k)\) to \(s(\mathtt {x}_i)\) is lost. This suggests that \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) can express whether, for example, any path from \(s(\mathtt {x}_i)\) to \(s(\mathtt {x}_j)\) also contains \(s(\mathtt {x}_k)\). We will introduce the test formula \(\mathtt {sees}_q(\mathtt {x}_i,\mathtt {x}_j) \ge \beta \) to capture this property.
Similarly, the memory states \((s_3,h_3)\) and \((s_4,h_4)\) can be distinguished by the formula \((\mathtt {size}= 1) *\big (\mathtt {reach}(\mathtt {x}_j,\mathtt {x}_k) \wedge \lnot \mathtt {reach}(\mathtt {x}_i,\mathtt {x}_k) \wedge \lnot \mathtt {reach}^+(\mathtt {x}_k,\mathtt {x}_k)\big )\). The memory state \((s_3,h_3)\) satisfies this formula by separating \(\{ \ell \mapsto \ell '\}\) from the rest of the heap, whereas the formula is not satisfied by \((s_4,h_4)\). Indeed, there is no way to break the loop from \(s(\mathtt {x}_k)\) to itself by removing just one location from the heap while retaining the path from \(s(\mathtt {x}_j)\) to \(s(\mathtt {x}_k)\) and loosing the path from \(s(\mathtt {x}_i)\) to \(s(\mathtt {x}_k)\). This suggests that the two locations \(\ell \) and \(\ell '\) are particularly interesting since they are reachable from several locations corresponding to program variables. Therefore by separating them from the rest of the heap, several paths are lost. In order to capture this, we introduce the notion of meet-points.
Let \(\mathrm{Terms}_{q}\) be the set \(\{ \mathtt {x}_1, \ldots , \mathtt {x}_q \} \cup \{ m_q(\mathtt {x}_i, \mathtt {x}_j) \ \mid \ i,j \in [1,q] \}\) understood as the set of terms that are either variables or expressions denoting a meet-point. We write \([\![\mathtt {x}_i]\!]^q_{s,h}\) to denote \(s(\mathtt {x}_i)\) and \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s,h}\) to denote (if it exists) the first location reachable from \(s(\mathtt {x}_i)\) that is also reachable from \(s(\mathtt {x}_j)\). Moreover we require that this location can reach another location corresponding to a program variable. Formally, \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s,h}\) is defined as the unique location \(\ell \) such that
-
there are \(L_1, L_2\ge 0\) such that \(h^{L_1}(s(\mathtt {x}_i)) = h^{L_2}(s(\mathtt {x}_j)) = \ell \), and
-
for all \(L_1' < L_1\) and for all \(L_2'\ge 0\), \(h^{L_1'}\big (s(\mathtt {x}_i)\big ) \not = h^{L_2'}\big (s(\mathtt {x}_j)\big )\), and
-
there exist \(k \in [1,q]\) and \(L\ge 0\) such that \(h^L(\ell ) = s(\mathtt {x}_k)\).
These conditions hold for at most one location \(\ell \). One can easily show that the notion \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s,h}\) is well-defined. The picture below provides a taxonomy of meet-points, where arrows labelled by ‘\(+\)’ represent paths of non-zero length and zig-zag arrows any path (possibly of zero length). Symmetrical cases, obtained by swapping \(\mathtt {x}_i\) and \(\mathtt {x}_j\), are omitted.

Notice how the asymmetrical definition of meet-points is captured in the two rightmost heaps. Consider the memory states from Fig. 1, \((s_3,h_3)\) and \((s_4,h_4)\) can be seen as an instance of the third case of the taxonomy and, as such, it holds that \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s_3,h_3} = \ell \) and \([\![m_q(\mathtt {x}_j,\mathtt {x}_i)]\!]^q_{s_3,h_3} = \ell '\).
Given \(q,\alpha \ge 1\), we write \(\text {Test}(q, \alpha )\) to denote the following set of atomic formulae (also called test formulae):
where \(v, v' \in \mathrm{Terms}_{q}\) and \(\beta \in [1,\alpha ]\). It is worth noting that the \(\mathtt {alloc}(v)\)’s are not needed for the logic \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\) but it is required for extensions.
We identify as special locations the \(s(\mathtt {x}_i)\)’s and the meet-points of the form \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s,h}\) when it exists (\(i,j \in [1,q]\)). We call such locations, labelled locations, and the set of labelled locations is written \(\text {Labels}^{q}_{s,h}\). The formal semantics of the test formulae is provided below:
where \(\text {Rem}^q_{s,h}\) is the set of locations that neither belong to a path between two locations interpreted by program variables nor are equal to program variable interpretations, i.e.  . There is no need for test formulae of the form \(\mathtt {sees}_q(v,v') \ge 1\) since they are equivalent to \(v \hookrightarrow v' \vee {\mathtt {sees}_q(v,v') \ge 2}\). One can check whether \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s,h}\) is defined thanks to the formula \(m_q(\mathtt {x}_i,\mathtt {x}_j) = m_q(\mathtt {x}_i,\mathtt {x}_j)\). By contrast, \(\mathtt {sizeR}_q \ge \beta \) states that the cardinality of the set \(\text {Rem}^q_{s,h}\) is at least \(\beta \). Furthermore, \(\mathtt {sees}_q(v,v')\ge \beta + 1\) states that there is a minimal path between \(v\) and \(v'\) of length at least \(\beta + 1\) and strictly between \(v\) and \(v'\), there are no labelled locations. The satisfaction of \(\mathtt {sees}_q(v,v')\ge \beta + 1\) entails the exclusion of labelled locations in the witness path, which is reminiscent to \(T \xrightarrow {\!\!h \backslash T''\!\!} T'\) in the logic GRASS [26]. So, the test formulae are quite expressive since they capture the atomic formulae from \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and the test formulae for
. There is no need for test formulae of the form \(\mathtt {sees}_q(v,v') \ge 1\) since they are equivalent to \(v \hookrightarrow v' \vee {\mathtt {sees}_q(v,v') \ge 2}\). One can check whether \([\![m_q(\mathtt {x}_i,\mathtt {x}_j)]\!]^q_{s,h}\) is defined thanks to the formula \(m_q(\mathtt {x}_i,\mathtt {x}_j) = m_q(\mathtt {x}_i,\mathtt {x}_j)\). By contrast, \(\mathtt {sizeR}_q \ge \beta \) states that the cardinality of the set \(\text {Rem}^q_{s,h}\) is at least \(\beta \). Furthermore, \(\mathtt {sees}_q(v,v')\ge \beta + 1\) states that there is a minimal path between \(v\) and \(v'\) of length at least \(\beta + 1\) and strictly between \(v\) and \(v'\), there are no labelled locations. The satisfaction of \(\mathtt {sees}_q(v,v')\ge \beta + 1\) entails the exclusion of labelled locations in the witness path, which is reminiscent to \(T \xrightarrow {\!\!h \backslash T''\!\!} T'\) in the logic GRASS [26]. So, the test formulae are quite expressive since they capture the atomic formulae from \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) and the test formulae for  .
.
Lemma 6
Given \(\alpha , q \ge 1\), \(i,j \in [1,q]\), for any atomic formula among \(\mathtt {ls}(\mathtt {x}_i, \mathtt {x}_j)\), \(\mathtt {reach}(\mathtt {x}_i, \mathtt {x}_j)\), \(\mathtt {reach}^{\scriptscriptstyle {+}}(\mathtt {x}_i, \mathtt {x}_j)\), \(\mathtt {emp}\) and \(\mathtt {size}\ge \beta \) with \(\beta \le \alpha \), there is a Boolean combination of test formulae from \(\text {Test}(q, \alpha )\) logically equivalent to it.
4.2 Expressive Power and Small Model Property
The sets of test formulae \(\text {Test}(q,\alpha )\) are sufficient to capture the expressive power of \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\) (as shown below, Theorem 2) and deduce the small heap property of this logic (Theorem 3). We introduce an indistinguishability relation between memory states based on test formulae, see analogous relations in [13, 15, 22].
Definition 3
Given \(q,\alpha \ge 1\), we write \((s,h) \approx _\alpha ^q (s',h')\)  for all \(\psi \in \text {Test}(q,\alpha )\), we have \((s,h) \models \psi \) iff \((s',h') \models \psi \).
for all \(\psi \in \text {Test}(q,\alpha )\), we have \((s,h) \models \psi \) iff \((s',h') \models \psi \).
Theorem 2(I) states that if \((s,h) \approx _\alpha ^q (s',h')\), then the two memory states cannot be distinguished by formulae whose syntactic resources are bounded in some way by q and \(\alpha \) (details will follow, see the definition for \(\texttt {msize}(\varphi )\)).
Below, we state the key intermediate result of the section that can be viewed as a distributivity lemma. The expressive power of the test formulae allows us to mimic the separation between two equivalent memory states with respect to the relation \(\approx ^q_\alpha \), which is essential in the proof of Theorem 2(I).
Lemma 7
Let \(q,\alpha ,\alpha _1,\alpha _2 \ge 1\) with \(\alpha = \alpha _1 + \alpha _2\) and \((s,h)\), \((s',h')\) be such that \((s,h) \approx ^q_\alpha (s',h')\). For all heaps \(h_1\), \(h_2\) such that \(h= h_1 + h_2\) there are heaps \(h'_1\), \(h'_2\) such that \(h= h'_1 + h'_2\), \((s,h_1) \approx ^q_{\alpha _1} (s',h'_1)\) and \((s,h_2) \approx ^q_{\alpha _2} (s',h'_2)\).
For each formula \(\varphi \) in \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\), we define its memory size \(\texttt {msize}(\varphi )\) following the clauses below (see also [32]).

We have \(1 \le \texttt {msize}(\varphi ) \le |\varphi |\). Theorem 2 below establishes the properties that formulae in \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\) can express.
Theorem 2
Let \(\varphi \) be in \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\) built over the variables in \(\mathtt {x}_1\), ..., \(\mathtt {x}_q\). (I) For all \(\alpha \ge 1\) such that \(\texttt {msize}(\varphi ) \le \alpha \) and for all memory states \((s,h)\), \((s',h') \) such that \((s,h) \approx ^q_\alpha (s',h')\), we have \((s,h) \models \varphi \) iff \((s',h') \models \varphi \). (II) \(\varphi \) is logically equivalent to a Boolean combination of test formulae from \(\text {Test}(q,\texttt {msize}(\varphi ))\).
The proof of Theorem 2(I) is by structural induction on \(\varphi \). The basic cases for atomic formulae follow from Lemma 6 whereas the inductive cases for Boolean connectives are immediate. For the separating conjunction, suppose \((s,h) \models \varphi _1 *\varphi _2\) and \(\texttt {msize}(\varphi _1*\varphi _2) \le \alpha \). There are heaps \(h_1\) and \(h_2\) such that \(h= h_1 + h_2\), \((s,h_1) \models \psi _1\) and \((s,h_2) \models \psi _2\). As \(\alpha \ge \texttt {msize}(\psi _1 *\psi _2) = \texttt {msize}(\psi _1) + \texttt {msize}(\psi _2)\), there exist \(\alpha _1\) and \(\alpha _2\) such that \(\alpha = \alpha _1 + \alpha _2\), \(\alpha _1 \ge \texttt {msize}(\psi _1)\) and \(\alpha _2 \ge \texttt {msize}(\psi _2)\). By Lemma 7, there exist heaps \(h'_1\) and \(h'_2\) such that \(h'=h'_1 + h'_2\), \((s,h_1) \approx ^q_{\alpha _1} (s',h'_1)\) and \((s,h_2) \approx ^q_{\alpha _2} (s',h'_2)\). By the induction hypothesis, we get \((s',h_1') \models \psi _1\) and \((s',h_2') \models \psi _2\). Consequently, we obtain \((s',h') \models \psi _1 *\psi _2\).
As an example, we can apply this result to the memory states from Fig. 1. We have already shown how we can distinguish \((s_1,h_1)\) from \((s_2,h_2)\) using a formula with only one separating conjunction. Theorem 2 ensures that these two memory states do not satisfy the same set of test formulae for \(\alpha \ge 2\). Indeed, only \((s_1,h_1)\) satisfies \(\mathtt {sees}_q(\mathtt {x}_i,\mathtt {x}_j) \ge 2\). The same argument can be used with \((s_3,h_3)\) and \((s_4,h_4)\): only \((s_3,h_3)\) satisfies the test formula \(m_q(\mathtt {x}_i,\mathtt {x}_j) \hookrightarrow m_q(\mathtt {x}_j,\mathtt {x}_i)\). Clearly, Theorem 2(II) relates separation logic with classical logic as advocated also in the works [10, 23]. Now, it is possible to establish a small heap property.
Theorem 3
Let \(\varphi \) be a satisfiable \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\) formula built over \(\mathtt {x}_1\), ..., \(\mathtt {x}_q\). There is \((s,h)\) such that \((s,h) \models \varphi \) and \(\mathrm{card}(\mathrm{dom}(h)) \le (q^2 + q) \cdot (|\varphi | + 1) + |\varphi |\).
The small heap property for \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\) is inherited from the small heap property for the Boolean combinations of test formulae, which is analogous to the small model property for other theories of singly linked lists, see e.g. [13, 27].
4.3 Complexity Upper Bounds
Let us draw some consequences of Theorem 3. First, for the logic \(\mathrm {SL}(*,\mathtt {reach}^{\scriptscriptstyle {+}})\), we get a PSpace upper, which matches the lower bound for \(\mathrm {SL}(*)\) [11].
Theorem 4
The satisfiability problem for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) is PSpace-complete.
Besides, we may consider restricting the usage of Boolean connectives. We note \(\mathsf {Bool(SHF)}\) for the Boolean combinations of formulae from the symbolic heap fragment [2]. A PTime upper bound for the entailment/satisfiability problem for the symbolic heap fragment is successfully solved in [12, 17], whereas the satisfiability problem for a slight variant of \(\mathsf {Bool(SHF)}\) is shown in NP in [26, Theorem 4]. Theorem 3 allows us to conclude this NP upper bound result as a by-product (we conjecture that our quadratic upper bound on the number of cells could be improved to a linear one in that case).
Corollary 4
The satisfiability problem for \(\mathsf {Bool(SHF)}\) is NP-complete.
It is possible to push further the PSpace upper bound by allowing occurrences of  in a controlled way. Let \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}}, \bigcup _{q,\alpha } \text {Test}(q,\alpha ))\) be the extension of \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) augmented with the test formulae. The memory size function is also extended:
in a controlled way. Let \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}}, \bigcup _{q,\alpha } \text {Test}(q,\alpha ))\) be the extension of \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}})\) augmented with the test formulae. The memory size function is also extended:  ,
,  ,
,  and
and  . When formulae are encoded as trees, we have \(1 \le \texttt {msize}(\varphi ) \le |\varphi | \alpha _{\varphi }\) where \(\alpha _{\varphi }\) is the maximal constant in \(\varphi \). Theorem 2(I) admits a counterpart for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}}, \bigcup _{q,\alpha } \text {Test}(q,\alpha ))\) and consequently, any formula built over \(\mathtt {x}_1\), ..., \(\mathtt {x}_q\) can be shown equivalent to a Boolean combination of test formulae from \(\text {Test}(q, |\varphi | \alpha _{\varphi })\). By Theorem 3, any satisfiable formula has therefore a model with \( \mathrm{card}(\mathrm{dom}(h)) \le (q^2 + q)\cdot (|\varphi | \alpha _{\varphi } + 1) + |\varphi | \alpha _{\varphi }\). Hence, the satisfiability problem for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}}, \bigcup _{q,\alpha } \text {Test}(q,\alpha ))\) is in PSpace when the constants are encoded in unary. Now, we can state the new PSpace upper bound for Boolean combinations of formulae from
. When formulae are encoded as trees, we have \(1 \le \texttt {msize}(\varphi ) \le |\varphi | \alpha _{\varphi }\) where \(\alpha _{\varphi }\) is the maximal constant in \(\varphi \). Theorem 2(I) admits a counterpart for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}}, \bigcup _{q,\alpha } \text {Test}(q,\alpha ))\) and consequently, any formula built over \(\mathtt {x}_1\), ..., \(\mathtt {x}_q\) can be shown equivalent to a Boolean combination of test formulae from \(\text {Test}(q, |\varphi | \alpha _{\varphi })\). By Theorem 3, any satisfiable formula has therefore a model with \( \mathrm{card}(\mathrm{dom}(h)) \le (q^2 + q)\cdot (|\varphi | \alpha _{\varphi } + 1) + |\varphi | \alpha _{\varphi }\). Hence, the satisfiability problem for \(\mathrm {SL}(*, \mathtt {reach}^{\scriptscriptstyle {+}}, \bigcup _{q,\alpha } \text {Test}(q,\alpha ))\) is in PSpace when the constants are encoded in unary. Now, we can state the new PSpace upper bound for Boolean combinations of formulae from  .
.
Theorem 5
The satisfiability problem for Boolean combinations of formulae from  is PSpace-complete.
is PSpace-complete.
To conclude, let us introduce the largest fragment including  and \(\mathtt {ls}\) for which decidability can be established so far.
and \(\mathtt {ls}\) for which decidability can be established so far.
Theorem 6
The satisfiability problem for the fragment of  in which \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is not in the scope of
in which \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is not in the scope of  is decidable.
is decidable.
5 Conclusion
We studied the effects of adding \(\mathtt {ls}\) to  and variants.
and variants.  is shown undecidable (Theorem 1) and non-finitely axiomatisable, which remains quite unexpected since there are no first-order quantifications. This result is strengthened to even weaker extensions of
is shown undecidable (Theorem 1) and non-finitely axiomatisable, which remains quite unexpected since there are no first-order quantifications. This result is strengthened to even weaker extensions of  such as the one augmented with \(n(\mathtt {x}) = n(\mathtt {y})\), \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\), or the one augmented with \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\). If the magic wand is discarded, we have established that the satisfiability problem for \(\mathrm {SL}(*,\mathtt {ls})\) is PSpace-complete by introducing a class of test formulae that captures the expressive power of \(\mathrm {SL}(*,\mathtt {ls})\) and that leads to a small heap property. Such a logic contains the Boolean combinations of symbolic heaps and our proof technique allows us to get an NP upper bound for such formulae. Moreover, we show that the satisfiability problem for
such as the one augmented with \(n(\mathtt {x}) = n(\mathtt {y})\), \(n(\mathtt {x}) \hookrightarrow n(\mathtt {y})\) and \(\mathtt {alloc}^{-1}(\mathtt {x})\), or the one augmented with \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 2\) and \(\mathtt {reach}(\mathtt {x},\mathtt {y}) = 3\). If the magic wand is discarded, we have established that the satisfiability problem for \(\mathrm {SL}(*,\mathtt {ls})\) is PSpace-complete by introducing a class of test formulae that captures the expressive power of \(\mathrm {SL}(*,\mathtt {ls})\) and that leads to a small heap property. Such a logic contains the Boolean combinations of symbolic heaps and our proof technique allows us to get an NP upper bound for such formulae. Moreover, we show that the satisfiability problem for  restricted to formulae in which \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is not in the scope of
restricted to formulae in which \(\mathtt {reach}^{\scriptscriptstyle {+}}\) is not in the scope of  is decidable, leading to the largest known decidable fragment for which
is decidable, leading to the largest known decidable fragment for which  and \(\mathtt {reach}^{\scriptscriptstyle {+}}\) (or \(\mathtt {ls}\)) cohabit. So, we have provided proof techniques to establish undecidability when \(*\),
and \(\mathtt {reach}^{\scriptscriptstyle {+}}\) (or \(\mathtt {ls}\)) cohabit. So, we have provided proof techniques to establish undecidability when \(*\),  and \(\mathtt {ls}\) are present and to establish decidability based on test formulae. This paves the way to investigate the decidability status of
and \(\mathtt {ls}\) are present and to establish decidability based on test formulae. This paves the way to investigate the decidability status of  as well as of the positive fragment of
as well as of the positive fragment of  from [30, 31].
from [30, 31].
References
Antonopoulos, T., Gorogiannis, N., Haase, C., Kanovich, M., Ouaknine, J.: Foundations for decision problems in separation logic with general inductive predicates. In: Muscholl, A. (ed.) FoSSaCS 2014. LNCS, vol. 8412, pp. 411–425. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54830-7_27
Berdine, J., Calcagno, C., O’Hearn, P.W.: A decidable fragment of separation logic. In: Lodaya, K., Mahajan, M. (eds.) FSTTCS 2004. LNCS, vol. 3328, pp. 97–109. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30538-5_9
Berdine, J., Calcagno, C., O’Hearn, P.W.: Smallfoot: modular automatic assertion checking with separation logic. In: de Boer, F.S., Bonsangue, M.M., Graf, S., de Roever, W.-P. (eds.) FMCO 2005. LNCS, vol. 4111, pp. 115–137. Springer, Heidelberg (2006). https://doi.org/10.1007/11804192_6
Brochenin, R., Demri, S., Lozes, E.: Reasoning about sequences of memory states. APAL 161(3), 305–323 (2009)
Brochenin, R., Demri, S., Lozes, E.: On the almighty wand. IC 211, 106–137 (2012)
Brotherston, J., Fuhs, C., Gorogiannis, N., Navarro Perez, J.: A decision procedure for satisfiability in separation logic with inductive predicates. In: CSL-LICS 2014 (2014)
Brotherston, J., Villard, J.: Parametric completeness for separation theories. In: POPL 2014, pp. 453–464. ACM (2014)
Calcagno, C., Distefano, D.: Infer: an automatic program verifier for memory safety of C programs. In: Bobaru, M., Havelund, K., Holzmann, G.J., Joshi, R. (eds.) NFM 2011. LNCS, vol. 6617, pp. 459–465. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20398-5_33
Calcagno, C., Distefano, D., O’Hearn, P., Yang, H.: Compositional shape analysis by means of bi-abduction. JACM 58(6), 26:1–26:66 (2011)
Calcagno, C., Gardner, P., Hague, M.: From separation logic to first-order logic. In: Sassone, V. (ed.) FoSSaCS 2005. LNCS, vol. 3441, pp. 395–409. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31982-5_25
Calcagno, C., Yang, H., O’Hearn, P.W.: Computability and complexity results for a spatial assertion language for data structures. In: Hariharan, R., Vinay, V., Mukund, M. (eds.) FSTTCS 2001. LNCS, vol. 2245, pp. 108–119. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45294-X_10
Cook, B., Haase, C., Ouaknine, J., Parkinson, M., Worrell, J.: Tractable reasoning in a fragment of separation logic. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 235–249. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23217-6_16
David, C., Kroening, D., Lewis, M.: Propositional reasoning about safety and termination of heap-manipulating programs. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 661–684. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46669-8_27
Demri, S., Deters, M.: Expressive completeness of separation logic with two variables and no separating conjunction. ACM ToCL 17(2), 12 (2016)
Demri, S., Galmiche, D., Larchey-Wendling, D., Mery, D.: Separation logic with one quantified variable. Theory Comput. Syst. 61, 371–461 (2017)
Distefano, D., O’Hearn, P.W., Yang, H.: A local shape analysis based on separation logic. In: Hermanns, H., Palsberg, J. (eds.) TACAS 2006. LNCS, vol. 3920, pp. 287–302. Springer, Heidelberg (2006). https://doi.org/10.1007/11691372_19
Haase, C., Ishtiaq, S., Ouaknine, J., Parkinson, M.J.: SeLoger: a tool for graph-based reasoning in separation logic. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 790–795. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_55
Hóu, Z., Goré, R., Tiu, A.: Automated theorem proving for assertions in separation logic with all connectives. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 501–516. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_34
Iosif, R., Rogalewicz, A., Simacek, J.: The tree width of separation logic with recursive definitions. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 21–38. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_2
Ishtiaq, S., O’Hearn, P.: BI as an assertion language for mutable data structures. In: POPL 2001, pp. 14–26. ACM (2001)
Le, Q.L., Tatsuta, M., Sun, J., Chin, W.-N.: A decidable fragment in separation logic with inductive predicates and arithmetic. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 495–517. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_26
Lozes, E.: Expressivité des Logiques Spatiales. Ph.D. thesis, ENS Lyon (2004)
Lozes, E.: Separation logic preserves the expressive power of classical logic. In: SPACE 2004 (2004)
Müller, P., Schwerhoff, M., Summers, A.J.: Viper: a verification infrastructure for permission-based reasoning. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 41–62. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_2
O’Hearn, P., Reynolds, J., Yang, H.: Local reasoning about programs that alter data structures. In: Fribourg, L. (ed.) CSL 2001. LNCS, vol. 2142, pp. 1–19. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44802-0_1
Piskac, R., Wies, T., Zufferey, D.: Automating separation logic using SMT. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 773–789. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_54
Ranise, S., Zarba, C.: A theory of singly-linked lists and its extensible decision procedure. In: SEFM 2006, pp. 206–215. IEEE (2006)
Reynolds, J.: Separation logic: a logic for shared mutable data structures. In: LICS 2002, pp. 55–74. IEEE (2002)
Schwerhoff, M., Summers, A.: Lightweight support for magic wands in an automatic verifier. In: ECOOP 2015, pp. 999–1023. Leibniz-Zentrum für Informatik, LIPICS (2015)
Thakur, A.: Symbolic Abstraction: Algorithms and Applications. Ph.D. thesis, University of Wisconsin-Madison (2014)
Thakur, A., Breck, J., Reps, T.: Satisfiability modulo abstraction for separation logic with linkedlists. In: SPIN 2014, pp. 58–67. ACM (2014)
Yang, H.: Local Reasoning for Stateful Programs. Ph.D. thesis, University of Illinois, Urbana-Champaign (2001)
Yang, H., Lee, O., Berdine, J., Calcagno, C., Cook, B., Distefano, D., O’Hearn, P.: Scalable shape analysis for systems code. In: Gupta, A., Malik, S. (eds.) CAV 2008. LNCS, vol. 5123, pp. 385–398. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70545-1_36
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Demri, S., Lozes, É., Mansutti, A. (2018). The Effects of Adding Reachability Predicates in Propositional Separation Logic. In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_26
Download citation
DOI: https://doi.org/10.1007/978-3-319-89366-2_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89365-5
Online ISBN: 978-3-319-89366-2
eBook Packages: Computer ScienceComputer Science (R0)





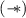 , is a convenient fragment (called herein
, is a convenient fragment (called herein 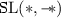 ) in which can be solved two problems of frame inference and abduction, that play an important role in static analysers and provers built on top of separation logic.
) in which can be solved two problems of frame inference and abduction, that play an important role in static analysers and provers built on top of separation logic.  can be decided in
can be decided in 
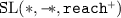 and
and 