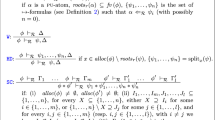A Decidable Fragment in Separation Logic with Inductive Predicates and Arithmetic

Abstract

We consider the satisfiability problem for a fragment of separation logic including inductive predicates with shape and arithmetic properties. We show that the fragment is decidable if the arithmetic properties can be represented as semilinear sets. Our decision procedure is based on a novel algorithm to infer a finite representation for each inductive predicate which precisely characterises its satisfiability. Our analysis shows that the proposed algorithm runs in exponential time in the worst case. We have implemented our decision procedure and integrated it into an existing verification system. Our experiment on benchmarks shows that our procedure helps to verify the benchmarks effectively.

1 Introduction

Separation logic [14, 27] is a well-established assertion language designed for reasoning about heap-manipulating programs. Combined with inductive predicates, separation logic has been shown to capture semantics of loops and recursive procedures naturally and succinctly. A decision procedure for satisfiability of separation logic with inductive predicates could be useful for multiple analysis problems associated with heap-manipulating programs, e.g., compositional verification [8, 19, 26], shape analysis [15], termination analysis [6] as well as to uncover reachability in bug finding tools [17]. It has been shown that the satisfiability of the fragment of separation logic which does not include inductive (user-defined) predicates is decidable [7, 17, 22, 23]. The main challenge on satisfiability checking of separation logic with inductive predicates is that it often requires reasoning about infinite heaps as well as infinite integer domain. Indeed, the problem in the full fragment of inductive predicates with shape and arithmetic properties is shown to be undecidable [29]. One research goal is thus to identify decidable yet expressive fragment of the logic, based on which we can have precise and always-terminating reasoning over heap-manipulating programs.

One way to show that a fragment of separation logic with inductive predicates is decidable is to infer, for each inductive predicate, a finite representation without any inductive predicates which precisely characterizes its satisfiability. For example, the authors in [1] showed that inductive predicates on linked lists can be precisely characterised by models of length zero or two and thus concludes that the fragment of separation logic with inductive predicates on linked lists only is decidable. Later, Brotherston et al. proposed SLSAT [5], a decision procedure to compute for every arbitrary heap-only inductive predicate a finite (disjunctive) set of base formulas which exactly characterises its satisfiability, and consequently showed that the fragment of separation logic with heap-only inductive predicates is decidable. Finally, the work in [29] extended SLSAT to show that a fragment of separation logic with inductive predicates and arithmetic properties under several restrictions is decidable. In particular, their fragment only allows inductive predicates satisfying the following conditions: for each inductive predicate, its heap part has two disjuncts and the arithmetic part is restricted in DPI predicates.

In this work, we present a decidable fragment of separation logic including inductive predicates with shape and arithmetic properties, which is more expressive than all fragments which have been shown to be decidable previously. The decidability is shown through a novel algorithm which computes for each inductive predicate a base formula (i.e. one without inductive predicates) which exactly characterizes its satisfiability. The idea is to compute for each heap-only inductive predicate a non-recursive base formula regardless of the infinite domains. In the case that the inductive predicate includes shape and arithmetic properties, if the arithmetical properties can be precisely computed in the form of arithmetic closures, we derive a combination of the base formula and the arithmetic closures which precisely characterises satisfiability for the inductive predicate.

In particular, we show how to derive a disjunctive base formula for each inductive predicate based on flat formulas, which are designed to capture the notion of a (infinite) set of formulas which can be represented by the same base formula (allocated memory, (dis)equalities and arithmetic closures). First, we describe a novel algorithm to derive for each inductive predicate a cyclic unfolding tree prior to flattening the tree into a disjunctive set of regular formulas. Every regular formula in this set has the same base pair of the allocated memory and (dis)equalities over a set of free variables (similar to [5]). Secondly, we define a decidable fragment where every regular formula derived for inductive predicates is flattable i.e., its arithmetic part is a conjunction of periodic constraints and the closure of the union of these conjunctions can be represented by some semilinear sets and thus is Presburger-definable (similar to [4, 29]). As a result, our algorithm derives for each inductive predicate a disjunctive set of flat formulas, and then a disjunctive set of base formulas.

Contributions. We make the following technical contributions.

• Firstly, we present a novel algorithm to generate cyclic unfolding trees for inductive predicates with shape and arithmetic properties. Our complexity analysis shows that the proposed algorithm runs in exponential time in the worst case.

• Secondly, based on the algorithm, we present a decision procedure for satisfiability checking of the fragment of separation logic with inductive predicates where arithmetic properties can be represented as semilinear sets.

• Thirdly, we have implemented our algorithm and applied it to verify several benchmark programs. In our implementation, we generate under-/over-approximated bases for those inductive predicates beyond the decidable fragment systematically.

Organization. The rest of the paper is organized as follows. Section 2 presents relevant definition. Section 3 shows an overview of our approach through an example. We show how to compute bases of regular formulas in Sect. 4 and subsequently compute regular formulas of inductive predicates in Sect. 5. Section 6 describes a decision procedure. Our implementation and evaluation are presented in Sect. 7. Section 8 reviews related work and lastly Sect. 9 concludes. For space reason, all missing proofs are presented in [20].

Fig. 1.

Syntax.

2 Preliminaries

We use $\bar{x}$ to denote a sequence of variables and ${x_i}$ to denote its $i^{th}$ element. We write $\bar{x}^N$ and $\bar{x}^S$ to denote the sequence of integer variables and pointer variables in $\bar{x}$, resp.

Syntax. A formula is defined by the syntax presented in Fig. 1. A symbolic heap $\varDelta$ is an existentially quantified conjunction of some spatial formula $\kappa$, some pointer (dis)equality $\alpha$ and some formula in Presburger arithmetic $\phi$. All free variables in $\varDelta$, denoted by function $\textit{FV}({\varDelta })$, are implicitly universally quantified at the outermost level. The spatial formula $\kappa$ may be conjoined ($*$) by $\mathtt{emp}$ predicate, points-to predicates ${x}{{\mapsto }}c(f_i{:}v_i)$ and inductive predicate ${\mathtt{P}}(\bar{v})_u^o$ where $o$ and $u$ are labels used for constructing unfolding trees in a breadth-first manner. While $o$ captures the ordering number, $u$ is the number of unfolding. We occasionally omit these numbers if there is no ambiguity. Whenever possible, we discard $f_i$ of the points-to predicate and use its short form as ${x}{{\mapsto }}c(\bar{v})$. We often use $\pi$ to denote a conjunction of $\alpha$ and $\phi$ formulas. Note that $v_1 {\ne } v_2$ and $v {\ne } {{\mathtt{null}}}$ are short forms for $\lnot (v_1{=}v_2)$ and $\lnot (v{=}{{\mathtt{null}}})$ respectively. $\_\,$ is used to denote a “don’t care” term.

We write $\mathcal {P}$ to denote a set of $n$ predicates in our system. Each inductive predicate is defined by a disjunction $\varPhi$ using the key word pred. In each disjunct, we require that variables which are not formal parameters must be existentially quantified.

Example 1

We define an increasingly sorted list using the fragment above.

$$\begin{aligned} \begin{array}{l} {\mathtt{pred}}~{\mathtt{sortll}}(\mathtt{root}{,}n{,}mi) \equiv \mathtt{root}{\mapsto }node2(mi,{{\mathtt{null}}}) ~{\wedge }~ {n{=}1} \\ \quad {\vee }~{\exists } ~q{,}n_1{,}mi_1 {\cdot }~ \mathtt{root}{\mapsto }node2(mi,q) *{\mathtt{sortll}}(q,n_1,mi_1)~{\wedge }~n{=}n_1{+}1~{\wedge }~ mi{\le }mi_1; \\ \end{array} \end{aligned}$$

where the data structure $node2$ is declared as: $data$ node2 { int val; node2 next;}. In the sorted list ${\mathtt{sortll}}(\mathtt{root}{,}n{,}mi)$, $\mathtt{root}$ is the pointer pointing to the head of the list, $n$ is the length of the list and $mi$ is the minimal value stored in the list.

We use $\varDelta [t_1 {/} t_2]$ for a substitution of all occurrences of $t_2$ in $\varDelta$ to $t_1$. Note that we always apply the following normalization after predicate unfolding: $(\exists \bar{w}_1{\cdot }~\kappa _1{\wedge }\pi _1) *(\exists \bar{w}_2{\cdot }~\kappa _2{\wedge }\pi _2) {\equiv } (\exists \bar{w}_1{,}\bar{v}_2{\cdot }~\kappa _1 {*}(\kappa _2\rho ) {\wedge }\pi _1 {\wedge } (\pi _2\rho ))$ where $\bar{v}_2$ is a vector of fresh variables and has the same length $n$ as $\bar{w}_2$; and $\rho$ is a substitution: $\rho {=} \circ \{[v_i/w_i] ~|~ \forall i \in \{1...n \} \}$.

Our proposal relies on the following definitions. ${\mathtt{P}}(\bar{v})$ is called (heap) observable if there is at least one free pointer-typed variable in $\bar{v}$. Otherwise, it is called unobservable. $v{\mapsto }c(\bar{t})$ is called (heap) observable if $v$ is free. Otherwise, it is unobservable.

• (base formula) $\varPhi$ is a base formula (or base for short) if it does not include any occurrences of inductive predicates. Otherwise, it is an inductive formula.

• ${\varvec{(\varDelta }^{\exists } \mathbf{formula) }}$ Let ${\varDelta ^{\exists }}$ be a base formula and is of the form:

  $$ {\varDelta ^{\exists }}{\equiv } \exists \bar{w} {\cdot } {x_1}{{\mapsto }}c_1(\bar{v}_1) {*}\dots {*}{x_n}{{\mapsto }}c_n(\bar{v}_n) {\wedge }\alpha {\wedge }\phi $$

  ${\varDelta ^{\exists }}$ is a totally (existentially) quantified heap base formula if $x_i {\in } \bar{w}$ for all $i {\in } \{1,\dots ,n \}$ and $\textit{FV}(\alpha ) {\subseteq } \bar{w}$. We show that existentially quantified pointer-typed variables are not externally visible wrt. the satisfiability problem (Sect. 4). This is the fundamental for the transformation of an inductive predicate into an equi-satisfiable set of base formulas.

• (regular formula) $\varPhi$ is a regular formula if it is of the form: $\varPhi {\equiv }{\varDelta ^b}{*}\varUpsilon ^\exists$ where ${\varDelta ^b}$ is a base formula and $\varUpsilon ^\exists$ is a disjunctive (possibly infinite) set of ${\varDelta ^{\exists }}$ formulas. For example ${{\varDelta ^b}}{*} (\exists \bar{w}{\cdot } {\mathtt{P_1}}(\bar{v}_1){*} \dots {*} {\mathtt{P_n}}(\bar{v}_n))$, where $\bar{v}^S_i {\subseteq } \bar{w}$ $\forall i {\in } \{1{\dots } n \}$, is a regular formula.

• (flat formula) $\varPhi$ is a flat formula if it is a regular formula and is flattable, i.e. can be represented by a base formula.

We use ${\varDelta ^b}$ to denote a conjunctive base formula, $\varDelta ^{re}$ a regular formula and $\varDelta ^{{flat}}$ a flat formula. The following definition is critical for the computation of base formulas.

Definition 1

The numeric projection $(\varPhi )^N$ is defined inductively as follows.

$$ \begin{array}{ll} \begin{array}{lcl} (\varDelta _1 \vee \varDelta _2)^N &{} \equiv &{} (\varDelta _1)^N \vee (\varDelta _2)^N \\ (\exists \bar{x} \cdot \varDelta )^N &{} \equiv &{} \exists \bar{x}^N \cdot (\varDelta )^N \\ (\kappa {\wedge }\alpha {\wedge }\phi )^N &{} \equiv &{} (\kappa )^N{\wedge }\phi \\ \end{array} &{} \qquad \begin{array}{lcl} (\kappa _1 {*} \kappa _2)^N &{} \equiv &{} (\kappa _1)^N {\wedge } (\kappa _2)^N \\ ({\mathtt{P}}(\bar{v}))^N &{} \equiv &{} {\mathtt{P^N}}(\bar{v}^N) \\ ({x}{{\mapsto }}c(\bar{v}))^N {\equiv } (\mathtt{emp})^N &{} \equiv &{} {\mathtt{true}}\,\\ \end{array} \end{array} $$

For each inductive predicate ${\mathtt{P}}(\bar{t}){\equiv }\varPhi$, we assume the inductive predicate symbols ${\mathtt{P}}^{\mathtt{N}}$ and predicate ${\mathtt{P^N}}(\bar{t}^N)$ for its numeric projection satisfy ${\mathtt{P^N}}(\bar{t}^N) {\equiv } \varPhi ^N$. The semantics of the numeric projection ${\mathtt{P^N}}(\bar{t}^N)$ is as follows. Let $\varUpsilon ^b_P$ be a (infinite) set base formulas derived from ${\mathtt{P}}(\bar{t})$. If all variables in $\bar{t}$ are pointer-typed, then ${\mathtt{P^N}}(\bar{t}^N){\equiv } {\mathtt{true}}\,$. Otherwise, ${\mathtt{P^N}}(\bar{t}^N) {\equiv } \bigvee \{({\varDelta ^b})^N \mid {\varDelta ^b}\in \varUpsilon ^b_P \}$.

Example 2

The numeric definition ${\mathtt{sortll}}^N$ corresponding to the above increasingly sorted list sortll is defined as follows.

$$ \begin{array}{l} {\mathtt{pred}}~{\mathtt{sortll}}^N(n{,}mi) \equiv {n{=}1} \\ \quad {\vee }~{\exists } ~n_1{,}mi_1 {\cdot }~ {\mathtt{sortll}}^N(n_1,mi_1)~{\wedge }~n{=}n_1{+}1~{\wedge }~ mi{\le }mi_1; \\ \end{array} $$

Fig. 2.

Semantics.

Semantics. Concrete heap models assume a fixed finite collection Node, a fixed finite collection Fields, a disjoint set Loc of locations (heap addresses), a set of non-address values Val, such that ${{\mathtt{null}}}{\in } {\textit{Val}}$ and Val $\cap$ Loc = $\emptyset$. Further, we define:

$$ \begin{array}{lcl} {\textit{Heaps}} &{} {\overset{{\text {def}}}{=}} &{} {\textit{Loc}} {\rightharpoonup _{fin}} ({\textit{Node}} ~{\rightarrow }~ \textit{Fields}~{\rightarrow }~ \textit{Val}\cup \textit{Loc}) \\ {\textit{Stacks}} &{} {\overset{{\text {def}}}{=}} &{} {\textit{Var}} ~{\rightarrow }~ \textit{Val}\cup \textit{Loc}\end{array} $$

The semantics is given by a forcing relation: $s{,}h~{\models }~ \varPhi$ that forces the stack $s$ and heap $h$ to satisfy the constraint $\varPhi$ where $h\in {\textit{Heaps}}$, $s\in {\textit{Stacks}}$, and $\varPhi$ is a formula.

The semantics is presented in Fig. 2. $dom(f)$ is the domain of function $f$; $h_1 {\#} h_2$ denotes that heaps $h_1$ and $h_2$ are disjoint, i.e., $\text {dom}(h_1) ~{\cap }~ \text {dom}(h_2) ~{=}~ \emptyset$; and $h_1 {\cdot } h_2$ denotes the union of two disjoint heaps. Semantics of pure formulas depend on stack valuations. It is straightforward and omitted for simplicity.

3 Overview and Illustration

In this section, we illustrate how our decision procedure works through checking the satisfiability of the following inductive predicate over the data structure $node$ which is declared as: $data$ node {node left; node right;}.

$$ \begin{array}{l} {\mathtt{pred}}~{\mathtt{Q}}(x{,}y{,}n) \equiv {\exists } ~y_1 {\cdot }x{\mapsto }node({{\mathtt{null}}}{,}y_1) {\wedge } y{=}{{\mathtt{null}}}{\wedge }x{\ne }{{\mathtt{null}}}{\wedge }{n{=}1} \\ \quad {\vee } ~{\exists } ~x_1{,}y_1{,}n_1 {\cdot } y{\mapsto }node(x_1{,}y_1) *{\mathtt{Q}}(x,y_1,n_1)^0_{\_}{\wedge }y{\ne }{{\mathtt{null}}}{\wedge }n{=}n_1{+}2 ;\\ \end{array} $$

First, we infer a disjunctive set of base formulas for the predicate $\mathtt Q$ which precisely characterizes $\mathtt Q$’s satisfiability. After that, we check satisfiability of each disjunct in the set. If one of the disjuncts is satisfied, so is $\mathtt Q$. We remark that as the base formulas do not contain any occurrences of inductive predicates, their satisfiability is decidable [17, 23]. We generate the base formulas for each inductive predicate by: (i) constructing a cyclic unfolding tree and (ii) extracting base formulas from the leaf nodes in the tree.

Fig. 3.

Cyclic unfolding tree $\mathcal{T}_{2}^{Q}$.

Constructing Cyclic Unfolding Tree. We construct the cyclic unfolding tree for inductive predicate $\mathtt Q$ as shown in Fig. 3. In an unfolding tree, a node $\mathtt{v}$ is a conjunctive formula. An edge from $\mathtt{v}_1$ to $\mathtt{v}_2$ where $\mathtt{v}_2$ is a child of $\mathtt{v}_1$ is obtained by unfolding $\mathtt{v}_1$, i.e., substituting an occurrence of an inductive predicate in $\mathtt{v}_1$ with one disjunct in the predicate’s definition (after proper actual/formal parameter substitutions). For instance, in Fig. 3, the root of the tree is $\varDelta _2{\equiv } {\mathtt{Q}}(x{,}y{,}n)^0_0$. We remark that the ordering number and unfolding number of the root are initially set to 0. The root has two children, $\varDelta _{21}$ and $\varDelta _{22}$, which are obtained by unfolding the occurrence of $\mathtt Q$ with its two branches.

$$ \begin{array}{l} \varDelta _{21}{\equiv } {\exists } ~y_1 {\cdot }x{\mapsto }node({{\mathtt{null}}},y_1)\wedge y{=}{{\mathtt{null}}}{\wedge }x{\ne }{{\mathtt{null}}}{\wedge } n{=}1\\ \varDelta _{22}{\equiv }{\exists } ~x_1{,}y_1{,}n_1 {\cdot } y{\mapsto }node(x_1{,}y_1) *{\mathtt{Q}}(x,y_1,n_1)^0_1{\wedge }y{\ne }{{\mathtt{null}}}{\wedge }n{=}n_1{+}2 \end{array} $$

In turn, $\varDelta _{22}$ has two children, $\varDelta _{23}$ and $\varDelta _{24}$, which are obtained by unfolding the occurrence of $\mathtt Q$ again.

$$ \begin{array}{l} \varDelta _{23}{\equiv }{\exists } ~x_1{,}y_1{,}n_1{,}y_2 {\cdot } y{\mapsto }node(x_1{,}y_1) *x{\mapsto }node({{\mathtt{null}}},y_2) ~{\wedge } \\ \qquad y_1{=}{{\mathtt{null}}}{\wedge }x{\ne }{{\mathtt{null}}}{\wedge } n_1{=}1 {\wedge }y{\ne }{{\mathtt{null}}}{\wedge }n{=}n_1{+}2\\ \varDelta _{24}{\equiv }{\exists } ~x_1{,}y_1{,}n_1{,}x_2{,}y_2{,}n_2 {\cdot } y{\mapsto }node(x_1{,}y_1) {*} y_1{\mapsto }node(x_2{,}y_2) {*} {\mathtt{Q}}(x,y_2,n_2)^0_2~{\wedge }\\ \qquad y_1{\ne }{{\mathtt{null}}}{\wedge }n_1{=}n_2{+}2 {\wedge }y{\ne }{{\mathtt{null}}}{\wedge }n{=}n_1{+}2 \end{array} $$

We remark that unfolding numbers annotated for occurrences of recursive predicates (e.g., ${\mathtt{Q}}(x,y_1,n_1)^0_1$ in $\varDelta _{22}$ and ${\mathtt{Q}}(x,y_2,n_2)^0_2$ in $\varDelta _{24}$) are increased by one after each unfolding.

A leaf in the unfolding tree is either a base formula (e.g., $\varDelta _{21}$ and $\varDelta _{23}$), or one whose all occurrences of inductive predicates are unobservable, or one which is linked back to an interior node (e.g., $\varDelta _{24}$). Intuitively, a leaf node v is linked back to an interior node $v'$ only if v is subsumed (wrt. the satisfiability problem) by $v'$ in terms of the constraint on the heap. These back-links generate (virtual) cycles in the tree. A leaf is marked either closed or open. It is marked closed if it is either unsatisfiable or is linked back to some interior node. Otherwise, it is marked open. For instance, $\varDelta _{24}$ is linked back to $\varDelta _{22}$ and thus marked closed. These two nodes are labeled with the fresh symbol $\clubsuit$ in Fig. 3. They are linked as they have (i) the same observable points-to predicate $y{\mapsto }node(\_\,{,}\_\,)$, (ii) the same observable occurrence of inductive predicate ${\mathtt{Q}}(x,\_\,,\_\,)$ and (iii) the same disequalities over free variables (i.e., $y\ne {{\mathtt{null}}}$).

Each path ending with a leaf node which is not involved in any back-link represents (a way to derive) a formula which can be obtained by unfolding the inductive predicates according to the edges in the path. A cycle in the tree thus represents an infinite set of formulas, since we can construct infinitely many paths by iterating through the cycle an unbounded number of times. For instance, in Fig. 3, we can obtain a different formula following the cycle from $\varDelta _{22}$ to $\varDelta _{24}$ and back to $\varDelta _{22}$ for a different number of times and then following the edge from $\varDelta _{22}$ to $\varDelta _{23}$. We show that all formulas obtained by iterating through the same cycle a different number of times have the same spatial base. Furthermore, if the closure of the arithmetic part of these formulas is Presburger-definable, we can construct one formula to represent this infinite set of formulas.

Flattening Cyclic Unfolding Tree. After constructing the tree, we derive the base for the inductive predicates, e.g. $\mathtt Q$ in this example. To do that, we flatten the tree iteratively until there is no cycle left. To flatten the tree iteratively, we keep flattening the minimal cyclic sub-trees, i.e. the sub-trees without nested cycles, in a bottom-up manner. For instance, in Fig. 3 the sub-tree in which $\varDelta _{22}$ is the root is a minimal cyclic sub-tree. In principle, we can derive an infinite number of base formulae, each of which corresponds to the formula constructed by iterating the cyclic a different number of times. For instance, the following is the disjunctive set of the formulas obtained by following the cycle zero or more times (and then visiting $\varDelta _{23}$).

$$\begin{aligned} \begin{array}{lcl} \varDelta ^{{flat}}_{23} &{} {\equiv } &{} \quad {\exists } ~x_1{,}y_1{,}n_1{,}y_2{\cdot } (y{\mapsto }node(x_1{,}y_1) {*} x{\mapsto }node({{\mathtt{null}}},y_2) {\wedge } x{\ne }{{\mathtt{null}}}{\wedge } \\ &{}&{} \qquad y{\ne }{{\mathtt{null}}}{\wedge } n{=}n_1{+}1) \wedge ( y_1{=}{{\mathtt{null}}}{\wedge } n_1{=}1) \\ &{} &{}{\vee }~ {\exists } ~x_1{,}y_1{,}n_1{,}x_2{,}y_2{,}n_2{,}y_3{\cdot } (y{\mapsto }node(x_1{,}y_1) {*} x{\mapsto }node({{\mathtt{null}}},y_3) {\wedge } x{\ne }{{\mathtt{null}}}{\wedge } \\ &{}&{} \qquad y{\ne }{{\mathtt{null}}}{\wedge } n{=}n_1{+}1) *(y_1{\mapsto }node(x_2{,}y_2) {*} {\wedge } y_2{=}{{\mathtt{null}}}{\wedge } n_1{=}n_2{+}2 \\ &{} &{} \qquad n_2{=}1) \\ &{} &{} {\vee } ... \end{array} \end{aligned}$$

Fig. 4.

Flattened tree.

Notice that each iteration of this cycle results in a formula which conjuncts $\varDelta _{23}$ with unobservable heaps (e.g., $y_1{\mapsto }node(\_\,{,}y_2){\wedge }y_2{=}{{\mathtt{null}}}$ where $y_1$, $y_2$ are existentially quantified variables) and a constraint which requires that the third parameter of $\mathtt Q$ is increased by two. We refer to $\varDelta ^{{flat}}_{23}$ as a flat formula. One of our main contribution in this work is to show that all formulae in the set have the same base. In particular, we state that a quantified heap base formula ${\varDelta ^{\exists }}_i$ is equi-satisfiable to its numeric projection, i.e. $({\varDelta ^{\exists }}_i)^N$. As a result, a flat formula is equi-satisfiable to a conjunction of a base formula (i.e., $\varDelta _{23}$) and the set of the numeric projections. Furthermore, in the proposed decidable fragment, closure of this numeric set is Presburger-definable. In this example, this numeric set can be represented by the arithmetic predicate: ${\mathtt{P_{cyc}}}(n_1){\equiv } n_1{=}1 ~ {\vee } ~ \exists n_2 {\cdot } n_1{=}n_2{+}2 {\wedge } {\mathtt{P_{cyc}}}(n_2)$. Following [29], we can show that this predicate is equivalent to the following Presburger formula: $\exists k {\cdot }n_1{=}2k{+}1 {\wedge } k{\ge }0$. As a result, $\varDelta ^{{flat}}_{23}$ is equi-satisfiable to the following base formula:

$$ \begin{array}{l} {\varDelta ^b}_{23}{\equiv } {\exists } ~x_1{,}y_1{,}x_2{,}y_2{,}n_1 {\cdot } (y{\mapsto }node(x_1{,}y_1) {*} x{\mapsto }node({{\mathtt{null}}},y_2) {\wedge }x{\ne }{{\mathtt{null}}}{\wedge }\\ \qquad y{\ne }{{\mathtt{null}}}{\wedge }n{=}n_1{+}1) {\wedge } (\exists k {\cdot }n_1{=}2k {+}1{\wedge } k{\ge }0) \end{array} $$

$\mathcal{T}_{2}^{Q}$ is flattened as the tree presented in Fig. 4 which has no cycle. Finally, the base of $\mathtt Q$ is computed based on the open leaf nodes of the tree shown in Fig. 4. It is the disjunction of $\varDelta _{21}$ and ${\varDelta ^b}_{23}$ as:

$$ \begin{array}{l} \{ {\exists } ~y_1 {\cdot }x{\mapsto }node({{\mathtt{null}}},y_1) {\wedge } y{=}{{\mathtt{null}}}{\wedge }x{\ne }{{\mathtt{null}}}{\wedge } n{=}1 ;\\ {\exists } ~x_1{,}y_1{,}y_2 {,}k{\cdot } y{\mapsto }node(x_1{,}y_1) {*} x{\mapsto }node({{\mathtt{null}}},y_2) {\wedge }x{\ne }{{\mathtt{null}}}{\wedge } y{\ne }{{\mathtt{null}}}{\wedge }n{=}2k{+}2 {\wedge } k{\ge }0 \} \end{array} $$

Since either disjunct of the set above is satisfiable, so is $\mathtt Q$.

4 Foundation of Base Computation

In this section, we show that existentially quantified pointer-typed variables are not externally visible wrt. the satisfiability problem. This finding is fundamental for the transformation of an inductive predicate into regular formulas and then flat formulas. The following two functions: $\mathbf{{\scriptstyle eXPure}}({\varDelta ^b})$ and ${\varPi }(\pi ,\bar{w})$, are relevant in our argument.

Reduction. We first define a function called , which transforms a base formula into an equi-satisfiable first-order formula. is defined as follows:

$$ \begin{array}[t]{l} \mathbf{{\scriptstyle eXPure}}(\exists \bar{w}{\cdot }~{x_1}{{\mapsto }}c_1(\bar{v}_1){*} ...{*} {x_n}{{\mapsto }}c_n(\bar{v}_n) ~{\wedge }~\pi ) ~{\equiv } \\ \quad {\mathtt{\exists }} ~ \bar{w}{\cdot }~ \bigwedge \{x_i{\ne }{{\mathtt{null}}}\mid i{\in }\{1...n\} \} \wedge \bigwedge \{x_i{\ne }x_j \mid i,j{\in }\{1...n\} \text { and } i{\ne }j \} ~{\wedge }~ \pi \\ \end{array} $$

Proposition 1

For all $s$ such that $s\models {\mathbf{{\scriptstyle eXPure}}}({{\varDelta ^b}})$, there exists $s'$,$h$ such that $s{\subseteq } s'$, $|\text {dom}(h)|{=}n{+}|\bar{w}|$, $(s(x_i) \rightarrow \_) \in \text {dom}(h) ~\forall i {\in } \{1...n\}$, and $s', h\models {\varDelta ^b}$ where $|\text {dom}(h)|$ is the size of heap $\text {dom}(h)$ and $|\bar{w}|$ is the length of sequence $\bar{w}$.

Proposition 2

For all $s, h$ such that $s, h\models {\varDelta ^b}$, ${s\models \mathbf{{\scriptstyle eXPure}}}({{\varDelta ^b}})$.

Lemma 1

${\varDelta ^b}$ is satisfiable if only if $\mathbf{{\scriptstyle eXPure}}({\varDelta ^b})$ is satisfiable.

Proof

The “if” direction follows immediately from Proposition 1. The “only if” direction follows immediately from Proposition 2.    $\square$

We remark that the proposed function $\mathbf{{\scriptstyle eXPure}}$ is similar to the well-formed function in [22]. Indeed, the well-formed function is more general than $\mathbf{{\scriptstyle eXPure}}$ as it additionally supports singly-linked lists $lseg$.

Quantifier Elimination. Function ${\varPi }(\pi ,\bar{w})$ eliminates the existential quantifiers on pointer-typed variables $\bar{w}^S$. It is defined as follows.

Definition 2

${\varPi }({\mathtt{true}}\,,\bar{w}) = {\mathtt{true}}\,$, ${\varPi }({\mathtt{false}}\,,\bar{w}) = {\mathtt{false}}\,$, ${\varPi }(v_1{\not =}v_1{\wedge }\pi _1,\bar{w}) = {\mathtt{false}}\,$, ${\varPi }(\exists \bar{w}{\cdot }~ \alpha {\wedge }\phi ,\bar{w})= \exists \bar{w}{\cdot }~{\varPi }(\alpha ,\bar{w}){\wedge }\phi$. Otherwise,

$$ \begin{array}{l} {\varPi }(v_1{=}v_2{\wedge }\alpha _1,\bar{w}) = \quad {\left\{ \begin{array}{ll} {\varPi }(\alpha _1[v_1/v_2],\bar{w}) &{} \quad {if }\ v_1\in \bar{w}^S\\ {\varPi }(\alpha _1[v_2/v_1],\bar{w}) &{} \quad {if }\ v_2\in \bar{w}^S\ { and }\ v_1 \not \in \bar{w}^S\\ v_1{=}v_2{\wedge } {\varPi }(\alpha _1,\bar{w}) &{} \quad \ {otherwise} \end{array}\right. } \\ {\varPi }(v_1{\not =}v_2{\wedge }\alpha _1,\bar{w}) = \quad {\left\{ \begin{array}{ll} v_1{\not =}v_2{\wedge } {\varPi }(\alpha _1,\bar{w}) &{} \quad \ {if }\ v_i{\not \in }\bar{w}^S, i{=}\{1,2\}\\ {\varPi }(\alpha _1,\bar{w}) &{} \quad \ {otherwise} \end{array}\right. } \end{array} $$

For soundness, we assume that $\alpha$ is sorted s.t. equality conjuncts are processed before disequality ones.

Lemma 2

For all $s$, $s\models \exists \bar{w} {\cdot } \alpha$ iff there exists $s' {\subseteq } s$ and $s' \models {\varPi }(\alpha ,\bar{w})$.

We remark that quantifier elimination in equality logic has been studied well and can be done in SMT solvers (i.e., Z3 [10]). In this paper, we present a simplified implementation for efficiency.

Lemmas 1 and 2 imply that it is sound and complete to discard existentially quantified heaps while solving satisfiability in our fragment. The base of a regular formula is computed as follows.

Lemma 3

For all $s$ and $h$, $s{,}h\models {{\varDelta ^b}}{*}\varUpsilon ^\exists$ iff there exist $s' {\subseteq } s$, $h' {\subseteq } h$ and $s'{,}h' \models {{\varDelta ^b}}{\wedge } \bigvee \{ ({\varDelta ^{\exists }})^N \mid {\varDelta ^{\exists }}\in \varUpsilon ^\exists \}$.

The proof, based on structural induction on the number of base formulas ${\varDelta ^{\exists }}$ of $\varUpsilon ^\exists$, is presented in [20]. We remark that this result can be implicitly implied from the results presented in [6, 17, 18]. Now, the problem of base computation in separation logic is reduced to the problem of closure computation for arithmetic constraints. We formally define this reduction as follows.

Definition 3

(Base Computation). Let $\varDelta ^{re}{\equiv }{{\varDelta ^b}}{*}\varUpsilon ^\exists$ be a regular formula. $\varDelta ^{re}$ is flattable, i.e. can be represented as a base formula, if $\bigvee \{ ({\varDelta ^{\exists }})^N \mid {\varDelta ^{\exists }}\in \varUpsilon ^\exists \}$ is equivalent to a Presburger formula.

We note that the disjunction set $\varUpsilon ^\exists$ may be infinite. In the next section we transform each inductive predicate into a set of regular formulas; each of these regular formulas is of the form: $\varDelta ^{re}~{\equiv }~ {{\varDelta ^b}}{*} (\exists \bar{w}{\cdot } {\mathtt{P_1}}(\bar{v}_1) {*} ... {*} {\mathtt{P_n}}(\bar{v}_n))$, where $\bar{v}^S_i {\subseteq } \bar{w}$ for all $i {\in } \{1...n \}$. Based on Definition 3, $\varDelta ^{re}$ is equivalent to $\varDelta ^{re}~{\equiv }~ {{\varDelta ^b}}{*} (\exists \bar{w}{\cdot } {\mathtt{P_1}}^N(\bar{v}^N_1) {\wedge } ... {\wedge } {\mathtt{P_n}}^N(\bar{v}^N_n))$. Thus, the problem of base computation for inductive predicates is reduced to the problem of closure computation for numeric predicates.

5 Transformation of Inductive Predicates

In this section, we present an algorithm, named pred2reg, to transform each inductive predicate into a disjunctive set of regular formulas. Each of these regular formulas is of the form: $\varDelta ^{re}~{\equiv }~ {{\varDelta ^b}}{*} (\exists \bar{w}{\cdot } {\mathtt{P_1}}(\bar{v}_1) {*} ... {*} {\mathtt{P_n}}(\bar{v}_n))$, where $\bar{v}^S_i {\subseteq } \bar{w}$ for all $i {\in } \{1...n \}$. For each inductive predicate in $\mathcal {P}$, pred2reg first uses procedure utree to construct a cyclic unfolding tree to characterise its satisfiability (Sect. 5.1). After that, pred2reg uses procedure $\mathtt {\mathtt{extract\_regular}}$ to flatten the tree into a set of regular formulas in a bottom-up manner (Sect. 5.2). The correctness of the transformation is presented in Sect. 5.3.

5.1 Constructing Cyclic Unfolding Tree

Procedure utree presented in Algorithm 1 aims to construct an unfolding tree given an inductive predicate. This algorithm is an instantiation of the S2SAT algorithm described in [17]. While S2SAT is designed for decision problems (SAT or UNSAT), utree works as a re-write procedure. It transforms an user-defined predicate into an unfolding tree with (virtual) cycles. Given an inductive predicate, say ${\mathtt{P}}(\bar{v})$, it constructs a cyclic unfolding tree for the formula $\varDelta {\equiv }{\mathtt{P}}(\bar{v})_0^0$. Each iteration (lines 2–12) conducts one of the following four actions. Function $\mathtt {\mathtt{OA}}$ over-approximates every leaf node and checks whether it is unsatisfiable. If it is the case, the function marks the leaf closed. Function ${\mathtt{link\_back}}$ links a leaf back to an interior node if they have the same free (externally) pointer-based variables. In each such back-link, the leaf node is called a bud and the interior node is called a companion. Function choose_bfs chooses an open leaf for the unfolding with function unfold.

Over-Approximation. Given an input tree $\mathcal{T}_{i}$, for each its leaf node $\varDelta$, function $\mathtt {\mathtt{OA}}$ obtains the over-approximation $\varDelta '$ by substituting all occurrences of inductive predicates appearing in $\varDelta$ with ${\mathtt{true}}\,$ prior to transforming $\varDelta '$ into an equi-satisfiable first-order formula $\pi '$ using function (defined in Sect. 4). Finally, $\pi '$ is discharged using an SMT solver. If $\pi '$ is unsatisfiable, so is $\varDelta$.

Unfolding. In each iteration, our algorithm selects one open leaf node including some occurrences of inductive predicates to expand the tree. The node is selected in a breadth-first manner. Among all open leaf nodes, a node is selected if it contains at least one observable occurrence of an inductive predicate, e.g. ${\mathtt{P}}(\bar{v})^{o}_{u}$, where $u$ is the smallest unfolding number. If there are more than one such occurrences, the one with the smallest ordering number is chosen. We remark that a leaf node whose occurrences of inductive predicates are all unobservable is never unfolded as this leaf is already a regular formula. For each new node derived, unfold marks it open and creates a new edge accordingly. Let ${\mathtt{Q}}(\bar{t})^{o_l}_{\_}$ denote a predicate occurrence of the derived node, its unfolding number is set to $\mathtt u{+}1$ if it is (not necessary directly) recursive. Otherwise, it is $\mathtt u$. Its sequence number is set to $o_l{+}o$.

Linking Back. Function ${\mathtt{link\_back}}$ connects an open leaf with at least one observable occurrence of inductive predicate (say, $\exists \bar{w}_1 {\cdot } \kappa _1{\wedge }\alpha _1{\wedge }\phi _1$) to an interior node (say, $\exists \bar{w}_2 {\cdot }\kappa _2{\wedge }\alpha _2{\wedge }\phi _2$) as follows.

• 1. First, it discards all unobservable points-to predicates and all unobservable inductive predicates, and then eliminates existentially quantified variables for pointer equalities and disequalities in the two formulas. Afterwards, the two formulas become $\kappa '_1{\wedge }\alpha _{1a}{\wedge }\phi _1$ and $\kappa '_2{\wedge }\alpha _{2a}{\wedge }\phi _2$ where $\alpha _{1a}{\equiv }{\varPi }(\alpha _1,\bar{w}_1^S)$, $\alpha _{2a}{\equiv }{\varPi }(\alpha _2,\bar{w}_2^S)$.

• 2. Secondly, it constructs $\alpha _{1b}$ (resp., $\alpha _{2b}$) by augmenting the closure for equalities on pointers into $\alpha _{1a}$ (resp., $\alpha _{2a}$): if $x{=}y \in \alpha$ and $y{=}z \in \alpha$ then $x{=}z \in \alpha$.

• 3. Thirdly, it builds a set of addresses, i.e. ${\mathtt{B}}_1$, ${\mathtt{B}}_2$, for each formula. Given a formula $\exists \bar{w} {\cdot } \kappa {\wedge }\alpha {\wedge }\phi$, its set of addresses ${\mathtt{B}}$ is collected as follows. If ${x}{{\mapsto }}c(\_\,) {\in } \kappa$ then $x \in {\mathtt{B}}$; if $x \in {\mathtt{B}}$ and $x{=}y \in \alpha$ then $y \in {\mathtt{B}}$.

• 4. Next, it adds into $\alpha _{1b}$ (resp. $\alpha _{2b}$) the Boolean abstraction of separating predicates, e.g. $\alpha _{1c}{\equiv }\alpha _{1b} {\wedge } \bigwedge \{x{\ne }{{\mathtt{null}}}~|~ x\in {\mathtt{B}}_1 \} {\wedge } \bigwedge \{x{\ne }y ~|~ x{,}y\in {\mathtt{B}}_1 \}$ and similarly for $\alpha _{2c}$. Note that we assume redundant constraints in $\alpha _{1c}$ and $\alpha _{2c}$ are discarded.

• 5. Finally, $\kappa '_1{\wedge }\alpha _{1c}{\wedge }\phi _1$ is linked to $\kappa '_2{\wedge }\alpha _{2c}{\wedge }\phi _2$ if the following conditions hold:

  • (i) ${\mathtt{B}}_1$ and ${\mathtt{B}}_2$ are identical; and

  • (ii) $\alpha _{1c}$ and $\alpha _{2c}$ are identical; and

  • (iii) For all occurrence ${\mathtt{P_i}}(\bar{t})^{o_2}_{u_2}$ in $\kappa _2'$, there exists one occurrence ${\mathtt{P_i}}(\bar{v})^{o_1}_{u_1}$ in $\kappa _1'$ such that $u_1 {>} u_2$ and for all free variable $v_i \in \bar{v}$, $t_i$ is a free variable and $\alpha _{1c} \implies t_i{=}v_i$.

Fig. 5.

Flattening minimal cyclic sub-tree.

5.2 Flattening Cyclic Unfolding Tree

To compute a set of regular formulas for a cyclic tree, procedure $\mathtt {\mathtt{extract\_regular}}$ flattens its cycles using procedure flat_tree iteratively in a bottom-up manner until there is no cycle left. Afterward, the set is derived from the disjunctive set of flattened open leaf nodes. In particular, it repeatedly applies flat_tree on minimal cyclic sub-trees. A cyclic sub-tree is minimal if it does not include any (nested) cyclic sub-trees and among other companion nodes, its companion node is the one which is closest to a leaf node. We use $\mathcal{C}(\varDelta _c{\rightarrow }\{\varDelta ^1_b,..,\varDelta ^n_b\})$ to denote a minimal cyclic sub-tree where back-links are formed between companion $\varDelta _c$ and buds $\varDelta ^i_b$. If there is only one bud in the tree, we write $\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b)$ for simplicity. Function flat_tree takes a minimal cyclic sub-tree as an input and returns a set of regular formulas, each of them corresponds to an open leaf node in the tree.

We illustrate procedure flat_tree through the example in Fig. 5 where the tree in the left (Fig. 5(a)) is a minimal cyclic sub-tree $\mathcal{C}(\varDelta _i{\rightarrow }\varDelta _{i_6})$ and is the input of flat_tree. For a minimal cyclic sub-tree, flat_tree first eliminates all closed leaf nodes (e.g., $\varDelta _{i_1}$ and $\varDelta _{i_5}$). We remark that if all leaf nodes of a cyclic sub-tree are unsatisfiable, the whole sub-tree is pruned i.e. replaced by a closed node with ${\mathtt{false}}\,$. After that, the open leaf nodes (e.g., $\varDelta _{i_3}$ and $\varDelta _{i_4}$) are flattened by the function flat. Finally, flattened nodes (e.g., ${\mathtt{flat}}(\mathcal{C}(\varDelta _i{\rightarrow }\varDelta _{i_6}),\varDelta _{i_3})$ and ${\mathtt{flat}}(\mathcal{C}(\varDelta _i{\rightarrow }\varDelta _{i_6}),\varDelta _{i_5}$)) are connected directly to the root of the minimal cyclic sub-tree (e.g., $\varDelta _i$); all other nodes (e.g., $\varDelta _{i_2}$ and $\varDelta _{i_6}$) are discarded. The result is presented in Fig. 5(b).

Function flat takes a minimal cyclic sub-tree, e.g. $\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b)$, and an open leaf node in the sub-tree, e.g. $\varDelta ^{re}_j{\equiv } \exists \bar{w} {\cdot } {{\varDelta ^b}} {*} {\mathtt{P_1}}(\bar{t}_1) {*} ... {*}{\mathtt{P_n}}(\bar{t}_n)$ where $\bar{t_i}^S {\subseteq } \bar{w}$ $\forall i \in \{1...n \}$, as inputs. It generates a regular formula representing the set of formulas which can be obtained by unfolding according to the path which iterates the cycle (from $\varDelta _{c}$ to $\varDelta _{b}$ and back to $\varDelta _{c}$) an arbitrary number of times and finally follows the path from $\varDelta _{c}$ to $\varDelta ^{re}_j$. As the formulas obtained by unfolding according to the paths of the cycle are existentially heap-quantified, following Lemma 3, they are equi-satisfiable with their numeric part. As so, flat constructs a new arithmetical inductive predicate, called $\mathtt P_{cyc}$, to extrapolate the arithmetic constraints over the path from $\varDelta _c$ to $\varDelta _b$. The generation of $\mathtt P_{cyc}$ only succeeds if the arithmetical constraints of $\varDelta _c$, $\varDelta ^{re}_j$ and $\varDelta _b$ are of the form $\phi _c$, $\phi _c{\wedge } \phi _{base}$ and $\phi _c {\wedge } \phi _{rec}$, respectively. Let $t_1{,}..{,}t_i$ be a sequence of integer-typed parameters of the matched inductive predicates in $\varDelta _c$ and $t_1'{,}..{,}t_i'$ be the corresponding sequence of integer-typed parameters of the matched inductive predicates in $\varDelta _b$. Then, flat generates the predicate ${\mathtt{P_{cyc}}}(t_1{,}...{,}t_i)$ defined as follows.

$$ {\mathtt{pred}}~ {\mathtt{P_{cyc}}}(t_1{,}...{,}t_i) \equiv \exists \bar{w}_b {\cdot } \phi _{base} \vee \exists \bar{w}_c {\cdot } \phi _{rec}{\wedge } {\mathtt{P_{cyc}}}(t_1'{,}...{,}t_i') $$

where $\bar{w}_b {=} \textit{FV}(\phi _{base}) \setminus \{ t_1{,}...{,}t_i\}$ and $\bar{w}_c {=} \textit{FV}(\phi _{rec}) \setminus \{ t_1{,}...{,}t_i\} \setminus \{ t'_1{,}...{,}t'_i\}$. Afterward, flat produces the output as: $\exists \bar{w} {\cdot } {{\varDelta ^b}} {\wedge }{\mathtt{P^N_1}}(\bar{t}^N_1) {\wedge } ... {\wedge }{\mathtt{P^N_n}}(\bar{t}^N_n){\wedge }{\mathtt{P_{cyc}}}(t_1{,}..{,}t_i)$.

Fig. 6.

Flattening a complex cyclic tree.

Finally, we highlight the flattening procedure with a fairly complex example in Fig. 6. The input tree, presented in Fig. 6(a), has three cycles. First, flat_tree flattens the lower tree $\mathcal{C}(\varDelta _2{\rightarrow }\varDelta _4)$ and produces the tree in the middle, Fig. 6(b), where $\varDelta _5'{\equiv }{\mathtt{flat}}(\mathcal{C}(\varDelta _2{\rightarrow }\varDelta _4),{\varDelta _{5}})$. After that, it flattens the intermediate tree and produces a cyclic-free tree in Fig. 6(c). In the final tree, $\varDelta '_3{\equiv }{\mathtt{flat}}(\mathcal{C}(\varDelta {\rightarrow }\{\varDelta _1,\varDelta _6\}),{\varDelta _{3}})$ and $\varDelta _5''{\equiv }{\mathtt{flat}}(\mathcal{C}(\varDelta {\rightarrow }\{\varDelta _1,\varDelta _6\}),{\varDelta '_{5}})$. As the latter tree has two back-links, the corresponding arithmetic predicate generated for it has two recursive branches.

5.3 Correctness

Procedure utree . First, it is easy to verify that the cyclic unfolding tree derived by the procedure utree preserves satisfiability and unsatisfiability of the given predicate.

Lemma 4

Let $\mathcal{T}_{i}$ be the cyclic unfolding tree derived by procedure utree for predicate ${\mathtt{P}}_i(\bar{t}_i)$. $\mathcal{T}_{i}$ contains at least one satisfiable leaf node iff ${\mathtt{P}}_i(\bar{t}_i)$ is satisfiable.

Next, we provide a complexity analysis for procedure utree. Intuitively, the procedure terminates if there is no more leaf node for unfolding. This happens when all leaf nodes are either base formulas, or formulas with unobservable occurrences of inductive predicates or linked back. The last case occurs if two nodes involved in a back link have similar arrangement over free predicate arguments. As the number of these free arguments are finite, so is the number of arrangements. In particular, suppose we have $N$ inductive predicates (e.g., $\mathtt P_1$,...,$\mathtt P_N$), and $m$ is the maximal length of predicate parameters (including one more for ${{\mathtt{null}}}$). The maximal free pointer-typed variables of an inductive predicate is also $m$. We compute the complexity based on $N$ and $m$.

Lemma 5

Every path of the cyclic unfolding tree generated by procedure utree (Algorithm 1) has at most $\mathcal {O}(2^{m} \times (2^{m})^N \times 2^{2m^2})$ nodes.

Procedure $\mathtt {\mathtt{extract\_regular}}$ . For simplicity, we only discuss the minimal cyclic sub-trees including one cycle. Let $\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b)$ be a minimal cyclic sub-tree and ${\varDelta ^b}_j$ be a satisfiable leaf node in the tree. Let ${\mathtt{lassos}}({\varDelta _c}{,}\varDelta _b{,}{\varDelta ^b}_j{,}k)$ be a formula which is obtained by unfolding the tree following the cycle (from $\varDelta _c$ to $\varDelta _b$ and back to $\varDelta _c$) $k$ times and finally following the path from $\varDelta _c$ to ${\varDelta ^b}_j$.

Lemma 6

$s, h\models \bigvee _{ k{\ge }0} {\mathtt{lassos}}({\varDelta _c}{,}\varDelta _b{,}{\varDelta ^b}_j{,}k)$ iff there exist $s' \subseteq s$ and $h'\subseteq h$ such that $s', h' \models {\mathtt{flat}}(\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b), {\varDelta ^b}_j)$.

Proof

By structural induction on $k$ and Lemma 3.    $\square$

The correctness of function ${\mathtt{flat\_tree}}$ immediately follows Lemma 6.

Lemma 7

Let $\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b)$ be a minimal cyclic sub-tree. $\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b)$ is satisfiable iff there exist $\varDelta ^{re}\in {\mathtt{{\mathtt{flat\_tree}}}}(\mathcal{C}(\varDelta _c{\rightarrow }\varDelta _b))$ and $s, h$ such that $s, h\models \varDelta ^{re}$.

6 Decision Procedure

Satisfiability of inductive predicates is solvable if all cycles of their unfolding trees can be flattened into regular formulas and all these regular formulas are flattable.

6.1 Decidable Fragment

Our decidable fragment is based on classes of regular formulas where each formula is flattable. We focus on the special class of regular formulas generated from the procedure pred2reg in the previous section (i.e., based on inductive predicates) and show how to compute bases for this class. In particular, each regular formula in this class is a set of base formulas unfolded from inductive predicates, e.g. $\varDelta ^{re}~{\equiv }~ {{\varDelta ^b}}{*} (\exists \bar{w}{\cdot } {\mathtt{P_1}}(\bar{v}_1) {*} ... {*} {\mathtt{P_n}}(\bar{v}_n))$, where $\bar{v}^S_i {\subseteq } \bar{w}$ for all $i {\in } \{1...n \}$. Following Lemma 3, we have: $\varDelta ^{re}$ is equi-satisfiable with ${{\varDelta ^b}}{\wedge } (\exists \bar{w} {\cdot } {\mathtt{P_1}}^N(\bar{t}^N_1) {*} ... {\wedge }{\mathtt{P_n}}^N(\bar{t}^N_n))$. Hence, $\varDelta ^{re}$ is flattable, i.e. can be represented by a base formula, if every ${\mathtt{P_i}}^N(\bar{t}^N_i)$ is equivalent with a Presburger formula $\phi _i$ for all $i {\in }\{1..n\}$. As so, $\varDelta ^{re}$ is equi-satisfiable to the base formula: ${\varDelta ^b}{\wedge }(\exists \bar{w}{\cdot } \phi _1{\wedge }...{\wedge }\phi _n)$. In consequence, we define a class of flattable formulas, called flat DPI formula, based on DPI predicates where each predicate is equivalent to a Presburger formula [29].

An arithmetic inductive predicate is DPI if it is not inductive or is defined as follows.

$$ \begin{array}{l} {\mathtt{pred}}~ P^N(\bar{x}) \equiv \mathop {\bigwedge }\nolimits _{1 \le i \le m} \phi _{0,i} \vee \exists \bar{z}\cdot \mathop {\bigwedge }\nolimits _{1 \le i \le m} \phi _i \wedge \mathop {\bigwedge }\nolimits _{1 \le l \le L} P^N(\bar{z}^l) \end{array} $$

where m is the arity of $P^N$, $\textit{FV}(\phi _{0,i}) {\subseteq } \{ x_i \}$, $\bar{z} {\supseteq } \bar{z}^l$, and there exists j such that $\phi _i$ is either of $x_i {=} f(\bar{z}_i)$, $x_i {\ge } f(\bar{z}_i)$, or $x_i {\le } f(\bar{z}_i)$ for all $i {\ne } j$, and $\phi _j$ is either of the following:

$$ \begin{array}{l} \begin{array}{lll} (1)~ x_j = f(\bar{z}_j) + c \wedge \phi ' &{}\qquad (2)~ x_j \ge f(\bar{z}_j) + c \wedge \phi '&{}\qquad (3)~ x_j \le f(\bar{z}_j) + c \wedge \phi ' \\ \end{array} \\ {}\\ (4) \text { a conjunction of the following forms with some integer constant } n>0:\\ \qquad \phi ', n x_j = f(\bar{z}_j), n x_j \ge f(\bar{z}_j),or ~n x_j \le f(\bar{z}_j) \end{array} $$

where c is some integer constant, $\bar{z}_j$ is $z_j^1,\ldots ,z_j^L$, $\phi '$ is an arithmetical formula such that $\textit{FV}(\phi ') \subseteq \bar{z}_j$ and $\phi '[z/\bar{z}_j]$ is true for any z, $f(\bar{z}_j)$ is a combination of $z_j^1,\ldots ,z_j^L$ with $\textit{max},\textit{min}$, defined by $f(\bar{z}_j) {:}\!{:=} z_j^l \ |\ \textit{max}(f(\bar{z}_j),f(\bar{z}_j)) \ |$ $\textit{min}(f(\bar{z}_j), f(\bar{z}_j))$, and f’s may be different from each other in the conjunction of (4).

The authors in [29] showed that each inductive predicate DPI exactly represents some eventually periodic sets which are equivalent to some sets characterized by some Presburger arithmetical formulas.

Lemma 8

[29]. For every DPI inductive predicate $P(\bar{x})$, there is a formula $\phi$ equivalent to $P(\bar{x})$ such that $\phi$ does not contain any inductive predicates.

Finally, we define flat DPI formulas based on the DPI predicates as follows.

Definition 4

(Flat DPI Formula). Let $\varDelta {\equiv } {\varDelta ^b}{*}(\exists \bar{w}{\cdot } {\mathtt{P_1}}(\bar{v}_1) {*} ... {*} {\mathtt{P_n}}(\bar{v}_n))$ where $\bar{v}^S_i {\subseteq } \bar{w}$ for all $i {\in } \{1...n \}$. $\varDelta$ is flattable if, for all $i \in \{1...n\}$, the arithmetic predicate ${\mathtt{P_i}}^N(\bar{v}_i^N)$ is a DPI predicate.

We remark that flat formulas can be extended to any class of inductive predicates whose numeric projections can be defined in Presburger arithmetic.

Now, we define a decidable fragment based on the flattable formulas.

Definition 5

(Decidable Fragment). Let $\mathcal {P}{=}\{{\mathtt{P_1}}, ...,{\mathtt{P_n}}\}$ and $\mathcal {P}^{cyc}{=}\{{\mathtt{P^{cyc}_1}}, ...,$ ${\mathtt{P^{cyc}_m}}\}$ be arithmetic predicates generated by function flat_tree while transforming the predicates in $\mathcal {P}$ using pred2reg. Solving satisfiability for every inductive predicate $\mathtt P_i$ in $\mathcal {P}$ is decidable iff every arithmetic predicate in $\mathcal {P}^N \cup \mathcal {P}^{cyc}$ is DPI where $\mathcal {P}^N{=}\{{\mathtt{P_1}}^N, ...,{\mathtt{P_n}}^N\}$.

We remark that the decidable fragment is parameterized by the classes of flattable formulas. It is extensible to any decidable fragment of arithmetic inductive predicates.

6.2 Decision Algorithm

Computing Bases for Inductive Predicates. We present a procedure, called $\mathtt {\mathtt{pred2base}}$, to compute for each inductive predicate in $\mathcal {P}$ a set of base formulas. $\mathtt {\mathtt{pred2base}}$ is described in Algorithm 2. It takes a set of predicates $\mathcal {P}$ as input and produces a mapping ${{\mathtt{base}}^{\mathcal {P}} }$ which maps each inductive predicate to a set of base formulas. $\mathtt {\mathtt{pred2base}}$ first uses procedure $\mathtt pred2reg$ (lines 2–5) to transform the predicates into regular formulas (which are stored in reg) together with a set of arithmetic inductive predicates (which are stored in ) while flattening cycles. We recap that for each inductive predicate function pred2reg first uses procedure utree in Sect. 5.1 to construct a cyclic unfolding tree and then uses procedure $\mathtt {\mathtt{extract\_regular}}$ in Sect. 5.2 to flatten the tree into a set of regular formulas. After that, it uses function pred2pres (lines 6–8) to compute for each inductive predicate in an equivalent Presburger formula. These relations is stored in the mapping Pres. Finally, at lines 9–11 it obtains a set of base formulas from substituting all arithmetic inductive predicates in the corresponding regular formulas by their equivalent Presburger formulas.

Satisfiability Solving. Let $\varDelta$ be a formula over a set of user-defined predicates $\mathcal {P}$ where $\mathcal {P}{=}\{{\mathtt{P_1}}, ..., {\mathtt{P_m}}\}$. The satisfiability of $\varDelta$ is reduced to the satisfiability of the predicate: ${\mathtt{pred}}~{\mathtt{P_0}}(\bar{t}_0) \equiv \varDelta ;$ where $\mathtt P_0$ is a fresh symbol and $\bar{t}_0$ is the set of free variables in $\varDelta$: $\bar{t}_0{\equiv }\textit{FV}(\varDelta )$.

6.3 Correctness

We now show the correctness of our procedure in the decidable fragment.

Theorem 1

Procedure $\mathtt {\mathtt{pred2base}}$ terminates for the decidable fragment.

Proposition 3

Let ${\mathtt{P_i}}(\bar{t}_i)$ be an inductive predicate in the decidable fragment. If ${\mathtt{P_i}}(\bar{t}_i)$ is satisfiable, ${\mathtt{reg}}({{\mathtt{P_i}}(\bar{v}_i))}$ produced by procedure pred2reg contains at least one satisfiable formula.

Proposition 4

Let ${\mathtt{P_i}}(\bar{t}_i)$ be an inductive predicate in the decidable fragment. If procedure pred2reg can derive for it a non-empty set of satisfiable regular formulas, then there exists an unfolding tree of ${\mathtt{P_i}}(\bar{t}_i)$ containing at least one satisfiable leaf node.

The proof is trivial.

Theorem 2

Suppose that $\mathcal {P}$ is a system of inductive predicates in the proposed decidable fragment. Assume that procedure $\mathtt {\mathtt{pred2base}}$ can derive for every ${\mathtt{P_i}}(\bar{t}_i)$ a base ${{\mathtt{base}}^{\mathcal {P}} {\mathtt{P_i}}(\bar{t}_i)}$. For all $s$, $h$ and ${\mathtt{P_i}} \in \mathcal {P}$, $s{,}h\models {\mathtt{P_i}}(\bar{t}_i)$ iff there exist $s' {\subseteq } s$, $h' {\subseteq } h$, and ${\varDelta ^b}\in {{\mathtt{base}}^{\mathcal {P}} {\mathtt{P_i}}(\bar{t}_i)}$ such that $s'{,}h' \models {\varDelta ^b}$.

Proof

The “if” direction follows immediately from Lemmas 3, 8 and Proposition 3. The “only if” direction follows immediately from Lemmas 3, 8 and Proposition 4.    $\square$

The above theorem implies that base generation for a system of heap-only inductive predicates is decidable with the complexity $\mathcal {O}(2^{m}\times 2^{2m^2} \times (2^{m})^N)$ time in the worst case. This finding is consistent with the one in [5].

7 Implementation and Evaluation

The proposed solver has been implemented based on the S2SAT framework [17]. We use Fixcalc [25] to compute closure for arithmetic relations. The SMT solver Z3 [10] is used for satisfiability problems over arithmetic. In the following, we first describe how to infer over-/under-approximated bases for those predicates beyond the decidable fragment. While over-approximated bases are important for unsatisfiability in verifying safety [8, 15, 26], under-approximated bases are critical for satisfiability in finding bugs [16]. After that, we show experimental results on the base computation and the satisfiability problem.

We sometimes over-approximate a base formula in order to show unsatisfiability, which helps to prune infeasible disjunctive program states and discharge entailment problems with empty heap in RHS [8]. In particular, the validity of the entailment checking $\varDelta ~{\vdash }~ \mathtt{emp}{\wedge } {\pi _c}$ is equivalent to the unsatisfiability of the satisfiability problem $\varDelta {\wedge } \lnot {\pi _c}$. Similarly, we sometimes under-approximate a base formula in order to show satisfiability, which helps to generate counter-examples that highlight scenarios for real errors. For the latter, our approach is coupled with an error calculus [16] to affirm a real bug in HIP/S2 system [8, 15]. When an error (which may be a false positive) is detected, we perform an additional satisfiability check on its pre-condition to check its feasibility. If it is satisfied, we invoke an error explanation procedure to identify a sequence of reachable code statements leading to the error [16]. With our new satisfiability procedure, we can confirm true bugs (which were not previously possible) so as to provide support towards fixing program errors.

It can be implied from Sect. 6 that generating approximated base for a formula relies on the approximation of the arithmetic part of inductive predicates, and then of regular formulas. To compute an under-approximation, we adopt the $k$-index bound approach from [4]. In particular, to compute a closure for a predicate $\mathtt P^N$, we only consider all unfolded formulas which have at most $k$ occurrences of inductive predicates. As the disjunction of the bounded formulas is an under-approximation, the closure computed is an under-approximated base. To compute an over-approximation, we adopt the approach in [30]. In particular, first we transform the system of arithmetic inductive predicates into a system of constrained Horn clauses. After that, we use Fixcalc [25] to solve the constraints and compute an over-approximated base.

Table 1. Bases inference for data structures

In the rest, we show the capability of our base inference and its application in program verification. We remark that, in [17] we show how a satisfiability solver in separation logic is applied into the verification system ${{\texttt {S2}_\mathtt{td}}}$. The experiments were performed on a machine with the Intel i7-960 (3.2 GHz) processor and 16 GB of RAM.

Base Inference. Using our proposed procedure, we have inferred bases for a broad range of data structures. The results are shown in Table 1. The first column shows the names of inductive predicates including cyclic linked-list, list segment, linked-list with even size, binary trees. TLL is binary trees whose nodes point to their parent and all leave nodes are linked as a singly-linked list. In all these predicates, $n$ is the length. The second column shows the inferred bases. Note that we use $\_\,$ for existentially quantified variables for simplicity. The third column presents type of the base (exact base or over-approximated base). The last column captures time (in seconds) of the computation.

While our proposal can infer bases for most predicates, there are also predicates where we have inferred approximated bases (AVL tree, heap tree, complete tree and red-black tree). These typically occur when they are outside of the decidable fragments. In all these cases, we had to infer over-approximation and under-approximations by $k$-index (under-approximated bases are not shown for brevity).

Table 2. Experimental results on satisfiability problems

Satisfiability Solving. We have implemented a new satisfiability solver based on the base inference. Our solver supports input as presented in Sect. 2 as well as in SMT2 format based on the description in [28]. We have integrated our proposed satisfiability procedure into HIP/S2 [8, 15], a verification system based on separation logic. Table 2 shows the experimental results on a set of satisfiability problems generated from the verification of heap-manipulating programs. The first column lists the data structures and their pure properties. The second column lists the total number of satisfiability queries sent to the decision procedure. The next two columns show the amount of unsat and sat queries, respectively. We use $k{=}10$ for the inference of under-approximation. The last column captures the processed time (in seconds) for queries of each data structure. The experimental results show that our satisfiability solver could exactly decide all sat and unsat problems from our suite of verification tasks for complex data structures. This is despite the use of approximated bases for four examples, namely Heap trees, Complete trees, AVL and RBT, that are outside of the decidable fragment.

8 Related Work

Solving satisfiability in fragments of separation logic with inductive predicates has been studied extensively. Several decidable fragments were proposed with some restrictions over either shape of inductive predicates, or arithmetic, or satisfiability queries. Proposals in [2, 5, 9, 11, 13, 17, 21, 29]¹ presented decision procedures for fragments including inductive predicates with heap properties, pure equalities but without arithmetic. Initial attempts like [2, 9, 21] focus only on linked lists. Smallfoot [2] exploits the small model property of linked lists. SPEN [11] enhances the decidable fragment above with nested lists and skip lists. [13] extends the decidable fragment with tree structures. The satisfiability problem is reduced to decidability of Monadic Second Order Logic on graphs with bounded tree width. Finally, SLSAT [5] proposes a decision procedure for arbitrary inductive definitions. The essence of SLSAT is an algorithm to derive for each predicate an equi-satisfiable base. Our work is an extension of SLSAT to support a combination of inductive predicates and arithmetic. To support arithmetical properties, instead of computing a least fixed point for heap property, our procedure first constructs a cyclic unfolding tree and then flattens the tree to derives the base. The decidable fragment in [29] has the following restrictions: for each inductive definition, (1) it has only a single induction case, (2) its inductive case has only a single occurrence of the inductive predicate unless the satisfiability of the spatial part becomes trivial, and (3) mutual inductive definitions are not allowed. Our decidable fragment removes these restrictions. Finally, [17] supports satisfiability checking of the universal fragment restricted in both shape and arithmetic. In comparison, our procedure supports arbitrary inductive definitions with relations based on semilinear sets over arithmetical parameters.

In terms of decision procedures supporting inductive predicates and arithmetic, GRASShoper [23] and Asterix [22] are among the first decision procedures where shape definitions are restricted to linked lists. The decidable fragments have been recently widened in extended GRASShoper [24], CompSPEN [12], ${{\texttt {S2SAT}}_{\texttt {SL}}}$ [17, 18, 29]. While CompSPEN extends the graph-based algorithm [9] to doubly-linked list, ${{\texttt {S2SAT}}_{\texttt {SL}}}$ is an instantiation of S2SAT [17]. For back-link construction, the instantiations [17, 18] are based on both heap and arithmetic constraints. Our algorithm in this work is more compositional i.e., it first forms back-links based only on the heap domain and then reduces the satisfiability problems into the satisfiability problems over arithmetic. By doing so, we can exploit well-developed results for the arithmetic domain. In this work, we reuse the result based on semilinear sets [29] for the arithmetic. In [20], we show how to adapt results based on periodic relations [4]. We are currently investigating how to use regular model checking [3] to enhance our decision procedure. The procedure ${{\texttt {S2SAT}}_{\texttt {SL}}}$ presented in [17] constructs back-links based on a combination of heap and arithmetic domains. In this work, back-links are constructed based on heap domain only. The satisfiability of the arithmetic part is processed in a separate phase. By doing so, the decidable fragment proposed in this paper is much more expressive when compared with the decidable fragment in [17]. For instance, while the decidable fragment in [17] includes a restricted fragment of heap-only predicates, the decidable fragment presented in this work includes arbitrary heap-only predicates. Our proposal may be viewed as an extension of the work [29] with the construction of cyclic unfolding trees to support arbitrary spatial predicates. To the best of our knowledge, our proposal is the most powerful decision procedure for satisfiability in separation logic.

9 Conclusion

We have presented a novel decision procedure for an expressive fragment of separation logic including shape and arithmetic properties. Our procedure is based on computing an equi-satisfiable base formula for each inductive predicate. This base computation, in turn, relies on the computation of the base for a set of flat formulas. We provide a complexity analysis to show that the decision problem for heap-based fragment is, in the worst case, in exponential time. We have implemented our proposal in a prototype tool and integrated it into an existing verification system. Experimental results shows that our procedure works effectively over the set of satisfiability benchmarks.