Statistical Framework for the Definition of Emphysema in CT Scans: Beyond Density Mask

Abstract

Lung parenchyma destruction (emphysema) is a major factor in the description of Chronic Obstructive Pulmonary Disease (COPD) and its prognosis. It is defined as an abnormal enlargement of air spaces distal to the terminal bronchioles and the destruction of alveolar walls. In CT imaging, the presence of emphysema is observed by a local decrease of the lung density and the diagnose is usually set as more than 5% of the lung below −950 HU, the so-called emphysema density mask. There is still debate, however, about the definition of this percentage and many researchers set it depending on the population under study. Additionally, the −950 HU threshold may vary depending on factors as the slice thickness or the respiratory phase of the acquisition. In this paper we propose (1) a statistical framework that provides an automatic definition of the density threshold based on the statistical characterization of air and lung parenchyma; (2) the definition of a statistical test for emphysema detection that accounts for the CT noise characteristics. Results show that this novel statistical framework improves the quantification of emphysema against a visual reference and improves the association of emphysema with the pulmonary function tests.

This study was supported by the National Institutes of Health NHLBI awards R01HL116931, R01HL116473 and R21HL140422.

1 Introduction

Emphysema is one of the most common disease manifestations that causes airflow limitation due to the destruction of alveolar walls and loss of elastic recoil. It is a common component of Chronic Obstructive Pulmonary Disease (COPD), a lung condition defined by expiratory airflow limitation associated with an inflammatory response to noxious particles such as cigarette smoke. COPD is currently the 3rd leading cause of death in the U.S. and represents an enormous societal burden. Recent evidences suggest a rapid decline in lung function occurs and may be prevented if acted upon [1]. Early diagnosis is, therefore, essential.

Although pulmonary function tests remain the standard diagnostic tool for COPD, image-based diagnosis of CT scans are increasingly used in diagnosing and categorizing COPD. The detection of emphysema is generally performed by visual inspection of CT images for Low-Attenuation Areas (LAA) [2]. Quantitatively, CT is a well-validated technique to assess the in vivo presence and extent of emphysema [3]. The identification of emphysema areas is usually prescribed to areas under a density level set to −950 Hounsfield Units (HU), the so-called density mask. This threshold has been selected by the community as the one with the highest correlation with microscopic emphysema analyzed though biopsies [4]. This threshold, however, may vary with the slice thickness (the original study was confined to scans with 1 cm), exposure dose and respiratory phase during the acquisition.

This work proposes to reduce the confounding factors that affect the emphysema detection by defining a statistical framework that provides a characterization of both lung parenchyma and air. The characterization will lead to the definition of an adaptive threshold that fits the particular conditions of the scan. The adaptive threshold will be defined as the one that reduces both type I and type II errors in a statistical hypothesis testing problem where the air probability distribution is acquired in the trachea, and the parenchyma distribution is inferred from the lung. This way, we palliate effect of the noise caused by lower effective radiation due to body mass, reconstruction deviations or respiratory phase. The statistical framework will also lead to define a statistical test for emphysema detection. Results show a significant improvement in the correlation with functional respiratory parameters used for the diagnosis of COPD.

2 Characterization of Emphysema in CT Scans

The definition of a statistical framework for the characterization of emphysema will require the determination of the probability distribution of air and lung parenchyma. In the case of air, the estimation of the probability distribution becomes easy since apparent anatomical structures like the trachea provide a suitable set of samples for the estimation. On the other hand, the parenchyma characterization is far more intricate because the lung tissue is a heterogeneous composition of tissues (connective tissue, capillaries, blood, and air). The intrinsic relationship between air and lung parenchyma is a critical factor that takes place in the variation of lung densities throughout the respiratory cycle due to the volume change.

We will disentangle the parenchyma composition of air by adopting a mixture model in the statistical description of emphysema proposed in [5]. This model is defined as a finite non-central Gamma Mixture Model (nc-$\varGamma$MM) whose probability density function (PDF) is:

$$\begin{aligned} p(x) = \sum _{j=1}^J \pi _j f_X(x|\alpha _j,\beta _j,\delta ) \end{aligned}$$

(1)

for J components, where $\pi _j$ are the weights of the mixture and $\alpha _j$, $\beta _j$ and $\delta$ are the shape, scale and location parameters of a non-central Gamma distribution with probability density function defined as:

$$\begin{aligned} f_X(x|\alpha ,\beta ,\delta ) = \frac{(x-\delta )^{\alpha - 1}}{\beta ^\alpha \varGamma (\alpha ) } e^{-\frac{x-\delta }{\beta }}, \qquad x \ge \delta \text { and } \alpha ,\beta > 0 \end{aligned}$$

(2)

The characterization of the air component of the mixture can be accurately calculated considering anatomical structures such as the trachea. The $\delta$ parameter estimated for air can be extended for the rest of components since the CT numbers are all relative to the lowest density level (air). Once the parameters of the air component are estimated, one can calculate the rest of components for the lung constraining the air to the parameters already derived. This will lead to a more accurate estimate of the air component that is not affected by the number of tissues of different densities.

Many methodologies can be applied for the estimation of the mixture model. Among them, probably the simplest is achieved with the Expectation Maximization method, which reduces the problem to solve a non-linear equation in each iteration, as proposed in [5]. In our work, we propose a modification of this Expectation Maximization methodology which comprises the following steps:

Estimation of the Air Component. Let $\varvec{x} = \left\{ x_i\right\} _{i=1}^N$ be the set of samples acquired in the trachea (following a nc-$\varGamma$ distribution). The parameters of the air component ($\alpha _\text {air}$, $\beta _\text {air}$, $\delta$) are calculated as the maximum log-likelihood estimates:

$$\begin{aligned} \left\{ \alpha _\text {air}, \delta \right\} = \mathop {\mathrm {argmax}}\limits _{\alpha , \delta \le \min {\varvec{x}}} \mathcal {L}(\alpha ,\delta | \varvec{x}) \end{aligned}$$

(3)

where

$$\begin{aligned} \mathcal {L}(\alpha ,\delta | \varvec{x}) = (\alpha - 1)\sum _{i=1}^N \log (x_i - \delta ) - N\alpha - N \alpha \log \left( \frac{1}{\alpha N}\sum _i^N (x_i - \delta ) \right) - N \log (\varGamma (\alpha )) \end{aligned}$$

(4)

and

$$\begin{aligned} \beta _\text {air} = \frac{1}{\alpha _\text {air} N}\sum _{i=1}^N (x_i - \delta ) \end{aligned}$$

(5)

Characterization of Lung Parenchyma. Once the parameters of the air component are known, the mixture model can be estimated constrained to the air parameters. To ensure that the heterogeneous composition of the lung is properly described in the mixture model, we set components from −950 to −750 HU in steps of 50 HU, and from −700 to −400 HU in steps of 100 HU. This is more than a reasonable range of attenuations considering that the normal lung attenuation is between −600 and −700 HU. So, the mixture model will be constrained to the mean values $\mu _j \in \{\mu _{\text {air}},-950, \dots , -400\}$.

The estimation of the shape parameters for each component, $\alpha _j$ (except the air component), are obtained by solving the following non-linear equation [5]:

$$\begin{aligned} \log (\alpha _j ) - \psi (\alpha _j) = \frac{\sum _{i=1}^N \gamma _{i,j} (x_i - \delta )/ \mu _j}{\sum _{i=1}^N \gamma _{i,j}} - \frac{\sum _{i=1}^N \gamma _{i,j} \log ( (x_i - \delta )/ \mu _j ) }{\sum _{i=1}^N \gamma _{i,j}} - 1 \end{aligned}$$

(6)

where $\psi (\cdot )$ is the digamma function, $\psi (\cdot ) = \varGamma '(x)/\varGamma (x)$, and $\gamma _{i,j} = P(j|x_i)$ are the posterior probabilities for the j-th tissue class:

$$\begin{aligned} \gamma _{i,j} = \frac{\pi _j f_X(x_i | \alpha _j,\beta _j,\delta )}{\sum _{j=1}^J\pi _j f_X(x_i | \alpha _j,\beta _j,\delta )} \end{aligned}$$

(7)

Finally, the scale factor is trivially calculated as $\beta _j = \mu _j/\alpha _j$ and the priors $\pi _j$ are updated as $\pi _j = \frac{1}{N}\sum _{i=1}^N \gamma _{i,j}$.

The fitting is performed iteratively until convergence in the parameters is reached. This is usually achieved in very few iterations since the shape parameter $\alpha _j$ is already constrained to the mean $\mu _j$, which ensures the robustness of the convergence. A suitable initialization of parameters for the iterative optimization is $\pi _j = 1/J$, $\alpha _j = 2$ and $\beta _j = \mu _j / \alpha _j$ for each component, $J=2,\dots ,J$ with the exception of the air component, $j=1$, which is set to $\alpha _1 = \alpha _\text {air}$ and $\beta _1 = \beta _\text {air}$.

Figure 1a shows a real CT scan where the lung and trachea masks are superimposed in blue and red respectively. In Fig. 1b, the histograms obtained from the trachea and lung parenchyma are depicted along with the nc-$\varGamma$ distribution fitted with Eqs. (3–5) plotted in solid red line, and the $\varGamma$MM fitted to the parenchyma data in solid blue line.

Air Component Removal. We can now disentangle the air component from the parenchyma description by imposing $\pi _\text {air} = \pi _1 = 0$ and updating the priors as $\pi _j^* = \pi _j/\sum _{k=2}^J \pi _k$ for $j=2, \dots , J$. The resulting mixture model now describes the composition of tissue without air:

$$\begin{aligned} p_\text {tissue}(x) = \sum _{j = 2 }^{J} \pi _j^* f_X(x|\alpha _j \beta _j, \delta ) \end{aligned}$$

(8)

Fig. 1.

Coronal view of a chest CT scan and histogram. Trachea and lung segmentations are shown in red and lung blue, respectively. Note that the density mask (−950 HU) underestimates the emphysema (more than 50% of trachea is classified as parenchyma).

3 Adaptive Threshold for Emphysema Detection

To improve the performance of the density mask threshold recommendation ($-950$ HU), we will consider the minimization of type I and type II errors of the statistical hypothesis testing for air and normal tissue for each subject. With the statistical framework established in the previous section, we can effectively characterize the air and parenchyma in each patient and a more accurate threshold can be established for emphysema detection. Formally speaking, let us consider the PDFs of air and tissue:

$$\begin{aligned} p_\text {air}(x) = f_X(x|\alpha _\text {air}, \beta _\text {air}, \delta ); \qquad \ p_\text {tissue}(x) = \sum _{j=2}^J \pi _j^* f_X(x|\alpha _j, \beta _j, \delta ), \end{aligned}$$

(9)

where $f_X(\cdot |\alpha , \beta , \delta )$ is the nc-$\varGamma$ PDF of Eq. (1). The optimal threshold is derived as:

$$\begin{aligned} t = \mathop {\mathrm {argmin}}\limits _{x} \left| 1-F_X(x,|\alpha _\text {air}, \beta _\text {air}, \delta ) - \sum _{j=2}^J \pi _j^* F_X(x|\alpha _j, \beta _j, \delta ) \right| , \end{aligned}$$

(10)

where $F_X(x,|\alpha , \beta , \delta )$ is the cumulative distribution function (CDF) of a nc-$\varGamma$ distribution:

$$\begin{aligned} F_X(x|\alpha _j,\beta _j,\delta ) = \int _{\delta }^x \frac{(y-\delta )^{\alpha - 1}}{\beta ^\alpha \varGamma (\alpha ) } e^{-\frac{y-\delta }{\beta }} dy = \frac{1}{\varGamma (\alpha )} \gamma \left( \alpha , \frac{x-\delta }{\beta }\right) , \ x \ge \delta \text { and } \alpha ,\beta > 0 \end{aligned}$$

(11)

The monotonic behavior of Eq. (11) ensures the existence of t in Eq. (10).

The statistical framework introduced in the previous section in combination to the definition of the optimal threshold in Eq. (10) allows us to define a statistical test for the detection of emphysema on a certain region of interest. The statistic will be defined as the degree of implication of emphysema, $\widehat{p}$, i.e. the percentage of emphysema within the region under study. According to the statistical model here derived, samples will have a probability of being emphysema $p_\text {emph} = F_X(t,|\alpha _\text {air}, \beta _\text {air}, \delta )$. Then, $\widehat{p}$ is distributed as a Binomial, $\mathcal {B}(p_\text {emph},n)$, of parameters $p_\text {emph}$ and the number of samples, n. Note that, as $n \rightarrow \infty$, $\widehat{p} \xrightarrow []{\mathcal {L}} \mathcal {N}\left( p_\text {emph},\sqrt{\frac{p_\text {emph}(1-p_\text {emph})}{n}} \right)$. Therefore, we can set a statistical test with null hypothesis H$_0$: “The region under study is normal parenchyma” whose critical point from which the null hypothesis is rejected if $\widehat{p} > p_0 + z_\alpha \sqrt{\frac{p_\text {emph}(1-p_\text {emph})}{n}}$, with $P(Z \le z_\alpha ) = \alpha$ and $Z \sim \mathcal {N}(0,1)$.

4 Results

The air and lung parenchyma were statistically characterized in 48 inspiratory scans acquired from subjects with diagnosed COPD with all the different severity levels according to the GOLD guidelines classification of patients¹. 5 Different devices from 2 different manufacturers were used: GE VCT-64, Siemens Definition Flash, Siemens Definition, Siemens Sensation-64, and Siemens Definition AS+. The dose was set to 200 mAs in all the acquisitions.

Lung segmentations and trachea segmentations were automatically obtained with an automatic method as implemented in the Chest Imaging Platform (www.chestimagingplatform.org). The distribution of air was defined by adjusting nc-$\varGamma$ statistical model as exposed in Eqs. (3–5) for the trachea samples, while the distribution of lung parenchyma was obtained by fitting the $\varGamma$MM to the lung parenchyma samples, Eqs. (6 and 7), and the tissue PDF is calculated by removing the air component, Eq. (8). The optimal threshold was computed as the optimal CT number that minimizes both type I and type II errors, Eq. (10).

We performed two different validations of the proposed methodology. First, we compareed the proposed method and the density mask within regions already labeled by an expert as severe emphysema, meaning most of the region affected; mild emphysema, where the tissue shows a mild low attenuation density; and normal parenchyma, where no parenchymal damage was perceived. The expert was free to select as many regions as necessary for each group on each subject. We used the degree of implication of emphysema as the validation metric defined as the percentage of voxels within the region that were considered emphysema according to each method. Finally, we provided an indirect validation of our method with a correlation analysis with respiratory function. We correlated the emphysema score obtained in each subject with FEV1%, a standard functional respiratory measure used for COPD diagnose. This measure is defined as the ratio between the volume of air that can forcibly be blown out in one second after full inspiration (the so-called Forced Expiratory Volume in 1 second, FEV1) and the volume of air that can forcibly be blown out after full inspiration (the so-called Forced Vital Capacity, FVC). Emphysema affects pulmonary function by compromising the lung elastic recoil and restricting flow by small airway collapse during expiration. Therefore, improved correlation with FEV1% can be seen as a functional validation of any approach that aims at quantifying emphysema.

Fig. 2.

Boxplots for the implication of emphysema detected in segmentations. The adaptive threshold detects more implication in severe and mild emphysema, while maintaining the normal parenchyma significantly below 5%.

Quantitative Validation in Classified Regions. The implication of emphysema was studied in the segmentations provided by the expert for all the 48 subjects. In Fig. 2 we show the boxplots for the three classes. Note that the implication of emphysema in regions labeled as severe and mild emphysema remarkably increases. We test the differences with a paired Wilcoxon signed-rank test at a significance level $\alpha = 0.05$ resulting in statistically significant differences for both severe and mild emphysema (p-values $<10^{-7}$ for both cases) between the proposed adaptive threshold and density masking. Additionally, Fig. 2c evidences that the increase in the sensitivity to emphysema detection still maintains a low type I error below 5% involvement (p-values $>0.3$), meaning that the null hypothesis H$_0$: “normal parenchyma” cannot be rejected.²

Fig. 3.

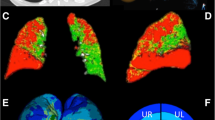
Emphysema classification for the density mask (−950 HU) and for the Adaptive Threshold of subject shown in Fig. 1. Density Mask underestimates the emphysema composition (a): Most of the samples in the trachea are labeled as tissue. (b) The Adaptive Threshold successfully labels the trachea samples. Besides, a prominent region of low attenuation density is now detected as emphysema.

Table 1. Linear-log regression analysis for the FEV1% with respect the emphysema for the density mask (−950 HU) and the adaptive threshold.

As an example of the performance of the proposed threshold, we show in Fig. 3 the density mask threshold at $-950$ HU and the optimal adaptive threshold $t = -870$ HU calculated with Eq. (10) for the same subject shown in Fig. 1. The density mask obtains a Type I error of $0.10\%$ and a Type II error $58.91\%$. Note that the $-950$ HU threshold is far below the extreme of the air and implies an unnecessary increase of type II error. This threshold is clearly underestimating the emphysema in this subject and, paradoxically, classifying more than $50\%$ of the trachea samples as tissue. On the other hand, the proposed threshold provides an optimal balance between both types of error, achieving a type I and type II errors equal to $4.69\%$. Note that the increase of type I error is still below the $5\%$ while the type II error is dramatically reduced to more reasonable values.

Physiological Validation. We performed a linear-log regression analysis of the FEV1% with respect to the emphysema detected in inspiratory scans for both the density mask and the adaptive threshold. Results are shown in Table 1 where the superiority of the adaptive threshold explains 44% of the variance in contrast to the 25% explained with the $-950$ HU one. We used the William’s test for dependent samples to test differences in correlations [6]. The statistic obtained for our dataset was $T = 2.024$, for $N=48$ and correlation between dependent variables $\rho =0.756$, implying that the adaptive threshold significantly improves the correlation with respiratory function when compare to density masking ($p=0.024$).

5 Conclusion

In this work, we show the problems derived from the definition of emphysema in CT scans by the density mask approach. As shown in Fig. 1, the threshold set by the density mask usually underestimates the distribution of air as a consequence of confounding factors such as slice thickness, device calibration, and noise due to body mass. The underestimation originates an important bias in the detection of emphysema that hinders the association with functional respiratory measures and early disease detection. Our work defines a statistical framework to circumvent this problem. We characterize both trachea and lung parenchyma, and derive a statistical test based on the optimal threshold that adapts to each acquisition and reduces type I and type II errors. Results show a consistent reduction of type II error in severe and mild emphysema regions while confines type I error to rates below 5% in normal parenchyma. Our adaptive threshold also shows a statistically significant improvement in association with pulmonary function. This result evidences the suitability of our methodology for clinical applications.