1. Introduction

Refractory dust grains in orbit around a star spiral into the star by the Poynting-Robertson drag (hereafter P-R drag) and sublime in the immediate vicinity of the star. Because the particles lose their mass during sublimation, the ratio β of radiation pressure to gravity of the star acting on each particle ordinarily increases. As a result, their radial-drift rates decrease and the particles pile up at the outer edge of their sublimation zone (e.g., Mukai and Yamamoto, 1979; Burns et al., 1979). This is a mechanism to form a dust ring proposed by Belton (1966) as an accumulation of interplanetary dust grains at their sublimation zone. Ring formation of drifting dust particles is not limited to refractory grains around the sun but it also takes place for icy grains from the Edgeworth-Kuiper belt and for dust in debris disks (Kobayashi et al., 2008, 2010). Therefore, dust ring formation due to sublimation of dust particles is a common process for radially drifting particles by the P-R drag.

The orbital eccentricity and semimajor axis of a dust particle evolve by sublimation due to an increase in its β ratio as well as by the P-R drag. We have derived the secular evolution rates of the orbital elements (Kobayashi et al., 2009). The derived rates allow us to find an analytical solution of the enhancement factors for the number density and optical depth of dust particles due to a pile-up caused by sublimation. Our analytical solution is found to reproduce numerical simulations of the pile-up well but its applicability is restricted for low eccentricities of subliming dust particles. The analytical solution shows that the enhancement factors depend on dust shapes and materials as expected from previous numerical studies (cf. Kimura et al., 1997). Although the solution includes physical quantities for the shapes and materials, it does not explicitly show which quantity essentially determines the enhancement factors.

The goal of this paper is to derive simplified formulae that explicitly indicate the dependence of dust ring formation on materials and structures of dust particles. In this paper, we adopt a simple model for the optical cross sections of fractal dust particles and analytically obtain not only the enhancement factors but also the location of the pile-up and sublimation temperature. In addition, we extend the model of Kobayashi et al. (2009) by taking into account orbital eccentricities of subliming dust particles.

In Section 2, we derive the sublimation temperature as a function of the latent heat. In Section 3, we introduce the characteristic radius of fractal dust and derive the sublimation distance for that dust. In Section 4, we simplify the formulae of enhancement factors derived by Kobayashi et al. (2009) and obtain the new formulae that show explicitly the dependence on materials and structures of the particles. We provide a recipe to use our analytical formulae in Section 5, apply our simplified formulae to both the solar system and extrasolar debris disks, and discuss observational possibilities of dust sublimation in Section 6. We summarize our findings in Section 7.

2. Sublimation Temperature

We consider dust particles in orbit around a central star with mass M*. Driven by the P-R drag, they drift inward until they actively sublime in the vicinity of the star. We have shown in Kobayashi et al. (2009) that the ring formation due to sublimation occurs only for their low orbital eccentricities e and obtained the secular change of semimajor axis a of the particle with mass m as

(1)

where η = −ln03B1;/lnm, −dm/dtǀr=a is the mass-loss rate of the particle at the distance r = a, G is the gravitational constant, and c is the speed of light. The β ratio is given by

(2)

where is the radiation pressure cross section averaged over the stellar radiation spectrum and L* is the stellar luminosity. The first and second terms on the right-hand side of Eq. (1) represent the drift rates due to sublimation and the P-R drag, respectively. Although we consider only the P-R drag from stellar radiation, the P-R drag due to the stellar wind also transports the particles. However, the magnitude of pile-up, its location, and sublimation temperature hardly depend on which drag determines their transport (Kobayashi et al., 2008, 2009).

A particle generated in a dust source initially spirals toward a star by the P-R effect. As it approaches the star due to the P-R inward drift, its temperature rises high and it finally starts active sublimation. The drift turns outward by sublimation when β increases with mass loss. The radial motion of the particles becomes much slower than the P-R drift alone, resulting in a pile-up of the particles. Note that other mass-loss mechanisms such as sputtering by stellar winds and UV radiation are negligible during active sublimation. 1 Footnote 1

The mass loss rate of a particle due to sublimation is given by

(3)

where A is the surface area of the particle, H is the latent heat of sublimation, μ is the mean molecular weight of the dust material, mu is the atomic mass unit, and k is the Boltzmann constant. Here the saturated vapor pressure at temperature T is expressed by P0(T) exp(− μmuH/kT) with P0 (T) being only weakly dependent on T.

During active sublimation, the first term on the right-hand side of Eq. (1) increases and then nearly vanishes. The temperature Tsubb at active sublimation is approximately determined by . Substituting Eq. (3) into Eq. (1) for , we have

(4)

Although Eq. (4) is a function of a as well as Tsub, the natural logarithmic function on the right-hand side has little sensitivity to a and Tsub. Therefore, the sublimation temperature may be approximated by

(5)

where

(6)

Here, we set m = 1.1 × 10−12g, α = 1/2, η = 1/3, Tsub = 1300 K and a = 15R⊙ with the solar radius R⊙ in the argument of the logarithmic function under the assumption of a spherical olivine dust particle around the sun; the other choice of these values does not change the result significantly because of the slowly-varying properties of the logarithmic function.

Equation (5) indicates that the active sublimation temperature is mainly determined by the latent heat of sublimation and mean molecular weight of the particles. This explains the findings by Kobayashi et al. (2008) that the temperature is insensitive to the stellar parameters, M*. and L*. As a consistency check, we calculate the sublimation temperatures according to Kobayashi et al. (2009) for materials listed in Table 1 and compare the temperatures with Eq. (5) (see Fig. 1). In spite of the simplification, Eq. (5) is in good agreement with the temperature given by the procedure of Kobayashi et al. (2009).

Table 1. Material parameters: the material density, μ is the mean molecular weight, H is the latent heat of sublimation, and P0 is the saturated vapor pressure Pv in the limit of high temperature.
Full size table
Fig. 1.
figure 1

Sublimation temperature Tsub as a function of μHξ−1, where ξ = 1 + 0.02ln(P 0/6.7 ? 1014 dyn cm ). The mean molecular weight μ, the latent heat H, and the vapor pressure in the limit of high temperature, P0, are listed in Table 1. The solid line indicates Eq. (5). Circles represent Tsub obtained from the method of Kobayashi et al. (2009) around the sun.

Full size image

3. Fractal Dust Approximation

We introduce the characteristic radius s of a dust particle, which is defined as

(7)

where ∫ dv means an integration over volume, is the distance from its center of mass, and ρi is its interior density. We consider that particles have a fractal structure; the mass-radius relation of the particles is given by m ∝sD for a constant fractal dimension D. For the fractal dust, , where sg is the gyration radius of the dust (Mukai et al., 1992). For homogeneous spherical dust, the characteristic radius reduces to the radius of the sphere. The cross sections of scattering and absorption of light are approximately described by a function of πs2 and 2πs/λ, where λ is the wavelength at the peak of light spectrum from the dust (Mukai et al., 1992).

The smallest dust particles before active sublimation contribute most to the enhancements of number density and optical depth at the pile-up (Kobayashi et al., 2009). Small particles produced by parent bodies in circular orbits are expelled by the radiation pressure if α > 1/2. Thus, the minimum characteristic radius s0min of dust particles prior to active sublimation corresponds to α = 1/2. The radiation pressure cross section is roughly given by in Eq. (2) for . Then, we have

(8)

where M⊙ and L⊙, respectively, denote the solar mass and luminosity. Note that is the effective density of a dust particle with the characteristic radius s0min and mass s0min in the following derivation. In addition, we discuss the application limit of our formulae in Appendix A.

3.1 Sublimation distance

We introduce the dimensionless parameter x,

(9)

where λsub is the wavelength at the peak of thermal emission from subliming dust with temperature Tsub. We approximate λsub = (2898 K/Tsub)μ m, which is the wavelength at the peak of a blackbody radiation spectrum with Tsub.

Since we deal with dust dynamics in optically thin disks, the equilibrium temperature T of a dust particle at a certain distance from a star is determined by energy balance among absorption of incident stellar radiation and emission of thermal radiation. Therefore, the relation between temperature T and distance r = a is approximately given by (e.g., Kobayashi et al., 2009)

(10)

if a is much larger than the radius of the central star. Here, σSB is the Stephan-Boltzmann constant and and are the absorption cross sections integrated over the stellar spectrum and the thermal emission from the dust particle, respectively.

Because s0min is larger than λ*, the cross section is approximated by the geometrical cross section;

(11)

The cross section may be for x≫1 and for x≪1. We connect them in a simple form as

(12)

When the temperature of the smallest drifting particles reaches Tsub, their pile-up results in a peak on their radial distribution (Kobayashi et al., 2009). With the application of the cross sections given by Eqs. (11), (12) to Eq. (10), the sublimation distance asub at the peak is obtained as

(13)

where R⊙ = 4.65 × 10−3 AU.

Inserting x given by Eq. (9) in Eq. (13), we have asub ∝ for x ≫ 1 and for x ≪ 1. In Kobayashi et al. (2008), our simulations have shown this dependence for dirty ice under the assumption that L* ∝ . We coupled Eqs. (4) and (10) and adopted the cross sections calculated with Mie theory 2 Footnote 2, and then obtained asub (Kobayashi et al., 2009). Equation (13) agrees well with asub derived from the method of Kobayashi et al. (2009) (see Fig. 2). However, Eq. (13) overestimates asub for less-absorbing materials (pure ice and obsidian) because our assumption of is not appropriate for such materials. Nevertheless, Eq. (13) is reasonably accurate for absorbing or compound dust (dirty ice).

Fig. 2.
figure 2

Sublimation distance asub in solar radii R⊙ as a function of where x is given by Eq. (9). The solid line indicates Eq. (13). Circles represent asub obtained from the method of Kobayashi et al. (2009) around the sun.

Full size image

4. Enhancement Factor

Dust particles with mass m0 in the range from m0min to m0max are mainly controlled by the P-R drag in their source and therefore spiral into the sublimation zone. As mentioned above, the smallest drifting dust with m0min corresponds to α = 1/2. If the drifting timescale of dust particles due to the P-R drag tPR is much shorter than the timescale of their mutual, destructive collisions tcol, the particles can get out of the dust source region by the P-R drag. The ratio of tPR to tcol increases with mass or size. Large dust particles with are collisionally ground down prior to their inward drifts. Therefore, the largest dust m0 max considered here roughly satisfies the condition tPR ~ tcol at the source region.

In the steady state, the number density of drifting dust particles is inversely proportional to the drift velocity (e.g., Kobayashi et al., 2009). Since the drift velocity of dust particles due to the P-R drag is proportional to α, their mass distribution is affected by the mass dependence η = −dlnα/dlnm. If the differential mass distribution of the dust source is proportional to m−b, that of drifting dust is modulated to m−b+η (e.g., Moro-Martin and Malhotra, 2003). Provided that successive collisions mainly produce dust particles in the dust source, we have b = (11 + 3p)/(6 + 3p) for the steady state of collisional evolution, where (Kobayashi and Tanaka, 2010). Here, is the specific impact energy threshold for destructive collisions and v is the collisional velocity. From the hydro-dynamical simulations and laboratory experiments, to m0 for small dust particles (Holsapple, 1993; Benz and Asphaug, 1999). Since p = −0.2 to 0 for a constant v with mass, b is estimated to be 1.8–1.9. This means that the smallest particles contribute most to the number density before dust particles start to actively sublime, while the largest particles dominate the optical depth prior to active sublimation.

When the temperatures of dust particles reach Tsub, they start to sublime actively. Their do not vanish perfectly, but they have very small relative to the initial P-R drift velocity. The magnitude of a pile-up due to sublimation is determined by the ratio of these drift rates (Kobayashi et al., 2009). Because the drift rate at the sublimation zone is independent of the initial mass and the initial P-R drift rate decreases with dust mass, the initially small dust piles up effectively. As a result, both the number density and the optical depth at the sublimation zone are determined by the initially smallest dust.

The number density is a quantity that can be measured by in-situ spacecraft instruments, while the optical depth is a key factor for observations by telescopes. In Kobayashi et al. (2009), we have provided enhancement factors for the number density and the optical depth due to sublimation. Here, we apply the simple model for optical cross sections in Eqs. (11), (12) and the properties of the fractal dust given by Eq. (B.7). Furthermore, we take into account an increase of eccentricities from e due to active sublimation. The number-density enhancement factor fN and the optical-depth enhancement factor fτ at the sublimation zone are then given by (see Appendix B for the derivation)

(14)
(15)

where the functions g(x) andh(e1) include the dependence on x and e1, respectively. They are given by

(16)
(17)

where αa = −dlnβ/dlns = D − 2 and I = μmuH/4kTsub ≃ 13. Since we assume that the mass differential number of the drifting particles is proportional to before active sublimation, the dependence of f τ on m0min/m0max seen in Eq. (15) differs from that of Kobayashi et al. (2009). This mass distribution is more realistic and consistent with that of dust particles measured by spacecraft around the earth (Grün et al., 1985). Equation (17) for h(e1) is applicable for e1 ranging from 1/2I+I ≃7× 10−6 to 1/2I ≃ 0.05. Dust particles do not pile up for e1 > 1/2I and hence we give h(e1) = 0 for e1 > 1/2I (Kobayashi et al., 2009). In addition, h(e1) = 1 for e1 < 1/2I+1I, while drifting dust particles hardly reach such small eccentricities (e1 < 1/2k+1I ~ 10−5) because their eccentricities naturally become as high as the ratio of the Keplarian velocity to the speed of light [~ 10−4(a/1AU)−1/2(M*/M⊙)1/2] by the P-R effect.

In Fig. 3, we compare the simplified formulae given by Eqs. (14) and (15) with the enhancement factors rigorously calculated by the formulae of Kobayashi et al. (2009). The x dependence of the enhancement factors given by Eqs. (14), (15) is shown in the function g(x), which is an increasing function ranging from 2β0) to I (x = ∞). Equations (14) and (15) briefly explain the tendency of the enhancement factors; materials with high x produce high enhancement factors.

Fig. 3.
figure 3

The enhancement factors for low orbital eccentricities as a function of x, where the dimensionless parameter x is determined by Eq. (9). Solid line represents Eqs. (14) and (15) with a use of m0min = m0max and h(e1) = 1. Circles indicate the factor numerically calculated by equations (68) and (69) of Kobayashi et al. (2009) around the sun for spherical dust listed in Table 1.

Full size image

Because x is proportional to Tsub/ρ (see Eq. (9)), the enhancement factors increase with Tsub/ρ. Thus, materials with high sublimation temperature tend to pile up sufficiently. In addition, fluffy dust particles with D ≃ 2 cannot effectively pile up even though ρ is low (Kimura et al., 1997). This is explained by the low α = D − 2 in the function g(x). Particles with D = 3 produce the highest enhancement factors. In spite of D = 3, compact particles are not the best for the pile-up due to a high density. Dust particles composed by ballistic particle-cluster aggregation have D ≃ 3 but low effective densities relative to compact ones. Therefore, such porous particles with D ≃ 3 may produce high enhancement factors due to large x resulting from their low densities. In addition, high x around a luminous star brings the enhancement factors to increase with stellar luminosity, which is shown for dirty ice, obsidian, and carbon in (Kobayashi et al. 2008, 2009).

In Kobayashi et al. (2008), we show the eccentricity dependence of enhancement factors from our simulations. The dependence is explained by h (e1) in the simplified formulae (see Fig. 4). Dust particles can pile up sufficiently for e1 < 10−3 because of h(e1) ≃ 1. Otherwise, the enhancement factors decrease with e1. For e1 ≳ 0.05, the sublimation ring is not expected.

Fig. 4.
figure 4

Dependence of enhancement factor on e1 for dirty ice, where e1 is orbital eccentricities of dust particles at the beginning of their active sublimation. Solid line indicates Eq. (14). Filled circles represent the results for the simulations calculated by Kobayashi et al. (2008).

Full size image

5. Recipe

We briefly show a recipe to obtain the sublimation temperature Tsub, its distance asub, and the enhancement factors fN, f. At first, the sublimation temperature Tsub is available from Eq. (5) adopting the material properties μ, H, and P0 listed in Table 1. Then, we calculate the dimensionless parameter x through Eq. (9), applying the stellar luminosity and mass of interest and the bulk density listed in Table 1 for compact spherical dust. Note that we should adopt a lower density for porous particles, taking into account their porosity. Inserting x in Eq. (13), we derive the sublimation distance asub. We further need orbital eccentricities e1 of dust particles at the beginning of active sublimation to calculate the enhancement factors, f N and f τ . The dust particles resulting from collisions have eccentricities e0 ~ α at the distance a0 of the dust production region. Since particles with the highest α contribute most to a sublimation ring, we estimate e0 ~ 0.5. Because eccentricities are dumped by the P-R drag, we can calculate e1 from the relation (Wyatt and Whipple, 1950). Inserting x and e1 to Eqs. (14) and (15), we obtain f N and f τ .

6. Discussion

The asteroid belt and the Edgeworth-Kuiper belt (EKB) are possible dust sources in the solar system. A dust counter on board spacecraft can measure the number density of dust particles. The sublimation of icy dust occurs at asub = 20 AU given by Eq. (13). Icy particles reaching the sublimation zone from the EKB still have high eccentricities e1≳ 0.1 (Kobayashi et al., 2008). Therefore, a substantial sublimation ring is unexpected because of f N = 1 for h(e1) = 0. Since the number density of dust particles decreases inside the sublimation zone, only a bump in the radial profile of the number density appears around asub (see Kobayashi et al., 2010). In contrast, dust particles composed of rocky, refractory materials actively sublime at several solar radii from the sun. Therefore, orbital eccentricities of dust particles coming from the asteroid belt drop to ~0.01 around the sublimation distance due to the P-R drag. Since we have h (0.01) ≃ 0.3 from Eq. (17) for b = 11/6 and D = 3, f N ≃ 1.3–3.0 is obtained from Eq. (14) for x ≳ 1. Therefore, future in-situ measurements of dust could find such a sublimation ring of refractory dust particles originating from the asteroid belt, but not a ring of icy dust particles from the EKB.

A dust ring was observed around 4R⊙ from the sun in the period 1966–1983, although it was not detected in the 1990s (Kimura and Mann, 1998 for a review). The optical depth is measured by dust emission observations. The enhancement factor fτ of the observed ring is estimated to be 2-3 (MacQueen, 1968; Mizutani et al., 1984). The mass distribution of drifting dust particles for b = 11/6 is consistent with the measurement of dust particles with masses ranging from m0min ~ 10−12g to m0max ~ 10−6g by spacecraft around the earth orbit (Grün et al., 1985). Using that, we estimate f τ ≲ 1.1 from Eq. (15) for e1 = 0.01. Thus, the enhancement by sublimation cannot account for the observed dust ring. However, this low f τ is mainly caused by the mass range of drifting dust particles. If m0 max decreased during the transport of dust particles from the earth’s orbit to the sublimation zone, higher f τ could be expected. For example, the largest particles in the mass distribution become smaller by the sputtering from the solar wind. The sputtering may decrease e1 as well as m0 max. Small particles with high eccentricities from the dust source are ground down by sputtering and blown out by the radiation pressure before reaching the sublimation zone, while large particles with low eccentricities gradually become small by sputtering without the increase of their eccentricities and drift into the sublimation zone. If the ratio of tPR to the timescale of decreasing size due to sputtering ranges in 0.1– 0.7, sublimation could form such a bright ring because of small m0max and e1. Indeed, the ratio derived by Mukai and Schwehm (1981) is consistent with the condition for the formation of a sublimation ring. That may be a clue to explain the observed ring.

Debris disks found around main sequence stars would be formed through collisional fragmentation in narrow planetesimal belts, which may resemble the asteroid and Edgeworth-Kuiper belts in the solar system. In young debris disks, fragments produced by successive collisions are removed from the disk by radiation pressure. We call such a disk a collision-dominated disk. Once the amount of bodies has significantly been decreased through this process, the P-R drag becomes the main removal process of fragments. Such a disk is referred to as a drag-dominated disk. We have investigated the dust ring formation in drag-dominated disks. To observe a sublimation ring requires a high enhancement factor f τ for the optical depth. As shown in Eq. (15), a small ratio of m0max to m0min yields high f τ . The condition of m0max ~ m0min is expected to form a bright ring. Since the drift time due to the P-R drag is comparable to the collisional time for bodies with m0max, the condition of m0max ~ m0min is achieved in transition from a collision-dominated disk to a drag-dominated one.

A significant sublimation ring consisting of icy particles is not expected in a debris disk due to high eccentricities if a planetesimal belt as a dust source is located within a few hundreds AU, similar to the solar system. On the contrary, dust particles composed of refractory materials have e1 ~ 0.01 or smaller if a planetesimal belt is around the distance of the asteroid belt or further outside. Furthermore, refractory dust particles have high sublimation temperatures and hence produce a higher enhancement factor. Recently, inner debris disks of refractory grains have been observed through interferometry around Vega, τ Cet, ζ Aql, and α Leo, and Formalhaut (Absil et al., 2006, 2008; Di Folco et al., 2007; Akeson et al., 2009). Such inner debris disks may have notable sublimation rings.

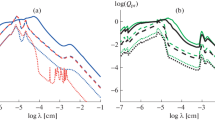
To check the observability of a sublimation ring in the spectral energy distribution (SED) of thermal emission expected from a disk around Vega located at the distance of 7.6 pc from the earth, we take our formulae with M*. = 2.1M⊙ and L* = 59 L⊙ for compact spherical olivine particles. We obtain Tsub = 1300 K, asub = 0.35 AU and f τ = 3.1, where we adopt m0max = m0min and h(e1) = 1 in Eq. (15). The smallest radius s0min = 10 μ m is much larger than the peak wavelength of thermal emission (λsub ≃ 2.3 μ m) and hence we simply treat dust particles as black-bodies to calculate the SED. The optical depth τd of dust particles drifting by the P-R drag without sublimation from the outer edge aout to the inner one ain is given by a constant τ0, where a equals asub. The total optical depth τ of the disk can be set as

(18)

where τe denotes the optical depth of dust particles forming a dust ring with width δasub. The width of the ring is roughly given by δasub = 0.05 asub (Kobayashi et al., 2008, 2009). We set asub = 1.5asub. Note that the other choice of aout does not change our result drastically. Choosing τ0 = 8 × 10−3, we can reproduce the flux density ~ 8.7 Jy measured by Absil et al. (2006) with the interferometry at a wavelength of 2.1 μ m. 3 Footnote 3Figure 5 depicts that the sublimation ring does not bring about a noticeable spectral feature in the SED, while the SED strongly depends on asub value. The flux density from the disk diminishes with decreasing wavelength for the wavelength smaller than λsub because of the absence of dust particles with temperature higher than Tsub due to sublimation. The result for ain = 0.6asub ≃ 0.21 AU is shown to better agree with the observational data. Since asub ≃ 0.22 AU (Tsub ≃ 1700 K) for pyroxene, the Vega disk seems to be abundant in pyroxene compared to olivine. That could be recognized as an evidence of sublimation unless the light scattering of dust particles exceed their thermal emission. 4 Footnote 4

Fig. 5.
figure 5

The spectral density distribution of the disk around Vega. The solid line indicates the flux density from a disk with the sublimation ring, choosing τ0 = 8 × 10−3 to fit the observational data at 2.1 μ m. Dotted lines represent that without a sublimation ring (fτ = 1 resulting in τe = 0) for τ0 = 1 × 10−2. To check the asub dependence, we set ain = 0.6asub for τ0 = 4 × 10−4 in the case without the sublimation ring (dashed lines). Circle corresponds to the interferometric measurement by Absil et al. (2006) and diamonds indicate the photometric data (Absil et al., 2006 and reference therein).

Full size image

7. Summary

  1. 1.

    We provide formulae of enhancement factors for the number density and the optical depth due to a pile-up of dust particles caused by sublimation and its location and sublimation temperature, applying a simple model for optical cross sections of fractal dust particles.

  2. 2.

    High sublimation temperatures result in substantial enhancement factors, though the pile-up is insensitive to the optical properties of dust particles.

  3. 3.

    If we adopt the mass distribution measured around the earth, the enhancement factor for the optical depth near the sun is smaller than 1.1. Therefore, the enhancement cannot explain the solar dust ring detected in the epoch of 1966–1983, unless the largest particles were destroyed by sputtering.

  4. 4.

    The number-density enhancement factor is expected to be 1.4–3 in the vicinity of the sun. Therefore, a sublimation ring could be found by in-situ measurements by spacecraft around several solar radii from the sun.

  5. 5.

    Sublimation removes dust particles with temperatures higher than their sublimation temperature. In the spectral energy distribution, the flux density from a disk reduces with decreasing wavelength, if the wavelength is shorter than the peak one of the blackbody spectrum with the sublimation temperature. That could be seen as a sublimation evidence. However, it is difficult to find signs from a sublimation ring in the spectral energy distribution.