Abstract
The 1 εm camera onboard the Japanese Venus Mission/Akatsuki scheduled to arrive at Venus in 2015 or 2016 is described. In addition to its scientific goals, the optical and mechanical designs, the calibration procedures, and some results of feasibility studies are presented. Those studies are about the source of the contrast in the dayside image, the resolution of the H2O detection on the nightside surface, and a possibility of finding an active volcano.
Similar content being viewed by others
1. Scientific Goals
Venus is a next-door planet of the Earth in the solar system with a similar mass and a little shorter distance from the sun. However, its surface environments are astonishingly different from those of the Earth. The atmosphere is as thick as 90 atm and as hot as 740 K on the surface (see, for example, “Venus” University of Arizona Press, 1983). From the atmospheric dynamics’ point of view, there is an interesting phenomenon called the ‘super-rotation’. This is a longstanding problem for meteorologists for more than 40 years (e.g. Gierasch, 1975). The atmosphere at the cloud top (at around 70 km above the surface) is rotating 60 times faster than the solid surface. There must be an effective mechanism to pump up the angular momentum of the surface to the atmosphere in the cloud top region. Various generation mechanisms have been proposed so far. The most common among them is so-called the “Gierasch Mechanism” where the angular momentum is pumped up from the surface by the meridional circulation (Gierasch, 1975). In other mechanisms the angular momentum is transported by equatorial atmospheric waves (Fels and Lindzen, 1973), by thermal tides (Baker and Leovy, 1987), and so on. However, its actual process has not been understood yet mostly because the thick clouds prevent mankind from looking deep into the atmosphere. However, in the middle of 1980s a break through was found by Allen and Crawford (1984) that those regions below the clouds can be seen through several spectral windows in the 1–2 εm region.
The main target of the present Venus mission/Akatsuki is to understand the generation mechanism of the superrotation of the Venus atmosphere by using those windows. For this purpose, five cameras utilizing different wavelengths and a radio beacon for occultation measurement are on board. Those different wavelengths provide information of different heights. Although the height resolution of about 10 km by those nadir-looking cameras are rather poor, it may be compensated by a better height resolution of 1 km by the radio occultation. The dynamical information obtained at the acceleration region (between the ground and the cloud-top region) will give us insights into the generation mechanism of this interesting phenomenon. Although an overview of the mission and the scientific instrumentation has already been described by Nakamura et al. (2007), the principal parts are noted below briefly.
The 1 εm camera named IR1 works both on the dayside and the nightside. On the dayside, it measures the 0.90 εm solar radiation scattered by the clouds, and quantifies the horizontal wind vectors by using the cloud-tracking technique. By combining the information obtained at various heights by the other cameras and by the radio occultation, meteorological information such as the wind field and the distribution of eddy diffusion may be deduced. This will make it possible to investigate the generation mechanism of the super-rotation.
On the nightside, it has three channels of 0.90, 0.97 and 1.01 εm to detect thermal emission mostly from the surface and a little from the lowest atmosphere. The latter two channels are a differential absorption pair for measuring the surface H2O abundance with the 1.01 εm channel as a reference. Although the center of the H2O band is located at 0.94 εm, the 0.97 εm channel is suitable for measuring the H2O abundance because of moderate absorption (it is too strong at the band center). H2O is one of the most important minor constituents in the lower atmosphere because of various reactions with surface minerals and a role for the greenhouse effects. Also it is related to the chemistry of the clouds, which are mostly made of H2SO4 and H2O.
These nightside channels are also used to investigate the distribution of surface emissivity. Surface emissivities may be deduced from the measured radiances with a known surface temperature and a correction of the influence of overlying clouds (Hashimoto and Sugita, 2003). Spatial variations of surface emissivities at near-infrared wavelengths were studied (e.g., Hashimoto et al., 2008); however, little has been discussed about its wavelength dependence so far. Since each material shows each wavelength dependence of emissivity, observation of wavelength dependence will help us to constrain the surface material more confidently. Especially, the spectra of ferrous mineral such as olivine = (Mg, Fe)2SiO4 and ferric mineral such as hematite = Fe2O3 show different wavelength dependence each other in the 0.9 to 1.0 εm region (see Fig. 8); it may be possible to discuss the redox state of Venus surface. Since redox state of Venus’ surface is likely related to the escape of water, the evolution of Venus would be inferred from IR1 observation.
Also IR1 will search for an active volcanism (Hashimoto and Imamura, 2001). On Venus, there are lots of landforms, which are related to volcanic activity; however, no active one has been found so far. Although Venus Express has not found any sign of active volcanism (Mueller et al., 2008), IR1 still has a chance to find it because of its much wider coverage of the surface owing to the equatorial orbit. Detection of active volcanism on Venus has a huge impact on the theory of evolution of planetary interior.
2. Instrumentation
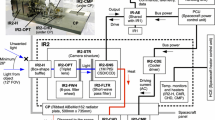
IR1 camera is composed of a baffle, filters, lenses, a detector and electronics (see Figs. 1 and 2). The specifications of IR1 camera are listed in Table 1. The baffle is an important component because the solar direction is not far away from the line of sight during the nightside observation. It is designed to reduce the solar contamination less than 2 × 10−6 of the initial when the solar direction is 26° or more away from the line of sight and within ±8° from the reference plane. The filter wheel has six positions on which four interference filters, a diffuser and a lid are placed. One of four filters is for the dayside measurement at 0.90 εm. Other three filters are for the nightside measurements at 0.90, 0.97 and 1.01 εm. Their transmission profiles are shown in Figs. 3 and 5; they are synthesized from the measured transmissions and the wavelength shifts expected for their inclination of 7° and the field of view of 6° in half-cone-angle. Note that the peak transmission of the dayside filter is as small as 0.27% because the same detector is used for both the dayside and the nightside measurements. The inclination of 7° aims at avoiding ghosts, which may be produced by unwanted multiple reflections between the optical components. The lens system is a triplet with a main wavelength at 0.90 εm and a focal length of 84 mm. Although the main wavelength was 1.01 εm at the earlier stage of the present project, it was changed to 0.90 εm. This was because gradation of the image due to diffusion of charge in pixels was worried much more for the 1.01 εm channel than for the 0.90 εm channel. Later, the actual spot sizes were measured by using a collimator with a focal length of 90 cm. Their FWHMs (full width of a half maximum) were 1.5 pixel at 0.90 εm and 2.5 pixel at 1.01 εm. That is, the worry did not come true fortunately. They correspond to 24 and 40 km, respectively, horizontal resolution on the Venus surface seen from the apoapsis (13 Venus radii = 79000 km above the surface). The 40 km spatial resolution of the 1.01 εm nightside channel is not so disappointing because of the smearing effect due to the clouds (Hashimoto and Imamura, 2001); a point light source on the surface appears as a spot of 100 km in diameter when it is seen through the clouds. The detector is a 1024 × 1024 array of Si-CSD (charge sweeping device) / CCD cooled down to 260 K to achieve S/N ratios of 300 for the dayside measurements and of 100 for the nightside measurements. Those S/N ratios are from scientific requirements based on previous measurements. For example, the former comes from the dayside contrast of 3% found by the measurements on board Galileo (Belton et al., 1991), and the latter from the nightside contrast of some tens percent found by the ground-based measurements (Meadows and Crisp, 1996). Estimation of the actual S/N ratio is described in the next chapter.
3. Calibration
The flat-field measurement and determination of the absolute sensitivity were carried out at Tsukuba Space Center by using a one meter integration sphere with a known radiance. IR1 has a diffuser to obtain a flat-field with a spatial scale of one degree or so during the flight with the Venus’ dayside as a light source. However, a flat-field with a larger spatial scale of several degrees is difficult to be obtained in flight, and is measured with the integration sphere. The sensitivity fluctuations measured are about 3% peak-to-peak in the main part of the field of view.
For the 0.90 εm dayside channel, input radiance of 37 mW cm−2εm−1 str−1 (77% of the nominal input) resulted an output of 633 ADU/s (analogue to digital conversion unit) = 44300 e−/s (65% of the nominal output); that is, the measured sensitivity was proved to be 84% of the designed. In case of IR1 camera 1 ADU = 70 e−.For the 0.90 εm nightside channel, an input radiance of 55 εW cm−2εm−1 str−1 (37 times as large as the nominal input) resulted an output of 565 ADU/s = 39600 e−/s (27 times as large as the nominal output); that is, the measured sensitivity was proved to be 73% of the designed. The nominal exposure durations are 3–6 s and 10–30 s, respectively, for the dayside and nightside measurements.
The thermal noise measured is 130 ADU/s at 290 K, which will be reduced to 1/10 when the detector is cooled down to 260 K. The depth of the well is measured to be around 10000 ADU = 700000 e−.
The S/N ratio of the actual measurements is mostly determined by the statistical noise. The thermal noise of 15 ADU/s at 260 K is usually unimportant. The expected S/N ratio for the measurements may be estimated as follows: Since the expected dayside output is 3000 ADU/3 s = 210000 e− /3 s, the expected S/N ratio due to statistical noise is 0.2% (=(210000)−1/2); this satisfies the scientific requirement of S/N = 300 for the 0.90 εm dayside measurements. The value 3000 ADU/3 s is based on the expected dayside radiance and the measured sensitivity noted above. Since the expected nightside output is 210 ADU/10 s = 15000 e−/10 s, the expected S/N ratio due to statistical noise is 0.8% (=(15000)−1/2); this satisfies the scientific requirement of S/N = 100 for the 0.90 εm nightside measurements. The value 210 ADU/10 s is also based on the expected nightside radiance and the measured sensitivity.
4. Feasibility Studies
4.1 Source of contrast for the 0.90 εm dayside image and the representative height
On the dayside, IR1 camera images the clouds illuminated by the sunlight, and various meteorological parameters such as the horizontal wind velocity are derived by tracking features on the clouds. Therefore, it is important to identify the source of such features and their representative height seen in the 0.90 εm image. As shown by the Venus’ global image taken during the Galileo’s flyby, the contrast found in the 986 nm dayside images was as small as 3% (Belton et al., 1991). They estimated the representative height for such 986 nm contrast as 50–55 km. This is based on the consideration about the wind speed difference between those seen in the UV and IR images, and the wind speed gradient with height found by the entry probes of Venera and Pioneer Venus (Schubert, 1983). Since detailed description has been published elsewhere (Takagi and Iwagami, 2011), some elementary results are noted below.
The dayside spectrum in the 0.9–1.0 εm region calculated is shown in Fig. 3. This is based upon a line-byline calculation using a molecular database HITRAN 2004 (Rothman et al., 2005), the VIRA1985 model atmosphere (Keating et al., 1985), a baseline cloud model (table 2a of Pollack et al., 1993), and a radiative transfer code RSTAR (Nakajima and Tanaka, 1986) to calculate the scattering process by the cloud particles. The molecular absorptions are so weak in this wavelength region that the solar spectrum appears almost as it is.
The expected output was calculated for various cloud thickness, cloud heights and atmospheric temperature profiles. The response of the output for changes in the clouds’ thickness is plotted in Fig. 4. The relative output changes by 13% and +8% when the cloud thickness changes to 0.5 and 2 times as large as the baseline cloud model, respectively. On the other hand, it responds little to the change in the cloud height; it is as small as 0.06% per 4 km (this is too small to be shown in Fig. 4). This is because the 0.90 εm region is a clear window for the CO2 absorption as seen in Fig. 3. Also, a temperature change causes little change in radiance; it is as small as 0.04% per 10 K. According to Pioneer Venus’ entry probe data (see figure 4 of Ragent and Blamont, 1980) or Venera’s entry probe data (see figure 103 of Krasnopolsky, 1986), those changes in the thickness by a factor of 1.5 or so appears to be realistic. Therefore, the 3% contrast in the 986 nm image seen by Galileo must be due to the change in the cloud thickness. This is a consideration about the total optical thickness of the clouds, and the representative height causing such change must be considered separately.
The representative height is investigated by using a mean cloud model composed of the lower (48–50 km), middle (50–57 km) and upper (57–70 km) clouds and the upper haze (70–84 km). Such mean cloud model and the expected changes are taken from the entry probe data summarized in table 4a of James et al. (1997). According to the present preliminary radiative transfer calculation, it is found that any layer (upper, middle and lower) except for the upper haze has a possibility to cause such a change of 3% in the measured radiance. The variability of the lower cloud is certainly larger than those of the others as seen in the entry probe data noted above; however, the optical thickness above the lower cloud is also larger than those of the others, and hides the variability most seriously. That is, it failed to identify the representative height based on the mean cloud model with its expected change and a radiative transfer calculation. Another source of information is needed for farther discussion.
The horizontal scale of the feature may provide a key. The scale of the 986 nm features tracked by Galileo was in the order of 300 km (this is read on figure 1 of Belton et al., 1991). By comparing the clouds data measured by a pair of entry probes worked nearly the same time (such as listed in table 4a of James et al., 1997), it is found that the lower clouds appear to be most variable as far as the distance between the entry probes is in the order of several hundred km (such as the case of Venera 11 and 12), and that whole the layers are variable if the distance exceeds 1000 km (such as the case of Venera 9 and 10). This fact is suggestive that the representative height of the 0.90 εm dayside images is in the lower cloud region 48–50 km. However, the number of examples is so limited that a definitive conclusion cannot be drawn.
4.2 H2O detection near the surface
The pair of 0.97 εm and 1.01 εm nightside channels is for H2O detection near the surface. The filter transmission profiles and the calculated nightside spectra are shown in Fig. 5. In the figure, the spectra are calculated for the H2O abundance of 0.5, 1 and 2 times as much as the nominal one; they appear at the top, middle and bottom, respectively. The nominal H2O mixing ratios are taken from Pollack et al. (1993), where those below the clouds are nearly constant at 30 ppm. This figure demonstrates that the H2O abundance can be obtained based on the differential absorption technique using the pair of 0.97/1.01 εm channels. The expected output ratio of 0.97/1.01 εm channels is plotted in Fig. 6 as a function of the H2O mixing ratio. It varies from 0.40 at 15 ppm to 0.23 at 60 ppm. The detection resolution is estimated to be 5 ppm for the case of a S/N ratio of 100.
The H2O abundance near the nightside surface has been measured in the 1.18 εm region based on the Galileo data (Drossart et al., 1993), and mixing ratios of 30±15 ppm with a latitudinal variation of 20% have been reported. Based on the Venus Express data, mixing ratios of 44±9 ppm with a latitudinal variation of ±1.5% (this corresponds to a variation of 44 × 0.03 = 1.3 ppm) over 60°S–25°N latitudes have been reported (Bezard et al., 2009). The resolution of 5 ppm by IR1 may not enough to find inhomogeneity in the H2O abundance if the latter estimation is true. However, the representative height for the IR1 measurement at 0.97/1.01 εm regions is lower than that of the 1.18 εm region by a few km, and may succeed to detect inhomogeneity in the H2O abundance in the lowest atmosphere. Longer exposure duration such as 100 s instead of 10 s may be effective to improve the resolution.
The contribution functions for the nightside channels are represented in Fig. 7. Their main parts come from the surface; their portions are 86, 76 and 89%, for the 0.90, 0.97 and 1.01 εm channels, respectively. The 0.97 εm channel shows larger atmospheric contribution than others due to the H2O absorption. The difference in the surface contributions between the 0.97 and 1.01 εm channels does not affect to the H2O retrieval as far as the mixing ratio has no height dependence as reported by Meadows and Crisp (1996).
4.3 Surface characterization and volcano quest
Contrast in surface emissivity may be measured by the pair of 0.90 and 1.01 εm channels. Although it is difficult to estimate absolute value of emissivities due to the interference of topography and overlying clouds, it is rather easy to determine the relative magnitude of emissivities. Since minerals have their emissivity spectra as shown in Fig. 8, surface material may be inferred from the ratio of the 0.90 and 1.01 εm radiances. However, as shown from the Venus Express data, emissivity differences are less important as compared to height variations (Haus and Arnold, 2010) and also to cloud opacity variations. However, most of them may be canceled out by calculating ratios of the 0.90 and 1.01 εm radiances. Since the wavelengths 0.90 and 1.01 εm are close by each other, the effects due to height variation and clouds’ opacity variation are expected to be the same as a first approximation. After such rationing procedure, it seems possible to pick up the emissivity difference due to the surface materials (see Fig. 8). However, even after such procedures, a statistical work may still be needed to delete secondary effects due to topography and clouds. Akatsuki has an advantage in such a statistical procedures because of its equatorial orbit to have wider surface coverage than Venus Express.
Emissivity spectra of surface minerals such as hematite, olivine, pyrite, pyroxene and magnetite (solid curves) after US Geological Survey Digital Spectrum Library (http://speclab.cr.usgs.gov) and the filter transmissions (dashed curves). Note that they are measured under room temperatures.
About the quest for an active volcanism, we depend on the significant temperature dependence of the thermal emission (Hashimoto and Imamura, 2001). Since the 0.90 εm channel locates at a wavelength of far shorter side of the peak (at around 4 εm) of the blackbody function of 740 K, the radiance varies significantly with temperature; it varies more than 3 orders of magnitude in the 0.9–1.0 εm region when temperature changes from 740 K to 1200 K (lava temperature) as seen in Fig. 9.
5. Summary
The 1 εm camera onboard the Venus Mission/Akatsuki is ready to start observation. On the dayside, it images features due to inhomogeneity in the clouds’ thickness to derive the horizontal wind velocity. It will provide useful information to investigate the acceleration mechanism for the super-rotation of the atmosphere. On the nightside, it also measures the thermal emission from the surface and the lower atmosphere to investigate the H2O abundance near the surface with a resolution of 5 ppm, and the distribution of the surface emissivity, which will be an important key to investigate the internal activity and the thermal history of Venus.
References
Allen, D. A. and J. W. Crawford, Cloud structure on the dark side of Venus, Nature, 307, 222–224, 1984., 10.1038/307222a0
Baker, N. L. and C. B. Leovy, Zonal winds near Venus’ cloud top level: A model study of the interaction between the zonal circulation and the semidiurnal tide, Icarus, 69, 202–220, 1987., 10.1016/0019-1035(87)90100-X
Belton, M. J. S., P. J. Gierasch, M. D. Smith, P. Helfenstein, P. J. Schinder, J. B. Pollack, K. A. Klaasen, J. Veverka, C. D. Anger, M. H. Carr, C. R. Chapman, M. E. Davies, F. P. Fanale, R. Greeley, R. Greenberg, J. W. Head III, D. Morrison, G. Neukum, and J. B. Pilcher, Image from Galileo of the Venus cloud deck, Science, 253, 1531–1536, 1991., 10.1126/science.253.5027.1531
Bezard, B., C. C. C. Tsang, R. W. Carlson, G. Piccioni, E. Marcq, and P. Drossart, Water vapor abundance near the surface of Venus from Venus Express/VIRTIS observations, J. Geophys. Res., 114, E00B39, 2009.
Drossart, P., B. Bezard, Th. Encrenaz, E. Lellouch, M. Roos, F. W. Taylor, A. D. Collard, S. B. Calcutt, J. Pollack, D. H. Grenspoon, R. W. Carlson, K. H. Bains, and L. W. Kamp, Search for spatial variation of H2O abundance in the lower atmosphere of Venus from NIMS-Galileo, Planet. Space Sci., 41, 495–504, 1993., 10.1016/0032-0633(93)90032-W
Fels, S. B. and R. E. Lindzen, The interaction of thermally excited gravity waves with mean flows, Geophys. Fluid Dyn., 6, 149–192, 1973., 10.1080/03091927409365793
Gierasch, P. J., Meridional circulation and the maintenance of the Venus atmospheric rotation, J. Atmos. Sci., 32, 1038–1044, 1975., 10.1175/1520-0469(1975)032<1038:MCATMO>2.0.CO;2
Hashimoto, G. L. and T. Imamura, Elucidating the rate of volcanism on Venus: Detection of lava eruptions by using near-infrared observations, Icarus, 154, 239–243, 2001., 10.1006/icar.2001.6713
Hashimoto, G. L. and S. Sugita, On observing the compositional variability of the surface of Venus using nightside near-infrared thermal radiation, J. Geophys. Res., 108 (E9), 5109, 2003., 10.1029/2003JE002082
Hashimoto, G. L., M. Roos-Serote, S. Sugita, M. S. Gilmore, L. W. Kamp, R. W. Carlson, and K. H. Baines, Felsic highland crust on Venus suggested by Galileo Near-Infrared Mapping Spectrometer data, J. Geophys. Res., 113, E00B24, 2008.
Haus, R. and G. Arnold, Radiative transfer in the atmosphere of Venus and application to surface emissivity retrieval from VIRTIS/VEX measurements, Planet. Space Sci., 58, 1578–1589, 2010., 10.1016/j.pss.2010.08.001
James, E. P., O. B. Toon, and G. Schubert, A numerical microphysical model of the condensational Venus cloud, Icarus, 129, 147–171, 1997., 10.1006/icar.1997.5763
Keating, G. M., J. L. Bertaux, S. W. Bougher, T. E. Cravens, R. E. Dickinson, V. A. Krasnopolsky, A. F. Nagy, J. Y. Nicholson III, L. J. Paxton, and U. von Zahn, Models of Venus neutral atmosphere: Structure and composition, Venus International Reference Atmosphere IV, Adv. Space Res., 5 (11), 117–172, 1985., 10.1016/0273-1177(85)90200-5
Krasnopolsky, V. A., Photochemistry of the Atmosphere of Mars and Venus, pp. 133, Springer-Verlag, Berlin, 1986., 10.1007/978-3-642-70401-7
Meadows, V. S. and D. Crisp, Ground-based near-infrared observation of the Venus nightside: The thermal structure and water abundance near the surface, J. Geophys. Res., 101, 4595–4622, 1996., 10.1029/95JE03567
Mueller, N., J. Helbelt, G. L. Hashimoto, C. C. C. Tsang, S. Erard, G. Piccioni, and P. Drossart, Venus surface thermal emission at 1 εm in VIRTIS imaging observations: Evidence for variation of crust and mantle differentiation conditions, J. Geophys. Res., 113, E00B17, 2008.
Nakajima, T. and M. Tanaka, Matrix formulation for the transfer of solar radiation in a plane-parallel scattering atmosphere, J. Quant. Spectrosc. Radiat. Transfer, 35, 13–21, 1986., 10.1016/0022-4073(86)90088-9
Nakamura, M., T. Imamura, M. Ueno, N. Iwagami, T. Satoh, S. Watanabe, M. Taguchi, Y. Takahashi, M. Suzuki, T. Abe, G. L. Hashimoto, T. Sakanoi, S. Okano, Y. Kasaba, J. Yoshida, M. Yamada, N. Ishii, T. Yamada, K. Uemizu, T. Fukuhara, and K.-I. Oyama, Planet-C: Venus Climate Orbiter mission of Japan, Planet. Space Sci., 55, 1831–1842, 2007., 10.1016/j.pss.2007.01.009
Pollack, J. B., B. Dalton, D. Grinspoon, R. B. Wattson, R. Freedman, D. Crisp, A. Allen, B. Bezard, C. De Bergh, L. P. Giver, Q. Ma, and R. Tipping, Near-infrared light from Venus’ nightside: A spectroscopic analysis, Icarus, 103, 1–42, 1993., 10.1006/icar.1993.1055
Ragent, B. and J. Blamont, The structure of the clouds of Venus: Results of the Pioneer Venus nephelometer experiment, J. Geophys. Res., 85, 8089–8105, 1980., 10.1029/JA085iA13p08089
Rothman, L. S., D. Jacquemart, A. Barbe, D. C. Benner, M. Birk, L. R. Brown, M. R. Carleer, C. Chackerian, K. Chance, L. H. Coudert, V. Dana, V. M. Devi, J. M. Flaud, R. R. Gamache, A. Goldman, J. M. Hartmann, K. W. Jucks, A. G. Maki, J. Y. Mandin, S. T. Massei, J. Orphal, A. Perrin, C. P. Rinsland, M. A. H. Smith, J. Tennyson, R. N. Tolchenov, R. A. Toth, J. V. Auwera, P. Varanasi, and G. Wagner, The HITRAN 2004 molecular spectroscopic database, J. Quant. Spectroscopy Radiative Trans., 96, 139–204, 2005., 10.1016/j.jqsrt.2004.10.008
Schubert, G., General circulation and the dynamical state of the Venus atmosphere, in Venus, pp 681–765, The University of Arizona Press, Tucson, USA, 1983.
Takagi, S. and N. Iwagami, Contrast sources for the infrared images taken by the Venus mission AKATSUKI, Earth Planets Space, 63, 435–442, 2011., 10.5047/eps.2011.01.007
Acknowledgements
The authors thank to the people working for manufacturing the camera. They are of Nikon Co. for the optics, Fujitoku Co. (Barr Associates Inc.) for the filters, Magoshi Co. for the baffle, Mitsubishi Electric Co. for the sensor, Sumitomo Heavy Industries Ltd. for the whole IR1system and NEC-Toshiba Space Systems Co. for the whole mission. They also thank to all the people of ISAS (Institute of Space Aeronautical Science) working for the mission.
Author information
Authors and Affiliations
Corresponding author
Appendix A. Additional Notes
Appendix A. Additional Notes
On 07 December 2010 Akatsuki failed to be inserted into the orbit around Venus, and is now orbiting the sun with a period of 203 Earth days. However, next trial of insertion is planned in 2015 or 2016 to start observation of Venus.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iwagami, N., Takagi, S., Ohtsuki, S. et al. Science requirements and description of the 1 μm camera onboard the Akatsuki Venus Orbiter. Earth Planet Sp 63, 487–492 (2011). https://doi.org/10.5047/eps.2011.03.007
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2011.03.007