Introduction

It is widely assumed that faces are processed more holistically—as perceptual wholes or integrals—than non-face objects such as houses, cars, or furniture (McKone & Robbins, 2011; Rossion, 2015), which in return are presumed to be processed in a more parts-based manner (Farah et al., 1998; Richler & Gauthier, 2014). Despite this, there is no commonly accepted definition of what ‘holistic’ processing is (Piepers & Robbins, 2012; Richler et al., 2012), and perhaps because of this some have argued that it is critical to ground the construct ‘holistic’ in experimental paradigms that can operationally define it. Three such paradigms are considered central (Rezlescu et al., 2017; Tanaka & Gordon, 2011): (i) the composite face paradigm (Young et al., 1987), the part–whole paradigm (Tanaka & Farah, 1993; Tanaka & Simonyi, 2016), and the face inversion paradigm (Yin, 1969).

In recent years, there have been several attempts to examine how the holistic effects measured by these paradigms relate to individual differences in face recognition performance. The results so far have been inconsistent. A few studies have found that (some) of the measures can account for some of the variance in face recognition (DeGutis et al., 2013; Rezlescu et al., 2017; Richler et al., 2011; Wang et al., 2012) but others have not (Konar et al., 2010; Rezlescu et al., 2017; Richler et al., 2015; Richler & Gauthier, 2014; Verhallen et al., 2017). To make matters worse, it has also been found that the three measures of holistic processing do not correlate to any great extent—if at all—which raises concern as to whether they tap the same construct, as is commonly assumed (for further discussion of this see Rezlescu et al., 2017). Such a concern has even been raised for one of the paradigms considered in isolation—the composite face paradigm—which may yield different results depending on which particular design of the paradigm (partial or complete) is applied (Richler & Gauthier, 2014; Rossion, 2013). Recently, we have been confronted with a similar concern regarding the face inversion paradigm, which is the paradigm of focus here.

The face inversion effect refers to the finding that processing of faces becomes disproportionally more disrupted by inversion than processing of non-face objects (Yin, 1969), a finding that has been replicated in a great number of studies (Bruyer, 2011) and examined in several (sub)disciplines including developmental psychology, cognitive psychology, neuropsychology, experimental psychology, comparative psychology and neuroscience (Cashon & Holt, 2015; Griffin, 2020; James et al., 2013; Klargaard et al., 2018; Leder et al., 2017; Rhodes et al., 1993). While the face inversion paradigm does not assess holistic processing directly—because it does not involve manipulations of holistic processes per se (McKone & Robbins, 2011; Tanaka & Simonyi, 2016)—the face inversion effect is usually taken to reflect that upright faces are processed holistically whereas a parts-based analysis is the only available processing option for inverted faces (Piepers & Robbins, 2012; Rossion, 2008). Indeed, inversion abolishes the holistic effects typically found with the composite face paradigm (Rossion & Boremanse, 2008) and the part-whole paradigm (Tanaka & Sengco, 1997).

If the face inversion effect does reflect holistic processing—a proposition that will be challenged in the Discussion—one might suspect this effect to be reduced in individuals with face processing deficits, provided of course that their deficits are related to holistic processing. In partial supportFootnote 1 of this proposition we recently found that the face inversion effect was reduced in a group of individuals with developmental prosopagnosia (Klargaard et al., 2018); a syndrome characterized by lifelong impairment in face recognition in the absence of brain damage. This was found across two widely used tasks in neuropsychological studies of face processing: The Cambridge Face Memory Test (CFMT) (Duchaine & Nakayama, 2006) and the Cambridge Face Perception Test (CFPT) (Duchaine, Germine, et al., 2007a). The interesting part of this study in the present context was that the magnitude of the inversion effects measured by the two tasks did not correlate, neither for the individuals with developmental prosopagnosia, the control participants or for the two groups combined. This might suggest that the ‘face inversion effect’—just like the composite face effect—does not reflect a singular phenomenon. It is also possible, however, that the lack of correlation between the two inversion effects was caused by limited statical power given that the sample consisted of only 16 individuals with developmental prosopagnosia and 32 controls. In addition, the reliability of the CFPT inversion measure was found to be rather unsatisfactory (rsb ranged from – .09 for the control sample to .19 for the sample with developmental prosopagnosia). This is problematic because the reliabilities of two measures limits the magnitude of the correlation that can be observed between them (Spearman, 1904). It is also worth noting that our measures of inversion effects were based on difference scores (accuracy for upright faces—accuracy for inverted faces) which are considered problematic for two reasons: (i) difference scores are often less reliable than their component scores (Peter et al., 1993), and (ii) difference scores may be confounded in the sense that both the condition of interest (here upright faces) and the control task (here inverted faces) may correlate with the difference score. If this is so, one could argue that the difference score is an unspecific measure. In the present case it would mean that the effects measured not only reflect holistic processing in the upright condition but also processes engaged by the inverted condition.

The general point regarding the unspecific nature of difference scores has been argued strongly by DeGutis et al. (2013) precisely with regards to the role of holistic processing in face recognition. They suggest that a better solution than to subtract scores is to regress the effect of the control condition (inverted faces) from the condition of interest (upright faces). The residuals left by regression should then yield a more specific measure of that part of the performance with upright faces that cannot be accounted for by performance with inverted faces, that is, the effect of holistic processing. By using such a regression approach, DeGutis et al. (2013) were able to establish that two measures of holistic processing—the part-whole and the composite face effect—both correlated with an independent measure of face recognition and with each other. This was not revealed by a similar analysis based on difference scores. In addition, the measures based on regression proved to have higher reliability than the measures based on subtraction (for similar results see Rezlescu et al., 2017).

Even though the regression approach seems attractive, it is not without concerns. Basically, it constitutes a departure from an individual difference approach in that the residual of a given participant reflects not only the individual’s performance but also the performance of the rest of group on which the regression model is based. Hence, the regression approach is subject to sampling error and this aspect should be considered in the context of the suggestion that stable estimates of correlations (based on Pearson’s r) may require sample sizes of N = 250 (Schönbrodt & Perugini, 2013); a sample size considerably beyond that used in most studies of holistic processing (for exceptions see Boutet et al., 2021; Rezlescu et al., 2017). This particular problem with sampling error is not an issue for the subtraction approach because it is ‘only’ affected by within-subject error owing to measurement imperfection (reliability being less than perfect). It is not the case, however, that the regression approach is unaffected by within-subject error. As mentioned above, the reliabilities of two measures limits the magnitude of the correlation that can be observed between them. Thus, as compared with the subtraction approach, where each subject serves as their own control, the estimate of an individual’s performance and its residual yielded by regression is affected by both sampling error and within-subject error. In this respect, it can seem surprising that measures based on regression can turn out more reliable than measures based on subtraction (DeGutis et al., 2013; Rezlescu et al., 2017) even if this is not always the case (Ross et al., 2015). However, and as pointed out by Hedge et al. (2018), the main reason why difference scores may have low reliability is that they can be quite successful in removing between-subject variance thus increasing the amount of (within-subject) measurement error relative to between-subject variance. Given these considerations it is not clear that the regression approach necessarily represents “...an improved analytic approach” relative to an approach based on difference scores as DeGutis et al. (2013, p. 88) claim (for a deeper discussion, see Willett, 1988). In fact, DeGutis et al. did not really test whether their measure of ‘holistic’ processing was face-specific or even specific for upright faces because they did not examine whether it correlated with processing of other stimuli besides upright faces, for example objects or inverted faces (Boutet et al., 2021). The same limitation was acknowledged by Rezlescu et al. (2017) in their study. They found that a regression-based measure of the face inversion effect correlated with processing of upright faces in an independent task, but they did not test whether it also correlated with for example processing of inverted faces.

Given the issues discussed above, the present work had four objectives. We wanted to examine: (i) if a correlation can be observed between inversion effects measured with the CFMT and the CFPT when using a larger sample (N = 420) than the one used by Klargaard et al. (2018), (ii) whether correlations between inversion effects will be specific to tasks using faces as stimuli, or/and (iii) will depend on the approach used (subtraction vs. regression), and (iv) the degree to which inversion effects based on subtraction and regression correlate with performance with both upright and inverted faces in independent tasks. The latter objective is motivated by an interest to see how specific the inversion measures are. If they are specific to holistic processing of upright faces, the inversion measures should correlate with processing of upright but not inverted faces.

Method

Tasks

The original versions of the CFMT (Duchaine & Nakyama, 2006) and the CFPT (Duchaine, Yovel, et al., 2007b) were used. To examine objective (ii)—whether potential correlations between measures of inversion effects would generalize to tasks with objects—we used the Cambridge Car Memory Test (CCMT), which is identical to the CFMT except that cars are used instead of faces as stimuli (Dennett et al., 2012). All instructions and feedback on the Cambridge tests were translated to Danish.

In the CFMT and the CCMT the participant is introduced to six target stimuli, and then tested with forced choice items consisting of three stimuli, one of which is the target. The tests comprise a total of 72 trials distributed over three phases: (a) an intro-phase with 18 trials where the study stimulus and the target stimulus are identical, (b) a novel-phase with 30 trials where the target differs from the study stimulus in pose and/or lighting, and (c) a novel+noise phase with 24 trials where the target differs from the study stimulus in pose and/or lighting and where Gaussian noise is added to the target. The dependent measure is the number of correct trials. The maximum score is thus 72; chance-level is 24 (33% correct responses).

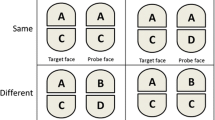
In the CFPT, the participant must arrange six facial images according to their similarity to a target face. The images were created by morphing six different individuals with the target face. The proportion of the morph coming from the target face varies in each image (88, 76, 64, 52, 40, and 28%). The test comprises 16 trials, half with upright and half with inverted faces. Scores for each item are computed by summing the deviations from the correct position for each face. Scores for the eight trials are then added to determine the total number of respectively upright and inverted errors. Hence, the dependent measure is a deviation-score where 0 represents perfect performance and 144 the worst possible performance. Chance performance corresponds to 35% correct.

Participants

A total of 420 first-year psychology students who were naïve to our hypotheses contributed data for this study as part of their course in cognitive psychology. The course is approved by the study board at the Department of Psychology, University of Southern Denmark, and the experiments conducted do not require formal ethical approval/registration according to Danish Law and the institutional requirements. Prior to participation, the students were informed that data collected in the experiments might be used in an anonymous form in future publications. Participants were free to opt-out if they wished, and participation in the experiments was taken as consent. Hence the sample size was determined by the number of students who took the course in the years 2014–2020 and provided data for all three tasks (CFMT, CCMT, and CFPT). No participants were excluded from the analyses reported below. Task order was counterbalanced for the CFMT and the CCMT. Except for 2 years, the CFPT was always performed a week prior to the CFMT and the CCMT, which were performed on the same day. The individual data for each of the 420 participants are provided in the Supplementary Data (https://osf.io/7ufv8/). To comply with GDPR, age was not logged for all the participants but the majority were in the age range of 20–30 and approximately two-thirds were women.

Statistical procedures

To make comparisons across tasks simple, all dependent measures were converted to percentage correct (Bate et al., 2019) and subsequent analyses were based on percentage correct responses; 95% confidence intervals were estimated based on bias corrected and accelerated bootstrapping (1000 samples) as implemented in the software package SPSS (version 28). Estimates of reliability were computed with the Spearman–Brown prediction formula (rsb) also as implemented in SPSS.

Two different measures of inversion effects were computed. The first was a simple difference score obtained by subtracting performance with inverted stimuli from performance with upright stimuli. This was done for all three tasks. In the following, these measures will be referred to with the subscript ‘SUB‘ for subtraction, such that CFMTSUB will refer for the difference score for performance with upright and inverted faces in the CFMT. The second measure was based on regressing out the effect of the control condition (inverted stimuli) from the condition of interest (upright stimuli) (DeGutis et al., 2013). The resulting standardized residual for each individual was taken as an index of ‘holistic’ processing. These measures will be referred to with the subscript ‘REG’ for regression.

As mentioned above, the correlation observed between two measures will scale with the reliabilities of the measures: The lower the reliabilities, the lower the possible correlation that can be observed between them will be. Because of this, many recommend that observed correlations be adjusted for measurement error (reliability) to give less biased estimates (Schmidt & Hunter, 1999). This can be achieved by using the disattenuation formula suggested by Spearman (1904), which is the observed correlation divided by the square root of the product of the two measures’ reliabilities. This formula will always adjust the observed correlation upward, and the lower the reliability the larger the adjustment. It is important to note that the adjusted correlation—which we will henceforth refer to as rAdjusted—is itself an estimate that is affected by sampling error, which will also affect the estimates of the reliabilities that it rests upon (Hedge et al., 2018). Hence, rAdjusted can yield values higher than 1 when reliability is low, and the adjustment in general does lead to overestimation when reliability is low (Wang, 2010). For these and related reasons, rAdjusted should be considered carefully (Winne & Belfry, 1982) but for completeness we do present the adjusted correlation when a significant correlation is found (for unadjusted measures).

To address the issue of specificity—which was our last objective—we examined how well the inversion effect indexes based on the CFPT (CFPTSUB and CFPTREG) correlated with processing of upright and inverted faces in the CFMT, and how well the inversion effect indexes based on the CFMT (CFMTSUB and CFMTREG) correlated with processing of upright and inverted faces in the CFPT. While we could have addressed specificity with another set of face processing tasks that were not also used to derive the inversion effect indexes from, we believe these comparisons are nevertheless fair because: (i) they are based on independent tasks (the indexes were derived from another task than the test conditions), and (ii) holistic processing is thought of as a perceptual phenomenon (Rezlescu et al., 2017) and both the CFMT and the CFPT require perceptual processing. In the following we will use the term “benchmark” to refer to these tests of specificity. Hence, the CFMT will serve as the benchmark task for evaluating the specificity of the CFPTSUB and CFPTREG measures and the CFPT will serve as benchmark task for evaluating the specificity of the CFMTSUB and CFMTREG measures.

Results

Inversion effects

As can be seen in Table 1, the mean performance with upright stimuli was highest for the CFMT (81% correct), intermediate for the CFPT (77% correct) and lowest for the CCMT (68% correct). These figures are similar to previous reports with similar age groups (see Table 2). Compared with the performance with upright stimuli, performance with inverted stimuli was rather similar across the three tasks ranging from 58–62% correct. Table 1 also shows there were credible inversion effects across all tasks (the 95% CI’s for reduction in % correct scores as a consequence of inversion did not contain 0), and the magnitude of these effects—around 20% for faces and 6% for objects—are comparable with what has been reported for faces and objects in previous studies (McKone & Robbins, 2011; Rezlescu et al., 2017). Hence, the inversion effects were disproportionally larger for faces than for objects which is the typical finding (Bruyer, 2011). Finally, because correlations can be affected by range restrictions, it is also worth noting that the coefficients of variation are rather similar across the six conditions (range 13–18) (see Table 2) and again comparable with previous findings (see e.g., Gauthier, 2018). Information regarding all correlations between tasks and conditions with upright and inverted stimuli can be found in the Appendix Table 6.

Table 1 Mean performance (% correct) with upright and inverted stimuli in the three tests and mean reduction in performance in the tests as a function of inversion. The 95% CIs of the means are given in brackets
Full size table
Table 2 The coefficient of variation for the six conditions in the present study and from other studies that have used the same test conditions in populations with a similar age range
Full size table

Reliabilities

The split-half reliabilities of the measurements were generally moderate to good for the CFMT and the CCMT (rsb ranged from .57 to .88) (see Table 3). However, the reliability of measurements based on the CFPT were considerably lower and for the CFPTSUB reliability could not be computed because of a negative correlation between odd and even trials. Finally, for all measures of inversion effects, the estimates based on regression were more reliable than the ones based on difference scores.

Table 3 The Spearman–Brown split-half reliabilities associated with the measures used in the present study
Full size table

Correlations between tasks in inversion effects

There was no significant correlation between the CFPTSUB and the CFMTSUB measures of inversion effects (see Table 4). However, a small significant correlation was found between the CFMTSUB and the CCMTSUB measures (r = .15, rAdjusted = .24). For the measures based on regression significant correlations were found both between the CFMTREG and the CFPTREG measures (r = .12, rAdjusted = .23) and between the CFMTREG and the CCMTREG measures (r = .11, rAdjusted = .14). The magnitudes of the two correlations found with the regression measures did not differ significantly (Z = .15, p = .88). This also held true when the comparison was performed on the adjusted correlations (Z = 1.3, p = .18). Likewise, the correlation between the CFMTSUB and the CCMTSUB measures was not significantly higher than the correlation found between the CFMTREG and the CCMTREG measures (Z = .59, p = .56: for the adjusted correlation Z = 1.5, p = .13).

Table 4 The correlations between tasks in inversion effects based on either subtraction (SUB) or regression (REG) measures
Full size table

Specificity

None of the measures based on difference scores (CFPTSUB and CFMTSUB) correlated significantly with processing of upright or inverted faces in the benchmark tasks (see Table 5). In comparison, the CFMTREG measure correlated with processing of upright faces in the CFPT (r = .18, rAdjusted = .27) and the CFPTREG measure correlated with processing of upright faces in the CFMT (r = .17, rAdjusted = .31). Hence, both regression measures of inversion effects were related to processing of upright faces in the benchmark tasks. However, the same measures were also related to processing of inverted faces (CFMTREG and CFPTInverted r = .16, rAdjusted = .26; CFPTREG and CFMTInverted r = .13, rAdjusted = .29) and the magnitude of these correlations did not differ considerably from correlations found with upright faces (cf. the 95% CIs in Table 5). In other words, the more poorly performance in the control condition (e.g., CFMTInverted) is at predicting performance in the condition of interest (e.g., CFMTUpright), the more likely it is that the individual will obtain a high score on the benchmark task (e.g., the CFPT) regardless of whether the stimuli are upright or inverted.

Table 5 Correlations between the different measures of inversion effects (SUB = subtraction score; REG = regression residual) and performance with upright and inverted stimuli in the Cambridge Face Memory Test (CFMT), the Cambridge Face Perception test (CFPT), and the Cambridge Car Memory Test (CCMT)
Full size table

To assess how systematic the correlations between the regression measures and performance on the benchmark tasks were, we examined whether the individuals who drove the correlation between CFPTREG and CFMTUpright performance were the same individuals who drove the correlation between CFPTREG and CFMTInverted performance. To do so, we computed the residuals from the correlation between the CFPTREG and CFMTUpright performance on the one hand (CFPTREG+CFMTUpright Residual), and the residuals from the correlation between the CFPTREG and CFMTInverted performance on the other (CFPTREG+CFMTInverted Residual). We then performed a correlation analysis with these two variables (CFPTREG+CFMTUpright Residual & CFPTREG+CFMTInverted Residual). This yielded a moderate to large effect (r = .47, 95% CI [.39, .54]). A similar sized effect was found when we looked at the relationship between the CFMTREG and CFPT performance with upright and inverted faces respectively (CFMTREG+CFPTUpright Residual & CFMTREG+CFPTInverted Residual: r = .49, 95%CI [.4, .56]). These results reveal some consistency across tasks. It is to a considerable degree the same individuals who drive the (modest) correlations observed between the CFPTREG and performance with of upright and inverted faces on the CFMT, and also the same individuals who drive the (modest) correlations observed between the CFMTREG and performance with upright and inverted faces on the CFPT.

Discussion

Our first objective was to examine whether inversion effects derived from different tasks measure the same construct. We found some evidence in favor of this proposition in that inversion effects derived from the Cambridge Face Memory Test (CFMT) did correlate with inversion effects derived from the Cambridge Face Perception Test (CFPT). This, however, was true only when the inversion effects were estimated by means of regression (CFMTREG & CFPTREG), and not when estimated by means of subtraction (CFMTSUB and CFPTSUB). The correlation based on regression was rather small, however, and the two measures shared only 1.4% of their variances. Even in the hypothetical event that the measures had had perfect reliability this would only have amounted to 5% of shared variance; an adjusted measure based on dividing the correlation observed by the product of the reliabilities of its two components (Spearman, 1904). Finally, the CFMTREG measure shared a comparable amount of variance (1.1%, 2%Adjusted) with the regression measure of inversion effects based on the Cambridge Car Memory Test (CCMTREG). A similar picture was obtained for measures based on subtraction where the CFMTSUB measure shared 2.1% (5.7%Adjusted) of its variance with the CCMTSUB measure. Given these findings there is limited evidence to support the notion that inversion effects derived from different tasks measure the same construct to any great extent or that they are category-specific. Also, the consistency across the two methods (subtraction and regression) was mixed in that the correlation between inversion effects for the CFMT and the CCMT was found with measures based on both regression and subtraction, whereas the correlation between inversion effects for the CFMT and the CFPT was found only with measures based on regression.

The finding that measures of inversion effects shared a comparable, but small, amount of variance across tasks with faces and objects is troubling if it is assumed that faces, and faces alone, are subject to holistic processing. Many researchers, however, take the stance that holistic processing is not limited to faces (Gerlach et al., 2022) but may be of greater importance for face than for object processing (e.g., McKone & Robbins, 2011). The present findings are compatible with such an interpretation as the drop in performance due to inversion was more pronounced for faces (around 20%) than for objects (6%). It is somewhat more troubling that the inversion effects observed are not more tightly coupled for faces in the two face processing tasks than they are for faces and objects in the recognition tasks. After all, the reductions in performance due to inversion were of similar magnitude for the CFMT (21%) and the CFPT (19%). It is also troubling, as we will discuss below, that the inversion indexes for faces correlate equally well with upright and inverted faces when based on the regression method.

As argued in the Introduction, it is generally assumed that the superior performance with upright compared with inverted faces reflects that upright (but not inverted) faces are processed holistically. Consequently, to the degree that measures of inversion effects do indeed provide indexes of holistic processing we would expect these measures to yield higher correlations with processing of upright faces—that according to theory are subject to holistic processing—than with processing of inverted faces that—again according to theory—are not subject to holistic processing but are processed in a parts-based manner (Piepers & Robbins, 2012; Rossion, 2008).

None of the measures based on subtraction revealed any significant correlation with processing of upright or inverted faces in the benchmark tasks. In comparison, both the CFPTREG and the CFMTREG accounted for a small but significant portion of the variance in processing of upright faces in the benchmark tasks (3%: 10%Adjusted and 7%Adjusted respectively for the CFPTREG and the CFMTREG). In this respect, the present findings add to an increasing number of studies which find that measures of holistic processing can only explain a modest degree of the variation in face processing ability observed among individuals if any at all (Konar et al., 2010; Rezlescu et al., 2017; Richler et al., 2015; Richler & Gauthier, 2014; Verhallen et al., 2017). Moreover, and perhaps more critically, the measures accounted for a similar amount of variance with inverted faces in the benchmark tasks (2%: 8%Adjusted and 7%Adjusted, respectively, for the CFPTREG and the CFMTREG) as they did with upright faces. Considered together, these findings suggests that while both the CFPTREG and CFMTREG measures can account for some of the variance found in other tasks of face processing, there is no evidence suggesting that these measures isolate something which is specific to upright faces. It is worth noting that even if these results may have been affected by the low reliability of the CFPT, this alone cannot account for the present findings. First of all, the regression-based measure derived from the CFPT did reveal credible correlations with the CFMT despite the measure’s poor reliability. Secondly, adjusting the correlations for the reliability of the measures did not change the pattern observed: The amount of variance explained in the benchmark tasks was quite similar for upright and inverted faces. This orientation-invariance also applies to overall task performance. The amounts of shared variance between the CFMTUpright and the CFPTUpright on the one hand and between the CFMTUpright and the CFPTInverted on the other were quite similar (r = .3 and r = .31, respectively; see the Appendix Table 6). The same was the case for the CFPTUpright and the CFMTUpright/CFMTInverted (r = .3 and r = .3 respectively, see the Appendix Table 6). For similar findings regarding orientation-invariance, see Meinhardt et al. (2019).

The finding that regression measures are apparently insensitive to the orientation of the stimuli in the benchmark tasks seems at odds with the claim by DeGutis et al. (2013) that regression yield specific measures of (holistic) processing. Admittedly, this finding of lack of specificity is surprising, as there can be no doubt that regression does ensure that the control condition (inverted faces) does not correlate with the measure of inversion effects (CFMTREG/CFPTREG)—which presumably reflects holistic processing—whereas the condition of interest (upright faces) does. In comparison, difference scores (CFMTSUB/CFPTSUB) may be affected by both the control condition and the condition of interest. As can be seen in Fig. 1, this is also the case with our data. Hence, as also demonstrated by DeGutis et al. (2013), the regression-based method does yield a somewhat more specific measure than the method based on subtraction in that the regression measure based on for example the CFMT only correlates with processing of upright stimuli and not inverted stimuli in the CFMT whereas the subtraction measure based on the CFMT correlates with processing of both upright and inverted stimuli in the CFMT. However, and as shown here, the regression measures are only specific in the context of the tasks that they were derived from, that is, the specificity does not generalize to other tasks. Consequently, even though the regression-based measure derived from the CFMT only correlated with processing of upright and not inverted stimuli in the CFMT it correlated with processing of both upright and inverted stimuli in the CFPT, and to similar degrees. These findings raise serious concerns as to what exactly is captured by these regression measures. Even though we cannot answer this question because the individual difference approach adopted here rests on common variance, what we can conclude is that it is not holistic processing if holistic processing is defined as processing that is limited to upright faces.

Fig. 1
figure 1

Scatter plots showing how the two types of indexes based on subtraction (left panels) and regression (right panels) correlated with their constituent conditions. As can be seen, the indexes based on subtraction correlated with both the control condition (inverted stimuli) and the condition of interest (upright stimuli). In comparison, the indexes based on regression yielded more pure measures reflecting variation in performance with upright but not inverted stimuli

Full size image

If the CFMTREG and CFPTREG do not measure holistic processing, does this mean that faces are not processed holistically? Probably not. It is entirely likely, as some have proposed, that both upright and inverted faces are processed holistically (Meinhardt et al., 2019; Murphy & Cook, 2017; Murphy et al., 2020; Sekuler et al., 2004). If this is indeed the case, then variance due to holistic processing will of course not be captured by the residuals in the CFMTREG and CFPTREG measures; only operations that differ between processing of upright and inverted faces will. This would certainly help explain why the CFMTREG and the CFPTREG measures do not seem sensitive to orientation across tasks. It is worth noting, though, that this suggestion does not mean that upright and inverted faces are processed equally well. Clearly, there are huge differences also in the present sample between the participants’ performance with upright and inverted faces (a 20% reduction due to inversion). It simply means that individual differences in holistic processing will contribute equally to performance differences across subjects in processing of upright and inverted faces.

Regardless of whether the CFMTREG and CFPTREG measures gauge holistic processing or not—and we are inclined to say ‘not’—what they measure seems rather task-dependent, as they could only account for about 2–3% (7–10%Adjusted) of the variance in performance with upright and inverted faces in the benchmark tasks. A similar figure was observed for the amount of variance shared by the measures directly (CFPTREG and CFMTREG), which was 1.4% (5%Adjusted). To this we must add the observation that the CFMTREG also shared variance with the CCMTREG (1%, 2%Adjusted). The only conclusion we can reach based on these findings is that inversion effects are quite task-specific and do not generalize better among face processing tasks than they do across face and object (car) processing tasks. Further, given that a similar amount of shared variance was found between the CFMTSUB and CCMTSUB measures (2%, 6%Adjusted) this finding is stable across both regression and subtraction.

Conclusions

We find clear inversion effects for faces in two widely used tests in the neuropsychological literature—the Cambridge Face Perception Test and the Cambridge Face Memory Test—and the magnitude of reduction due to inversion in these tests is much larger (20%) than what is observed for objects (cars) in the Cambridge Car Memory Test (6% reduction). However, the inversion effects were quite task-dependent, and did not correlate better among face processing tasks than across face and object processing tasks. Finally, in contrast to previous studies, we also explicitly tested whether the measures of inversion effects provided specific measures of holistic processing—that is, tapped into operations confined to processing of upright faces. We found no evidence supporting this proposition. In conclusion, the present findings suggest that inversion effects are highly context-dependent and do not reflect holistic processing if holistic processing is defined as processing that is specific to upright faces. These observations are done in a much larger sample than previous studies (N = 420) and are thus unlikely to be caused by low power or sampling error.

The present findings do not bring us closer to why faces are often much more affected by inversion than objects are or whether inversion leads to qualitative or quantitative shifts in processing. They do suggest, however, that we cannot treat the inversion effect with faces as a pure or generalizable measure of holistic face processing. This is an important lesson, not least for studies that wish to understand what inversion effects reflect.