A note on the identification of change detection task models to measure storage capacity and attention in visual working memory

Abstract

The change detection task is a common method for assessing the storage capacity of working memory, but estimates of memory capacity from this task can be distorted by lapses of attention. When combined with appropriate mathematical models, some versions of the change detection task make it possible to separately estimate working memory and the probability of attentional lapses. In principle, these models should allow researchers to isolate the effects of experimental manipulations, group differences, and individual differences on working memory capacity and on the rate of attentional lapses. However, the present research found that two variants of a widely accepted model of the change detection task are not mathematically identified.

Working memory plays a key role in many large-scale theories of cognition (Anderson, Matessa, & Lebiere, 1997; Meyer & Kieras 1997), and individual differences in the storage capacity of working memory are widely thought to play a major role in determining individual and group diffe- rences in cognitive ability (Baddeley 2003; Cowan 2012; Engle, Tuholski, Laughlin, & Conway, 1999). The visual change detection paradigm has become a popular approach for estimating working memory capacity (Cowan, Naveh-Benjamin, Kilb, & Saults, 2006; Cusack, Lehmann, Veldsman, & Mitchell, 2009; Luck & Vogel 2013). In the canonical version of this paradigm (Luck & Vogel 1997; Vogel, Woodman, & Luck, 2001), each trial consists of a sample array of visually presented objects followed by a short delay and then a test array (see Fig. 1a). The sample and test arrays are identical except that on some percentage of trials (typically 50%), one item differs between the sample and test arrays. On each trial, participants make an unspeeded two-alternative forced-choice response to indicate whether a change was present or absent. Working from this general paradigm, Pashler (1988, p. 370) developed a simple equation for estimating the number of items stored in memory. The logic behind this equation is that if the participant has a working memory capacity of K items and the array contains S items, there will be a K/S probability that the changed item is one of the items being held in working memory and that the change will therefore be detected. This equation has become widely used to assess how memory storage capacity, K, varies across experimental conditions, across groups of participants, and across individuals within a group (Alvarez & Cavanagh 2004; Cowan et al.,, 2006; Cusack et al.,, 2009; Johnson, McMahon, Robinson, Harvey, Hahn, Leonard, . . . , Gold, 2013).

One advantage of the change detection task is that—when used in conjunction with appropriate mathematical models (Rouder, Morey, Cowan, Zwilling, Morey, & Pratte, 2008) —it can be used to measure attentional engagement concurrently with working memory storage capacity. By attentio- nal engagement, we mean that the participant is actively encoding the stimuli and following the rules of the task. When attention is not engaged, a lapse of attention occurs. Following previous work (Rouder et al., 2008; Rouder, Morey, Morey, & Cowan, 2011), we assume that a participant is either “on task” or “off task” on a given trial. When participants are on task, they (a) perceive the sample array, (b) encode as much of that information as possible, (c) maintain as much of this information as possible over the delay, (d) compare the memory of the sample array to the test array to arrive at a decision, and (e) make the appropriate response for this decision. Alternatively, when they are off task, they fail at one or more of the aforementioned task components.

In recent years, many variants of the change detection task have been described in the literature, and quantitative methods have been developed to estimate working memory capacity and attentional engagement in at least three of these variants (Gibson, Wasserman, & Luck, 2011; Rouder et al., 2008, 2011). These models have not been widely used in the empirical literature, in which researchers often simply estimate capacity without considering lapses of attention (Adam, Mance, Fukuda, & Vogel, 2015; Fukuda, Vogel, Mayr, & Awh, 2010; Fukuda, Vogel, Mayr, & Awh, 2011). However, there is growing evidence that mind wandering and other forms of attentional disengagement play a significant role in both typical and disordered cognition (Erickson, Albrecht, Robinson, Luck, & Gold, 2017; Mrazek, Smallwood, Franklin, Chin, Baird, & Schooler, 2012), and future research on individual and group differences in working memory would benefit greatly from models that can separately estimate capacity and attentional engagement. The present note demonstrates that attentional engagement is not necessarily estimated accurately in models of two of three variants of the change detection task. In these variants, the underlying mathematical model is not identified, meaning that different parameter values will predict the same pattern of behavioral performance. Stated differently, in these models, widely different levels of attentional engagement may be consistent with a given pattern of observed data. This occurs because the attentional engagement parameter depends mathematically on the two guessing parameters. In the remainder of this paper, we prove that these models are not identified and we demonstrate the consequences of this inconvenient mathematical truth for model estimation and interpretation. We then describe simple model modifications that ensure parameter identification. We end by describing the overall strengths and weaknesses of the three variants of the change detection task with respect to psychological factors that may impact their validity. The models considered in this study are mathematical instantiations of a class of theories of visual working memory that are often called “slot” or “item-limit” theories (reviewed by Luck & Vogel 2013). These theories assume that there is a limit on the number of items that can be stored in working memory; when the sensory input exceeds this limit, a subset of items are stored with some reasonable precision, and no information is retained about the other items. In contrast, “resource” theories assume that all items are stored in working memory, but that the quality of the individual item representations declines as the number of items in memory increases because of resource limitations or noise (Bays, 2014; van den Berg, Awh, & Ma, 2014). These two classes of theories have been hotly debated, and the field has not reached a consensus. Importantly, researchers in a variety of domains have a pressing need to be able to estimate working memory capacity and attentional engagement, and this research cannot wait decades for memory experts to reach unanimity. Researchers should certainly not use parameter estimates from models that are not mathematically identified. Thus, the present note is timely even if the debate between item-limit theories and resource theories has not been completely resolved.

Three variants of the change detection task

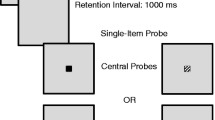
Figure 1 shows the three variants of the change detection task that we consider in this report. The first variant (Luck & Vogel, 1997; Vogel et al., 2001) is illustrated in Fig. 1a. We call this model the canonical changedetection task because it was the first variant to become widely used (and it is still the most commonly used of the three variants). The second variant limits the decision to a single item in the test array (Fig. 1b), which is typically accomplished either by presenting a postcue around the one item in the test array that might have changed or by presenting only one item in the test array (see Experiments 4-6 in Vogel et al., (2001). We call this the partial report change detection task because it is analogous to the partial report paradigm made famous in Sperling’s classic iconic memory experiments (Sperling, 1960). The third variant, called the multiple change detection task, is similar to the canonical change detection task, except that multiple items can change on a given trial (Fig. 1c). Rather than varying the set size, this task fixes the number of items in the display and varies the number of items that change (Gibson et al., 2011). However, the task remains the same as in the other variants; participants report whether a change was present (irrespective of the number of changes) or absent. Figure 2 illustrates the pattern of data expected from the model of the canonical change detection task. In this model, the probability of reporting a change is a function of S (the set size), whether a change actually occurred, and four person parameters: the individual’s level of storage capacity (K), attentional engagement (A), and two guessing parameters (G and U). This figure shows trial response probabilities for five hypothetical individuals with K values that range from 1 to 5, A = .85, G = .15, and U = .35. In general, the probability of detecting a change on change-present trials declines systematically as the set size (S) increases beyond a given individual’s storage capacity (K). At this point in the manuscript, it is not important to understand the other parameters. Rather, it is sufficient to recognize that under the canonical change detection paradigm, trial response probabilities can be modeled as a function of set size, whether or not a true change occurred, and the previously described four person parameters. Notice in Fig. 2 that that the probability of a change response on change-absent trials does not depend on set size or storage capacity. The general logic for estimating attentional engagement (Gibson et al.,, 2011; Rouder et al.,, 2008, 2011) is that participants will attend to the task on a certain proportion of trials (denoted A), and they will have lapses of attention for the remaining proportion of trials (1 − A). When participants are attending (i.e., they are on task), they are expected to exhibit perfect performance if the set size is less than or equal to their storage capacity (i.e., when S ≤ K). Accuracy is predicted to fall off at higher set sizes. When participants lapse (i.e., they are off task), they presumably guess randomly and are predicted to produce a constant error rate at all set sizes. Pashler’s (1988, p. 370) original equation for estimating working memory storage capacity (K) assumed that the participant was consistently on task and would respond correctly on a change-present trial if a change was present and if the changed item was in working memory. However, because a change might occur in an item that was not stored in memory, it would be reasonable for participants to occasionally guess that a change was present even if none of the items in memory changed. In Pashler’s model, this guessing rate is denoted G. Pashler assumed that G could be estimated by the probability of a change-present response on trials without a change. Cowan (2001) created a modification of this equation for the partial report variant of the task.

Fig. 1

Illustration of three visual change detection task variants

Fig. 2

Probability of change detection in the canonical change detection model. In this example, S ∈{1,2,3,4,5,6}, K ∈{1,2,3,4,5}, A = .85, G = .15, and U = .35. Importantly, the same picture arises from different (A,G,U) triples. For example, (A,G,U) triples of (.903,.199,.000), (.785,.080,.546), and (.722,.000,.649) make identical predictions as (.85,.15,.35)

The Cowan (2001) and Pashler (1988) models did not take into account the possibility of lapses of attention. Rouder et al., (2011) extended these models to include the possibi- lity of lapses, assuming that participants guess when they are off task (see also Rouder et al.,, 2008). Rouder et al., (2011) used the letter U to denote the probability of a change-present guess when a participant is off task (i.e., when a participant is not attending to the task). In this scheme, U refers to uninformed guessing and G refers to informed guessing. When a participant is on task, guesses are informed by factors such as the number of items in the array and the fact that no changes were detected in the K items that were present in working memory. The guessing rate when a participant is on task (G) may be quite different from the guessing rate when a participant is experiencing attentional lapses (U). Importantly, lapses in attentional engagement may occur for many reasons such as an ill-timed blink that prevents perception of the sample array, mind wandering that prevents encoding of the sample array in memory, or response-mapping confusions at the time of report. In the partial report change detection model, all guessing is considered uninformed guessing (Rouder et al., 2011). In other words, the partial report change detection model includes U but not G. In this model, if the probed item is not in working memory due to capacity limits, then the subject presumably guesses in the same manner as when the item is not in working memory due to an attentional lapse. As will be proven below, in the models of the canonical and multiple change detection tasks, the attention (A), and two guessing (G, U) parameters are not mathematically identified without additional constraints. In less formal language, this implies that different values of these parameters can produce the same pattern of responses on a change detection task (and a given set of observed data is therefore consistent with multiple combinations of parameter values). In the next section we demonstrate this point mathematically.

Model underidentification in the canonical and multiple change detection tasks

Both the canonical and multiple change detection tasks include four individual-level parameters. In the following mathematical equations, no subscripts are used for the individual or trial to avoid notational clutter. As described earlier, the four person parameters of these models are:

• K: capacity, the number of objects held in visual working memory,

• A: attention, the probability that attention is engaged on a trial (0 ≤ A ≤ 1),

• G: informed guessing, the probability of correctly guessing that an object changed, on a given trial, if that object is not in working memory when the participant is on task (0 ≤ G ≤ 1), and

• U: uninformed guessing, the probability of indicating that a change has occurred, on a given trial, when the participant has no information to constrain the guessing (0 ≤ U ≤ 1).

In the following, we assume that on a given trial S objects are shown on a computer display. For the test array, C objects change. In the canonical change detection task C ∈{0,1} and S varies. In the multiple change detection task C ∈{0,1,…,S} for a constant S. Let D_C,S denote the probability that an object has changed and exists in working memory for a trial with set size S in which C objects have changed. In Gibson et al., (2011) D_C,S is modeled as a function of K, C, and S:

$$\begin{array}{@{}rcl@{}} \text{if} C&=&0,D_{0,S}= 0 \end{array} $$

(1a)

$$\begin{array}{@{}rcl@{}} \phantom{0}\text{if}C&>&0,D_{C,S}\!=\!\left\{\begin{array}{ll} \min\left[1,1\!-\!\prod_{i=S-C + 1}^{S}\frac{i-K}{i}\right] & \text{if}C\!\leq\! S\!-\!K\\ 1 & \text{otherwise}. \end{array}\right.\\ \end{array} $$

(1b)

Note that this model is a generalization of the equations provided by Rouder et al., (2011) for modeling change detection performance in the canonical task when lapses of attention are possible. That is, when only a single change is possible, Eq. 1a and 1b reduce to the equations provided by Rouder et al. (2011 see p. 328). The K, A, G, and U parameters are estimated from the observed responses to each experimental trial type (where trial types are defined by C and S combinations). For a trial with C changes, we write P_C,S to denote the probability of a “change” response. These probabilities (i.e., change proportions) are modeled as functions of the four person-level parameters described above: A, G, U, and (indirectly via D_C,S) K,

$$ P_{C,S}=A[D_{C,S}+(1-D_{C,S})G]+(1-A)U. $$

(2)

We now demonstrate that in the multiple change and the canonical change detection tasks, three of the four person-level parameters (A, G, U) cannot be uniquely estimated without making additional assumptions. Recall that Fig. 2 shows the hit rates and false alarm rates as a function of S for five K values in the canonical change detection task. Notably, for any K value, the values in Fig. 2 could arise from sets of parameters other than the figure-generating values of A = .85, G = .15, and U = .35. For example, the data shown in Fig. 2 could be generated by (A,G,U) values of (.903,.199,.000), (.785,.080,.546) or (.722,.000,.649). Moreover, this pattern of data is consistent with values of A ranging from .722 to .903, and it is impossible to determine the actual value of A that generated the data (even with an infinite number of trials). This is a very broad range of possible A values, and it is unlikely that researchers who employ these tasks could draw meaningful conclusions about individual or group differences in attentional engagement given this degree of indeterminacy. To clarify the underlying cause of this underidentification, we introduce a mathematical coefficient to these models, B, that makes it possible to generate all sets of fungible (A,G,U) triples that can produce a given set of data.¹ The coefficient B is related to A, G, and U as follows:

$$ \tilde{A}=A/B, $$

(3)

$$ \tilde{G}= 1-B(1-G), $$

(4)

and

$$ \tilde{U}=\frac{A-\frac{A}{B}+(1-A)U}{1-\frac{A}{B}}. $$

(5)

As is formally proved in the Appendix, with a suitable choice of B, any triple of ($\tilde {A}$, $\tilde {G}$, $\tilde {U}$) that is generated from Eqs. 3–5 will yield the same values of P_C,S (for all values of C and S) for given values of (A, G, U). This fact justifies our claim that the multiple change and the canonical change detection models are not identified. Further illustration of the implications of model non-identification are given in Online Appendix A. Note, however, that the choice of B is subject to the constraints that $\tilde {A}$, $\tilde {G}$, and $\tilde {U}$ must each lie between 0 and 1. As shown in Online Appendix B, these constraints will be satisfied whenever

$$ \frac{A}{A+(1-A)U}\leq B\leq\frac{1}{1-G}. $$

(6)

In the Online Appendix B, we also derive the bounds on the $\tilde {A}$, $\tilde {G}$, and $\tilde {U}$ parameters that are implied by these bounds on B.

Identified visual short-term working memory model

Solution 1: Equal guessing probabilities

One way to eliminate the indeterminacy of the change detection models is by adding constraints on the relationship between the two guessing rate parameters, G and U. Specifically, when G = U there are three identified person-level parameters when there are at least three trial types. This identification constraint is justified whenever the probability of a “change” response due to inattention equals the probability of a “change” response when a changed object is not in working memory. In this updated model, the probability P of a “change” response to trial type C equals

$$ P_{C,S} =AD_{C,S}(1-G)+G. $$

(7)

Solution 2: An ideal guesser

Another way to resolve the non-identification of the canonical and multiple change detection models follows a suggestion by Rouder et al., (2011) about the normative relationship between the G and U parameters. In an ideal guesser, the informed guessing probability G will depend on set size, capacity, and the estimated base rate of changes. Specifically, Rouder et al. (2011, p. 327) propose that, for an ideal guesser,

$$ G_{C,S}=\frac{(1-D_{C,S})U}{(1-D_{C,S})U+(1-U)}, $$

(8)

and therefore

$$ P_{C,S}=A[D_{C,S}+(1-D_{C,S})G_{C,S}]+(1-A)U. $$

(9)

The identification constraint given in Eq. 8 is psychologically valid only if participants guess in a manner that is ideal. However, to our knowledge, there is no empirical evidence that this ideal relationship holds in change detection tasks, and it is well known that humans and other species often deviate from normative behavior across a wide range of probabilistic decision-making scenarios (Estes, 1962; Kahneman and Tversky, 2000). As a consequence, this solution is not necessarily on stronger psychological footing than Solution 1.

Simulations

To evaluate the performance of each of these solutions, we conducted two small simulation studies in which we varied the extent to which the assumptions of the solutions were violated. These simulations were designed to evaluate whether the suggested model identification restrictions lead to accurate working memory capacity estimates even if the model identification assumptions do not hold exactly. In both studies, trial responses were simulated for the canonical change detection task with set sizesS = {1,2,3,4,5,6,7}. At each set size, we simulated responses to 30 change-present and 30 change-absent trials for a total of 420 trial responses. In the first simulation, we generated a trial response grid of K, A, G, and U values such that K ∈{1,2,3,4,5}, A ∈{.6,.7,.8,.9,1}, G ∈{0,.1,.2,.3,.4,.5}, and U ∈{0,.1,.2,.3,.4,.5}. That is, in the first simulation, we assumed that informed guessing did not depend on set size and we systematically examined violations of the G = U assumption of Solution 1. All levels of K, A, G, and U were fully crossed, leading to 900 unique conditions. Capacity values K were then estimated using model identification Solution 1. In the second simulation, we generated data according to the same grid of K, A, and U values. We also assumed that informed guessing rates depended on set size and K according to Eq. 8, but multiplied the resulting G_C,S values by a factor j, j ∈{0.6,0.8,1.0,1.2,1.4}, to systematically examine the effects of violating Solution 2’s assumption of the relationship between G andU. For j = 1, the ideal observer assumption holds, and for j≠ 1, the informed guessing rate is systematically higher or lower than the ideal rate. All levels of K, A, U, and j were fully crossed, leading to 750 unique conditions. In both simulations, response data for 100 subjects were generated for each unique condition (i.e., set of parameters {K,A,G,U} or{K,A,U,j}). Capacity values K were then estimated using model identification Solution 2. For each subject in both simulations, maximum likelihood parameter estimates were obtained using the Nelder–Mead optimization routine as implemented in the dfoptim package (Varadhan & Borchers, 2016) in R R Core Team (2016)². To avoid local maxima, for each simulated response vector we obtained ten sets of parameter estimates from ten different sets of start values. We retained the set of parameter estimates that produced the largest log likelihood value. This design makes it possible to investigate how well the two model identification solutions perform as their model identification restrictions are or are not met. Note that we simulated a relatively large number of subjects (100 per condition) to obtain reliable estimates of bias and variance in the parameter estimates, not because this would ordinarily be required in an empirical study that was designed to estimate the parameters themselves. Results of the first simulation are shown in Fig. 3, and results for the second simulation are shown in Fig. 4. Both figures show box plots of the distribution of bias ($\hat {K}-K$), and within each box, the black horizontal line represents the median bias value and the whiskers extend to 1.5 times the interquartile range of bias values. Figure 3 shows the distribution of bias for all combinations of data-generating K, A, and the absolute difference between G andU (|G − U|). In this figure, the bottom row of panels represents data simulated under the condition that G = U, and thus the boxes in the bottom row represent recovery for when theG = U assumption is met. As Fig. 3 shows, median $\hat {K}$ values are very close to their data-generating values across all conditions, even if the G = U assumption is not met. In other words, if data are generated under the assumption that G is independent of the other parameters, medianK values can be estimated without significant bias by assuming that G = U. Average (mean) estimates, however, are somewhat biased, and bias tends to be negative. Interestingly,K values estimated under Solution 1 tend to be negatively biased whereas K values estimated under Solution 2 tend to be positively biased. Although median $\hat {K}$ is nearly unbiased at all combinations of K, A, G, and U, there are some differences in the variability of $\hat {K}$ across conditions, as shown by the sizes of the conditional box plots. Most prominently, $\hat {K}$ variability increases substantially as the data-generating A decreases from 1.0 to 0.6. In other words, smaller attention values (A) are associated with greater variability in $\hat {K}$ than larger attention values. Figure 4 shows the distribution of bias for all combinations of data-generating K, A, and j, where j is multiplied by the ideal informed guessing rate G_C,S (as described above, if j = 1, then the ideal observer of Solution 2 holds). Consequently, the middle row of panels represents recovery when the ideal observer assumption of Solution 2 holds. Overall, the results displayed in Fig. 4 are similar to those displayed in Fig. 3. Namely, median K estimates are nearly unbiased in most conditions, especially at higher values of A. Moreover, even if the assumption of Solution 2 does not hold exactly, capacity estimates are largely unaffected by this misspecification. Perhaps the most prominent conclusion from both of these simulations is that when a subject does not pay attention on some proportion of trials, it becomes increasingly difficult to reliably estimate working memory capacity because many of the trial responses are the result of inattentiveness. This suggests that researchers should design experiments that maximize person attentiveness when trying to obtain the most accurate estimates of working memory capacity. In other words, although an appropriate model can avoid the problem of lapses of attention leading to an underestimate of the true working memory storage capacity, low attentiveness remains a problem in terms of reliability.

Fig. 3

Conditioning plot of $\hat {K}$ bias ($\hat {K}-K$) for various combinations of data-generating K, A, and the absolute difference between G and U (i.e., |G − U|) values for the canonical change detection task. Each cell represents five levels of K. Data were generated according to the unidentified canonical change detection model. Parameters were estimated under the Solution 1 assumption that G − U, and the bottom row of panels represents simulations for which the Solution 1 assumption holds. The furthest right column of cells displays results for perfect attentional engagement (A = 1), and columns of cells further to the left correspond to lower attentional engagement

Fig. 4

Conditioning plot of $\hat {K}$ bias ($\hat {K}-K$) for various combinations of data-generating K, A, and j values for the canonical change detection task, where j is the factor by which the ideal observer guessing rates G_C,S are multiplied (if j = 1), then the Solution 2 assumption holds. Each cell represents five levels of K. Parameters were estimated under the ideal relationship between set size, capacity, and informed guessing defined by Solution 2. The furthest right column of cells displays results for perfect attentional engagement (A = 1), and columns of cells further to the left correspond to lower attentional engagement

Discussion

The ability to separately assess working memory capacity and attentional engagement is both practically and theoretically important, and change detection tasks can make this possible when combined with appropriate mathematical models. However, the present findings show that the canonical and the multiple change detection tasks are not mathematically identified if these models take attentional capacity into account. Stated plainly, in this model of working memory capacity, widely different estimates of attentional engagement can lead to identical data sets. We have suggested two model identification solutions: the first assumes that the two guessing parameters, G and U, are equal to each other, and the second assumes that informed guessing is a normatively ideal function of uninformed guessing, working memory capacity, and set size. However, neither of these solutions has been supported by empirical evidence, and further research is needed to determine what model identification method is most psychologically plausible. The typical model for the partial report variant of the change detection task is identified because all guessing in this variant is uninformed, eliminating the need to have separate G and U parameters. This variant uses a postcue to indicate which item should be reported. If the cued object is not present in memory, the participant has no information about whether or not that item might have changed, just as a participant has no information about the presence or absence of a change if attention has lapsed. Assuming that this logic is justified, the partial report change detection task is identified and should therefore be used when the goal of the research is to estimate both working memory storage capacity and attentional engagement. Each of the three variants discussed here—the canonical variant, the multiple change variant, and the partial report variant—has advantages and disadvantages that are not captured in the typical mathematical models used to describe task performance. An advantage of the partial report variant is that only one item from the sample array must be compared with the test array, which minimizes contributions from “decision noise” (Vogel et al., 2001). However, the partial report version assumes that participants can completely ignore the uncued items. This assumption may not be true in some groups of participants. In addition, some experiments implement the partial report task by means of a test display that contains only the one item to be compared with memory, and this may lead to difficulty in knowing exactly which item from the sample array corresponds to the one item in the test display (Levillain and Flombaum, 2012). It should also be noted that location binding errors, in which the features are remembered but their locations are lost (Bays, Catalao, & Husain, 2009), will contribute to capacity estimates in the partial report task but should have little or no impact on performance in the multiple change detection task. The role of these bindings is less clear in the canonical change detection task. An advantage of the multiple change detection version is that every trial appears to be equally easy to the participant because the set size is held constant, and the participant has no way of knowing in advance how many items will change. This avoids the possibility that some participants will “give up” on trials with large set sizes, a scenario that would violate the assumption of the existing models that attentional engagement is independent of the set size. Such violations will lead to poor model fit and an underestimation of actual storage capacity (see Rouder et al., 2008). Moreover, participants with low storage capacity should be able to detect changes quite well when most or all of the items change between the sample and test arrays, avoiding the feeling of frequent failure that these participants experience at large set sizes in the canonical and partial report versions of the task. Consequently, the multiple change detection task may yield more accurate estimates of storage capacity in participants who are not highly motivated to maximize their performance, whereas capacity estimates with the other tasks may be distorted by individual differences in effort. Thus, although the mathematical model of the partial report variant makes it possible to separately estimate working memory capacity and attentional engagement, it may involve assumptions about task performance such as equivalent attentional engagement across different set sizes or an ideal observer that may be inappropriate in some studies. As a result, if the main goal of a study is to estimate working memory capacity in a manner that is unbiased by the degree of attentional engagement, and not to estimate attentional engagement per se, the canonical variant or the multiple change variant might be more appropriate than the partial report variant. An alternative to the model identification solutions proposed in this paper is to use tasks that are not variants on change detection. For example, considerable research now uses delayed estimation tasks, in which the participant provides a continuous estimate of the remembered feature value (e.g., by clicking on the corresponding location on a color wheel; see Wilken & Ma, 2004; Zhang & Luck, 2008). These tasks make it easy to create models that capture the precision of the memory representations as well as storage capacity, and models are also available that do not assume a fixed number of discrete representations (van den Berg et al., 2014). However, the existing models of delayed estimation do not take lapses of attention into account, and this would be a useful avenue for future model development.

Conclusions

Presently, there is no perfect means of concurrently assessing working memory capacity and attentional engagement, although considerable progress has been made over the past decade. The issue of lapses of attention was largely ignored prior to the study of Rouder et al., (2008), and several different methods are now available to separately estimate working memory capacity and attentional engagement. Our work has demonstrated that the canonical change detection task and the multiple change detection task cannot be used to estimate attentional engagement. It has also demonstrated that when best practices are used, researchers can use working memory tasks to make reliable inferences about working memory capacity and attentional engagement.

Appendix

In this appendix we provide a formal proof that the multiple change and the canonical change detection models are not identified. Using the notation introduced in the main paper, rewrite (2) as

$$\begin{array}{@{}rcl@{}} P_{C,S} & = & AD_{C,S}+AG-AD_{C,S}G+(1-A)U, \end{array} $$

(A1)

$$\begin{array}{@{}rcl@{}} & = & AD_{C,S}(1-G)+P_{0,S}. \end{array} $$

(A2)

Next, rewrite (3), (4), and (5) as

$$ A=\tilde{A}B, $$

(A3)

$$ G=\frac{B-1+\tilde{G}}{B}, $$

(A4)

and

$$ U=\frac{(1-\tilde{A})\tilde{U}-\tilde{A}B+\tilde{A}}{1-\tilde{A}B}. $$

(A5)

Substituting (A3), (A4), and (A5) into (A1) with C = 0 yields,

$$\begin{array}{@{}rcl@{}} P_{0,S} & = & AG+(1-A)U \end{array} $$

(A6)

$$\begin{array}{@{}rcl@{}} & = & \tilde{A}B\left( \frac{B-1+\tilde{G}}{B}\right)+(1-\tilde{A}B)\frac{(1-\tilde{A})\tilde{U}-\tilde{A}B+\tilde{A}}{1-\tilde{A}B}\\ & = & \tilde{A}(B-1+\tilde{G})+(1-\tilde{A})\tilde{U}-\tilde{A}B+\tilde{A}\\ & = & \tilde{A}\tilde{G}+(1-\tilde{A})\tilde{U}. \end{array} $$

(A7)

Note that Eqs. A6 and A7 have the same mathematical form. This result proves our conjecture that this model is not identified for P_0,S. To show that our conjecture also holds for P_C,S, using the result from Eq. A7, let

$$\begin{array}{@{}rcl@{}} P_{C,S} & = & AD_{C,S}(1-G)+P_{0,S} \end{array} $$

(A8)

$$\begin{array}{@{}rcl@{}} & = & \tilde{A}BD_{C,S}(1-\frac{B-1+\tilde{G}}{B})+P_{0,S}\\ & = & \tilde{A}BD_{C,S}(\frac{1-\tilde{G}}{B})+P_{0,S}\\ & = & \tilde{A}D_{C,S}(1-\tilde{G})+P_{0,S}, \end{array} $$

(A9)

As before, note that Eqs. A8 and A9 have the same mathematical form. Because $\tilde {A}$, $\tilde {G}$, and $\tilde {U}$ do not depend on C, S, or K, this result holds generally for the multiple change and canonical change detection models, regardless of the type of trials or number of replications. This completes our proof: the multiple change and the canonical change detection models are not identified.