Abstract
A novel method for the maximum likelihood estimation of structural equation models (SEM) with both ordinal and continuous indicators is introduced using a flexible multivariate probit model for the ordinal indicators. A full information approach ensures unbiased estimates for data missing at random. Exceeding the capability of prior methods, up to 13 ordinal variables can be included before integration time increases beyond 1 s per row. The method relies on the axiom of conditional probability to split apart the distribution of continuous and ordinal variables. Due to the symmetry of the axiom, two similar methods are available. A simulation study provides evidence that the two similar approaches offer equal accuracy. A further simulation is used to develop a heuristic to automatically select the most computationally efficient approach. Joint ordinal continuous SEM is implemented in OpenMx, free and open-source software.
Similar content being viewed by others
Introduction
In psychology, both continuous and ordinal variables are commonplace. Skin conductance, eye location, and facial muscle position are most naturally recorded as continuous variables. In contrast, survey data from questionnaires that assess, for example, personality characteristics or clinical symptom severity, are most naturally recorded as ordinal or binary responses. Item response theory (IRT) is a popular way of analyzing ordinal data (e.g., Baker & Kim, 2004; Lord, Novick, & Birnbaum, 1968). However, researchers often want to incorporate both ordinal and continuous measures, and then estimate how latent variables relate to other latent variables using a path or structural equation model. Within the IRT framework, some approaches are available (e.g., Cai, 2010), but computational limits preclude models with more than about ten latent variables. Some extensions of regression are available (e.g., Little and Schlucter, 1985), but are limited to categorical (not continuous) latent variables. In contrast, structural equation models (SEM) excel at covariance-based modeling of continuous latent variables (Kline, 2015). However, the best way to incorporate ordinal data into the SEM framework is not obvious.
Ordinal and binary data can be included into SEM models using either Bayesian or frequentist approaches. Bayesian SEM may be the more flexible approach (Muthén & Asparouhov, 2012), but it requires greater computational resources. Here we restrict our scope to frequentist estimation. Weighted least squares (WLS) and maximum likelihood (ML) are two popular approaches to frequentist estimation (Jöreskog & Moustaki, 2001). WLS is much less computationally demanding than ML, especially when the number of measured variables is large. When the data are complete, WLS and ML exhibit identical accuracy (Bradley, 1973). However, in psychology and longitudinal studies generally, it is common for some data to be missing. Missingness can be divided into categories determined by the presumed cause (Rubin, 1976). To review, when missingness does not depend on any of the predictor or response variables then the situation is called missing completely at random (MCAR). When observed variables can account for missingness of other variables then the situation is called missing at random (MAR). Finally, when missingness depends on unobserved or missing variables then the situation is called missing not at random (MNAR).
WLS uses the univariate and bivariate marginals of summary statistics (i.e., means, covariance, and thresholds) as data to fit against the model implied distribution (e.g., Jöreskog, 1990; Lee, Poon, & Bentler, 1992; Muthén, 1984). However, in the presence of missing data, summary statistics of the data are not defined. Hence, data that are missing are typically imputed to obtain complete data and then multivariate normal summaries of the complete data are analyzed with WLS. Parameter estimates from multiple imputations (MI) with different random seeds are typically combined for an accurate assessment of parameter variability (van Stef, 2012).
How well does ML work in comparison to the combination of MI and WLS? A small simulation study will shine some light on this question. Missing data pose no special problem for full-information ML. ML estimates are asymptotically unbiased in both MCAR and MAR situations (e.g., Enders & Bandalos, 2001). MI+WLS should also perform well, but in contrast to ML, MI+WLS is not a fully automatic procedure. Here the MICE package assists with imputation (van Buuren & Groothuis-Oudshoorn, 2011). The analyst must decide on an imputation model, the number of imputations, and the structure of the weight matrix. For the imputation model, at least five options have been studied for ordinal indicators (Wu et al., 2015). However, among these five, MICE only offers the proportional odds model (i.e., method polr). For continuous indicators, we use MICE’s default, predictive mean matching (i.e., method pmm). As for the number of imputations, here we follow the heuristic suggested by Bodner (2008, Table 3). Finally, the weight matrix can be an identity (i.e., ordinary least squares), diagonal, or unrestricted matrix. Here we use a diagonal weight matrix due to its superior performance on small samples (Flora & Curran, 2004).
Our initial foray employs a trivial one parameter model. Suppose we wish to estimate the correlation \(\theta \) between two ordinal variables (i.e., a polychoric correlation) with data missing at random. To keep things simple, means and variance were fixed to standard normal and thresholds fixed to the \(\frac {1}{3}\) and \(\frac {2}{3}\) standard normal quantiles. Sample size was 2000 rows with 90% of indicator #2 set to missing when indicator #1 obtained category 1. Euclidean or \(l^{2}\)-norm was used to summarize results across trials. Using 50 imputations, MI+WLS obtained a bias \(||\mathbb {E}\hat \theta -\theta _{true}||_{2}\) of 1.15 while ML performed slightly better with a bias of 0.87 (see Fig. 1). Given the possible superior accuracy of ML, it is worth exploring efficient ways to incorporate ordinal data into the ML SEM framework.
One line of research has incorporated link functions of the generalized linear model into SEM (e.g., Kirkpatrick & Neale, 2016; Skrondal & Rabe-Hesketh, 2004). Not only can ordinal variables be accommodated, but the analyst may choose from a wide variety of link functions including Poisson, logit, and gamma. However, the generalized linear model approach, by default, makes the assumption that items are conditionally independent. Conditional independence precludes the possibility of correlated error variance between ordinal indicators. This assumption can be relaxed, but at a high computational cost (Hagenaars, 1988). Instead of assuming that items are conditionally independent, a multivariate probit model, with unrestricted variance, can be evaluated using ML (Lee et al., 1990). However, the computational burden for ML increases rapidly with only 3 or 4 latent variables, even with the simplifying assumption of zero residual correlation between ordinal indicators (Asparouhov & Muthén, 2010, p. 13). One way around this performance obstacle is a technique known as item parceling. Averaging groups of 2 or more ordinal items together produces continuous-like indicators (e.g., Matsunaga 2008). When item parcels are entered into a model as continuous indicators, hundreds of latent variables can be accommodated without a heavy computational burden. However, many researchers have cautioned that parceling adds nuisance variability (e.g., Nasser & Wisenbaker, 2003; Sterba & MacCallum, 2010).
Here we introduce a novel method for the ML estimator that offers better performance than existing methods. Similar to (Lee et al., 1990), ordinal variables are modeled by the multivariate probit distribution. Covariances with other ordinal or continuous variables are unrestricted. As an ML family model, the usual asymptotic results provide for standard errors (Wald, 1943) and the likelihood ratio test (Wilks, 1938). Performance is limited by the number of ordinal variables, not by the number of continuous observed or latent variables.
The method partitions the ordinal and continuous parts of the Gaussian distribution by conditioning one on the other (Aitken, 1935). It is currently implemented for up to about 20 ordinal variables in the structural equation modeling program OpenMx (Neale et al., 2016). The paper is organized as follows: in Methods we provide the mathematical background for our approach and describe two different approaches to joint likelihood computation. We next provide a simulation study comparing the Accuracy of the two approaches, propose A Heuristic to select the most computationally efficient approach, and provide an Example of use in a real data set. Finally, we detail the performance characteristics of the method and describe our approach to take advantage of parallel processing for Rapid Evaluation of Large Data Sets. Complete scripts to reproduce the analyses contained in this paper are available at https://osf.io/3qat8/.
Methods
The authors are not aware of a computationally efficient way to directly evaluate the multivariate Gaussian likelihood of ordinal and continuous indicators together. However, the likelihood can be broken apart by the axiom of conditional probability, \(P(A\cap B) = P(A)P(B|A)\). In particular,
The expressions \(P(\text {continuous})\) and \(P(\text {ordinal})\) are well documented in the literature and will be summarized below. To obtain the conditional distributions, \(P(\text {continuous}|\text {ordinal})\) and \(P(\text {ordinal}|\text {continuous})\), we review the multivariate Gaussian selection formulae. Our initial presentation of the formulae will be abstract and then we will detail its application for each conditional distribution.
Let the \(n \times n\) covariance matrix R be partitioned into non-empty, disjoint sets p and q. Let \(R_{ij}\) denote the covariance matrix between the p and q variables where the subscripts denote the variable subsets (e.g. \(R_{pq}\)). Let column vectors \(\mu _{p}\) and \(\mu _{q}\) contain the means of p and q variables, respectively. We wish to compute the conditional covariances of the variables in q for a subset of the population where \(R_{pp}\) and \(\mu _{p}\) are known (or partially known)—that is, we wish to condition the covariances and means of q on those of p. Let \(V_{pp}\) be an arbitrary covariance matrix of the same dimension as \(R_{pp}\). By the selection formulae (Aitken, 1935), if we replace \(R_{pp}\) by \(V_{pp}\) then the mean of q is transformed as
and the covariance of p and q are transformed as

If p and q are chosen such that each represents either only ordinal or continuous indicators, the same likelihood is obtained using either Eqs. 1 or 2. However, one or the other approach is more computationally efficient depending on the number of unique ordinal patterns per rows of data and the number of continuous variables. Therefore, both approaches deserve examination. The expressions \(P(\text {continuous})\) and \(P(\text {ordinal})\) are likelihoods that are well documented in the literature (see Ferron & Hess, 2007; Lee, Poon, & Bentler, 1990, respectively). These likelihoods are usually based on the multivariate normal probability density function, or integrals thereof in the case of ordinal data. We provide concise reviews of the \(P(\text {continuous})\) and \(P(\text {ordinal})\) cases and then detail how to obtain and evaluate the conditional distributions.
A few more details bear mention. In all cases, missing data are easily accommodated by omission of the missing variables from the model implied distribution on a per-row basis. Then at the end of optimization, no special treatment is needed to obtain the parameter covariance matrix. The standard estimators for exponential models are available. The Hessian, numerically approximated using Richardson extrapolation, is used by default in OpenMx.
P(continuous)
Let \({\Sigma }\) and \(\mu \) be the model implied covariance and mean column vector, respectively. Assuming that these variables follow a multivariate normal distribution, the likelihood of a vector of m continuous observed variables y is the multivariate Gaussian density function,
P(ordinal)
In this approach, an ordinal variable is considered to measure an underlying normal distribution. Ordinal category labels are assigned to different portions of the distribution based on a probit model with specific thresholds \(\tau \), such that a value falling between the \(k^{th}\) and \((k + 1)^{th}\) threshold is assigned the \(k^{th}\) ordinal category. To evaluate the multivariate probit likelihood of n ordinal data y, we therefore require thresholds \(\tau \) in addition to the model implied mean vector \(\mu \) and covariance \({\Sigma }\). To evaluate the likelihood, the covariance may be decomposed into a correlation matrix \({\Omega }\) and vector of standard deviations \(\sigma \),
As a matter of expediency, the thresholds for all variables are stored together in a single matrix, in category \(\times \) item order. Since each indicator may have a different number of outcome categories, and consequently, a different number of thresholds, some of the entries in the matrix may be unused. For brevity, columns are indexed with a dot when an expression is intended to apply to all items. For an indicator with C response categories \((c = 0, \dots , C-1)\), at most \(C-1\) thresholds can be freely estimated. Thresholds \(\tau _{.,0}\) and \(\tau _{.,C}\) are fixed to \(-\infty \) and \(\infty \), respectively. Thresholds must be strictly ordered such that \(\tau _{.,j} < \tau _{.,k}\) when \(j<k\).
An adjacent pair of thresholds are used as integration limits, after being standardized. For example, if the observed response \(y_{1}\) is 0 then the integration limits \(a_{1}\) and \(b_{1}\) are \(\frac {\tau _{1,0}-\mu _{1}}{\sigma _{1}}\) and \(\frac {\tau _{1,1}-\mu _{1}}{\sigma _{1}}\), respectively. Similarly, if \(y_{2}\) is 2 then the integration limits \(a_{2}\) and \(b_{2}\) are \(\frac {\tau _{2,2}-\mu _{2}}{\sigma _{2}}\) and \(\frac {\tau _{2,3}-\mu _{2}}{\sigma _{2}}\), respectively. The likelihood of response pattern y is
where \({\Phi }\) is the multivariate Gaussian density function. Conceptually, Eq. 9 finds the area under the curve (or hyper-surface) within the region delimited by the thresholds along each dimension. Refer to (Mehta et al., 2004) for a more elaborate and gentle introduction to this procedure. Evaluation of the ordinal likelihood (9) requires computation that is exponential in the number of ordinal variables (Fig. 2; Genz, 1992).
P(ordinal|continuous)
Let y be one row of observed measures. Let \({\Sigma }\) and \(\mu \) be the model implied covariance matrix and mean, respectively. Subscripts o and c are used to indicate the ordinal and continuous parts of these objects, respectively. \(L(y_{c})\) is the multivariate Gaussian density (6) evaluated with \(y_{c}\), \(\mu _{c}\), and \({\Sigma }_{cc}\). We evaluate \(L(y_{c})\) and then condition the ordinal distribution using the selection formulae to obtain \(L(y_{o}|y_{c})\). We partition \({\Sigma }\) as,

To condition on the continuous distribution and obtain the conditional ordinal distribution, Eqs. 3 and 4 are applied with p set to continuous and q set to ordinal,
In this case, we consider the process to be selecting from the multivariate normal distribution only those cases where \(y_{c}\) is precisely equal to the values of the continuous indicators actually observed in the data for a given measurement. Since we know these values precisely, we consider them to have zero variance and covariance. We therefore set the matrix \(V_{pp}\) in Eq. 4 to zero. The likelihood of the row may then be evaluated. \(L(y_{o}|y_{c})\) is the multivariate probit (9) evaluated with \(y_{o}\), \(\mu _{o}^{\prime }\), Σoo′, and \(\tau \). Finally, the joint likelihood is the product \(L(y_{c}) L(y_{o}|y_{c})\).
P(continuous|ordinal)
In some cases, it may be more efficient to compute the likelihood of the continuous values conditioned on the ordinal likelihood instead of the other way around. \(L(y_{o})\) is the multivariate probit (9) evaluated with \(y_{o}\), \(\mu _{o}\), \({\Sigma }_{oo}\), and \(\tau \). We evaluate \(L(y_{o})\) and then condition the continuous distribution using the selection formulae to obtain \(L(y_{c}|y_{o})\). In contrast to the P(ordinal|continuous) case, we do not know the precise latent value described by ordinal observation \(y_{o}\), and therefore cannot set the matrix \(V_{pp}\) in Eq. 4 to zero. Instead, \(V_{pp}\) is set to reflect the variation remaining after conditioning on \(y_{o}\).
The conditioning procedure for \(V_{pp}\) may be illustrated with an example using R,


Suppose we have a two-dimensional covariance matrix (line 1). Let us sample some observations (line 2). Given the categories selected by ordinal data, we set thresholds for each ordinal variable (lines 3 and 4). Only observations within the region described by the thresholds are retained (line 5). The resulting covariance matrix (line 7) is known as the truncated distribution. The same truncated distribution, including the truncated mean, can be obtained more efficiently using a lengthy mathematical procedure (line 8) fully described elsewhere (Manjunath & Wilhelm, 2012; Wilhelm & Manjunath, 2015; Neale & et al. 1989). Of particular interest here is the fact that evaluating the truncated multivariate normal distribution is a computationally intensive procedure. Numerical integration (similar to Eq. 9) is required to obtain each entry of the mean vector and off-diagonal entry of the covariance matrix.
To condition on the ordinal distribution and obtain the conditional continuous distribution, we truncate \(\mu _o\) and \({\Sigma }_{oo}\) respect to \(y_o\). Let the truncated result be \(\mu _t\) and \({\Sigma }_{tt}\), respectively, and apply Eqs. 3 and 4 with p set to ordinal and q set to continuous,
Note that the vector \(\mu _t\) was already centered with respect to \(\mu _o\) when the thresholds were standardized. As before, the likelihood of the row may then be evaluated. \(L(y_c|y_o)\) is the multivariate Gaussian density (6) evaluated with \(y_c\), \(\mu _c^{\prime }\), and \({\Sigma }_{cc}^{\prime }\). Finally, the joint likelihood is the product \(L(y_o) L(y_c|y_o)\).
Simulation
Accuracy
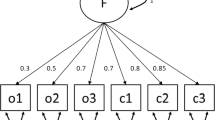
A simulation study was conducted to compare the accuracy of the parameter estimates when conditioning on the continuous or ordinal indicators. Data were simulated and parameters recovered from a single factor model as shown in Fig. 3. For data generation, ordinal thresholds were set to the \(\frac {1}{3}\) and \(\frac {2}{3}\) standard normal quantiles. For the small model with 15 parameters and approximately 5 degrees of freedom, ordinal and continuous loadings were set to 0.77, 0.87, 1.07, 1.41, 0.7; continuous means to \(-\)0.32, 0.19, \(-\)0.12; and continuous residual variances to 3.57, 1.51, 0.21. For the large model with 27 parameters and approximately 27 degrees of freedom (similar to Fig. 3 except with more indicators), ordinal and continuous loadings were set to 0.77, 0.87, 1.07, 1.41, 0.7, 1.4, 1.44, 1.16, 1.13; continuous means to \(-\)0.29, 0.15, \(-\)0.37, \(-\)0.23, \(-\)0.11, \(-\)0.49; and continuous residual variances to 0.21, 0.4, 0.74, 0.99, 11.07, 2.15. After complete data were generated, indicators other than \(o1\), \(c1\), and \(c2\) were set missing when the linear combination \(1_{(o1 = 3)} + c1 + c2\) was greater than 1. On average, this resulted in \(16.49\%\) missing data in the small model and \(25.01\%\) in the large model.
Small factor model used in parameter recovery simulation study. The latent factor G and ordinal indicators (o1, o2) variances were fixed to standard normal. Means and variances of continuous indicators (c1, c2, and c3) were estimated. Ordinal indicators had three possible outcomes; the two thresholds were estimated. The large model was similar in structure except with three ordinal and six continuous indicators
Monte Carlo bias and variance of estimates were assessed from 500 replications. Results are summarized in Table 1 and detailed per parameter bias is given for the small model with a sample size of 250 in Fig. 4. It is not surprising that ML-based estimators perform well when missingness is determined by a linear combination of the observed data. The advantage of ML over MI+WLS would likely be narrower in practice with non-simulated data.
A heuristic
While both ways to evaluate the joint likelihood, \(P(\text {ordinal}) P(\text {continuous}|\text {ordinal})\) and \(P(\text {continuous})\)P(ordinal|continuous), are mathematically equivalent and describe the same function, for a particular data set, one approach is quicker to evaluate than the other. A simulation study was conducted to determine when each conditioning approach would be the most efficient. When there are few continuous variables, the numerical integration for ordinal variables is the clear performance bottleneck. Data were generated using a single latent factor model with 1, 36, and 100 continuous indicators; 250, 1000, 2500, and 10000 rows; and a nearly continuous spectrum of unique ordinal patterns from 2 to 835. An average rowsPerOrdinalPattern was computed once per data set. To obtain accurate elapsed times, the likelihood function was evaluated 3 times per condition, alternating between conditioning on the continuous or ordinal variables, and the median taken. All computations were done on a single CPU core.
These predictors were input into a logistic regression. The regression obtained was,
Sample size was not a statistically significant predictor. This regression correctly predicted the faster conditioning strategy in 94% of the trials. The user retains the option to specify whether to condition on the continuous or ordinal variables, but OpenMx uses this regression equation as the default choice heuristic. If selecting manually, a simplified approximation can be used. In a model with fewer than 50 continuous indicators, if each ordinal pattern appears at least ten times in the data, ordinal conditioning will likely be faster.
Example
The National Youth Survey (NYS; Elliott, 2008), a probability sample of households in the continental United States, tracked the development of 1,725 adolescents with in-depth questionnaires. Using NYS data, Duncan et al., (2001) examined the development of problem behavior in a family’s youngest adolescent (N = 770). The distribution of ages at the beginning of the study (Wave 1) were 245, 218, 167, and 140 for 11–14-year-olds, respectively. The analyses encompassed the first 5 years of data, during which the families were assessed annually in a cohort-sequential design. At each age, a problem behavior latent factor was defined in terms of self-reported alcohol and marijuana use, deviant behavior, and academic failure. Thereafter, a latent growth curve was built across ages to assess change over time. The slope of the curve was of primary substantive interest. Here we reanalyzed these data with some minor changes.
Duncan et al., (2001) described an alcohol indicator scored on a six-point scale ranging from 0 (never) to 5 (more than once a day). Such an indicator is indeed present in Wave 1 of these data, but in Wave 2 and later, the alcohol items are replaced by more specific items about beer, wine, and hard liquor. Here we chose to retain the beer item from Waves 2-5 and set beer missing in Wave 1. The other indicators were present in all waves. Marijuana use was scored the same as beer. The deviant behavior indicator was a parcel comprised of the maximum score of four items (running away, lying about age, skipping school, and sexual intercourse), each scored on a scale from 1 (never) to 9 (2-3 times a day). Academic failure was scored on a five-point scale ranging from 1 (mostly As) to 5 (mostly Fs).
The factor model and growth curve structures were also modified slightly. In Duncan et al., (2001), the problem behavior variance was set to the alcohol indicator variance. This causes the variances of the other indicators to be estimated relative to the alcohol variance. We felt this design unnecessarily colored the parameters with an alcohol interpretation, and instead, fixed the problem behavior variance to 1.0 and estimated the indicator variances. Both formulations of the model involve the same number of parameters, but we find the latter model easier to interpret. Duncan et al., (2001) placed the zero loading for the latent slope on Age 11. This makes the sign of the slope depend on the level at age 11 compared with the mean of the other ages. In contrast, we placed the zero loading on age 14. There is much more data available at age 14 compared to age 11, providing more power to estimate the slope without changing the number of parameters. In summary, our model resembles Fig. 1 from Duncan et al., (2001) with three changes: (a) alcohol is replaced by beer, (b) the variance of age is standardized instead of set to the variance of alcohol, and (c) slope is centered at age 14 instead of age 11.
Our 17 parameter model obtained a log likelihood of \(-20885.06\). Factor loadings from latent problem behavior to indicators correlated at 1 with the loadings published in Duncan et al., (2001). The growth curve mean slope was 0.83 with variance 0.81. However, this model treated ordinal data as continuous. Given that these items have 5 categories or more, this is permissible only when the distribution of data is symmetric (Rhemtulla et al., 2012). Skew of indicators were 2.46, 2.1, 0.95, and \(-0.33\) for marijuana, deviance, beer, and academic failure, respectively. Therefore, we decided to try a model that treated marijuana and deviance as ordinal.
Although adolescent ages spanned from 11 to 18 years old, no adolescent had more than 5 years of data. Hence, the maximum number of non-missing ordinal variables per row was 10 (instead of 18). A small number of ordinal variables per row is important to maintain adequate integration accuracy (9). For comparison, we also fit a time variant model, corresponding to the second model in Duncan et al., (2001). A comparison of these models is exhibited in Table 2. With such dramatically improved fit, the ordinal model offers more power to accurately estimate growth curve coefficients. Mean slope was 1.4 with variance 0.9. Factor loadings from latent problem behavior to indicators changed little, obtaining a correlation of 0.98 with the loadings published in Duncan et al., (2001). Thresholds are exhibited in Fig. 5.
The same ordinal model could be fit using multiple imputation and WLS. However, modest extensions such as latent classes or per participant measurement occasions would require maximum likelihood. For example, latent classes might be appropriate if we suspected that there were two kinds of adolescents, those who exhibit stable problem behavior (slope = 0) and those who exhibit growth (slope > 0). However, in these data, the slope factor scores appear normally distributed. Per participant measurement occasions would be appropriate if interviews were unevenly spaced out across individuals. Measurement at irregular intervals can be a powerful technique to assess temporal trends, but require more sophisticated modeling (e.g., Driver, Oud, & Voelkle, 2017; Mehta & West, 2000).
Rapid evaluation of large datasets
When rows are sorted appropriately, intermediate results required to evaluate the previous row can often be reused in the current row. For example, when conditioning on the continuous indicators and the missingness pattern is the same, then the inverse of the continuous variables’ covariance matrix and the ordinal covariance conditioned on the continuous covariance (11) can be reused. A great deal of computation can be saved. The savings can be even greater when conditioning on the ordinal indicators. When the responses to the ordinal variables are the same as those in the previous row then the ordinal likelihood \(L(y_o)\) (9) and truncated ordinal distribution \(\mathcal N(\mu _t,{\Sigma }_{tt})\) can be reused, avoiding expensive numerical integrations. Since the likelihood function is often evaluated many times during optimization, row sorting and comparisons between adjacent rows can be carried out once in time asymptotically proportional to \(n\log n\) for n rows of data and applied throughout optimization.
To improve performance further, OpenMx implements support for multi-threaded, shared memory parallelism. Rows of data are partitioned into a number of contiguous ranges that match the number of available threads. Ranges are evaluated in parallel. Several factors limit the efficiency of parallel evaluation. Parallel evaluation is only faster than serial evaluation on large datasets because of the operating system overhead involved in starting and managing threads. In addition, some sharing of intermediate calculations across rows is prevented because threads cannot share data with other threads without the use of costly synchronization primitives. Finally, all threads must finish before the total likelihood value can be computed. If some threads finish early and sit idle then the potential capability of the hardware is not fully realized.
Some of these limitations, such as operating system overhead, are unavoidable. However, we implement an adaptive heuristic to help balance the work among threads. Each thread records its execution time in nanoseconds during each set of likelihood evaluations. Thread elapsed time is estimated by the median of measurements made during the most recent five likelihood evaluations. The elapsed time of the fastest \(t_f\) and slowest \(t_s\) threads are identified. An imbalance estimate i may be computed as
with damping factor d set to 5. Proportion i of the slower thread’s rows are reallocated to the faster thread. Work is only moved once from the slowest to the fastest thread because different rows are allocated across all threads necessitating further measurement. A damping factor of five seems to allow gross imbalances to be addressed while minimizing adjustment oscillation.
A study was conducted to demonstrate the efficacy of multi-threaded evaluation. One hundred thousand rows were simulated from a single factor model with six ordinal and four continuous indicators. The number of ordinal categories was set to obtain about 12 rows per unique ordinal pattern. This dataset was evaluated conditioning on ordinal or continuous variables using 1–8 CPUs. Each of the conditioning \(\times \) CPU conditions were evaluated three times and the median elapsed time taken. To give an opportunity for the adaptive load balancing to take effect, each logical evaluation actually consisted of 176 function evaluations. Results are exhibited in Fig. 6.
Reduction in function evaluation elapsed time by number of CPUs (a) and the same data rescaled to times faster with a gray stripe showing ideal linear scaling (b) for 100,000 rows of six ordinal and four continuous indicators. Conditioning on ordinal indicators does not scale as well as continuous because larger granularity work units make the work more difficult to balance across threads. Measurements were done on an Intel Xeon X5647 2.93GHz CPU running GNU/Linux 2.6.32 with ample RAM
Discussion
We introduce a new approach to incorporate ordinal data in structural equation models estimated using maximum likelihood. Covariances between indicators are unrestricted. Our approach accommodates 13 ordinal indicators before integration time increases beyond 1 s per row. Two ways to evaluate the likelihood are identified. Using the axiom of conditional probability, the ordinal indicators can be conditioned on the continuous indicators or vice versa. Both approaches offer nearly equal accuracy, but differ in CPU performance, which mainly depends on the number of rows per unique ordinal pattern. Rapid evaluation of large datasets is facilitated in OpenMx by an implementation of multi-threaded, shared memory parallelism. We now discuss a number of limitations and potential extensions.
Here we assume a multivariate probit distribution for ordinal indicators. An extension to Student’s t distribution seems feasible (e.g., Zhang et al. 2013). However, it is not clear how to allow other distributions commonly applied to categorical data (e.g., Poisson, gamma, or beta) without restriction of the covariance structure. The Pearson–Aitken selection formulae do not require multivariate normality, but do require multivariate linearity and homoscedasticity, to which our conditional probability approach seems limited.
The numerical integration for the ordinal likelihood (9) is often the computational bottleneck in models with more than a few ordinal indicators. OpenMx currently uses integration code that is about 25 years old (Genz, 1992). Faster, higher accuracy code may have been developed since then. To reduce integration time, advantage might be taken of special purpose hardware (graphics processing units, field-programmable gate arrays, or hardware accelerators) (e.g., KruŻel & Banaś, 2013). Work along these lines could increase the practical limit on the number of ordinal indicators to up 20 and, perhaps, beyond.
OpenMx currently uses Broyden family optimizers (Broyden, 1965) with a gradient approximated by finite differences (Gilbert and Varadhan, 2012; Richardson, 1911). Instead of numerical approximation, the gradient could be more quickly and accurately obtained using analytic derivatives or automatic differentiation (e.g., Griewank, 1989). More accurate derivatives would also contribute to more accurate standard errors. However, the flexibility of OpenMx’s modeling interface, which permits user-specified matrix algebras for the expected means, thresholds, and covariances, would require symbolic matrix calculus algorithms to be developed for a general implementation. Implementation of derivatives for certain fixed algebra specifications (e.g., RAM; Oertzen & Brick, 2014) would be more straightforward.
The heuristic used here (17) obtained by logistic regression does not always select the fastest approach. A more robust test would be to time both evaluation approaches and select the one that is empirically faster on the particular model and data. In many cases, the small additional cost to set up and test both conditioning schemes (instead of blindly following the heuristic) would pay off in reduced total optimization time. In the current implementation, the choice of conditioning approach can only be made for an entire data set or by manually partitioning the data into groups. However, it might be worth investigating a mode of operation where the choice of conditioning approach is automatically made on a per ordinal pattern basis. This approach may perform better if the number of rows per ordinal pattern varies substantially.
At the time of writing, multi-threaded, shared memory parallelism is available in OpenMx on GNU/Linux and Mac OS/X, but not on Microsoft’s Windows operating system. Little can be done until OpenMP is supported by the Rtools for Windows project.Footnote 1 Until then, those who wish to take advantage of multiple CPUs will need to select a supported operating system.
Here we assume that rows of data are independent. This need not be the case with multilevel data. For example, if measurements of students and characteristics of teachers are available then the students are conditionally independent given a teacher. Crossed multilevel structures can involve even more entangled dependency relationships. For example, a single student may have membership in a number of classrooms. We do not consider data with such complex dependence relationships here, but leave them as future work.
With a more efficient approach to evaluating models that combine continuous and ordinal indicators, modeling options are expanded. Researchers have more scope to include ordinal indicators in their data collection and analysis. We hope this will lead to new, innovative designs that accelerate scientific progress.
References
Aitken, A. C. (1935). Note on selection from a multivariate normal population. In Proceedings of the Edinburgh Mathematical Society (series 2) 4.2 (pp. 106–110). https://doi.org/10.1017/S0013091500008063
Asparouhov, T., & Muthén, B. (2010). Bayesian analysis of latent variable models using Mplus. Retrieved November 1, 2016 from http://statmodel.com/download/BayesAdvantages6.pdf
Baker, F. B., & Kim, S. H. (2004) Item Response Theory: Parameter Estimation Techniques. 2nd. Boca Raton: CRC Press.
Bodner, T. E. (2008). What improves with increased missing data imputations? In Structural Equation Modeling 15.4 (pp. 65–675). https://doi.org/10.1080/10705510802339072
Bradley, E. L. (1973). The equivalence of maximum likelihood and weighted least squares estimates in the exponential family. In Journal of the American Statistical Association 68.341 (pp. 199–200).
Broyden, C. G. (1965). A class of methods for solving nonlinear simultaneous equations. In Mathematics of Computation 19.92 (pp. 577–593). https://doi.org/10.2307/2003941
van Stef, B. (2012) Flexible imputation of missing data. Boca Raton: CRC Press.
Cai, L. (2010). High-dimensional exploratory item factor analysis by a Metropolis–Hastings Robbins–Monro algorithm. In Psychometrika 75.1 (pp. 33–57). https://doi.org/10.1007/s11336-009-9136-x
Driver, C. C., Oud, J. H. L., & Voelkle, M. C. (2017). Continuous time structural equation modeling with R Package ctsem. In Journal of Statistical Software 77.5 (pp. 1–35). https://doi.org/10.18637/jss.v077.i05
Duncan, S. C., Duncan, T. E., & Strycker, L. A. (2001). Qualitative and quantitative shifts in adolescent problem behavior development: a cohort-sequential multivariate latent growth modeling approach. In Journal of Psychopathology and Behavioral Assessment 23.1 (pp. 43–50). https://doi.org/10.1023/A:1011091523808
Elliott, D. (2008). National Youth Survey [United States]: Waves I-V, 1976-1980. Inter-university Consortium for Political and Social Research (ICPSR) [distributor]. https://doi.org/10.3886/ICPSR08375.v2
Enders, C. K., & Bandalos, D. L. (2001). The relative performance of full information maximum likelihood estimation for missing data in structural equation models. In Structural Equation Modeling 8.3 (pp. 430–457). https://doi.org/10.1207/S15328007SEM0803_5
Ferron, J. M., & Hess, M. R. (2007). Estimation in SEM: a concrete example. In Journal of Educational and Behavioral Statistics 32.1 (pp. 110–120). https://doi.org/10.3102/1076998606298025
Flora, D. B., & Curran, P. J. (2004). An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. In Psychological Methods 9.4 (pp. 466-491). https://doi.org/10.1037/1082-989X.9.4.466
Genz, A. (1992). Numerical computation of multivariate normal probabilities. In Journal of Computational and Graphical Statistics 1.2 (pp. 141–149). https://doi.org/10.1080/10618600.1992.10477010
Gilbert, P., & Varadhan, R. (2012). numDeriv: accurate Numerical Derivatives. R package version 2012.9-1. http://CRAN.R-project.org/package=numDeriv
Griewank, A. (1989). On automatic differentiation. In Mathematical Programming: Recent Developments and Applications 6.6 (pp. 83–107).
Hagenaars, J. A. (1988). Latent structure models with direct effects between indicators local dependence models. In Sociological Methods & Research 16.3 (pp. 379–405). https://doi.org/10.1177/0049124188016003002
Jöreskog, K. G. (1990). New developments in LISREL: analysis of ordinal variables using polychoric correlations and weighted least squares. In Quality & Quantity 24.4 (pp. 387–404). https://doi.org/10.1007/BF00152012
Jöreskog, K. G., & Moustaki, I. (2001). Factor analysis of ordinal variables: a comparison of three approaches. In Multivariate Behavioral Research 36.3 (pp. 347–387). https://doi.org/10.1207/S15327906347-387
Kirkpatrick, R. M., & Neale, M. C. (2016). Applying multivariate discrete distributions to genetically informative count data. In Behavior Genetics 46.2 (pp. 252–268). https://doi.org/10.1007/s10519-015-9757-z
Kline, R. B. (2015) Principles and practice of structural equation modeling. New York: The Guilford Press.
KruŻel, F., & Banaś, K. (2013). Vectorized openCL implementation of numerical integration for higher-order finite elements. In Computers & Mathematics with Applications 66.10 (pp. 2030–2044). https://doi.org/10.1016/j.camwa.2013.08.026
Lee, S. -Y., Poon, W. -Y., & Bentler, P. M. (1990). Full maximum likelihood analysis of structural equation models with polytomous variables. In Statistics & Probability Letters 9.1 (pp. 91–97). https://doi.org/10.1016/0167-7152(90)90100-L
Lee, S. -Y., Poon, W. -Y., & Bentler, P. M. (1992). Structural equation models with continuous and polytomous variables. In Psychometrika 57.1 (pp. 89–105). https://doi.org/10.1007/BF02294660
Little, R. J. A., & Schlucter, M. D. (1985). Maximum likelihood estimation for mixed continuous and categorical data with missing values. In Biometrika 72.3 (pp. 497–512). https://doi.org/10.1093/biomet/72.3.497
Lord, F. M., Novick, M. R., & Birnbaum, A. (1968) Statistical theories of mental test scores. Oxford: Addison-Wesley.
Manjunath, G. B., & Wilhelm, S. (2012). Moments Calculation For the Doubly Truncated Multivariate Normal Density. arXiv:1206.5387[stat.CO].
Matsunaga, M. (2008). Item parceling in structural equation modeling: a primer. In Communication Methods and Measures 2.4 (pp. 260– 293). https://doi.org/10.1080/19312450802458935
Mehta, P. D., Neale, M. C., & Flay, B. R. (2004). Squeezing interval change from ordinal panel data: Latent growth curves with ordinal outcomes. In Psychological Methods 9.3 (p. 301). https://doi.org/10.1037/1082-989X.9.3.301
Mehta, P. D., & West, S. G. (2000). Putting the individual back into individual growth curves. In Psychological Methods 5.1 (p. 23). https://doi.org/10.1037/1082-989X.5.1.23
Muthén, B. (1984). A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. In Psychometrika 49.1 (pp. 115–132). https://doi.org/10.1007/BF02294210
Muthén, B., & Asparouhov, T. (2012). Bayesian structural equation modeling: a more flexible representation of substantive theory. In Psychological Methods 17.3 (pp. 313–335). https://doi.org/10.1037/a0026802
Nasser, F., & Wisenbaker, J. (2003). A Monte Carlo study investigating the impact of item parceling on measures of fit in confirmatory factor analysis. In Educational and Psychological Measurement 63.5 (pp. 729–757). https://doi.org/10.1177/0013164403258228
Neale, M. C., et al. (1989). Bias in correlations from selected samples of relatives: the effects of soft selection. In Behavior Genetics 19.2 (pp. 163–169). https://doi.org/10.1007/BF01065901
Neale, M. C., et al. (2016). OpenMx 2.0: extended structural equation and statistical modeling. In Psychometrika 81.2 (pp. 535–549). https://doi.org/10.1007/s11336-014-9435-8
von Oertzen, T., & Brick, T. R. (2014). Efficient Hessian computation using sparse matrix derivatives in RAM notation. In Behavior Research Methods 46.2 (pp. 385–395). https://doi.org/10.3758/s13428-013-0384-4
Rhemtulla, M., Brosseau-Liard, P. É., & Savalei, V. (2012). When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. In Psychological Methods 17.3 (pp. 354– 373). https://doi.org/10.1037/a0029315
Richardson, L. F. (1911). The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. In Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character (Vol. 210, pp. 307–357). https://doi.org/10.1098/rsta.1911.0009
Rubin, D. B. (1976). Inference and missing data. In Biometrika 63.3 (pp. 581–592). https://doi.org/10.2307/2335739
Anders, S., & Rabe-Hesketh, S. (2004) Generalized latent variable modeling: multilevel, longitudinal, and structural equation models. Boca Raton: CRC Press.
Sterba, S. K., & MacCallum, R. C. (2010). Variability in parameter estimates and model fit across repeated allocations of items to parcels. In Multivariate Behavioral Research 45.2 (pp. 322–358). https://doi.org/10.1080/00273171003680302
van Buuren, S., & Groothuis-Oudshoorn, K. (2011). mice: multivariate imputation by chained equations in R. In Journal of Statistical Software 45.3 (pp. 1–67). http://www.jstatsoft.org/v45/i03/
Wald, A. (1943). Tests of statistical hypotheses concerning several parameters when the number of observations is large. In Transactions of the American Mathematical Society 54.3 (pp. 426–482). https://doi.org/10.2307/1990256
Wilhelm, S., & Manjunath, G. B. (2015). tmvtnorm: truncated Multivariate Normal and Student t Distribution. R package version 1.4-10. http://CRAN.R-project.org/package=tmvtnorm
Wilks, S. S. (1938). The large-sample distribution of the likelihood ratio for testing composite hypotheses. In The Annals of Mathematical Statistics 9.1 (pp. 60–62).
Wu, W., Jia, F., & Enders, C. (2015). A comparison of imputation strategies for ordinal missing data on Likert scale variables. In Multivariate Behavioral Research 50.5 (pp. 484–503). https://doi.org/10.1080/00273171.2015.1022644
Zhang, Z., et al. (2013). Bayesian inference and application of robust growth curve models using Student’s t distribution. In Structural Equation Modeling: a Multidisciplinary Journal 20.1 (pp. 47–78). https://doi.org/10.1080/10705511.2013.742382
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported in part by National Institute of Health grants R01-DA018673 and R25-DA026119 (PI Neale), R01-DA022989 (PI Boker), and by the Center for Lifespan Psychology at the Max Planck Institute for Human Development. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Institutes of Health. J.P. and T.B. contributed equally.
Rights and permissions
About this article
Cite this article
Pritikin, J.N., Brick, T.R. & Neale, M.C. Multivariate normal maximum likelihood with both ordinal and continuous variables, and data missing at random. Behav Res 50, 490–500 (2018). https://doi.org/10.3758/s13428-017-1011-6
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13428-017-1011-6