Abstract
Semantic feature norms (e.g., STIMULUS: car → RESPONSE: <has four wheels>) are commonly used in cognitive psychology to look into salient aspects of given concepts. Semantic features are typically collected in experimental settings and then manually annotated by the researchers into feature types (e.g., perceptual features, taxonomic features, etc.) by means of content analyses—that is, by using taxonomies of feature types and having independent coders perform the annotation task. However, the ways in which such content analyses are typically performed and reported are not consistent across the literature. This constitutes a serious methodological problem that might undermine the theoretical claims based on such annotations. In this study, we first offer a review of some of the released datasets of annotated semantic feature norms and the related taxonomies used for content analysis. We then provide theoretical and methodological insights in relation to the content analysis methodology. Finally, we apply content analysis to a new dataset of semantic features and show how the method should be applied in order to deliver reliable annotations and replicable coding schemes. We tackle the following issues: (1) taxonomy structure, (2) the description of categories, (3) coder training, and (4) sustainability of the coding scheme—that is, comparison of the annotations provided by trained versus novice coders. The outcomes of the project are threefold: We provide methodological guidelines for semantic feature classification; we provide a revised and adapted taxonomy that can (arguably) be applied to both concrete and abstract concepts; and we provide a dataset of annotated semantic feature norms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
The reliability of data annotations is often overlooked and is not discussed in several studies involving content analyses and coding tasks (Krippendorff, 2004). This is also the case for linguistic data, in which not all annotation projects include formal tests of intercoder agreements (Artstein & Poesio, 2008). We show how this phenomenon also applies to psychological data, such as the linguistic data collected within the semantic feature norms paradigm. With this contribution we aim to provide guidelines to remedy this methodological gap, specifically in relation to the annotation of semantic feature norms.
Semantic feature norms are data collected in order to address the following question: What are concepts made of? Among the different accounts of semantic memory structure and processes proposed in the literature (for an extensive review of different models of semantic memory, see Jones et al., 2015; McRae & Jones, 2013), the featural view is one of the most popular (see for example Murphy, 2002). A well-established paradigm since the 1970s, the featural view was first introduced to make predictions about semantic categorizations in time-constrained tasks (Smith, Shoben, & Rips, 1974). A few years later the same paradigm was used to investigate the structure of semantic categories and conceptual representations based on prototype theories, as well as the notion of family resemblanceFootnote 1 (see, e.g., Medin & Schaffer, 1978; Rosch & Mervis, 1975). Modern versions of the semantic feature paradigm use normed data—that is, aggregate data collected in property generation tasks from several raters (e.g., McRae et al., 2005; Vinson & Vigliocco, 2008) or through online games (e.g., Recchia & Jones, 2012). In these tasks, participants are typically instructed to imagine a given concept and then produce properties to describe it (for example: car → <has four wheels>; car → <is used for transportation>). This can be achieved in think-aloud experiments (e.g., Barsalou & Wiemer-Hastings, 2005), in which the participants are asked to describe given stimuli, which are then segmented and standardized by the analysts, or in more constrained settings, in which the participants are provided prearranged blank lists to fill up with a given number of features (e.g., McRae et al., 2005), or are asked to complete predetermined sentence stems (e.g., Garrard et al., 2001). Even though semantic features cannot be considered as exhaustive readouts of a concept’s content, they provide valuable insights into salient aspects of meaning (e.g., Cree & McRae, 2003; Garrard et al., 2001; McRae et al., 2005). As a theory of meaning and conceptual representation, the featural view has been evaluated against models of human similarity judgments (e.g., Tversky, 1977; Tversky & Gati, 1982), and in more recent times it has been used to explain category-specific semantic disorders (e.g., Caramazza & Shelton, 1998; Garrard et al., 2001; Laiacona et al., 1993; Sartori & Lombardi, 2004). Recently, semantic features have been integrated within classic distributional models based on text corpora (such as LSA; Landauer & Dumais, 1997), to address the symbol-grounding problem that characterizes the distributional models of the first generation (cf. De Vega et al., 2008), and to enhance the symbolic representations derived from word co-occurrences with grounded, sensorimotor properties conveyed by the feature-based representations (Andrews et al., 2009; Baroni et al., 2010).
The sets of semantic features collected in property generation tasks are typically post-processed and categorized into feature types, according to established taxonomies and related coding schemes. For example, Garrard and colleagues (Garrard et al., 2001) propose a four-way knowledge-based classification of semantic features, that takes into account sensory, functional, encyclopaedic and categorizing information. Wu and Barsalou (2009) propose a more articulated knowledge-based taxonomy (refined in subsequent phases), which was also (marginally) applied to features produced in response to abstract concepts (Barsalou & Wiemer-Hastings, 2005). In addition to an adapted version of Wu and Barsalou’s taxonomy, which has also been adopted by Kremer and Baroni (2011), Cree and McRae (2003) propose a brain region taxonomy, which takes into account insights from neuroscience and neuropsychology to determine sets of feature types that are plausibly computed in different brain areas. Lebani and Pianta (2010a) propose an easy-to-use and cognitively plausible classification that combines insights from Cree and McRae (2003) and Wu and Barsalou (2009), as well as lexical semantics (e.g., WordNet relations). This taxonomy is applied by the authors in the STaRS.sys project, in which semantic features are used to support speech therapists in preparing materials for rehabilitation purposes (Lebani & Pianta, 2010b). Vinson and Vigliocco (2008) proposed a five-category taxonomy that accounts for feature types produced for nouns and verbs, referring to their sensorimotor and functional roles. Recchia and Jones (2012) propose a 19-category taxonomy that constitutes an adapted version of existing coding schemes, applied extensively to semantic features of both concrete and abstract concepts.
Such a higher-order classification of semantic features into feature types can be used to infer differences between concepts, based on the differences among the types of features that they evoke. For example, Barsalou and Wiemer-Hastings (2005) showed that abstract concepts evoke qualitatively different types of concept properties (features) than do concrete concepts. The authors suggest that abstract concepts seem to be grounded in situations and involve subjective experiences and emotions (see also Vinson et al., 2014), whereas concrete concepts evoke features that are more directly related to the referent that they define. Moreover, abstract concepts have more relational features than do concrete concepts, which, by contrast, have more internal attributes. In this view, the perception of abstract and concrete concepts differs in focus, the former being more spread across a situation and its related entities, the latter being directed onto the concept’s referent (Wiemer-Hastings & Xu, 2005).
However, there seem to be different ways in which the annotation process (i.e., how the semantic features are classified into types) is approached, conducted, and reported throughout the literature. Therefore, because the reliability of the annotations (measured in terms of intercoder agreements) sometimes seems to be underestimated, under-reported, or reported in different ways, the validity of the observations based on such data remains questionable. A contingent problem is the fact that the proposed coding schemes suggested in the literature are often underspecified, and therefore their applicability to new datasets is extremely challenging. In addition, some of the coding schemes outlined above were initially created on the basis of semantic features collected in response to concrete concepts only, and applying the same categories to semantic features produced for abstract concepts presents new challenges that depend on the intrinsic peculiarities of such concepts (i.e., the fact that they lack a concrete and easily imaginable referent).
It is the aim of this methodological article to explain in detail why consistent reliability checks are necessary for this type of research, how the results of these tests can be improved within this paradigm, and which theoretical and methodological implications the results bring. We exemplify our claims by means of a practical case study, in which we applied existing coding schemes to a set of semantic features that we collected using a property generation task in response to a sample of concrete and abstract concepts.Footnote 2 In this case study, it is our goal to strive for optimal agreement among annotators.
Theoretical background
Various empirical studies support the claim that semantic features provide insights into core aspects of the content of concepts. Semantic feature effects reported in the literature include the following: a semantic priming effect (concepts that share semantic features prime one another, as opposed to concepts that do not share semantic features; Cree et al., 1999; McRae & Boisvert, 1998), a number of features effect (decision times and errors in lexical decision tasks are lower for concepts with many features; Pexman et al., 2002; Pexman et al., 2003), and a distinctive features effect (pairs of concepts sharing distinctive features are judged to be more similar than concepts sharing an equal number of relatively frequent features (Mirman & Magnuson, 2009). Because of their acknowledged importance in cognitive processing, semantic feature norms have been collected throughout the years for different languages (see, e.g., Kremer & Baroni, 2011, for Italian and German; Montefinese et al., 2013, for Italian) and different varieties of language (see, e.g., BLIND, a corpus of semantic features norms produced by congenitally blind participants: Lenci et al., 2013).
As we anticipated in the introduction, different taxonomies have been proposed in the literature to classify semantic features into types. Such coding schemes have then been adapted in other studies to accommodate the annotation of features produced in other languages, as well as features produced for different types of concepts (typically concrete and abstract ones). In Table 1, we report (a selection of) well-known taxonomies and relative adaptations, retrieved from published studies in which the authors reported the results of the annotation process and the relative reliability tests (if applied).
As can be observed in Table 1, the ways in which the annotation processes and reliability tests have been conducted and reported have been quite variable. Moreover, even when the intercoder agreement is checked and then reported in the study, some questions remain open.
Wu and Barsalou (2009), in particular, reported the agreement in percentages (see Table 1). However, agreement percentages have been widely criticized due to their inability to account for agreement by chance (e.g., Cohen, 1960). In this light, Spooren and Degand (2010) stated that in cases in which the interpretation (as opposed to formal characteristics) of the phenomenon under scrutiny is central, low agreement scores are sometimes inevitable. This is often the case when using content analysis to look at linguistic data. Because interpretation is arguably more likely to vary across coders, as opposed to formal characteristics of the data, and because such interpretations are likely to involve a degree of random guessing, we argue that interrater agreement is to be preferred over percentages, because it takes into account and balances agreement by chance. However, in tasks in which the coding scheme is very simple and the decision is therefore limited to a few possible categories (e.g., a team of doctors who have to decide between a limited set of options for a patient’s treatment) that are very familiar to the annotator, agreement percentages might still be valuable. In these cases the coders (i.e., the doctors) are (hopefully) very well trained and experienced, so that less random guessing is likely to occur, whereas it is more likely that the annotations are based on guessing when the coding scheme includes many categories. In the latter case, a measure of agreement that balances agreement by chance should be preferred to raw percentages (for a discussion, see McHugh, 2012).
Recchia and Jones (2012) reported that after multiple rounds of classification of a subset of properties by two coders, reliable annotations were eventually achieved (see Table 1). However, the two coders arguably developed more similar ways of thinking round after round and gave similar annotations that would not necessarily have been reproduced by novice coders. Therefore, a coding scheme cannot be considered reliably replicable unless the annotations provided by trained coders who worked together are compared to the annotations given by novice coders.
In Montefinese et al. (2013), the disagreement between the first two coders (which was not quantified) was first mediated in a discussion with a third coder, after which the annotations achieved through discussion among three coders were compared to those of a (fourth) “secondary” coder, generating an extremely high kappa coefficient (see Table 1). However, the authors do not specify whether the secondary coder was a novice, or whether she had been trained, because she had participated in the previous tasks. Moreover, it is not quite clear how the third annotator mediated the codings of the first two coders (reliability ratings are not reported for these stages of the annotation process).
Finally, in Kremer and Baroni (2011) the reliability of the annotations into feature types (in relation to the semantic feature norms released by the authors) was calculated on a sample of 100 concept–feature pairs, which covers around 1% of the total dataset in each language (see Table 1). This may be sufficient for the specific dataset analyzed by Kremer and Baroni, but raises the general issue of sample representativeness: to determine the reliability of a coding scheme and its reliable application (by trained and novice coders), the sample of data on which the annotations are performed should be a fair subset of the whole dataset. In this way, if the intercoder reliability is sufficiently high, the remaining annotations performed by a single coder can be assumed to be replicable. In general, we would assume that the bigger the sample size of the subset used for intercoder reliability checks, the more likely it is to be representative for the whole dataset and other data that it can be applied to.
Methodological guidelines about reliability in content analysis
In recent times, scientific journals ranging from communication to medical science have typically required their contributors to report intercoder reliability scores (Feng, 2015, p. 13; Hayes & Krippendorff, 2007, p. 78). The idea behind this requirement is that research can only be published if there is sufficient agreement between independent observers about the units of analysis studied; if no such agreement existed, the research would normally be thought of as insufficiently reproducible, and might even be unreliable.
Reliability grounds the confidence of a given set of annotated data by providing acceptable scores in terms of stability (the same annotations do not change over time if re-applied by the same analysts to the same data), replicability (annotations remain the same when different analysts annotate the same data), and of course accuracy (the extent to which the annotation process conforms to its specifications and yields what it is designed to yield). In other words, “the importance of reliability rests on the assurance it provides that data are obtained independent of the measuring event, instrument or person. Reliable data, by definition, are data that remain constant throughout variations in the measuring process” (Kaplan & Goldsen, 1965, pp. 83–84).Footnote 3
Finally, a commonly acknowledged drawback of pursuing high reliability is that of giving up interesting but nonreplicable interpretations to provide, instead, highly reliable (i.e., replicable) but oversimplified coding schemes. The analysts should, therefore, find a compromise between highly replicable and highly accurate coding schemes (Krippendorff, 2013).
In computational linguistics, it has been argued that alpha-like coefficients, although traditionally used less than kappa-like measures, may be more appropriate for corpus-based annotation tasks (Artstein & Poesio, 2008). This could also be the case for semantic feature norms classification into feature types.
A number of reliability measurements have been proposed in the literature to determine intercoder reliability. The simplest of these is determining the percentage of agreement between independent observers. This measurement, however, does not take into account that the chance that agreement is reached decreases when the number of categories increases (Hayes & Krippendorff, 2007:80), nor that the chance that agreement is reached is affected by overrepresentation of categories (Artstein & Poesio, 2008; Gwet, 2015). Reliability indexes such as Scott’s (1955) π, Cohen’s (1960) κ, Fleiss’s (1971) κ, and Krippendorff’s (1970, 2004) α have been proposed to remedy this problem. In essence, each of these reliability indexes corrects the percentage of agreement by the probability of chance agreement.
Like Fleiss’s κ, Krippendorff’s α has the advantage that it allows checking for reliability between more than two coders (which Scott’s π and Cohen’s κ do not) and it allows checking for reliability between these multiple coders without them having to rate exactly the same number of items.
Yet, unlike Fleiss’s κ, Krippendorff’s α takes into account disagreement magnitude as well as potential missing values (Artstein & Poesio, 2008). For these reasons, we prefer using Krippendorff’s α as a measure to evaluate agreement, even though we can just as well report Fleiss’s κ in our present study, since disagreements between coders in this study do not differ in magnitude, and there are no missing data. In fact, we will also report Fleiss’s κ for direct comparison with the reliability tests reported in related studies (see Table 1).
Another important methodological issue that needs to be addressed when referring to content analysis and reliability tests is that of the quality of the analysts who perform the annotation and the training they receive. The analysts who develop the taxonomy that is then used to code the data need to be experts in the field, but at the same time they need to undergo a training session, during which the coding scheme is discussed, modified, and refined, in accordance with what the data reveal (e.g., Krippendorff, 2013, pp. 128–132). During the training, it is important to detail the descriptions of each category, providing examples and counterexamples, so that the categories are mutually exclusive. This can be a very arduous task, especially when dealing with real-world communications, such as speaker-generated semantic features and their relation to the concepts used as stimuli. As a matter of fact, as described below, the semantic relation between a feature and a concept is not always straightforward, and can be coded in different ways, especially when the concept is abstract. It is therefore very difficult to render the categories mutually exclusive when the data to which they need to be applied is inherently ambiguous and allows for different interpretations. We hereby suggest, as was pointed out in supplementary materials provided by Barsalou (1992), to try to infer what the informant meant when he/she produced a specific feature, although of course the coder cannot know for sure what the informants were thinking during the coding task. This can be done by taking a probabilistic approach (based on knowledge of the world, language use, context, etc.) and coding the semantic relation that is perceived as more salient for a given concept–feature pair.
As was pointed out in the manual for content analysis written by Krippendorff (2013, p. 131), the analysts who code the data should ideally not be the same people who constructed (or adapted) the taxonomy. This distinction is necessary because two (or more) researchers who worked together to develop a coding scheme and engaged in discussions that led to mutual clarifications and agreements on the same perspectives will often generate a higher score in intercoder agreement tests than a fresh set of coders. For this reason, once the taxonomy is developed and refined through the training process that the expert analysts undergo, the data should be annotated (again) by novice coders, who should be able to rely solely on the taxonomy, its descriptions and the examples provided. Reliability should then be checked among the annotations provided by the novice coders. In this way, the annotation process can be considered replicable.
Project outline
In this project, we apply the general methodological guidelines provided in relation to content analyses—surveyed in the previous section—to the annotation processes aimed at classifying semantic features into feature types. In this process, we develop and provide specific guidelines for annotators, applicable to the semantic feature norm paradigm, who need to apply coding schemes to datasets of semantic features.
The study that we report here tackles the following methodological issues in semantic feature classification:
-
1.
the structure (hierarchical or horizontal) of the taxonomy and related coding scheme, and the overall number of categories;
-
2.
the degree of in-depth description of the categories, as well as the availability of examples and counterexamples provided with the supplementary materials;
-
3.
the role of coders training;
-
4.
the evaluation of the developed materials by means of comparison between the annotations provided by trained versus novice coders.
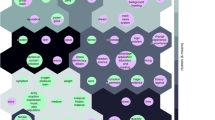
We exemplify these issues by reporting the coding process aimed at annotating a dataset of semantic features produced in a property generation task, in relation to concrete as well as abstract concepts. The project was divided into four phases, which are verbally outlined and summarized in Fig. 1. A detailed description of each phase is reported in the Method section. Each phase targeted one of the four methodological issues described above. Specifically, in Phase 1 we underwent an exploratory analysis, in which we surveyed existing coding schemes, selected a relevant one (previously applied to semantic features produced for both concrete and abstract concepts), applied it to a set of data, and calculated intercoder agreement scores. In Phase 2, as is illustrated in Fig. 1, we discussed the results of the coding task and the intercoder reliability scores that we obtained. We identified the problems with the first annotation task and planned how to remedy them (mainly the necessity to use a coding scheme with fewer categories to facilitate the annotators, and the option of having a hierarchically structured coding scheme). In Phase 3, we underwent intensive training sessions to develop detailed materials that would address the issues identified in the previous phase and that would need to be tested in Phase 4 (and used in future replication studies). In Phase 4, as is summarized in Fig. 1, we evaluated the newly developed coding scheme by means of annotation tasks performed by three trained coders and by three novice coders. Finally, we performed formal reliability tests among all six annotators, as well as between the trained versus the novice coders.
Method
The materials on which the annotation tasks reported here were performed were a set of semantic features produced by American English native speakers in response to a sample of 185 concrete and abstract concepts. These concepts appear to be one of the two metaphor terms in a sample of A-is-B metaphors that were randomly selected from the Metaphor Corpus of linguistic metaphors and the VisMet corpus of visual metaphors (for further details, see Bolognesi, 2016). Some of the stimuli included in this dataset were also included in established datasets of semantic features (41 items also appear in McRae et al., 2005, and 46 items also appear in Recchia & Jones, 2012). On these shared items, a correlation study was performed to check how the collected data related to the two established datasets of semantic features. The Pearson’s coefficients were, respectively, r = .94 (in relation to McRae et al.’s, 2005, dataset) and r = .96 (in relation to Recchia & Jones’s, 2012, dataset). The semantic features were formulated as one word or as compounds (typically adjective–noun), and therefore required minimal intervention for their standardization.
Phase 1
In the first exploratory phase, three independent annotators applied an existing taxonomy, previously used for the annotation of semantic features, to concrete and abstract concepts. Reliability tests were performed on the annotations provided by the three independent coders.
The problems encountered during the task were discussed, and turned into variables that were addressed in Phases 2 and 3.
We opted for the Recchia and Jones’s (2012) taxonomy, that was derived from existing coding schemes previously applied to the annotation of concrete concepts, and was adapted by the authors for the purpose of accommodating the annotation of semantic features for both concrete and abstract concepts crowdsourced through online gaming. The taxonomy consists of 19 categories, and therefore 19 different coding labels that can be attributed to a concept–feature pair (e.g., “Communication”: magazine → <gossip>; “Materials”: hell → <brimstone>). Categories are presented on the same level and enhanced with a short description of the category, one example featuring a concrete concept and one example featuring an abstract concept. With these materials, three independent annotators with different academic backgrounds (linguistics, argumentation, and journalism) at a postgraduate level performed the annotation task and joined as co-authors of this article. We annotated roughly 30% of our database (a batch of 50 concepts, amounting to 608 features) independently and without any previous training, using only the information provided by the taxonomy and its related coding scheme.
Phase 2
In this phase, we first discussed the problems encountered in the previous annotation task and turned the problems into variables, so as to test them in the following tasks. Since the main problem encountered appeared to be the high number of categories that are not hierarchically structured encompassed by the Recchia and Jones’s (2012) taxonomy, we opted for the Wu and Barsalou (2009) knowledge-based taxonomy in the next annotation task, which is structured into four macrocategories and 27 nested categories.Footnote 4 More specifically, the four macrocategories that constitute the core of this taxonomy refer to properties of the entity (or concept), properties of the situation in which the entity typically occurs, introspections (such as emotions and cognitive operations), and taxonomic features that identify relations, such as synonymy and hyperonymy. Each macrocategory is then divided into nested categories that define specific types of properties.
The inner hierarchical structure of this taxonomy allows one to assess the semantics of a concept–feature pair in two steps (with a macrocategory and then with a nested category), which allows for a double reliability check at each of the two levels. In this phase, we applied the Wu and Barsalou (2009) taxonomy at the macro level (four categories) to a new batch of 25 randomly selected concept–feature pairs (265 features, around 13% of the whole dataset).
Reliability tests were performed on the new annotations provided by the three independent coders.
Phase 3
In this phase, we took five training sessions, which were scheduled on a weekly basis and had an average duration of 2.5 h. Together we applied and discussed the nested categories described in the Wu and Barsalou (2009) taxonomy. During the training session and discussions, we revised some of the nested categories to accommodate the annotation of features related to abstract concepts. We added examples/counterexamples to exemplify the taxonomy (Appendix 1), and developed a decisional flowchart (Appendix 2)Footnote 5 to facilitate the application of the coding scheme in future tasks performed by untrained (novice) coders.
Phase 4
In this phase, the revised and adapted coding scheme was evaluated in an annotation task performed by three trained coders and three novice coders. Because the annotation task was performed by two different types of coders (trained vs. novice), some qualitative observations could be made about the importance of the training session.
The adapted taxonomy, enriched with the developed materials, was applied to a new batch of 259 randomly selected concept–feature pairs (~13% of the whole database). In this study, six coders annotated the batch: three trained coders (who developed the materials for the adapted taxonomy and performed the previous annotation tasks) and three novice coders, who were not familiar with the task nor the aim of the study, and had never performed a task like this before. The three novice coders had a postgraduate educational background in different disciplines: philosophy, linguistics, and literature.
Analysis
Phase 1
The application of the Recchia and Jones’s (2012) coding scheme to our data resulted in very low agreement among the annotators (Krippendorff’s α = .36; Fleiss’s κ = .36). The difficulties encountered by the three annotators were then discussed. The following problems emerged:
First, the number of categories (19) was too high, and therefore it was difficult for the annotators to familiarize themselves with the taxonomy and keep in mind all the coding options when coding a concept–feature pair. As a consequence, we observed that coders tended to stick with some “preferred” categories, which they perceived as more familiar. Figure 2, for example, shows the different distributions of the annotations provided by Coders 1 and 2 over the 19 categories. As Fig. 2 shows, Category 19 (“super/subordinates”) was frequently used by both coders, but it was the most frequent category only in the annotations of Coder 1. The most frequent category used by Coder 2, on the other hand, was Category 9 (“contingency”).
Number of categories: The value should be limited, so that all the categories can be available in the mind of the coder during the task.
Next, some categories seemed to be missing. Annotators had to add some concept–feature combinations to other categories because they did not find a category that exactly suited their interpretation. This was the case, for example, for antonyms that emerged in our dataset, such as hardness → <softness>, for which there was no dedicated category. However, this category has a major cognitive value, as is described for example in Cann et al. (2011), in which the authors reported that antonyms hold a special status in word association tasks, especially in relation to adjectives and verbs, and plausibly for their nominalizations as well.
Category exhaustiveness: The categories should cover all the domains to which they refer.
Third, the categories descriptions were too generic, and there was an overlap (they were not mutually exclusive). This was reflected in the overall poor agreement among annotators, as well as in some notes that the annotators reported on the annotation form, suggesting alternative coding options for the same concept–feature pair. For example, factory→ <efficient> could be annotated as an evaluation, a manner or a nonvisual perceptual property; similarly, cookie→ <chocolate chips> could be interpreted as a material or a component, and ice cream→ <treat> could be seen as either an evaluation or a superordinate.
Category description: This needs to be as precise as possible, so as to render the categories conceptually mutually exclusive.
Finally, as was already observed in Recchia and Jones’s (2012) article, the relation between features and abstract concepts was more difficult to determine than the relation between features and concrete concepts. The materials might not include enough examples and counterexamples, which would help the annotators understand when a category applies to the data and when it does not.
Category exemplification: Categories should be exemplified through several examples that cover different cases (e.g., abstract and concrete features, applied to abstract and concrete concepts) and counterexamples.
In general, the major problem with this taxonomy seemed to be the large number of categories the coders needed to browse over to annotate each concept–feature pair, and the lack of structure among the categories. To resolve these issues, we decided to adopt another taxonomy (Wu & Barsalou, 2009), which was originally derived from the observation of features produced for concrete concepts.
Phase 2
Crucially, reliability tests showed that (given the much smaller number of possible codings, as compared to the previous task) the agreement among annotators had improved (Fleiss κ = .76, Krippendorff α = .76).
Still, the agreement was not perfect (i.e., it was not above .80), and a closer look at the differences between annotations revealed that the disagreements primarily occurred related to the annotation of features referring to abstract concepts, as already pointed out in the annotation process reported in Recchia and Jones (2012). More specifically, a qualitative analysis of the disagreements showed that the disagreements mainly concerned the choice between the category of “Introspection” and the category of “Situation” properties. For example, given the concept provider, features such as <need> or <safety> were coded as “Introspection” or as “Situation” by different annotators. Similarly, given the concept purpose, the feature <motivation> was coded as “Introspection” or as “Situation” by different coders. This phenomenon was observed only qualitatively, but it suggests that “Introspection” and “Situation” properties could, in principle, explain the same concept–feature relations, and therefore might be perceived to be more similar to one another. This qualitative observation of problematic annotations led us to discuss the disagreements and seek to resolve the underlying problem. This was the goal of Phase 3 (training) and Phase 4 (Final annotations and training evaluation).
Phase 3
During the training sessions in which the coding scheme was discussed, the annotators agreed that some of the nested categories were not perceived as mutually exclusive. These nested categories were therefore merged into a single one. For example, the differences between <External component> and <Internal component> were not clear when coding features of abstract concepts (e.g., army→ <soldier>) nor when coding features of concrete ones (clock→ <hands>, barcode→ <numbers>). Similarly, the difference between “Materials” and “Internal components” or “External components” was not always clear (coffee→ <beans>, air→ <oxygen>). For this reason, these three categories were merged into a single one, which included components, materials, and substances. In other cases, categories were dropped because they appeared to be included in other categories. For instance, “Individuals” was dropped because the annotators perceived this category to be included in “Subordinates” and therefore opted for a better description of the latter category, which included features describing categories placed one or more levels below the target concept in a taxonomy (e.g., body organ→ <lungs>, tablet→ <Ipad>, gorilla→ <King Kong>).
Finally, the descriptions of the nested categories were refined and, where possible, suggestions were given as to what types of predication would trigger such a category (e.g., “it causes X,” and what would be the opposite category.
The final revised taxonomy (and related coding scheme) included four macrocategories and 20 nested categories (Appendix 1). To aid the coding process, we also constructed a flowchart that could be used during the annotation process (Appendix 2). In this flowchart, the categories from the revised taxonomy are ordered on the basis of (a) hierarchy (the annotator would encounter the macrocategories before the subcategories) and (b) frequency of occurrence of the macro and nested categories based on the annotations that were obtained in Phase 2 (the more frequent the category occurred, the earlier the annotator would encounter that category in the flowchart). Additionally, the (c) resemblance between different categories was pointed out in the flowchart to diminish the chance that coders would accidentally select a category that is similar to the one they would like to use, but not entirely the same (for example, in case of coding a property as a synonym, the question whether it is not a contingency appears in the flowchart). This flowchart was used in Phase 4. together with the table that explains the revised taxonomy (Appendix 1).
Phase 4
The three trained coders applied, independently, the revised taxonomy to a new set of data (259 concept–feature pairs, ~13% of the whole dataset). The intercoder agreement was calculated at both the macro level, on the basis of four categories (Fleiss κ = .88, Krippendorff α = .88), and the nested category level, on the basis of 20 categories (Fleiss κ = .84, Krippendorff α = .84).
Moreover, three novice coders applied, independently, the revised taxonomy to the same set of data used by the three trained coders. These coders were instructed to apply the revised taxonomy and to use both of the provided tools: the table and the flowchart. Then the intercoder agreement was calculated among the three novice coders on both the macro level (Fleiss κ = .84, Krippendorff α = .84) and the nested category level (Fleiss κ = .81, Krippendorff α = .81).
The overall reliability of the annotations provided by the six coders (three trained and three novices) was finally calculated, resulting in Fleiss κ = .83, Krippendorff α = .83. Table 2 shows the reliability values calculated between pairs of coders as well. Cohen’s kappa coefficients between coder pairs are reported.
The differences among the annotations of the trained and the novice coders (reported in Table 2) were observed on a qualitative basis and statistically evaluated (see Table 3). It emerged that the novice coders were less consistent in annotating taxonomic features at the nested category level, which they tended to code as either “Subordinates” or “Synonyms” (e.g., place→ <home>). This tendency was not observed among the trained coders. On the other hand, the novice coders confirmed and extended the lack of agreement in distinguishing consistently between “Situations” and “Introspections,” which had already been observed in the previous task with the three main coders before their training session. In particular, the disagreements emerged when coding concept–feature pairs that were coded either as “S-obj” (i.e., objects that appear together with the concept in a given situation) or as “I-cont” (features expressing contingencies and other cognitive operations that could be signaled by links such as “requires,” “provides,” “is correlated with,” and so on). This was observed in pairs including concrete concepts, such as plant→ <water>, and in pairs including abstract concepts, such as sight→ <light>.
To compare the interrater agreements achieved by the trained and the novice coders, we applied the linearization method (Gwet 2015), implemented to address the problem of testing the difference between two sets of agreement coefficients for statistical significance.Footnote 6 The linearization method is similar to the classical t test for means, and in our case it allowed to compare the reliability coefficients obtained within pairs of trained coders to the reliability coefficients obtained with pairs of novice coders. Table 3 summarizes the results of the application of the linearization method, where the term StdErr (d) represents the standard error of the differences of participant-level linear elements defined in the linearization method. As can be observed from the table, the t statistics in both cases were always below 1.96, which indicated that the difference between the two groups (trained vs. novice coders) was not statistically significant. The test delivers similar results for Fleiss and Krippendorff coefficients, which does not come as a surprise, because no ratings are missing from our dataset. Moreover, the test shows that the difference between groups of coders is not statistically significant at both, the macro level and the nested category level.
Discussion and conclusions
This contribution argues in favor of performing reliability tests in content analyses, specifically in the case of semantic features annotation. In this respect, we first reviewed how (and if) reliability tests were performed and reported in contributions that address the topic of semantic feature categorization. We then explained the possible methodological drawbacks that derive from the lack (or partial application) of reliability checks, and finally we reported a four-phase project, in which we performed several annotation tasks with the intention of improving our annotations by manipulating different parameters. The results of the four-phase project reported in the Analysis section allowed us to develop a set of methodological guidelines for scholars who need to perform annotation tasks on datasets of semantic feature norms. Our guidelines relate to the following points: (1) choosing (and possibly adapting) a coding scheme that suits the data; (2) choosing the types of coders (for example trained vs. novice); (3) choosing the data sample on which the annotation task will be performed; and (4) choosing the measure to weigh the reliability of the annotations.
The first methodological contribution of this study relates to the general question of which taxonomy (and related coding scheme) should be chosen to annotate a given dataset of semantic features into feature types. The literature reviewed in the Theoretical Background section shows that several coding schemes have been suggested throughout the years and also that it is a frequent practice to perform revisions and adaptations of existing coding schemes, in order to render the taxonomy suitable for a given dataset (see, e.g., Barsalou & Wiemer-Hastings, 2005; Recchia & Jones, 2012). We argue that this practice is legitimate if it preserves a cognitively valid and psychologically motivated coding scheme. In phase three of our study, for example, we merged nested categories that belong to the same macrocategory under one label (internal and external components of an entity, within the encompassing label ‘Components’). This allowed us to preserve the cognitive validity of the coding scheme, and achieve higher reliability in the annotation task, by simply producing a less refined distinction between nested categories. In line with this guideline, we acknowledge the fact that in content analysis, the analysts are faced with the dilemma of achieving high reliability scores by sacrificing refined distinctions. This is a trade-off that the analysts need to discuss in relation to their primary goals. In addition to this, we argue and show that a hierarchically structured taxonomy is easier to apply and therefore should be preferred to a horizontal taxonomy with several categories presented on the same level of specificity. Moreover, we argue in favor of the development of detailed materials to support the coders in the annotation tasks. The more the coding scheme is described in detail, with examples and counterexamples, the easier it is for the annotators to understand the distinctions among categories, and apply the coding scheme correctly.
With regard to coder training, the question arises to what extent training is necessary and desirable. On the one hand, coders need to have a clear idea about what to code, so training is both necessary and desirable. On the other hand, training might diminish the value of high agreement between coders; if they are trained in the same way, it is likely that they code in the same way, and therefore agreement might not be an indication of an appropriate coding scheme, but rather of a successful training.
On the basis of the present research, we believe that the danger of coder training should not be overestimated. In phase four of the present research, we contrasted codings by trained and novice annotators by means of the linearization method (Gwet, 2015). This showed no significant difference between trained and novice coders; both on the macro level and at the nested category level, the trained and novice annotators code the data in similar ways. Since training can enhance understanding of the coding scheme and provide annotators with a more concrete idea of the kind of data that belongs to each coding category, we are of the opinion that training could be helpful when dealing with a complex taxonomy or complex data. Coder training could, moreover, aid in fine-tuning the coding scheme. As was demonstrated in Phases 1–3 of the present research, training can point toward difficulties in the researched taxonomy and may, for example, also help to identify (counter)examples of the different coding categories.
Another issue relates to the sample size of the dataset to be coded by multiple coders. A typical experimental setup is that multiple coders do not code the entire dataset, but just a subset of it. The idea behind this is that if intercoder reliability is sufficient for this subset, each coder could individually annotate the remainder of the dataset in a reliable way as well. It is thus an efficient way to check for reliability. This is, however, only the case if the subset that is coded by multiple coders is representative of the entire dataset. As we pointed out earlier, we assume that the bigger the sample size of the subset, the more likely it is to get a fair idea about the reliability of each individual coder. After all, provided that the subset is randomly selected, we can predict with greater confidence that annotators would code the remaining data in the same way. The exact size of the subset should be determined by taking into account the complexity of the coding scheme and the complexity of the data. In general, the more complex the scheme and data, the larger the subset needs to be to provide fair coverage of the dataset’s inner variability, and therefore a fair idea about the reliability of the annotators’ application of the coding scheme. Complexity of the scheme might result from a large number of categories (again, the more categories, the more complex the scheme). Complexity of the data might result, for example, from semantic features produced for both concrete and abstract concepts.
Apart from the size of the subset, the measure that is chosen to weigh intercoder reliability needs to be discussed: what, in the end, is the overall value of testing intercoder reliability be means of alpha-like or kappa-like measures? The advantage of using such measures is, of course, that they provide a more or less standardized measure to check for reliability. However, it should be emphasized that alpha-like or kappa-like measures are by no means direct measures of truth or quality: a coding scheme might have no theoretical or cognitive foundations, and yet coders might use it in the same way and thereby obtain high intercoder reliability. This, however, does not mean that these measures cannot provide any useful information: sufficiently high scores can be regarded as an indication of the adequacy of the examined taxonomy.
In the present study, the reported Krippendorff’s α and Fleiss’s κ scores were identical. This was expected, since disagreements between coded categories were considered equal and all data was coded. We nevertheless recommend reporting Krippendorff’s α, in case the disagreements might be of different magnitudes (e.g., in the case of coding sets of categories in which disagreement might be partially or fully) or in case some data are missing.
A final point that we wish to rise with the present contribution relates to the overall need and importance of performing reliability checks, especially in the present crowdsourcing era. As a matter of fact, it has been recently suggested that crowdsourced annotations—that is, annotations performed by several remote workers that are recruited online (i.e., a large sample of novice coders)—can overcome the problems related to the “antiquated ideal of a single correct truth” (Aroyo & Welty, 2015:15), typically performed by (one or) a few experts and measured by means of intercoder agreement coefficients. With this study, we argue in favor of the need for reliability checks, and we report a study in which the reliability scores achieved by experts—that is, trained coders—do not substantially differ from the reliability scores achieved by novice coders (Phase 4). In this perspective, we argue that, from a theoretical and methodological point of view, the optimal situation is realized precisely when trained and novice coders do not differ in their performances, as this implies that the annotations are replicable and do not rely on a single truth mastered by a few experts, and that the coding scheme and the other developed materials are clear.
To conclude, the contributions of this study are threefold: We suggest methodological guidelines to tackle several issues that researchers who deal with content analysis of semantic features typically run into; we propose a revised coding scheme (based on Wu & Barsalou, 2009, knowledge-based taxonomy), which can be applied to the annotation of semantic features collected for both abstract and concrete concepts; and finally we release a dataset of 185 abstract and concrete concepts and their related semantic features, collected in a property generation task and fully annotated with the revised coding scheme.
Notes
“A family resemblance relationship consists of a set of items of the form AB, BC, CD, DE. That is, each item has at least one, and probably several, elements in common with one or more items, but no, or few, elements are common to all items” (Rosch & Mervis, 1975, p. 575).
The dataset of annotated semantic features has been released on GitHub at the following URL: https://github.com/mariannabolognesi/Semantic-Feature-Norms.
A crucial aspect needs to be underlined here: Reliability, in contrast to validity, does not concern truth per se. As was pointed out by Kaplan and Goldsten (1965), reliability relates to the measuring process, not to the quality of the taxonomy or the data to which it is applied. It is not correct to ascertain validity of the taxonomy (or the data collected) only by reporting high degree of intercoder agreement during the annotation process. In content analysis, the two variables (reliability and validity) are often related in the following way: Unreliability (disagreements among observers or annotators) limits the chance of validity, but, at the same time, reliability does not guarantee validity (observers might be influenced by the same subjective biases).
The taxonomy is theoretically motivated by a number of factors, which are also summarized in Cree and McRae (2003). In general, the four macrocategories do not simply emerge from the collected data, but take into account how the information is conveyed by sensory channels and how it reflects aspects of introspective experiences, and they meet the variation of information found in ontologies (Keil, 1979) as well as event frames and verb arguments (Barsalou, 1992; Fillmore, 1968; Schank & Abelson, 1977). Moreover, this taxonomy is described in quite some detail by the authors, who revised their own taxonomy over the years, also releasing additional materials to facilitate the annotation process.
Both, the taxonomy and the flowchart have also been released online, on the COGVIM website: https://cogvim.org/materials/.
Kilem Gwet, who developed the linearization method, collaborated with us and applied the method to our dataset. We are extremely grateful to him for his availability and willingness to collaborate with us.
References
Andrews, M., Vigliocco, G., & Vinson, D. (2009). Integrating experiential and distributional data to learn semantic representations. Psychological Review, 116, 463–498. doi:10.1037/a0016261
Aroyo, L., & Welty, C. (2015). Truth is a lie: Seven myths about human annotation. AI Magazine, 36, 15–24.
Artstein, R., & Poesio, M. (2008). Inter-coder agreement for computational linguistics. Computational Linguistics, 34, 555–596.
Baroni, M., Barbu, E., Murphy, B., & Poesio, M. (2010). Strudel: A distributional semantic model based on properties and types. Cognitive Science, 34, 222–254.
Barsalou, L. (1992). Frames, concepts, and conceptual fields. In A. Lehrer & E. F. Kittay (Eds.), Frames, fields, and contrasts (pp. 21–74). Hillsdale, NJ: Erlbaum.
Barsalou, L. W., & Wiemer-Hastings, K. (2005). Situating abstract concepts. In D. Pecher & R. Zwaan (Eds.), Grounding cognition: The role of perception and action in memory, language, and thought (pp. 129–163). New York, NY: Cambridge University Press.
Bolognesi, M. (2016). Using semantic feature norms to investigate how the visual and the verbal modes afford metaphor construction and expression. Language and Cognition. doi:10.1017/langcog.2016.27
Cann, D., McRae, K., & Katz, A. (2011). False recall in the Deese–Roediger–McDermott paradigm: The roles of gist and associative strength. Quarterly Journal of Experimental Psychology, 64, 1515–1542.
Caramazza, A., & Shelton, J. (1998). Domain-specific knowledge systems in the brain: The animate–inanimate distinction. Journal of Cognitive Neuroscience, 10, 1–34. doi:10.1162/089892998563752
Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20, 37–46.
Cree, G. S., & McRae, K. (2003). Analyzing the factors underlying the structure and computation of the meaning of chipmunk, cherry, chisel, cheese, and cello and many other such concrete nouns. Journal of Experimental Psychology, 132, 163–201. doi:10.1037/0096-3445.132.2.163
Cree, G. S., McRae, K., & McNorgan, C. (1999). An attractor model of lexical conceptual processing: Simulating semantic priming. Cognitive Science, 23, 371–414. doi:10.1207/s15516709cog2303_4
De Vega, M., Glenberg, A., & Graesser, A. (2008). Symbols and embodiment: debates on meaning and cognition. Oxford, UK: Oxford University Press.
Feng, G. (2015). Mistakes and how to avoid mistakes in using intercoder reliability indices. Methodology, 11(1), 13–22.
Fillmore, C. (1968). The case for case. In E. W. Bach & R. T. Harms (Eds.), Universals in linguistic theory (pp. 1–88). New York, NY: Holt, Rinehart & Wynston.
Fleiss, J. (1971). Measuring nominal scale agreement among many raters. Psychological Bulletin, 76, 378–382.
Garrard, P., Lambon, R., Hodges, J., & Patterson, K. (2001). Prototypicality, distinctiveness, and intercorrelation: Analyses of the semantic attributes of living and nonliving concepts. Cognitive Neuropsychology, 18, 125–174.
Gwet, K. (2015). Testing the difference of correlated agreement coefficients for statistical significance. Educational and Psychological Measurement, 76, 609–637.
Hayes, A., & Krippendorff, K. (2007). Answering the call for a standard reliability measure for coding data. Communication Methods and Measures, 1, 77–89.
Jones, M., Willits, J., & Dennis, S. (2015). Models of semantic memory. In J. R. Busemeyer & J. T. Townsend (Eds.), Oxford handbook of mathematical and computational psychology (pp. 232–254). Oxford, UK: Oxford University Press. doi:10.1093/oxfordhb/9780199957996.013.11
Kaplan, A., & Goldsen, J. (1965). The reliability of content analysis categories. In H. D. Lasswell & N. Leites (Eds.), Language of politics: Studies in quantitative semantics. New York, NY: G. W. Stewart.
Keil, F. C. (1979). Semantic and conceptual development: An ontological perspective. Cambridge, MA: Harvard University Press.
Kremer, G., & Baroni, M. (2011). A set of semantic norms for German and Italian. Behavior Research Methods, 43, 97–109. doi:10.3758/s13428-010-0028-x
Krippendorff, K. (1970). Bivariate agreement coefficients for reliability data. In E. R. Borgatta & G. W. Bohrnstedt (Eds.), Sociological methodology (pp. 139–150). San Francisco, CA: Jossey Bass.
Krippendorff, K. (2004). Reliability in content analysis: Some common misconceptions and recommendations. Human Communication Research, 30, 411–433.
Krippendorff, K. (2013). Content analysis: An introduction to its methodology (3rd ed.). Thousand Oaks, CA: Sage.
Laiacona, M., Barbarotto, R., & Capitani, E. (1993). Perceptual and associative knowledge in category specific impairment of semantic memory: A study of two cases. Cortex, 29, 727–40.
Landauer, T. K., & Dumais, S. T. (1997). A solution to Plato’s problem: The latent semantic analysis theory of the acquisition, induction and representation of knowledge. Psychological Review, 104, 211–240. doi:10.1037/0033-295X.104.2.211
Lebani, G., & Pianta, E. (2010a). A feature type classification for therapeutic purpose: A preliminary evaluation with non-expert speakers. In Proceedings of the 4th ACLLAW Workshop (pp. 157–161). New York, NY: ACM Press.
Lebani, G., & Pianta, E. (2010b). Human language technologies supporting therapeutic practices for language disorders: The Project STaRS.sys. In Proceedings of the 7th Annual Meeting of the Italian Society of Cognitive Science (AISC 2010) (pp. 52–56). Rome, Italy: Istituto di Scienze e Tecnologie della Cognizione.
Lenci, A., Baroni, M., Cazzolli, G., & Marotta, G. (2013). BLIND: A set of semantic feature norms from the congenitally blind. Behavior Research Methods, 45, 1218–1233.
McHugh, M. (2012). Interrater reliability: The kappa statistic. Biochemia Medica, 22, 276–282. doi:10.3758/BF03192726
McRae, K., & Boisvert, S. (1998). Automatic semantic similarity priming. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24, 558–572. doi:10.1037/0278-7393.24.3.558
McRae, K., Cree, G., Seidenberg, M., & McNorgan, C. (2005). Semantic feature production norms for a large set of living and nonliving things. Behavior Research Methods, 37, 547–559. doi:10.3758/BF03192726
McRae, K., & Jones, M. (2013). Semantic memory. In D. Reisberg (Ed.), The Oxford handbook of cognitive psychology (pp. 206–219). Oxford, UK: Oxford University Press.
Medin, D. L., & Schaffer, M. M. (1978). Context theory of classification learning. Psychological Review, 85, 207–238. doi:10.1037/0033-295X.85.3.207
Mirman, D., & Magnuson, J. (2009). Dynamics of activation of semantically similar concepts during spoken word recognition. Memory & Cognition, 37, 1026–1039. doi:10.3758/MC.37.7.1026
Montefinese, M., Ambrosini, E., Fairfield, B., & Mammarella, N. (2013). Semantic memory: A feature-based analysis and new norms for Italian. Behavior Research Methods, 45, 440–461. doi:10.3758/s13428-012-0263-4
Murphy, G. (2002). The big book of concepts. Cambridge, MA: MIT Press.
Pexman, P. M., Lupker, S., & Hino, Y. (2002). The impact of feedback semantics in visual word recognition: Number of features effects in lexical decision and naming tasks. Psychonomic Bulletin & Review, 9, 542–549.
Pexman, P. M., Holyk, G. G., & Monfils, M.-H. (2003). Number of features effects and semantic processing. Memory & Cognition, 31, 842–855. doi:10.3758/BF03196439
Poesio, M. (2004). Discourse annotation and semantic annotation in the GNOME corpus. In Proceedings of the 2004 ACL Workshop on Discourse Annotation (pp. 72–79). Barcelona.
Recchia, G., & Jones, M. N. (2012). The semantic richness of abstract concepts. Frontiers in Human Neuroscience, 6, 315.
Rosch, E., & Mervis, C. B. (1975). Family resemblances: Studies in the internal structure of categories. Cognitive Psychology, 7, 573–605. doi:10.1016/0010-0285(75)90024-9
Sartori, G., & Lombardi, L. (2004). Semantic relevance and semantic disorders. Journal of Cognitive Neuroscience, 16(3), 439–52.
Schank, R., & Abelson, R. (1977). Scripts, plans, goals, and understanding: An inquiry into human knowledge structures. Hillsdale, NJ: Erlbaum.
Scott, W. (1955). Reliability of content analysis: The case of nominal scale coding. Public Opinion Quarterly, 19, 321–325.
Smith, E. E., Shoben, E. J., & Rips, L. J. (1974). Structure and process in semantic memory: A feature model for semantic decisions. Psychological Review, 81, 214–241.
Spooren, W., & Degand, L. (2010). Coding coherence relations: Reliability and validity. Corpus Linguistics and Linguistic Theory, 6, 241–266.
Tversky, A. (1977). Features of similarity. Psychological Review, 84, 327–352. doi:10.1037/0033-295X.84.4.327
Tversky, A., & Gati, I. (1982). Similarity, separability, and the triangle inequality. Psychological Review, 89, 123–154. doi:10.1037/0033-295X.89.2.123
Vinson, D., Ponari, M., & Vigliocco, G. (2014). How does emotional content affect lexical processing? Cognition and Emotion, 28, 737–746. doi:10.1080/02699931.2013.851068
Vinson, D. P., & Vigliocco, G. (2008). Semantic feature production norms for a large set of objects and events. Behavior Research Methods, 40, 183–190. doi:10.3758/BRM.40.1.183
Wiemer-Hastings, K., & Xu, X. (2005). Content differences for abstract and concrete concepts. Cognitive Science, 29, 719–736.
Wu, L.-L., & Barsalou, L. W. (2009). Perceptual simulation in conceptual combination: Evidence from property generation. Acta Psychologica, 132, 173–189. doi:10.1016/j.actpsy.2009.02.002
Author note
This study is sponsored by an EU Marie Curie Intra European Fellowship, awarded to Dr Marianna Bolognesi (COGVIM n° 629076, Project Acronym: COGVIM; Call identifier FP7-PEOPLE-2013-IEF). The authors are extremely grateful to Professor Lawrence Barsalou for providing supplementary materials and notes about the Wu and Barsalou taxonomy, Christian Burgers for his comments on a previous draft of the article, and Kilem Gwet for applying the linearization method to our dataset. The authors are also grateful to the two anonymous reviewers, thanks to whom the quality of the article has been substantially improved. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Appendices
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bolognesi, M., Pilgram, R. & van den Heerik, R. Reliability in content analysis: The case of semantic feature norms classification. Behav Res 49, 1984–2001 (2017). https://doi.org/10.3758/s13428-016-0838-6
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13428-016-0838-6