In the last decade, the field of visual word recognition has seen a surge in so-called megastudies (see Balota, Yap, Hutchison, & Cortese, 2012, for an overview). Generally speaking, a typical megastudy comprises several thousand items for which lexical decision, naming, and/or word identification responses are collected. The rationale behind megastudies is that they complement (traditional) factorial studies in which stimuli are selected on the basis of specific lexical or semantic characteristics. That is, factorial studies require one to experimentally control for a number of variables that could potentially obscure the effect(s) of interest. Megastudies, on the other hand, aim to gather data for as many stimuli as possible, without many constraints. The idea is that one can then statistically control for confounding variables by conducting a multiple regression analysis. In addition, continuous variables such as word frequency need not be divided into distinct categories (i.e., high-frequency vs. low-frequency words). This is a critical advantage of the megastudy approach, because artificially dichotomizing continuous variables has been shown to reduce power and increase the probability of Type I errors (Maxwell & Delaney, 1993).

In the present study we sought to build on this work, and we describe a megastudy involving the speeded word fragment completion task (Heyman, De Deyne, Hutchison, & Storms, 2015). Each trial in this task features a word from which one letter has been deleted (e.g., tom_to).Footnote 1 Participants are asked to complete each word fragment as quickly and accurately as possible by pressing a designated response key. Heyman and colleagues used two variants of this task: one in which one of five vowels could be missing (i.e., a, e, u, i, or o), and one in which one of two vowels could be missing (i.e., a or e). It is important to note that there was always only one correct completion, such that items like b_ll were never used. Heyman et al.’s main purpose was to develop a task that could successfully capture semantic priming effects. The idea was that the speeded word fragment completion task requires more elaborate processing than do traditional paradigms such as lexical decision and naming. This would, in turn, allow the prime to exert its full influence, and thus produce more robust priming effects. Indeed, Heyman et al. found a strong priming effect for short, highly frequent words, whereas the lexical decision task failed to show a significant effect for those items.

In addition, Heyman and colleagues (2015) identified some other advantages over the lexical decision task. Specifically, the task is more efficient than lexical decision because it requires no nonwords, and participants rate it as more engaging and easier than the lexical decision task (Heyman et al., 2015). Given the promising results and potential advantages, it would be fruitful to build a database of speeded word fragment completion responses. Having such norms readily available would, for instance, be invaluable when conducting studies with a between-items manipulation. That is, most researchers aim to equate their stimuli on baseline response times in such instances, to avoid finding spurious effects. This is especially relevant in the semantic priming domain, because the magnitude of the priming effect correlates with the baseline response times to both the primes and targets (Hutchison, Balota, Cortese, & Watson, 2008). As a consequence, databases such as the Dutch Lexicon Project (henceforth DLP; Keuleers, Diependaele, & Brysbaert, 2010) and the English Lexicon Project (Balota et al., 2007) are frequently used in studies examining semantic priming (e.g., Hutchison, Heap, Neely, & Thomas, 2014; Thomas, Neely, & O’Connor, 2012). Likewise, a speeded word fragment completion database could be used by semantic priming researchers to derive prime and target baseline latencies for this task.

Besides compiling a large database, another goal of the present study was to gain more insight into the processes underlying the speeded word fragment completion task. Although Heyman and colleagues (2015) provided a first, modest indication of potentially relevant factors, their analyses were based on a limited item sample and considered only five predictor variables. To extend this previous work, a large-scale norming study was conducted involving a total of 8,240 stimuli. Participants were assigned to one of two task versions, each featuring over 4,000 stimuli. Both variants required participants to make a two-alternative forced choice decision. The response options were a and e, in one version, and i and o, in the other. As was the case for Heyman et al., participants were instructed to respond as quickly and accurately as possible. The resulting response times were then used as the dependent variable in item-level regression and mixed-effects analyses featuring 23 predictor variables. All stimuli were selected from the DLP (Keuleers, Diependaele, & Brysbaert, 2010), which allowed us to run the same analyses on lexical decision data, thereby providing a benchmark to evaluate the speeded word fragment completion results. In the remainder of the introduction, we will describe the 23 predictors that were used in the analyses. For the sake of clarity, we divided the predictors into six groups, such that every variable got one of the following labels: standard lexical, relative distance, word availability, semantic, speeded word fragment completion, or interaction. The first four categories all comprise variables derived from the visual word recognition literature. The speeded word fragment completion variables, on the other hand, are based on preliminary work by Heyman et al. and the researchers’ own intuitions about the task. Finally, the sixth set of variables consists of theoretically motivated interaction terms. Each of the six variable groups will be discussed in turn.

Standard lexical variables

Length

Word length, expressed in terms of number of characters, is one of the most studied variables in the visual word recognition literature (see New, Ferrand, Pallier, & Brysbaert, 2006, for an overview). Despite the plethora of research, no clear picture has emerged. That is, both inhibitory and null effects have been reported, as well as facilitatory effects under very specific conditions.Footnote 2

Quadratic length

New et al. (2006) attributed these diverging results to the lack of a linear relation between length and word recognition response times. Instead, they found a U-shaped relation such that length had a facilitatory effect for words of three to five letters, had no effect for words of five to eight letters, and had an inhibitory effect for words of eight to 13 letters. Because of this quadratic pattern, we included quadratic length (based on standardized length values) as a variable in the present study.

Number of syllables

Whereas the two previous variables measure orthographic word length, counting the number of syllables of a word provides a phonological word length measure. Previous studies have shown an inhibitory effect of number of syllables when statistically controlling for orthographic word length (New et al., 2006; Yap & Balota, 2009). The DLP database only features mono- and bisyllabic words; thus, number of syllables was a binary variable in this case.

Summed bigram frequency

This variable measures the orthographic typicality of the target word (e.g., tomato, when the word fragment is tom_to). Every word consists of N – 1 bigrams, where N is the number of characters of a word (e.g., to, om, ma, at, and to for tomato). Evidence is mixed as to how bigram frequency relates to visual word recognition. More specifically, studies have found a positive relation (Rice & Robinson, 1975; Westbury & Buchanan, 2002), a negative relation (Conrad, Carreiras, Tamm, & Jacobs, 2009), and no relation (Andrews, 1992; Keuleers, Lacey, Rastle, & Brysbaert, 2012; Treiman, Mullennix, Bijeljac-Babic, & Richmond-Welty, 1995) between bigram frequency and response times. In the present study, we estimated the occurrence frequency of every bigram using the SUBTLEX-NL database, featuring only letter strings with a lemma contextual diversity above 2 as a corpus (Keuleers, Brysbaert, & New, 2010). All those letter strings were split up in bigrams with the orthoCoding function of the R package ndl (Shaoul, Arppe, Hendrix, Milin, & Baayen, 2013). The frequency of occurrence of the word, operationalized as its contextual diversity (Adelman, Brown, & Quesada, 2006), was taken into account when calculating bigram frequencies, such that bigrams appearing in highly frequent words were given a greater weight. For example, the word the has a contextual diversity count of 8,070, so the bigrams th and he were considered to occur 8,070 times (just for the word the).Footnote 3 The employed procedure did not take the position of the bigram into consideration, meaning that the bigram to in, for instance, store did count toward the bigram frequency of to in tomato. This yielded a frequency table for all bigrams, which was then used to derive the summed bigram frequencies for all target words.

Summed monogram frequency

Monogram frequency is the analogue of bigram frequency for individual letters. Even though it is conceivable that monogram and bigram frequency are correlated (unless they are disentangled in a hypothetical factorial experiment), none of the studies cited above focused on the potential confounding influence of monogram frequency. Andrews (1992) explicitly acknowledged this by noting that “even though the samples were selected according to bigram frequency, they were also relatively equivalent in single-letter frequency” (p. 237). In the present study, we sought to address this issue by entering both variables simultaneously in the analyses.

Relative distance variables

Orthographic Levenshtein distance 20 (OLD20)

OLD20, a variable introduced by Yarkoni, Balota, and Yap (2008), measures the orthographic neighborhood density of the target word (e.g., tomato). Levenshtein distance reflects the number of deletions, substitutions, insertions, and transpositions that are necessary to transform one letter string into another. For instance, the closest orthographic neighbors for call are hall, calls, all, ball, . . . (i.e., their Levenshtein distance is 1), whereas bell, called, mail, . . . are more distant neighbors (i.e., their Levenshtein distance is 2). OLD20 expresses the average Levenshtein distance of a target word to its 20 closest orthographic neighbors. In general, words are recognized faster when their orthographic neighborhood size is relatively large (Yarkoni et al., 2008). Even though there are different ways to look at the orthographic neighborhood (e.g., counting the number of words of the same length that can be formed by changing one letter of the target word; Coltheart, Davelaar, Jonasson, & Besner, 1977), in the present study we used OLD20 because Yarkoni and colleagues’ results suggested that this measure explained more variance in word recognition response times. OLD20 values were calculated using the R package vwr (Keuleers, 2011) with the SUBTLEX-NL database featuring only letter strings with a lemma contextual diversity above 2 as a corpus (Keuleers, Brysbaert, & New, 2010).

Phonological Levenshtein distance 20 (PLD20)

PLD20 is the phonological analogue of OLD20. Yap and Balota (2009) found a positive relation between PLD20 and lexical decision and naming latencies when controlling for a host of other variables including OLD20 (for which they also found a positive relation with response times). Note, however, that the orthography-to-phonology mapping is more opaque in English than it is in Dutch. Yap and Balota examined data from the English Lexicon Project (Balota et al., 2007), so the question is whether their findings might generalize to a shallower language such as Dutch. To calculate PLD20 measures, a lexicon of word forms in DISC notation was created with WebCelex (Max Planck Institute for Psycholinguistics, 2001). Then, PLD20 estimates were again calculated using the vwr package (Keuleers, 2011).

Word availability variables

Contextual diversity

Word frequency has proven to be one of the most potent predictors of response times in visual word recognition studies (e.g., Balota, Cortese, Sergent-Marshall, Spieler, & Yap, 2004). Words that occur often are recognized faster, presumably because repeated exposure increases accessibility. However, Adelman and colleagues (2006) suggested that contextual diversity (i.e., the number of different contexts in which a word occurs) is a better predictor of response times. Moreover, word frequency did not have a facilitatory effect when contextual diversity and length were accounted for, whereas contextual diversity did have a facilitatory effect when controlling for word frequency and length (Adelman et al., 2006). Contextual diversity values were obtained from the SUBTLEX-NL database (Keuleers, Brysbaert, & New, 2010) and were log-transformed (as was also the case in Adelman et al., 2006).

Age of acquisition

The estimated age at which a particular word was learned has been shown to be strongly correlated with various word frequency measures (Brysbaert & Cortese, 2011). Nevertheless, several studies have shown a positive relation between age of acquisition and word recognition response times when statistically controlling for word frequency, suggesting that age of acquisition has a unique effect (Brysbaert & Cortese, 2011; Juhasz, Yap, Dicke, Taylor, & Gullick, 2011; Kuperman, Stadthagen-Gonzalez, & Brysbaert, 2012). Estimates of age of acquisition were obtained from Brysbaert, Stevens, De Deyne, Voorspoels, and Storms (2014).

Cue centrality

Previous work by De Deyne, Navarro, and Storms (2013) has shown that centrality measures derived from word associations can explain variability in lexical decision latencies when controlling for contextual diversity and word frequency. On the basis of a large word association database, De Deyne and colleagues created a network of connected nodes (see also De Deyne & Storms, 2008). Various cue centrality statistics could then be computed for every individual node in the network, where a node corresponds to a word. Perhaps the two most obvious measures are in-degree (i.e., the number of incoming links) and out-degree (i.e., the number of outgoing links). Yet, in this article, we will use the clustering coefficient implemented by Fagiolo (2007). Although it is related to in- and out-degree, this measure is argued to be more sophisticated, since it also captures the connectivity of the neighboring nodes (De Deyne et al., 2013).

Semantic variable

Concreteness

Generally speaking, semantic variables such as the concreteness of a word, but also its imageability and meaningfulness, have been found to be related to word recognition response times (Balota et al., 2004; Schwanenflugel, 1991). That is, concrete words are recognized faster than abstract words, but only when deeper semantic processing is required by the task (Schwanenflugel, 1991). Hence, if the speeded word fragment completion task indeed involves more elaborate processing, as was suggested by Heyman et al. (2015), one would expect a stronger relation between judged concreteness and response times. Concreteness ratings were again obtained from Brysbaert et al. (2014).Footnote 4

Speeded word fragment completion variables

Orthographic Levenshtein distance 20 distractor (OLD20D)

In this context, the term “distractor” refers to the nonword formed by filling in the incorrect letter (e.g., tometo). Thus, OLD20D quantifies the orthographic neighborhood density of the distractor in a similar way as for the target (i.e., OLD20). Because the target and distractor are identical except for one letter, both measures will be highly correlated. Nevertheless, the potential importance of this variable was illustrated by Heyman et al. (2015), who found a strong inhibitory effect of the neighborhood size of the distractor when controlling for the neighborhood size of the target. That is, response times were slower when the distractor had many close orthographic neighbors.

Relative position deleted letter

This variable expresses the relative position of the deleted letter within the word. Its values are obtained by dividing the absolute position of the deleted letter by the word length (e.g., for tom_to it is 4/6 or .67). Given the reading direction, which is from left to right for Dutch, one might expect a negative correlation between this metric and response times. The rationale was that omitting a letter at the beginning of a word would be more disruptive than deleting a letter at the end. That is, in the latter case, participants could use the first (unfragmented) part of the word to better predict the actual word, and thus also the deleted letter.

Quadratic relative position deleted letter

Analogous to the word length effect, we also anticipated a (potential) quadratic relation between response latencies and the relative position of the deleted letter. Concretely, one might expect an inverted U-shaped relation. The reason is that when the deleted letter is located toward the boundaries of the word, a relatively long substring is preserved. For instance, suppose the target word is orange and the word fragment is _range or orang_. In either case, a long substring remains intact (i.e., range and orang, respectively). However, when the deleted letter is located toward the middle of the word, as in or_nge, the resulting substrings, or and nge, appear less revealing when it comes to deciding which letter is omitted. As was the case for word length, quadratic relative position deleted letter was calculated after first standardizing the values of the relative position deleted letter variable.

Local bigram frequency

Whereas the summed bigram frequency counts all bigrams of a word (see above), the local bigram frequency specifically focuses on the bigram(s) that contain the missing letter (e.g., ma and at in tom_to). The idea is that people might restrict their attention to the letter(s) that immediately surround the blank. As a consequence, their response times might be influenced by the so-called local bigrams, such that responses to stimuli with a higher local bigram frequency are faster. Naturally, local bigram frequencies will be correlated with summed bigram frequencies, yet it is important to disentangle their effects by adding them both to the regression equation. For one thing, the variables might have opposite effects: facilitatory for local bigram frequency, and null or even inhibitory for summed (global) bigram frequency. Local bigram frequencies were obtained in a way similar to that for summed bigram frequencies. Word fragments with a missing letter at the word boundary (e.g., orang_) have only one local bigram, and thus their frequency estimates would be lower in comparison to other word fragments, such as or_nge. Therefore, the average bigram frequency was computed in the latter cases [e.g., for or_nge: (bigram frequency of ra + bigram frequency of an)/2].

Deleted letter

There were two variants of the speeded word fragment completion task: one in which the deleted letter was a or e, and one in which the deleted letter was i or o. The variable deleted letter indicated the correct response to each word fragment. We used a dummy coding scheme, such that the letters a and i served as the baseline in the analyses of, respectively, the a/e and i/o data. If there were a consistent response bias across participants or if omitting one specific letter were more detrimental than the other, this would show up in the regression weight for this predictor. Note, however, that we tried to eliminate response bias by selecting equal numbers of stimuli per response option. Also note that this variable will be related to summed monogram frequency in the a/e version of the task, because the letter e occurs considerably more often than the letter a in Dutch. Consequently, the monogram frequency variable only captured the (potential) effect of the nondeleted letters in a regression analysis with deleted letter as another predictor.

Alternative completion

The premise of the speeded word fragment completion task is that there is always only one correct response. However, in some cases other completions could be possible if they were permitted as a response option. For instance, the correct completion of p_int is paint and not peint, but filling in the letter r would yield the orthographically legal word print. Despite the fact that the letter r was not allowed as a response, it might still create conflict, and thus slow down response times. Furthermore, the degree of response conflict might depend on the occurrence frequency of the alternative completion such that highly accessible alternatives would have more adverse effects. To evaluate these assumptions, the alternative completion variable was added to the equation. This is a categorical variable with three possible values: 0, indicating that there are no alternative completions; 1, indicating an alternative completion with a low occurrence frequency; and 2, indicating an alternative completion with a high occurrence frequency. The frequency of occurrence was again operationalized as the log-transformed contextual diversity (Adelman et al., 2006), where values below 2 were considered low. When there were two or more alternative completions (e.g., print and point for p_int), the one with the highest contextual diversity was used.

Vowel type

This variable concerns the vowel configuration of which the missing letter is a part. The deleted letter in the present experiment was always a vowel. Consequently, it could be surrounded by consonants (e.g., tom_to) or it could be part of a double, triple, or quadruple vowel (e.g., p_int, s_eing, or qu_uing). Here, we distinguished three types: single vowels (as in tom_to), repeated double vowels (as in b_etle), and an “other” category that included nonrepeated double vowels, triple vowels, and quadruple vowels. The repeated double vowels category served as the baseline in the dummy coding scheme used here. Previous work from Heyman et al. (2015) suggested that word fragment completion takes longer when the missing letter is part of a double vowel than when it is a single vowel. However, these results came from a word fragment completion task with five response options, and the authors made no distinction between repeated and nonrepeated double vowels.

Interaction variables

In theory, we could include all two-way interactions as well as all higher-order interactions. However, this would yield a very complex model, which could lead to convergence issues when conducting mixed-effects analyses. Therefore, we only added five theoretically motivated two-way interactions.

Contextual Diversity × Length

Several previous studies have examined the (potential) interaction between word frequency and word length (Balota et al., 2004; Weekes, 1997; Yap & Balota, 2009). However, as was the case for the main effect of word length, no clear picture has emerged. On the one hand, Balota and colleagues found an inhibitory length effect that diminished when word frequency increased. In contrast, even though Weekes initially observed a similar pattern, no significant length effect remained for both low- and high-frequency words when covariates such as neighborhood size were introduced. Yap and Balota’s results were also mixed, in particular they found a significant Frequency × Length interaction in the naming task, but the interaction did not reach significance in the lexical decision analysis (despite going in the same direction). In the present study, we further explored this apparent discrepancy using the contextual diversity measure advocated by Adelman et al. (2006) instead of word frequency.

Contextual Diversity × Quadratic Length

A potential explanation for the lack of a consistent Frequency × Length interaction is that there is no linear length effect in the first place. As we discussed above, New and colleagues (2006) found a quadratic effect of word length. It is theoretically possible that this effect varies with word frequency such that, for instance, mainly (or only) low-frequency words show this U-shaped relation. A study from Hyönä and Olson (1995) examining eye fixation patterns when reading aloud provided some suggestive evidence for such an interaction. First-fixation durations showed the typical quadratic length effect, but only when medium- and low-frequency words were considered. High-frequency words, on the other hand, showed an inverted U-shaped length effect. One might wonder whether this is a general pattern that would also emerge in a speeded two-alternative forced choice task such as word fragment completion.

Contextual Diversity × OLD20

Several studies in the visual word recognition domain have examined whether word frequency and orthographic neighborhood size interact (Andrews, 1992; Balota et al., 2004; Sears, Hino, & Lupker, 1995; Yap & Balota, 2009). The general finding is that neighborhood size facilitates lexical decision and naming performance for low-frequency words. The picture for high-frequency words is less clear. The common understanding is that high-frequency words do not benefit as much from orthographic neighbors as low-frequency words do. However, considered in isolation, facilitatory and inhibitory effects of neighborhood size have been reported for high-frequency words (as well as null effects). Yarkoni et al. (2008) suggested that a more powerful metric such as OLD20 could resolve these inconsistencies. Their analyses indeed showed a significant Frequency × OLD20 interaction that explained more variance than the traditional Frequency × Neighborhood Size interaction. Given that contextual diversity explains more variance than word frequency (Adelman et al., 2006), one might expect the Contextual Diversity × OLD20 interaction to be even more potent in this regard.

Contextual Diversity × PLD20

To clearly disentangle orthographic and phonological neighborhood density effects, we also included a Contextual Diversity × PLD20 interaction. There has been some debate as to the nature of neighborhood density effects, because both density measures are usually strongly correlated (e.g., Mulatti, Reynolds, & Besner, 2006). Mulatti and colleagues argued that phonological neighborhood density, but not orthographic neighborhood density, affects naming performance. So, when examining the potential influence of orthographic neighborhood density, it is important to control for phonological neighborhood density.

Contextual Diversity × Concreteness

As we discussed above, concrete words tend to be recognized faster than abstract words. However, this effect mainly (or only) manifests itself in low-frequency words (Schwanenflugel, 1991). In a similar vein, Strain, Patterson, and Seidenberg (1995) suggested that atypical low-frequency words benefit more from a rich semantic representation than do high-frequency words. It should be noted, though, that more recent evidence has cast some doubt on this conclusion. For instance, Balota et al. (2004) did not find a significant interaction between word frequency and semantic variables (see also Yap & Balota, 2009).

Method

Participants

Forty paid volunteers participated in the experiment (eight men, 32 women; mean age 21 years). The experiment consisted of two separate 1-h sessions, and participants received a payment of €16 when they completed both sessions. All participants were native Dutch speakers. The study was approved by the Ethical Committee of the Faculty of Psychology and Educational Sciences of the University of Leuven, and participants provided written informed consent before starting the experiment.

Materials

The stimuli for the speeded word fragment completion task were words from which one letter had been deleted (e.g., tom_to). The omitted letter was always either an a, e, i, or o. The rationale behind using these specific letters was that they all had a high occurrence frequency in Dutch, which would allow us to select as many stimuli as possible. To make the task similar to other two-alternative forced choice tasks, we decided to make two separate item pools. One set contained only words from which the letter a or e had been deleted, and the other set contained words from which an i or an o had been deleted. There was one restriction in the selection of stimuli, in that only word fragments with a single correct completion were used. For example, a stimulus such as m_n was unsuitable because both response options, in this example the letters a and e, would be plausible (yielding, respectively, man and men). In contrast, a stimulus such as l_ck was a good candidate for the a/e version of the task, because lack is an existing word but leck is not. Note, though, that in this particular instance the word fragment would have other correct completions if the design had no response restrictions (i.e., lock, luck, or lick; see the alternative completion variable above). Yet, within the context of the a/e task, there was only one correct response.

All stimuli were chosen from the DLP (Keuleers, Diependaele, & Brysbaert, 2010), which made it possible to compare the present data with lexical decision data. Stimulus selection occurred as follows. First, all words were removed that contained no as, es, is, or os. For the remainder of the stimuli, we checked whether the distractor was an existing word. The term “distractor” here refers to the stimulus formed by filling in the nontarget letter. The stimulus man would yield m_n as its word fragment and men as a distractor, whereas lack would yield l_ck as the word fragment and leck as a distractor. Since the distractor in the former case is an existing word, it was removed from the candidate pool. To check whether distractors were indeed nonwords, we used the SUBTLEX-NL database listing all letter strings with a lemma contextual diversity greater than 2 (Keuleers, Brysbaert, & New, 2010). Thus, only stimuli with a distractor that was not listed in this database were used. One additional restriction applied to words that contained the same target letter more than twice (e.g., repressed). Whether the distractor was an existing word was only assessed for the first two occurrences of the target letter. That is, for repressed, we checked whether rapressed and reprassed existed, but not whether repressad existed.

In a next step, all stimuli were divided in two pools: the a/e pool and the i/o pool. Some stimuli could be part of both pools (e.g., tomato could be put in the a/e pool, tom_to, or the i/o pool, t_mato). The majority of those stimuli were randomly assigned to one pool, except for 800 stimuli that were placed in both pools. Each letter combination (i.e., a + o as in tomato, a + i, e + o, and e + i) occurred 200 times in those 800 common stimuli.

Then, the stimuli within a pool were assigned to a target letter. In some instances there was no choice (e.g., for lack), but in others both letters, either a and e or i and o, could be deleted (e.g., deaf could yield the word fragments de_f, in which a was the target letter, and d_af, in which e was the target letter). Once stimuli had been assigned to a unique letter, the position of the deleted letter might need to be determined. Again, this only applied to a subset of the stimuli—that is, words containing the same target letter twice (e.g., repressed could yield the word fragments r_pressed and repr_ssed). We opted to delete the first letter (as in r_pressed) in 75 % of those instances if the target letter were e or i, and in 50 % of the cases if the target letter were a or o. The reason for this unequal distribution was to keep the average position of the deleted letter more or less similar within an item pool, because in Dutch, many verbs and plurals end in -en, and many adjectives end in -ig.

Finally, all remaining stimuli were manually checked to make sure that the distractor was indeed a nonword and that no proper names were included. To assure that participants would be unbiased, equal numbers of stimuli per response option were selected. This ultimately led to 4,200 stimuli in the a/e item pool, half of which required an a response, and 4,040 stimuli in the i/o item pool, half of which required an i response. Because the experiment consisted of two sessions, each item pool was split up in two lists (henceforth, List A and List B). Stimuli were randomly assigned to a list, with equal numbers of stimuli for both response options.

Procedure

The entire experiment consisted of two sessions that lasted approximately 1 h each. Participants were tested individually, and the time between the sessions was minimally one day and maximally two weeks. They were informed that the experiment involved completing words from which one letter had been deleted as quickly and accurately as possible. In addition, the instructions stated that only two response options were possible (i.e., a/e or i/o) and that there was always only one correct completion. Participants used the arrow keys to respond.

We created eight different versions of the experiment, resulting from combining three between-subjects factors: Item Pool (a/e vs. i/o), List Order (List A in the first session vs. List B in the first session), and Response Keys (left arrow corresponding to a or i vs. left arrow corresponding to e or o). Experiment version was counterbalanced across participants. On every trial, a word fragment was shown until the participant responded, and the intertrial interval was 500 ms. The order of the stimuli within a session was random. Each session was split into 14 blocks of 150 stimuli (except the last block of the i/o version, which consisted of only 70 stimuli). After each block, participants were allowed to take a self-paced break, and they also received feedback about their performance. If their accuracy for a certain block dropped below 85 %, they were encouraged to be more accurate. Before the start of each session, participants got a practice block comprising 30 different trials, 15 per response option. In contrast to the actual experiment, during the practice phase participants got immediate feedback if they made an error (i.e., the message “Wrong answer” was displayed for 1,000 ms). The experiment was run on a Dell Pentium 4 computer with a 17.3-in. CRT monitor using PsychoPy (Peirce, 2007).

Results

Reliability and descriptive statistics

First, the reliability of the response times was assessed by calculating Cronbach’s α. The a/e and i/o datasets yielded αs of, respectively, .83 and .82. Log-transforming the response times slightly increased α to .87 for both datasets; however, all further analyses were performed on the untransformed response times. The obtained reliability estimates are comparable to those reported in lexical decision megastudies (Keuleers, Diependaele, & Brysbaert, 2010; Keuleers et al., 2012). Note though, that in the present study only 20 participants were required in order to reach such high reliability estimates, whereas the latter lexical decision megastudies needed about twice that number.

In a next step, outliers and errors were excluded, after which the average response time per item was calculated. Outliers were removed in two steps. First responses faster than 250 ms or slower than 4,000 ms were omitted, as well as erroneous responses. Then, participant-specific cutoff values, defined as the mean plus three standard deviations, were calculated. Response times exceeding this criterion were also discarded. As a result of this procedure, 4.8 % and 8.1 % of the data were removed from the a/e and i/o datasets, respectively. The resulting average response times per item as well as the standard deviation and accuracy are available as a supplementary Excel file. The response times averaged across items were 739 and 823 ms, for, respectively, the a/e and i/o items. The average accuracies were, respectively, 95.2 % and 94.7 %. Despite the high overall accuracy, some item-level accuracies were as low as 5 % (e.g., t_am, which should be completed as team, an English loanword). Because the averaged response times for such items were only based on a limited number of data points, all further analyses were performed on items for which the accuracy was higher than 70 %. As a result, 106 and 103 items were omitted from the a/e and i/o lists, respectively.

Item-level regression analyses

In order to understand the underlying mechanisms of the speeded word fragment completion task, we sought to relate a number of predictors to the response times obtained in this norming study. Some of the predictors were derived from the existing word recognition literature, whereas others were selected on the basis of our intuitions about the nature of the speeded word fragment completion task itself. Before turning to the actual regression analyses, we first wanted to explore the relation between the speeded word fragment completion task and the lexical decision task. From previous research (Heyman et al., 2015), one would expect a statistically significant correlation between the response times in both tasks. Yet, if both tasks partly differ in their underlying processes, one would only expect a small to moderate correlation. The analyses revealed correlations of .36 {a/e items: t(4092) = 24.78, p < .001, 95 % CI [.33, .39]} and .41 {i/o items: t(3935) = 28.25, p < .001, 95 % CI [.38, .44]}. Both correlations were subsequently corrected for attenuation (Spearman, 1904) using the reliabilities reported above and in Keuleers, Diependaele, and Brysbaert (2010). The resulting disattenuated correlations were .44 for a/e items and .51 for i/o items. To test whether the disattenuated correlations were imperfect, we applied Kristof’s (1973, Case II) method. This procedure required trial-by-trial data from both the lexical decision and the speeded word fragment completion task. First, errors and outliers were removed using the criteria described earlier. Then, the participants were randomly split into two groups to create two parallel halves of each task. This was done for both the a/e and i/o versions separately. Applying Kristof’s test showed that we could reject the null hypothesis, meaning that the disattenuated correlations differed significantly from 1 [t(4093) = 45.76, p < .001, for a/e items; t(3936) = 41.89, p < .001, for i/o items]. Taken together, the results confirmed that there are both similarities and differences between lexical decision and word fragment completion.

In addition, we examined the response times to the items that occurred in both the a/e and i/o lists. The correlation between the speeded word fragment completion response times to those items was .34 {t(767) = 9.94, p < .001, 95 % CI [.27, .40]}. Applying Spearman’s correction for attenuation with the reliability estimates reported above resulted in a correlation of .41 [Kristof’s test: t(768) = 20.73 p < .001]. We interpreted these findings to mean that word-specific variables can only explain a limited amount of variance in the word fragment completion response times.

To examine in more detail which variables were related to the response times, a multiple regression analysis was performed. All 23 variables were simultaneously entered into the regression equation (because of missing values for some predictors, the actual analyses were performed on a subset of the data; see Table 1 for summary statistics on the predictors, and Tables 2 and 3 for zero-order correlations). The three categorical variables (i.e., deleted letter, alternative completion, and vowel type) were dummy coded, whereas all other variables were standardized. This resulted in 25 regression weights being estimated, since the variables alternative completion and vowel type both comprised three categories. In order to limit the Type I error probability, only p values below .002 (.05/25) were considered to provide significant evidence against the null hypothesis. Furthermore, the data from the two item pools were analyzed separately to give us an idea about the generalizability of the effects. The results are summarized in Table 4. Overall, they are very consistent across item pools and fit nicely with the predictions from the word recognition literature (see below for a more detailed evaluation).

Table 1 Means and standard deviations for the predictors in the regression analyses
Full size table
Table 2 Zero-order correlations between predictors and dependent variables for a/e items (N = 3,379)
Full size table
Table 3 Zero-order correlations between predictors and dependent variables for i/o items (N = 3,082)
Full size table
Table 4 Item-level regression results for the speeded word fragment completion task
Full size table

In order to directly compare the speeded word fragment completion task with the lexical decision task, additional analyses were conducted using the DLP lexical decision latencies as the dependent variable. All 23 predictor variables were again included in these analyses, even though the speeded word fragment completion variables are senseless in a lexical decision context. This was done to ensure that the latter variables were indeed specific to the fragment completion task and that they do not measure some general word recognition property. Also, to assure comparability, the a/e and i/o division was kept in the analyses, despite the fact that this distinction is actually irrelevant in the lexical decision task. The results, summarized in Table 5, are a bit surprising in some ways. Considered as a whole, the findings were rather consistent across the item pools, but the regression weights for some variables did not follow the predicted pattern. More specifically, the length variables (i.e., quadratic word length and number of syllables) and the Levenshtein distance measures (i.e., OLD20 and PLD20) seemed to have either no effect or an unexpected facilitatory effect. One might argue, however, that the inclusion of the speeded word fragment completion variables and/or the interaction terms somehow distorted the results of the lexical decision analyses. To address this concern, we reanalyzed the lexical decision data using only the regular word recognition variables (see Table 6). Taken together, the results remained essentially the same when removing the speeded word fragment completion and interaction variables.

Table 5 Item-level regression results for the lexical decision task
Full size table
Table 6 Item-level regression results for the lexical decision task without the speeded word fragment completion and interaction variables
Full size table

Thus far, the analyses allowed us to evaluate the roles of the different variables, yet it remained unclear how much total variance they explain. To get an idea about the contributions of the six variable groups, hierarchical regression analyses were performed. Contrary to the previous analyses, in which all predictors were entered at once, we now added predictors in a stepwise fashion. In a first step, only the standard lexical variables were included, and the resulting R 2 was calculated. Then, the other groups were added in the following order: relative distance variables, word availability variables, semantic variable, word fragment completion variables, and interaction variables. The R 2 estimates, calculated after each step and separated by task and item pool, are reported in Table 7. The proportion of variance explained by all predictors was slightly lower in the speeded word fragment completion task than in the lexical decision task (i.e., respectively, .421 vs. .475 for a/e items, and .399 vs. .471 for i/o items). Intriguingly, the word availability variables accounted for the vast majority of the variance explained in the lexical decision task, whereas in the speeded word fragment completion task the proportion of explained variance was more evenly distributed across the standard lexical variables, the word availability variables, and the variables specific to speeded word fragment completion. The fact that the latter variable group contributed only very meagerly toward the total R 2 in the lexical decision task confirms that these variables do not tap into general word recognition processes.

Table 7 R-squared values at each step of the hierarchical item-level regression analysis, with R-squared changes in parentheses
Full size table

Mixed-effects analyses

The previous set of analyses required us to collapse over participants to obtain the average response time per item. Not only does such an approach ignore (potential) interindividual differences, it also neglects longitudinal effects. For instance, practice and/or fatigue can influence response times, but these effects go undetected when one averages over participants. A key advantage of mixed-effects modeling is that it allows researchers to statistically control for such longitudinal effects (Baayen, Davidson, & Bates, 2008). Therefore, we reanalyzed the speeded word fragment completion and lexical decision latencies using mixed-effects models. Again, the analyses were split up per task and item pool, but now the trial-by-trial data were used. In addition to the independent variables that were used before, we also included trial number as a predictor.Footnote 5 The three categorical variables (i.e., deleted letter, alternative completion, and vowel type) were dummy coded, and all other variables were standardized. One notable difference was that we no longer included speeded word fragment completion variables in the analyses of lexical decision latencies, because the item-level regression analyses confirmed that those variables are meaningless within the context of a lexical decision task. The results of the mixed effects analyses are shown in Table 8, for speeded word fragment completion, and Table 9, for lexical decision.Footnote 6

Table 8 Mixed-effects results for the speeded word fragment completion task
Full size table
Table 9 Mixed-effects results for the lexical decision task
Full size table

Summary

The item-level regression and mixed-effects analyses yielded very similar outcomes. Looking at the speeded word fragment completion results, we see that 11 variables were consistently related to the response latencies. That is to say, 11 variables showed a significant effect across both item pools and analysis methods (using a significance level of .002; see above): length, quadratic length, OLD20, contextual diversity, age of acquisition, OLD20D, quadratic relative position deleted letter, local bigram frequency, deleted letter, alternative completion, and vowel type. Turning to the lexical decision task, only four variables yielded consistent effects: contextual diversity, age of acquisition, cue centrality, and concreteness. Obviously, speeded word fragment completion variables are meaningless in the context of lexical decision, but it is remarkable that several other predictors did not show the expected effects. For one, neither (quadratic) word length nor number of syllables consistently predicted response times in the lexical decision task. In contrast, we did observe a significant U-shaped relation between word length and speeded word fragment completion latencies (see Fig. 1). Similarly, we found a significant inhibitory OLD20 effect in the speeded word fragment completion task, but not in the lexical decision task (we will elaborate on this issue in the Discussion section). It is also noteworthy that the theoretically motivated interaction effects were never consistently significant in either the speeded word fragment completion task or the lexical decision task.

Fig. 1
figure 1

Relation between word length, in number of characters (x-axis), and predicted standardized response times (y-axis) for a/e stimuli in the lexical decision task (black bars) and the speeded word fragment completion task (gray bars). The predictions are based on the item-level regression results, thereby ignoring the (nonsignificant) interactions

Full size image

Discussion

In the present study, we gathered speeded word fragment completion data for 8,240 stimuli. The goal of this undertaking was twofold. On the one hand, we sought to provide norms that can be used in subsequent studies—for instance, to match stimuli on baseline response time and accuracy. The other aim of this megastudy was to gain more insight into the underlying processes of the speeded word fragment completion task. To this end, item-level regression and mixed-effects analyses were carried out on the response times using 23 predictor variables. In addition, since all stimuli were selected from the DLP (Keuleers, Diependaele, & Brysbaert, 2010), a direct comparison with the lexical decision task was possible. The results showed moderate correlations between lexical decision latencies and speeded word fragment completion latencies, indicating that the tasks have both similarities and differences. When the same analyses were performed on the lexical decision data, some remarkable discrepancies emerged. In what follows, we first offer some explanations for the diverging findings. Then we close with a discussion of potential (nonimplemented) process models of the speeded word fragment completion task.

Comparing speeded word fragment completion with lexical decision

As we mentioned above, some variables did not show the predicted relation with lexical decision performance. This was especially the case for the relative distance measures OLD20 and PLD20. Not only were these variables not consistently related to lexical decision times, the obtained regression weights were nearly always numerically negative. In contrast, OLD20 was a reliable predictor of speeded word fragment completion response times. More specifically, a fragment was completed faster when the target word (e.g., tomato for tom_to) had a small OLD20 value, which is indicative of a dense orthographic neighborhood.

Our unexpected findings for the lexical decision task could potentially be due to a multicollinearity issue. Indeed, Yap, Tan, Pexman, and Hargreaves (2011) found no significant effects of OLD20 and PLD20, which they attributed to the high correlations among the predictor variables. Note that Yap and colleagues (Yap & Balota, 2009; Yap et al., 2011) also included number of orthographic neighbors and number of phonological neighbors as predictors, thereby potentially aggravating the multicollinearity issue. To assess whether our parameter estimates were distorted as a consequence of multicollinearity, variance inflation factors (henceforth, VIFs; Freund, Wilson, & Sa, 2006) were calculated for the 11-variable analysis (see Table 6). All VIFs were smaller than 7, where values of 10 or higher are generally considered problematic. This suggests that the results for the lexical decision task were not distorted because of multicollinearity.

Another possibility is that the unexpected findings are due to the specific stimulus selection procedure used here. As we described in the Method section, the stimuli for the speeded word fragment completion task had to meet certain criteria. The resulting item pool is thus a selective sample of all possible word stimuli. One might therefore argue that the uncharacteristic results for the lexical decision task are due to a biased set of stimuli. However, it is important to recognize that the majority of the DLP word stimuli were included and that the analyses were performed on over 3,000 stimuli per item pool. Even though this sample could potentially be biased in one way or another, the number of stimuli is nevertheless substantial. Furthermore, although a biased item pool could in principle explain differences between the present lexical decision results and those observed in other studies, it is not clear how such an explanation resolves the inconsistencies between the lexical decision and speeded word fragment completion results. The analyses involved exactly the same stimulus set, so if this explanation were true, one would expect the effects of word-specific variables such as OLD20 to be distorted in both tasks. This was clearly not the case, as can be seen in Tables 4 and 5 and Tables 8 and 9.

Finally, one might speculate that the speeded word fragment completion task is better-equipped than the lexical decision task to capture certain effects, perhaps because participants rely on different strategies to optimize their performance. Specifically, the nature of the nonwords could play a pivotal role in the lexical decision task. For instance, if words on average have a denser orthographic neighborhood (indicated by lower OLD20 values) than nonwords, participants might become aware of this contingency and use it to their advantage. If it is the other way around (i.e., lower OLD20 values for nonwords), a dense orthographic neighborhood would be indicative of a nonword. In the latter case, it is not unthinkable for OLD20 to have no or even a facilitatory effect on response times for word stimuli. Some of the observed inconsistencies might thus be attributed to differences in the task characteristics.

Taken together, we proposed three possible explanations for the discrepancies between the speeded word fragment completion task and the traditionally used lexical decision task. We would emphasize, though, that there are also parallels between the tasks, so both are in a sense complementary. More importantly, none of the three suggestions invalidates the results obtained with the speeded word fragment completion paradigm. This is a critical conclusion, because it affirms that the proposed paradigm can be used not only within the context of semantic priming, but also to examine visual word recognition in general. In this regard, it is noteworthy that the present paradigm is more efficient than the lexical decision task. That is to say, it does not require nonwords, so the number of stimuli is reduced by half (assuming that equal numbers of words and nonwords are used in lexical decision). Moreover, one needs about half the number of participants to obtain reliability estimates similar to those in the lexical decision task. Yet, several decades of research using the lexical decision task have offered insight into its underlying processes, whereas not much is known about the speeded word fragment completion task. In the remainder of the discussion, we try to provide a first step in the direction of uncovering the mechanisms that play a role in the latter task. Concretely, we will first summarize the findings regarding the speeded word fragment completion variables. Then we will put forth a set of explanations of the task and discuss their validity in light of the data.

Speeded word fragment completion variables

The set of seven variables that were designed to measure specific aspects of the speeded word fragment completion task indeed accounted for a considerable amount of variance in this task. That is, R 2 estimates increased from .23–.26 to .40–.42 (see Table 7), values that are comparable to those obtained for the lexical decision task (i.e., .46–.47). As expected, adding these variables to the analyses of the lexical decision data did not improve the model predictions much. Given this observation, and the fact that we observed no consistent effects across item pools, one can safely assume that these variables are indeed irrelevant to lexical decision. The remainder of this section will therefore focus only on the results for the speeded word fragment completion task. We will summarize the results here, but defer a discussion about the underlying processes to the last section of this discussion.

OLD20D

A very potent predictor of word fragment completion response times was the orthographic neighborhood density of the distractor (e.g., OLD20 of tometo when the fragment was tom_to). Responses to word fragments were relatively slower when the distractor had a dense orthographic neighborhood. Note that we did not derive a similar measure for the phonological neighborhood of the distractor, because Dutch does not have exact spelling-to-sound mapping. As a consequence, it was not always clear how one would pronounce the distractor.

Relative position deleted letter

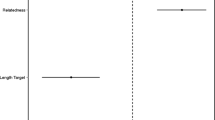
The results provided evidence for an inverted U-shaped relation between the relative position of the deleted letter within the word fragment and response times. Responses were faster when the omitted letter was located toward the boundaries of the word (e.g., _range or orang_). This is illustrated in Fig. 2. It depicts the model predictions for the different values of the relative position deleted letter variable when controlling for all other variables. As we suggested in the introduction, one might explain this finding in terms of substrings that are more or less intact. Substrings in the word fragment completion task are created by the blank (e.g., tom and to in tom_to). Unless the deleted letter is the first or last letter of a word, there are always two substrings. The proposal is that a longer substring puts more constraints on the identity of the complete word, which in turn results in faster response times. To illustrate this, consider again the three potential word fragments for orange: or_nge, _range, and orang_. The latter two word fragments yield longer intact substrings (i.e., range and orang) that readily elicit the complete word, whereas shorter substrings (i.e., or and nge) appear more equivocal in this respect.

Fig. 2
figure 2

Relation between the relative position of the deleted letter (x-axis) and the predicted standardized response times (y-axis) for the a/e version (red dots) and the i/o version (blue triangles), based on the item-level regression analyses. Every symbol represents an actual value of the relative position deleted letter variable in the dataset

Full size image

Local bigram frequency

Local bigram frequency facilitated responses, such that word fragments with local bigrams that occurred often were completed faster. This was taken to mean that the letter(s) closest to the blank play a special role. Participants seem to rely somehow on the co-occurrence frequency of the target letter with the surrounding letter(s).

Deleted letter

The sign of the corresponding regression weights indicated that the a and i responses were given faster than the e and o responses. This could imply that word fragments in which the a or i was deleted were easier to complete (after controlling for a host of other variables). Alternatively, participants could have had a systematic preference for one letter. With regard to the latter possibility, it is noteworthy that the occurrence frequency of the letter was inversely related to response times in the a/e case. If participants were to use the base rate to guide their responses, one would expect a bias in favor of the letter e, because it is by far the most prevalent letter in Dutch.

Alternative completion

Word fragments with alternative, yet unacceptable, solutions are responded to more slowly than fragments with only a single legal completion. For some stimuli (e.g., p_int), one can create an existing word by filling in a letter that was not part of the response options. For instance, inserting r would yield the word print, but because only a and e were allowed as responses, the correct answer is paint in this case. Furthermore, a distinction was made between low- and high-frequency alternative completions. The alternative seemed to interfere more if it occurred in many different contexts.

Vowel type

We discerned three vowel types: single vowels (e.g., tom_to), repeated double vowels (e.g., b_etle), and an “other” category consisting of nonrepeated double vowels, triple vowels, and quadruple vowels (e.g., p_int, s_eing, or qu_uing). The results revealed that word fragments from the second group (i.e., repeated double vowels) were completed faster. There appeared to be no systematic difference between the single-vowel category and the “other” category. The observed effects can be explained in several ways. One possibility is related to the local bigram frequency effect. The repeated double-vowel bigram (e.g., ee in b_etle) occurs considerably more often in Dutch than the equivalent distractor vowel combination (e.g., ae). This is not so pronounced, or is even reversed, for the simple-vowel and “other” categories. When participants rely to a certain extent on the frequency of local bigrams and factor in the distractor letter, it becomes clear why such a vowel-type effect would occur. Alternatively, the sound of the vowels may have an impact (too). In Dutch, there is generally no uncertainty about how a repeated double vowel is pronounced, but this is not true for all vowel types. For instance, the letters a in the words taken (“tasks” in English) and takken (“branches”) are pronounced differently (i.e., their phonetic transcriptions in the International Phonetic Alphabet are [ta:kən] and [tɑkən], respectively). This might potentially lead to confusion and slower responses.

Toward a process model of the speeded word fragment completion task

The goal of this study was not to provide a complete, theoretically sound model of the workings of the speeded word fragment completion task. Still, the present results do give us insight into the underlying processes, and also rule out some a priori plausible models. In this section, we put forth a (nonexhaustive) set of explanations of the task and discuss their validity in light of the data.

One might view the speeded word fragment completion task as a word identification task augmented with a late decisional component. Deleting a letter from a word is conceivably a form of visual degradation. The only difference is that participants would ultimately have to decide between two response options. In this sense, it involves a mostly bottom-up process, since task specificities enter relatively late in the decision. Such an account would predict the striking similarities observed between our results and those obtained with other visual word recognition paradigms. It can also explain the alternative completion effect. Initially, for instance, paint, print, and point all emerge as potential completions of the word fragment p_int, with perhaps a preference for the word with the highest occurrence frequency. Only during the final decision stage is the sole suitable completion selected (i.e., paint), which is arguably more time-consuming when there are multiple candidates. Crucially, the distractor (peint, in this example) plays no role in this explanation, an assumption that seems untenable, given its strong inhibitory orthographic neighborhood density effect. The latter effect suggests that the distractor is at least considered at some point in the word fragment completion process. In other words, it cannot be a purely bottom-up process. A complete account of the speeded word fragment completion task needs a top-down component (too).

Another approach to the two-alternative speeded word fragment completion task is to fill in both letters and check which option yields an existing word (e.g., paint or peint). This could be done in a serial or a parallel fashion. That is, one might consider only one potential completion at a time, or evaluate them concurrently. The former account resembles a lexical decision task in which inserting a certain letter yields an existing word or a nonword. Depending on the outcome, either the considered letter or the alternative option will be given as a response. Such an account could explain a response bias by assuming that the same letter is always filled in and that affirmations (“yes this is a word”) result in faster (or slower) responses. The other possibility is that both completions are taken into account simultaneously. This is also a form of lexical decision, since participants have to select the actual, legal word out of the two possible completions. If the speeded word fragment completion task is indeed some sort of lexical decision task in disguise, one would expect the pattern of results observed here, which was largely consistent with other word recognition studies. This top-down account, in both its serial and parallel variants, can even clarify why the orthographic neighborhood of the distractor has an impact. Namely, a distractor with many neighbors is more word-like, which probably complicates the decision, leading to slower response times. However, if the speeded word fragment completion task is purely top-down-driven, what about the effect of the deleted letter’s relative position? Why would responses to fragments such as or_nge be slower than those to _range or orang_? All three examples yield the same word (i.e., orange); hence, lexical decision latencies should be similar. Put differently, the place of the blank should not matter, unless one was to assume that it would affect the insertion process. Given the quadratic trend of the effect, the latter claim would entail that filling in a letter at the boundary of a word requires less time than filling in a letter toward the middle of a word.

To account for the complete pattern of results observed in the present study, one could also envision a “compromise” model with both top-down and bottom-up processes. A key characteristic of the speeded word fragment completion task is that it requires a decision between two alternatives. Therefore, one might view the two-alternative speeded word fragment completion as a diffusion process, which encompasses both top-down and bottom-up influences. Previous research has already successfully applied the diffusion model to the lexical decision task (Ratcliff, Gomez, & McKoon, 2004; Wagenmakers, Ratcliff, Gomez, & McKoon, 2008). One could extend this approach to the speeded word fragment completion task, though some modifications would be in order. The diffusion model postulates the existence of two decision boundaries, which determine the amount of evidence necessary for a certain response option (Ratcliff, 1978). In the lexical decision task, the two boundaries correspond to word and nonword. The central premise of the diffusion model is that information is accumulated over time until one of the boundaries is reached. The response option associated with this boundary is then selected. The speed with which information is accumulated is called the “drift rate”, and previous research has shown that it is influenced by word frequency in the lexical decision task (Ratcliff et al., 2004; Wagenmakers et al., 2008). A translation to the speeded word fragment completion task would involve changing the boundaries from word/nonword to a/e or i/o. The idea is that words with high values for contextual diversity would have high absolute drift rates. Similarly, low values for age of acquisition and OLD20 would result in high absolute drift rates. Note that this is markedly different from the application of the diffusion model in the context of a lexical decision task. In the latter case, one could unambiguously say that high-frequency words are associated with higher drift rates (when “word” responses correspond to the upper boundary; the direction of the relation is reversed when “word” responses correspond to the lower boundary). Here, one needs to consider the absolute values of the drift rate. The reason is that half of the trials have the letter a as the target letter, whereas in the other trials it is the distractor letter. Consequently, when the upper boundary is associated with, for instance, the letter a, one would expect a positive relation between contextual diversity and drift rate when a is the correct response, and a negative relation when e is the correct response. Note that the direction of the relations would reverse if the upper boundary corresponded to the letter e. Put differently, it is assumed that contextual diversity influences the decision process, but that the direction of the drift rate depends on the correct response.

In contrast to contextual diversity, OLD20, and the like, other variables would reduce the absolute drift rate. For example, having alternative completions presumably curtails drift rate, which results in slower response times. In addition, the diffusion model can easily explain a response bias in favor of the letter a by assuming that the starting point of the diffusion process is located closer toward the a boundary. Taken together, the diffusion model could potentially provide a good account of the speeded word fragment completion data. Even though such an approach would not grant us direct insight into the underlying lexical and semantic processes (Ratcliff et al., 2004), it would offer a solid starting point.