Discrete latent variables have been used in psychology and the social sciences to represent distinct latent constructs. Examples of discrete latent variables include profiles of thinking styles (Sternberg, 1998), attachment styles (secure, anxious–resistant, and avoidant; Ainsworth, Blehar, Waters, & Wall, 1978), teaching styles (Bennett & Jordan, 1975), styles of teaching and learning (Fischer & Fischer, 1979), and psychological types (Jung, 1971). In these examples, the latent categories of theoretical concepts, constructs, entities, or subgroups are represented by the levels of discrete latent variables.

Discrete latent constructs are often developed to characterize the underlying relationships in observed data. As these constructs are not directly observable, statistical models employing latent variables are needed to analyze the data, in order to help understand the relationships. These models are generally referred to as “models with discrete latent variables” (MDLVs). In this article, MDLVs are grouped into four families based on two dimensions of the data structure. Along the time dimension, data may be collected at a fixed time (cross-sectional) or at multiple time points (longitudinal). In terms of sampling structure, data may be hierarchical (nested) or nonhierarchical (nonnested). Models for nested data are known as “multilevel models.” Models for the four kinds of data are presented in a 2 × 2 matrix framework, for convenient reference (see Fig. 1). A MATLAB toolbox referred to as the “MDLV toolbox” has been developed to implement the estimation procedures when applying the four families of MDLV models in data analysis.

Fig. 1
figure 1

A framework of models with discrete latent variables

Full size image

The first dimension of the model framework concerns whether data are collected at a fixed or at multiple time points. For cross-sectional data that are collected at a single time point, levels of a discrete latent variable represent the underlying distinct latent categories and are generally called “latent classes” in the literature. The latent structure of the model explains the observed relationships among the manifest (indicator) variables with mutually exclusive and exhaustive latent classes. In other words, each latent class is associated with a unique response profile of the manifest variables. Because the observed responses are subject to random errors, statistical models are employed to relate the latent classes to the realized responses. The models assume that responses are independent, given the latent class (known as the “conditional independence assumption”).

Data collected from the same individuals at multiple time points are called “longitudinal data.” As these data are sequentially ordered in the time dimension, the repeated measurements provide data for studying the intraindividual changes over time. The distinct latent states at different time points represent an individual’s path of transition among latent states. The dynamics of latent transitions among states are characterized by the different patterns of the latent states across time. Studying the transitional dynamics is the key to understanding developmental stages in life. Examples of theories (models) for developmental stages can be found in children’s cognitive development (Piaget, 1973), the eight psychosocial stages of lifespan social development (Erikson, 1950), and sequential stages of moral development (Kohlberg, 1984). Although these theories may imply that the latent state transitions follow a deterministic sequence of directions (e.g., monotonic), the models represent transition patterns by the probabilities of moving to another state or of staying at the same state between two consecutive times, without imposing directional constraints. The theories may be revised by examining the patterns of transitional probabilities as estimated from empirical data.

The second dimension concerns the sampling characteristics of the data. Often, observed data have a natural nested structure in which individual observations are clustered within higher-level units. The nested data structure is referred to as a “multilevel,” “clustered,” or “hierarchical” structure. A notable example of nested structure is the educational system, in which students are organized into classes, classes are organized into schools, and schools are organized into districts. Data with such nested structure are generally not completely independent of each other. For example, data on students in the same school tend to be correlated (not independent), because of shared family and school characteristics as well as interactive relationships. Incorporating possible dependency in the nested data into the modeling procedure is important in obtaining results that can be interpreted properly. The MDLV models discussed here appropriately account for data dependency by way of conditional independence (as opposed to total independence) assumptions. Explicitly, responses are assumed to be independent within latent classes, but not across them. Thus, data across latent classes within a cluster may be dependent.

In the following sections, four families of models included in the toolbox are presented one by one, according to the framework in Fig. 1. First, however, a general description of the European Values Study (2011; EVS) is given. Several data sets were created by extracting sample data from two waves of this study (the 1999 and 2008 surveys) for use in demonstrating the modular functions of the toolbox. Each data set was analyzed with models in a specific family in order to illustrate how to apply the models to fit the data and how the results may be interpreted. The four families of models are explained in four separate sections. Each section provides the model representation and statistical assumptions of a particular family of models. Then, the toolbox is invoked to fit the data with each of the models under discussion. An analysis example in each section illustrates how to use the toolbox to perform the specific modeling tasks and how to interpret the results. The next-to-last section presents a summary description of the MDLV toolbox (details are provided in Appendix C of the supplemental materials), and the last section concludes the study with a brief discussion of applications of the models included in the MDLV toolbox. Alternative software is also discussed that is available for applying various models with discrete latent variables in data analysis.

Models with discrete latent variables for data analysis

The models included in the MDLV toolbox are organized into four families based on the structure of the data to be analyzed. These families of models are presented in Fig. 1 using a 2 × 2 matrix framework with time (T) and sampling scheme (S) as its dimensions. The time dimension differentiates cross-sectional data (T = 1) from longitudinal data (T > 1). Cross-sectional data are obtained at a fixed time point, while longitudinal data are obtained repeatedly at two or more occasions for each individual. The sampling dimension differentiates nested (hierarchical) data from nonnested (nonhierarchical) data. Nested or hierarchical data involve multiple levels of sampling, and models applicable to these data are called “multilevel.” Nonnested or nonhierarchical data do not consider organizational levels of the sampling units and are regarded as being single-level.

The models shown in the upper right quadrant in Fig. 1 are developed for the analysis of nested longitudinal data and are called the “multilevel latent Markov models” (MLMMs). The MLMM can be considered either as an extension of the latent Markov model (LMM) to explain possible dependency attributable to the nested data structure, or as an extension of a multilevel latent class model (MLCM) to describe discrete latent change when models are applied to longitudinal data. Therefore, the LMM in the lower right quadrant and the MLCM in the upper left quadrant are the two special cases of MLMM.

The LMM describes possible changes among discrete latent states from one time to the next. The MLCM take into account the possible dependency due to nested structure when modeling data with discrete latent variables. The latent class model (LCM) is the classical model for modeling categorical data with discrete latent variables. As can be been in Fig. 1, the LCM situated in the lower left quadrant are the basic models of the proposed framework. The LCM can also be considered as the special case of MLMM when data are nonnested and collected at a single time point.

The theoretical background and statistical representation of each of these families of models are discussed separately in the following sections. Applications of the models are illustrated by fitting them to data extracted from the European Value Study (2011) using the functions available in the MDLV toolbox.

Data for illustrative examples: The European Values Study

The EVS consisted of four waves of surveys between 1981 and 2008. The aims of the EVS were to explore the moral and social values of Europeans and to cover various topics, such as attitudes toward family, work, religion, politics, and society. The first wave was conducted in 1981 in a total of 16 countries; the second wave was collected in 1990 and included 27 countries. The participating countries in the third (1999) and fourth (2008) waves increased to 33 and 47, respectively. We will use data extracted from the 1999 and 2008 surveys to demonstrate the functions in the MDLV toolbox. Further information about this study is available at the EVS website (www.europeanvaluesstudy.eu). Sample data on ten items related to marriage were obtained from each of the two surveys for analysis with the four families of models included in the toolbox.

The original questionnaires have 12 items on attitudes toward the important criteria for a successful marriage. Participants were asked to rate the importance of each of the criteria. Ten of the items that are common to both waves are analyzed in the examples and listed in Table 1. The original response categories have three levels: very important, rather important, and not very important. Since participants tended to consider many factors important, we recoded the responses into two categories: Very important was recoded to 1, and rather important and not very important were coded to 0.

Table 1 Items in the European Values Study questionnaire on “important criteria for a successful marriage”
Full size table

The survey data are cross-sectional within a country, though 31 countries participated in both the third (1999) and fourth (2008) waves. For analysis with LMM and MLMM, synthetic longitudinal data were created by linking the responses of each participant in the 1999 survey sample to corresponding responses of a matched participant in 2008. Participants were matched by income ranking within the same country. The steps (including the SAS codes used) to construct the synthetic longitudinal data are detailed in Appendix A1 of the supplemental materials. The synthetic longitudinal data are fitted with the LMM without consideration for the countries of the participants. Countries constitute the second level in the data structure when the data are fitted with the MLMM.

The LCM and MLCM were fitted to data on the sampled responses separately for the third (1999) and fourth (2008) waves. Data over the surveyed countries were combined and fitted separately for the two waves with the LCM. The same data were also fitted separately for the two waves with the MLCM by taking into consideration the countries of the participants (i.e., participants were nested within countries).

Appendix A in the supplemental materials presents the SAS syntax for sampling, linking, and recoding the EVS data. The MATLAB scripts and syntax for preparing the sampled data to be analyzed with various models using the MDLV toolbox are also shown in Appendix A. In the following sections, each of the four families of models presented in Fig. 1 is discussed. Then, examples of the model fitting are used to explain how to fit the models using functions available in the MDLV toolbox.

Multilevel latent Markov models

MLMMs (Yu, 2007) address both temporal and structural dependency in a single model. Let Y g denote the response vector of all participants in group g over T occasions, when there are n g participants in group g. Let Y igj,t denote the observed response to the jth item of participant i in group g at the tth time point. Each participant responds to the same J items at each time point. The latent variable (H) is used to differentiate groups in latent class distributions. Let H g be the random variable representing the latent cluster membership of group g, and l be a particular latent cluster. The variable H g is assumed to follow a multinomial distribution with L components. Each component represents a latent cluster. As is specified in the MLCM, different clusters have different lower-level parameters.

At the individual level, let X igt denote the latent state for participant i of group g at time t, in which a particular latent state at time t is denoted as m t . For simplicity, the numbers of latent states and clusters are fixed as equaling M and L, respectively, across all occasions. In addition, each participant is assumed to belong to only one group (e.g., to attend only one school), and his or her group membership is assumed to be the same over time (e.g., to attend the same school). With these assumptions, the probability of observing the response vector of participant i of group g over T occasions is

$$ \begin{array}{*{20}c} {P\left( {{{\mathbf{y}}_g}} \right)=\sum\nolimits_{l=1}^L {\left( {P\left( {{H_g} = l} \right)\prod\nolimits_{i=1}^{{{n_g}}} {\sum\nolimits_{{{m_1}=1}}^M {\sum\nolimits_{{{m_2}=1}}^M {\quad \sum\nolimits_{{{m_T}=1}}^M {\left[ P \right.} } } }\ \left( {{X_{ig,1 }} = {m_1}\ \left| {{H_g} = l} \right.} \right)} \right.} } \hfill \\ {\quad \quad \quad \quad \left. {\left. {\times \prod\nolimits_{t=2}^T {P\left( {{X_{ig,t }} = {m_t}\left| {{X_{{ig,t\text{--} 1}}} = {m_{t-1 }},{H_g} = l} \right.} \right)\prod\nolimits_{t=1}^T {\prod\nolimits_{j=1}^J {P\left( {{y_{igj,t }}\left| {{X_{ig,t }} = {m_t}} \right.} \right)} } } } \right]} \right),} \hfill \\ \end{array} $$
(1)

where P(H g  = l) denotes the latent cluster probabilities, which can be conceptualized as cluster sizes. The conditional probabilities, P(X ig,1 = m 1 | H g  = l), indicate that the latent clusters may have different latent class distributions at Time 1. The clusters can also differ in the transition process; that is, cluster membership can have systematic effects on the process of moving between the latent statesFootnote 1 across two time points. This effect is expressed by a conditional probability as P(X ig,t  = m t  | X ig,t–1 = m t–1, H g  = l). However, it is assumed that cluster membership (H g ) has no effects on the conditional response probabilities P(y igj,t  | X ig,t  = m t ). That is, how individuals respond to items is only affected by their latent class statuses, not by their group membership. This “time-invariant” assumption of conditional response probabilities is made in order to avoid potential confusion about the attribution of differences observed over time. Conditional on the latent class, item responses are not affected by the clusters at the group level. The constraints of \( \sum\nolimits_{l=1}^L {P\left( {{H_g} = l} \right) = 1\ \mathrm{and}\;\sum\nolimits_{m=1}^M {P\left( {{x_{ig }} = m\ \left| {{H_g} = l} \right.} \right) = 1} } \) are needed for model identifications. Note that the rows of the transition matrix must also sum to 1.

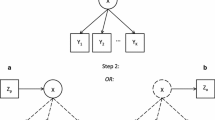
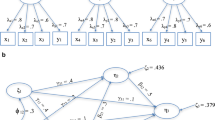
The various components of the MLMM are graphically depicted in Fig. 2 to present a simple and intuitive conceptualization of the components and their effects. The squares are the observed manifest variables. The arrows indicate that some relationships may exist between two connected variables. To emphasize the discrete nature of the latent variable, the latent variable is expanded as an ellipse, with each latent class explicitly depicted inside the ellipse. The discrete group-level latent variable (H) is represented by the horizontal ellipse, and the circles inside represent the different latent clusters. The two vertical ellipses are the latent variables of individual’s latent status at Times 1 and 2. Each latent state is depicted as a small circle inside the ellipses. The long horizontal dashed line divides the two levels of hierarchy. The arrows from the discrete random variable (H) at group level pointing toward the discrete latent variable (X 1) and the transition paths (dashed lines) at the lower level represent the effects of the latent clusters.

Fig. 2
figure 2

Graphical representation of a multilevel latent Markov model

Full size image

The special cases of MLMM (i.e., LCM, LMM, and MLCM) that will be discussed in the following sections can be represented by portions of the components in Fig. 2. For example, the MLCM can be represented by removing the portion of T = 2; the LMM can be depicted by the components below the dashed line; and the LCM can be portrayed by the portion below the dashed line at a given time.

Fitting the MLMM with the MDLV toolbox

Taking into consideration the nested structures (participants nested within countries), the EVS data were fitted by an MLMM. The codes for fitting the MLMM using the MDLV toolbox are available in Appendix B1. Models with two and three latent clusters combined with two and three latent classes were fitted to the pseudolongitudinal data, and the likelihood values, numbers of parameters, and Akaike and Bayesian information criteria (AIC and BIC) are presented in the top panel of Table 2. According to the AIC and BIC, the best-fitting model is the one with two latent clusters and three latent classes. The estimated parameters of the two-cluster and three-state MLMM and the corresponding conditional response probabilities of these three classes are listed in Table 3.Footnote 2

Table 2 Likelihood values (−LL), numbers of parameters, and fit indices (Akaike and Bayesian information criteria [AIC, BIC]) for models in the MDLV framework
Full size table
Table 3 The estimated model parameters of the two-cluster and three-class multilevel latent Markov model (MLMM) and multilevel latent class model (MLCM)
Full size table

The patterns of conditional response probabilities of the three latent states show differences in emphasis on the important criteria for a successful marriage. The probability pattern for the state S1 is characterized by generally rating most of the ten criteria as being very important (with the notable exception of political agreement). This latent state resembles the “general class” found in the LCM results (cf. class C1 for Wave 3 and C3' for Wave 4 in Table 5). S1 is the only latent class likely to consider the finance items (adequate income and good housing) as being very important. Personal compatibilities with regard to religion and social background are also likely to be important for this class, though to a lesser extent. The other two states, S2 and S3, do not view finance and compatibility as being very important. The second state S2 places importance primarily on family life, particularly on faithfulness, the sexual relationship, and children. For state S3 (with relatively small sizes: 16 % and 4 %, respectively, for the two latent clusters), only faithfulness is emphasized by the majority of the members, while a relatively small proportion (.22) consider having children as being important.

Table 3 also presents estimates of latent cluster probabilities and the corresponding latent class distributions for each cluster. The results suggest that about two thirds (.67) of the countries are in cluster A and one third (.33) are in cluster B. Looking at the initial latent state distributions (for Wave 3 [1999 survey]), it was found that 67 % of the participants in Cluster A countries were in S2, and the remainder were evenly distributed between S1 (17 %) and S3 (16 %). For the countries in cluster B, S1 (42 %) and S2 (54 %) were the dominant classes, with S3 (4 %) being almost negligible.

The posterior latent cluster membership probabilities were obtained for each of the 31 participating countries. Each country was then classified into the cluster for which it had higher membership probabilities. The classification results are summarized in Table 4. As can be seen from Table 4, cluster A includes most of the countries in Eastern and Northern Europe, whereas the cluster B countries are mostly in Western, Central, and Southern Europe. A closer look within the clusters also suggests that religion plays a role. In general, countries assigned to cluster A tend to be in the region in which the traditional religion of the majority is Orthodox Christianity. Countries in cluster B tend to be in the region in which the religion of the majority is traditional Protestant or Catholic Christianity. This pattern of clustering along the dimension of religious belief can also be seen in Wave 4. However, there are some limitations to using traditional majority religion to characterize the two latent clusters. For example, many countries that are historically Catholic (e.g., Italy, Spain, and Portugal) and historically Protestant (e.g., Germany and Great Britain) are grouped in cluster A (Orthodox Christianity), and the major centers of Eastern Orthodoxy (e.g., Greece and Ukraine) are categorized into cluster B (Protestant or Catholic Christianity).

Table 4 Estimated latent cluster memberships of the 31 participating countries (multilevel latent Markov model [MLMM] and multilevel latent class model [MLCM])
Full size table

The estimated transition probabilities P(X t  | X t–1) are presented in Table 3. For both clusters, latent state S2 shows great stability (the probabilities of staying at the same state are .91 for cluster A and .90 for cluster B). This finding suggests that those whose values of a successful marriage are focused on family life consistently expressed the same views over time.

Regarding the change in the latent state membership from Wave 3 to Wave 4, several similar transitions are apparent in both latent clusters. More specifically, it is very unlikely in both clusters to observe a transition from S1 to S3 or from S3 to S1, and the probabilities are also low for participants in S2 to transit to other states between the two waves. This pattern suggests that participants in S2 for both clusters were very likely to stay in the same state over time. For instance, participants in the “family-oriented” state tend to hold the same view about the criteria for a successful marriage over time. When examining the transition pattern separately for each cluster, we found that participants from countries in cluster B were relatively more stable than those in cluster A. About 33 % of the participants in cluster A moved from S1 to S2, but only 15 % of the participants in cluster B did so. However, participants in cluster A appear to be more likely to change their view of a successful marriage.

Multilevel latent class models

The MLCM is a special case of MLMM applying to data collected at a single time point, but possible data dependency due to the nested data structure is also taken into account in the MLCM. More specifically, model parameters are allowed to be different for participants in different groups (higher-level units). In order to identify and differentiate the clustering effects at different levels, the nested data structure needed to be clearly represented in the notation system. Therefore, the observed response vector is denoted as Y ig (instead of Y i ) to indicate a participant’s higher-level membership g (i.e., participant i is a member of group g).

A version of multilevel extension of LCM was proposed by Vermunt (2003). In his version of the MLCM, Vermunt (2003) used random effects to account for higher-level effects, as is done in the classical multilevel modeling framework. The random-effects MLCM can be regarded as an extension of a random-coefficient logistic regression model (Agresti, Booth, Hobert, & Caffo, 2000; Hedeker, 1999, 2003; Hedeker & Gibbons, 1994; Wedel & DeSarbo, 1994; Wong & Mason, 1985) with a latent, instead of observable, dependent variables.

The higher-level effects used to account for the group effects can come from some forms of parametric or nonparametric distributions (Vermunt, 2003). The MLCM discussed in this article are conceptually equivalent to the nonparametric MLCM discussed in Vermunt’s (2003) article, in which the group-level differences in lower-level parameters are explained by discrete random effects. As is also discussed in Vermunt’s (2003) article, the higher-level effects can be imposed on either the latent class probabilities or the conditional response probabilities. However, the special case of having a common measurement model (i.e., conditional response probabilities) across clusters is considered in the toolbox.

More specifically, a discrete random variable H g having L possible outcomes is hypothesized to represent the L unique higher-level latent clusters. Each outcome of the discrete random variable can be conceptualized as a latent cluster consisting of homogeneous (Level 2) groups sharing the same latent class distribution. This discrete random variable requires a parameter P(H g  = l) to describe the distributions (i.e., cluster sizes) of the latent clusters. The differences between clusters are demonstrated in a cluster’s latent class probabilities. Explicitly, the latent class probabilities P(X ig  = m) can differ depending on the latent cluster membership (H g ), and are represented specifically as P(X ig  = m | H g  = l). Let y igj denote the response of participant i of group g to the jth item. Assuming that there are n g participants in the gth group, the probability of observing the response vector of all participants of group g is

$$ P\left( {{{\mathbf{y}}_g}} \right) = \sum\nolimits_{l=1}^L {\left( {P\left( {{H_g} = l} \right)\prod\nolimits_{i=1}^{{{n_g}}} {\left[ {\sum\nolimits_{m=1}^M {P\left( {{X_{ig }} = m\ |{H_g} = l} \right)\prod\nolimits_{j=1}^J {P\left( {{y_{igj }}\ |{X_{ig }} = m} \right)} } } \right]} } \right)}\ . $$
(2)

A matrix P(X | H) of size M × L is used to represent the estimated M latent class probabilities for each of the L clusters. The columns of the matrix P(X | H) describe the within-cluster distributions of the latent classes. Accordingly, the entries in each column sum to 1. Conceptually, each latent cluster can have a unique pattern of conditional response probabilities. However, as was also discussed in Vermunt’s (2003) article, different conditional response probabilities among clusters can be ambiguous and subject to questionable interpretations. Therefore, invariant conditional response probabilities are assumed in the models fitted with the MDLV toolbox.

Fitting MLCM using the MDLV toolbox

The various MLCMs with different numbers of clusters and classes were fitted to the EVS data separately for Wave 3 and Wave 4. The MATLAB codes for fitting each model are presented in Appendix B2. The results of the model fit indexes are summarized in Table 2. As is shown there, both the AIC and BIC values suggest that the two-cluster and three-class model provided the best fit for both Wave 3 and Wave 4 data. The estimated latent cluster probabilities P(H g  = l), conditional latent class probabilities P(X ig  = m | H g  = l), and conditional response probabilities P(y ij  | X i  = m) are listed in Table 3, separately for each wave.

The estimated parameters for the MLCM listed in Table 3 suggest that the three classes have similar patterns for conditional response probabilities in both waves, like the three classes analyzed by the LCM below. That is, C1 is the “all aspects” class, C2 values the “family-oriented criteria,” and C3 is the class that values mainly “faithfulness,” as well as the two specific criteria of “children” and “happy sexual relationship.” The estimated P(H g  = l) is \( \left[ {\begin{array}{*{20}c} {.64} \hfill \\ {.36} \hfill \\ \end{array}} \right] \) for Wave 3; that is, about 2/3 of the countries are in cluster A, and 1/3 are in cluster B. The estimated P(X | H) for Wave 3 is \( \left[ {\begin{array}{*{20}c} {.08} \hfill & {.22} \hfill \\ {.46} \hfill & {.59} \hfill \\ {.46} \hfill & {.19} \hfill \\ \end{array}} \right] \)

As can be seen from this matrix, classes C2 and C3 are the dominant classes, with similar sizes (about 46 % each) for countries in cluster A. Class C1 is much smaller (about 8 %) for countries in cluster A. In contrast, class C2 is the major class (about 59 %) for countries in cluster B. The other two classes for countries in cluster B are of similar sizes (22 % in C1 and 19 % in C3). The pattern of P(X |H) for Wave 4 is similar to that for Wave 3. However, the latent cluster distributions are quite different between the two waves: Cluster A is the larger of the two clusters for Wave 3, but cluster B is the larger one for Wave 4.

Following model fitting, the posterior probabilities of being in each of the two latent clusters were obtained for each country. Each country was then assigned to the cluster with higher posterior probability. The resulting latent cluster memberships for the 31 countries are presented in Table 4. The cluster compositions found in Table 4 suggest that major factors for differentiating the clusters may be religion, geopolitics, and socioeconomic system. In Wave 3, the countries categorized into cluster A are identical to the findings with the MLMM, except for one country (Sweden). Therefore, the interpretation for the two clusters can follow the possible lines related to geographical location and historical majority religion described earlier for the MLMM. As was described earlier, cluster B is larger in Wave 4: Seven countries move from cluster A to cluster B, and only one moves from cluster B to cluster A.

Latent Markov models

Wiggins (1973) extended the simple Markov model to an LMM to take into account measurement imperfection (i.e., assuming latent variables). An LMM can be viewed as the combination of the unrestricted latent class model and a single Markov chain. In other words, the LMM is an extension of the LCM in the time dimension to account for temporal dependency. Under the framework of discrete latent variables, the LMM is a special case of MLMM that applies to data without nested structure.

To formally define the LMM, let y ijt denote the response of participant i on item j at time t, and let y it  = (y i1t , y i2t , . . . , y iJt ) denote the observed response vector of participant i to J items at time t, where i = 1, . . . , I and t = 1, . . . , T. Furthermore, let y i  = (y i1, y i2, . . . , y iT ) denote the response vector of a single participant i over T occasions. The discrete latent variable for participant i at time t is denoted by X it , where a particular latent state at time t is denoted as m t . For simplicity, the numbers of latent states are assumed to be equal, with M latent states at each time point. Making the assumption of conditional independence and combining similar terms, the probability of observing the response vector of participant i over T occasions is

$$ P\left( {{{\mathbf{y}}_i}} \right) = \sum\nolimits_{{{m_1}=1}}^M {\sum\nolimits_{{{m_2}=1}}^M {\quad \sum\nolimits_{{{m_T}=1}}^M {\ \left( {P\left( {{X_{i1 }} = {m_1}} \right)\prod\nolimits_{t=2}^T {P\left( {{X_{it }} = {m_t}\ \left| {{X_{i,t-1 }} = {m_{t-1 }}} \right.} \right)\;\prod\nolimits_{t=1}^T {\prod\nolimits_{j=1}^J {P\left( {{y_{ijt }}\ |{X_{it }} = {m_t}} \right)} } } } \right)} } }, $$
(3)

The three terms of Eq. 3 explicitly show the three components in an LMM. The first component, P(X i1 = m 1), is called the latent class probability,Footnote 3 which can be conceptualized as the probability of randomly selecting an individual who belongs to the latent class m at the first time point. It can also be viewed as the prevalence of classes at the first time point—in other words, “class size.” The second term, P(X it  = m t  | X i,t–1 = m t–1), is called the transition probability, giving the probabilities of moving between latent states between two adjacent occasions. The specification of P(X it  = m t  | X i,t–1 = m t–1) implies that the current state (m t ) is only affected by the state at the previous time point (m t–1). This specification is usually known as the “lag 1 Markov model.” A more restricted and simpler model assuming identical transition probabilities between any two adjacent time points is considered in this article. This is typically referred to as a “time-homogeneous” Markov chain.

The last term, P(y ijt  | X it  = m t ), is the conditional response probability that characterizes the measurement model for the occasion t. The conditional response probability represents how individuals respond to items when the individuals belong to a certain latent state at a particular time point. Typically, the conditional response probabilities of items at each time point are fixed to be the same across occasions. Thus, the differences in responding to items between the two time points can be attributed to the transitions between latent states.

Fitting LMM using the MDLV toolbox

The synthetic longitudinal data created by linking Wave 3 and Wave 4 data were fitted with LMM by ignoring the nested structure of the data. The codes used to fit LMM are included in Appendix B3 of the supplemental materials. The likelihood, numbers of parameters, and fit indices (AIC and BIC) for two- to five-state LMMs are presented in Table 2. The AIC and BIC both suggest that a five-state LMM has the best fit among the four models. The estimated conditional response probabilities and transition matrix for the five-state model are presented at the bottom of the LMM column in Table 5.

Table 5 The estimated model parameters of the fitted latent Markov (LMM) and latent class (LCM) models
Full size table

The estimated latent class probabilities [.33 .30 .22 .08 .06] listed in Table 5 indicate that Wave 3 includes three relatively larger states and two smaller states. The latent state S4 is similar to the “all aspects” class (C1) described below in the results of the analysis with LCM. The state S3 resembles the “family-oriented” class (C2), and the state S2 is most similar to class C3, expressing “faithfulness” as being the single most important criterion, and “children” and “happy sexual relationship” as being minor criteria for a successful marriage.

The estimated transition matrix P(X it  = m t  | X i,t–1 = m t–1) is displayed in the bottom panel of Table 5. The data shown in the diagonal suggest that the three larger states (S1, S2, and S3) are more stable than the two smaller states (S3 and S4). Participants in states S1, S2, and S3 at Wave 3 are more likely to stay in the same states or to move to the other two larger states at Wave 4 (see the upper-diagonal 3 × 3 matrix). In addition, participants in states S4 and S5 at Wave 3 tend to move to one of the three larger states at Wave 4.

Latent class models

The LCM seeks to explain the observed relationships among the discrete manifest variables with a set of mutually exclusive and exhaustive latent classes, and is the base model in the proposed discrete latent variable framework. The LCM was first considered in the 1950s by Green (1951), Anderson (1954), and Gibson (1959). Lazarsfeld and Henry (1968) provided more comprehensive examinations and reviews. The LCM gained increasing popularity because of the subsequent work of Goodman (1974b), Haberman (1974, 1979), and Clogg (1979, 1981).

To formally represent the LCM, let X be the latent variable consisting of M mutually exclusive and exhaustive latent classes. The latent classes are indexed by m, where m = 1, 2, . . . , M. In addition, Y ij denotes the random variable representing the response of participant i to the jth item (1 ≤ j ≤ J), and y ij represents a realization of the random variable Y ij . The class-specific conditional probability of observing y ij for item j and participant i in class m is P(Y ij  = y ij  | X = m), which is also called the conditional response probability or latent conditional probability. In the LCM, the probability of obtaining the response pattern y i for participant i, P(Y i  = y i ), is a weighted average of the M class-specific conditional response probabilities, P(Y i  = y i  | X = m); that is,

$$ P\left( {{{\mathbf{y}}_i}} \right) = \sum\nolimits_{m=1}^M {P\left( {X_i=m} \right)\prod\nolimits_{j=1}^J {P\left( {{y_{ij }}\ \left| {X_i = m} \right.} \right),} } $$
(4)

where P(X = m) denotes the probability of a randomly sampled participant in the sample belonging to latent class m, which is usually called the latent class probability. Conceptually, latent class probabilities can be considered as the class size of the latent class in the population. An LCM assumes local independence within each class, so that the joint probability of response pattern y i in class m is the product of all conditional probabilities of items within this class (the second term of Eq. 4). An LCM also needs to satisfy the identification constraints of Goodman (1974a, 1974b), who showed that latent class models are identifiable by the constraint \( \sum\nolimits_{m=1}^M {P\left( {X = m} \right) = 1} \).

Fitting LCM using the MDLV toolbox

Appendix B4 of the supplemental materials shows the MATLAB codes used to fit LCM to the sampled data from the 1999 and 2008 waves of the EVS. The log-likelihood values, numbers of parameters, AIC, and BIC of fitting models having two to five classes for each wave are presented in Table 2. The AIC preferred the five-class solution, but the BIC suggested that the three-class model is appropriate for the Wave 3 EVS data. On the other hand, both indices suggested that the five-class model is preferred among the four models for the Wave 4 EVS data. The estimated conditional response probabilities [P(Y = y | X = m)] and latent class probabilities [P(X)] of the three-class fit for Wave 3 and the five-class fit for Wave 4 are summarized in Table 5. The estimated latent class probabilities for Wave 3 indicated that about half (50 %) of the participants were in class C2, 13 % in class C1, and 37 % in class C3.

From examining the item response probabilities, the three classes (C1, C2, and C3) represented high, medium, and low tendencies to rate the various criteria as being important for successful marriage in general. When comparing the relative ratings among criteria within each class, class C1 could be considered as a class of individuals who value all of the ten criteria as being important for a successful marriage. Class C2 consisted of half of the participants and was characterized by having the attitude that a successful marriage does not require husbands and wives to share the same religious belief, to agree in politics, or to come from similar social backgrounds. Class C3 represented individuals who regard “faithfulness” as being the most important criterion for a successful marriage, and “children” and a “happy sexual relationship” as being relatively more important than the remaining seven criteria.

The results of the five-class solution for conditional response probabilities of the ten items for Wave 4 are listed in Table 5. It should be noted that the labeling is arbitrary for these five classes. By examining the item response probabilities, it was found that class C3' resembled the “all aspects are important” class (C1) in Wave 3, and Class C5' was similar to Class C2, which emphasized mainly family-oriented values for a successful marriage. Class C2' was quite similar to C3, in that it seemed to be based on a view that only faithfulness is very important, and that having children is the next most important criterion, but less so than for Class C3. The classes C1' and C4' may be regarded as emphasizing the utilitarian and romantic aspects of marriage, respectively, since the members of C1' valued faithfulness, adequate income, and good housing more, whereas the members of C4' valued criteria such as faithfulness and sexual relationship.

The MDLV MATLAB toolbox

The Models With Discrete Latent Variables (MDLV) MATLAB toolbox comprises a collection of functions to estimate parameters of the four families of models depicted in Fig. 1. The MDLV MATLAB toolbox was implemented using MATLAB Version V7.2 (R2006a; The MathWorks, Natick, MA) on an IBM-compatible PC running on the Windows XP Professional OS. The toolbox has been tested with MATLAB V7.6 (R2008a) and MATLAB V7.13 (R2011b). The MDLV toolbox can be downloaded directly from www.psych.mcgill.ca/labs/yulab/software_MDLV.html. In addition to the main estimation functions, the toolbox also includes functions to simulate data for each model with specified parameters. A collection of utility functions is also included, to facilitate data preparation or to serve as supporting subroutines for the main estimation functions. The codes and scripts of all illustrative examples used in this article are also included in the toolbox.

The parameters of the four models are estimated using the expectation maximization (EM) algorithm (Dempster, Laird, & Rubin, 1977). The forward–backward, or Baum–Welch, algorithm (Baum, Petrie, Soules, & Weiss, 1970) is used to estimate the parameters for LMM. The standard EM algorithm was found to be impractical for MLMM, however, due to its complexity. For the MLMM, the E-step is modified using the upward–downward algorithm (Vermunt, 2002, 2003, 2004). The upward–downward algorithm is analogous to the forward–backward algorithm (or Baum–Welch algorithm) for the estimation of hidden Markov models with large numbers of time points (Baum et al., 1970; Frühwirth-Schnatter, 2006). Details of the parameter estimation procedure can be found in Yu (2007).

The current version of the MDLV toolbox handles only binary data and is limited to a two-level data structure (e.g., students within schools, citizens within countries). The numbers of individuals in groups are assumed to be equal. However, functions can be modified to accommodate unequal group sizes. Details of the required data formats, the inputs and outputs of the main estimation functions, and functions to simulate data for the four models, as well as some useful utility functions included in the toolbox are described in Appendix C of the supplemental materials.

Discussion and conclusions

Discrete latent constructs or concepts have advantageous properties for capturing distinct latent quantities, and thus have great potential to be utilized in order to form theories or hypotheses in the social sciences. A framework based on a 2 × 2 matrix of models for analyzing data with discrete latent variables has been introduced in this article. By categorizing different features of the data according to temporal and structural characteristics, the LCM, LMM, MLCM, and MLMM are placed in the corresponding quadrants of this modeling framework. The modeling framework not only offers a concise matrix for conceptualizing theories, it also assists and guides researchers in selecting an appropriate model for data analysis.

Several commercial statistical software packages can be used to fit individual models under this framework. For example, LEM (Vermunt, 1997) can be used to fit an LCM, the Hidden Markov Model Toolbox for MATLAB (Murphy, 1998) can fit an LMM, and the PROC LCA (Lanza, Collins, Lemmon, & Schafer, 2007) and PROC LTA (Lanza & Collins, 2008) procedures in SAS are available, respectively, for an LCM and an LMM. No single software covers all four of these models, except for the newer version of Latent GOLD 4.5 with syntax module (Vermunt & Magidson, 2008). However, the developed MDLV MATLAB toolbox covers all four models in this framework of modeling discrete latent structures, and it offers a convenient and accessible instrument for parameters estimations. The illustrations of how to fit various models with the MDLV MATLAB toolbox provide step-by-step examples of empirical applications to real data.

Modeling with discrete latent variables offers many interesting possible applications in psychology and the social sciences. The two types of models, distinguished by the temporal characteristics of the data, offer excellent approaches to study the static latent structure and the dynamic transitions among latent states. In addition, since dependencies in multilevel data structures have gained substantial attention in the social sciences, the proposed framework and toolbox have the desirable capability of accommodating possible nested dependencies in the data. This possibility of handling a nested data structure widens the range of applications available when studying static and dynamic latent structure.

In sum, the proposed framework offers comprehensive coverage of different models under the common theme of modeling data with discrete latent variables. The implemented MDLV MATLAB toolbox bridges the theoretical models to empirical applications by providing accessible tools and resources. It is hoped that bringing together the statistical modeling framework and the corresponding estimating toolbox will facilitate applications of discrete latent variables in empirical studies.