The question of how spatial representations are maintained and updated in the visual system is crucial for our understanding of human vision and memory. There are abundant studies on spatial working memory (SWM), which is considered as a memory buffer for temporarily holding and manipulating information that concerns the spatial location of an object. These studies often involve reproducing the location of a briefly presented object by a mouse click or a finger touch (Schneegans & Bays, 2016; Schurgin & Flombaum, 2014). The performance is quite accurate, although there is a systematic distortion that the stored locations are found to be either attracting one another (memory averaging effect; Liverence & Scholl, 2011; Sheth & Shimojo, 2001) or being attracted to boundaries and landmarks (landmark effect; Diedrichsen, Werner, Schmidt, & Trommershäuser, 2004; Huttenlocher, Hedges, & Duncan, 1991; Nelson & Chaiklin, 1980).

Most studies on SWM presented visual stimuli on a two-dimensional (2-D) fronto-parallel plane with no depth perception involved; therefore, the storage mechanism of depth information remains poorly understood. Since the visual system has distinct processing mechanisms for depth information and 2-D (fronto-parallel) spatial information (Finlayson & Golomb, 2016; Finlayson, Zhang, & Golomb, 2017; Simon & Rudell, 1967; Umemura, 2015), working memory for depth information may also have a mechanism different from that for spatial locations or visual information within a 2-D context. Indeed, previous studies showed that our ability of detecting changes in metric depth (Qian & Zhang, 2019) or recalling a numeral associated with a certain depth is severely limited (Reeves & Lei, 2017). Compared with the near-perfect performance for memorizing up to four objects (Luck & Vogel, 1997) or five 2-D locations (Simons, 1996), the change-detection accuracy for one depth position is below 80% even though depth perception is quite accurate, suggesting that the ability of holding representations of metric depth information with a typical retention of 900 ms is much lower than that of an object or a 2-D location (Qian & Zhang, 2019; Reeves & Lei, 2017, suggested that the memory performance might be slightly improved with a longer retention of 2,000 ms, although the accuracy was still below 80%). However, such a poor memory performance contradicts our apparently smooth daily experience that involves memorizing objects’ three-dimensional (3-D) locations, one might suspect that other type of depth information may come to aid the apparently inaccurate metric depth representation. In other words, aside from metric depth, there may be other depth representation available to enhance our memory for depth. The question of the nature of internal representation for depth is crucial for our understanding of 3-D spatial information, and therefore needs to be addressed.

Evidence on perceptual tasks has shown that estimation of depth or distance can be improved with the addition of a comparison or reference point (Blank, 1958; Foley, 1985; Gogel, 1972; Sousa, Brenner, & Smeets, 2011), indicating an important role of utilizing the relation between depth positions. Similarly, studies on visual working memory (VWM) showed that change detection performance on object’s features (e.g., color) was affected by the spatial configuration of the memory display, suggesting that the brain may use the relational information of individual visual items on the basis of global spatial configuration to enhance VWM (Jiang, Olson, & Chun, 2000; Li, Qian, & Liang, 2018; Qian, Wang, Liu, & Lei, 2017; Qian, Zhang, Wang, Li, & Lei, 2018). Based on these findings, here we speculate that the relational information based on 3-D spatial configuration is of central importance for working memory for depth positions. Particularly, we propose that relative depth order, which determines in part the relation between depth positions, is stored as one of the depth representations and may play an important role in working memory. Investigating the effect of depth order is essential in uncovering the mechanism of how location information in a 3-D context is held in working memory.

To investigate the memory representation of depth, we used a change-detection paradigm adapted from Luck and Vogel (1997). The change-detection task (CDT), which has been frequently used in studies on VWM (Luck & Vogel, 1997, 2013), is proved to be a valid tool for investigating working memory and has been used to test spatial memory (Di Lollo, 1977; Peterson, Rawlings, & Cohen, 1977). In a CDT, observers were instructed to detect any change between a briefly presented memory array and a test display after a period of retention. In our study, multiple memory items were simultaneously presented with each occupying a different stereoscopic depth plane, and participants were required to retain the positions in depth of these items. Employing a CDT allows us to test the memory performance as a function of the magnitude of depth change, and meanwhile examine how change in relation of depths among items and whether the direction of change (closer or farther) could affect the performance.

Through this approach, we evaluated whether working memory represents individual depth positions independently or relationally with an emphasis on its ordinal information within the global configuration. We hypothesize that (1) metric depth is stored in working memory; (2) ordinal depth is stored in working memory; (3) the latter has a more prominent effect on memory performance. The first hypothesis predicts better memory performance for a larger change in magnitude. The second hypothesis predicts that the memory performance should be improved when the relation of memory items in depth (i.e., its depth order) had changed. The third hypothesis predicts that whether the ordinal depth changes or not should modulate the effect of metric depth. In addition, we also examined whether the direction of change could affect the performance. Because past research showed that items at a closer depth were better retained in visual working memory (Qian et al., 2017; Qian et al., 2018), it is possible that change of position to a closer depth is easier to detect, as such changes can be ecologically more important and relevant.

Method

Participants

Twelve students from Sun Yat-Sen University (SYSU), with normal or corrected- to-normal vision took part in the experiments. Eleven of them were naïve to the purpose of the study and received payment for their participation; only one was an experienced psychophysical observer (one of the authors). Because no previous study has investigated an effect similar to our experiment, we based our sample size on the results of a power analysis given the effect size on change in depth order (η2 = 0.6) estimated from our pilot study, which was of the same task as in the main experiment. The power analysis was performed using G*Power (Faul, Erdfelder, Lang, & Buchner, 2007), which revealed that at least nine participants would be required to have an 90% power to detect an effect in our study.

This research was approved by the SYSU Institutional Review Board (IRB). Written informed consent approved by the IRB was obtained from each participant prior to all the experiments.

Apparatus

Participants viewed the stimuli against a uniform gray background (102 cd/m2) through a Wheatstone stereoscope on a pair of 21-inch ViewSonics monitors. The display resolution was set to 1,920 × 1,080 pixels, with a refresh rate of 60 Hz.

Stimuli

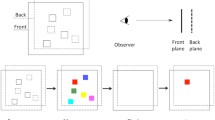
In the main experiment, the memory array was composed of a set of blue squares arranged in a circular configuration with a radius of 3.5° from the center of the screen (see Fig. 1). There were two (Set Size 2) and three (Set Size 3) memory items presented in separate experimental blocks. The memory items were presented at various depth planes perpendicular to the line of sight, with one item per depth plane. The depth position of a memory item was randomly selected from a set of seven depth planes without replacement. The depth planes were separated by a binocular disparity ranging from −0.51° to 0.51° with a step of 0.17°, which corresponded to −7.0, −4.8, −2.5, 0, 2.7, 5.5, 8.6 cm from the monitor screen with a typical interpupillary distance of 6.5 cm and a viewing distance of 75 cm. These disparities were selected so that the left-eye and right-eye images could be reliably fused and the items clearly appeared to be separated in depth (Blakemore, 1970). Each item subtended 0.65°× 0.65° of visual angle. In addition, the items at the farther planes might appear to be larger than those at the nearer ones due to the mechanism of size–distance scaling. We decreased the size of the items by 1% for each receding plane so that the size of the items at different planes appeared to be the same (for details, see Qian & Zhang, 2019).

Fig. 1
figure 1

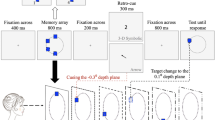
Stimuli and procedure in the experiments. Top: task sequence. Bottom: the front view and side view of the memory display. Here, we show an example of the stimuli with a set size of 2. The memory items are outlined with various types of lines to indicate their different depth profiles. No line was presented in the formal experiments

Full size image

Procedure

Participants were seated in a dark room to complete the experiment. Before the experiments, they were required to pass a screening test to ensure that they could well perceive the stereoscopic depth. On each trial, two horizontally displaced blue squares were presented for 500 ms. The depth position of one item was randomly selected from the seven depth planes, and the other item was separated by a relative disparity of 0.17°. Participants were instructed to judge which item was farther as quickly as possible, and were required to achieve an accuracy of above 90% for 48 trials in order to continue with the formal experiment. The 12 participants passed the screening test and were recruited for the experiments.

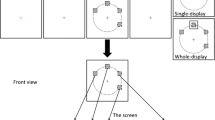
They were then trained for a short time (2–5 min) to get acquainted with the stimuli and the task. Each trial began with a fusion phase where a red cross, subtending 0.65° × 0.65°, was presented at the center of the screen. The participants were instructed to fixate at the red cross and fuse the left-eye and right-eye images of the cross until no double image was perceived. They then confirmed the success of fusion by pressing a key, and the red cross turned black and persisted throughout the trial. Following a 400-ms presentation of the black fixation cross, the memory array composed of blue squares was then presented for 800 ms. It was followed by a 900-ms retention interval, and then the test phase where a test item was shown until the participant responded. In the whole-display experiment, the test item was shown together with the rest of memory array. It was indicated by a black box (1.3° × 1.3°), which was located at the same depth plane as the test item. In the single-display experiment, only the test item was presented. There was a 1,000-ms blank intertrial interval. A diagram of the task sequence was shown in Fig. 1.

The depth position of the test item would either remain the same as in the memory array or change to a different one selected from the rest of depth planes. Figure 2 shows an example of memory array and test array for the whole-display experiment with a set size of 2 under different experimental conditions. In the cross condition, the test item would change to a depth plane so that the perceived depth order of the items changed (see Fig. 2, the cross condition). For the two uncross conditions, the test item would change its depth position, but the perceived depth order of the items remained. Specifically, in the uncross-inward condition, the test item would change to a depth plane nearer to the other memory item (i.e., within the depth volume of the original memory array; see Fig. 2, the uncross-inward condition); in the uncross-outward condition, the test item would change to a depth plane further away from the other memory item (i.e., beyond the depth volume of the original memory array; see Fig. 2, the uncross-outward condition). A change magnitude of 0.34° or 0.51° was tested for each set size, and the direction of the change was also manipulated. A forward direction indicated that the test item moved closer to the participant, and a backward direction indicated that the test item moved further away from the participant.

Fig. 2
figure 2

Memory array and test array in different experimental conditions. Here, an example of the whole-display experiment with a set size of 2

Full size image

The participants were asked to memorize the depth positions of the memory items and to judge whether the depth position of the test item had changed, by pressing “1” on the keyboard to indicate a change, and pressing “3” to indicate no change. Each participant completed a total of 1,024 trials for each test display, including 512 trials for each set size (i.e., 32 trials per cross type, magnitude, and direction). There were half 'no change' trials and half 'change' trials. The participants completed the single-display and whole-display experiments on two different days, and the order of experiments was counterbalanced across participants. The trials of all conditions were mixed, and the order was randomized for each set size block.

Data analysis

Because the conditions of cross type, magnitude, and direction were only meaningful for the 'change' trials, the results of the 'change' and 'no-change' trials were analyzed separately. We performed a separate 2 × 3 × 2 × 2 (set size × cross type × magnitude × direction) repeated-measures ANOVA on the accuracy for the 'change' trials in the whole-display experiment and the single-display experiment to examine the effect of each variable. The results of all post hoc comparisons were Bonferroni corrected.

Results

Whole-display experiment

The accuracies of the 'no-change' trials are shown in Table 1. The accuracies of the 'change' trials are shown in Fig. 3. The results showed a significant main effect of set size, F(1, 11) = 10.96, p = .007, \( {\eta}_p^2 \) = 0.50, magnitude of change, F(1, 11) = 30.98, p < .001, \( {\eta}_p^2 \) = 0.74, and cross type, F(2, 22) = 15.89, p < .001, \( {\eta}_p^2 \) = 0.59. Post hoc comparisons showed that the accuracy in the cross condition (91.5±4.5%) was significantly higher than that in the uncross-inward condition (70.2±17.0%, p = .003), and uncross-outward condition (77.5±15.4%, p = .039); and the accuracy in the uncross-outward condition was significantly higher than that in the uncross-inward condition, p = .001. The main effects of change direction were not significant, F(1, 11) = 3.09, p = .107, \( {\eta}_p^2 \) = 0.22.

Table 1 Means ± SD of the accuracies of the 'no-change' trials
Full size table
Fig. 3
figure 3

Results of the whole-display experiment. Upper panels: the accuracies of the 'change' trials for a set size of 2. Lower panels: the accuracies of the 'change' trials for a set size of 3. Error bars indicate standard errors of the mean

Full size image

The two-way interaction between cross type and magnitude of change was significant, F(2, 22) = 3.84, p = .037,\( {\eta}_p^2 \) = 0.26. For the cross condition, the accuracy was high regardless of change magnitude (all above 90% for the set size of 2 and above 85% for the set size of 3). Pairwise comparison showed that the accuracy for a small magnitude of change was not significantly different from that for a large magnitude (p = .060). But for the two uncross conditions, a large magnitude of change yielded significantly better performance (uncross-outward: p = .012; uncross-inward: p = .006). No other two-way, three way or four-way interaction was found to be significant, ps > .05.

Single-display experiment

In the whole-display experiment, since the test item was presented along with the other memory items, it was possible that the participants were memorizing the whole depth configuration of the memory display instead of memorizing the specific depth position of each item. If this strategy was employed, we would expect a better performance in the cross condition since the whole depth configuration had changed. To rule out this possibility, we tested the memory performance using a single display where only the test item was presented during the test phase. In this case, participants would not be able to use the depth configuration or relative distance information between the elements of the memory array to fulfill the task and the absolute depth positions must be retained.

The accuracies of the 'no-change' trials are shown in Table 1. The accuracies of the 'change' trials are shown in Fig. 4. The results were generally in accordance with that in the whole-display experiment: significant main effects of set size, F(1, 11) = 38.17, p < .001, \( {\eta}_p^2 \) = 0.78; magnitude, F(1, 11) = 35.89, p < .001, \( {\eta}_p^2 \) = 0.77; and cross type, F(2, 22) = 13.25, p < .001, \( {\eta}_p^2 \) = 0.55; no significant main effect of change direction, F(1, 11) = 1.07, p = 0.323, \( {\eta}_p^2 \) = 0.09; significant interaction effect between cross type and magnitude, F(2, 22) = 9.44, p = .001,\( {\eta}_p^2 \) = 0.46; no other significant interaction, ps > .05. Despite the overall consistent results, there was a small exception. Post hoc comparisons on the effect of cross type showed that the accuracy in the cross condition was significantly higher than that in the uncross-inward (p = .001) and uncross-outward conditions (p = .006), but no significant difference was found between the two uncross conditions (p = .44).

Fig. 4
figure 4

Results of the single-display experiment. Upper panels: the accuracies of the 'change' trials for a set size of 2. Lower panels: the accuracies of the 'change' trials for a set size of 3. Error bars indicate standard errors of the mean

Full size image

Importantly, the interaction effect between cross type and magnitude was significant, demonstrating a result pattern consistent with the whole-display experiment. Pairwise comparison showed that for the cross condition, the accuracy for a small magnitude of change was not significantly different from that for a large magnitude (p = .064), but for the two uncross conditions, a large magnitude of change yielded significantly better performance (uncross-outward: p = .006; uncross-inward: p = .042).

Discussion

The present study investigated how depth information is stored in working memory by employing a change-detection paradigm. We found that memory performance is significantly improved when the depth order of an item changes, and increasing the magnitude of change only improves memory performance when the depth order is unchanged. When the test item was presented along with the other memory items (whole-display), there was a memory benefit for detecting an expansion (uncross-outward) of the overall depth volume over a contraction (uncross-inward) of the volume. However, this benefit was not observed when the test item was presented alone (single-display), indicating that presenting the whole set of items facilitates the detection of depth volume change. In addition, the lack of a significant effect of direction of change suggests that moving to a proximal or distal location during memory retrieval does not affect the memory performance for depth.

The smallest magnitude of change used in our experiment was '0.34', which typically corresponds to 5.2 cm with a viewing distance of 75 cm. This amount of change is nonnegligible and can be easily perceived; however, the accuracy for detecting such a change was low when there was no change in depth order present. This was consistent with the previous studies that have investigated working memory for depth. For example, Qian and Zhang (2019) showed that the accuracy in a change detection task was about 78% with a set size of one. Consistently, Reeves and Lei (2017) also demonstrated the poor retention of numerals associated with depths even for a set size of one using a partial report paradigm. In their study, numerals were shown at different depth planes, followed after various delays by an arrow cue to indicate one of the depth planes, and the participants needed to report the numeral whose depth cued by the arrow. These highly nonintuitive findings indicate that our ability for storing precise metric depth information is severely limited. The exact depth position of a single item is either not encoded into absolute spatial metrics efficiently, or is poorly retained even if it is encoded. To further look into this question, we performed a regression analysis and found that the correlations between the perceptual performance in the screening test and the memory performance in the two main experiments were not significant (ps > .296). This might provide some evidence suggesting that the unsatisfying performance is probably due to poor retention of metric representation of depth.

Conversely, change in depth order can be well detected regardless of the change magnitude. This effect was reliably observed in the single-display and whole-display experiments, suggesting that depth order is registered in working memory whether the task encouraged or discouraged a strategy for memorizing the global depth configuration. In the single-display experiment, observers knew that only a single depth position was to be tested and no other memory item was available to provide relational cues during the test phase, the memory performance in the cross condition was nevertheless higher than the uncross conditions. This indicates that the information of relative depth order is encoded and represented in working memory. However, since the comparisons between different experimental conditions were made on the accuracies of 'change' trials, one might suspect whether there was any response bias confounding the results. To address this issue, we carried out a control experiment for a set size of 2 with a block design (i.e., different experimental conditions were tested in separate blocks). We calculated the detection sensitivity, d', and the response bias, β, based on the hit and false-alarm rates. The results showed that β did not significantly vary between conditions, and the results for d' were consistent with the main experiment (see the Supplementary Materials for detailed reports). This suggests that the better performance when changing depth order was not due to response bias, indicating that ordinal depth is stored in working memory.

The interaction between cross type and change magnitude shows that if the depth order is unchanged, metric information matters: the larger the change magnitude is, the better the memory performance. This suggests that metric depth is also stored in working memory. However, if the depth order is changed, the memory performance is high even with a small change magnitude. This further suggests that observers were not able to register each depth position in working memory independently of the others, indicating that change in depth order is a better indicator for working memory performance than the magnitude of change. But one thing to be noted is that the set sizes and change magnitudes tested in our study were relatively small, we might need more evidence to conclude that the predominance of ordinal representation for depth working memory persists for larger set sizes or change magnitudes.

Studies on VWM have shown that items in memory are more closely bound to locations within a spatial configuration rather than to absolute locations in space, suggesting that VWM might be configuration-based (Jiang et al., 2000). The formation of 2-D spatial configuration is immediate, within the first few hundred milliseconds of visual presentation (Chun & Jiang, 1998). The configural effect was also observed in recognition of novel objects and faces (Carlson-Radvansky, 1999; Gauthier & Tarr, 1997; Palmer, 1977; Tanaka & Farah, 1993), that observers became less accurate at identifying parts of the object when the configuration of the global object changed. Although the configural effect is seemingly similar to the effect of depth order found in our experiment, they differ in several fundamental ways. First, the configural effect demonstrates that the memory can be enhanced when the spatial configuration is kept constant, whereas in our experiment the spatial configuration was only kept constant on the 'no-change' trials, but always changed on the 'change' trials, and nevertheless the memory performance differed. Second, the previous findings were all within a context of 2-D spatial configuration, and did not specify in what form the relational information being encoded and stored. Here, we show that spatial configuration is important to working memory in a 3-D spatial context, and suggest that the relational information for depth positions can be registered as their relative depth order, which may be a basic representational unit and play a primitive role in working memory in a 3-D spatial context. Finally, in addition to the effect of depth order, we found that a memory benefit for detecting an expansion of the overall depth volume over a contraction of the volume only in the whole-display experiment, indicating that presenting the whole set of memory items facilitates the detection of depth volume change. This memory benefit cannot be attributed to the configural effect, since facilitation on item localization by encoding the global configuration would predict better performance for the whole display than for the single display, but not for volume expansion. The memory benefit for volume expansion may be due to that expansion requires an update on the registered depth range, whereas contraction within the registered depth range does not, therefore there is a higher detection sensitivity for the former. The fact of presenting the whole set of memory items during retrieval (whole display) may facilitate this process because items within a configuration could serve as references for each other and the visual system becomes more sensitive to the relation among items.

The present findings have important implications for the nature of working memory for depth information. Depth order is an inherent characteristic in a depth configuration, which specifies the relation of one location among other locations and the observer. The crucial role of depth order may be associated with the attentional processes that are used to detect objects in depth. Studies indicate that we tend to attend to object in depth serially rather than to simultaneously spread attention across multiple depths (He & Nakayama, 1995), which is also consistent with our daily experience. Because attention can be constrained within a depth plane and the depth order of objects may determine the temporal order in which each object receives attentive processing, this information is essential for locating and identifying objects in depth. Although metric depth is also retained in working memory, we suggest that ordinal information plays an important role in encoding and retention of depth information.

To conclude, our study suggests that depth information is not registered independently in working memory, but rather in relation to other items in the same spatial configuration. The relational information is encoded in the form of depth order. The memory representation for depth is inherently relational and wedded to global 3-D spatial configuration, revealing a fundamental organizing principle for depth information in the visual system.