Imagine an athlete waiting in the starting blocks of a sprint race. After perceiving the word “Set,” the athlete takes his final position, as this is a warning that the go signal is about to occur. During the brief interval between “Set” and “Go,” the athlete is preparing to take off as fast as possible the instant the gunshot is heard. This process is known as temporal preparation (Dalmaijer, Nijenhuis, & Van der Stigchel, 2015; Niemi & Näätänen, 1981).

Temporal preparation has been investigated extensively in reaction time (RT) tasks by manipulating the foreperiod, the interval between a warning stimulus (S1) and a target stimulus (S2). It has consistently been shown that RTs with respect to S2 are influenced both by the duration and distribution of foreperiods. For example, in a variable-foreperiod paradigm with a uniform distribution, where all foreperiods vary randomly and equiprobably within blocks, RTs typically decrease as the foreperiod increases—the classic variable-foreperiod effect (e.g., Woodrow, 1914). Moreover, in the case of an antiexponential distribution, where the occurrence of short foreperiods is low, this decrease in RTs with increasing foreperiods becomes even steeper (e.g., Los, Kruijne, & Meeter, 2017. By contrast, in the case of an exponential distribution, where the occurrence of short foreperiods is high, the RT-foreperiod function is approximately flat (e.g., Näätänen, 1971; Trillenberg, Verleger, Wascher, Wauschkuhn, & Wessel, 2000).

Whereas previous research has firmly established these and similar foreperiod effects (for reviews, see Los, Kruijne, & Meeter, 2014; Niemi & Näätänen, 1981), the underlying cognitive mechanism is still largely unknown. Most inquiries have started from the idea that the increase of temporal preparation is closely related to the hazard function (e.g., Nobre, Correa, & Coull, 2007; Vallesi, Lozano, & Correa, 2013), which describes the increasing conditional probability of S2 occurrence over time, given that it has not occurred yet (e.g., Luce, 1986). In particular, there exists a close reciprocal relationship between current hazard and mean RT across a variety of foreperiod distributions (Coull, 2009; Cui, Stetson, Montague, & Eagleman, 2009; Janssen & Shadlen, 2005; Näätänen, 1971; Trillenberg et al., 2000), which has led to the widespread belief that hazard drives temporal preparation or temporal expectancy (e.g., Coull, Cheng, & Meck, 2011; Niemi & Näätänen, 1981; Stuss et al., 2005; Vallesi et al., 2013; Vallesi & Shallice, 2007).

A problem with this hazard-based view is that it lacks a cognitive basis (Los, 2013). It has been argued that the changing hazard is used by a controlled process that allows participants to strategically apply knowledge about the hazard function to enhance their preparatory state (e.g., Coull et al., 2011; Vallesi et al., 2013; Vallesi, McIntosh, Shallice, & Stuss, 2009; Vallesi & Shallice, 2007). This view requires that participants have access to the changing hazard as time elapses during the foreperiod, but no one has ever specified how people acquire knowledge of the hazard function and how they are able to subsequently apply it.

Starting from an alternative point of view, Los, Kruijne, and Meeter (2014) recently proposed that temporal preparation on the current trial is directly driven by representations of previous experiences stored in long-term memory (see also Howard & Eichenbaum, 2013; Taatgen & Van Rijn, 2011). They elaborated this view in a new multiple trace theory of temporal preparation (MTP), which is based on the following assumptions. First, on each trial, inhibition is applied during the foreperiod, serving to prevent premature responses (see also Duque & Ivry, 2009; Narayanan & Laubach, 2006), and activation at the onset of S2, to support the response. Second, these actions along with their temporal profile are stored as unique memory traces on each individual trial. Third, during the foreperiod on each new trial the stored inhibition and activation values are retrieved and aggregated across memory traces and together determine the current preparatory state. As time elapses during the foreperiod, the aggregated inhibition values decrease relative to the aggregated activation values, such that preparation increases (for details, see Los et al., 2014). This in turn, can explain the variable-foreperiod effect and the modifying influence of the distribution of foreperiods. Furthermore, by adding the assumption that recent memory traces contribute more strongly to current preparation than older ones, MTP also provides a natural explanation for typical short-term effects of foreperiod (i.e., the asymmetric sequential effect; e.g., Los, 2010; Steinborn & Langner, 2012; Zahn, Rosenthal, & Shakow, 1963), which have been problematic for hazard-based explanations.

In an initial test of MTP, Los et al. (2017) studied transfer effects of different foreperiod distributions. According to MTP, memory traces of previous distributions of foreperiods should be relatively persistent across blocks, and therefore, when participants are presented with a change in distribution, RTs should still show signs of the old distribution. By contrast, according to hazard-based explanations, participants should be able to quickly tune in on the prevailing hazard function, so there should be no transfer between blocks. Los et al. presented two groups of participants with either the exponential or the antiexponential distribution for a couple of blocks during an acquisition phase. They found that the RT-foreperiod function was approximately flat in the exponential blocks and steep in the antiexponential blocks, which is consistent with earlier findings in the literature (e.g., Niemi & Näätänen, 1981). Then, in the transfer phase, both groups were presented with the same uniform distribution. Although full information was provided about this change in foreperiod distribution at the start of these blocks, the results showed clear transfer effects of the previous distributions. Specifically, the RT-foreperiod function was still flatter after a preceding exponential distribution than after a preceding antiexponential distribution. This finding clearly shows that old timing experiences continue to contribute to current temporal preparation, which supports a key prediction of MTP and is hard to reconcile with the hazard-based view.

At the most general level, the findings by Los et al. (2017) show that temporal preparation is modified by the history of previous timing experiences. MTP is well equipped to account for effects of trial history, because all previous memory traces, created across all previous trials and blocks, contribute to preparation as a function of their recency. By contrast, hazard is a mathematical function derived from the current distribution of foreperiods without regard to their history. Therefore, effects of trial history, whether short term (asymmetric sequential effects) or long term (transfer effects of foreperiod distributions across blocks) severely challenge the validity of hazard as an explanatory construct in temporal preparation.

How persistent is the transfer effect in temporal preparation? The transfer effects observed by Los et al. (2017) lasted for more than two hundred trials, but occurred within a single experimental session of maximally one hour. If temporal preparation is driven by traces retrieved from long-term memory, it should be possible to observe transfer effects over a longer period of time. In the current study, we tested this corollary in the same way as in the study by Los et al., except for one crucial difference. After completing the acquisition phase, participants were dismissed and came back a full week later for the transfer phase. In the acquisition phase, one group was presented with the exponential distribution of foreperiods, whereas the other group was presented with the antiexponential distribution. In the transfer phase, both groups received, after explicit instruction, the same uniform distribution. According to MTP the pattern of RTs in the transfer phase should still show signs of the old distributions presented one week earlier. This outcome would confirm the importance of long-term memory in temporal preparation.

Method

Participants

The initial sample consisted of 28 students, who participated in an experiment that required attendance in two sessions separated by 7 days. One participant was excluded from the analyses because her data did not meet our criteria (see Results section). Therefore, the final sample included 27 participants (23 female, 4 male), between 19 and 28 years of age (M = 22.26, SD = 2.26), and with normal or corrected-to-normal eyesight. Participants were randomly assigned to Group 1 (n = 13) or Group 2 (n = 14). All participants gave informed consent and received either course credits or a monetary compensation of €10 for participation.

Design

The foreperiod, here defined as the interval between the onset of S1 and the onset of S2, varied within subjects and within blocks at four levels of 400, 800, 1200, or 1600 ms. Foreperiods varied randomly within blocks according to one of three different distributions: uniform (foreperiod ratio 1: 1: 1: 1), exponential (foreperiod ratio 8: 4: 2: 1; i.e., predominantly trials with shorter foreperiods), or antiexponential (foreperiod ratio 1: 2: 4: 8; i.e., predominantly trials with longer foreperiods). Session 1 (the acquisition phase) consisted of five blocks, and Session 2 (the transfer phase) consisted of four blocks (see Fig. 1, top panel). In the first block of Session 1, both groups received the same uniform distribution as a baseline condition. Then, in Blocks 2–5, Group 1 received the exponential distribution and Group 2 the antiexponential distribution. In Blocks 6–9 of Session 2 (one week later), both groups received the same uniform distribution. The dependent variables were mean RT and error proportion.

Fig. 1
figure 1

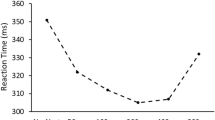
Top panel. Successive foreperiod distributions across blocks for Groups 1 and 2 (Uni = uniform; Exp = exponential; Anti-exp = antiexponential). Note that Session 1 (acquisition phase) and Session 2 (transfer phase) were separated by a full week. Bottom panel. Mean response time as a function of foreperiod, group, and block. Error bars represent ±1 standard error. Note that the interaction between foreperiod and group observed in Blocks 2–5 of Session 1 was still statistically significant a week later in Blocks 6–8 of Session 2, reflecting a long-term transfer effect of foreperiod distribution

Full size image

Procedure

Participants were seated in a dimly-lit cubicle with a personal computer, which was connected to a 22 inch, 120 Hz LCD monitor and a standard QWERTY keyboard. Participants placed their heads on a chin rest at a viewing distance of 70 cm from the screen and held their left and right index finger on the z and m key, respectively. At the start of each session, participants received task instructions on the computer screen.

Each trial started with the presentation of S1, a 0.4° × 0.4° black fixation cross (+), presented against a white background at the center of the screen. Then, after a variable foreperiod of either 400, 800, 1200, or 1600 ms, S2 was presented. S2 was a 0.8° black square, placed to the left or right of fixation with equal probability, at about 2.0° eccentricity. Participants were instructed to press the z or m key when S2 appeared left or right of fixation, respectively, and to do so as quickly as possible while maintaining high accuracy. After the participant responded, S1 and S2 were immediately removed, leaving the screen blank for 1500 ms before the onset of a new trial.

Participants completed nine blocks of 120 trials each, taking approximately 40 minutes in Session 1 (five blocks), and 30 minutes in Session 2 (four blocks). During Session 1, participants received no information about the distributions of foreperiods. However, at the start of Session 2, participants were debriefed about the distribution they had received in Blocks 2–5 of Session 1 and they were informed that in each block of Session 2, short and long intervals would occur equally often. In both sessions, mean RT and the percentage of correct responses were shown on the screen after the completion of each block. Participants copied these scores on a sheet of paper to allow them to keep track of their performance, which served the purpose of keeping participants motivated to respond as accurately and quickly as possible. This also allowed the experimenter to review performance at a glance after each experimental session. Participants were fully debriefed after Session 2.

Results

Data from one participant in Group 1 were excluded from the analyses because her RTs were above 800 ms in more than 10% of the trials. For all other participants, the first trial of each block was discarded as well as trials where participants made an erroneous key press (0.81%) or responded during the foreperiod (0.39%). Trials with RTs shorter than 150 ms or longer than 800 ms were also discarded (0.26%). Because these percentages were very low, they were not analyzed any further. From the data of the remaining trials, mean correct RTs were calculated and used for subsequent analyses.

We performed mixed ANOVAs on each block separately, with foreperiod included as a linear (1 df) within-subjects factor and group as a between-subjects factor. This analysis allowed us to unambiguously test whether the slope of the RT-foreperiod function (i.e., the linear effect of foreperiod on RT) was modified by group. In all analyses, alpha was set at .05. The results of these analyses revealed a strong main effect of foreperiod in Block 1, F(1, 25) = 52.80, p < .001, η2 p = .68, showing the typical reduction of RT as a function of foreperiod. By contrast, neither the main effect of group, nor the interaction between group and foreperiod were significant (F < 1), indicating that temporal preparation was initially equivalent in both groups. As expected, the results showed a significant interaction between foreperiod and group in the subsequent blocks (2–5) of Session 1, minimal F(1, 25) = 19.07, p < .001, η2 p = .43, across all four blocks, reflecting the approximately flat and steep RT-foreperiod function in Group 1 and Group 2, respectively. As Fig. 1 shows, this interaction was already strong in Block 2, when the differential foreperiod distributions were used for the first time.

Crucially, a week later, the interaction between foreperiod and group was still significant in Blocks 6–8 of Session 2, when both groups received the uniform distribution, minimal F(1, 25) = 12.92, p = .001, η2 p = .34, across all three blocks. As shown in Fig. 1, this interaction still reflects an approximately flat and a much steeper RT-foreperiod function in Group 1 and Group 2, respectively. This indicates that the pattern of RTs in the transfer phase still showed signs of the old distributions presented in the acquisition phase, even though it was emphasized at the start of Session 2 that the distribution would be uniform. The interaction between foreperiod and group was nonsignificant in the final block, F(1, 25) = 3.51, p = .073, η2 p = .12, which indicates that the transfer effects diminished toward the end of Session 2. The fact that this happened after no less than 360 intervening trials with the uniform distribution suggests that this diminishing effect occurs very slowly.

Finally, we corroborated these results with more stringent analyses by referring the interaction effects in each test block to the corresponding effect in the first block of the acquisition phase. To this end we used mixed ANOVAs with foreperiod, group, and block as factors. The three-way interaction among foreperiod, group, and block was significant when comparing Block 1 to Block 6, F(1, 25) = 8.57, p = .007, η2 p = .26, or to Block 7, F(1, 25) = 6.15, p = .020, η2 p = .20, it approached significance when comparing Block 1 to Block 8, F(1, 25) = 3.78, p = .063, η2 p = .13, but not any longer when comparing Block 1 to Block 9, F(1, 25) = 2.30, p = .14, η2 p = .084. Thus, even this more stringent analysis indicates that the two-way interaction between foreperiod and group was initially stronger than in the baseline condition (Block 1) and gradually became less strong across subsequent test blocks.

Discussion

The present data provide compelling evidence for a profound role of long-term memory in temporal preparation. Consistent with earlier findings by Los et al. (2017), the effects of the different foreperiod distributions presented in Session 1 (the acquisition phase) were still apparent in Session 2 (the transfer phase), where both groups received the same uniform distribution and were provided full information about the change in foreperiod distribution. The critical new finding of the present study is that this transfer effect was observed when the two sessions were separated by no less than a full week. Thus, extending the previous findings by Los et al., we showed that the transfer effect does not only occur within one experimental session but even a week later. This strongly suggests that the memory traces postulated by MTP are very stable over time.

The observed transfer effect is hard to reconcile with models of temporal preparation based on the hazard function (e.g., Coull et al., 2011; Cui et al., 2009; Janssen & Shadlen, 2005; Vallesi & Shallice, 2007). The hazard function is derived from the current distribution of foreperiods without regard to their history. Therefore, if temporal preparation is driven by hazard, there should be no transfer from previous distributions of foreperiods. The present data are clearly inconsistent with this prediction.

It may be noted that the two-way interaction between foreperiod and group, as observed in Session 1, was considerably reduced in Session 2. However, this finding is not inconsistent with the predictions of MTP, because recent memory traces—especially the most recent one—are assumed to carry more weight than older traces in their contribution to preparation on the current trial (see also Los et al., 2014). This mechanism allows MTP to account for short-term effects lasting a few trials (i.e., asymmetric sequential effects), which have been shown to make a robust contribution to RT (e.g., Los, 2010; Los & Van den Heuvel, 2001; Steinborn & Langner, 2012; Vallesi & Shallice, 2007; Woodrow, 1914; Zahn et al., 1963). These sequential effects also contribute to the difference in RT-foreperiod functions between the exponential and antiexponential distributions (i.e., there are more primed short-short transitions in the exponential than antiexponential distribution; see Los & Agter, 2005, for a detailed discussion). This contribution of sequential effects strongly diminishes as soon as the transition to the uniform distribution is made in Session 2. However, within Session 2, the transfer effect turned out to be quite persistent. It remained statistically reliable for hundreds of trials and was nonsignificant only toward the end of Session 2. This means that the transfer effect not only survives a delay of a week, but also is not easily overwritten by new traces.

It is of interest that a pervasive role of long-term memory is also emerging in other domains of human performance. For instance, in the domain of specific temporal expectancy, it has been observed that participants respond faster to a specific target stimulus, the higher it is correlated with a specific temporal interval (e.g., Thomaschke, Wagener, Kiesel, & Hoffmann, 2011). This effect has been observed to persist for many trials into a transfer phase, where the time-event correlation no longer applies (Thomaschke & Dreisbach, 2013). Furthermore, in the domain of time perception, Taatgen and Van Rijn (2011) observed long-term effects of trial history (along with short-term ones) reflected in the time estimates of temporal intervals. Intriguingly, the pool model that Taatgen and Van Rijn proposed as an account for these effects is based on principles of memory storage similar to those of MTP. Finally, in the more distant domain of visual search, it has been observed that selection is faster when target features are repeated from one trial to the next, and in the case of conjunction search these effects even occur on the long term, that is, up to at least a week, as in the present experiment (Kruijne & Meeter, 2015, 2016).

In conclusion, the view that temporal preparation is driven by the hazard function cannot account for the transfer effects found in our study. Participants used neither the information provided at the start of Session 2 nor their initial experiences during Session 2 to quickly adjust to the new hazard regime. Consequently, the effect of the foreperiod distribution experienced a week earlier continued to influence behavior for several hundreds of trials. Therefore, our results provide compelling evidence that temporal preparation is not driven by hazard but instead by memory traces stored in long-term memory as assumed by MTP. MTP seems promising not only because it makes correct predictions about transfer effects, but it also relies on well-established cognitive principles of learning and memory. On this account, we conclude that temporal preparation is actually a reliving of our past.