A generative joint model for spike trains and saccades during perceptual decision-making

Abstract

Theory development in both psychology and neuroscience can benefit by consideration of both behavioral and neural data sets. However, the development of appropriate methods for linking these data sets is a difficult statistical and conceptual problem. Over the past decades, different linking approaches have been employed in the study of perceptual decision-making, beginning with rudimentary linking of the data sets at a qualitative, structural level, culminating in sophisticated statistical approaches with quantitative links. We outline a new approach, in which a single model is developed that jointly addresses neural and behavioral data. This approach allows for specification and testing of quantitative links between neural and behavioral aspects of the model. Estimating the model in a Bayesian framework allows both data sets to equally inform the estimation of all model parameters. The use of a hierarchical model architecture allows for a model, which accounts for and measures the variability between neurons. We demonstrate the approach by re-analysis of a classic data set containing behavioral recordings of decision-making with accompanying single-cell neural recordings. The joint model is able to capture most aspects of both data sets, and also supports the analysis of interesting questions about prediction, including predicting the times at which responses are made, and the corresponding neural firing rates.

Introduction

For more than 50 years, mathematical theories of simple decision-making have been based on the notion of “evidence accumulation”. Evidence accumulation explains behavioral and neurophysiological data by assuming that decisions are made by gradually accumulating evidence from the environment in favor of each possible choice. The first choice to accumulate a threshold amount of evidence is selected (see Fig. 1a). Through variations on this basic theme, accumulator models of decision-making have explained dozens of robust empirical phenomena (Palmer and Shadlen 2005; Ratcliff 1978; Ratcliff and Rouder 1998; Van Zandt 2000), and have been used as measurement tools to understand important problems including clinical disorders (Ho et al. 2014), alcohol intoxication (van Ravenzwaaij et al. 2012), sleep deprivation (Ratcliff and Van Dongen 2011), and many others.

Fig. 1

Some previous research linking decision-making models with neural data

More recently, neurophysiological research has provided insights into the neural underpinnings of decision-making (for reviews, see: Glimcher, 2003; Shadlen & Kiani, 2013; Purcell et al. 2012; Mulder et al. 2014). Links between neurophysiology and cognitive models allow the possibility of testing cognitive models on their ability to simultaneously account for both behavioral and neural data. Many researchers agree that this “neuro-cognitive modeling” approach has the potential to provide important insights into psychological and neuroscientific questions. However, the information gained by this joint approach requires coherent solutions for integrating the neural and behavioral data.

Detailed links between neurophysiology and cognitive decision-making models

The initial links between neurophysiology and cognitive decision-making were drawn when researchers noticed that certain cortical neurons in monkeys behaved similarly to the basic structures assumed in evidence accumulation models (Boucher et al. 2007; Britten et al. 1992; Glimcher 2003; Hanes and Schall 1996; Kim and Shadlen 1999; Schall 2001; Shadlen and Newsome 2001; Schall 2003). For example, certain types of neurons in the frontal eye fields (FEF) and lateral intraparietal (LIP) areas of macaque monkeys behave analogously to the “accumulator” structures in evidence accumulation models: those neurons accumulate evidence towards a threshold, and a behavioral response follows soon after (see Fig. 1b). Of course, the analogy is much more sophisticated than this:

• A neuron in FEF reaches a stereotyped and invariant firing rate just before a response is initiated.

• The time the neuron takes to reach maximum firing rate is related to the decision time of the monkey.

• The activity of the neuron can predict behavioral responses, even when those responses contradict stimulus evidence, and even when the stimulus contains no evidence (for reviews, see: Gold & Shadlen, 2007; Schall, 2003.

(Usher and McClelland 2001) explored the relationship between neurophysiology and cognitive decision-making by developing their accumulator model of simple decision-making with careful consideration of the dual constraints imposed by neurophysiology and psychology. (Hanks et al. 2011) identified particular neural trajectories with the trajectories of accumulator processes in their model. Other researchers have linked neural and behavioral models by identifying experimental manipulations which should induce corresponding qualitative differences in model parameters and neurophysiological measurements (Ho et al. 2009; Roitman and Shadlen 2002; Heitz and Schall 2013).

The tightest links between neural and behavioral data can be made by jointly (i.e., simultaneously) modeling the two data sets. As well as increasing the breadth of explanation offered by a theory, jointly modeling neural and behavioral data more tightly constrains the theory’s predictions. This constraint improves model identifiability and can shine light on aspects of the theory that are not otherwise easy to examine (a point also made by Purcell et al. 2010). For example, cognitive models of decision-making include a latent parameter which represents the composite of two distinct processes (a “non-decision time” parameter, which represents time taken for stimulus input processes and also for response output processes). As we will show, these two processes can be separately identified when the neurophysiological data and the behavioral data are addressed simultaneously. Another key advance of this approach over post hoc (or two-stage) linking approaches is that joint models allow neural data to inform understanding of the behavioral aspects of the model, and vice versa.

(Turner et al. 2013) developed an innovative approach to joint modeling in which separate neural and behavioral models were linked—by allowing covariance between the models’ parameters—and the entire ensemble was estimated together. The joint model and one-stage estimation procedure allows for exploratory analysis of relationships between neural and behavioral models. Turner et al.’s approach also has the benefit of allowing the two different data streams to jointly influence parameter estimates in both models. We expand on this, and other important comparisons between two-stage and joint modeling approaches in Two-stage modeling and joint modeling in the discussion section.

Jointly modeling neural and behavioral data

(Purcell et al. 2010) proposed a model for confirmatory analysis with specific and tightly constrained links between the neural and behavioral elements. The model assumed precise quantitative links between accumulators in cognitive models and physiological structures (see Fig. 1c). The theory is evaluated by recording the timing of action potentials (spikes) from both the evidence-producing neurons (visual neurons in the FEF of the macaque) and the evidence-accumulating neurons (movement neurons). The recorded spikes from the visual neurons are used to drive evidence accumulation in a cognitive accumulator model, and the resulting evidence accumulation trajectories are compared against the measured trajectories of the movement neurons.

Purcell et al.’s work marked an important theoretical advance: theirs was the first work to quantify, within a model, the assumed link between neural data and a cognitive accumulator model (the trajectory of an evidence accumulator). Our work builds on the work of Purcell et al. by including an explicit model of the neural data (Purcell et al. mapped the cognitive model directly to neural firing rates) and a function for linking parameters of the neural and accumulator models. The explicit joint model allows us to address interesting questions that were not previously possible, such as “conditional on observing a certain response time, what neural data are likely?”, and the converse question, “conditional on observing certain neural data, what response time is likely?”. By quantifying answers to these questions, the joint model supports multiple ways of testing theories against observed data. We use a computationally tractable decision-making model (the linear ballistic accumulator, or LBA, model: Brown & Heathcote, 2008) and a simple neural model (an inhomogeneous Poisson process). The joint model was implemented in a Bayesian framework and includes hierarchical structures to account for random variation between neurons from different recording sessions and different stimuli conditions.

Our hierarchical structure directly models variability between neurons. This has some advantages over other methods, because the behavior of neurons is extremely variable (Stein 1965; Stein et al. 2005; Tomko and Crapper 1974), even for those neurons within a specific class, which are assumed to have a common purpose. This variability is reflected in neurons with distinct firing characteristics. In response to the same stimuli, some neurons may have very little change between baseline and peak firing rate, whilst neighboring neurons may have quite a dramatic change. Accounting for this variability within computational models, especially in models tightly linking behavioral and neural data, can be a difficult statistical problem. Typically, this problem has been circumvented, removing the variability between neurons by normalizing the firing rates of all neurons within a data set. Although this allows for easier implementation of computational models, it is at the cost of lost information. Although describing neuronal variability within a model is more veridical, the question is do models without descriptions of neuronal variability provide just as good approximations of the phenomenon of interest compared to models with descriptions of neuronal variability? The framework presented here allows for a more full, and quantitative investigation of this model comparison question which we present later.

A decision-making model for neural and behavioral data

Data

We evaluated our model using data from a seminal experiment reported by (Roitman and Shadlen 2002). In the “response time” segment of their experiment, Roitman and Shadlen had two monkeys, denoted “B” and “N”, make thousands of binary decisions about the motion direction of a random dot kinematogram. On each trial, a random dot kinematogram appeared on screen and the monkey indicated whether the coherently moving dots were drifting left or right. There were six levels of decision difficulty manipulated by changing the proportion of coherently moving vs. randomly moving dots. Response times and choices were recorded from each trial, as well as the timing of action potentials from carefully selected neurons in the lateral intraparietal area of the cortex. A different neuron was selected for recording during each experimental session. Some further details of the procedure and data structure are given in Appendix A, but for full details see the original publication¹.

Model

The core element of our model is a simple accumulator model of decision-making, the linear ballistic accumulator (LBA: Brown & Heathcote, 2008). The LBA model has been successfully applied to a large range of simple perceptual choice tasks, including the random dot kinematogram (Ho et al. 2009; Forstmann et al. 2008; Forstmann et al. 2010), and to behavioral decision-making data from monkeys (Heitz and Schall 2012; Cassey et al. 2014). The LBA models the decision between left- vs. right-moving motion as a race between two accumulators, one of which represents the decision to respond “left” and the other which represents the decision to respond “right” (see Fig. 1a). When the stimulus is presented, activity in these accumulators grows linearly. When the activity of either accumulator reaches a pre-set threshold, a decision is made and a response is triggered. The rate of growth in activity is called the “drift rate”, and it is typically larger for the accumulator whose response matches the stimulus than for the accumulator whose response does not, however there is trial-by-trial random variation in the drift rate, which leads to occasional incorrect choices. By specifying the parameters of the model (the height of the response threshold, the distribution of the drift rates, etc.) the model makes predictions for the joint distribution over response choice and response time (see Appendix B for details).

We expand the LBA model to include neural data in two steps (see Fig. 2). We first define a statistical model for the neural data (single cell recordings) collected by (Roitman and Shadlen 2002). That model is a time-inhomogeneous Poisson process, where the spiking rate of the process follows a stereotyped path during each decision (see Fig. 2b). The spike rate is initially constant at a pre-stimulus baseline rate. Firing then dips and recovers just after the onset of the stimulus, then the spike rate increases steadily during the decision-making period itself, before finally falling rapidly to a low baseline after a decision is made. This firing rate path is specified by parameters that correspond to the pre and post-decision baseline firing rates, the size and duration of the post-stimulus dip, and the time to reach the decision threshold (see Fig. 3 for an illustration, and Appendix C for details).

Fig. 2

Our modeling approach

Fig. 3

Piecewise linear function for firing rate of the time-inhomogeneous Poisson process. Red text indicates links with behavioral model

Linking neural and behavioral data

The key step in linking the cognitive model to the neural data is to link the firing rate during the period that represents information accumulation (i.e., the steady increase in firing rate that takes place between stimulus onset and the response) with the instantaneous amount of evidence in the accumulators of the LBA model. This linking is illustrated by the red-colored elements in Fig. 2b and c: the red line segment in Fig. 2b shows the section of the neural firing rate that is linked to evidence accumulation, and the red accumulator trajectory in Fig. 2c shows the LBA model element linked to the firing rate. It is possible to explore all kinds of complex links between these two elements, but we restricted our investigation to a simple linear link. That is, we assumed that a one-unit change in the amount of evidence in an LBA accumulator was equal to a fixed amount of change in the firing rate of the neuron (only during the evidence accumulation or ramping phase). This fixed amount is a parameter of the model (the linking parameter, 𝜃). Prior to any evidence accumulation (i.e. t = 0) the LBA assumes there is some starting amount of evidence in each accumulator, which is a random sample from the interval [0,A]. Evidence then accumulates at a rate given by the drift rate, v. At the time a decision is made, that is when the response threshold is reached, there are b units of evidence in the accumulator. At any given time over the course of a decision, the amount of evidence in an accumulator can be calculated using geometry. The key element of linking the model to the neural data is the dynamic link to the amount of evidence in the accumulator at any given time. This dynamic link is only for the pre-decision evidence accumulation phase.

Formally, the linking function between the state of the evidence accumulator at time t and the Poisson firing rate at time t is given by the following equation, but only for that period during which evidence accumulation occurs (the red segment in Fig. 2).

$$ \lambda(t) = \theta \times \left( x(t) - \frac{A}{2} \right) + \alpha $$

(1)

where λ(t) is the neural firing rate, x(t) is the current amount of evidence in the accumulator, A is the average starting activation of the LBA accumulators and α is the pre-stimulus baseline firing rate of the neuron. LBA accumulators have starting activation randomly (uniformly) distributed between zero and A, so their average is just A/2. Below, we explore two different models, one with A = 0 and one with A = 1. Future work could explore other linking functions—e.g., such as assuming that firing rate is a sigmoidal function of the evidence accumulator’s state.

The result of tightly linking the cognitive model to the neural and behavioral data is a coherent model that does not require separate estimation of the parameters of a neural model and a behavioral model. Instead, we jointly estimate posterior distributions over all parameters in a hierarchical Bayesian framework. We use the resulting estimates to illustrate how the model can address interesting questions about prediction. For example, the model can predict imminent behavioral responses and these behavioral predictions increase in accuracy as the model is conditioned on more and more neural data.

We show that previously inscrutable aspects of the LBA model are revealed in greater detail by the joint model of the neural and behavioral data. For example, the LBA includes an offset parameter (known as t ₀ or T _{e r} ) that represents the time taken for non-decision processes, such as encoding of the stimulus and executing the motor response. Our statistical model for the neural data includes separate components representing the time taken for stimulus perception and the time taken for response execution. These two components remove the need for a single offset parameter, instead allowing us to fractionate the estimated offset time into a stimulus encoding period (δ) and a motor execution period(β).

Model variants

We investigated five model variants in total. The main model we will report is the joint model as defined in the manuscript. The joint model addresses both data streams simultaneously and has hierarchical structures, which are important for exploring the variability between neurons. The second model variant included trial-to-trial variability in start point, by setting the parameter A = 1 in the LBA model. This is more typical of regular usages of the LBA model, where parameter A (the width of the random start-point distribution) is freely estimated. Computational constraints limited us from freely estimating the A parameter, but investigating the A = 1 model variant was important to establish that setting A = 0 in the main model did not limit generalizability. In addition, we also thoroughly investigated three additional models. The third model variant we investigated was the same as the main model, but without a hierarchical structure to accommodate variability between neurons. Instead, that model estimated a single set of parameters for all neurons, treating each as identical. The fourth model was a standard LBA account of the behavioral data only (no neural model, and no linking). The fifth model was a neural-only model, using the time inhomogeneous Poisson model (no behavioral model, and no linking). The neural-only and behavioral-only models were identical to the neural and behavioral components of the main model. We detail results from the main model with comparisons to the variant, which does not take into account neuronal variability. The remaining variants are addressed briefly and results from these are shown in Appendix F and G.

We estimated the posterior distributions over the parameters of all the models in a hierarchical Bayesian framework. Separate parameters were estimated for each recording session (i.e., each neuron). These session-wise parameters were constrained to follow truncated normal distributions. The session-wise parameters, as well as the mean and standard deviation parameters of the group-level truncated normal distributions were estimated simultaneously. This procedure was repeated for monkeys “B” and “N”.

Results

Goodness of fit

We first examined the goodness-of-fit of the main model (i.e., including neuron-to-neuron variability and setting A = 0). We sampled posterior predictive data from the model by replicating the number of sessions and trials per session for each monkey 100 times. Each replication used an independent random draw of parameters from the appropriate session-specific posterior distribution. Conditional on these parameters, we used the LBA model to generate synthetic response times and choices, and used the evidence trajectories from the LBA model to specify the firing rate of the Poisson process which was used to generate neural data. We compared mean RT, full RT distributions, and spike rates between the posterior predictive data and the observed data.

Figure 4c compares posterior predictive and observed behavioral data. Mean RT (top panel) and mean accuracy (bottom panel) are plotted for each monkey and each coherence condition. Throughout, we use black plots for Monkey B and red plots for Monkey N. The error bars illustrate uncertainty in the model predictions due to both finite sample size and posterior parameter variance. The model’s predictions for mean RT match the data very closely. For Monkey B, the mean RT from the data and from posterior predictive data agree to within less than 6 ms. across all coherence levels, and for Monkey N to within 26 ms. The match in predicted choice accuracy is also excellent for Monkey B (within 3 % across all coherence levels), and is fair for Monkey N (except for a 6 % mis-fit in the 0.064 coherence condition). For reference, these fits compare favorably with the simple statistical models traditionally fit to the such data summary statistics (e.g., see Fig. 3 of Roitman & Shadlen, 2002).

Fig. 4

A summary comparison of the fit to data for the main model (more detail in Appendix F). a Full distributions of response times for monkey “N”, separately for 0, .064, and .512 coherence conditions (columns) and correct vs. incorrect responses (rows). All x-axes show decision time (time of saccade) in seconds. Histograms show data, smooth lines show posterior predictive distributions from the joint model. Increasing coherence (across each row) leads to more correct responses and fewer incorrect responses, as well as faster response time distributions. b Neural data (spikes per second) for monkey “N”, separately for 0, .064, and .512 coherence conditions (columns) and correct vs. incorrect responses (rows). The top two rows show neural activity aligned against stimulus onset, the bottom two rows show neural activity aligned against response (saccade), with all x-axes showing time in seconds. Histograms show data, smooth lines show posterior predictive data from the joint model. Data and model predictions are all cut off at the median response time for each condition, following Roitman and Shadlen (2002). Vertical green lines mark stimulus onset (top two rows) and response time (lower two rows). c A comparison of data from both Monkeys ,“B” and “N” (black and red solid lines, respectively), against model predictions (circles). The top panel graphs mean response time (in seconds) and the bottom panel graphs mean accuracy (proportion), both against all stimulus coherence conditions. The circles show the mean statistics calculated from all posterior predictive samples, and the error bars contain 95 % of statistics from all posterior predictive samples

Figure 4a shows a more detailed comparison of response times between the model predictions and observed behavioral data for monkey N (for complete fits to neural and behavioral data for each coherence level for both monkeys see Fig. 7 and 9 in Appendix F). Each panel in Fig. 4a shows a histogram of observed response times (grey bars) overlaid by the corresponding response time density calculated from the posterior predictive model data. All panels use the same axes, which illustrates how the number of correct responses increases in the easier decision conditions (i.e., with increasing stimulus coherence, shown in the top row). The number of incorrect responses shrinks correspondingly, with no incorrect responses at all in the easiest condition. The noise in the data is much more apparent in these plots than in the plots of mean response time and accuracy, and it is clear that some conditions elicited response time distributions that do not resemble the kinds of distributions usually observed in human decision-making studies. For example, in the two most difficult decision condition shown in Fig. 4a, Monkey N produced response time distributions that were negatively skewed. The LBA model misses the data in some of those conditions, which is unsurprising: the LBA is a model of human decision-making and is constrained by its architecture to predict peaked, positively skewed distributions. Nevertheless, the data and model agree in most conditions to a reasonable degree.

We also fit the standard LBA to the behavioral data alone (a “behavioral-only” model; see Fig. 8 in Appendix F), as a benchmark comparison. The behavior-only model must fit the behavioral data at least as well as the joint model, because the behavioral-only model is unconstrained by the neural data—the joint model must compromise on some behavioral parameters to better account for the neural data. Despite the additional constraint imposed by the linking function, the joint model captures the behavioral data almost as well as the standard LBA, which is apparent by comparison of Fig. 8 with Fig. 7.

Figure 4b compares the observed neural data and associated predictions from the main model fit. The data in Fig. 7b replicates the “T1” (or within receptive field) elements of Roitman and Shadlen’s (2002) Fig. 7a. In order to also include model fits on our graph, we have used a less compact arrangement, where each panel shows changes in neural spiking rate for monkey N and a selection of stimulus coherences, as time unfolds during decision-making. As columns move left to right decisions become more difficult (from 0 to 0.064 to 0.512 coherence). The first row shows data aligned on stimulus onset, while the second row shows data aligned on saccadic response. Following (Roitman and Shadlen 2002), and since fewer and fewer trials contribute to the graphs at longer and longer response times, we have trimmed each graph at the median response time for its particular condition.

The data aligned on stimulus onset (top row) show a steady, moderate firing rate before the stimulus, which rises approximately linearly before falling away. The model captures this trend well, but appears to miss the post-stimulus dip in firing rate which occurs in the first 100-150 ms. after the stimulus appears. We attribute this to two factors. Prior to the post-stimulus decrease in firing rate there is slight and almost immediate increase in firing rate, just after the stimulus appears. Our piecewise linear model of the neural data does not include this additional artifact. Also, this may illustrate one aspect where the joint nature of the model has imposed difficult constraints: the model has estimated the dip-and-recover parameters (β and δ) to be small. This is due to the tendency of the LBA to estimate small values for non-decision time, which are reflective with the behavioral artifacts of stimulus encoding and motor execution. This causes a superior fit to the behavioral data. However the cost of estimating a small non-decision time is that it forces a reduction of δ (the duration of the post-stimulus dip) causing the post-stimulus dip to be missed. This requires further investigation in future work with the possibility of directly modeling this additional artifact.

The data aligned to responses (bottom row) show an approximately linear increase in firing rate until just a few milliseconds before the onset of the saccade, which is marked by the vertical green lines. The saccade is followed by a rapid decline in firing rate to a new, much lower baseline. The model captures these effects very closely, via the timing and rate parameters, β, γ, and ω.

The posterior distributions over the parameters corresponding to the model fits above are detailed in Table 2 of Appendix E. These parameter estimates illustrate some interesting patterns. For example, Monkey B waited for more evidence to accumulate before making a decision than did Monkey N (higher evidence threshold, b; this pattern also holds for the model that includes start point variability, see Appendix G). The time taken for firing rate to reduce to baseline after a response (parameter γ) was about 0.12 s, for both monkeys, but there was very large variability between neurons in this quantity (the corresponding σ estimate, which measures standard deviation across neurons, is about 0.24 s). Similarly, the critical parameter linking neural and behavioral data (𝜃) varied greatly between neurons. The posterior distribution over 𝜃 suggests that about one neuron in six changed its firing rate by less than ten spikes per second during the course of evidence accumulation. By comparison, the median change in firing rate during evidence accumulation was around 30 spikes per second.

We also fit a neural-only model, corresponding to just the neural elements of the joint model. The neural-only model must always fit the neural data at least as well as the joint model, for the same reason of statistical nesting as above: the joint model is forced to accommodate constraints from the behavioral data. Fig. 10 in Appendix F shows the fit to the neural data for the neural only model. Comparison with Fig. 9 again shows that the decrement in fit for the joint model is not overly large.

Out-of-sample prediction tests

Predicting upcoming neural and behavioral data

In this section, we test generalizability of the model by predicting data that were not used for model fitting. We do this separately for the main model, which allows neuronal variability, as well as for the model which does not allow neuronal variability and treats all neurons identically. The hierarchical model (with neuronal variability) is expected to outperform the non-hierarchical model (without neuronal variability) as the hierarchical model can learn about individual neuron differences which allow it to differentiate its predictions for each particular neuron in the held out trial.

Because the joint model makes predictions for both neural and behavioral data, the predictive performance can be assessed by the difference between the predicted and observed response times and also by the difference between the predicted and observed spike counts. We use the models to predict both response times as well as spike rates using maximum a posteriori (MAP) estimates for the model with neuronal variability. To evaluate the averaged model, we calculated MAP predictions, except that we conditioned on parameter estimates that were MAP across all neurons (rather than for the particular neuron associated with the left-out data).

For each session (i.e., neuron) and for each monkey, we randomly selected one-fifth of the trials as a test set, to be excluded from training. The posterior distributions over the model parameters were then calculated from the remaining data, and used to make predictions for the left-out data. For each left-out trial, we predicted the time at which the response would occur, and also the firing rate of the neuron (estimated by the number of spikes observed in each small window of time) at each time point in a 0-2 s window from stimulus onset. After these predictions, we allowed the model to refine its predictions by conditioning each trial’s predictions on more and more of the data observed during that trial. That is, for any given left-out trial, the first prediction of response time and firing rate was made without allowing the model any knowledge of the data from the left-out trial. The next prediction was made allowing the model to condition its predictions on the first few spikes recorded during the first 100 ms of the left-out trial. The next prediction conditioned on a few more spikes that occurred during the next 100 ms, and so on until the model incorporated all data from the left-out trial (including the observed response and response time).

We evaluated the model’s prediction performance in two ways. For the neural data, we compared the number of spikes that the model predicted to occur in each 100 ms bin to the actual number that was observed in that bin, during the left-out trial. For the behavioral data, we compared the absolute difference between the RT predicted by the model, and the observed RT from the left-out trial. After sufficient data had been revealed to the model on any given trial, the actual response for that trial—and the associated RT—must also have been revealed. The best “prediction” from any reasonable model at this stage is the actual, observed RT. Similarly, the best “prediction” for any already-revealed spikes are those actual spike counts. For this reason, the prediction error of the model falls to zero as more and more data are revealed.

We made predictions for response times by finding, for each trial, that response time with the maximum a posteriori probability, conditioned on the maximum a posteriori parameter estimates calculated from the calibration data, calculated using Eq. 3 from Appendix E. That equation depends on the observed spiking data for the trial in question, C _{i j} , and this dependence allows us to condition the response time predictions on different amounts of revealed decision time. The effect of this is shown on the x-axes in Fig. 5a for a subset of coherences for Monkey “N”. For example, x = 0.5 shows the accuracy of response time predictions when the likelihood calculations include data that were observed during the first 0.5 s after stimulus onset. Fig. 5b shows the same effect of conditioning model predictions on increasing amounts of revealed data for the neural data. The solid lines in Fig. 5a and b summarize the performance of the response time and spike count predictions, respectively, across all trials and across all samples of left-out data for the model which allows for neuronal variability. The dashed lines indicate the performance of the model without neuronal variability. It illustrates that a model which fails to take into account the differences between neurons makes poorer predictions (i.e., larger prediction errors). Indeed the performance of the two models only becomes commensurate until after the majority of the data have been revealed, that is, only when the model without neural variability can condition its predictions on the majority of the data (be it behavioral or neural) is its prediction accuracy similar to the model with neuronal variability. This effect is larger for Monkey “N” than for Monkey “B”, because the amount of between-neuron variability in parameters was larger for Monkey “N”.

Fig. 5

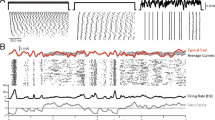
Predictive model performance for Monkey “N”. a Prediction error (mean absolute difference, in seconds) when predicting response times from unseen data for coherence levels 0 and 0.256. Predictions are given by the MAP estimator conditioned on increasing durations of revealed data from each trial (x-axes). The solid line in each panel shows prediction error from the joint model that allows for individual neuron differences. The dashed line shows prediction error from an average (non-hierarchical) version of the joint model, which does not account for parameter differences between neurons. As more data is revealed, prediction error drops and approaches zero when the temporal window includes the actual response and response time as observed information. b Neural data prediction error for coherence levels 0 and 0.256, measured by the mean absolute difference between the observed and predicted spike counts in 0.05-s bins. Predictions are given by the MAP estimator conditioned on increasing durations of revealed data from each trial (x-axes). The solid line in each panel shows prediction error from the joint model. The dashed line shows prediction error from a non-hierarchical version of the joint model which does not account for parameter differences between neurons. c Response time distributions conditioned on spike trains. For the early stages of trials (i.e., < 0.6 s), for coherence level 0.256, resulting RTs are grouped based on whether the corresponding spike train portion had either few (≤14) or many (≥ 28) spikes, plotted as grey histograms. Posterior predictive RTs group according to the same criteria are overlaid as solid lines. d Spike trains conditioned on response times. Empirical spike trains whose corresponding saccade was made in the RT range 0.2–0.5 s or 0.7–1 s are plotted. Posterior predictive spike trains from the same RT ranges are overlaid as solid lines

It is clear that the main model, which includes neuronal variability, makes better predictions before any data are revealed about the particular left-out trial (i.e., at x = 0) and continues to do so as more data are revealed. It took, on average, 0.64 s and 0.92 s (for monkeys “B” and “N”, respectively) of revealed data for a model which did not account neuronal variability to perform with commensurate success to that of a model which did account for this variability. This is an important result, demonstrating that valuable information is lost when neuronal variability is not accounted for. Indeed inclusion of this variability greatly improves the performance of the model.

Predicting response time distributions and neural firing rate trajectories:

The incorporation of both behavioral and neural data in the joint model means that the model predictions for behavioral data change based on the neural data, and vice versa. Fig. 5c demonstrates this effect of conditioning RTs on neural dynamics. We separated observed RTs based on whether the neural data had either few (≤14) or many (≥ 28) spikes occurring in the first 0.6 s of the trial. These response times are plotted as grey histograms in Fig. 5c. We made the same separation for the posterior predictive RT data, based on the posterior predictive neural data. The predicted distributions from the main model are shown as red lines in Fig. 5c. The distributions of data are clearly different between the many and few spike conditions, and the model’s predictions are sensitive to this difference.

Figure 5d demonstrates the corresponding effect of conditioning neural data on behavioral data. We separated trials according to whether they had fast RTs (0.2–0.5 s) or slow RTs (0.7–1 s). The neural data from these trials are shown as gray histograms, aligned both on stimulus onset (upper row) and response (bottom row). As before, we compared the observed data with the posterior predictive data by taking spike trains generated out of the model and grouping based on the same RT ranges, using the model’s predicted RTs. The model (red lines) identifies the different characteristics between the two ranges, with a faster ramping in spike rate for the faster RTs and a slower ramping of spike rate for the slower RTs.

Discussion

As with many research topics in psychology and neuroscience, the study of decision-making has been informed by both behavioral and neural data. Over past decades, different approaches have been taken to integrate the behavioral and neural evidence, with increasing statistical sophistication allowing tighter integration in recent years. Tighter integration can be important as it allows, among other things, more precise, quantitative testing of deep model assumptions about the link between behavior and neuroscience (e.g., Purcell et al. 2010; Turner et al. 2013; Turner et al. 2016).

We evaluated our modeling approach using data from a seminal experiment reported by (Roitman and Shadlen 2002). This experiment had two monkeys making thousands of decisions about random dot motion, with simultaneous recordings of behavioral data and action potentials from neurons involved in the decision-making process. The joint model was able to fit the full distributions of response times, for both correct and incorrect responses, across the six different levels of decision difficulty. Simultaneously, the model fit the change in firing rate of decision-related neurons both across conditions as well as across time during each decision trial.

Not all of the behavioral model fits were quite as close to the data as is typical for the LBA (e.g., the fifth panel in the top row, and the second and fourth panels in the second row of Fig. 7). We attribute this to two causes. Firstly, behavioral data from monkeys are not quite the same as behavioral data from humans, for which the LBA model was developed. In addition to species differences, it is typical for monkeys to undergo training which can be orders of magnitude greater than is standard for human participants. It is possible that such training results in response time data with different characteristics to standard human experimentation, or perhaps there are differences in the underlying cognitive processes (cf. Hawkins et al. 2015). However, the instances of misfit are most likely attributed to the fact that this instance of the LBA model is very tightly constrained because it must jointly account for the behavioral data and the neural data. This causes tension between adjusting parameters to optimize agreement with the behavioral data and adjusting parameters to optimize agreement with the neural data.

Two-stage modeling and joint modeling

It is important to highlight some similarities and differences between our approach and previous approaches to linking behavioral and neural data streams. One common element in the work to date that has linked behavioral and neural data streams is the use of a two-stage approach (however see Turner et al. 2013). In such approaches, first a model is fit to one of the data streams (typically a cognitive model is fit to the behavioral stream, such as response times). Secondly, based on the outcomes of the model fit, considerations are made about how elements of the model fit map onto elements of the other data stream (typically the neural stream). These considerations may be how accurately elements of the model predicts changes in (assumed) analogous elements of the neural data, such as changes in firing rates of single neurons (e.g., Hanes & Schall, 1996) or changes in amplitudes of EEG recordings (e.g., Logan et al. 2015).

(Purcell et al. 2010) used a more sophisticated two-stage approach. In addition to fitting the behavioral data, one element of the neural data was also used to inform specific mechanisms of various cognitive models. As such, elements of both data streams informed the initial first-stage model fitting. Following this, the model fits were compared to different neural data, which were not used to inform the model fitting. Purcell et al. were able to perform informative model comparison as well as answer interesting prediction questions using this two-stage linking process.

The joint modeling framework outlined in this paper builds on the foundational work of (Purcell et al. 2010) and (Turner et al. 2013). Like Turner et al., our approach links both data streams in a single step, within one framework. The joint model defines a specific, quantitative link between the neural and behavioral data, and allows parameters to be estimated simultaneously from both data sets. This framework allows the model to address interesting questions, such as making predictions for neural data on the basis of observed behavioral data, and importantly, make predictions for behavioral data on the basis of observed neural data, something which was not possible with Purcell et al.’s approach. Our approach puts the behavioral and neural data sets on an equal footing, allowing information from each data set to inform estimation of all of the model parameters. It is this equality that means that the model can make predictions for neural data as well as for behavioral data. Our approach also brings extra constraint to the model. For example, the parameter governing non-decision time in evidence accumulation models (t ₀ here, often called T _{e r} in diffusion models) is under-constrained by behavioral data, but might be constrained by neural data. The model also allowed us to address interesting prediction questions. We illustrated how the model can make predictions for response times as well as for neural firing rates, and how these predictions can be conditioned on partially observed data. When the predictions were conditioned on more and more partial data from each trial, the predicted response times and firing rates became more and more accurate.

Both approaches are informative for cognitive-neuroscience. As we see it, however, there are some important advantages to our novel framework. One of the promises of cognitive-neuroscience is that new (neural) data streams should constrain models. This constraint requires that neural data inform model fitting, not just model development. In many instances of the two-stage approach, neural data, or at least a portion of the neural data, are used as a post-hoc performance metric. This means that constraint is provided by the neural data after fitting, to be applied to the following iteration of model development. In our approach, all data (neural and behavioral) equally constrain model estimation. This has important consequences for model selection issues. For example, in the two-stage approach there is the potential for a tension between the importance of the two data streams. If one model provided a better fit for the behavioral data, but another model provided a better fit for the neural data, then what should we conclude? Further to this point, suppose one model provided a good fit to the behavioral data, then in second stage the model performed poorly in the prediction of the neural data. In the usual version of the two-stage approach, this would lead to the model being rejected. However, it is entirely possible there were other model parameters, which would have allowed an acceptable compromise—providing an almost-as-good fit to the behavioral data, and a much better account of the neural data. Rejecting this model seems wrong, and a joint modeling framework can avoid that outcome.

Model comparison was a key feature of (Purcell et al. 2010), who compared multiple model architectures using their two-stage linking approach. While we did not try to distinguish between competing model architectures, our framework has great potential for solving model selection issues. As well as those outline above, the Bayesian implementation of our framework provides important and powerful statistical advantages in terms of model selection, with Bayesian model selection methods such as Bayes factors (O’Hagan 1995; Wasserman 2000), Deviance Information Criterion (Spiegelhalter 1998) and Widely Applicable Information Criterion (Watanabe 2010) all applicable.

We compared the performance of a model that accounted for neuronal variability and a model which did not, as well as models that accounted only for neural data or only for behavioral data. The main model performed much better than the model which treated neurons as identical, which fits with the well-known variability in the performance characteristics of cortical neurons. Despite being well known, it can be a difficult statistical matter to coherently deal with inter-neuron variability. Typically, firing rates are normalized within-neuron, circumventing the problem. This, of course, results in the loss of potentially important information. We demonstrated that when this neuronal variability is taken into account, the predictive performance is far superior to that of a model which is naïve to the variability between neuron.

A final distinction can also be drawn between our approach and that of (Purcell et al. 2010) in terms of theory development. Both approaches had different levels of theoretical focus. Purcell et al. were interested in studying different system level implementations, that is, different cognitive model architectures. In this approach, the model itself is being studied as an object of interest. In the literature on the philosophy of computational modeling this approach has been termed abstract direct representation (cf., Godfrey-Smith, 2009; Irvine, 2014; Weisberg, 2007). Whereas, we focused on how data streams interact, the individual model architectures within the joint framework are somewhat auxiliary to the framework itself. This model-based theorizing focuses more on “...making novel claims about underlying, and as yet unobserved, structures or causal mechanisms” (p.17, Irvine, 2014).

Cause and effect in joint models

At the level of the entire brain, it is clear that the causal relationship between neuronal firing and behavior runs from the former to the latter—(Purcell et al. 2010) use this structure in their model. However, it is possible to set up a joint model, such as ours, with many different causal structures, embodying different assumptions. Some of these structures are statistically equivalent, and so will not be discriminable. The model we have proposed assumes a structure which may, at first, seem counterintuitive. Our model assumes that the evidence accumulation process is the root cause of both the behavioral data, and (with conditional independence) the neural spiking data. While this might seem to violate the causal relationship between brain and behavior, our approach has practical strengths, and makes philosophical sense when we acknowledge that we are working with data from only a single neuron in each session. The single neuron clearly is not the cause of the behavioral response, because the influence of the multitude of other neurons not being measured. With this in mind, our approach can be seen as an approximation, in which the many unmeasured influences on behavior are approximated by assuming independence between the single observed neuron and the behavioral data, after conditioning on the state of the evidence accumulation process.

An important consideration is that the neural data are incomplete with respect to the accumulator model, because they correspond to just one of the two decision responses (accumulators). The consequence of this is that we are lacking information about the complementary accumulator; on roughly half the trials, the monkey’s response corresponded to the accumulator that was not being recorded. This is a computationally tricky problem to solve, requiring numerical integration over both the unobserved neural data (i.e., the data from the unrecorded neuron corresponding the receptive field to which a saccade was made) as well as the unobserved finishing time for the accumulator corresponding to those neuronal data. Again, assuming conditional independence between the response times and the spikes trains, or put differently, assuming response times and spikes trains interact indirectly via linking separately to the root node of accumulated evidence allows for a more tractable model. More direct linking between behavioral and neural data is desirable, however we leave this for future research (Fig. 6).

Fig. 6

Illustrative ways in which the causal structure of a joint model might be conceived. The simplest approach follows a simplified version of reality (left). A more realistic account of reality includes a very large number of unmeasured, and unmodeled, causes (center). Our approach (right) might be seen as an approximation of this, where the single observed data, and all the unmeasured data are treated as effects of a single underlying phenomenon

Conclusions

We have described a novel joint model which simultaneously accounts for both behavioral (response times and saccades) and neural (spike trains) data from a perceptual decision-making task. The predictive ability of the model is bi-directional; response times and saccades can be predicted from spike train data and vice versa. The key advance of our work is the importance attributed to both streams of data, allowing neural and behavioral data to simultaneously inform model estimation and our understanding of perceptual decision-making.

Appendices

Appendix A: Data

Let P be the number of neurons for a particular monkey (P=23 and P=31 for Monkey B and N respectively). Let N _j be the number of trials recorded in a single session for neuron j. Unless otherwise noted, all behavioral and neural data are indexed by two subscripts: j representing sessions (j = 1…P) and i representing trials within sessions (i = 1…N _j ).

Each trial involved the presentation of a random dot kinematogram with a particular direction and coherence. The stimulus direction was always either left or right, and coherence was one of six values (0,0.032,0.064,0.128,0.256,0.512). We use S _{i j} and Q _{i j} to denote direction and coherence, respectively. The behavioral data include vectors R T _{i j} of response times and R _{i j} of responses. The neural data are represented as a set of vectors, C. Each element, C _{i j} , is a vector of random length containing the times of spike events recorded during a trial, measured relative to stimulus onset. Let n _{i j} be the number of spikes recorded in trial i during session j so that vector C _{i j} has length n _{i j} . To model the spike data, we also introduce vectors T ^start and T ^end for the times at which recording began and ended. (Roitman and Shadlen 2002) recorded continuously from the neurons during sessions, but we have clipped the recordings to always have $T^{start}_{ij}=-0.11 \mathrm {sec.}$ and $T^{end}_{ij}=RT_{ij}+0.31 \mathrm {sec.}$

The neural data are limited to recordings from one side of the decision process. In terms of the accumulator model, the neural data correspond to just one of the two accumulators. Thus, for about half of the trials, the monkey’s response corresponded to the accumulator that was not being recorded (i.e., the response was away from the receptive field of the recorded neuron). These trials present a problem for modeling, as calculating likelihoods for observed behavioral data requires integration over the unobserved neural data as well as the unobserved finishing time for the accumulator corresponding to those neural data (unobserved, as this accumulator lost the race to threshold). To ease the computational burden associated with the integration, we restrict our modeling to trials on which the observed response was a saccade towards the receptive field of the neuron being recorded. Using the terminology of (Roitman and Shadlen 2002), we are using data from “T1” trials in which the monkey responded correctly, as well as from “T2” trials in which the monkey answered incorrectly. This restriction solves a problem of unobserved data, which would require integration otherwise.

Appendix B: Behavioral Model

The LBA model has three parameters that specify the accumulators: non-decision time offset, t ₀; the range of starting points, A; and the response threshold, b. In pilot work, we found that setting A = 0 (i.e., no random variability in starting points for the accumulators) provided a reasonable fit to the data, and greatly simplifies the computational algorithm (by removing the need to integrate firing rate calculations across different evidence trajectories). This setting (A = 0) also has precedent in modeling highly over-practiced data from non-human primates (Cassey et al. 2014), however, see Appendix G.

We constrained the other two parameters (t ₀ and b) to be constant across all six coherence conditions. A benefit of our joint model is that the neural data constrains one of these parameters. The parameter t ₀ is assumed to represent the time taken for two different processing stages: the time to perceive and encode the stimulus before decision-making can begin, and the time to execute the response after a decision is reached. The neural data allow separate estimation of those two components—see parameters β and δ below.

LBA drift rates are distributed across trials according to truncated normal distributions (positive values only). A full model could include 24 drift rate parameters: a mean and a standard deviation for each of the two racing accumulators, for each of the six stimulus conditions. We have limited the complexity of the model by assuming that the standard deviation of the drift rate distributions is 1.0 for the accumulator corresponding to the correct response in all coherence conditions. In the zero-coherence condition, we assumed that the drift rates are identically distributed for the two responses, reflecting the lack of information (note that this is not strictly necessary, as the monkeys could have been biased). This makes for 16 drift rate parameters in total, for the six coherence conditions. That is, a single mean drift rate parameter for all distributions in the zero-coherence condition (unit standard deviation for all those distributions), and then in each of the other five coherence conditions there are three parameters: one mean drift rate for the accumulator corresponding to the correct response, and one mean drift rate and one standard deviation for the accumulator corresponding to the incorrect response.

With those assumptions, the likelihood of a particular response time and response choice was derived by (Brown and Heathcote 2008). The amount of evidence in an accumulator (also called its activation) is a line with intercept given by the start point and slope given by the drift rate. Call this quantity x(t).

Appendix C: Neural Model

We model spike arrival as a time inhomogeneous Poisson processes with a piecewise linear firing rate λ(t,Θ), where t represents time during each decision, measured relative to stimulus onset, and Θ is a short-hand notation for the entire set of model parameters (which are defined below). The parameters that specify λ(t,Θ) are the junctions of the linear segments (see Fig. 3 in the main text). These parameters vary across sessions (neurons) but not across trials, so they are indexed by j = 1…P only.

From the start of recording until the stimulus appears, the neuron has a baseline firing rate given by parameter α. The first period following stimulus onset is marked by a dip-and-recovery in firing rate, which is unrelated to decision-making (see also Roitman & Shadlen, 2002, p.9486). The dip-and-recovery is modeled by a linear “V” shape, governed by two parameters: its width (δ) and depth (Δ).

The period following the dip-and-recover is the sole period of firing which is assumed to be related to evidence accumulation. During this period, the firing rate increases linearly toward threshold value. If the threshold is reached, a decision response is triggered. No parameters are required for the height of the threshold or the time taken to reach threshold, as these quantities are constrained by the link with the LBA model. The height is inferred from the LBA model’s threshold parameter, b, via the linking assumption. The time taken to reach threshold is inferred from the observed response time, i.e.: R T _{i j} −δ−β. When the threshold is reached, an overt behavioral response (i.e., a saccade) occurs after a delay of length β. The firing rate drops from its threshold value to a post-decision baseline rate of ω. This drop is linear over the period from β before the saccade to γ after the saccade.

The above assumptions determine the instantaneous firing rate function, λ(t) over the recording period. With this calculated, the likelihood of the spike times observed during trial i of session j is given by:

$$ L(\boldsymbol{C}_{ij} | {\Theta}) = \frac{ {\prod}_{k=1}^{n_{ij}} \lambda(\boldsymbol{C}_{ij}[k],{\Theta})}{n!} e^{-{\int}_{\boldsymbol{T}} \lambda(z,{\Theta}) dz} $$

(2)

The integral is over the recording interval, $\boldsymbol {T} = (T^{start}_{ij},T^{end}_{ij})$. We use C _{i j} [k] to indicate the k ^th element of the vector of spike arrival times C _{i j} , k = 1…n _{i j} . Eq. 2 is just the standard density function for a non-homogeneous Poisson process (Weinberg et al. 2007).

Appendix D: Linking

The key link between the LBA model and the neural data is between the evidence accumulation trajectory of the LBA accumulator and the evidence accumulation segment of the Poisson firing rate (see red elements in Fig. 2 in the main text). It is possible to instantiate and test all kinds of quantitative linking functions, but we have constrained the model to the simplest possible linking assumption. We assume a linear relationship between neural firing rate and the evidence trajectory of the LBA model. This relationship is specified by a single parameter (𝜃) for the scale: a one-unit change in evidence in the LBA accumulator corresponds to a firing rate change of 𝜃 spikes per second. Denote by x(t) the activation of the LBA accumulator after an accumulation time of t seconds. This corresponds to a firing rate at time t + δ of α + 𝜃 × x(t). With an evidence threshold in the LBA model of b, these assumptions imply a firing rate threshold of α + 𝜃 × b

Appendix E: Estimating the Model

Calculating the joint likelihood over the behavioral and neural data is made easier by our assumption of no start point variability in the LBA model (A = 0). Without that assumption, the likelihoods must be integrated over the different evidence trajectories implied by different start points. This integration is simple to accomplish numerically, but is computationally costly.

Without start point variability, as here, the joint likelihood for a single trial’s neural and behavioral data can be specified in closed form. Let ϕ ₊(.|μ,σ) represent the density of a normal distribution truncated to positive values, with mean μ and standard deviation σ, and let Φ₊(.|μ,σ) represent the corresponding cumulative distribution function. Let v _r and s _r be the mean and standard deviation parameters of the truncated normal distribution of drift rates for the accumulator corresponding to the recorded neuron, and v _o and s _o be the corresponding parameters for the other accumulator. If we denote by Θ a vector of all the model parameters, then the joint likelihood is given by:

$$\begin{array}{@{}rcl@{}} L(RT_{ij},\boldsymbol{C}_{ij} | {\Theta}) = \frac{b}{(RT_{ij}-\beta-\delta)^{2}} \end{array} $$

$$\begin{array}{@{}rcl@{}} {\Phi}_{+}(\frac{b}{RT_{ij}-\beta-\delta} |v_{o},s_{o}) \\ \phi_{+}(\frac{b}{RT_{ij}-\beta-\delta} |v_{r},s_{r}) L(\boldsymbol{C}_{ij} | {\Theta}) \end{array} $$

(3)

where L(C _{i j} |Θ) is given by Eq. 2. The first three terms of Eq. 3 correspond to the standard LBA model density (Brown and Heathcote 2008).

We estimated the posterior distributions over the parameters of the joint model in a hierarchical Bayesian framework. The hierarchy allows all model parameters to vary with session (i.e., neuron) and imposes truncated normal distributions on these session-wise parameters. The session-wise parameters, as well as the mean and standard deviation parameters of the group-level truncated normal distributions were estimated simultaneously, but separately for monkeys “B” and “N”. Samples were drawn using Markov chain Monte-Carlo with proposals generated by differential evolution (Turner et al. 2013). We used 60 sampling chains, drew 5,000 samples from each, and used random, widely distributed start points. We discarded the first 4,000 samples from each chain as burn-in, and confirmed convergence of the Markov chains by graphical inspection.

We imposed moderately informed priors on the mean and standard deviation parameters of the group-level distributions. These priors were informed by results from (Roitman and Shadlen 2002) (for the neural parameters) and from previous fits of the LBA model (for the behavioral parameters). In all cases, the prior distributions were wide enough to encompass more than double the range of plausible values. The priors for all mean (μ) parameters were positive-only truncated normal distributions and for all standard deviation (σ) parameters were gamma distributions, with settings given in Table 1. Note that the priors on the drift rate distributions’ means and standard deviations (v and s) are identical for all coherence conditions, and for both accumulators. Table 2 summarizes the posterior distributions for all monkey-level parameters. Therefore, the table contains two rows for each session-level parameter: one row for the mean and one row for the standard deviation parameter of the corresponding monkey-level truncated normal distribution.

Table 1 Priors

Table 2 Posterior parameter estimates (medians, and 95 % highest posterior density intervals), for both monkeys. These are given for both the mean (μ) and standard deviation (σ) of the truncated normal distribution across sessions (i.e., across neurons)

Appendix F: Model performance

Below we display the complete model fits to the behavioral (Figs. 7 and 9) and neural (Fig. 8) data for the main model. Fits to the behavioral data for the standard LBA (Fig. 9), and to the neural data for the standard Poisson neural model (Fig. 10) are also shown for comparison.

Fig. 7

Full distributions of response times for both monkeys, separately for each stimulus coherence condition (column) and correct vs. incorrect responses (rows). Histograms show data, smooth lines show posterior predictive data from the joint model. Increasing coherence (across each row) leads to more correct responses and fewer incorrect responses, as well as faster response time distributions

Fig. 8

Same format as Fig. 7, displaying fits to the behavioral data for the standard LBA

Fig. 9

Neural data (spikes per second) for both monkeys, separately for each stimulus coherence condition (column) and correct vs. incorrect responses (rows). The top two rows show neural activity aligned against stimulus onset, the bottom two rows show neural activity aligned against response (saccade), with all x-axes showing time in seconds. Histograms show data, smooth lines show posterior predictive data from the joint model. Data and model predictions are all cut off at the median response time for each condition, as per Roitman and Shadlen (2002). Vertical green lines mark stimulus onset (top two rows) and response time (lower two rows)

Fig. 10

Same format as Fig. 9, displaying fits to the neural data for the piecewise linear neural model only

Figure 11 is the comprehensive version of Fig. 5a showing prediction error for both monkeys and across all coherence conditions.

Fig. 11

Prediction error (mean absolute difference, in seconds) when predicting response times from unseen data. Predictions are given by the MAP estimator conditioned on increasing durations of revealed data from each trial (x-axes). The solid line in each panel shows prediction error from the joint model that allows for individual neuron differences. The dashed line shows prediction error from an average (non-hierarchical) version of the joint model which does not account for parameter differences between neurons. As more data is revealed, prediction error drops and approaches zero when the temporal window includes the actual response and response time as observed information

Appendix G: Allowing for start point variability

The parameterization used for all fits reported in the main text had no variability in the start point of the accumulators (i.e., A = 0). This was computational practical. With no start point variability, it is not necessary to integrate over all possible start points (U[0,A]) in firing rate at the start of evidence integration. The benefit of this was a substantial decrease in the time it took to fit the joint model. However, this speed up does come at a theoretical cost; with no start point variability, the LBA has no other mechanisms to capture the speed-accuracy trade-off, a ubiquitous decision-making phenomenon in both humans and non-human primates (e.g., Cassey et al. 2014). Here we report fits from the joint model with identical parameterization to the main text fits except for start point variability where A = 1. The inclusion of start point variable does improve the fit, although this is not surprising given the extra flexibility. However, as shown in Figs. 12, 13 and 14, the improvement in fit is marginal. As such, due to commensurate model performance and computational efficiency we chose to analyze the model with no start point variability.

Fig. 12

A comparison of data from Monkeys “B” and “N” (black and red solid lines, respectively) against predictions (circles) from a model which allows start point variability (A = 1). The left panel graphs mean response time (in seconds) and the right panel graphs mean accuracy (proportion), both against stimulus coherence. The circles show the mean statistics calculated from all posterior predictive samples, and the error bars contain 95 % of statistics from all posterior predictive samples

Fig. 13

Full distributions of response times for both monkeys, separately for each stimulus coherence condition (column) and correct vs. incorrect responses (rows). Histograms show data, smooth lines show posterior predictive data from the joint model with start point variability (A = 1). Increasing coherence (across each row) leads to more correct responses and fewer incorrect responses, as well as faster response time distributions

Fig. 14

Neural data (spikes per second) for both monkeys, separately for each stimulus coherence condition (column) and correct vs. incorrect responses (rows). The top two rows show neural activity aligned against stimulus onset, the bottom two rows show neural activity aligned against response (saccade), with all x-axes showing time in seconds. Histograms show data, smooth lines show posterior predictive data from the joint model with start point variability (A = 1). Data and model predictions are all cut off at the median response time for each condition, as per Roitman and Shadlen (2002). Vertical green lines mark stimulus onset (top two rows) and response time (lower two rows)