Abstract
Most mathematics assignments consist of a group of problems requiring the same strategy. For example, a lesson on the quadratic formula is typically followed by a block of problems requiring students to use that formula, which means that students know the appropriate strategy before they read each problem. In an alternative approach, different kinds of problems appear in an interleaved order, which requires students to choose the strategy on the basis of the problem itself. In the classroom-based experiment reported here, grade 7 students (n = 140) received blocked or interleaved practice over a nine-week period, followed two weeks later by an unannounced test. The mean test scores were greater for material learned by interleaved practice rather than by blocked practice (72 % vs. 38 %, d = 1.05). This interleaving effect was observed even though the different kinds of problems were superficially dissimilar from each other, whereas previous interleaved mathematics studies had required students to learn nearly identical kinds of problems. We conclude that interleaving improves mathematics learning not only by improving discrimination between different kinds of problems, but also by strengthening the association between each kind of problem and its corresponding strategy.
Similar content being viewed by others
Learning techniques inspired by research in the laboratory can improve learning in the classroom (for recent reviews, see Dunlosky, Rawson, Marsh, Nathan, & Willingham, 2013; Roediger & Pyc, 2012). In the study reported here, a simple intervention designed to improve mathematics learning was assessed in a classroom-based experiment. We first describe the intervention and the relevant research.
Interleaved practice
The solution of a mathematics problem requires two steps, as is illustrated by the following example:
A bug flies 48 m east and then flies 14 m north. How far is the bug from where it started?
This problem is solved by using the Pythagorean theorem to find the length of a hypotenuse (\( \sqrt{48+14}=50 \)). In other words, students first choose a strategy (Pythagorean theorem) and then execute the strategy. The term strategy is used loosely here to refer to a theorem, formula, concept, or procedure. Learning to choose an appropriate strategy is difficult, partly because the superficial features of a problem do not always point to an obvious strategy (e.g., Chi, Feltovich, & Glaser, 1981; Siegler, 2003). For example, the word problem about the bug does not explicitly refer to the Pythagorean theorem, or even to a triangle or hypotenuse. Additional examples are given in Fig. 1.
The two steps in the solution of a problem. To solve a problem, students must choose a strategy and then execute it. Superficially similar problems may require different strategies (A and B, or C and D), and superficially dissimilar problems may require the same strategy (A and C). Regardless of similarity, students know the strategy in advance when working a block of problems requiring the same strategy
Although students must learn to choose an appropriate strategy, they are denied the opportunity to do so if every problem in an assignment requires the same strategy. For example, if a lesson on the Pythagorean theorem is followed by a group of problems requiring the Pythagorean theorem, students know the appropriate strategy before they read each problem. The grouping of problems by strategies is termed blocked practice, and the large majority of practice problems in most mathematics textbooks are blocked. Blocked practice served as the control in the study reported here.
In an alternative approach that is evaluated in the present study, a majority of the problems within each assignment are drawn from previous lessons, so that no two consecutive problems require the same strategy—a technique known as interleaved practice. With this approach, students must choose an appropriate strategy and not only execute it, just as they must choose an appropriate strategy when they encounter a problem during a cumulative exam or high-stakes test. Put another way, blocked practice provides a crutch that might be optimal when students first encounter a new skill, but only interleaved practice allows students to practice what they are expected to know. To create assignments with interleaved practice, the problems within a set of blocked assignments can be rearranged (Fig. 2).
A hypothetical set of assignments providing interleaved practice. Each column represents an assignment, and each table entry indicates the lesson number on which the problem is based. For example, if Lesson 50 is on ratios, the corresponding assignment includes four ratio problems and one problem on each of eight lessons seen earlier in the school year (or during the previous school year). Another eight ratio problems (Lesson 50) are distributed across future assignments, with decreasing frequency. In other words, problems of different kinds are interleaved (which requires students to choose a strategy), and problems of the same kind are spaced (which improves retention). Note that the arrangement shown here is not the one that was used in the present study
In addition to providing opportunities to practice choosing a strategy, interleaved mathematics assignments guarantee that problems of the same kind are distributed, or spaced, across different assignments (Fig. 2). Spacing typically improves performance on delayed tests of learning (e.g., for recent reviews, see Dunlosky et al., 2013; Roediger & Pyc, 2012), and several studies have shown that spacing can improve the learning of mathematics, in particular (Rohrer & Taylor, 2006, 2007; Yazdani & Zebrowski, 2006). To summarize thus far, interleaved practice has two critical features: Problems of different kinds are interleaved (which requires students to choose a strategy), and problems of the same kind are spaced (which usually improves retention).
Previous studies of interleaved practice
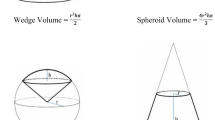
Four previously published studies compared the effects of interleaved and blocked mathematics practice (Le Blanc & Simon, 2008; Mayfield & Chase, 2002; Rohrer & Taylor, 2007; Taylor & Rohrer, 2010). In each of the studies, participants received interleaved or blocked practice of different kinds of problems, and interleaving produced better scores on a delayed test. However, in each of these studies, the different kinds of problems (and the corresponding strategies) were nearly identical in appearance (Fig. 3). In one study, for example, every problem included a variable raised to an exponent, and, in another, every problem referred to a prism. We refer to problems with shared features as superficially similar problems, and this similarity might hinder students’ ability to distinguish or discriminate between different kinds of problems. Indeed, the benefit of interleaved practice is often attributed to improved discrimination, as we will detail in the Discussion section. Therefore, the superficial similarity of the problems used in previous studies leaves open the possibility that the test benefit of interleaving is limited to scenarios in which students learn to solve kinds of problems that look alike, and such a boundary condition would curtail the utility of interleaved practice in the classroom, where students encounter problems that are often easily distinguished from other kinds of problems.
Problems learned in previous studies of interleaved mathematics: Students learned to solve several kinds of problems relating to (A) exponent rules (Mayfield & Chase, 2002), (B) the volume of obscure solids (Le Blanc & Simon, 2008; Rohrer & Taylor, 2007) or (C) prisms (Taylor & Rohrer, 2010) [EE2] In each study, the different kinds of problems (as well as the corresponding strategies) were nearly identical. Note that each of the studies included four or five kinds of problems, but only three are shown here
Present study
We compared interleaved and blocked mathematics practice in a classroom-based experiment with a counterbalanced, crossover design. Students learned to solve different kinds of problems drawn from their mathematics course, and they received the lessons and assignments from their regular teacher over a period of nine weeks. Two weeks after the last assignment, students sat for an unannounced test. Unlike previous studies of interleaved mathematics practice, the different kinds of problems were superficially dissimilar.
Method
Participants
The study took place at a public middle school in Tampa, Florida. Three teachers and eight of their seventh-grade mathematics classes participated. Each teacher taught two or three of the classes. Of the 175 students in the classes, 157 students participated in the study. Of these, 140 students attended class on the day of the unannounced test, and only these students’ data were analyzed. Nearly all of the students were 12 years of age at the beginning of the school year.
Material
Students learned to solve four kinds of problems drawn from their course (Fig. 4). To confirm that students could not solve these kinds of problems before the experiment, we administered a pretest with one of each kind of problem. Averaged across problems, just 0.7 % of the students supplied both the correct answer (e.g., x = 7) and the correct solution (the steps leading to the answer). When scored solely on the basis of answers (which presumably included guesses), the mean score was 3.2 %.
Examples of the four kinds of problems used in the present studies. (A) Solve a linear equation requiring four steps. (B) Solve a word problem using a proportion. (C) Graph an equation of the form, y = mx + b, where m and b are integers. (D) Determine the slope of the line defined by two given points with integer coordinates
The four kinds of problems were not only superficially different from each other, but also quite unlike other kinds of problems that the students had seen prior to the completion of the experiment. For example, although students ultimately learn how to solve many kinds of equations, a linear equation was the only kind of equation that these students had encountered previously in school (Fig. 4A). Likewise, a linear equation was the only kind of equation that the students had previously graphed (Fig. 4C). The slope problem (Fig. 4D) was also moderately unique, because the term “slope” is used only in limited contexts. However, the proportion word problem (Fig. 4B) does resemble other kinds of word problems.
Design
For the study, we used a counterbalanced crossover design. We randomly divided the eight classes into two groups of four, with the constraint that each group included at least one of the classes taught by each teacher. One group interleaved their practice of problems kinds A and B and blocked their practice of kinds C and D, and the other group did the reverse.
Procedure
During the nine-week practice phase, students received ten assignments with 12 problems each. Across all assignments, the students saw 12 problems of each of the four kinds (Fig. 4). The remaining problems were based on entirely different topics. Students received the ten assignments on Days 1, 15, 24, 30/31, 36, 37, 57, 58, 60, and 64. Every student received the same problems, but we rearranged the problems to create two versions of each assignment—one for each group. The first four problems of kinds A, B, C, and D were the first four problems of Assignments 1, 2, 4, and 5, respectively. If a problem kind was learned by blocked practice, the remaining eight problems appeared in the same assignment as the first four, meaning that the assignment included one block of 12 problems. If a problem kind was learned by interleaved practice, the remaining eight problems of the same kind were distributed across the remaining assignments. This meant that students saw the last problem of each kind on a later date in the interleaved condition than in the blocked condition, which is an intrinsic feature of assignments with interleaved practice (Fig. 2). The effect of this difference in “true test delay” is detailed in the Results.
Shortly before the scheduled date of each assignment, teachers received paper copies for their students and a slide presentation with solved examples and solutions to each problem. We asked teachers to present the examples before distributing the assignment. On the following school day, teachers presented the solution to each problem while encouraging students to make any necessary corrections to their own solutions. Teachers then collected the assignments. Within two days, one or more of the authors visited the school, scored each assignment (without marking it), and returned the assignments to the teachers. Although these scores do not measure students’ mastery, because students could correct their errors while the teacher presented the correct solutions, this scoring of the assignments provided us with evidence of teacher compliance with the experimental procedures.
Students were tested two weeks after the last assignment. We asked teachers not to inform students of the test in advance, because we did not want the final test to be affected by cramming just prior to the test. Teachers did not see the test before it was administered. The students were tested during their regular class, and the teacher and one author proctored each test. All of the test problems were novel. The test included three problems of each of the four kinds, and each of the four pages included a block of three problems of the same kind. We created three versions by reordering problems within each block, and students in adjacent chairs received different versions. Students were allotted 36 min and allowed to use their school-supplied basic calculator. Each test was scored on site that day by two raters who were blind to each student’s group assignment. The two raters scored each answer as correct or not correct and later resolved the few discrepancies (17 of 1,680). Test score reliability was moderately good (Cronbach’s alpha = .78).
Results
A repeated measures comparison of the two halves of the test showed that interleaved practice was nearly twice as effective as blocked practice, t(139) = 10.49, p < .001 (Table 1). The effect size was large, d = 1.05, 95 % CI = [0.80, 1.30]. This benefit of interleaving was observed for each of the four kinds of problems, ps < .01. The effect sizes for the four kinds (A, B, C, and D) exhibited a positive trend (0.72, 0.45, 1.00, and 1.27, respectively). This means that the interleaving benefit was larger for problem kinds introduced later in the practice phase. In other words, although the true test delay (the interval between the last practice problem and the test) was larger in the blocked condition than in the interleaved condition (see the Procedure section), the problem kinds with larger test delay differences (i.e., that were seen earlier in the practice phase) were associated with smaller effect sizes. Although this negative association might reflect order effects—that is, all participants saw the four problem kinds in the same order—we cannot think of a reason why order would matter. In brief, the effect sizes for problem kinds introduced later in the practice phase were larger than the effects for the earlier ones, and this trend was in the opposite direction from what would be expected if the difference in test delays contributed to the observed effect. Furthermore, if this difference did play a role, it might be seen not as a confound, but as an intrinsic feature of interleaved assignments (Fig. 2).
Discussion
Whereas previous studies of interleaved mathematics practice had required students to learn kinds of problems that were nearly identical in appearance (Fig. 3), the results reported here demonstrate that this benefit also holds for problems that do not look alike (Fig. 4). That is, the benefit of interleaved mathematics practice is not limited to the ecologically invalid scenario in which students encounter only superficially similar kinds of problems. Although it might seem surprising that a mere reordering of problems can nearly double test scores, it must be remembered that interleaving alters the pedagogical demand of a mathematics problem. As was detailed in the introduction, interleaved practice requires that students choose an appropriate strategy for each problem and not only execute the strategy, whereas blocked practice allows students to safely assume that each problem will require the same strategy as the previous problem.
However, the interleaved practice effect observed here might reflect the benefit of spaced practice rather than the benefit of interleaving per se. As we explained in the introduction, the creation of interleaved mathematics assignments guarantees not only that problems of different kinds will be interleaved, but also that problems of the same kind will be spaced across assignments, and spacing ordinarily has large, robust effects on delayed tests of retention. We therefore believe that spacing contributed to the large effect observed here (d = 1.05). Still, we have reason to suspect that interleaving, per se, contributed as well. In one previous interleaved mathematics study, students in both the interleaved and blocked conditions relied on spaced practice to the same degree, and interleaving nevertheless produced a large positive effect (d = 1.23; Taylor & Rohrer, 2010). In the present study, though, we chose to compare interleaved practice to the kinds of assignment used in most textbooks, which is a massed block of problems.
Theoretical accounts of the interleaved mathematics effect
How does interleaving improve mathematics learning? The standard account holds that the interleaving of different kinds of mathematics problems improves students’ ability to distinguish or discriminate between different kinds of problems (e.g., Rohrer, 2012). Put another way, each kind of problem is a category, and students are better able to identify the category to which a problem belongs if consecutive problems belong to different categories. This ability to discriminate is a critical skill, because students cannot learn to pair a particular kind of problem with an appropriate strategy unless they can first distinguish that kind of problem from other kinds, just as Spanish-language learners cannot learn the pairs PERRO–DOG and PERO–BUT unless they can discriminate between PERRO and PERO.
This discriminability account parsimoniously explains the interleaving effects observed in previous mathematics interleaving studies, because participants in these studies were required to discriminate between nearly identical kinds of problems (Fig. 3). For instance, one of these previous studies included an error analysis, and it showed that the majority of test errors in the blocked condition, but not in the interleaved condition, occurred because students chose a strategy corresponding to one of the other kinds of problems that they had learned—for example, using the formula for prism edges rather than the formula for prism faces (Taylor & Rohrer, 2010). Furthermore, the students in this study were given a second final test in which they were given the appropriate strategy for each test problem and asked only to execute the strategy, and the scores on this test were near ceiling in both conditions. In sum, the data from this earlier experiment are consistent with the possibility that interleaving improves students’ ability to discriminate one kind of problem from another (or discriminate one kind of strategy from another).
However, in the present study, discrimination errors appeared to be rare. In a post-hoc error analysis, three raters (two of the authors and a research assistant, all blind to conditions) examined the written solution accompanying each incorrect answer and could not find any solutions in which students “used the wrong strategy but one that solves another kind of problem.” The raters then expanded the definition of discrimination error to include solutions with at least one step of a strategy that might be used to solve any kind of problem other than the kind of problem that the student should have solved. With this lowered threshold, discrimination errors still accounted for only 33 of the 756 incorrect answers (4.4 %), with no reliable difference between conditions (5.1 % for interleaved, 4.0 % for blocked). For the other incorrect answers, students chose the correct strategy but incorrectly executed it (45.9 %), or they relied on a strategy we could not decipher, often because they did not show their work (49.7 %). The virtual absence of discrimination errors is arguably not surprising, partly because the different kinds of problems did not look alike, and partly because some strategies were obviously an inappropriate choice for some kinds of problems (e.g., trying to graph a line by creating a proportion). The rarity of discrimination errors in the present study raises the possibility that improved discrimination cannot by itself explain the benefits of interleaved mathematics practice.
We suggest that, aside from improved discrimination, interleaving might strengthen the association between a particular kind of problem and its corresponding strategy. In other words, solving a mathematics problem requires students not only to discriminate between different kinds of problems, but also to associate each kind of problem with an appropriate strategy, and interleaving might improve both skills (Fig. 5). In the present study, for example, students were asked to learn to distinguish a slope problem from a graph problem (a seemingly trivial discrimination) and to associate each kind of problem with an appropriate strategy (e.g., for a slope problem, use the strategy “slope = rise/run”), and the latter skill might have benefited from interleaved practice. Yet why would interleaving, more so than blocking, strengthen the association between a problem and an appropriate strategy? One possibility is that blocked assignments often allow students to ignore the features of a problem that indicate which strategy is appropriate, which precludes the learning of the association between the problem and the strategy. In the present study, for example, students who worked 12 slope problems in immediate succession (i.e., used blocked practice) could solve the problems without noticing the feature of the problem (the word “slope”) that indicated the appropriate strategy (slope = rise/run). In other words, these students could repeatedly execute the strategy (y 2 – y 1)/(x 2 – x 1) without any awareness that they were solving problems related to slope. In brief, blocked practice allowed students to focus only on the execution of the strategy, without having to associate the problem with its strategy, much like a Spanish-language learner who misguidedly attempts to learn the association between PERRO and DOG by repeatedly writing DOG.
It might be possible to experimentally tease apart the effects of interleaving on discrimination and association. In one such experiment, participants would receive either blocked or interleaved mathematics practice during the learning phase, as they typically do, and then take two tests. The first test would assess only discrimination. For example, students might be shown a random mixture of five problems—four problems of one kind (e.g., word problems requiring a proportion) and one problem of a different kind (e.g., a word problem requiring the Pythagorean theorem)—and then be asked to identify the problem that does not fit with the others (the Pythagorean theorem problem). Students would repeat this task many times with different kinds of problems. On a second test measuring both discrimination and association, students would see problems one a time and, for each problem, choose the correct strategy, but not execute it. Scores on the first test (discrimination only) should be greater than scores on the more challenging second test (discrimination and association), with larger differences between the two test scores reflecting a poorer ability to associate a kind of problem and its strategy. Therefore, if interleaving improves association, the difference between the two test scores should be smaller for students who interleaved rather than blocked.
Category learning
Finally, although we focused here on mathematics learning, several studies have examined the effect of interleaved practice on category learning. For example, participants might see photographs of different kinds of birds (jays, finches, swallow, etc.) one at a time, in an order that was either blocked (each of the jays, then each of the finches, etc.) or interleaved (jay, finch, swallow, etc.), and interleaving would produce greater scores on a subsequent test requiring participants to identify previously unseen birds (e.g., Birnbaum, Kornell, Bjork, & Bjork, 2013; Kang & Pashler, 2012; Kornell & Bjork, 2008; Wahlheim, Dunlosky, & Jacoby, 2011; but see Carpenter & Mueller, 2013). As with the results of previous interleaved mathematics tasks, the positive effect of interleaving on category learning could also be attributed to an improved ability to discriminate between, say, a jay and a finch. To our knowledge, though, it remains an untested possibility that this effect might also reflect a strengthened association between each category (e.g., finches) and the category name (“finch”). The relative contributions of enhanced discrimination and stronger associations to interleaving effects could be disentangled by an experiment analogous to the mathematics experiment proposed in the previous section: Participants would receive two tests: a discrimination-only test requiring them to sort birds (or identify the one bird that is different from others), and the usual test requiring them to name novel birds, which would require both discrimination and association. In summary, although strong evidence exists showing that interleaved practice can improve both mathematics learning and category learning, it seems unclear why either of these effects occur.
References
Birnbaum, M. S., Kornell, N., Bjork, E. L., & Bjork, R. A. (2013). Why interleaving enhances inductive learning: The roles of discrimination and retrieval. Memory & Cognition, 41, 392–402. doi:10.3758/s13421-012-0272-7
Carpenter, S. K., & Mueller, F. E. (2013). The effects of interleaving versus blocking on foreign language pronunciation learning. Memory & Cognition, 41, 671–682. doi:10.3758/s13421-012-0291-4
Chi, M. T. H., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121–152.
Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D. T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, 14, 4–58.
Kang, S. H. K., & Pashler, H. (2012). Learning painting styles: Spacing is advantageous when it promotes discriminative contrast. Applied Cognitive Psychology, 26, 97–103.
Kornell, N., & Bjork, R. A. (2008). Learning concepts and categories: Is spacing the “enemy of induction”? Psychological Science, 19, 585–592. doi:10.1111/j.1467-9280.2008.02127.x
Le Blanc, K., & Simon, D. (2008). Mixed practice enhances retention and JOL accuracy for mathematical skills. Chicago: Paper presented at the 49th Annual Meeting of the Psychonomic Society.
Mayfield, K. H., & Chase, P. N. (2002). The effects of cumulative practice on mathematics problem solving. Journal of Applied Behavior Analysis, 35, 105–123.
Roediger, H. L., III, & Pyc, M. A. (2012). Inexpensive techniques to improve education: Applying cognitive psychology to enhance educational practice. Journal of Applied Research in Memory and Cognition, 1, 242–248.
Rohrer, D. (2012). Interleaving helps students distinguish among similar concepts. Educational Psychology Review, 24, 355–367.
Rohrer, D., & Taylor, K. (2006). The effects of overlearning and distributed practice on the retention of mathematics knowledge. Applied Cognitive Psychology, 20, 1209–1224.
Rohrer, D., & Taylor, K. (2007). The shuffling of mathematics practice problems boosts learning. Instructional Science, 35, 481–498.
Siegler, R. S. (2003). Implications of cognitive science research for mathematics education. In J. Kilpatrick, G. W. Martin, & D. E. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 219–233). Reston: National Council of Teachers of Mathematics.
Taylor, K., & Rohrer, D. (2010). The effect of interleaving practice. Applied Cognitive Psychology, 24, 837–848.
Wahlheim, C. N., Dunlosky, J., & Jacoby, L. L. (2011). Spacing enhances the learning of natural concepts: An investigation of mechanisms, metacognition, and aging. Memory & Cognition, 39, 750–763. doi:10.3758/s13421-010-0063-y
Yazdani, M. A., & Zebrowski, E. (2006). Spaced reinforcement: An effective approach to enhance the achievement in plane geometry. Journal of Mathematical Sciences and Mathematics Education, 37–43.
Author Note
This work was supported by the Institute of Education Sciences, U.S. Department of Education, through Grant No. R305A110517 to the University of South Florida (PI: D.R.). The opinions expressed are those of the authors and do not necessarily represent the views of the U.S. Department of Education. We thank Sandra Stershic for her help with the data analysis, and we thank Jennifer DeMik, Brendan Paul, Nancy Self, Liberty Middle School, and Hillsborough County Public Schools for their participation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rohrer, D., Dedrick, R.F. & Burgess, K. The benefit of interleaved mathematics practice is not limited to superficially similar kinds of problems. Psychon Bull Rev 21, 1323–1330 (2014). https://doi.org/10.3758/s13423-014-0588-3
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13423-014-0588-3