Introduction

Working memory refers to information consciously available for a brief interval in time. It is well known that there are limits on working memory, but elucidating the nature, causes, and correlates of these limits remains timely, topical, and controversial (Cowan, 2001; Miyake & Shah, 1999; Osaka, Logie, & D’Esposito, 2007). Current research addresses not only the nature of working memory itself, but how working memory subserves other domains of mental life, including long-term memory, language comprehension, and problem solving. Researchers explore how capacity limits in working memory affect processing and performance in these other domains.

Fig. 1
figure 1

Change detection paradigms. In both paradigms, participants briefly study a set of objects and, after a brief delay, are tested. a Single-probe recognition. b Whole-display recognition

Full size image
Fig. 2
figure 2

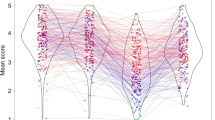
Conclusions about capacity depend on the choice of estimate. a Averaged hit and false alarm rates as a function of set size from Cowan et al. (2006). b Averaged Pashler (\( {\widehat{k}_p} \)) and Cowan (\( {\widehat{k}_c} \)) estimates. The Cowan measure yields an invariance of capacity with set size; the Pashler measure yields a dependence

Full size image
Fig. 3
figure 3

The dependence of informed guessing, g, on set size, capacity, and uninformed guessing base rate (u) in the whole-display paradigm

Full size image

To explore the nature and role of working memory in cognition, researchers study the effects of experimental manipulations on capacity, as well as the relationship between capacity and other performance measures, physiological signals, and participant variables (e.g., age). A conventional paradigm for measuring visual working memory capacity is the change detection paradigm, first introduced by Phillips (1974) and popularized by Luck and Vogel (1997). As is shown in Fig. 1, there are two versions of the paradigm. In both versions, a set of items is displayed for study. In Fig. 1, the items are squares with stripes of various orientations. After study and a brief retention interval, a test display is presented. In the paradigm on the left, called single-probed recognition, one target is presented at a studied location. This target is either the studied item or a novel item. The participant must make a recognition judgment, and the correct answer for the example in Fig. 1 is that the target is novel.Footnote 1 In the paradigm on the right, called whole-display recognition, a full set of items are presented at test. Either this set is the same as the original studied set, or, alternatively, one item is novel, as it is in Fig. 1. The difference between the tasks is that in single-probed recognition, the participant knows which item may change, if one does. Hence, the participant need only evaluate the status of a single item. In whole-display recognition, the participant does not know which item may change and, consequently, must evaluate the status of all items. Given this difference in demands, it is not surprising that the two tasks yield somewhat different outcomes, with better performance in the single-probed recognition paradigm (Wheeler & Treisman, 2002).

One popular conceptualization of working memory is that it consists of a limited number of slots (e.g., Cowan, 2001), although there are alternatives that are discussed subsequently. Within this discrete-slots conceptualization, researchers may study how the number of available slots changes across conditions and participant variables. There are two formulae for measuring the number of slots. Pashler (1988) proposed the following measure, denoted \( {\widehat{k}_p} \), for a whole-display task:

$$ {\widehat{k}_p} = N\left( {\frac{{\widehat{h} - \widehat{f}}}{{1 - \widehat{f}}}} \right), $$
(1)

where \( \widehat{h} \) and \( \widehat{f} \) are observed hit and false alarm rates and N is the number of to-be-remembered items, referred to as the set size. Cowan proposed an alternative measure, denoted \( {\widehat{k}_c} \), for the single-probe task:

$$ \mathop{{\hat{k}}}\nolimits_c = N\left( {\hat{h} - \hat{f}} \right). $$
(2)

Although measures \( {\widehat{k}_p} \) and \( {\widehat{k}_c} \) were proposed for different tasks, they are commonly seen as competitors, or at least as different alternatives for measuring the same construct. Consider the following inconsistencies in the field. Some researchers using the whole-display recognition have opted for \( {\widehat{k}_p} \) (e.g., C. C. Morey, Cowan, Morey, & Rouder, in press; Palva, Monto, Kulashekar, & Palva, 2010; Sligte, Scholte, & Lamme, 2009), while others using the same paradigm have opted for \( {\widehat{k}_c} \) (e.g., Saults & Cowan, 2007; Vogel, McCollough, & Machizawa, 2005). Most researchers using single-probe recognition have opted for \( {\widehat{k}_c} \) (e.g., Awh, Barton, & Vogel, 2007; Cowan, Fristoe, Elliott, Brunner, & Saults, 2006; Rouder, Morey, Cowan, Zwilling, Morey, & Pratte, 2008), whereas Treisman and Zhang (2006) opted for \( {\widehat{k}_p} \). Some researchers have even reported both measures for the same data set (e.g., Lee et al., 2010; Vogel, Woodman, & Luck, 2006).

The choice between \( {\widehat{k}_p} \) and \( \mathop{{\hat{k}}}\nolimits_c \) may prove critical in assessing how capacity covaries with other factors. Consider, for example, the data and analysis of Cowan, Fristoe, Elliott, Brunner, and Saults (2006), who assessed whether capacity changes across set size in 11-year-old children, using the single-probe recognition task. Cowan (2001) advocated a model in which capacity is a fundamental latent property that does not change with stimulus variables such as set size. Fig. 2a shows the observed hit and false alarm rates from 52 children. We computed values of \( {\widehat{k}_p} \) and \( {\widehat{k}_c} \) for each child at each set size. The averages of these capacity measures are shown in Fig. 2b. As can be seen, capacity is nearly constant, as predicted by Cowan’s (2001) model, if measured by \( {\widehat{k}_c} \). If capacity is measured with \( {\widehat{k}_p} \), however, capacity increases with set size, seemingly violating Cowan’s model.

In summary, although the measurement of capacity may prove critical in assessing topical questions, there are inconsistencies, with different researchers opting for different formulae in identical paradigms. The choice of capacity measure is consequential, since different measures may yield different conclusions. Fortunately, this choice is not arbitrary, and here we provide the appropriate guidance. First, we show that both the Pashler and Cowan formulae are not competitors but may be derived from a common discrete-slots assumption. We consider measures to be principled if they can be logically derived from a reasonable processing model of a specific task and unprincipled if there exists no corresponding processing model. Measure \( {\widehat{k}_p} \) is principled for whole-display recognition. Measure \( {\widehat{k}_c} \) is principled for single-probe recognition. Conversely, \( {\widehat{k}_p} \) is unprincipled for single-probe recognition; \( {\widehat{k}_c} \) is unprincipled for whole-display recognition. Second, we show that there are subtle but important flaws in the common model underlying both formulae. We propose modifications of this model and discuss capacity estimation in light of these modifications.

A discrete-slots working memory model

The theoretical basis for both capacity measures is a discrete-slots working memory model, first advocated by Miller (1956). The main postulate is that working memory consists of a small number of slots that holds a single item or a single chunk of bound items. In the change detection task, where the stimuli are simple, presented in parallel, and held for about a second or so, it is reasonable to assume that items are not grouped or chunked and that performance reflects the small number of slots. When there are more items than slots, some items are represented in a slot, and others are not. When an item is unrepresented in working memory, participants have no knowledge whatsoever about it.

The discrete-slots assumption may be used to derive estimates of capacity in a variety of tasks. For the change detection tasks, it is common to use items that are highly distinguishable, such as categorically different colors. For such highly distinguishable stimuli, it makes sense to couple the discrete-slot assumptions with a threshold assumption. If an item is in memory, we assume that there is sufficient information to correctly assess whether it matches a probe item at test.

This threshold assumption is appropriate for the change detection tasks with highly distinguishable stimuli. It is not appropriate for other stimuli, such as those that may differ subtly (Olsson & Poom, 2005). Likewise, the threshold assumption is not appropriate for other tasks, such as Zhang and Luck’s (2008) production task, in which the participant must indicate which color was studied by endorsing an option on a smoothly varying color wheel. In these cases, a discrete-slot memory model may be coupled with a finite-precision assumption in which color information for items in memory is represented up to some finite precision (e.g., Awh et al., 2007; Zhang & Luck, 2008). We focus on the change detection task with distinguishable stimuli because these are commonly used to assess changes in capacity across manipulations and group variables.

The discrete-slots memory model is not the only approach to modeling working memory. There are alternatives in which working memory reflects a limit of resources, which are spread more thinly as more items enter working memory (e.g., Bays & Husain, 2008; Wilken & Ma, 2004). There are two main advantages to considering the discrete-slots model for measurement purposes. First, the model receives support from diverse lines of inquiry (e.g., Awh et al., 2007; Rouder, Morey, Cowan, Zwilling, Morey, & Pratte, 2008; Vogel, McCollough, & Machizawa 2005; Xu & Chun, 2006; Zhang & Luck, 2008). Second, capacity is conceptualized as a limit in the number of slots, which is a highly interpretable quantity that may be compared across different conditions and groups. In limited-resources models, in contrast, there is no single natural capacity measure. For example, in Bays and Husain’s power law theory of resource distribution, capacity consists of two parameters that describe how resources are allocated. These two parameters are domain specific, and patterns of variations across domains are not as interpretable as a number-of-slots measure.

Single-probed recognition

For single-probed recognition, the participant need only consider the status of the probed item. The participant’s performance on each trial is conditional on whether the probed item is in memory or not. If the probed item is in memory, the participant performs perfectly, and the hit and false alarm rates from these probes are 1 and 0, respectively. When the item is not in memory, the participant guesses, and we denote the rate of change responses from guessing as u. Let d denote the probability that the probed item is in memory. Combining yields

$$ h = d + u\left( {1 - d} \right) , $$
(3)
$$ f = u\left( {1 - d} \right) . $$
(4)

The equations above describe a double-high threshold model. It is straightforward to show that the maximum-likelihood (ML) estimator of d is given by \( \widehat{d} = \widehat{h} - \widehat{f} \) (see Egan, 1975), so long as \( \widehat{h} \geqslant \widehat{f} \). The probability that the probed item is in memory, d, is k / N if the set size exceeds capacity and 1.0 if set size is no larger than capacity. These two conditions are expressed as

$$ d = min\left( {\frac{k}{N},1} \right). $$
(5)

It is straightforward to show that the ML estimator of \( \widehat{k} \) is

$$ \widehat{k} = N\left( {\widehat{h} - \widehat{f}} \right),\,k \leqslant N,\,\widehat{h} \geqslant \widehat{f}. $$
(6)

This estimator is the Cowan measure, subject to the qualification that k ≤ N and \( \widehat{h} \geqslant \widehat{f} \). The last qualification is of little importance, since observed hit rates almost always exceed false alarm rates in empirical studies. The first qualification, k ≤ N, has important ramifications, which are discussed subsequently. Kyllingsbaek and Bundesen (2009) described the statistical properties of the measure.

Whole-display recognition

The participant’s behavior in the whole-display recognition task is conditional on whether the participant has detected that one of the items has changed or not. The threshold assumption, discussed above, is very convenient for derivations. It guarantees that participants detect change only when it truly happens, no matter how many items are in the display. For change trials, the probability that the participant detects the change is d, the probability that the changed item is in memory. For same trials, the probability that the participant detects a change is necessarily zero. If a change is detected, the participant responds accordingly. If a change is not detected, the participant must guess whether the trial is a same trial or whether a change occurred in one of the items not in memory. We denote the probability of responding change when engaging in this type of guessing as g. The predicted hit and false alarm rates are

$$ h = d + \left( {1 - d} \right)g, $$
(7)
$$ f = g, $$
(8)

The equations above describe a high-threshold model; the maximum-likelihood estimator of d is given by \( \widehat{d} = {\left( {\widehat{h} - \widehat{f}} \right)}/{\left( {1 - \widehat{f}} \right)} \) for \( \hat{h} \geqslant \hat{f} \) (Egan, 1975). It is straightforward to show that the ML estimator of k is

$$ \widehat{k} = N\left( {\frac{{\widehat{h} - \widehat{f}}}{{1 - \widehat{f}}}} \right),\,k \leqslant N,\,\widehat{h} \geqslant \widehat{f},\,\widehat{f} < 1. $$
(9)

This estimator is the Pashler measure, subject to the qualification that k ≤ N , \( \hat{h} \geqslant \hat{f} \), and \( \widehat{f} < 1 \). Implications of the first qualifier are important and are discussed below.

Guessing in whole-display recognition is qualitatively different from guessing in single-probe recognition. In the single-probe paradigm, guessing is uninformed, and this uninformed rate is denoted by u. In whole-display recognition, however, the guessing rate may be informed by the capacity and set size. To see how this information affects guessing, consider a participant with k = 3 and N = 4. This participant will detect the majority of changes when they are presented. For this participant, observing that all items are the same indicates one of two possibilities: Either there was no change in the display, or the change occurred in the one item that was not in working memory. Whereas not storing the specific item is a low-probability event (.25 in this example), the participant has relatively high confidence that there was no change in the display. Consequently, g should be low. If this participant was presented many more items—say, N = 10—then most of the changes would occur in items that are not in working memory. In this case, the value of g should be higher, because it is increasingly probable that changes were missed. Hence, the value of g should reflect the set size and capacity.

While the discrete-slots model is agnostic to the guessing strategies across set sizes, it is helpful to describe normative behavior of g in assessing performance. The normative predictio isFootnote 2

$$ g = \frac{{(1 - d)u}}{{(1 - d)u + (1 - u)}}. $$
(10)

The dependence of informed guessing (g) on set size, capacity and uninformed guessing (u) is shown in Fig. 3. If capacity is at least as large as set size, then g = 0. As a smaller percentage of items are in working memory, g increases. In the large set size limit, this informed guessing probability converges to u, the uninformed guessing rate. Whether participants follow such a normative prescription remains unexplored.

Problematic averaging

The derivations above show that the Pashler and Cowan measures are valid only when the set size N is as big as or bigger than true capacity k. If k > N, the estimates are limited by N, which, by definition, is biased too low.

The qualification that k ≤ N is especially problematic when capacity is averaged across a group of participants. To see this, consider a set of participants who have capacities of three, four, and five items, in equal numbers. The true average capacity is, therefore, 4.0. Suppose there are four items at study—that is, N = 4. For the two thirds of the participants with true capacities of three and four items, the closed-form estimators yield valid estimates. For the one third with a capacity of five items, however, the estimator may be no larger than N, which is 4 in this example. In the large sample limit, the average across the sample has a value of 3.67, which is below the true average. The easiest solution is to use designs with only larger set sizes or to ignore estimates from smaller set sizes. This solution may not be practical, since it is not always obvious which set sizes are sufficiently large. A more principled solution comes from R. Morey (2011), who developed a hierarchical version of the discrete-slots model for use across several participants and across several set sizes. In Morey’s version, each individual has his or her own capacity k, but these are not unconstrained. Instead, each is assumed to come from a common parent distribution. When people display perfect performance, the estimate of capacity is not N. Instead, it is adjusted upward by an amount reflecting the estimated parent distribution, and this process yields accurate averaged estimates.

The problematic prediction of error-free performance

The discrete-slots model, as specified, makes a surprisingly problematic prediction. If capacity is larger than set size, performance is perfect. Conversely, if observed performance is not perfect, then, as a matter of mathematical logic, capacity must be less than the set size. This implication is problematic, since participants do make an occasional mistake in the small set size condition. For example, in Rouder et al. (2008), 23 participants performed change detection with two items. Every single participant made at least one error out of 180 trials. The presence of errors implied that capacity must be less than two, even though this estimate does not accord well with capacity estimates measured from larger set sizes.

We believe that it is reasonable to assume that participants will eventually make a mistake even in small set size conditions, due to a momentarily lapse in attention or intention. Unfortunately, such lapses dramatically affect the capacity estimate. A principled solution is to explicitly model stray errors. Rouder et al. (2008) provided perhaps the simplest modification. In their model, attention was modeled as an all-or-none process: Either attention was paid on a trial, in which case the responses reflected the discrete-slots model, or was not, in which case the responses reflected an uninformed guess. The probability that attention was paid on a trial is denoted by a. This attention-mixture model for single-probed recognition is

$$ \begin{array}{*{20}c} {h = a{\left[ {d + {\left( {1 - d} \right)}u} \right]} + {\left( {1 - a} \right)}u,} \\ {f = a{\left[ {{\left( {1 - d} \right)}u} \right]} + {\left( {1 - a} \right)}u.} \\ \end{array} $$

The same model for whole-display recognition is

$$ \begin{array}{*{20}c} {h = a{\left[ {d + {\left( {1 - d} \right)}g} \right]} + {\left( {1 - a} \right)}u,} \\ {f = ag + {\left( {1 - a} \right)}u.} \\ \end{array} $$

Note that, in whole-display recognition, guessing is informed if the trial is attended and is uninformed otherwise.

Although the attention-mixture model avoids the predicted-perfect-performance pitfall in a principled manner, capacity cannot be estimated by convenient closed-form equations such as (1) and (2). Instead, algorithmic approaches are needed. Rouder et al. (2008) used numerical methods to maximize likelihood across several conditions simultaneously. R. Morey (2011) proposed hierarchical versions of the models that allow for individual attention, capacity, and guessing parameters. These parameters are assumed to result from parent distributions, and this hierarchical structure provides for stable and accurate estimation of these parameters and their dependence on covariates.

Critical benchmarks

The main tenet of the underlying discrete-slot model is that the number of slots in working memory, the capacity, is fixed. The current models provide a means of measuring this capacity as a function of set size. The critical benchmark in each is that capacity should remain constant across changes in set size. This benchmark has been tested fairly thoroughly for the single-probe task. Cowan et al. (2005) showed an approximate constancy for set sizes between 4 and 12. Rouder et al. (2008), using some of the advanced measurement models discussed above, showed the same for set sizes between 2 and 8. Rouder et al. also showed the constancy of capacity across different base-rate conditions. To our knowledge, there are no published assessments of capacity constancy in the whole-report task across set size manipulations.

A secondary issue is whether guessing in each model follows a prescribed form with changes in set size. When the pattern of guessing is easily understood and makes theoretical sense, the capacity estimate has increased interpretability. If guessing rates fail to follow such a pattern, the capacity estimate may still be interpreted, but in a qualified manner. Rouder et al. (2008) showed an invariance of u to set size manipulations in the single-probe task. To our knowledge, there is no corresponding detailed assessment of whether g follows the predictions in (10). Given that the single-probe task and the associated model have been benchmarked better than the whole-display task, researchers at this date can have more confidence in the capacity estimates from the former than in those from the later.

Recommendations

The analysis above of the discrete-slots model yields the following practical recommendations for the measurement of capacity.

  1. 1.

    The Pashler and Cowan capacity measures are derived from the same discrete-slots model. The Pashler measure is principled for the whole-display recognition paradigm; the Cowan measure is principled for the single-probe recognition paradigm. Contrary to popular usage, these measures are not competitors or alternatives, and their use is strictly dictated by the paradigm. It is unprincipled to report \( {\widehat{k}_c} \) for whole-display designs or to report \( {\widehat{k}_p} \) for single-probe designs.

  2. 2.

    There are two problems with the closed-form estimators \( {\widehat{k}_p} \) and \( {\widehat{k}_c} \). First, they are contingent on large set sizes (k ≤ N), and this constraint poses challenges to estimating average capacity across a group of participants. Second, and perhaps more important, the discrete-slots model predicts error-free performance for small set sizes. As a consequence, occasional errors, which may occur from occasional lapses in attention, greatly affect capacity measurements. One solution for both of these problems is to simply ignore small set size conditions. A more principled solution is to adopt R. Morey’s (2011) hierarchical discrete-slots model. This model explicitly models attentional lapses, as well as variations across participants and conditions.