Performance factors in associative learning: Assessment of the sometimes competing retrieval model

Abstract

Previous simulations revealed that the sometimes competing retrieval model (SOCR; Stout & Miller, Psychological Review, 114, 759–783, 2007), which assumes local error reduction, can explain many cue interaction phenomena that elude traditional associative theories based on total error reduction. Here, we applied SOCR to a new set of Pavlovian phenomena. Simulations used a single set of fixed parameters to simulate each basic effect (e.g., blocking) and, for specific experiments using different procedures, used fitted parameters discovered through hill climbing. In simulation 1, SOCR was successfully applied to basic acquisition, including the overtraining effect, which is context dependent. In simulation 2, we applied SOCR to basic extinction and renewal. SOCR anticipated these effects with both fixed parameters and best-fitting parameters, although the renewal effects were weaker than those observed in some experiments. In simulation 3a, feature-negative training was simulated, including the often observed transition from second-order conditioning to conditioned inhibition. In simulation 3b, SOCR predicted the observation that conditioned inhibition after feature-negative and differential conditioning depends on intertrial interval. In simulation 3c, SOCR successfully predicted failure of conditioned inhibition to extinguish with presentations of the inhibitor alone under most circumstances. In simulation 4, cue competition, including blocking (4a), recovery from relative validity (4b), and unblocking (4c), was simulated. In simulation 5, SOCR correctly predicted that inhibitors gain more behavioral control than do excitors when they are trained in compound. Simulation 6 demonstrated that SOCR explains the slower acquisition observed following CS–weak shock pairings.

The observation that cues trained in compound often compete with each other for the potential to control a conditioned response was once accepted as support for an acquisition-focused approach to associative learning. According to this view, response deficits caused by treatments like simple compound training (e.g., overshadowing [Pavlov, 1927]), blocking (Kamin, 1968), and degraded contingency (Rescorla, 1968) reflect a failure of animals to learn the association between the test conditioned stimulus (CS) and the unconditioned stimulus (US). This view was widely accepted until the observation of retrospective revaluation (changes in the response potential of an absent stimulus due to further training of other stimuli; Kaufman & Bolles, 1981; Matzel, Schachtman, & Miller, 1985) prompted some researchers to reconsider the role of performance factors in associative learning situations. The comparator hypothesis (Miller & Matzel, 1988) is among the more influential associative theories that emphasize performance factors in associative learning. According to this model, when animals receive the test target CS at test, they compare the representation of the US directly activated by the target CS with the representation of the US indirectly activated through target CS–comparator stimulus–US associative linkage, where comparator stimuli are other cues present during CS–US training. Presumably, the strength of an animal’s response is determined not by the absolute strength of the target CS–US association, but by the strength of the target CS–US association relative to the associative strength to the US of other stimuli that were present during training. That is, responding is based on the increase in expectation of the US signaled by the target CS, relative to the expectation of the US in the context of training without the CS. For example, the blocking effect involves reduced responding to a target CS (X) after training in the presence of a well-established signal (A) for the US, relative to a control condition in which subjects receive target training in compound with a neutral stimulus (B). The comparator hypothesis explains this effect by asserting that pretraining A establishes a strong A–US association; thus, the US representation indirectly activated through the X–A–US linkage at test is stronger than the US representation indirectly activated through the X–B–US linkage (because the B–US association is weaker than the A–US association). In other words, A blocks responding to X because the X–US association is weak, relative to the A–US association. Importantly, changes in associative strength are driven by contiguity alone; therefore, the model deemphasizes competitive factors during acquisition in determining the conditioned response controlled by a target stimulus. Instead, competition-like processes occur at test.

The comparator hypothesis was designed to account for the outcome of experiments in which a test CS is trained in the presence of one comparator stimulus. Thus, it was unable to explain the results of experiments in which multiple nontarget cues are involved in training, as is often the case. For example, Williams (1996) observed that the potential of a stimulus to block a target stimulus can be disrupted when it is blocked by a third stimulus. In his experiments, subjects received either simple blocking training (phase 1 AB+, phase 2 AX+) or training in which the putative blocking stimulus was blocked by a third stimulus (phase 1 B+, phase 2 AB+, phase 3 AX+). Williams observed less blocking of X when B was pretrained (i.e., when B blocked A) than when B was associatively neutral prior to the AB compound training. Within the comparator framework, this suggests that the potential of a comparator stimulus to compete with a target stimulus is determined not by the absolute strength of the comparatorstimulus–US association but by the strength of the comparator stimulus–US association, relative to other [higher-order] comparator stimuli. This idea provided the basis for the extended comparator hypothesis (ECH; Denniston, Savastano, & Miller, 2001; see Fig. 1), which goes beyond the original comparator hypothesis by specifying the nature of competition among multiple comparator stimuli (i.e., comparator stimuli have their own comparator stimuli). Stimuli that are directly associated with the target CS are considered first-order comparator stimuli, which operate exactly like the comparator stimuli in the original comparator hypothesis. Associates of first-order comparator stimuli (i.e., second-order comparator stimuli) can reduce the effectiveness of both the target stimulus–first order comparator stimulus within-compound association (link 2) and the comparator stimulus–US association (link 3). Applied to Williams’s data, the X–A–US associative linkage should be strong in both groups. But pretraining of B (i.e., the B–US association) should strengthen the US representation activated through the X–A–B–US associative linkage, which should down-modulate the effect of the X–A–US linkage, thereby decreasing the blocking effect on the X–US association. Alternatively stated, pretraining of B reduces the effective strength of the A–US association, which decreases its effectiveness as a comparator stimulus for X.

Fig. 1

The extended comparator hypothesis. Arrows represent the associations between stimuli. The strengths of the directly and indirectly associated outcome representations are compared to determine the strength of responding to the target cue. Ovals depict stimulus representations; rectangles depict physical events; diamonds represent the comparator process

The ECH was limited in at least two ways. First, it was not formalized; thus, it was not possible to generate quantitative predictions using ECH. Second, it failed to predict the facilitative effect that compound training can have on a test CS. For example, in second-order conditioning situations, pairing a test CS with a well-established signal for the US usually results in strong excitatory responding to the test CS. Sometimes competing retrieval (SOCR; Stout & Miller, 2007) is a formalization of the ECH that allows for both competition (e.g., blocking) and facilitation (e.g., second-order conditioning) as a result of compound training. The model also goes one step beyond ECH by assuming that experience that indirectly activates a representation of the US through the target CS–comparator stimulus–US associative linkage causes animals to switch from a facilitative to a competitive response pattern. This modification allows the model to explain basic facilitation effects and the transition from facilitation to competition that is often observed when the number of trials is increased. Consistent with the original comparator hypothesis, SOCR assumes that the formation of associations is noncompetitive (i.e., cues do not compete with each other for associative strength during acquisition). Thus, contiguity and local error (the difference between the magnitude of the US received and the expectation of the US based on each cue separately) are the necessary and sufficient conditions for associative learning (see the Method section for formal details of SOCR).

Tests of SOCR have been reported in several empirical (e.g., Witnauer & Miller, 2007) and theoretical (e.g., Witnauer & Miller, 2010) articles. SOCR provides explanations for a number of important cue interaction phenomena and some phenomena related to extinction; however, the scope of previous simulations of SOCR has been largely limited to cue interactions. The purpose of the present simulations was to apply SOCR to a broader range of phenomena than in previously reported simulations. Moreover, following Polack, Laborda, and Miller (2011), here we modified SOCR to explain interactions among cues that are simultaneously present at test. An important limitation of SOCR’s implementation in Stout and Miller’s (2007) simulations was that it did not specify how cues interact when they are tested simultaneously (i.e., they applied the model only to situations in which the target cue was tested in isolation of cues and contexts that shared associations with the target CS or the US). In the present simulations, we applied SOCR to situations in which the test stimulus interacted with the test context (e.g., renewal) and to compound testing (e.g., negative patterning). Thus, as was suggested by Polack et al., we extended SOCR by making two simple assumptions about cue interactions during testing. First, we assumed that the response potentials of multiple cues summate in their potentials to control a conditioned response. Second, we assumed that the representation of a present comparator stimulus is more strongly activated than the representation of an absent comparator stimulus. Importantly, the implementation of the model was identical in all simulations. Importantly, we did not change the model across phenomena or procedures. Each phenomenon was simulated twice, once using a consistent set of free parameters and again using different best-fitting (discovered through hill climbing) free parameters for each situation in which CSs, USs, and independent variables differed, which captures the truism that different CSs, USs, and other independent variables often result in different behaviors (e.g., Brandon & Wagner, 1998). See the General Discussion for an explanation of the consequences of allowing the model’s free parameters to change across simulations. We also matched the procedural parameters (treatment of control cues and contexts, number of trials, and counterbalancing of cues) of the actual experiments as closely as possible in the present simulations.

Simulations

In the present simulations, as instructed by the editors of this invited article, we applied SOCR to a collection of experiments from a wide variety of paradigms. SOCR assumes that learning is driven by contiguity and local error. Thus, increases in the strength of the association between two stimuli (Stim1 and Stim2; e.g., X and the US, X and A, etc.) were modeled using the following equation:

$$ \Delta {{V}_{{{\text{Stim1}} - {\text{Stim2}}}}} = {\text{Salienc}}{{\text{e}}_{\text{Stim1}}}*{\text{ Salienc}}{{\text{e}}_{\text{Stim2}}}*\left( {\lambda --{{V}_{{{\text{Stim1}} - {\text{Stim2}}}}}} \right), $$

(1)

where Salience is a free parameter representing salience of the stimulus in question (0.1 < Salience < 0.9), λ is a fixed parameter (set at 1 by convention) that represents the maximum associative strength supportable by Stim2, and V _Stim1-Stim2 is the pretrial strength of the Stim1–Stim2 association. Thus, V represents the proportion of asymptotic associative strength. Note that the boundary conditions used in the present simulations are different from those used in previous simulations (e.g., Stout & Miller, 2007). This prevented us from using unrealistically high or low values for the model’s free parameters. The update equation for SOCR in the present simulations takes the familiar form:

$$ {{V}_{{{\text{Stim1}} - {\text{Stim2}}}}}^{{n + {1}}} = \Delta {{V}_{{{\text{Stim1}} - {\text{Stim2}}}}}^{\text{n}} + {{V}_{{{\text{Stim1}} - {\text{Stim2}}}}}^n. $$

(2)

Decrements in the strength of the Stim1–Stim2 association occurred when Stim1 was presented in the absence of Stim2 and are modeled by the equation:

$$ \Delta {{V}_{{{\text{Stim1}} - {\text{Stim2}}}}} = {\text{Salienc}}{{\text{e}}_{\text{Stim1}}}* - k{1}*{{V}_{{{\text{Stim1}} - {\text{Stim2}}}}}, $$

(3)

where k1 (0.1 < k1 < 1) is a free parameter representing the rate of extinction, where the 0.1 lower limit was to prevent extinction from ever being turned off. Note that these learning rules assume that contiguity and local error (the difference between actual and asymptotic associative strength for a single cue) are the two factors that drive learning, which is based on Bush and Mosteller’s (1955) learning rules. The extent to which a stimulus (X) can activate an absent stimulus was determined by the strength of the association between those stimuli (V _X-i ). We also assumed that activation of a present stimulus is determined by both associative activation and unconditioned activation. Associative activation of a present stimulus (i) by another present stimulus (X, in this case) plus unconditioned activation is stronger than associative activation of an absent stimulus alone and is given by the following equation:

$$ {\text{Activatio}}{{\text{n}}_{{{\text{X}} - i}}} = {{V}_{{{\text{X}} - i}}} + k{4}*{\text{Salienc}}{{\text{e}}_i}, $$

(4)

where k4 (0 < k4) is a free parameter. Activation of an absent stimulus i given presentation of X is equal to V_Xi .

SOCR assumes that compound training can either facilitate or reduce responding to a target cue. This is assumed to reflect processing that occurs at the time of retrieval. Thus, the model assumes that responding to X (R _X) is determined by the following response rule:

$$ {{R}_{\text{X}}} = {\text{Activatio}}{{\text{n}}_{{X - US}}}-k{2}*\left( {\Sigma O{{\text{p}}_{{{\text{X}} - i - {\text{US}}}}}*r{{V}_{{{\text{X}} - i}}}*r{{V}_i}_{{ - {\text{US}}}}} \right), $$

(5)

where k2 is a free parameter that weights comparison processes so they have less impact (0 < k2 < 1) than the direct CS–US association. Op_X-i-US (termed the operator switch) is a variable that represents the degree of discrimination between directly and indirectly activated US representations. This variable controlled whether the interaction between X and i was facilitative (e.g., second-order conditioning) or competitive (e.g., cue competition and conditioned inhibition). rV _X-i represents X’s potential to activate a representation of a comparator stimulus (i), and rV _i-US represents the potential of a comparator stimulus to activate a representation of the US. r was calculated following Eqs. 6 and 7. This response rule assumes that responding to X is determined by a comparison (through subtraction) between the US representation activated through the X–US association (V _X-US) and the US representation activated through the effective X–comparator stimulus (rV _X-i ) and comparator stimulus–US (rV _i-US) associative linkages. Basically, SOCR states that responding to X is not a function of the absolute value of V _X-US. Rather, it reflects the value of V _X-US relative to other cues that were present when X was trained. Thus, computations reflect the view that behavioral control by a target CS (X) is determined not by the absolute strength of the direct X–US association, but by the strength of that association relative to the relationship between background cues and the US (rV _i-US), where background cues are retrieved through within-compound associations (rV _X-i ) and dampened by a factor of k2.

Similar to the first-order processes that determine responding to X, the potential of X to activate first-order comparator stimuli (rV _X-I , where r denotes reiteration) and the potential of comparator stimuli to activate the US (rV _i-US) are determined by comparison processes involving second-order (j) comparator stimuli, which are other stimuli that are associated with the first-order comparator stimuli and the target cue and/or the US. Specifically, the following equation was used to calculate X’s potential to activate comparator stimuli:

$$ r{{V}_{{{\text{X}} - i}}} = {\text{Activatio}}{{\text{n}}_{{X - i}}} - k{2}*\left( {O{{\text{p}}_{{{\text{X}} - j - i}}}*{\text{Activatio}}{{\text{n}}_{{X - j}}}*{\text{Activatio}}{{\text{n}}_{{j - i}}}} \right). $$

(6)

This equation captures the view that the effective first-order comparator stimulus representation is determined by the representation of the first-order comparator activated directly through the association between X and the first-order comparator (Activation _X-i ), as compared with the representation of the first-order comparator activated through higher-order linkage (i.e., Activation _X-j and Activation _j-i ). The strength of the effective indirectly activated representation of the US (rV _i-US) was determined by similar higher-order comparator processes:

$$ r{{V}_{{i - }}}_{\text{US}} = {\text{Activatio}}{{\text{n}}_{{i - US}}} - k{2}*\left( {O{{\text{p}}_{{i - j - }}}_{\text{US}}*{\text{Activatio}}{{\text{n}}_{{i - j}}}*{\text{Activatio}}{{\text{n}}_{{j - US}}}} \right). $$

(7)

Importantly, the operator switch (Op_X-i-US) changes with experience in activating a representation of the US. Changes in the operator switch were modeled using the equation

$$ \Delta O{{\text{p}}_{{{\text{X}} - i - {\text{US}}}}} = k{3}*{\text{Salienc}}{{\text{e}}_{\text{X}}}*{{V}_{{{\text{X}} - i}}}*{{V}_{{i - }}}_{\text{US}}*\left( {{1} - O{{\text{p}}_{{{\text{X}} - i - {\text{US}}}}}} \right), $$

(8)

where k3 (0 < k3 < 1) is the rate with which changes occur in the operator switch. Note that this equation applies only when V _X-US = 0. Otherwise, Δ Op_X-i-US = 1 − Op_X-i-US. This rule for the operator switch assumes that subjects must learn to discriminate between directly activated representations and indirectly activated representations unless X is directly paired with the US, in which case the discrimination is complete in a single trial. Initial values of operator switches were −1, which allowed for facilitative interactions among stimuli (e.g., second-order conditioning). ,The total responding evoked at test was determined by simple summation such that

$$ {\text{Respons}}{{\text{e}}_{\text{Total}}} = \sum {{R}_i}, $$

(9)

where i represents all stimuli present at test.

Scaling

In the present simulations, we were interested in differences between the model’s predictions and empirical data. Consequently, we needed to scale the predictions of the model to match the scales used in the empirical research. The critical measurement in some of the present simulations was the log₁₀ latency to consume water for five cumulative seconds in the presence of the test CS. Following Larrauri and Schmajuk (2008), we assumed that lick suppression (LS) multiplied by a scaling factor is equal to the response potential of X (R _X) as predicted by the model. In addition, we assumed that the LS predicted by such proportional scaling is added to the scale’s minimum (i.e., log₁₀ 5) set by researchers’ measuring latency to complete 5 s of drinking in the presence of the CS. Thus, in the present simulations, we approximated the LS scale using the equation

$$ {\text{LS}} = {\text{lo}}{{\text{g}}_{{{1}0}}}{5} + \left( {{\text{Scaling}}*{{R}_{\text{X}}}} \right), $$

(10)

where Scaling is a free parameter used to approximate the log₁₀ latency scale measured in LS situations.

To approximate the suppression ratio (SR) scale used as the critical measure in simulations of leverpress suppression situations, the response outputs of the model used in the present simulations were scaled using the following equation:

$$ {\text{SR}} = \left( {{\text{Scaling}} - {{R}_{\text{X}}}} \right) \div \left[ {\left( {{\text{Scaling}} - {{R}_{\text{X}}}} \right) + \left( {{\text{Scaling}} - {{R}_{\text{Context}}}} \right)} \right], $$

(11)

where Scaling is a free parameter that was used to represent baseline levels of leverpressing (i.e., in the absence of any behaviorally relevant cue). Following Larrauri and Schmajuk (2008), in the present simulations that used this scaling technique, testing was conducted in a context that was not excitatory, so R _Context was assumed to be zero in all of the SR simulations. All other simulated scales were assumed to be proportional to the target cue’s behavioral control such that

$$ {\text{Behavior}} = {\text{Scaling}}*{{R}_{\text{X}}}. $$

(12)

Model selection

The Bayesian information criterion (BIC) was calculated for SOCR’s fit to each data set. We assumed that

$$ {\text{BIC}} = n*{ \log }\left( {SSE/n} \right) + P*{ \log }(n), $$

(13)

where n represents the number of data points that were simulated, SSE represents the sum of the squared differences between observed and predicted means, and P is the number of free parameters used to fit the data (Waekliem, 2004). Effectively, n * log (SSE/n) represents a badness-of-fit measurement, and the far right term [P * log (n)] represents a penalty for model complexity. The BIC is useful because it controls for differences in the number of free parameters. Lower BIC numbers indicate a fit. Because we optimized the values of cue and outcome salience, we treated these values as free parameters. Arguably, such values are not free parameters because, ideally, they are constrained to be consistent with subjects’ perception (e.g., more intense stimuli are constrained to be of higher salience than less intense stimuli).

Free parameters

We used a fixed set of parameters to simulate basic phenomena (e.g., blocking) in all of the present simulations. Saliences were selected arbitrarily, with the constraint that the relative values of saliences be realistic (i.e., context salience < cue salience < outcome salience). They (k1–k4) reflected algebraic means of the best-fitting parameters of what we considered to be a representative sample of simulations, which included simulations 1–6 (except for simulation 3a).In these simulations, the saliences of all cues were 0.35, the saliences of contexts were 0.15, and the saliences of outcomes were 0.5, which captures the view that outcomes (including USs) are more salient than cues, which are more salient than diffuse contexts. The value of the extinction rate parameter (k1) was 0.22, the value of the comparator weight parameter (k2) was 0.56, the value of the operator learning rate parameter (k3) was 0.46, and the value of the weighting of a present comparator stimulus in determining its activation (k4) was 1.60. In addition to using a fixed set of parameters to simulate each basic effect, we fit specific experiments using a hill-climbing algorithm, which discovered presumably ideal values for parameters. Importantly, we applied narrower boundary conditions on these parameters than were used in previous reports (e.g., Stout & Miller, 2007) in order to avoid potentially unrealistic values for best-fitting parameters.

Simulation 1: Acquisition

Basic acquisition in Pavlovian situations is characterized by an increase in the magnitude of a conditioned response as a function of the number of CS–US pairings. There are several aspects of acquisition that associative models should be able to fit. First, conditioned responding often emerges with relatively few CS–US pairings, and it often partially wanes with extensive training (i.e., the overtraining effect; Pavlov, 1927). SOCR explains the emergence of conditioned responding on the basis of its use of Bush and Mosteller’s (1955) learning rule, which predicts that a CS–US association will grow as a negatively accelerated function of the number of pairings. The overtraining effect falls straightforwardly from SOCR because, in addition to the target CS–US association, animals presumably learn and perform on the basis of the target CS–training context and training context–US associations. The latter two associations strengthen slowly, relative to the target CS–US association, due to the usual low salience of the context and the fact that it is partially extinguished during the intertrial intervals. Thus, the training context becomes a strong comparator stimulus only after extensive training based on the comparator impact being determined by the product of V _X-Context and V _Context-US. Consequently, at least superficially, SOCR can explain both simple acquisition curves and the overtraining effect. Importantly, recent experiments suggest that the overtraining effect is disrupted (i.e., conditioned responding is strengthened) when testing occurs in a context different from that used for target CS–US pairings (Bouton, Frohardt, Sunsay, Waddell, & Morris, 2008). Bouton et al. administered light–US pairings in context A and tone–US pairings in context B. Testing of both stimuli occurred in both contexts such that each stimulus was tested in both the acquisition context for that stimulus (e.g., light in context A) and in a different context (e.g., light in context B). Conditioned responding was stronger when testing occurred in the different context than when testing occurred in the acquisition context, which suggests that the overtraining effect is at least partially context specific. This effect is potentially explained by the augmentation of link 2 implemented in the present simulations. In overtraining situations, the training context functions as a strong comparator stimulus and down-modulates responding to the target stimulus. This effect should be stronger when the representation of the acquisition context is more strongly activated (when testing occurs in the acquisition context). In simulation 1, SOCR was fit to Bouton et al.’s data in an effort to determine whether or not SOCR explains simple acquisition, the overtraining effect, and recovery from the overtraining effect with a change in context.

Figure 2 depicts the results of a simulation (with the fixed set of parameters) of basic acquisition, overtraining, and reduced overtraining with a change in context. The top panel of Fig. 2 depicts the change in responding to the CS as a function of the number of acquisition trials. Importantly, responding is expected to increase with a moderate amount of training and then decrease with massive training (the overtraining effect; Pavlov, 1927). Inspection of the bottom panel of Fig. 2 reveals that SOCR anticipates stronger responding in an associatively neutral context than in the acquisition context; thus, the model anticipates that the overtraining effect wanes with a change in context (Bouton et al., 2008). The top panel of Fig. 3 summarizes Bouton et al.’s results and the best-fitting predictions of SOCR during acquisition. Both observed and predicted conditioned responding increased as a function of the number of CS–US pairings during the first 12 sessions, which demonstrates that SOCR can explain basic acquisition. In addition, both observed and predicted performance declined with extensive training; thus, SOCR explains the overtraining effect. Finally, observed and predicted responding was weaker in the acquisition context than in a different context, thereby demonstrating that SOCR explains the observation that the overtraining effect diminishes with a change in context (see Fig. 2b). These results, in conjunction with previous simulations (e.g., Stout & Miller, 2007; Witnauer & Miller, 2010), suggest that SOCR provides a good account of phenomena related to acquisition.

Fig. 2

Predicted responding based on a fixed set of parameters during 100 acquisition trials with 3 context extinction trials per intertrial interval. The top panel represents predicted responding to a CS as a function of the number of CS–US pairings. The bottom panel represents responding to the CS in the acquisition context and an associatively neutral context

Fig. 3

Best-fitting predictions and observed results of Bouton, Frohardt, Sunsay, Waddell, and Morris’s (2008) Experiment 1. The top panel represents predicted and observed conditioned suppression to two different CSs (tone and light) during CS–US training sessions in different contexts. The bottom panel represents responding during a separate test session in which both the light and tone were tested in the context used for training that CS (same) or in the context used to train the other CS (different). Note that lower values indicate stronger conditioned suppression

Simulation 2: Extinction

Extinction occurs when the behavioral control by a target stimulus decreases as a result of nonreinforced presentations of that stimulus following acquisition. SOCR asserts that basic extinction is driven by two mechanisms. The first is based on the strengthening of the target CS–context association that presumably occurs during nonreinforced trials, which increases the strength of the indirectly activated US representation at test, thereby decreasing responding. This is at least superficially consistent with the widely held view that extinction is not completely driven by unlearning (e.g., Delamater, 1996). Second, as a consequence of local error reduction, SOCR assumes that unlearning contributes to extinction, which is consistent with the observation that recovery from extinction is rarely complete.

Importantly, the information that animals learn during extinction is often not expressed outside of the extinction context. Renewal occurs when testing outside of the extinction context results in greater behavioral control by the target stimulus than when the target stimulus is tested in the extinction context. In simulation 2, we applied SOCR to extinction and renewal. Figure 4 depicts the results of a simulation with the fixed parameters in which SOCR predicts less responding as a function of the number of nonreinforced presentations of the CS (Fig. 4, top panel) and more responding when testing after extinction occurs in the acquisition context than in the extinction context (Fig. 4, bottom panel). Three contextual manipulations are known to produce renewal in at least some situations. When extinction occurs in the context of acquisition (context A) and testing occurs in a different context (context C), responding is sometimes greater than when testing occurs in context A (AAC renewal). Similarly, if acquisition, extinction, and testing each occur in distinct contexts (ABC renewal), responding is often greater than when extinction and testing occur in the same context that is distinct from the acquisition context. In addition, if acquisition occurs in context A and extinction occurs in context B, responding is greater in context A than in context B (ABA renewal). AAC, ABC, and ABA renewal strongly suggest that the information learned during extinction is not completely erased by nonreinforced trials and that extinction is context dependent. SOCR is able to explain renewal on the basis of its use of the augmentation rule for interactions among stimuli during testing.

Fig. 4

Predicted responding based on a fixed set of parameters during extinction and in ABA renewal. The top panel depicts responding after 10 acquisition trials and during 30 extinction trials in Context B (after training in Context A). Three context extinction trials occurred during each intertrial interval. The bottom panel depicts responding to the CS during a subsequent test in the extinction context (right) or the acquisition context (left)

Rescorla (2008) conducted three experiments aimed at demonstrating renewal, using a within-subjects design in which the associative histories of the test CSs and contexts were equated across renewal conditions. For example, in his demonstration of ABC renewal, subjects received training of two different stimuli (X and Y) in context A. X was extinguished in context B, and Y was extinguished in context C. Both stimuli were tested in both contexts B and C; thus, renewal could be assessed by comparing responding to the CSs across the two contexts. Consistent with other reports of renewal (e.g., Bouton & Bolles, 1979), Rescorla (2008) observed weaker responding when a CS was tested in the context in which it was extinguished than when it was tested in the other context. Rescorla’s (2008) demonstrations of AAC and ABA renewal used a similar design.

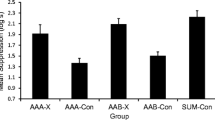
SOCR’s best-fitting predictions and Rescorla’s (2008) results are depicted in Fig. 5. The decline in predicted values as a function of nonreinforced trials matches the decline in observed conditioned responding, thereby demonstrating that SOCR explains simple extinction. Importantly, predicted response strength increased when testing occurred outside of the extinction context, which matches the ordinal differences observed by Rescorla (2008) and demonstrates that SOCR is able to explain renewal, although, lamentably, the size of the predicted differences between conditions do not match well Rescorla’s (2008) observations. In other simulations, SOCR provided a better fit to these differences by allowing for smaller values of k1 (the extinction rate parameter), which is consistent with the view that renewal suggests that extinction involves more than unlearning. These data, in conjunction with several recent experiments (e.g., Laborda, Witnauer, & Miller, 2011; Witnauer & Miller, in press), support the explanation of extinction provided by SOCR, with one important qualification. In its current form, SOCR does not have a mechanism to explain how changes in time and emotion can influence the context. For example, training with an aversive US presumably creates a relatively temporary emotional context. Reinstatement treatments, which create an aversive emotional context in fear conditioning, might cause the emotional context of testing to be more similar to the emotional context of original acquisition than to the emotional context of extinction (in which aversive stimuli are omitted). Thus, one could view reinstatement as a form of ABA renewal in which the emotional context (instead of the physical context) is being changed between phases. Similarly, spontaneous recovery could be viewed as a form of ABC renewal in which the temporal context changes between phases (Bouton, 1993). Thus, the model fails to explain spontaneous recovery and reinstatement, but, in explaining ABA, AAC, and ABC renewal, the model could likely explain other recovery from extinction effects with slight modifications, since it has been argued by Bouton that spontaneous recovery and reinstatement are variants of renewal.

Fig. 5

Best-fitting predictions and observed results of Rescorla (2008). The first 12 x-axis values represent average responding during blocks of extinction trials in ABA (Experiment 1; top panel), AAB (Experiment 2; middle panel), and ABC (Experiment 3; bottom panel) renewal experiments. The last two x-axis values represent average responding in the extinction and renewal contexts, respectively

Simulation 3: Second-order conditioning and conditioned inhibition

Second-order conditioning is the increase in responding that sometimes occurs when a target stimulus is nonreinforced in the presence of a well-established excitor (Pavlov, 1927). Interestingly, conditioned inhibition is often observed after similar training procedures. For example, nonreinforced XA presentations interspersed among reinforced presentations of A will cause X to be inhibitory with respect to the US such that it will reduce responding to an independently trained excitor (i.e., it will negatively summate) and be slower to acquire excitatory behavioral control than a neutral stimulus. Second-order conditioning and conditioned inhibition occur after similar training, with the critical procedural variable being the number of nonreinforced trials (e.g., Stout, Escobar, & Miller, 2004; Yin, Barnet, & Miller, 1994). Interestingly, conditioned inhibition is relatively insensitive to presentations of the conditioned inhibitor alone (i.e., conditioned inhibition fails to extinguish; Zimmer-Hart & Rescorla, 1974). Figure 6 depicts a simulation of the change from second-order conditioning to conditioned inhibition that occurs with increasing numbers of training trials. The simulation used the fixed parameters. All simulations involved an equal number of reinforced (A+) and nonreinforced (XA−) trials. Training consisted of either 10 (few) or 100 (many) trials and the test stimulus was either X alone (elemental) or X in compound with an independently trained excitor (compound). Importantly, the model is able to explain simple second-order conditioning (excitatory responding in few–elemental), conditioned inhibition (attenuated responding to the independently trained excitor in group many–compound). Simulations 3a, 3b, and 3c used a hill-climbing algorithm to fit SOCR’s predictions to the results of experiments in conditioned inhibition and second-order conditioning.

Fig. 6

Predicted responding based on a fixed set of parameters to X after A+ / AX−training. Elemental indicates testing of X alone. “Compound” indicates testing of X in the presence of an independently trained excitor. “Few” depicts responding after 10 simulated training trials. “Many” depicts responding after 100 trials

Simulation 3a: Second-order conditioning and conditioned inhibition after feature-negative training

In a feature-negative discrimination task, animals receive reinforced presentations of A and nonreinforced presentations of AX. In these situations, X sometimes becomes inhibitory with respect to the US, such that it will reduce responding to an independently trained excitor (i.e., it will negatively summate) and be slower to acquire excitatory behavioral control than a neutral stimulus. However, responding to X after feature-negative training seems to depend on several procedural variables, including the number of trials and whether A+ and AX− trials are interspersed or arranged serially with all A + followed by all AX− trials (Yin et al., 1994). With relatively few AX− trials, X often evokes an excitatory conditioned response (i.e., second-order conditioning). After many AX− trials, conditioned inhibition to X is observed, and it is stronger when trials are interspersed than when they are serially organized (i.e., blocked rather than interspersed). The purpose of simulation 3a was to test whether or not SOCR can explain these observations.

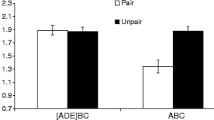
The results of Yin et al.’s (1994) Experiment 2 and SOCR’s best-fitting predictions are summarized in Fig. 7. In their experiment, Yin et al. administered no trials (None [N]) or Few (F) or Many (M) AX− trials that were either serial (S) or interspersed (I). In addition, subjects were tested on either X alone or X in compound with an independently trained excitor (BX). Excitatory responding to X alone was stronger after Few trials than after None or Many. Moreover, excitatory responding was evident after both interspersed and serial training. That is, X evoked a strong excitatory conditioned response in Groups IF-X and SF-X and a weak excitatory response in all other groups that were tested on X alone, thereby replicating basic second-order conditioning. Importantly, the predictions of SOCR closely match the observations within the groups that were tested on X, indicating that SOCR explains the emergence of second-order conditioning after relatively few trials and the decline in second-order conditioning after many trials. This is driven by SOCR’s use of the operator switch, which assumes that activation of the US through higher-order associative structures (i.e., the X–A–US associative linkage) has a facilitative effect on the target stimulus when animals lack much experience with an indirectly activated US representation. Facilitation is expected to change to competition as animals gain experience with the indirectly activated US representation; thus, second-order conditioning should be weak after many training trials. When X was tested in compound with B, strong excitatory responding was observed after None and Few training trials because X was either neutral (Condition None) or moderately excitatory (Condition Few). Inhibition to X developed after many training trials, which was evidenced by the relatively weak responding to XB observed after many training trials (i.e., responding in Group IM-XB was weaker than in IF-XB and IN-XB). Importantly, inhibition was weaker when training trials were presented serially than when they were interspersed (i.e., responding was weaker in IM-XB than in SM-XB). All of the critical results within the compound testing condition were anticipated by SOCR. The increase in predicted inhibition achieved by increasing the number of trials was driven by the operator switch, and the relatively weak inhibition observed after serial training (i.e., all A–US followed by XA−) was expected because the A–US association extinguished during XA− trials, thereby decreasing the strength of the indirectly activated US representation at test.

Fig. 7

Best-fitting predictions and observed mean log latencies to resume drinking in the presence of the test CS in Yin, Barnet, and Miller (1994). Condition I received interspersed and Condition S received serial presentation of A+ and AX− trials. Condition N received zero, Condition F received few, and Condition M received many pairings of X and A. X indicates that subjects were tested on X alone, and BX indicates that subjects were tested on a compound consisting of X and an independently trained condition excitor (B)

SOCR explains several important phenomena related to feature-negative training, including second-order conditioning with only relatively few interspersed or serial trials and a conditioned inhibitor negatively summating with an independently trained excitor and additional inhibition occurring only with relatively many interspersed trials. In other simulations, SOCR was also shown to explain other aspects of discrimination learning. On the basis of its use of the augmentation rule, SOCR explains basic negative patterning, which involves reduced responding on compound AB− trials, relative to elemental A–US and B–US trials during A–US/B–US/AB − training. The augmentation rule allows for negative patterning because indirect activation of the US representation through the A–B–US and B–A–US linkages should be stronger when A and B are presented in compound; thus, responding should be relatively weak during compound trials. Moreover, SOCR explains positive patterning (weak responding to elements and strong responding to the compound during A−/B−/AB–US training) because it assumes that the excitatory response potentials of A and B should summate when they are presented in compound. Importantly, this account is challenged by experiments in which both effects are observed (e.g., Bellingham, Gillette-Bellingham, & Kehoe, 1985). SOCR seems unable to explain both positive and negative patterning with the same set of free parameters, because the best-fitting parameters for negative patterning allow for strong competition on compound trials, which is contradicted by the observation of strong responding on compound trials in positive patterning. This is likely driven by SOCR’s use of simple elemental representations. Presumably, if SOCR assumed that animals learn about configurations of stimuli, it would allow the model to explain both negative and positive patterning with a single set of parameters.

Simulation 3b: The role of the context in conditioned inhibition

According to SOCR, conditioned inhibition occurs when a target stimulus indirectly activates the US representation (through the target stimulus–comparator stimulus–US linkage) more strongly than it directly activates the US representation (through the direct target stimulus–\US association). Conditioned inhibition procedures involve at least two types of trials: reinforced presentations of a training excitor and nonreinforced presentations of the target stimulus in compound with the training excitor, which strengthen the comparator stimulus–US and the target stimulus–comparator stimulus associations, respectively. In these situations, the training excitor can consist of either a punctate stimulus (e.g., feature-negative training) or a training context (e.g., the explicitly unpaired procedure for conditioned inhibition and inhibition produced through differential conditioning). Thus, two distinct procedures that often produce conditioned inhibition are the feature-negative (A+/AX−) and differential conditioning (A+/X−) procedures. Interestingly, the procedural parameters that promote conditioned inhibition with feature-negative training seem to mitigate conditioned inhibition with differential training.

The results of Urcelay and Miller (2006) demonstrated that A+/X − training with a short intertrial interval (ITI; massed) is more effective in establishing inhibition to X than is training with a long ITI (spaced). Conversely, massed feature-negative training is less effective than spaced training. Urcelay and Miller’s (2006) summation tests in Experiments 1 and 2 are summarized in Fig. 8. Subjects received either massed or spaced training and, orthogonally, either feature-negative (FN) or differential training (Diff). Also, a transfer excitor was tested in compound with either the target stimulus (Sum) or a control stimulus (Ctrl). Responding in Groups FN Spaced Sum and Diff Massed Sum was reduced relative to their respective control groups, indicating that inhibition was observed after spaced feature-negative training and massed differential training. Moreover, responding was greater in Group FN Massed Sum relative to Group FN Spaced Sum, which suggests that massed trials reduce the effectiveness of feature-negative training. Also, responding was greater in Group Diff Spaced Sum than in Group Diff Massed Sum.

Fig. 8

Best-fitting predictions and observed log latency to resume drinking in Urcelay and Miller’s (2006) summation conditions. Groups in the FN condition received feature-negative (A+ / AX−) training and groups in the Diff condition received differential (A+ / X−) training. Subjects were tested on either the target inhibitor (Sum) or an irrelevant control stimulus (Sum Ctrl) in compound with an independently trained transfer excitor. Additionally, subjects received either a short (Massed) or a long (Spaced) interval between trials

Inspection of Fig. 8 reveals that SOCR provided a reasonably good fit to Urcelay and Miller’s (2008) data. SOCR explains inhibition produced by differential training because, when trials are massed, A+/X− training presumably establish strong X–training context and training context–US associations, which conjointly allow for a strong indirectly activated US representation. When trials are spaced, the training context–US association extinguishes during the ITI, thereby diminishing indirect activation of the US at test. Thus, SOCR explains the diminished conditioned inhibition that was observed with spaced, relative to massed, differential trials. SOCR explains inhibition produced by spaced FN training for the reasons detailed in simulation 3. Importantly, those processes can be influenced by competition among comparator stimuli for the potential to mediate indirect activation of the US. When a target stimulus is trained in the presence of two comparator stimuli that can independently make the target a conditioned inhibitor, the comparator stimuli can compete with each other for the potential to drive support responding indicative of conditioned inhibition to the target stimulus. Applied to feature-negative training, when trials are spaced, only the training excitor (A) will be an effective comparator stimulus, because the context extinguishes during the intertrial interval. In contrast, when trials are massed, the training excitor and the training context will compete with each other for the potential to serve as effective comparator stimuli to the target stimulus, consequently reducing the inhibitory potential of the target (Urcelay & Miller, 2008). Thus, SOCR predicts that the amount of inhibition produced by feature-negative and differential training depends on the ITI.

Simulation 3c: Extinction of conditioned inhibition

Many associative models (e.g., Rescorla & Wagner, 1972) predict that presentations of a conditioned inhibitor by itself will reduce its effectiveness as a conditioned inhibitor. Figure 9 summarizes the results of Zimmer-Hart and Rescorla’s (1974) experiment that failed to detect evidence of extinction of conditioned inhibition (cf. Polack et al., 2011). Subjects first received A − US/AX − inhibition training, which presumably made X inhibitory. Following inhibition training, subjects received either the target stimulus alone in the context (extinction) or mere exposure to the context (no extinction). Then subjects were tested on either an independently trained transfer excitor (B) or the training excitor (A). Orthogonally, these excitors were tested in compound with either the conditioned inhibitor (summation) or a control stimulus (summation control). Critically, the pattern of responding was similar in the extinction and no extinction conditions, which suggests that presentations of the target stimulus alone had no effect on conditioned inhibition. Moreover, they observed that negative summation was stronger when the target stimulus was tested with the training excitor than when it was tested with the independently trained transfer excitor. SOCR’s predictions match Zimmer-Hart and Rescorla’s results. SOCR explains the failure to observe extinction of conditioned inhibition by assuming that presentations of the target stimulus in the training context simultaneously decrease the strength of the X–A association (which undermines conditioned inhibition mediated by A) and increase the strength of the X–training context association (which strengthens conditioned inhibition mediated by the context). During extinction of the inhibitor, the training context–US association should extinguish, which should undermine inhibition to the target stimulus. However, this effect should be equal across groups (all groups received the same exposure to the training context), so extinction of the training context–US association should not differentially affect the magnitude of inhibition across groups. Also, SOCR explains the observation that negative summation is stronger when the target stimulus is tested in compound with the training excitor than when it is tested in compound with the transfer excitor on the basis of its use of the augmentation rule. Thus, the present simulations revealed that SOCR explains many important characteristics of inhibition and discrimination learning. In addition, previous simulations (Stout & Miller, 2007) have demonstrated that SOCR can explain the reduced conditioned inhibition that is observed after extinction of the training excitor (Lysle & Fowler, 1985) and conditioned inhibition established using a surrogate outcome (Espinet, Iraola, Bennett, & Mackintosh, 1995). Space precludes revisiting these effects.

Fig. 9

Best-fitting predictions and observed suppression in Zimmer-Hart and Rescorla’s (1974) Experiment 1. “Summation” indicates that the target inhibitor (X) and “Summation Control” indicates that an irrelevant control stimulus were tested in compound with either the excitor used in inhibitory training (A) or an independently trained transfer excitor (B). “Condition Extinction” indicates received presentations of X alone and “Condition No Extinction” indicates received exposure to the context. Note that lower values indicate more suppression

Simulation 4: Cue competition

SOCR explains basic cue competition by assuming that the compound training ordinarily involved in cue competition studies establishes strong target stimulus–comparator stimulus and comparator stimulus–US associations that allow for the target stimulus to indirectly activate the US representation, the strength of which is subtracted from the directly activated US representation. Thus, SOCR explains overshadowing, blocking, overexpectation, relative stimulus validity, and backward blocking (as reviewed by Stout & Miller, 2007). The results of a simulation using the fixed set of parameters are summarized in Fig. 10. Notably, SOCR explains both overshadowing (reduced responding after compound, relative to elemental, training) and blocking (reduced responding after training a target in the presence of a well-established signal for the US, relative to simple compound training). SOCR also explains the reduced blocking (increased responding) observed after posttraining associative deflation of the blocking cue (i.e., recovery from blocking). The purpose of simulation 4 was to test whether SOCR with the augmentation rule can explain basic blocking (simulation 4a), the reduced relative stimulus validity effect seen with posttraining extinction of the excitatory unique element (simulation 4b), and unblocking with increases and decreases in US magnitude (simulation 4c).

Fig. 10

Predicted responding based on a fixed set of parameters after elemental (X+) training, overshadowing (BX+), blocking (A+ | AX+), and recovery from blocking (A+ | AX+ | A−). In the blocking condition, there were 10 phase 1 trials followed by 5 AX–US trials and 18 context extinction trials per ITI. Notably, more context extinction trials were used in this simulation than in other simulations because cue competition is attenuated when training is relatively massed (e.g., Stout, Chang & Miller 2003)

Simulation 4a: Blocking

Cue competition often wanes with increases in the amount of training of the compound stimulus, beyond some moderate amount (e.g., 4 trials; Stout, Arcediano, Escobar & Miller 2003). SOCR explains this phenomenon by assuming that massive amounts of training cause the training context and the competing cue to counteract (Stout & Miller, 2007). Previous simulations did not examine SOCR’s potential to explain the effect of increasing the amount of compound training from a small to moderate number of trials. Azorlosa and Cicala (1986); see Fig. 11) demonstrated blocking in fear conditioning with 1 compound trial and a decrease in blocking with 10 compound trials. In their critical experiment, subjects received either 1 or 10 compound blocking trials. In addition, three control groups were included in which subjects were tested with a novel stimulus or with a stimulus that was trained in the presence of an irrelevant control cue using 1 or 10 compound trials. Blocking was clearly weaker after 10 than after 1 compound blocking trial, and SOCR provided a good fit to their results. SOCR assumes that after 10 compound blocking trials, the training context has become excitatory and can compete with the blocking cue for the potential to reduce responding to the target cue (i.e., the training context and the blocking cue counteract for the potential to compete with the target cue).

Fig. 11

Best-fitting predictions and observed suppression in Azorlosa and Cicala’s (1986) Experiment 1. Subjects in the blocking groups received phase 1 A+ trials followed by either 1 or 10 phase 2 AX+ trials. Subjects in Group Novel Stim were tested on an associatively neutral stimulus at test. Subjects in Group 10 Blocking Control (Unsignaled) received treatment identical to that in Group Blocking 10, except that A and the US were unpaired in phase 1. Groups 10 Blocking Control (No Ph1) and 1 Blocking Control (No Ph1) received treatment identical to Groups 10 Blocking and 1 Blocking, except that phase 1 training was omitted

Simulation 4b: Recovery from the relative validity effect

The relative validity effect involves less responding to X after AX+/BX− training than after AX+/AX−/BX+/BX− training. SOCR explains the basic effect by assuming that A has a stronger comparator impact after continuous reinforcement than do A and B after partial reinforcement (Stout & Miller, 2007). More important, the relative validity effect is attenuated when A is extinguished (McConnell, Urushihara, & Miller, 2010). In their critical experiment, McConnell et al. administered AX+/ BX−/CY+/DY− training in phase 1, which was designed to establish weak responding to both X and Y through relative validity. In phase 2, subjects received either extinction of the AD compound (extinction) or exposure to the context (no extinction), and orthogonally, subjects received either X (Test X) or Y (Test Y) during a subsequent test session. Inspection of Fig. 12 reveals that subjects suppressed more to X after compound extinction than after context exposure, thereby demonstrating recovery from the relative validity effect. Importantly, this effect was specific to X; responding to Y did not change as a result of extinction. These findings are, to the authors’ knowledge, uniquely anticipated by SOCR. Other models of retrospective revaluation assume that a common error term drives changes in the associative status of absent cues (e.g., Van Hamme & Wasserman, 1994), which should apply equally to X and Y. In contrast, SOCR explains these findings by assuming that extinction of A influences X and extinction of D is irrelevant. This explanation is supported by the results of simulation 6b.

Fig. 12

Best-fitting predictions and observed suppression in McConnell, Urushihara, and Miller’s (2010) Experiment 1. All subjects received phase 1 training consisting of AX+ / BX− / CY+ / DY−. Subjects in the extinction condition received phase 2 compound extinction of AD and subjects in the no-extinction condition received mere exposure to the context. Subjects were tested either on X (Test X) or Y (Test Y)

Simulation 4c: Unblocking

Some models assume that blocking involves a learned reduction in associability to the blocked stimulus because it does not predict a change in the occurrence of the US (e.g., Pearce & Hall, 1980). This account of blocking is supported by the observation that blocking is attenuated by both increases and decreases in US magnitude during compound trials (Holland, 1984). Toward demonstrating this phenomenon, Holland exposed subjects to phase 1 elemental training consisting of A+/B++ and phase 2 training consisting of AX++/B++ (Group Up), A++/BX++ (Group Up Control), A+/BX+ (Group Down), or AX+/B+ (Group Down Control), where + represents one food pellet and ++ represents one food pellet followed by two additional food pellets. The results of this experiment and SOCR’s best-fitting predictions are illustrated in Fig. 13. Holland observed less blocking in Groups Up and Down, relative to their respective controls. SOCR anticipates less blocking in Group Up because A should be a less effective blocking stimulus than B on the basis of its being paired with a weaker US in phase 1. SOCR anticipates less blocking in Group Down because B should be better able than A to counteract with the training context (which was made excitatory during phase 1 training). The best-fitting parameters for this simulation involved an unusually high value for the salience of the context. This allows the model to predict a strong context–US association and, consequently, counteraction between the context and the blocking stimulus.

Fig. 13

Best-fitting predictions and observed results of Holland’s (1984) Experiment 1. “Up” indicates an increase and “Down” indicates a decrease in the number of USs that followed the CS. See the text for details. Note that the predicted value for Up Control is slightly negative and very close to zero

Simulation 5: Unequal associative changes

Rescorla (2000) observed a greater increase in the excitatory behavioral control by an inhibitor (B) than by an excitor (A) when the two stimuli were conditioned in compound. This is problematic for associative theories, which assume that total error reduction drives learning (e.g., Rescorla & Wagner, 1972), because A and B should share a common error term when they are trained in compound; thus, changes in A and B should be equal (assuming equal saliences or appropriate counterbalancing). In simulation 5, SOCR was applied to the appetitive conditioning portion of Rescorla’s (2000) experiments. The results of the experiment and accompanying simulation are summarized in Figs. 14 (depicting the results of a simulation using the fixed set of parameters) and 15 (depicting Rescorla’s results accompanied by best-fitting predictions). All subjects received training designed to establish B and D as inhibitors and A and C as excitors in phase 1, followed by AB+ training in phase 2. Subjects subsequently responded less to AD than to BC during test (D was an inhibitory stimulus). Critically, the only difference between the training of AD and BC was the difference in the amount that was learned about A and B during AB+ trials. SOCR is able to explain this difference (using either hill climbing or the fixed set of parameters) on the basis of its use of a local error reduction rule, which predicts greater increases in the strength of the B–US association than of the A–US during AB + trials.

Fig. 14

Predicted responding based on a fixed set of parameters after compound training with an excitor (A) and an inhibitor (B) to compounds consisting of the target excitor and a control inhibitor (AD) and a target inhibitor and a control excitor (BC). Greater responding to BC indicates that B gained more behavioral control than A during AB+ trials. In phase 1, 100 iterations of X+ / XB− / XD− / A+ / C+ were simulated. Three phase 2 AB+ trials were simulated. There were three context extinction trials per ITI

Fig. 15

Best-fitting predictions and observed results of Rescorla’s (2000) Experiment 1. Condition BC was tested on a compound consisting of the target inhibitor (B) and an independently trained excitor (C). Condition AD was tested on the target excitor (A) and an independently trained inhibitor (D). Note that SOCR fit all control experiments in Rescorla’s (2000) article with a single set of parameters, but for simplicity of presentation, only the data from Experiment 1 are presented

Simulation 6: Latent inhibition

Previous reports have documented that SOCR can explain the observation that CS–US pairings are less effective in establishing excitatory conditioned responding when they are preceded by presentations of the CS alone (latent inhibition; Stout & Miller, 2007). Figure 16 summarizes the results of simulated latent inhibition using the fixed set of parameters. In addition, SOCR predicts that the CS–training context and training context–US associations are critical for latent inhibition, which is supported by the observation that latent inhibition is attenuated when a context shift occurs between pretraining exposure and training (undermining the effect of CS preexposure on the CS–training context association) and when context extinction follows CS–US pairings (reducing the strength of the training context–US association). Importantly, latent inhibition-like effects also occur when CS–weak US pairings are administered instead of CS-alone presentations (Hall & Pearce, 1979). Figure 17 summarizes the critical results of Hall and Pearce’s demonstration of latent inhibition produced by CS–weak US pairings and SOCR’s predictions. In phase 1, subjects received pairings of an irrelevant control stimulus with a weak US (Light+), simple preexposure to the target stimulus (Tone−), or pairings of the target stimulus with a weak US (Tone+). In phase 2, all subjects received tone–strong US pairings, followed by testing of the tone using a barpress suppression procedure. Suppression to the tone was weakest in Group Tone−, which replicates basic latent inhibition. Moreover, suppression was weaker in Group Tone + than in Group Light+, which indicates that tone–weak US pairings cause latent inhibition. SOCR explains this effect by assuming that the tone–weak US pairings strengthen the tone–US, tone–context, and context–US associations. Strengthening the tone–US association increases responding at test, but this is more than offset by the stronger context–US association and particularly the tone–context association. Thus, the net effect of tone–weak US pairing is to reduce responding, relative to training an irrelevant stimulus.

Fig. 16

Predicted responding based on a fixed set of parameters to a target CS during training to a preexposed CS (CS Preexposure) and a novel CS (Acquisition). Sixty-six CS-alone presentations preceded five CS–US pairings with three context extinction trials per ITI occurring in the present simulations

Fig. 17

Best-fitting predictions and observed suppression to the tone in phase 2 of Hall and Pearce’s (1979) Experiment 2. Group Tone + received pretraining consisting of tone–weak shock pairings in phase 1,whereas Group Tone − received preexposure to the tone alone, and Group Light + (Control) received pretraining consisting of light–weak shock pairings. Phase 2 consisted of pairings of the tone with a strong shock

General discussion

The results of the present simulations demonstrate that SOCR explains a wide variety of associative phenomena, some of which are outside the domain of cue interaction that SOCR was originally designed to explain. The performance of SOCR across the present simulations is summarized in Table 1, and the best-fitting parameters of SOCR are presented in Table 2. BIC values allow for comparisons across simulations and models because it involves a penalty for number of free parameters and increases as a function of the amount of data explained with a single set of parameters. SOCR explains acquisition and related phenomena, including the overtraining effect and reduced overtraining with a context shift (Bouton et al., 2008) and reduced responding after pretraining pairing of the target with a weak US (Hall & Pearce, 1979). SOCR explains extinction and renewal (e.g., Rescorla, 2008), select aspects of discrimination learning (e.g., conditioned inhibition produced by feature-negative training), and second-order conditioning produced by feature-negative training, and the emergence of conditioned inhibition only after many trials (Yin et al., 1994). SOCR explains several previously unsimulated aspects of cue competition, including reduced blocking produced by changes in US intensity (Holland, 1984) and recovery from the relative validity effect as a result of posttraining deflation of the continuously reinforced element (McConnell et al., 2010). In addition, SOCR correctly anticipates that response strength of a target cue is determined by the associative status of other cues present during training, as well as the associative history of the target cue (e.g., Rescorla, 2000). Importantly, the augmentation rule used in the present simulations allowed SOCR to explain interactions between a target cue and other stimuli that are present at test, including renewal and the attenuated overtraining effect observed after a change in context.

Table 1 Summary of the fit of SOCR

Table 2 Best-fitting parameters for SOCR

Inspection of Table 2 reveals that there was variability in the values for the best-fitting parameters. This is a consequence of two important aspects of the present simulations. First, the hill-climbing algorithm does not attempt to minimize differences across simulations with respect to best-fitting parameters. Thus, the hill climbing will not necessarily find similar values for parameters across different simulations. We chose this strategy for assessing SOCR because only optimal parameters (as discovered by hill climbing) allow us to assess the underlying principles of the model independently of the appropriateness of the model’s parameters. Second, this reflects the fact that we simulated experiments that used different procedural parameters (e.g., differing CSs, differing USs, different stimulus intensities, different stimulus durations, different interstimulus intervals, or differing numbers of trials), which presumably cause the model to have different best-fitting parameters. Indeed, some of the predictions of SOCR are parameter dependent. For example, the strength of the predicted overshadowing effect partially depends on the strength of the context–US association. While this could be viewed as a weakness of SOCR, we prefer to view this as a strength of the model because most (if not all) associative phenomena are observed only within specific procedural constraints. For example, overshadowing has been shown to depend on the number of trials, intertrial interval, CS duration, and CS–US contingency; all of these variables presumably influence the context–US association. In some unreported simulations, best-fitting values near zero for some ki parameters were found, which effectively disables some aspect of the model. For example, a best-fitting value of 0.1 for k1 was found in simulation 1, which allowed for only very slow extinction. Importantly, we replicated these simulations with greater constraints on the hill-climbing algorithm and reported them here and showed that the model still predicted the central effects that were simulated. This resulted in worse fits of the model. We elected to report the more-constrained simulations because they are based on more realistic values for the free parameters. Table 3 represents a comparison of the results of simulations with fixed and best-fitting parameters.

Table 3 Effects simulated with best-fitting and fixed parameters

Some important phenomena are outside of the domain of Stout and Miller’s (2007) SOCR. In its current implementation, SOCR is a trial-wise model. Thus, the model is unable to explain phenomena related to the distribution of responding within a CS (e.g., inhibition of delay; e.g., Drew, Zupan, Cooke, Couvillon, & Balsam, 2005). Moreover, SOCR assumes a simple elemental representation instead of a microelemental (e.g., Wagner, 1981) or a configural (e.g., Pearce, 1987) representation. Ultimately, this representational scheme was chosen in order to develop and test the simplest version of SOCR possible. That is, we wanted to determine the set of phenomena that are explained by the core principles of SOCR. Adding more sophisticated assumptions about representation would allow SOCR to explain more experiments (especially those related to generalization and discrimination). However, it would create a more complex model, and it would not allow us to easily determine whether SOCR’s performance is attributable to its most important assumptions (e.g., local error reduction at acquisition, comparisons performed at test, and facilitative or competitive cue interactions as a function of the operator switch) or to the more complex (and less central) assumptions concerning representation. This also allowed us to use a smaller number of free parameters (five, excluding saliences of stimuli: k1, extinction rate; k2, comparator weight; k3, operator rate; k4, augmentation; and scaling) than is sometimes used in contemporary associative modeling.