Introduction

Uncertainty is traditionally investigated in regards to its relationship to value (Bernoulli, 1738; Kahneman & Tversky, 1979; Levy et al., 2010; Rushworth & Behrens, 2008; Sokol-Hessner et al., 2009; Tversky & Kahneman, 1992; Tymula & Glimcher, 2016). There is now a robust literature illustrating that a choice’s value decreases as the uncertainty associated with that choice increases (Gneezy et al., 2006; Newman & Mochon, 2012; Tversky & Kahneman, 1992). And yet, there is still large behavioral variability in how much people (dis)like uncertainty (Chapman et al., 2022). These differences might be the result of having specific experiences with uncertainty. Given that concepts correspond to our knowledge about and experiences with the world (Grand et al., 2022), here we depart from classic theories of uncertainty to ask: Do conceptual representation of uncertainty predict risky decision-making?

The idea that conceptual representations of uncertainty might by linked to risky choice was inspired by prior work (Bhatia et al., 2019; Brooks & Freeman, 2018). Some research has recovered conceptual representations of risk (hazards) from natural language data and correlated these representations to perceptions of risk (Bhatia, 2019a). We extend this work by directly investigating the relationship between an individual’s conceptual representation of uncertainty and their actual risky choices. Our logic is built on the notion that conceptual representations are the result of direct experience, which is at the cornerstone of many conceptual learning theories (Andrews et al., 2009; Griffiths et al., 2007). For example, experts perceive stimuli differently than novices because they have acquired a detailed representational structure through extensive experience (Wing et al., 2022). These distinct conceptual representations can in turn impact cognitive processes like memory (Konkle et al., 2010) and perception (Cohen et al., 2015), which can then further influence the conceptual representation of uncertainty. To examine the link between experience and representation, we take a data-driven approach to test whether people’s uncertainty representations predict decision-making, probing whether individuals with similar conceptual representations of uncertainty also display similar patterns of decision-making under uncertainty.

To provide the most detailed account of this relationship, we also investigated which dimensions conceptually structure uncertainty representations. There are several possible dimensions that may structure how people represent uncertainty. Given that uncertainty is often defined in statistical terms, one likely candidate dimension is probability or likelihood. Prospect theory, for example, transforms objective probabilities to subjective probabilities, thus capturing the known psychological phenomena of subjectively overweighting low probabilities and underweighting high probabilities, which has led to many useful insights about how uncertainty biases choice (Kahneman & Tversky, 1979). Another candidate dimension is affect. It is well-documented that people exhibit negative emotions when they do not know what will happen (FeldmanHall et al., 2016; Feldmanhall et al., 2018; Loewenstein et al., 2001; Slovic et al., 2007; Slovic & Peters, 2006). Although there are many ways to define affect, a predominate framework (Barrett et al., 2007; Russell, 1980; Russell et al., 1989) carves the affective space along the dimensions of valence and arousal, where valence is construed on a negative to positive continuum and arousal on a low intensity (e.g., sleepiness) to high intensity (e.g., alertness) continuum. Evidence spanning multiple methodologies finds that uncertainty causes aversive feelings characterized by negative valence and high arousal (FeldmanHall et al., 2016; Feldmanhall et al., 2018; Huettel et al., 2006; Levy et al., 2010). One additional candidate dimension which could structure how uncertainty is represented is the source of the uncertainty; that is, whether uncertainty is construed as external or internal (Fox & Ulkumen, 2021). External uncertainty refers to an unpredictable feature of the world (e.g., will it rain tomorrow?), while internal uncertainty refers to our confidence about our own knowledge (e.g., is Melbourne is the capital of Australia?). Research has distinguished between these two types of uncertainties (Ülkümen et al., 2016), revealing that people use clauses like “I’m confident” or “I’m not sure” to signal internal uncertainty, while external uncertainty is communicated using clauses such as “it is likely” or “it is not probable.” We begin by testing which of these dimensions conceptually structure uncertainty representations, before detailing the relationship between these representations and decision-making under risk.

Experiment 1

Material and methods

Participants

Participants (N = 49) were recruited using the undergraduate credit pool from Brown University (unfortunately, due to a data collection error no demographics were recorded for this study). All participants passed the attention check and therefore were included in the final sample. Participants received course credit and provided informed consent in a manner approved by Brown University’s Institutional Review Board.

Stimuli

The words presented to participants to measure the conceptual representation of uncertainty were selected by canvassing past work on uncertainty language (Herbstritt & Franke, 2019; Karelitz & Budescu, 2004) and a pre-rating study. The final selection process involved three main criteria: 1) balancing the number of words associated with probabilities falling above and below 50% based on our pre-rating study; 2) sufficient variability in the ratings of the selected words; and 3) exclusion of word pairs that are antonyms (e.g., unknown and known). Adherence to these criteria led to the inclusion of 18 words categorized by probabilities above 50% (frequent, likely, predictable, possible, inevitable, definite, confident, certain) and those with probabilities below 50% (risky, erratic, improbable, unexpected, doubtful, uncertain, questionable, unknown, ambiguous, and vague).

Procedure

Spatial arrangement task

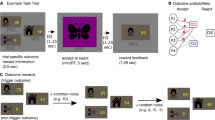
Participants were asked to arrange these 18 words according to their perceived similarity by clicking and dragging them within a circle (Fig. 1A). Perceived similarity was defined by the Euclidean distances between words; participants were instructed to place words perceived as similar closer together, while words perceived as dissimilar were instructed to be placed farther apart (Kriegeskorte & Mur, 2012). Participants completed only one trial of this spatial arrangement task.

Fig. 1
figure 1

Methods. Participants completed these tasks during Experiments 1 and 2. A. The Spatial Arrangement Task required participants to place words within a sphere to denote their similarity to the other words, which allowed us to assess a participant’s conceptual representation of words relating to uncertainty. B. Participants then rated each uncertainty word separately along three discrete dimensions: probability, source (internal or external), and affect (valence and arousal). C. Finally, in Experiment 2, participants completed a risky decision-making task in which they had to select between two gambles that varied in their payoffs and probability

Full size image

Explicit ratings

After participants completed the spatial arrangement task, they were asked to rate each uncertainty word on different dimensions (the order of presentation was randomized across participants): probability, affect (both valence and arousal simultaneously), and source. For probability, participants were instructed to report on a scale from 0 (not probable at all) to 100 (very probable) the extent to which a word reflects a certain probability. For example, a subject might be shown the word “sure” and asked to report the probability associated with “sure.” For source, participants were first given descriptions of the meaning of internal and external uncertainty (e.g., “Our uncertainty about the world comes from two main sources: our own lack of knowledge (an internal source) or randomness in the world (an external source)”). This description is accompanied with a classic example regarding the flip of a coin (external uncertainty) or the knowledge of a fact (internal uncertainty). Source was rated on a scale from 0 (very internal) to 100 (very external). Lastly, for valence and arousal, we followed the methodology from our prior research using self-reports for emotion words (Heffner et al., 2021; Heffner & FeldmanHall, 2022; Russell et al., 1989), where ratings were collected for each word using a 500 by 500 pixel 2-dimensional circumplex grid: the horizontal axis represents valence and ranged from unpleasant (−250) to pleasant (250), and the vertical axis represents arousal and ranged from low (−250) to high (250) intensity. Participants were instructed on the meaning of valence and arousal and how to use the two-dimensional circumplex, where the right half of the grid represents pleasant feelings (the farther to the right the more pleasant…), and the vertical dimension of the circumplex represents the degree of arousal. Participants were told that arousal has to do with how wide awake, alert, or activated a person feels, independent of whether the feeling is positive or negative. The top half of the circumplex is for feelings that are above average in arousal, and the lower half for feelings below average).

Results

Uncertainty representations are one-dimensional

We first analyzed the structure of uncertainty representations by computing a group-level distance matrix from participant’s spatial arrangement data. This distance matrix captures the average distance in Euclidean space between all 18 uncertainty words and represents the dissimilarities between words (i.e., representational dissimilarity matrix [RDM]). We then applied multidimensional scaling on this RDM to determine how many latent dimensions are needed to capture people’s uncertainty representations. Results show that one-dimension accounts for 58% of the variance in uncertain dissimilarities and that there is a considerable drop in accounted variance for the second and all successive dimensions (<10% of variance is explained by each of these additional dimensions). Taken together, it appears that uncertainty representations are structured in a one-dimensional manner.

Probability and valence contribute to structuring uncertainty representations

How can we interpret this one-dimensional solution that appears to be structuring uncertainty representations? To understand which dimension best describes how people conceptually represent uncertainty at the group level, we looked at Spearman correlations between the average ratings for each labeled dimension and the first principal component across all words. A high correlation between the ratings of the uncertainty words and their positions along the one-dimensional solution can be interpreted as evidence that this dimension provides a good interpretation of the representational space. Results of the four correlations (one for each dimension, with valence and arousal performed separately) reveal that probability and then valence are the most likely dimensions structuring uncertainty representations, with both analyses revealing a correlation coefficient greater than 0.5 (valence: rs(16) =  − 0.59, p = 0.01, probability: rs(16) =  − 0.88, p < 0.001), while the correlation for arousal and source (internal and external) were not significant (arousal: rs(16) =  − 0.02, p = 0.95, internal: ri(16) =  − 0.03, p = 0.91, external : re(16) = 0.09, p = 0.73). Furthermore, the group-level ratings of probability and valence are very highly correlated as well (rs(16) = 0.69, p = 0.001), suggesting that both of these a priori-selected dimensions are capturing a similar underlying component. Thus, it appears that uncertainty representations are conceptually structured along a single probability/valence dimension.

Experiment 2

Results suggest that uncertainty is represented along a probability/valence dimension. However, it remains unknown whether a person’s uncertainty representations can be linked to their behavior under uncertainty. Experiment 2 was conducted to replicate the main finding of Experiment 1 and test whether conceptual representations of uncertainty predict risky decision-making.

Materials and methods

Participants

Participants (N = 176) were recruited using the online testing platform Prolific (100 females, 73 males, 3 prefer not to say; mean age 35.2, SD = 12.3). We removed 41 participants from analysis for failing to pass attention checks used in prior research (Heffner & FeldmanHall, 2022) and the gambling task (Lejarraga et al., 2019), resulting in a final sample of 135 participants. Participants received monetary compensation and provided informed consent in a manner approved by Brown University’s Institutional Review Board. Under protocol 1607001555.

Stimuli

We selected the same set of 18 (un)certainty words than in Experiment 1 to measure the conceptual representation of uncertainty.

Procedure

Spatial arrangement task

As in Experiment 1, participants were asked to arrange these 18 words according to their perceived similarity by clicking and dragging them within a circle. This time, however, we extended and increased its robustness by using a well-vetted method (Kriegeskorte & Mur, 2012). Participants first rated the perceived similarity of all 18 words on the first trial, establishing an initial dissimilarity matrix between all words. All subsequent trials involved a subset of these 18 words. This was done to allow participants to convey high-dimensional representations, which could cause two words to be perceived as similar in one subset, but dissimilar in another subset with different word combinations. Subsets were determined on a trial-by-trial basis according to the lift-the-weakest adaptative algorithm (Kriegeskorte & Mur, 2012), such that specific subsets are specifically selected to further probe the similarity ratings where the algorithm has the least confidence. For example, if a participant indicated that two words are similar, a future trial might have those two words presented again amongst a smaller subset that includes different words. If the participant continues to place those two words close together, it provides stronger evidence that these words are represented as similar, regardless of the other words that surround it. Readers are referred to Kriegeskorte and Mur (2012) for technical details of the adaptive algorithm.

Explicit ratings for each uncertainty dimension

After participants completed the spatial arrangement task, they were asked to rate each uncertainty word on the different candidate dimensions following a similar method in Experiment 1. The only difference we made was that source, which was originally rated on separate scales for internal and external uncertainty, was combined into a single scale (0 = very internal, 100 = very external).

Risky decision-making task

After rating words on each candidate dimension, participants completed a gambling task (based on Lejarraga et al., 2019) in which they had to select between two risky gambles that varied in terms of the probability and magnitude of monetary reward (Fig. 1C). The task was comprised of 91 trials (see Appendix 1 for design information), and participants were told that one trial would be paid out based on their choice on that trial (monetary reward varied between losing $100 and gaining $100, while probabilities varied between 0.1-0.99). To prevent participants from losing money, they were endowed with $100 at the beginning of the task. One participant of the sample was paid at the end of the experiment, which participants were instructed about at the beginning of the task.

Results

Uncertainty representations are unidimensional based on valence and probability

We first analyzed the structure of uncertainty representations by computing a group-level dissimilarity matrix from the average of participant’s spatial arrangement data, which represents the average dissimilarity between two words (e.g., uncertain and likely). We then applied metric multidimensional scaling on this representational dissimilarity matrix (Fig. 3C). Replicating Experiment 1, results show that one dimension explains more than 40% of the variance in uncertainty representations, with a considerable drop for the second and all successive dimensions (<10% of variance is explained by each of these additional dimensions; Fig. 2A). The multidimensional solution finds two general clusters, similar to Experiment 1: one with uncertain words (e.g., ambiguous, unknown, vague), and the other with certain words (e.g., predictable, certain, definite; Fig. 2B). Hierarchical clustering of the RDM reflects the same pattern in a different visualization (Fig. 2C). To understand the uncertainty representation solution, we examined group-level correlations between average ratings of uncertainty words and the first MDS dimension. Again, results reveal that probability and valence are the most likely dimensions structuring uncertainty representations, with both analyses revealing a Spearman correlation coefficient greater than 0.7 (valence: rs(16) =  − 0.71, p < 0.001, probability: rs(16) =  − 0.90, p < .001; Fig. 2E-F), whereas the correlation for arousal and source were not significant (arousal: rs(16) =  − 0.37, p = 0.14, source: rs(16) = 0.30, p = 0.22). Using a subset of uncertainty words and an independent online population, we replicate the finding that uncertainty representations are conceptually structured along a single probability/valence dimension.

Fig. 2
figure 2

Conceptual representations of uncertainty are one dimensional and organized by valence or probability. A. The percentage of variance explained for principal dimension from the similarity data reveals a sharp kink after the first component, illustrating that the variance is best explained by one component. B. Plot of solution of multidimensional scaling of the similarity. Data using the first two dimensions. C. Group-level representational dissimilarity matrix of uncertainty words, organized by hierarchical cluster.

Full size image
Fig. 3
figure 3

Conceptual representations of uncertainty are one dimensional and organized by valence or probability. A. The percentage of variance explained for principal dimension from the similarity data reveals a sharp kink after the first component, illustrating that the variance is best explained by one component. B. Plot of solution of multidimensional scaling of the similarity. Data using the first two dimensions. C. Group-level representational dissimilarity matrix of uncertainty words, organized by hierarchical cluster

Full size image
Fig. 4
figure 4

Conceptual representations of uncertainty predict risky decision-making. A. The correlation coefficients matrix for all tasks. Results reveal that gambling behavior is predicted by conceptual representations of uncertainty, probability, and valence. B. The archetypal group had greater separation between uncertain and certain words for both valence and probability than the atypical group. C. Two exemplar participants who are dissimilar to each other in their uncertainty representations and decision-making are depicted. Dots represent the ratings of each word, where the large dots reflect the means of the ratings.

Full size image

Uncertainty representations predict decisions under uncertainty

Although our results suggest that uncertainty is represented along a probability/valence dimension, it remains unknown whether an individual’s representation of uncertainty is related to their behavior under uncertain conditions. If the conceptual representation affects the subjective valuation of choices, then people who represent uncertainty in a similar fashion also should display similar patterns of behavior under uncertainty. We leveraged this logic by taking a correlational approach (van Baar et al., 2019; van Baar et al., 2021). First, we calculated the Spearman correlation between each participant and each other participant within each task: the spatial arrangement task (uncertainty representations), the dimension rating task (valence, arousal, probability, and source), and the gambling task. This resulted in six correlation matrices capturing the similarity in behavior between participants from very dissimilar (r = −1) to very similar (r = +1). Two participants were dropped from this analysis because they did not vary their ratings in one of the tasks (e.g., rating each word 50 on probability), meaning their correlations with other participants were undefined. Next, we examined the correlation between one correlation matrix (e.g., gambling behavior matrix) and another (e.g., conceptual uncertainty representation matrix) as a method for determining how much similarity in one task predicts similarity in the other. We controlled for the large number of degrees of freedom by using a permutation test to determine significance. We permutated the correlation matrices by randomly shuffling participant identifiers and recalculating this correlation of correlations 100,000 times, building a null distribution of Spearman correlation that could be expected by chance. We used the 99th percentile of this null distribution as our criterion for determining if our empirical result was significant.

When examining the relationship between uncertainty representations and decision-making under uncertainty, we found that people who represent uncertainty similarly to one another also behave more similarly during an uncertain decision-making task (rs = 0.21, p < 0.001). We found that this (and all) empirical correlation exceeds the 99th percentile of the null distribution of correlation values calculated through permutation testing, meaning our empirical correlation was statistically significant and unlikely due to chance. Uncertainty representations were the most predictive measure of decisions to gamble (Fig. 4A), closely followed by the probability dimension, which was the primary dimension structuring uncertainty (rs = 0.17, p < 0.001). In contrast, the correlation with valence was small, albeit still significant (rs = 0.07, p < 0.001). Overall, these results reveal that conceptual representations of uncertainty predict consequential decision-making.

To gain better insight of where the representational differences lie between participants who behaved differently under uncertainty, we examined how participants who exhibited different conceptual representations of uncertainty differed. First, we calculated how unique each participant’s uncertainty representation was by computing their average correlation between one participant’s uncertainty representation and the representation of all the other participants. Next, we used a median split (r = 0.47) of this average correlation to create two groups: the archetypal group whose uncertainty representations were above the median in similarity, and the atypical group, whose uncertainty representations fell below the median in similarity. We calculated the valence and probability differences for uncertain and certain words for the archetypical and typical groups. Results from a Welch two-sample t-test reveal that the archetypal group had significantly greater differences between uncertain and certain words for both valence and probability than the atypical group (valence t(127.61) = 2.74, p = 0.006, probability t(119.01) = 2.48, p = 0.01; Fig. 4B). In other words, participants who are more typical in their uncertainty representations rated uncertain words more negative and less likely, whereas participants who had a more unique representation did not exhibit such grave differences between these words, rating uncertain words as more positive and more likely. To further illustrate, we took two specific participants from each group and plotted the probability and valence ratings of these participants (Fig. 4C). While archetypal person shows a sharp distinction between certain and uncertain concepts along the probability and valence dimensions, the atypical person exhibits a representation in which certain and uncertain words overlap along these dimensions.

Discussion

Decision-making is classically described by a value-maximization framework: possible outcomes are transformed into subjective values, and the option that leads to the highest subjective value is ultimately selected (Levy et al., 2010; Tversky & Kahneman, 1992; Tymula & Glimcher, 2016). Although we now know that individuals who are uncertainty averse decrease the subjective value of uncertain options, an open question revolves around how people mentally represent uncertainty. Over a lifetime, each person has their own experiences with uncertainty. These experiences with uncertainty are likely to shape its conceptual representation. The ensuing representation, in turn, may end up influencing how people make decisions under uncertainty. Our results reveal that representations of uncertainty are simple, rather than multifaceted. Across two experiments, people structured their representations of uncertainty along a dimension that tracks both probability and valence. We do note, however, that had we selected an entirely different set of words, the strength of the correlations between dimensions might change and well as the dimensionality solution. Yet, these words, which are commonly used to express uncertainty, were sufficient to demonstrate how individual differences in uncertainty representations are capable of predicting how people make decisions under uncertainty.

The fact that different conceptual representations of uncertainty are associated with distinct behavioral fingerprints suggests a strong link between how uncertainty is conceptually represented and its effect on choice. This is supported by current models that understand decision-making as a process guided by an internal sampling from memory (Olivola & Chater, 2016; Stewart et al., 2006), which predict that the kind of memories sampled change depending on people’s conceptualization of uncertainty. Our data suggest that some individuals conceptually structure uncertainty as more negative and emotionally aversive than others, which aligns with the general tendency for negative affect to lead to avoidant behavior, while positive affect leads to approach-like behavior (Carver, 2006; Carver & Scheier, 1990). This stands in stark contrast to those classified as “atypical” in our cohort. These individuals do not have such distinct representations between certain and uncertain concepts. Future work can test whether having a representation strongly structured along the valence dimension may lead to a more automatic reaction to approach certainty and avoid uncertainty, whereas a more neutral representation between certainty and uncertainty may lead to a more deliberative, context-dependent response to uncertainty.

Probability also was found to structure uncertainty representations. At first blush, this finding dovetails with the classic conceptualization of uncertainty. However, a closer look at our data reveals a gap between these more traditional accounts and people’s lay understanding of probability—namely that uncertain concepts appear to be associated with low probabilities, whereas chance is generally thought to hover at around 50%. This link between low probabilities and uncertainty concepts aligns more with the notion of surprise than chance, which would suggest that risk-seeking and risk-averse individuals’ representations may be capturing different expectations, much like an optimism/pessimism bias (Sharot, 2011; Sharot et al., 2007), a mechanism that can be teased out in future work.

Our main goal was to test the link between the conceptual representation of uncertainty and risky decision-making. Testing this relationship dovetails with recent work looking at how semantic memory processes influence preferential decision-making (Bhatia, 2019b), where memory can internally bias the options that are generated before a choice is even made (e.g., to decide which restaurant to go, one needs to first create a list of options). We extend this work by demonstrating that abstracted, conceptual representations can predict behavioral patterns amongst individuals, even when people face the exact same decisions.

Uncertainty stems from many sources, from uncertainty surrounding decision outcomes to sensorial uncertainty (Bach & Dolan, 2012). Research measuring how the brain processes these different types of uncertainties reveals discrete networks that encode uncertainty, depending on its source. For example, decision-outcome uncertainty is processed in the anterior insula, prefrontal cortex, and cingulate cortex (d’Acremont et al., 2009; Preuschoff et al., 2006, 2008), whereas sensorial uncertainty is mainly processed by intraparietal sulcus, middle frontal gyrus, anterior cingulate cortex, and anterior insula (Kayser et al., 2010). Because our findings reveal that how an individual conceptualizes uncertainty biases how they experience uncertainty, it is likely that most, if not all, of these brain regions are modulated by the conceptual representation of uncertainty. Future work can help to characterize which of these brain regions are most sensitive to individual differences in how uncertainty is conceptualized.

Bernoulli started a tradition of formalizing uncertainty aversion using a subjective value function, which led to a proliferation of decision-making models under this framework. Although these models have been wildly successful, in large part because of their simplicity and generalizability, they also have limited our insight into how uncertainty influences choice. We broaden the scope of inquiry by showing that the nature of an individual’s uncertainty representations predicts risky decision-making. Establishing this relationship is a starting point for unveiling the dynamics between abstracted representations and choice.