P300 amplitude variations, prior probabilities, and likelihoods: A Bayesian ERP study

Abstract

The capability of the human brain for Bayesian inference was assessed by manipulating probabilistic contingencies in an urn-ball task. Event-related potentials (ERPs) were recorded in response to stimuli that differed in their relative frequency of occurrence (.18 to .82). A veraged ERPs with sufficient signal-to-noise ratio (relative frequency of occurrence > .5) were used for further analysis. Research hypotheses about relationships between probabilistic contingencies and ERP amplitude variations were formalized as (in-)equality constrained hypotheses. Conducting Bayesian model comparisons, we found that manipulations of prior probabilities and likelihoods were associated with separately modifiable and distinct ERP responses. P3a amplitudes were sensitive to the degree of prior certainty such that higher prior probabilities were related to larger frontally distributed P3a waves. P3b amplitudes were sensitive to the degree of likelihood certainty such that lower likelihoods were associated with larger parietally distributed P3b waves. These ERP data suggest that these antecedents of Bayesian inference (prior probabilities and likelihoods) are coded by the human brain.

Probabilistic inference is a well-established research area in cognitive psychology (see Anderson, 2015, for a textbook introduction; Kahneman, Slovic, & Tversky, 1982). The topic has only recently begun to receive attention in cognitive neuroscience (Bach & Dolan, 2012; Glimcher, 2004). Current research focuses on the neural implementations of probabilistic inference in two main areas. At the cellular level, studies examine neural codes for probabilistic inference (Gerstner & Fremaux, 2015; Kappel, Habenschuss, Legenstein, & Maass, 2015; Pouget, Beck, Ma, & Latham, 2013). At the level of large-scale neural circuits, studies identify neural response variability related to probabilistic inference with high spatial resolution (functional magnetic resonance imaging; fMRI) or with high temporal resolution (event-related potentials; ERP).

Statement of the Problem

Bayesian inference (Jaynes, 2003; Robert, 2007) is the focus of much of this research. Bayes’ theorem updates the probability for a hypothesis as more evidence becomes gradually available. Bayes’ theorem derives posterior probabilities for the hypothesis as consequences of two antecedents, that is, the prior probabilities for the hypothesis and the likelihoods for the evidence should a hypothesis prove true. Figure 1 provides a geometric visualization of Bayes’ theorem. Readers who are unfamiliar with Bayes’ theorem are advised to inspect Fig. 1 before proceeding. A more formal introduction to Bayes’ theorem can be found below.

Fig. 1

A geometric illustration of Bayesian inference. In our study, the ‘Mondrian diagram’ on the left-hand side shows probability distributions and likelihoods on trial n – 1. In our study, trial n – 1 refers to the situation before the first piece of evidence has been received, implying that these parameters were instructed. The ‘Mondrian diagram’ on the right-hand side shows the same parameters on trial n, that is, after a first piece of evidence was observed (i.e., in the example here, an s ₁ stimulus, indicated by the dotted black arrow). The receipt of this piece of evidence triggers Bayesian inference. Solid black horizontal lines define prior (left ‘Mondrian diagram’) and posterior (right ‘Mondrian diagram’) probabilities. Relative proportions of colored rectangles along the horizontal axis represent likelihoods. Bayesian inference thus equals shifts of the solid black horizontal line along the vertical axis. In the given example, the black horizontal line was dragged downwards from trial n – 1 to trial n, such that P(h₁ǀs₁) > P(h₁) and P(h₂ǀs₁) < P(h₂). The degree of belief in hypothesis h₁ being true increased, and accordingly the degree of belief in hypothesis h₂ being true decreased, after obtaining evidence s ₁ due to unbalanced likelihoods, that is, P(s₁ǀh₁) > P(s₁ǀh₂). (Color figure online)

According to the Bayesian brain hypothesis, the brain codes and computes Bayesian parameters such as prior probabilities and likelihoods (Doya, Ishii, Pouget, & Rao, 2007; Friston, 2005; Knill & Pouget, 2004). Hence, fMRI or ERP discoveries showing that the manipulation of prior probabilities and likelihoods is associated with separately modifiable and distinct neural responses would strengthen the support for the Bayesian brain hypothesis.

Overview of the Existing fMRI Research

We briefly review the literature in chronological order. Summerfield and Koechlin (2008) showed multiple representations of prior expectations within the visual hierarchy in extrastriate and anterior temporal lobe regions with fMRI. Stern, Gonzalez, Welsh, and Taylor (2010) measured fMRI while subjects accumulated sequential pieces of probabilistic evidence and then made a decision under uncertainty. Increased uncertainty during evidence accumulation was associated with activity in dorsal cingulate cortex, whereas greater uncertainty when executing a decision was related to enhanced lateral frontal and parietal activity. These results suggest that neural mechanisms of uncertainty depend on the parameters and on the stage of decision making. Participants in the study by Furl and Averbeck (2011) viewed sequences of bead colors drawn from hidden urns and attempted to infer the majority bead color in each urn. When viewing each bead color, participants chose either to seek more evidence about the urn by drawing another bead (draw choices) or to infer the urn contents (urn choices). When faced with urns that had bead color splits closer to chance (i.e., 60/40 vs. 80/20), participants increased their evidence-seeking behavior. Urn choices evoked larger hemodynamic responses than did draw choices in the insula, striatum, anterior cingulate, and parietal cortex. These parietal responses were greater for participants who sought more evidence on average and for participants who increased their evidence seeking when draws came from 60/40 urns.

Vilares, Howard, Fernandes, Gottfried, and Körding (2012) designed a sensorimotor decision-making task in which human subjects had to estimate positions of hidden visual targets. Uncertainty (a parameter that is also referred to as precision in other publications) was systematically varied in a two-by-two factorial design, with the factors prior and likelihood uncertainty, such that the conditions were matched for performance accuracy but differed in prior and likelihood uncertainty. Their fMRI study revealed that prior and likelihood uncertainty had distinct neural representations. Whereas likelihood uncertainty activated brain regions along the visuomotor pathway, representations of prior uncertainty were identified in brain areas outside this pathway, including putamen, amygdala, insula, and orbitofrontal cortex. O’Reilly et al. (2013) separately modified surprise, that merely reflects the unexpectedness of an observation and shifts in beliefs or Bayesian updating (see Fig. 1), in a saccadic planning task. They observed that distinct brain regions are associated with surprise and Bayesian updating. Whereas surprise was associated with a hemodynamic response in the posterior parietal cortex, the anterior cingulate cortex was activated during Bayesian updating.

D’Acremont, Schultz, and Bossaerts (2013) asked their subjects to estimate the probability of uncertain stimuli based on prior knowledge as well as on repeated empirical observations. They found hemodynamic correlates of prior knowledge in the striatum, whereas areas in the default mode network (angular gyri, posterior cingulate cortex, and medial prefrontal cortex) encoded stimulus frequencies. Schwartenbeck, FitzGerald, and Dolan (2016) developed a novel paradigm that allowed decomposing surprise and Bayesian updating (akin to O’Reilly et al., 2013). Using fMRI, they showed that dopamine-rich midbrain regions encode Bayesian updating, whereas surprise is encoded in prefrontal regions, including the presupplementary motor area and dorsal cingulate cortex. In the context of the dopaminergic system, another line of research has shown that this system conveys stochastic parameters of upcoming rewards, such as reward uncertainty (Fiorillo, Tobler, & Schultz, 2003; Preuschoff, Bossaerts, & Quartz, 2006; Preuschoff, Quartz, & Bossaerts, 2008). Trapp, Lepsien, Kotz, and Bar (2016) addressed the neural underpinnings of prior probability in category-specific areas (i.e., the fusiform face area and the parahippocampal place area). Their findings showed that hemodynamic activity in the fusiform face area was higher when faces had higher prior probability.

The available fMRI research shows that various probabilistic parameters may in fact be associated with separately modifiable and anatomically distinct hemodynamic responses. With regard to the exact localization of these responses, the data are less consistent, putatively because of the enormous heterogeneity of the tasks considered. The available data seem to converge in fronto-striatal representations of prior parameters and predominantly parietal representations of likelihood parameters, although there are exceptions from this rule. Furthermore, these parameters are not necessarily equivalent to proper prior probabilities and likelihoods because a majority of tasks that were used in these studies must be considered as being only indirectly related to Bayes’ theorem.

Overview of the Existing ERP Research

The relevant ERP research is very much focused on the P300 component (see Kopp, 2008; Polich, 2007, for an overview). Donchin (1981) argued that P300 amplitude is not crucially determined by the inherent attributes of eliciting events. He ascertained that “surprising events elicit a large P300 component” (p. 498). Squires, Wickens, Squires, and Donchin, (1976) had presented a model of trial-by-trial P300 (which is also referred to as P3b, i.e., the parietally distributed P300) amplitude variations, based on the concept of expectancy, which was thought to be determined by multiple factors, most notably by the memory for event frequency and by the “global” event probability. Mars et al. (2008) indeed found that surprise that merely reflects the unexpectedness of an observation was encoded in the parietally distributed P3b (see also Seer, Lange, Boos, Dengler, & Kopp, 2016).

Achtziger, Alós-Ferrer, Hügelschäfer, and Steinhauser (2014) measured ERPs during performance of a belief-updating task and found evidence that participants who overweight new information display a lower sensibility to conflict detection, captured by the N2 (see Folstein & Van Petten, 2008, for overview), whereas participants who overweight prior probabilities initiated action choice well before new information was presented (captured by lateralized readiness potentials; see Eimer, 1998, for an overview). Ostwald et al. (2012) found evidence for spatiotemporal and functional segregation in human somatosensory processing. Their data suggest that early processing stages (somatosensory cortex) may implement short-term Bayesian perceptual learning, intermediate processing stages (right inferior frontal cortex) index active stimulus engagement, and late processing (cingulate cortex) may reflect learning-induced updating of top-down attentional control mechanisms (as expressed in scalp-recorded P3b responses).

Kolossa, Fingscheidt, Wessel, and Kopp (2013) modeled the surprise-sensitivity of trial-by-trial P3b amplitude variations as originating from the operation of multiple digital filters in the brain (i.e., two parallel first-order infinite impulse response low-pass filters and an additional fourth-order finite impulse response high-pass filter). Kolossa, Kopp, and Fingscheidt (2015) replicated the surprise-sensitivity of P3b amplitude variations and showed that the anteriorly distributed P3a encodes Bayesian updating, a finding that was also reported by Bennett, Murawski, and Bode (2015).

The available ERP research shows in a remarkably consistent pattern that various probabilistic parameters may in fact be associated with separately modifiable and functionally distinct electrophysiological responses. Multiple studies showed that amplitude variations in the frontally distributed P3a are related to Bayesian updating, hence to changes in prior probabilities as a result of the gradual receipt of new evidence (as illustrated in Fig. 1). In contrast, amplitude variations in the parietally distributed P3b are related to surprise that reflects the unexpectedness of the evidence.

The Current Study

We sought to bring additional insight into how the human brain produces Bayesian inference by searching for potential ERP correlates of Bayesian parameters. Our study aims to contribute to the existing literature in the following ways. First, previous ERP studies were mainly interested in revealing neural mechanisms underlying the dynamics of Bayesian updating and less attention was given to the neural correlates of the two antecedents of Bayesian inference (i.e., the prior probabilities for the hypothesis and the likelihoods for the evidence should a hypothesis prove true). Second, our study examined potential ERP correlates of preexperiential forms of instructed Bayesian parameters (FitzGerald, Seymour, Bach, & Dolan, 2010; Hertwig, Barron, Weber, & Erev, 2004; Hertwig & Erev, 2009). Third, we also advocate an explicitly Bayesian approach to statistical inference in place of classical methods. Bayesian inferential approaches have been proposed as early as 1985 for psychophysiological research (O’Connor, 1985), but have not gained importance in the relevant literature until recently (see Maris, 2012, for an overview; Constantino & Daw, 2015).

We will formalize our research hypotheses (see Derivation of Eight Hypotheses of Interest) as so-called informative—that is, (in-)equality constrained—hypotheses (Hoijtink, 2012) that are quite distinct from traditional null and alternative hypotheses. Subsequently, support in the data (in the form of Bayes factors and posterior model probabilities) for each of these hypotheses is computed. This is a purely confirmatory inferential approach in which the researcher’s degrees of freedom are limited to the specification of the informative hypotheses of interest. Hence, we also try to demonstrate the utility of applying a Bayesian statistics approach to ERP research.

The Urn-Ball Task

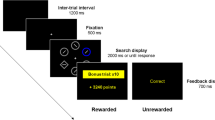
Figure 2 shows our experimental paradigm, which employed an urns-and-balls (or urn-ball) task (Phillips & Edwards, 1966). Samples of balls were drawn from two types of urns. We manipulated probabilistic contingencies at two levels. First, we introduced various degrees of uncertainty (Bach & Dolan, 2012) about the type of urn by sampling urns from two probability distributions with different uncertainty parameters. Second, we manipulated the proportion of ball colors within the two types of urns at different levels of uncertainty. We refer to these probabilistic contingencies as prior probabilities and likelihoods, respectively. Figure 2b shows that the urn-ball task requested binary decisions about the colors of all balls across the entire sequence of four draws of balls. After four draws of balls, subjects had to infer the origin of these samples of balls (i.e., they were forced to choose the type of urn from which they believed these four balls had actually been sampled).

Fig. 2

(a). The four tableaus that were shown to participants in the four probability conditions of the urn-ball task—certain priors (Pc: P = 0.9, P = 0.1), uncertain priors (Pu: P = 0.7, P = 0.3), certain likelihoods (Lc: P = 0.9, P = 0.1), uncertain likelihoods (Lu: P = 0.7, P = 0.3); see text for details. (b). Each of the four probability conditions (here, uncertain priors & uncertain likelihoods condition, PuLu, serves as an example) comprised 50 consecutive episodes of sampling that consisted of the invisible drawing of one urn, the visible drawing of a sample of four balls from that urn (sequential drawing with replacement), and a forced choice on the type of urn from which this sample might have originated (Color figure online)

Non-Bayesian Interpretation of the Urn-Ball Task

The non-Bayesian analysis of the urn-ball task rests upon the sampling of balls from the population of balls. As shown in Fig. 2a, a non-Bayesian could ignore the existence of the urns in the tableau, and he or she could simply count or estimate the overall numbers of red and blue balls in order to predict the result of the first draws (see Fig. 2b). These quantities correspond to the marginal probabilities P(s ₁ ) and P(s ₂ ) in Fig. 1. The reader who wants to know more about these marginal probabilities in the urn-ball task is referred to Kolossa et al. (2015). It will suffice to point out that these marginal probabilities correspond to the unexpectedness of the evidence (i.e., surprise).

Bayesian Formulation of the Urn-Ball Task

As illustrated in Fig. 1, the Bayesian analysis of the urn-ball task evaluates the probability of a hypothesis (such as that a particular sample of balls was drawn from one type of urn). It rests upon the idea that these probabilities are updated in the light of new evidence, and Bayes’ theorem prescribes that posterior probabilities are proportional to the product of likelihoods (distribution of ball colors, given one urn) and prior probabilities (distribution of urns). Given prior probabilities P(h ₁) = 1 − P(h ₂) for two hypothetical urns h ∈ {h ₁, h ₂} and the availability of one piece of evidence or a stimulus (i.e., an observed ball) s ∈ {s ₁, s ₂}, we can compute the posterior probabilities as

$$ P\left({h}_1|s\right)=\frac{P\left(s|{h}_1\right)\cdot P\left({h}_1\right)}{P(s)} $$

(1)

$$ P\left({h}_2|s\right)=\frac{P\left(s|{h}_2\right)\cdot P\left({h}_2\right)}{P(s)}. $$

(2)

and

Formulating these posterior probabilities in the log-odds form (Jaynes, 2003), using the notation Lo(h ₁|s) = ln(P(h ₁|s)/P(h ₂|s)) for the posterior log-odds that favor h ₁, given evidence s, we obtain

$$ \mathrm{L}\mathrm{o}\left({h}_1|s\right)= \ln \frac{P\left(s|{h}_1\right)\cdot P\left({h}_1\right)}{P\left(s|{h}_2\right)\cdot P\left({h}_2\right)}= \ln \frac{P\left(s|{h}_1\right)}{P\left(s|{h}_2\right)}+ \ln \frac{P\left({h}_1\right)}{P\left({h}_2\right)}. $$

(3)

Hence, Bayesian probability updating (in log-odds form and for binary decisions) simply equals adding the logarithm of the likelihood ratio, that is, ln(P(s|h ₁)/P(s|h ₂)), to the logarithm of the prior odds, that is, ln(P(h ₁)/P(h ₂)).

Derivation of Predictions for ERP Amplitudes

We recorded 20-channel electroencephalographic data from human participants who performed the urn-ball task. We deliberately restricted our analyses to cortical responses to just the initial items of the samples of balls. Figure 2B illustrates that this confinement served to identify potential ERP correlates of the unexpectedness of the evidence, prior probabilities, and likelihoods as they were instructed via the tableaus in our urn-ball task (FitzGerald et al., 2010; Hertwig et al., 2004; Hertwig & Erev, 2009). We measured cortical responses to simple colored stimuli that were processed for probabilistic inference at a later time. We aimed to test whether instructed unexpectedness of the evidence, prior probabilities, and likelihoods separately modify distinct neural responses.

We hypothesized that the unexpectedness of the evidence, prior probabilities, and likelihoods should reveal itself as amplitude variations in P300 waves. We expected that P3a amplitudes are modified by the manipulation of prior probabilities and that P3b amplitudes are modified by the manipulation of the unexpectedness of the evidence and/or likelihoods. The P3a prediction is related to empirical and theoretical grounds for expecting sensitivity to prior probabilities. Empirically, some if not most of the cited fMRI work may be used to derive this prediction if one assumes that frontal sources contribute to the generation of scalp-recorded P3a waves (Polich, 2007). Theoretically, Bayesian updating can be described as transforming prior probabilities to posterior probabilities (see Fig. 1). Because the cited ERP work has shown that amplitude variations in the P3a are related to Bayesian updating, they may also be related to prior probabilities. Surprise reflects the unexpectedness of the evidence—see the marginal probabilities P(s ₁ ) and P(s ₂ ) in Fig. 1—and relationships between surprise and P3b amplitude variations are manifest in many previous ERP studies. The concept of likelihood has hitherto been neglected in ERP studies, yet amplitude variations in the P3b may be sensitive to likelihoods, too. Most of the cited fMRI work may be used to derive this prediction if one assumes that parietal sources contribute to the generation of scalp-recorded P3b waves (Polich, 2007).

Method

Participants

Sixteen undergraduate psychology students participated to gain course credits (15 female, 1 male). Their age ranged from 19 to 50 years (M = 24.7, SD = 9.3 years of age). One participant was left-handed and two were ambidextrous. All participants indicated having normal or corrected-to-normal vision. The procedure was approved by the local ethics committee.

Task Procedures

As shown in Fig. 2a, we manipulated the task’s probabilistic contingencies at two levels. We refer to these probabilistic contingencies as prior probabilities and likelihoods, respectively, and to their unique combination as a probability condition. At the beginning of each probability condition, a tableau of 10 urns containing a total of 100 colored balls was shown to participants. First, we introduced varying degrees of uncertainty about the type of urn by manipulating their prior probabilities. Second, we manipulated the proportion of ball colors within each urn, thereby manipulating likelihoods. Visualization of prior probabilities and likelihoods in the form of these tableaus allowed participants to build internal representations of probabilistic contingencies.

Uncertainty in prior distributions was manipulated by presenting 10 urns, composed of different numbers of type h ₁ and type h ₂ urns. On uncertain prior probability conditions (Pu), seven type h ₁ urns and three type h ₂ urns—that is, P(h ₁ ) = .7, P(h ₂ ) = .3—were presented. Note that usage of the term more uncertain would be technically accurate; however, we use the technically inaccurate, but simpler uncertain throughout the article. On the certain prior probability condition (Pc), nine type h ₁ urns and one type h ₂ urn—that is, P(h ₁ ) = .9, P(h ₂ ) = .1—were presented. Note that usage of the term more certain would be technically accurate; however, we use the technically inaccurate, but simpler certain throughout the article. Uncertainty in likelihoods was manipulated in the following way: On uncertain likelihood conditions (Lu), urn type h ₁ contained seven red (s ₁ ) and three blue (s ₂ ) balls—P(s ₁ |h ₁ ) = .7, P(s ₂ |h ₁ ) = .3—whereas urn type h ₂ contained three red and seven blue balls—that is, P(s ₁ |h ₂ ) = .3, P(s ₂ |h ₂ ) = .7. On certain likelihood conditions (Lc), urn type h ₁ contained nine red balls and one blue ball—that is, P(s ₁ |h ₁ ) = .9, P(s ₂ |h ₁ ) = .1—whereas urn type h ₂ contained one red ball and nine blue balls—that is, P(s ₁ |h ₂ ) = .1, P(s ₂ |h ₂ ) = .9. We chose these quite strongly unbalanced prior probabilities and likelihoods to optimize the discriminability of the informative hypotheses (see Derivation of Eight Hypotheses of Interest). The results may have been biased by the selection of these values. Ball colors were counterbalanced across participants. To avoid confusion, s ₁ (s ₂) always refers to that ball color in a tableau that was present in more (fewer) cases, regardless of the actual color. We refer to the frequent stimulus as s ₁ and to the rare stimulus as s ₂ in the remainder of this article.

Figure 2b illustrates the urn-ball paradigm and outlines the experimental setup for all four probability conditions. Repeated sampling consisted of the following sequence of events: First, one of the 10 urns was selected randomly, but the outcome of this selection remained hidden to the participants. Subsequently, a random sample of four balls was sequentially drawn, with replacement, from the selected urn, and balls were presented visually, one after the other, on the computer screen. Visual stimuli (i.e., the sampled balls) were presented at the center of a computer screen (Eizo FlexScan T766 19-in.; Hakusan, Ishikawa, Japan) against gray background (stimulus size = one degree, stimulus duration = 100 ms, stimulus onset asynchrony = 2,500 ms). Cortical responses to these visual stimuli constituted the brain activations that we measured. Participants were asked to indicate the color of each ball by pressing a key corresponding to one of the two colors. Participants also repeatedly had to perform probabilistic inverse inference. That is, they were asked after each sample of four balls to decide from which type of urn this sample might have originated (forced choice). No feedback as to the correctness of the choices was provided.

Each of the four probability conditions c ∈ {PcLc, PcLu, PuLc, PuLu} comprised 50 episodes of random sampling, each consisting of four draws, yielding a total of 800 sequentially presented colored ball stimuli. We restricted our analyses to cortical responses to just the initial draws within the 200 (i.e., four times 50) episodes of sampling in an attempt to identify potential neural correlates of prior probabilities and likelihoods on the processing of the initial ball of each sample. Prior probabilities and likelihoods could solely be learned by instruction (i.e., inspection of the tableaus), whereas the expected values of relative frequencies of red and blue balls—PcLc: P(s ₁) = .82, P(s ₂) = .18; PcLu & PuLc: P(s ₁) = .66, P(s ₂) = .34; PuLu: P(s ₁) = .58, P(s ₂) = .42, respectively—could be learned by inspection of the tableaus as well as from experience. This holds true for large numbers of episodes of sampling where observed relative frequencies of red and blue balls should approximate their expected values.

Each participant completed four practice episodes of sampling under the supervision of and in a task-related dialogue with the experimenter to become accustomed to the task at the beginning of the experiment. The tableau of each practice sampling consisted of one single h ₁ urn and one single h ₂ urn (yielding uniform prior probabilities). Successful completion of these practice episodes of samplings demonstrated that the participants understood the procedure and their task. Each participant performed all four probability conditions with breaks of approximately 2 minutes between conditions. The order of probability conditions was counterbalanced across participants. The experiment was run using Presentation® (Neurobehavioral Systems, Albany, CA).

Instructions read as follows: “You will experience a series of chance experiments. You will see ten urns, each of which is filled with 10 balls. Urns predominantly contain red or blue balls. One of the urns will be selected by chance, but you will never see which urn was sampled. Four balls will be randomly sampled with replacement from the selected urn, and these balls will be shown to you one after the other. You will have to identify the color of each of these balls by appropriate responding. After having seen a sample of balls, you will have to infer from which type of urn (the predominantly red or blue type) that particular sample may have originated. These episodes of sampling will be repeated many times.”

Electrophysiological Recordings and Data Preanalysis

The electroencephalogram (EEG) was recorded continuously, using a QuickAmps-72 amplifier (Brain Products, Gilching, Germany) and the Brain Vision Recorder Version 1.02 software (Brain Products, Gilching, Germany) from frontal (F7, F3, Fz, F4, F8), fronto-central (FCz), central (T7, C3, Cz, C4, T8), parietal (P7, P3, Pz, P4, P8), occipital (O1, O2), and mastoid (M1, M2) sites. Ag-AgCl EEG electrodes were used, which were mounted on an EasyCap (EasyCap, Herrsching-Breitbrunn, Germany). Electrode impedance was kept below 10 kΩ. All EEG electrodes were referenced to average reference during the recording. Participants were informed about the problem of noncerebral artifacts, and they were encouraged to reduce the occurrence of movement artifacts. Ocular artifacts were monitored by means of bipolar pairs of electrodes positioned at the sub- and supraorbital ridges (vertical electrooculogram; vEOG) and at the external ocular canthi (horizontal electrooculogram; hEOG). The EEG and EOG channels were subject to a band-pass filter of .01 Hz to 30 Hz and digitized at 250 Hz sampling rate with t as discrete time index and a resulting sampling period T = 4 ms.

Initial off-line analysis of the EEG data was performed by means of the Brain Vision Analyzer Version 2.0.1 software (Brain Products, Gilching, Germany). EEG electrodes were offline rereferenced to average mastoid reference. Careful manual artifact rejection was performed before averaging to discard trials during which eye movements or any other noncerebral artifact except blinks had occurred. One hundred and eleven trials of the 3,200 trials that were originally recorded had to be rejected (i.e., around 3.5%) so that 3,089 trials entered subsequent levels of analysis. Deflections in the averaged EOG waveforms were small, indicating that fixation was well maintained on those trials that survived the manual artifact rejection process. Semi-automatic blink detection and the application of an established method for blink artifact removal were employed for blink correction (Gratton, Coles, & Donchin, 1983). Error trials were excluded so that solely artifact-free trials on which stimuli were correctly identified entered the final level of analysis—error rates for frequent (s ₁) stimuli: PcLc = .01, PcLu = .02, PuLc = .02, PuLu = .02; for rare (s ₂) stimuli: PcLc = .05, PcLu = .04, PuLc = .04, PuLu = .04.

Data Reduction

The continuous EEG obtained at the finally selected electrodes Fz, F4, and Pz (cf. Selection of EEG/ERP Data for Statistical Analysis) was divided for each individual participant i ϵ {1,…,N} with N = 16 into epochs x _i,c,s,m (t) of 700 ms duration starting 100 ms before stimulus onset with m ϵ {1,…,M _i,c,s }, where M _i,c,s denotes the number of epochs of stimulus type s ∈ {s ₁, s ₂} presented to participant i in probability condition c ϵ {PcLc, PcLu, PuLc, PuLu}. Epochs were corrected using the interval [−100, 0] ms before stimulus presentation as the baseline.

Event-related potential (ERP) waveforms ${\overline{x}}_{i,c,s}(t)$ were created for each individual participant, separately for each stimulus type and for each probability condition, by averaging over epochs ${\overline{x}}_{i,c,s}(t)=\frac{1}{M_{i,c,s}}{\displaystyle {\sum}_{m=1}^{M_{i,c,s}}{x}_{i,c,s,m}(t)}$. Because of enormous interindividual variability in ERP waveforms from individual participants, the corresponding stimulus-type-specific and probability-condition-specific waves were separately averaged over participants yielding grand-average waveforms ${x}_{c,s}(t) = \frac{1}{N}{\displaystyle {\sum}_{i=1}^N{\overline{x}}_{i,c,s}(t)}$.

A moving average ${\overset{\sim }{x}}_{c,s}(t)=\frac{1}{9}{\displaystyle {\sum}_{\tau =-4T}^{4T}{x}_{c,s}\left(t+\tau \right)}$ was applied to these grand average ERP waveforms to reduce high-frequency noise to find the time of maximum variance, ${t}_{\sigma_{\max}^2,s}$, between probability conditions.

Following

$$ {t}_{\sigma_{\max}^2,s} = \arg\ { \max}_{t\ \epsilon\ \left[290,\dots, 400\right]\mathrm{ms}}\left\{\mathrm{V}\mathrm{a}\mathrm{r}\left({\tilde{x}}_{\mathrm{PcLc},s}(t),{\tilde{x}}_{\mathrm{PcLu},s}(t),{\tilde{x}}_{\mathrm{PuLc},s}(t),{\tilde{x}}_{\mathrm{PuLu},s}(t)\right)\right\}, $$

ERP latencies with the maximum variance between the four probability conditions were separately identified for frequently (s ₁) and rarely (s ₂) occurring stimuli for t ϵ [290, 400] ms corresponding to a wide latency range for measuring the P300 (Polich, 2007).

In the next step, participant-specific single-trial voltages were registered at the emergent grand-average latencies of maximum variance ${t}_{\sigma_{max}^2,s}$ (Fz: s ₁: 312 ms, s ₂: 356 ms; F4: s ₁: 332 ms, s ₂: 352 ms; Pz: s ₁: 360 ms, s ₂: 364 ms; visual inspection of the variance over time confirmed these points in time as distinctive points of maximum between-condition variability) separately for each probability condition. These single-trial voltages were smoothed in order to reduce high frequency noise following

$$ {\overset{\sim }{x}}_{i,c,s,m}=\frac{1}{9}{\displaystyle {\sum}_{\tau =-4T}^{4T}{x}_{i,c,s,m}\left({t}_{\sigma_{\max}^2,s}+\uptau \right)}, $$

and subsequently averaged over epochs ${\overline{x}}_{i,c,s}=\frac{1}{M_{i,c,s}}{\displaystyle {\sum}_{m=1}^{M_{i,c,s}}{\tilde{x}}_{i,c,s,m}}$. Bayesian model selection was conducted based on these means (see below).

Signal-to-Noise Ratio Estimation

The signal-to-noise ratio (SNR) for ERPs can be defined as the ratio of the ERP power P _ERP to the noise power P _D (beim Graben, 2001; Kolossa, 2016)

$$ \mathrm{S}\mathrm{N}\mathrm{R}=\frac{P_{\mathrm{ERP}}}{P_{\mathrm{D}}}, $$

which can be specified in decibel (dB) according to

$$ \mathrm{S}\mathrm{N}\mathrm{R}\ \left[\mathrm{dB}\right]=10{ \log}_{10}\left(\frac{P_{\mathrm{ERP}}}{P_{\mathrm{D}}}\right). $$

We calculated the condition- and stimulus-specific power estimates, ${\widehat{P}}_{\mathrm{ERP},i,c,s}$ and ${\widehat{P}}_{\mathrm{D},i,c,s}$, respectively, for individual participants based on the single trial ERP estimates ${\tilde{x}}_{i,c,s,m}$ following Möcks, Gasser, and Köhler (1988). These authors suggested that

$$ {\widehat{P}}_{\mathrm{D},i,c,s}=\frac{1}{M_{i,c,s}-1}{\displaystyle \sum_{m=1}^{M_{i,c,s}}}{\left({\overset{\sim }{x}}_{i,c,s,m}-{\overline{x}}_{i,c,s}\right)}^2, $$

and

$$ {\widehat{P}}_{\mathrm{ERP},i,c,s}=\frac{1}{M_{i,c,s}}\left({\displaystyle {\sum}_{m=1}^{M_{i,c,s}}{\left({\tilde{x}}_{i,c,s,m}\right)}^2-{\widehat{P}}_{\mathrm{D},i,c,s}}\right). $$

Under the assumption that noise in any epoch is not correlated with the ERP nor with noise in any other epoch, averaging over M _i,c,s epochs improves the condition- and stimulus-specific SNR _i,c,s of ERP average waveforms for individual participants by $\sqrt{M_{i,c,s}}$, yielding

$$ {\mathrm{SNR}}_{i,c,s}\ \left[\mathrm{dB}\right]=10{ \log}_{10}\left(\frac{M_{i,c,s}\cdot {\widehat{P}}_{\mathrm{ERP},i,c,s}}{{\widehat{P}}_{\mathrm{D},i,c,s}}\right). $$

The mean SNR over individual participants further simply follows

$$ {\mathrm{SNR}}_{c,s}\ \left[\mathrm{dB}\right]=\frac{1}{N}{\displaystyle {\sum}_{i=1}^N{\mathrm{SNR}}_{i,c,s}}\kern0.5em \left[\mathrm{dB}\right]. $$

Table 1 shows the condition- and stimulus-specific mean SNR _c,s  [dB] as well as the standard deviation, minimum and maximum values of individual SNR _i,c,s  [dB] separately at the finally selected electrodes Fz, F4 and Pz (cf. Selection of EEG/ERP Data for Statistical Analysis). This is a theoretical upper bound on the SNR under ideal assumptions, which are not met in real data (beim Graben, 2001). Actual SNRs are expected to be lower. Table 1 presents SNRs, mean, minimum and maximum number of trials per probability condition and stimulus type, M _i,c,s , that went into ERP averaging at the level of individual participants.

Table 1 The mean, standard deviation, minimum and maximum values of signal-to-noise ratios (SNRs) at electrodes Fz, F4, and Pz are presented separately for each stimulus type s and probability condition c. Additionally, the respective means as well as minimum and maximum numbers of trials M_i,c,s are given

Selection of EEG/ERP Data for Statistical Analyses

Late positive potentials of the ERP are decomposable into at least two separable components (Dien, Spencer, & Donchin, 2004; Polich, 2007; Sutton & Ruchkin, 1984). Those ERP components are a parietally distributed positivity (P3b, with maximum peak at electrode Pz) and a frontally distributed positivity (P3a, with maximum peak at more anterior midline electrodes). Three principles for selecting data for statistical analyses governed our initial attempts to reveal statistically significant effects of prior probabilities and likelihoods on P3a and P3b amplitude variations: (1) Analyze EEG data as recorded in single trials, (2) analyze EEG data recorded at midline electrodes, and (3) analyze all eight measured conditions (four probability conditions times two stimulus types). Application of these principles was associated with difficulties to consistently disprove the null hypothesis, which we attributed to the abundantly large random variation in these measurements, mostly because of the notoriously low SNR of single-trial EEG data.

Therefore, the principles for selecting data for statistical analyses were changed, as follows: (1) Analyze averaged ERP data with sufficient SNRs, and (2) analyze ERP data recorded at the electrodes where prior probabilities and likelihoods exerted maximum effects on face value. Application of these principles led to the following decisions: (1) As shown in Table 1, only ERP averages in response to the frequent stimuli s ₁, but not those in response to the rare stimuli s ₂, possessed sufficient SNRs throughout all four probability conditions. The SNR of ERP averages in response the rare stimuli s ₂ in the PcLc probability condition fell below acceptable levels because of insufficient numbers of trials that entered these ERP averages (fewer than 10 trials on average). Based on these data, we decided to restrict the statistical analyses to the s ₁ ERP averages that were measured in the four probability conditions. (2) Fig. 3 (middle panels) shows topographic maps of difference waves (likelihood difference waves and prior probability difference waves). Inspection of Fig. 3 (middle panels) reveals that the likelihood manipulation exerted maximum effects on face value at electrode Pz. The prior probability manipulation exerted maximum effects on face value at electrode F4 in close proximity to electrode Fz. Therefore, in addition to electrodes Fz and Pz, electrode F4 was selected for statistical analyses.

Fig. 3

(Left panels). Grand-average ERP wave shapes at electrodes F4 (upper panel) and Pz (lower panel) in response to frequent stimuli s ₁ in the four probability conditions (all Pc waves in red lines; all Pu waves in blue lines; all Lc waves in solid lines; all Lu waves in dashed lines). Both diagrams show the latency range for measuring the P300 (i.e., from 290 to 400 ms; in light gray) as well as the latencies of maximum variance as defined in the text (i.e., F4: 332 ms; Pz: 360 ms). (Middle panels). Topographic maps of difference waves (on the left: prior probability difference waves, i.e., Pc–Pu; on the right: likelihood difference waves, i.e., Lu–Lc). The prior probability manipulation exerted maximum effects at electrode F4 in close proximity to electrode Fz around the latency of maximum variance (i.e., 316–348 ms). The likelihood manipulation exerted maximum effects at electrode Pz around the latency of maximum variance (i.e., 344–376 ms). (Right panels). ERP images at F4 and Pz electrodes in response to frequent stimuli s ₁ from the four probability conditions. ERP images at F4 (upper panel) show color-coded single-trial EEG data separately for certain (Pc) and uncertain (Pu) prior probability conditions, sorted according to the response times on these trials (from fastest to slowest). ERP images at Pz (lower panel) show color-coded single-trial EEG data separately for uncertain (Lu) and certain (Lc) likelihood conditions, sorted according to the response times on these trials (from fastest to slowest). (Color figure online)

Derivation of Eight Hypotheses of Interest

We used information-theoretic measures (see Fig. 4a; see also MacKay, 2003) such as surprise (Kolossa et al., 2013), entropy (Kopp & Lange, 2013), and redundancy (Barlow, 2001) as response functions for modeling the measured ERP responses (Friston, 2005). Surprise (I) equals a logarithmic measure of the probability p(x) that a binary random variable X takes on the value x. Therefore, I(x) = − log ₂ p(x); I(x) ∈ [0, + ∞] (with minimum surprise (I(x) = 0 at p(x) = 1.0 and maximum surprise (I(x) → + ∞ at p(x) = .0). Entropy (H) equals the summation of surprise values over all the possible values x that X can take multiplied with their respective probability. For a binary random variable X it is H(X) = − ∑ ² _{k = 1} p(x _k )log₂(p(x _k )); H(X) ∈ [0, 1] (with minimum entropy (H(X) = 0) at p(x _k ) = .0 and at p(x _k ) = 1.0 and maximum entropy (H(X) = 1) at p(x _k ) = .5). Redundancy (R) is sort of a reciprocal value to entropy, and it equals R(X) = 1 − H(X); R(X) ∈ [0, 1] (with minimum redundancy (R(X) = 0) at p(x _k ) = .5 and maximum redundancy (R(X) = 1 at p(x _k )=.0 and at p(x _k ) = 1.0).

Fig. 4

(a). Surprise (I, red curve), entropy (H, blue curve) and redundancy (R, green curve) over the probability P of a binary random variable. (b). Ordinal inequality predictions of P300 amplitude variations for the frequent stimulus s ₁ in the four probability conditions (PcLc, PcLu, PuLc, PuLu) as a function of surprise (I, red curve), entropy (H, blue curve) and redundancy (R, green curve) with P = unexpectedness of s ₁ at the abscissa. (c). Ordinal inequality predictions of P300 amplitude variations for the frequent stimulus s ₁ in the four probability conditions as a function of surprise (I, red curve), entropy (H, blue curve) and redundancy (R, green curve) with P = prior probability at the abscissa. (d). Ordinal inequality predictions of P300 amplitude variations for the frequent stimulus s ₁ in the four probability conditions as a function of surprise (I, red curve), entropy (H, blue curve) and redundancy (R, green curve) with P = likelihood at the abscissa. (Color figure online)

Informative hypotheses pose specific (in-)equality constraints on the measured cortical responses that we obtained from the frequent stimulus s ₁ in the four probability conditions (PcLc, PcLu, PuLc, PuLu). We use the following notation here: Certain condition (.9 and .1 probability distribution), uncertain condition (.7 and .3 probability distribution), s _cc = s ₁ in the certain prior and certain likelihood condition; s _cu = s ₁ in the certain prior and uncertain likelihood condition; s _uc = s ₁ in the uncertain prior and certain likelihood condition; s _uu = s ₁ in the uncertain prior and uncertain likelihood condition. Equivalently, μ _cc , μ _cu , μ _uc , and μ _uu correspond to the predicted condition-specific mean ERP voltages. There are three groups of conceivable informative hypotheses.

The first group of hypotheses subsumes non-Bayesian hypotheses. We refer to this group of hypotheses as non-Bayesian hypotheses because their (in-)equality constraints are based on the unexpectedness of the evidence or surprise—that is, the marginal probability P(s ₁ ) in Fig. 1. The unexpectedness of s ₁ draws varies between .82 and .58 on the four experimental conditions, with P(s _cc) = .82, P(s _cu) = .66, P(s _uc) = .66, P(s _uu) = .58 (see Fig. 2a). Application of the three information-theoretic transformations (I, H, R; see Fig. 4b) to these probabilities yields two distinct hypotheses, namely:

• H ₁ : μ _uu  > {μ _cu  = μ _uc } > μ _cc

• [(I;H) hypotheses: I _.58 > {I _.66 = I _.66} > I _.82; H _.58 > {H _.66 = H _.66} > H _.82]

• H ₂ : μ _uu  < {μ _cu  = μ _uc } < μ _cc

• [(R) hypothesis: R _.58 < {R _.66 = R _.66} < R _.82].

Surprise- and entropy-transformed non-Bayesian hypotheses are associated with indistinguishable (in-)equality constraints, but their predictions can be differentiated from those of the redundancy-transformed non-Bayesian hypothesis.

The second group of hypotheses subsumes two prior probability hypotheses. Recall that the condition-specific prior probabilities amounted to P(s _cc) = .90, P(s _cu) = .90, P(s _uc) = .70, P(s _uu) = .70. Application of the three information-theoretic transformations (I, H, R; see Fig. 4c) to these prior probabilities yields two distinct hypotheses, namely:

• H ₃ : {μ _uu  = μ _uc } > {μ _cu  = μ _cc }

• [(I;H) hypotheses: {I _.7 = I _.7} > {I _.9 = I _.9} ; {H _.7 = H _.7} > {H _.9 = H _.9}]

• H ₄ : {μ _uu  = μ _uc } < {μ _cu = μ _cc }

• [(R) hypothesis: {R _.7 = R _.7} < {R _.9 = R _.9}].

Surprise- and entropy-transformed prior probability hypotheses are associated with indistinguishable (in-)equality constraints, but their predictions can be differentiated from those of the redundancy-transformed prior probability hypothesis.

The third group of hypotheses subsumes two likelihood hypotheses. Recall that the condition-specific likelihoods amounted to P(s _cc) = .90, P(s _cu) = .70, P(s _uc) = .90, P(s _uu) = .70. Application of the three information-theoretic transformations (I, H, R; see Fig. 4d) of the likelihoods yields two hypotheses, namely:

• H ₅ : {μ _uu  = μ _cu } > {μ _uc  = μ _cc }

• [(I;H) hypotheses: {I _.7 = I _.7} > {I _.9 = I _.9}; {H _.7 = H _.7} > {H _.9 = H _.9}]

• H ₆ : {μ _uu  = μ _cu } < {μ _uc  = μ _cc }

• [(R) hypothesis: {R _.7 = R _.7} < {R _.9 = R _.9}]

Surprise- and entropy-transformed likelihood hypotheses are associated with indistinguishable (in-)equality constraints, but their predictions can be differentiated from those of the redundancy-transformed likelihood hypothesis.

The null hypothesis equals the traditional equality constraint, i.e.,

• H ₀ : {μ _uu  = μ _cu  = μ _uc  = μ _cc }

In contrast, the unconstrained hypothesis does not impose any constraints, i.e.,

• H _u : {μ _uu  , μ _cu  , μ _uc  , μ _cc }

Bayesian Evaluation of the Eight Hypotheses of Interest

For each of the Fz, F4, and Pz electrodes, averaged ERP voltage measurements are obtained for each of 16 participants in the four probability conditions (see section Selection of EEG/ERP Data for Further Analyses). Averaged means that within each condition, single-trial measurements for each participant are averaged for the frequent stimulus (s ₁). This results for each electrode in a data matrix consisting of 16 rows (one for each participant) containing the averaged ERP voltage measurements ${\overline{x}}_{i,c}$ in each of four conditions.

Eight informative hypotheses (Hoijtink, 2012, pp. 5–8, 23) with respect to the structure in the means have been formulated. These hypotheses will be evaluated using Bayes factors factor (BF; Hoijtink, 2012, pp. 51–52) that can be transformed into posterior model probabilities (PMPs; Hoijtink, 2012, pp. 52–53). This is done using five steps (see Appendix A for a technical elaboration of the description given below):

• Step 1. Model each data matrix with a specific instance of the multivariate normal linear model (Hoijtink, 2012, pp. 22–23), namely, the repeated-measures model (Hoijtink, 2012, pp. 29–32). The main parameters of the repeated measures model are μ _cc , μ _cu , μ _uc , and μ _uu , that is, the mean of the 16 measurements in each condition and ∑ the covariance matrix of the voltage measurements in each of the four conditions (see Appendix A, Section 1).

• Step 2. Specify the unconstrained prior distribution (Hoijtink, 2012, pp. 46–48) of the parameters under H _u , that is, a low informative prior distribution for the means and a noninformative prior distribution for the covariance matrix (see Appendix A, Section 2).

• Step 3. Combine the density of the data (Hoijtink, 2012, pp. 44–45) of the repeated-measures model with the prior distribution under H _u to obtain the unconstrained posterior distribution (Hoijtink, 2012, pp. 49–51) of the parameters under H _u (see Appendix A, Section 3).

• Step 4. Use the result from Hoijtink (2012, pp. 51–52) to compute BF _mu  = f _m /c _m for m = 0, …, 6, that is, the Bayes factor quantifying the relative support in the data for H _m and H _u , where f _m denotes the fit of H _m (the proportion of the posterior distribution in agreement with the constraints in H _m ) and c _m denotes the complexity of H _m (the proportion of the prior distribution in agreement with the constraints in H _m ). A Bayes factor of 5 indicates that after observing the data the support for H _m is 5 times higher than the support for H _u if the fit and complexity of both hypotheses are accounted for (see Appendix A, Section 4).

• Step 5. To facilitate the interpretation of the seven resulting Bayes factors for H ₀ to H ₆ , they can be transformed into posterior model probabilities PMP _m (Hoijtink, 2012, pp. 52–53) for each of the 7 constrained hypotheses and H _u . Assuming that a priori each hypothesis is equally likely, PMP _m   = BF _mu / (1+∑ _m‘ BF _m’u ) for m’ = 0, …, 6, and PMP _u = 1 / (1+∑ _m’ BF _m’u ) for H _u . These posterior model probabilities are numbers on a scale from 0 to 1 that quantify the support in the data for each of the hypotheses under consideration (see Appendix A, Section 5).

BFs and PMPs properly weighting the fit and complexity of each hypothesis under consideration can be computed using the software package BIEMS (Mulder, Hoijtink, & de Leeuw, 2012). The results are displayed in Table 2. As can be seen in the last two columns, for example, both H ₁ (with a Bayes factor of 1.63) and H ₅ (with a Bayes factor of 10.31) receive more support than H _u . This implies that the constraints used to formulate both hypotheses are supported by the data. By transforming the Bayes factors to posterior model probabilities, it can be seen that the support for H ₅ (with a posterior model probability of .71) is much larger than for H ₁ (with a posterior model probability of .11). The next section will provide an elaborate interpretation of the results in Table 2.

Table 2 Bayes factors (BFs) and posterior model probabilities (PMPs) for the eight hypotheses tested at electrodes Fz, F4, and Pz

Results

Descriptive ERP Results

Figure 3 (left panels) depicts grand-average ERP wave shapes at F4 and Pz electrodes in response to frequent stimuli s ₁ in the four probability conditions (all Pc waves in red lines; all Pu waves in blue lines; all Lc waves in solid lines; all Lu waves in dashed lines). Both diagrams show the latency range for measuring the P300 (i.e., from 290 to 400 ms; in light gray) as well as the latencies of maximum variance as defined above (i.e., F4: 332 ms; Pz: 360 ms). Inspection of the ERP wave shapes at electrode F4 reveals that the ERP waves in response to s ₁ stimuli in the certain prior probability condition (Pc) were more positive than the ERP waves in response to s ₁ stimuli in the uncertain prior probability condition (Pu) at the latency of maximum variance, identifiable as a difference between red and blue ERP wave shapes. Inspection of the ERP wave shapes at electrode Pz reveals that the ERP waves in response to s ₁ stimuli in the uncertain likelihood condition (Lu) were more positive than the ERP waves in response to s ₁ stimuli in the certain likelihood condition (Lc) at the latency of maximum variance, identifiable as a difference between dashed and solid ERP wave shapes.

Figure 3 (middle panels) shows topographic maps of difference waves (likelihood difference waves, i.e., Lu−Lc, and prior probability difference waves, i.e., Pc−Pu). Inspection of the maps reveals that the likelihood manipulation exerted maximum effects at electrode Pz around the latency of maximum variance (i.e., from 344 to 376 ms). The prior probability manipulation exerted maximum effects at electrode F4 in close proximity to electrode Fz around the latency of maximum variance (i.e., from 316 to 348 ms).

Figure 3 (right panels) depicts ERP images at F4 and Pz electrodes in response to the frequent stimulus s ₁ from the four probability conditions. The ERP images at F4 (upper panel) show color-coded single-trial EEG data separately for certain (Pc) and uncertain (Pu) prior probability conditions, sorted according to the response times on these trials (from fastest to slowest). It can be seen that there is a trend toward more positive single-trial EEG deflections in response to s ₁ stimuli in certain as compared to uncertain prior probability conditions at the latency of maximum variance, thus ruling out the possibility that the apparent prior probability effect that was observed in grand-average ERP wave shapes (see upper left panel) might simply be related to boosted latency jitter in the uncertain prior probability condition in comparison to the certain prior probability condition. The ERP images at Pz (lower panel) show color-coded single-trial EEG data separately for uncertain (Lu) and certain (Lc) likelihood conditions, sorted according to the response times on these trials (from fastest to slowest). It can be seen that there is a trend toward more positive single-trial EEG deflections in response to s ₁ stimuli in uncertain as compared to certain likelihood conditions at the latency of maximum variance, thus ruling out the possibility that the apparent likelihood effect that was observed in grand-average ERP wave shapes (see lower left panel) might simply be related to boosted latency jitter in the certain likelihood condition in comparison to the uncertain likelihood condition.

Bayesian Hypothesis Evaluation

Table 2 displays BFs and PMPs for each of the eight competing hypotheses H ₁ through H ₆ as well as H ₀ and H _u separately at each of the three electrodes that were examined (i.e., Fz, F4, Pz). Guidelines for interpreting the magnitudes of BFs can be found in Kass and Raftery (1995). BF values between 1 and 3 denote a degree of support that is barely worth mentioning. BF values between 3 and 10 denote substantial support for the hypothesis under investigation (H _i ) compared to a reference hypothesis such as for example H _u . BF values between 10 and 100 denote strong evidence in favor of H _i compared to H _u , whereas BF values larger than 100 denote decisive evidence. BF values smaller than one denote marginal to decisive evidence against H _i . As can be seen from inspection of Table 2, the non-Bayesian hypotheses H ₁ and H ₂ did generally not receive support from the data (.03 ≤ BFs ≤ 1.63, below .01 ≤ PMPs ≤ .11).

The results at electrode Fz remain inconclusive. The prior probability (redundancy) hypothesis H ₄ receives the most support from the data, with BF ₄  = 1.55 and ₄  = .26. One should be reluctant to conclude from these data that ERP amplitude variations at Fz are associated with prior probabilities. Recall that BF < 3 denotes a degree of support for any H _i that is barely worth mentioning. The support for H ₄ is just .26/.12 = 2.2 times higher than the support for H ₀ , and the support for H ₄ is just .26/.17 = 1.53 times higher than the support for H _u . The support for the best likelihood (surprise, entropy) hypothesis H ₅ , was virtually indistinguishable from that for hypothesis H ₄ , with BF ₅  = 1.52 and PMP ₅  = .25.

The results at electrode F4 lend substantial support for prior probability (redundancy) hypothesis H ₄ , with BF ₄  = 5.01 and PMP ₄  = .68. Recall that 3 < BF < 10 denotes a substantial degree of support for any H _i . The support for H ₄ is .68/.04 = 17 times higher than the support for H ₀ , and the support for H ₄ is .68/.14 = 4.86 times higher than the support for H _u . The support for the prior probability (redundancy) hypothesis H ₄ was 11.3 times higher than the support for the best likelihood (surprise, entropy) hypothesis H ₅ , with BF ₅  = .46 and PMP ₅  = .06. One can conclude from these data that ERP amplitude variations at F4 are associated with prior probabilities.

The results at electrode Pz provide strong support for likelihood (surprise, entropy) hypothesis H ₅ , with BF ₅  = 10.31 and PMP ₅  = .71. Recall that BF > 10 denotes a strong degree of support for any H _i . The support for H ₅ is .71/.05 = 14.2 times higher than the support for H ₀ , and the support for H ₅ is .71/.07 = 10.14 times higher than the support for H _u . The support for the likelihood (surprise, entropy) hypothesis H ₅ was 11.3 times higher than the support for the best prior probability (surprise, entropy) hypothesis H ₃ , with BF ₃  = .40 and PMP ₃  = .03. One can conclude from these data that ERP amplitude variations at Pz are associated with likelihoods.

Discussion

Our data show that the manipulation of prior probabilities and likelihoods is associated with separately modifiable and distinct ERP responses, thereby demonstrating that the antecedents of Bayesian inference are coded by the brain. We found that the manipulation of prior probabilities was associated with P3a amplitude variations, whereas the manipulation of likelihoods was related to P3b amplitude variations. P3a amplitudes were sensitive to the degree of prior certainty such that more certain prior probabilities were related to larger frontally distributed P3a waves, irrespective of the level of certainty in the likelihoods. P3b amplitudes were sensitive to the degree of likelihood certainty such that less certain likelihoods were associated with larger parietally distributed P3b waves, irrespective of the level of prior certainty.

The Current Study in the Context of the Existing Literature

Two Bayesian parameters were instructed, that is, prior probabilities and likelihoods (FitzGerald et al., 2010; Hertwig et al., 2004; Hertwig & Erev, 2009). Therefore, our findings are novel because there are no previous studies that demonstrate ERP correlates of instructed Bayesian parameters. This may help to understand why our P3b negative results with regard to the unexpectedness of the evidence seem to be in disagreement with the existing P3b literature (see Kolossa et al., 2013; Kolossa et al., 2015). Most P3b studies show that P3b amplitude variations are sensitive to the unexpectedness of the evidence or surprise, but none of these studies has examined instructed unexpectedness or surprise against instructed likelihoods.

The available fMRI research suggests fronto-striatal representations of prior parameters and predominantly parietal representations of likelihood parameters. These broad anatomical distinctions are in accordance with our findings if one assumes that frontal sources contribute to the generation of scalp-recorded P3a waves and that parietal sources contribute to the generation of scalp-recorded P3b waves (Polich, 2007). The P3a finding needs further specification because previous ERP studies revealed an association between Bayesian updating and P3a amplitudes rather than between prior probabilities and P3a amplitudes (Bennett et al., 2015; Kolossa et al., 2015). The P3a waves in this study were more anteriorly distributed than the P3a waves in the previous studies, but this issue clearly needs to be further examined by future studies. It also remains open why higher prior certainty was associated with larger frontal P3a amplitudes rather than with smaller P3a amplitudes. The direction of the effect of likelihood uncertainty on P3b amplitude variations is congruent with the results that were obtained from fMRI studies because higher likelihood uncertainty was repeatedly associated with larger parietal activation (Furl & Averbeck, 2011; Stern et al., 2010).

The P3b Component in the Urn-Ball Task

Manipulation of the likelihoods resulted in P3b amplitude variations at electrode Pz. Specifically, s ₁ stimuli in uncertain likelihood conditions evoked more prominent P3b responses compared to s ₁ stimuli in certain likelihood conditions. This finding is in accord with previous research on the P3b ERP component, which revealed that P3b amplitude variations are related to the uncertainty or surprise of its eliciting events (Donchin, 1981; Kolossa et al., 2013; Sutton, Braren, Zubin, & John, 1965).

Likelihoods express conditional probabilities, that is, P(s|h ₁) and P(s|h ₂) in the current urn-ball task. Applied to stimuli s ₁, likelihoods amounted to P(s ₁|h ₁) = .7 and P(s ₁|h ₂) = .3 in uncertain likelihood conditions, and they amounted to P(s ₁|h ₁) = .9 and P(s ₁|h ₂) = .1 in certain likelihood conditions. The urn-ball task can be understood as a binary classification test, and sensitivity [here, P(s ₁|h ₁) = .7 vs. P(s ₁|h ₁) = .9] and specificity [here, P(s ₁|h ₂) = .3 vs. P(s ₁|h ₂) = .1] are well-known statistical measures of the performance of such tests (e.g., Green & Swets, 1966). Low sensitivity was coupled with low specificity in uncertain likelihood conditions, thereby minimizing the information that can be gained from an observed s ₁ event in this condition. High sensitivity was coupled with high specificity in certain likelihood conditions, thereby maximizing the information that can be gained from an observed s ₁ event in this condition. P3b amplitude variations in the urn-ball task reflect variations in sensitivity and specificity of an observed s ₁ event because we measured more prominent P3b responses under relatively low levels of sensitivity and specificity in comparison to higher levels of these probabilistic quantities. It is easy to see how sensitivity and specificity can be combined to compute the logarithm of the likelihood ratio (logLR), that is, ln(P(s|h ₁)/P(s|h ₂)), that was formalized in Equation 3.

Studies of perceptual decisions in primates (Kira, Yang, & Shadlen, 2015; Yang & Shadlen, 2007) and in rodents (Hanks et al., 2015) showed that the firing rates of neurons in the parietal cortex reflected the gradual accumulation of logLR when different logLRs were assigned to various sensory cues. Although the underlying neural mechanisms are less understood, a similar framework explains a variety of P3b-like phenomena that are related to perceptual decisions in humans (Kelly & O’Connell, 2013; O’Connell, Dockree, & Kelly, 2012). Our P3b findings can thus be viewed as reflecting activities of a neural module, putatively located in the parietal cortex, which traces the accumulation of sensory evidence in terms of logLR. Our P3b results also imply that this posterior probabilistic module does not seem to be sensitive to prior probabilities, and this question was never addressed before.

The P3a Component in the Urn-Ball Task

Manipulation of prior probabilities resulted in P3a amplitude variations at electrode F4. Specifically, s ₁ stimuli in certain prior probability conditions evoked more prominent P3a responses compared to s ₁ stimuli in uncertain prior probability conditions. There is not much previous knowledge about the relationships between P3a amplitude variations and probabilistic quantities, such as uncertainty and surprise. Two earlier studies from our group suggested that P3a amplitude variations are related to the resolution of uncertainty (Kopp & Lange, 2013; Lange, Seer, Finke, Dengler, & Kopp, 2015).

Prior probabilities amounted to P(h ₁) = .7 and P(h ₂) = .3 in uncertain prior probability conditions, and they amounted to P(h ₁) = .9 and P(h ₂) = .1 in certain prior probability conditions. P3a amplitude variations in the urn-ball task reflected these variations in prior probabilities at the point in time when the initial stimuli s ₁ in the samples of balls were processed. This finding establishes a connection between prior probabilities and the brain activations that we measured. Equation 3 tells us that the logarithm of the prior odds, that is, ln(P(h ₁)/P(h ₂)), is the second summand that contributes to Bayesian inference. Given that P3b responses code logLR (see above), the discovery that P3a amplitude variations in the urn-ball task reflect variations in prior probabilities provides the missing piece of evidence that the human brain codes both summands that are required for Bayesian inference.

Although one cannot draw strong conclusions from 20-channel electroencephalographic data about the underlying neural mechanisms, the present P3a findings do justify some propositions. Our P3a findings can be viewed as reflecting neural activities of a neural module, which traces prior probabilities (anterior probabilistic module), putatively in terms of log prior odds. The anterior probabilistic module is dissociable from the posterior probabilistic module, both in terms of the cortical areas that are involved and in terms of their functions: While the posterior probabilistic module is sensitive to logLR, but insensitive to log prior odds, the anterior probabilistic module is sensitive to log prior odds, but insensitive to logLR.

Prefrontal regions do contribute to the generation of scalp-recorded P3a wave shapes (Polich, 2007), suggesting that the anterior probabilistic module might be located in the prefrontal cortex. It is not possible to draw firm conclusions about the underlying neural mechanisms from the fact that the manipulation of prior probabilities exerted maximum effects at electrode F4 (i.e., right-lateralized). There exist some hints that the right cerebral hemisphere might be dominant for statistical processing in general (Anderson, 2008; Danckert, Stöttinger, Quehl, & Anderson, 2012; Roser, Fiser, Aslin, & Gazzaniga, 2011; Shaqiri & Anderson, 2013).

Implications and Suggestions

We found evidence for two dissociable probabilistic modules in the human brain that code instructed prior probabilities and likelihoods. Our ERP data demonstrate that all information necessary for Bayesian inference is coded by the human brain (i.e., that the antecedent conditions for Bayesian inference are met). The results suggest that the human brain computes Bayesian updating on the basis of these probabilistic quantities. A demonstration that the human brain computes Bayesian updating requires tracing the dynamic evolution of Bayesian probabilities and brain activations over the complete sequences of ball samples (Kolossa et al., 2015).

Another implication of our results is that the brain uses the information that was conveyed by the tableaus (i.e., instruction-based knowledge). Neither likelihoods nor prior probabilities could be learned through statistical learning (i.e., through accumulation of experience across episodes of sampling within probability conditions). In that regard it is worth mentioning that participants never received feedback as to the correctness of their urn choices. Hence, statistical learning yields an estimate of the expected value of relative frequencies of ball colors (plus sampling error), whereas neither likelihoods nor prior probabilities are observable quantities. This aspect of our results suggests that the viewing of the tableaus led to the formation of probabilistic models of ball sampling, and that both probabilistic modules form part of these probabilistic models. The measured brain activations may disclose neural correlates of a model-based probabilistic system for guiding behavior at choice points (Dolan & Dayan, 2013; Doll, Duncan, Simon, Shohamy, & Daw, 2015; O’Doherty, Lee, & McNamee, 2015; Tolman, 1948).

Limitations and Future Directions

The SNR is an important, yet often neglected, factor in ERP research. As detailed in the Signal-to-Noise Ratio Estimation paragraph of the Method section, the current urn-ball task was associated with insufficient SNRs of some average ERPs because of insufficient numbers of trials for averaging (see Table 1). Insufficient SNRs led to the exclusion of all ERPs that were recorded in response to rarely occurring stimuli s ₂. Future urn-ball studies should take the SNR problem into account. In that regard, it might be of interest that Paukkunen, Leminen, and Sepponen (2010) suggested an adaptive method that is based on monitoring the SNR online on a trial-by-trial basis. Their method allows continuing ERP recordings until the SNR quality of an accumulating ERP average meets some predefined criterion, such that the sufficiency of the number of trials for ERP averaging can be better guaranteed.

The stability and validity of the results need to be examined through appropriate replication and generalization studies. Decisive support that the brain activations that we measured code prior probabilities and likelihoods was not achieved. The results at electrode F4 lent substantial support for a prior probability hypothesis, and the results at electrode Pz provided strong support for a likelihood hypothesis. Replication in an independent, preferentially larger sample is desirable. An examination of the generalization across different probability distributions and task domains (urn-ball problems vs. real-world-like problems) is warranted.

Future studies should aim to integrate these and related findings with the broader theoretical concepts that have been developed for an understanding of P300 amplitude variation. Polich (2007) attributed P3a amplitude variations to attentional mechanisms in the service of evaluating incoming stimuli, and subsequent studies should clarify how Bayesian and other schemes of information processing could be brought together to provide novel theoretical accounts of P3a amplitude variation. P3b amplitude variation is traditionally understood as being related to memory storage in the service of context updating (Donchin & Coles, 1988; Polich, 2007). It remains to be delineated how our findings can be reconciled with this more traditional view. P300 amplitude variation is known to be related to many other variables, such as the difficulty of a task (Kopp, Kizilirmak, Liebscher, Runge, & Wessel, 2010) or the specific temporal regimes on a task (Gonsalvez, Barry, Rushby, & Polich, 2007). A comprehensive theory of P300 amplitude variation still needs to be developed (see Johnson, 1986; Polich, 2007, for corresponding attempts).

Conclusions

Our approach allowed us to assess relationships between antecedents of probabilistic inference and electrophysiological measures. Our results open new windows onto the neural correlates of probabilistic inference in humans by isolating distinct electrophysiological signatures of how the human brain processes instructed prior probabilities and likelihoods. These signals could be measured with a minimum of signal processing and with high temporal resolution. The influence of instructed prior probabilities and likelihoods is dissociable and may be mapped onto the classical distinction between anteriorly and posteriorly distributed scalp-recorded P300 waves. The picture that emerges is one of a Bayesian brain as revealed by the sensitivity of anteriorly distributed P3a waves for variations in prior probabilities, as well as by the sensitivity of posteriorly distributed P3b waves for variations in likelihoods.