Introduction

Dopamine has been implicated in motivated learning, especially in incremental learning from reinforcement. Electrophysiolgical recordings in nonhuman primates have established that responses of midbrain dopamine neurons reflect a reward prediction error (PE), a signal representing the difference between a received and an expected reward (Schultz, Dayan, & Montague, 1997; Schultz, 1998, 2001, 2006). PEs signaled by dopamine neurons are thought to provide an incremental learning signal that guides subsequent value-based decisions and actions. Human neuroimaging research has linked reward anticipation and PEs to changes in BOLD activity in the ventral striatum (Delgado, Li, Schiller, & Phelps, 2008; O’Doherty, Dayan, Friston, Critchley, & Dolan, 2003; Rutledge, Dean, Caplin, & Glimcher, 2010), and pharmacological research has demonstrated that striatal PE responses are modulated by dopaminergic drugs (Menon et al., 2007; Pessiglione, Seymour, Flandin, Dolan, & Frith, 2006). However, little is known about how dopamine antagonists influence dynamic learning from feedback and reward in patient populations who take these drugs.

Many psychiatric and neurological illnesses have been associated with abnormalities in dopamine neurotransmission and with deficits in reinforcement learning (Frank, Seeberger, & O’Reilly, 2004; Maia & Frank, 2011). Schizophrenia (SZ) is a prime example, since it involves excessive amounts of striatal dopamine and altered dopamine receptor profiles (Abi-Dargham, 2003; Abi-Dargham & Moore, 2003; da Silva Alves, Figee, van Amelsvoort, Veltman, & de Haan, 2008; Guillin, Abi-Dargham, & Laruelle, 2007; Nikolaus, Antke, & Müller, 2009). Accordingly, dopamine receptors are the primary target of antipsychotic treatment (Kapur & Mamo, 2003; Seeman, 1987, 2010). SZ has also been linked to impairments in reward-related processes, including affective responses and feedback-based reward learning (Dowd & Barch, 2012; Gold et al., 2012; Gold, Waltz, Prentice, Morris, & Heerey, 2008; Murray et al., 2008a, b; Ursu et al., 2011; Waltz, Frank, Robinson, & Gold, 2007; Waltz, Frank, Wiecki, & Gold, 2011). Given the demonstrated impact of dopamine dysfunction in SZ and the strong convergence between dopamine and reinforcement processing in the brain, reinforcement learning tasks provide a particularly promising means of studying motivational deficits in SZ and the impact of pharmacological treatment (Gold, Hahn, Strauss, & Waltz, 2009; Maia & Frank, 2011; Ziauddeen & Murray, 2010).

There has been a recent surge in studies investigating reinforcement learning deficits in SZ. There is evidence to suggest that abnormalities in reinforcement and reversal learning emerge in patients with first-episode psychosis (Murray et al., 2008a, b). Prior work has demonstrated that patients with SZ show impaired learning from gains, yet they exhibit intact learning from losses (Gold et al., 2012; Reinen et al., 2014; Waltz et al., 2007). Results from imaging studies have suggested that SZ patients show intact BOLD signal in the ventral striatum during the coding of negative PE but that this activity is attenuated for responses to reward receipt (Waltz et al., 2010). In addition, there is evidence that SZ patients display learning patterns suggestive of stimulus–response associations, whereas healthy controls typically exhibit learning that reflects updating of expected value, which incorporates outcomes from past trials to inform their subsequent choice decisions (Gold et al., 2012). Notably, this effect is related to negative symptom severity, such that patients with higher levels of negative symptoms exhibit altered strategies during reinforcement learning, while patients who score low on negative symptom scales more closely resemble controls. Moreover, these effects are attributed to a deficit in value expectation, which may be mediated by top-down influence of the orbitofrontal cortex (Gold et al., 2012).

Prior research on the links between dopamine, reward processing, and reinforcement learning has provided a helpful framework for elucidating the cognitive and motivational deficits in SZ (Barch & Dowd, 2010; Gold et al., 2009; Ziauddeen & Murray, 2010). However, one primary obstacle in this line of work is that many patients with SZ are treated with antipsychotic medications, which act on dopamine receptors. Yet little is known about the exact ways in which pharmacological dopamine blockade impacts reinforcement learning and the corresponding neural bases in patient populations. A better understanding of the interaction between antipsychotic medication and reinforcement learning may lead to progress in elucidating the mechanisms contributing to motivational processes in patients with SZ, allowing for a closer examination of the implications of treatment. One possibility is that pharmacological dopamine blockade may interfere with PE coding during learning, which may impact value representation and decision making at the behavioral and neural levels.

Until now, relatively few studies have directly investigated the effects of antipsychotics on the dynamic process of reinforcement learning in SZ. There is some evidence suggesting that antipsychotic medication can influence cognitive processes, including nondeclarative memory and reward-related anticipation in patients (Beninger et al., 2003; Juckel et al., 2006; Kirsch, Ronshausen, Mier, & Gallhofer, 2007; Schlagenhauf et al., 2008); however, less is known about how drug treatment impacts the behavioral and neural bases of reward and punishment learning.

To address this, we completed an exploratory study to investigate whether antipsychotic medication impacts behavioral and neural signatures of reinforcement learning in patients with SZ. We tested outpatients taking atypical antipsychotic medication while undergoing fMRI to determine whether medication-related differences in BOLD signal could be detected in the striatum during learning. Treatment was uncontrolled in that patients were receiving antipsychotic medications in accordance with their diagnostic and therapeutic needs. Nonetheless, these patients provided an opportunity to examine how learning -related signals in the brain vary as a function of medication status. We used a reinforcement learning paradigm to assess the use of trial-by-trial feedback to guide learning of probabilistic associations between cues and reward outcomes. The task was completed in separate reward and punishment conditions to examine whether there was a difference in learning when approaching monetary gain or avoiding monetary loss.

Specifically, we sought to explore whether the dose of medication might modulate sensitivity to reward- and punishment-related feedback and PE during learning. We hypothesized that higher doses of antipsychotic medication would impair anticipation of rewards and approach behaviors and would bias learning from negative reinforcement, since increased D2 blockade in animals and healthy controls has been associated with impaired learning from rewards and improved learning from punishments (Amtage & Schmidt, 2003; Centonze et al., 2004; Waltz et al., 2007; Wiecki, Riedinger, von Ameln-Mayerhofer, Schmidt, & Frank, 2009).

Method

Patients

Participants consisted of 28 outpatients with schizophrenia (see Table 1). All patients were recruited through the Lieber Center for Schizophrenia Research and Treatment at the New York State Psychiatric Institute (NYSPI). Patients met DSM–IV criteria for schizophrenia or schizoaffective disorder using the Structured Clinical Interview for DSM–IV and medical records (First, Spitzer, Gibbon, & Williams, 2002). As part of a screening procedure, clinical ratings were performed, including the Simpson Angus Scale (SAS), the Scale for the Assessment of Positive Symptoms (SAPS), the Scale for the Assessment of Negative Symptoms (SANS), and the Calgary Depression Scale (CDS) (Addington, Addington, Maticka-Tyndale, & Joyce, 1992; Andreasen & Olsen, 1982). Eligible patients were required to have CDS scores less than 10 and SAS ratings less than 6.

Table 1 Patient demographics and clinical ratings
Full size table

All patients tested had been taking one atypical antipsychotic (excluding clozapine) for at least 2 months, with stable doses for at least 1 month before the day of testing. Medications taken included aripiprazole, olanzapine, lurasidone, ziprasidone, and risperidone. Some patients also took antidepressants, mood stabilizers, and anticholinergics at the time of testing. All patients were English speaking, had no history of neurological illness or severe head trauma, and had no metal implants. Most participants were right-handed, but 1 participant was left-handed. All participants provided written informed consent under the research protocol that was approved by the Institutional Review Board of NYSPI and Columbia University. Participants received a total of $250 for study participation and won additional earnings based on task performance.

Two participants were excluded from analyses due to self-reports of not following instructions during task completion when asked to report on their experience during the debriefing interview and evidence from their performance that they did not learn during the task. Additionally, 4 patients were excluded from fMRI analyses due to technical problems during fMRI data acquisition and/or excessive motion. Thus, the final sample was 26 for behavioral analyses and 22 for fMRI analyses.

Medication equivalence conversion

Antipsychotic medication doses were converted to chlorpromazine (CPZ) equivalents to normalize antipsychotic dosing across participants (Woods, 2003; see Table 2 for the conversion table used).

Table 2 Chlorpromazine (CPZ) dose equivalency table
Full size table

Procedures

Screening and practice session

All participants underwent a screening session, which included drug screening and clinical assessment. Patients who met eligibility criteria came back for a practice session on a separate day. During the practice session, participants completed questionnaires, working memory tasks (operation span and n-back), and a practice version of the reinforcement-learning task.

The practice task used a different set of stimuli, feedback contingency, structure, and outcomes than the main task. This practice was meant to ensure that all participants would be familiar with the general setting of playing a computer game, making responses with the keyboard, and receiving feedback, before the actual task was administered, in order to minimize potential “learning set” differences. The practice consisted of 100 trials during which participants chose one of two butterfly images and then received feedback (“correct” or “incorrect”). The probability contingencies were .8/.2 and remained constant throughout the task.

Scanning session

The second session involved completing the experimental task while in the MRI scanner.

Experimental task

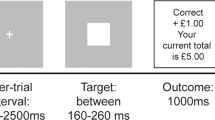
The reinforcement learning task, illustrated in Fig. 1, took place in two separate conditions, gain and loss. In both the gain and loss conditions, participants first chose one of two geometric shapes, then received feedback on their choice (“Correct!” or “Incorrect!”), and then were notified of the reward outcome (monetary gain or loss); thus, each trial consisted of three components in succession: choice, choice feedback, and monetary outcome.

Fig. 1
figure 1

Experimental paradigm. a Gain condition. The task schematic depicts the gain condition when the participant chooses the triangle, receives correct feedback, and is rewarded with $1. b Loss condition. In the loss condition, the participant chooses the triangle, receives correct feedback, and loses $0

Full size image

Feedback and reward were both delivered probabilistically. For feedback, choosing the optimal shape resulted in correct feedback 70 % of the time and incorrect feedback 30 % of the time, whereas the suboptimal shape had the reverse probability contingencies (.3/.7, correct/incorrect). Reward receipt was also probabilistic and depended on the given feedback. In the gain condition, there was a 50/50 chance of winning a high ($1.00) or medium ($0.50) amount following correct feedback and a low ($0) or medium ($0.50) amount following incorrect feedback. For the loss condition, correct feedback resulted in a 50/50 chance of losing a low or medium amount (−$0 or −$0.50), and incorrect feedback led to a 50/50 chance of losing a medium or high amount (−$1.00). Additionally, prior to beginning the loss condition, participants received an $80 endowment from which they tried to avoid losing money. Money earned during the task was paid to participants upon completion of the experiment.

The order of conditions and the experimental stimuli were counterbalanced across participants. Prior to starting each block (gain or loss), participants received general instructions about the task. Choice, feedback, and outcome epochs were separated by jittered interstimulus intervals, and each trial was followed by a jittered intertrial interval. Each condition occurred in a block consisting of 110 trials, which were split into five runs per block.

The experimental task was presented with MATLAB and PsychToolbox software, and responses were recorded with a scanner-compatible button box system. Participants viewed the task on a projected screen visible through a mirror attached to the head coil.

FMRI data acquisition

All fMRI scanning took place at the Columbia Radiology MRI Center at the Neurological Institute at the Columbia University Medical Center. FMRI scanning was performed on a 1.5-T GE Signa Twin Speed Excite HD scanner using a one-channel head coil. A high-resolution T1-weighted structural image was acquired using a spoil gradient recoil sequence (1 × 1 × 1 mm voxel). Functional blood oxygenation level dependent (BOLD) images were collected using a T2*-weighted spiral in-and-out sequence (TR = 2,000 ms, TE = 28 ms, flip angle =84°, slice thickness 3, FOV 22.4, matrix 64 × 64). Each block (gain and loss) of the task consisted of 110 trials across 10 runs, with 264 volumes acquired per run. On each functional scanning run, five discarded volumes were collected prior to the onset of the first trial to allow for magnetic field stabilization.

Behavioral analysis

Percentage of optimal choice was used to assess overall task performance. This measure was calculated by determining the percentage of trials on which the participant selected the choice that was most often followed by correct feedback (.7 probability).

Sensitivity to feedback measures were calculated to assess the impact of positive and negative feedback on subsequent choices. At the extreme, a participant who is maximally sensitive to feedback on any given trial will tend to repeat the same choice following positive feedback (referred to as win-stay) and to shift choices immediately following negative feedback (referred to as lose-shift). To calculate each participant’s tendency to win-stay and lose-shift, we quantified the percentage of times a participant would choose the same shape on the subsequent trial after receiving correct feedback (win-stay) and the percentage of times they chose the other shape following incorrect feedback (lose-shift).

A temporal difference (TD) model was used to assess changes in dynamic trial-by-trial learning from feedback over time. This model allowed us to calculate values for PEs from feedback at each trial and overall LR values for each participant (Daw, 2011; O’Doherty et al., 2003; Schönberg, Daw, Joel, & O’Doherty, 2007; Schonberg et al., 2010; Sutton & Barto, 1998). PE was calculated by finding the difference between the expected outcome at the time of choice and the actual outcome received at the time of feedback. LR was used to assess the degree to which individuals updated their choices in response to trial-by-trial feedback. A higher LR indicates that an individual is more responsive to trial-by-trial changes, updating expectations rapidly after each event. A lower LR indicates more gradual updating based on feedback over the course of learning (Daw, 2011). For example, a participant with an LR of 1 would be more likely to stay with a choice following correct feedback and would switch his or her choice after negative feedback.

By assuming that correct feedback was a reinforcer, the TD model was used to (1) calculate a trial-specific cumulative value (v) for the chosen stimulus, given the subject's history of choices made and feedback received up to that point in the experiment, and (2) calculate PE (δ) which, as described previously, is the value expected at that point in time, as compared with the value of the feedback (fb) that was then received, or δ = fb − v. For the purposes of this article, the parameter we will focus on is the LR (α), or the degree to which a participant incorporates the information from these prediction errors into his or her subsequent choice behavior over the course of the experiment. In order to estimate the LR parameter, we used the equation v t + 1 = v t + αδ t and calculated these values at each trial t. A function in MATLAB was then used to generate an optimal fit to each participant's entire set of data for each task condition separately. Note that for the data presented below, a value of 1 is not necessarily better than an LR of .5; rather, 1 represents a subject who stays or shifts following correct or incorrect feedback (Daw, 2011). To further probe the effects of positive PE and negative PE on learning, additional Q learning models were used to calculate separate LRs for learning from positive prediction error (positive LR) and for learning from negative prediction error (negative LR) (Cazé & van der Meer, 2013; Jones et al., 2014).

We conducted multiple regression analyses to assess the effect of dose on learning performance measures. Given that our data were not normally distributed and that our sample size was relatively small, we fit the linear models using a permutation test with 5,000 iterations. For these analyses, we included the following factors in our model, in addition to the performance measure of interest: task condition (gain or loss), age, SAPS global scores, and SANS global scores. To assess the effects of dose on positive and negative LRs, we conducted an analysis of covariance (ANCOVA) using a permutation test with dose and task condition as factors in our model.

FMRI preprocessing and data analysis

Functional imaging data were preprocessed with SPM 8 (Wellcome Department of Imaging Neuroscience, London, U.K.) and were analyzed with the NeuroElf software package (http://neuroelf.net/). Functional images underwent slice-time correction and were realigned to the first volume of each run to correct for head movement. Images were then warped to the Montreal Neurological Institute template and were smoothed with a 6-mm Gaussian kernel. Data were forced to single precision in order to decrease the impact of rounding errors. Participants with excessive motion or poor quality fMRI data were excluded from further analyses.

Following preprocessing, the data underwent a first-level statistical analysis using the standard general linear model. The model included regressors for choice (3,000 ms), feedback (1,000 ms), and outcome (3,000 ms). These regressors were modeled as separate factors for the gain and loss conditions. A parametric regressor for PE was modeled during the feedback period. Motion parameters were also incorporated into the model as a regressor of no interest, and a temporal filter was used (Fourier transform, 200 ms). Robust regression was performed at the first level in order to limit the effects of outliers (Wager, Keller, Lacey, & Jonides, 2005).

For the fMRI analyses, we estimated separate individual LRs for the gain and loss conditions for each participant and then generated trial-by-trial PEs, which were later used as parametric regressors in the GLM. We also computed a separate GLM using PE regressors generated from the group’s average LR, since fitting individual LRs is a statistically noisier approach. The two models produced very similar and convergent results; however, only the data from the model using individual LR PE regressors are reported below.

To assess the relationship between medication dose and BOLD response during feedback, we performed exploratory whole-brain analyses. Because we were primarily interested in feedback PEs, we computed contrasts for the feedback period while including a parametric regressor for trial-by-trial PE. We then computed a whole-brain Pearson correlation for dose to assess how PE coding related to medication status in gain and loss conditions separately. We computed separate contrasts for the gain and loss conditions.

For whole-brain correction, family-wise error (FWE) thresholds of p < .05 were estimated using AlphaSim Monte Carlo simulation (Ward, 2000) with a smoothness level specified for each contrast as was estimated from the data, ranging from 8.6 to 10.3. Reported clusters were thresholded at p < .005 and a cluster size of k > 46–67 (the specific cluster size was determined by running AlphaSim separately for each contrast computed).

Results

Behavioral results

Medication dose and clinical ratings

Patients tested were prescribed a range of 50–800 mg in equivalent CPZ dose, with an average of 251.6 mg and a standard deviation of 182.8 mg.

There were no significant relationships between CPZ dose and symptom ratings from any clinical scales, including SANS or SAPS scores, or the global subscores: SANS global score (r = .20, p = .33), affective flattening (r = .30, p = .14), apathy (r = .20, p = .32), anhedonia (r = .01, p = .96), attention (r = −.29, p = .15), or alogia (r = .21, p = .31). SAPS global score (r = .03, p = .90), hallucinations (r = .09, p = .67), delusions (r = −.23, p = .26), bizarre behavior (r = .07, p = .75), or positive formal thought disorder (r = .16, p = .43). This confirmed that there was no relationship between medication dose and symptom severity.

Optimal performance

To assess task performance, we calculated the percentage of trials on which participants selected the optimal choice. Calculations of mean percentage of optimal choice revealed that patients performed above chance in both the gain condition, t = 6.8, p < .001, and in the loss condition, t = 8.0, p < .001, indicating that overall, participants were able to learn during the task (Fig. 2). The results of a multiple regression indicated that dose was not associated with percentage of optimal choice (p = .75).

Fig. 2
figure 2

Optimal choice across dose. Percentage of optimal choice is displayed as a function of dose for the gain condition (green) and the loss condition (red). There was no significant relationship between dose and percentage of optimal choice

Full size image

Sensitivity to feedback

Multiple regression tests assessing the effects of medication dose on sensitivity to feedback showed that dose was not associated with percentage of win-stay (p = .34). However, there was a significant association between dose and percentage of lose-shift (β= 0.0004, p < .001), but the effect of task condition (gain vs. loss) was not significant (p = .88) (Fig. 3). This model, which included factors for task condition, age, global SAPS scores, and global SANS scores, explained 27.8 % of the variance, R 2 = .277, F(5, 46) = 3.53, p = .009.

Fig. 3
figure 3

Percentage of lose-shift across dose. Percentage of lose-shift is displayed as a function of dose for the gain condition (green) and loss condition (red). There was a significant association between dose and percentage of lose-shift (p < .001)

Full size image

Learning rate

When using multiple regression tests to assess the relationship between LR and dose, dose was significantly associated with LR (β = 0.0008, p < .001), but the effect of task condition was not significant (p = .90) (Fig. 4). This model also included factors for age, global SAPS scores, and global SANS scores and explained 20.1 % of the variance, R 2 = .208, F(5, 46) = 2.41, p = .05.

Fig. 4
figure 4

Learning rate across dose. Learning rate, as calculated from a temporal difference model, is displayed as a function of dose for the gain (green) and loss (red) conditions. There was a significant association between dose and learning rate (p < .001)

Full size image

In testing the effects of dose on positive LR and negative LR, the results of an ANCOVA test revealed that the main effect of dose was not significant for positive LR. However, for negative LR, there was a significant interaction between dose and task condition (gain vs. loss), F = 7.98, p = .007, such that negative LR increased with dose in the loss condition but decreased with dose in the gain condition (Fig. 5).

Fig. 5
figure 5

Negative learning rate across dose. Negative learning rate (LR), as calculated from responses to negative prediction errors, is shown across dose for the gain (green) and loss (red) conditions. There was a significant interaction, such that negative LR increased with dose in the loss condition but decreased with dose in the gain condition

Full size image

FMRI results

We first examined PE responses during feedback, collapsed across the entire group, to determine whether patients showed intact BOLD responses to trial-by-trial fluctuations in PE estimates in the striatum. Analysis of brain activation during the feedback period with a parametric regressor for feedback PE indicated that activation in the bilateral ventral striatum correlated with trial-by-trial fluctuations in PE estimates from the learning model during the loss condition. For the contrast of feedback with PE estimates in the gain condition, activation in the caudate tracked with feedback PE, and BOLD activity in the ventral striatum was trending but did not survive correction for multiple comparisons (Fig. 6, Tables 3 and 4).

Fig. 6
figure 6

Prediction error coding during feedback. Whole-brain contrasts displayed illustrate BOLD signal during the time of feedback when including a parametric regressor for prediction error. Patients showed significant recruitment of the bilateral ventral striatum for feedback prediction error in the loss condition (right). For the gain condition, recruitment of the ventral striatum was trending but did not survive multiple comparisons correction (left)

Full size image
Table 3 BOLD activity for feedback prediction error, gain condition (local maxima with 10 or more voxels are listed underneath each cluster)
Full size table
Table 4 BOLD activity for feedback prediction error, loss condition (local maxima with 10 or more voxels are listed underneath each cluster)
Full size table

We then examined the relationship between medication dose and BOLD responses to feedback PE during learning. While including medication dose as a whole-brain covariate, we examined the association between dose and PE coding during feedback separately for the gain and loss conditions. For the gain condition, the only activation clusters that survived whole-brain correction included the superior temporal gyrus, the superior parietal lobule, and the middle temporal gyrus (Table 5). In the loss condition, we found a significant negative relationship between medication dose and activation in the ventral and dorsal striatum. Specifically, there was a negative association between dose and PE signal in the bilateral caudate, left putamen, and left globus pallidus. Additionally, there was a negative association with dose and the parametric PE response during feedback in the rostral medial prefrontal cortex (Fig. 7 and Table 6).

Table 5 Feedback prediction error correlated with medication dose, gain condition (local maxima with 10 or more voxels are listed underneath each cluster)
Full size table
Fig. 7
figure 7

Dose-related modulation of feedback prediction error during losses. Whole-brain maps are shown for the loss condition illustrating correlations between dose and BOLD signal during feedback while including a parametric regressor for prediction error. Clusters in the dorsal and ventral striatum and the medial prefrontal survived family-wise error correction. Patients on higher doses showed attenuated recruitment in these regions

Full size image
Table 6 Feedback prediction error correlated with medication dose, loss condition (local maxima with 10 or more voxels are listed underneath each cluster)
Full size table

Results summary

Behavioral results showed that medication dose was associated with differences in sensitivity to feedback. Percentage of lose-shift was positively associated with medication dose across the gain and loss conditions. Analyses of dynamic learning behavior using a TD model indicated that dose was positively associated with LR across both gain and loss conditions. When examining positive and negative LRs separately, there was a significant interaction between dose and condition for negative LR, such that dose was negatively associated with negative LR in the gain condition but positively associated with negative LR in the loss condition. FMRI results showed that medication dose was associated with attenuated recruitment of portions of the ventral and dorsal striatum and medial prefrontal cortex during feedback PE coding in the loss condition.

Discussion

This study found that higher doses of atypical antipsychotic drugs may be associated with altered trial-by-trial learning and strategic approach implemented during feedback-driven reinforcement learning in patients with SZ. While medication dose was not related to overall performance, medication dose was associated with learning measures, suggesting altered learning approaches. Sensitivity to feedback analyses revealed a significant relationship between dose and lose-shift scores, indicating that patients taking higher doses of medication were more likely to respond to negative feedback by switching their choice on the subsequent trial. Furthermore, no such relationship was found between dose and win-stay measures, illustrating the specificity of the relationship between medication dose and responses to negative feedback.

We used a reinforcement learning model (Daw, 2011; O'Doherty et al., 2003; O'Doherty et al., 2006; Schönberg et al., 2007; Schonberg et al., 2010) to formally quantify trial-by-trial estimates of learning driven by PEs. Using this model, we found a significant association between dose and LR. These results suggest that patients taking higher doses of medication tended toward more rapid updating of responses on a trial-by-trial basis. In addition, analyses comparing learning from positive PE and negative PE showed that, for negative LR, there was an interaction between dose and task condition (gain vs. loss), such that negative LR increased with dose in the loss condition but decreased with dose in the gain condition.

The fMRI data suggest that medication status is associated with changes in neural signatures of PE when learning from losses. While patients taking lower doses of antipsychotic medication showed intact recruitment of the striatum, those on higher doses showed attenuated activation in the striatum and mPFC. A large body of research has shown that these regions support PE coding, responses to reward, and tracking of expected value (Daw & Doya, 2006; Delgado, Locke, Stenger, & Fiez, 2003; Delgado, Nystrom, Fissell, Noll, & Fiez, 2000; O’Doherty et al., 2003; O’Doherty et al., 2004). It is possible that the observed attenuated recruitment of this reward-related network may underlie the reported behavioral associations between medication dose and strategic approaches to reinforcement learning.

PE serves as a learning signal, reflecting a response to an unexpected outcome. While some work suggests that the ventral striatum tracks with PE independently of valence (both positive and negative) (e.g., O’Doherty et al., 2003), there is evidence demonstrating that the ventral striatum typically tracks more closely with the coding of positive PE (e.g., Seymour, Daw, Dayan, Singer, & Dolan, 2007). Negative PE coding is, instead, often associated with responses in the dorsal striatum (Delgado, 2007; Delgado et al., 2008). Following this theoretical model from prior research, one potential interpretation of these results is that patients show a medication effect that may result in higher dose being associated with blunted coding of PE in the canonical reward-related neural circuitry. Therefore, the neural results suggest that higher doses may potentially be associated with an altered ability to track expected value of the associated cues, possibly contributing to the need to use immediate feedback to adjust decisions, which, in turn, could hinder flexible learning. Furthermore, this altered learning signal may suggest a potential underlying mechanism by which patients taking higher doses are more likely to lose-shift or update rapidly on a trial-by-trial basis. If they are not accurately encoding PE signals, they are less likely to gradually learn the contingencies of the task and, thus, rely on rapid updating at each trial to accomplish learning. In sum, attenuated PE coding in the striatum and mPFC, which was associated with medication dose, may possibly contribute to the observed increased lose-shift tendencies and higher LRs in patients taking higher doses of antipsychotics.

Prior work on reward learning in schizophrenia has implicated deficits in reward network recruitment during reward-based tasks. There is converging evidence suggesting that schizophrenics show deficient learning when approaching gains but that schizophrenics are able to learn from negative feedback and their learning remains intact when avoiding monetary losses (Reinen et al., 2014; Waltz et al., 2007). Neuroimaging research has linked behavioral learning deficits in SZ to underlying neural systems and has demonstrated that schizophrenics show altered neural responses to PE in the midbrain and ventral striatum (Corlett et al., 2007; Murray et al., 2008a, b). Additionally, patients with SZ exhibit abnormalities in value representation in the orbitofrontal cortex during probabilistic learning (Gold et al., 2008; Waltz et al., 2010). Furthermore, SZ patients show intact striatal coding of negative PE, but they exhibit attenuated responses to rewarding outcomes (Waltz et al., 2009). Studies examining the impact of medication on reward anticipation have shown that the ventral striatum is particularly responsive to changes in medication status (Juckel et al., 2006; Kirsch et al., 2007; Schlagenhauf et al., 2008). Expanding on this experimental framework, our findings suggest that increased antipsychotic medication may possibly further bias learning from negative outcomes, which may potentially result from spared striatal coding of negative PEs. Our imaging results show regions that largely overlap with areas found in prior work on reward impairments in SZ and, thus, provide preliminary evidence that antipsychotic medication status might further contribute to altered behavioral and neural processes during reward-based learning.

Reinforcement learning and, specifically, responses to positive and negative PEs have been directly linked to dopamine activity. Prior literature has suggested that D2 blockade may enhance sensitivity to negative feedback during learning (Maia & Frank, 2011; Wiecki et al., 2009). While atypical antipsychotic drugs act on an array of neurotransmitter receptors, D2 blockade is common to all of these drugs. Furthermore, there is evidence suggesting that action at D2 receptors may be the fundamental mechanism underlying the therapeutic effects of these drugs (Kapur & Mamo, 2003; Seeman, 1987, 2010). One potential mechanism may be that D2 blockade modulates tonic dopamine transmission and tonic dopamine levels are tied to processing of negative PEs (Frank & O’Reilly, 2006; Frank et al., 2004; Kapur & Seeman, 2001). Another putative mechanism is that D2 blockade alters both the phasic firing of dopamine neurons and the tonic dopamine levels via depolarization blockade, which may, in turn, weaken the effect of positive PE signaling on subsequent learning from reward or punishment (Grace, 1991). While fMRI data cannot elucidate the underlying molecular substrate, D2 blockade may be a potential mechanism driving the observed behavioral and neural effects of antipsychotic dose on responses to reward-related feedback. However, further molecular research must be conducted to examine the effects of D2 blockade and the synaptic level contributions to reinforcement learning.

There are several limitations that need to be considered when interpreting the results of this exploratory study. First, the patient sample size was relatively small, and further studies in larger samples need to be conducted to replicate these results. Second, we did not include data from healthy controls or from unmedicated patients in these analyses. Third, medication status was not standardized across patients. While these results suggest that medication status is associated with altered responses to feedback, it remains difficult to parse out the exact mechanism driving this effect. This question is very challenging to address in human patient populations, since schizophrenia is a heterogeneous disease. Even more challenging is that medication was not controlled in this outpatient research study. While we found no significant relationship between medication dose and symptom severity, it is difficult to determine whether these effects stem from the antipsychotic drugs or whether these findings reflect other potential individual differences within our patient group. It is quite possible that medication dose may be associated with underlying symptoms or individual differences, which may be contributing to these reported effects. Another constraint in interpreting these findings is that the atypical antipsychotics act on multiple neurotransmitter systems, making it difficult to piece apart a causal neurobiological substrate.

Despite these inherent challenges, these exploratory findings establish a preliminary and informative characterization of the impact of antipsychotic medication on reinforcement learning in SZ. Following this, these findings have direct relevance to the clinical and theoretical framework of cognitive deficits in SZ and could help constrain future research. Future pharmacological studies should be conducted in larger samples of healthy controls and patients with SZ to further elucidate the impact of dose-related D2 blockade on reward learning and motivated behavior. In addition, future studies should examine the effects of D2 antagonists in patients with diagnoses other than SZ who take these drugs, including patients with bipolar disorder and treatment-resistant depression, to fully understand the effects of antipsychotic medication across diagnoses and to address disease-specific differences in underlying dopamine dysregulation. Furthermore, animal models may provide a promising means to better parse out the putative contribution of D2 blockade to the observed impact of antipsychotic dose on reinforcement learning.

Ed Smith was the intellectual driving force behind this study. Ed was passionate about understanding the neural bases of cognitive impairments in SZ and believed strongly in the potential of leveraging cognitive neuroscience to understand mental disorders. His research interests inspired a collaborative initiative to characterize the motivational deficits associated with SZ that focused on dissociating the impact of reward anticipation and hedonic experience on cognition and behavior, which this study was a part of. I had the amazing opportunity to work with Ed as a research assistant on this project. As my first research mentor, Ed taught me how to think critically about the links between the brain and human behavior, which ultimately motivated me to pursue training in cognitive neuroscience. His passion for science was infectious, and his mentorship will have a lasting impact on my career. I am so fortunate to have had the opportunity to work with Ed; he was an incredible scientist, a supportive mentor, and a truly kind friend. While we miss him greatly, his advice and insights on science and life in general have provided lasting inspiration.