Abstract
The popular random-dot motion (RDM) task has recently been applied to multiple-choice perceptual decision-making. However, changes in the number of alternatives on an RDM display lead to changes in the similarity between the alternatives, complicating the study of multiple-choice effects. To disentangle the effects of similarity and number of alternatives, we analyzed behavior in the RDM task using an optimal-observer model. The model applies Bayesian principles to give an account of how changes in the stimulus influence the decision-making process. A possible neural implementation of the optimal-observer model is discussed, and we provide behavioral data that support the model. We verify the predictions from the optimal-observer model by fitting a descriptive model of choice behavior (the linear ballistic accumulator model) to the behavioral data. The results show that (a) there is a natural interaction in the RDM task between similarity and the number of alternatives; (b) the number of alternatives influences “response caution”, whereas the similarity between the alternatives influences “drift rate”; and (c) decisions in the RDM task are near optimal when participants are presented with multiple alternatives.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In order to transform the continuous stream of perceptual information into goal-directed action, people need to make decisions. These decisions may involve any number of alternative options, often more than two. This may be the reason that psychological theorizing and experimenting about perceptual decision-making has recently shifted focus from binary choice (e.g., Britten, Shadlen, Newsome, & Movshon, 1992; Ratcliff, 1978) to multiple choice (e.g., Brown, Steyvers, & Wagenmakers, 2009; Ditterich, 2010; Hawkins, Brown, Steyvers, & Wagenmakers, in press; Ho, Brown, & Serences, 2009; Leite & Ratcliff, 2010). Multiple-choice decision-making is also an important research topic because it allows researchers to validate theories initially developed for binary choices (e.g., Ratcliff, 1978; Smith & Vickers, 1988). Assuming that multiple-choice decision-making is a natural generalization of binary choice, these models should also generalize to multiple-choice contexts in order to have validity as a description of the underlying decision process.
Random-dot motion
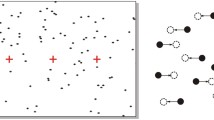
A task often used in the study of perceptual decision-making is the random-dot motion (RDM) task (Ball & Sekuler, 1982; Britten et al., 1992; Churchland, Kiani, & Shadlen, 2008; Forstmann et al., 2010; Forstmann et al., 2008; Ho et al., 2009; Mulder et al., 2010; Niwa & Ditterich, 2008; Pilly & Seitz, 2009; Roitman & Shadlen, 2002; Salzman & Newsome, 1994; Shadlen & Newsome, 2001; van Maanen, Brown, et al., 2011). In this task, participants are required to indicate the apparent direction of motion of a cloud of dots that is presented on a computer screen. Typically, a percentage of the dots move in a designated direction (the target direction), while the remaining dots move randomly. The percentage of coherently moving dots is often used as a measure of task difficulty (see, e.g., Britten et al., 1992). In many experiments, the potential target directions are indicated on an imaginary circle surrounding the dot cloud (Fig. 1). In particular, the RDM task is an experimental paradigm often used to study behavior associated with multiple-choice (n > 2) decision-making (Ball & Sekuler, 1982; Churchland et al., 2008; Ho et al., 2009; Niwa & Ditterich, 2008; Salzman & Newsome, 1994; Shadlen & Newsome, 2001). One reason for this may be that the paradigm extends rather naturally to more alternatives. However, one complicating factor in applying RDM to multiple-choice decision-making is that as the number of response alternatives changes, so does their similarity.
Configurations of alternatives in a typical random-dot motion display. Note that as the number of alternatives increases, the angular distance (i.e., similarity) between two adjacent alternatives decreases. These particular configurations were also used in Experiment 1.
Similarity and number of alternatives interact
In spite of the ease with which the RDM paradigm can be extended to multiple-choice tasks, it is difficult to study the effects of increasing the number alternatives. This is because introducing an extra target inevitably decreases the relative angular distance of the alternatives, which increases the similarity of the alternatives in terms of location.
Overview
To disentangle the effects of similarity and number of alternatives, we will analyze optimal behavior in the RDM task. First, we introduce a model of an optimal observer in the RDM task. The model applies Bayesian principles to give an account of how changes in the stimulus (such as the similarity between alternatives) influence the decision-making process. We also show how this model can be neurally implemented. The model predictions will be experimentally verified in the following sections. Because the optimal-observer model describes behavioral changes under a rationality assumption, we additionally fit a linear ballistic accumulator (LBA; Brown & Heathcote, 2008) model to the data. The LBA model is a process model of decision-making that can be fit to the response time distributions of correct and error responses (cf. Ratcliff, 1978). This model allows us to study whether the changes that are predicted by the optimal-observer model are reflected by changes in latent variables in the decision process. These should appear as parameter changes of the LBA model.
Optimal behavior in RDM
The RDM stimulus consists of a set of dots, each moving in a particular direction. A proportion of the dots move in the same direction, and the remaining dots move in random directions. To make a decision, an optimal observer could simply count the number of dots that move in each direction and choose the direction with the most dots. However, the perceptual system introduces variance in the perceived motion—for instance, because motion-sensitive neurons in the brain not only respond to their preferred motion direction, but also to similar directions. Thus, in order to make a correct decision, the observer needs to decide whether a certain amount of evidence for a particular response alternative outweighs the evidence for other alternatives. One way to define optimal performance would be to achieve the minimum average response time for a prespecified error rate (cf. Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006). A process that implements this strategy can be described as follows. The optimal observer computes for each response alternative the posterior probability that this alternative is the target, on the basis of the evidence observed so far:
with H i being the hypothesis that motion direction i generated the RDM stimulus, and D being the set of observed dot movements. Here we assume that the prior probabilities for each alternative are equal—as they will be in subsequent experiments—and hence can be ignored. Equation 1 then simplifies to
On the basis of new incoming evidence, the model continuously recomputes the posterior probability of each response alternative until the probability of one of the alternatives crosses a preset response criterion.
The above scheme implements the multihypothesis probability ratio test (MSPRT; Baum & Veeravalli, 1994), which generalizes the sequential probability ratio test (SPRT; Wald, 1947) to more than two alternatives. Given a particular response criterion, the model stops sampling and initiates a decision when the posterior probability of any of the alternatives crosses the response criterion. Because the posterior probability reflects the probability that a particular choice is correct, the model reports the correct alternative on a proportion of the trials that is on or above the response criterion.
In addition to the MSPRT, other definitions of optimal behavior exist. For example, the observer could take the cost of making an error into account and weigh that against the cost of sampling more evidence (and responding later). An optimal strategy to do this would include maximizing the proportion of correct responses per unit time (the reward rate; Bogacz et al., 2006; Gold & Shadlen, 2002; Hawkins et al., in press; Simen et al., 2009). The choice of strategy most likely differs between experimental contexts as well as individuals (Hawkins et al., in press). In contexts in which the quality of the stimulus is uncertain, such as in typical RDM tasks in which the stimulus coherence is manipulated on a trial-to-trial basis (e.g., Palmer, Huk, & Shadlen, 2005), SPRT does not provide an accurate description of the data (cf. Bogacz et al., 2006; Hanks, Mazurek, Kiani, Hopp, & Shadlen, 2011). In the present setup, however, the quality of the stimulus is constant, and SPRT thus allows for a straightforward analysis of the decision-making process. In the Simulation section below, we will provide simulations using both implementations of optimal choice.
Evidence accumulation
The posterior probability for each alternative is computed on the basis of the evidence contained in the stimulus. In the RDM paradigm, this means that a participant perceives moving dots and the directions of movement are combined into evidence for each alternative.
Each movement is encoded in the brain by motion-sensitive neurons (Britten et al., 1992). Each motion-sensitive neuron is tuned to a particular motion direction, which means that each neuron has a preferred motion direction. The functional form of these tuning curves follows a von Mises function (Swindale, 1998). The von Mises function for an angle ϕ is given by
where I 0(x) is the modified Bessel function of order 0, μ indicates the preferred orientation of the neuron, and κ is the neuron’s response specificity, which may be used to express individual differences in motion perception ability.
In response to a stimulus with orientation ϕ, each neuron i produces a spike train that follows a Poisson process with a firing rate equal to f(ϕ | μ i , κ). That is, within a time step of length ∆t starting at times t = 1, . . . , T, the number of spikes n it is distributed according to a Poisson random variable:
The likelihood of a particular motion direction ϕ for the spikes in a single time step (i.e., from t to t + ∆t) is then
Here we assume that the spike trains in each direction-sensitive neuron are independently distributed, which is approximately the case for cortical pyramidal cells (Beck et al., 2008; Jazayeri & Movshon, 2006).
Over time, the observer perceives a set of motion directions D, a subset of which is coherent and moving in the target direction, whereas the complement is uniformly distributed and moving in random directions. The observer’s challenge is to accumulate evidence for each of the possible directions of movement. The optimal observer computes Bayes’s rule (Eq. 2) for all choice alternatives on the basis of the likelihood of each alternative j Footnote 1:
The posterior probabilities in Eq. 2 can now be expressed as
which simplifies to
Equation 8 can be interpreted as follows: Each response alternative (μ j ) is represented by a counter that collects all spikes from the neurons encoding for that direction. Thus, the posterior probability for each alternative depends on the ratio of the spike counts of all alternatives.Footnote 2 Beck et al. (2008) showed that this model can be implemented by networks of neuronal populations, giving credence to the idea that the brain computes optimal choice.
The optimal-observer model is intended to analyze the RDM task in terms of optimal performance. That is, given the noisy nature of the stimulus and a particular response criterion, the model shows what the optimal behavior should be to minimize response times. This is not to say that the model is the definitive account of human behavior. There are a number of ways in which observers can deviate from the model’s predictions. For instance, individual observers may have different ways of taking the cost of sampling into account, and therefore could weigh the cost of time in different ways.
Simulations with the optimal-observer model: I. Similarity
As time progresses, more and more observations of moving dots become available. When, for a particular duration T and movement direction μ j , the the posterior probability reaches a response criterion, the model provides response j with decision time T. This is illustrated in Fig. 2. The top left panel shows a condition with two alternatives (A and B). The mean direction of motion is μ A = 0, and the alternative choice is located at μ B = π (note that, due to the circular arrangement of alternatives, we can also say that μ B = –π). For example, if we assume that the specificity of the von Mises function is κ = 1, the probability of drawing a sample that is closer to the incorrect alternative is only .11. This means that the majority of evidence samples (i.e., movement) indicates that A is the correct alternative. Therefore, this target configuration represents a relatively easy decision-making task, and the response criterion indicated by the horizontal gray line is reached quickly (Fig. 2, top right panel).
The left column presents sampling distributions of perceived motion and the location alternatives for three different situations; the right column shows illustrations of evidence accumulation in the model. (Top panels) Two response alternatives with an angular distance of π. (Middle panels) Two response alternatives with an angular distance of \( \frac{1}{2}\pi \). (Bottom panels) Four response alternatives with an angular distance of \( \frac{1}{2}\pi \). In the right panels, the gray lines represent the criterion value (set at 0.9). The dotted vertical lines represent the time step at which one of the posterior probabilities crosses (or has crossed) the response criterion for the first time (that is, the decision time). The meandering lines represent different choice alternatives
If the angular distance between alternatives changes, so does the probability that a response alternative is correct, given a sample from a distribution with a particular concentration. In the example in the top panels of Fig. 2, an evidence sample with perceived movement x = 1 contributes more to the posterior probability of A than to the posterior probability of B, because the distance between x and μ A is smaller than the distance between x and μ B. As the angular distance between A and B decreases, the probability increases that a particular evidence sample contributes more to B than to the target A. This is depicted in the middle left panel of Fig. 2. Here, the foil B with \( {\mu_B} = \frac{1}{2}\pi \) is a more likely alternative given evidence sample x, since μ B – x < μ A – x. Consequently, average decision times take longer, because the target locations are more similar than in the situation depicted in the top panels. Note that because the top and middle panels represent binary choices, every increase in the posterior probability of one alternative is mirrored as a decrease in the posterior probability of the other alternative.
We explored the model’s behavior as a function of angular distance by running a binary choice simulation. That is, the model had two response options, and we manipulated their angular distance. The angles were chosen to be representative of the similarities between alternatives in a typical multiple-choice RDM experiment: \( \frac{2}{3}\pi, \,\frac{2}{5}\pi, \,\frac{2}{7}\pi, \,{\text{and}}\,\frac{2}{9}\pi \). The κ parameter that controls the concentration of the von Mises distribution was kept constant at κ = 0.5. Each data point in Fig. 3 is based on 10,000 simulated decisions.
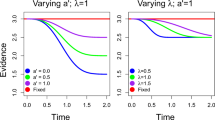
The optimal-observer model predicts a linear decrease of the logarithm (of the mean decision time (MDT) with the log of the angular distance between alternatives. (Left) MDT versus angular distance. (Middle) Log(MDT) versus log(Angular distance). (Right) Accuracy versus angular distance. Note: In the legend, c represents the response criterion value
As Fig. 3 shows, the optimal-observer model predicts that the mean decision time (MDT) decreases as the angular distance between the alternatives increases. In particular, the models predict that log MDT will decrease approximately linearly with the logarithm of the angular distance (Fig. 3, middle panel). Because the model strives for a fixed proportion of correct responses, the accuracy rates are constant over different angular distances.
Simulations with the optimal-observer model: II. Number of alternatives
If the number of alternatives increases, the prior probability of each alternative decreases. As a consequence, the time needed to cross the distance between the start point and response criterion is greater, and therefore MDT is larger. The bottom panels of Fig. 2 illustrate this with a choice between four alternatives. MDT is prolonged because the prior probabilities are lower and the increase in the likelihood of each alternative is lower. This is because the circular target arrangement in the RDM task necessarily results in an interaction between similarity and number of alternatives.
In Simulation I, we focused on how decision-making in RDM depends on the similarity between alternatives by manipulating the angular distance between the choice alternatives. Now, we will simulate the additional effect of increasing the number of alternatives, as in a typical RDM experiment. We ran the model 10,000 times for three, five, seven, and nine response alternatives in a circular arrangement. This arrangement represents the convential way of extended the number of alternatives in the RDM paradigm. Because the alternatives are spaced over the full circle, the angular distances between two successive alternatives were \( \frac{2}{3}\pi, \,\frac{2}{5}\pi, \,\frac{2}{7}\pi, \,{\text{and}}\,\frac{2}{9}\pi \), respectively, as in the similarity simulation discussed before. On each trial, the mean of the sampling distribution was randomly chosen to be one of the alternative directions. The concentration of the sampling distribution was again κ = 0.5.
We simulated behavior for two response strategies that may be considered optimal. The first strategy minimizes response time for a given response criterion. This strategy implements the MSPRT (Dragalin, Tartakovsky, & Veeravalli, 1999). Whereas the MSPRT is a straightforward notion of optimal behavior, participants could also take other information into account while making a decision. The second strategy explores optimal choice by assuming that decision-makers maximize the reward rate over the course of an experiment (Bogacz et al., 2006; Gold & Shadlen, 2002; Hawkins et al., in press; Simen et al., 2009). The reward rate is defined as the average proportion of correct responses (P c) per unit time (here defined as the sum of the mean response time MRT and the intertrial interval ITI):
Maximizing reward rate entails that the proportion of correct responses be balanced against the time required to provide a correct response. Therefore, as P c decreases—for example, due to the increased difficulty of the task—the maximal reward rate is obtained through faster responding, allowing for more responses, and therefore more correct responses per unit time. In this simulation, the intertrial interval was set at ITI = 50.
Independently of the choice of optimal strategy (fixed or reward-rate-based), the model predicts a linear increase of response time with number of alternatives (or even an exponential increase; see Fig. 4). This result is inconsistent with previous work on multiple-choice behavior that found that mean response times increased with the log of the number of alternatives (sometimes referred to as Hick’s law; Brown et al., 2009; Hick, 1952; Hyman, 1953; Teichner & Krebs, 1974). The model does not predict Hick’s law in this simulation, because the decision-making process is influenced by both changes in likelihood accumulation (because of changing similarity) and changes in prior probability (because of changing the number of alternatives).
The optimal-observer model predicts a linear or supralinear increase in mean decision time (MDT) with increasing numbers of alternatives (N). (Left) MDT versus N. (Middle) MDT versus log N. (Right) Accuracy versus N. RR, reward-rate-based criterion value; MSPRT, fixed criterion value, set at the average of the criteria estimated for the RR strategy (0.72)
With respect to predictions of choice accuracy, the optimal strategies diverge. The fixed-criterion strategy predicts that accuracy will be equal for all N, consistent with the idea that the model strives for a particular proportion of correct responses. The reward-rate-based strategy predicts that accuracy will decrease with increasing N, because this is equivalent to minimizing the total experiment time. This can be appreciated by observing the differences in the predicted MDTs between the models: The sum of MDT over all N is higher for the fixed-criterion than for the reward-rate-based strategy.
From the analysis of the optimal-observer model, two important properties of behavior in the RDM task emerge: First, the change over time in posterior probability is affected by the location of the choice alternatives, and therefore indirectly by the number of alternatives, because changing the number of alternatives affects the location of the alternatives. Second, the amount of evidence that is required for a decision is directly affected by the number of alternatives. This is because more alternatives decreases the initial value of the posterior probabilities that are monitored in the optimal-observer model. These properties were empirically tested in two experiments. Experiment 1 showed, in a conventional multiple-choice RDM task, that participants adjust the required amount of evidence in the face of more alternatives. In addition, Experiment 1 showed that the speed with which the posterior probabilities increase changes with more alternatives, which independently affects behavior. In Experiment 2, we tested the hypothesis that the similarity between alternatives affects the increase in posterior probability, whereas the number of alternatives affects the required amount of evidence.
The linear ballistic accumulator model
To corroborate the predictions for Experiments 1 and 2, we analyzed the data using the linear ballistic accumulator model (LBA; Brown & Heathcote, 2008). While the optimal-observer model can be considered a normative model of decision-making, as it describes optimal choice, the LBA model is a descriptive model and can be successfully fit to experimental data. In particular, the LBA model accounts for response time distributions for both correct and incorrect responses, as well as for the proportion of correct responses.
Similar to the optimal-observer model, the LBA model assumes that a decision is made via the accumulation of evidence for a particular alternative (Fig. 5). The LBA model assumes that each alternative is represented by its own accumulator. During a trial, evidence for each choice alternative j accumulates at a fixed rate (drift rate v j ) until a critical value (the decision criterion b) has been reached. To account for variability in the data, the LBA model assumes that the drift rates on a trial are drawn from a normal distribution. The mean of that distribution differs per accumulator, while the variance (s) is typically kept constant. In addition, the LBA model assumes that the start point is noisy as well and is drawn from a uniform distribution with bounds [0, A]. These two sources of variability prove sufficient to account for many benchmark phenomena in decision-making tasks (Brown & Heathcote, 2008). LBA also estimates the time that cannot be explained by any of the other components (nondecision time T er).
Following the prediction from the optimal-observer model, we hypothesized that the drift rate would decrease with an increasing number of alternatives, reflecting the decreased likelihood of the alternatives in the optimal-observer model. In addition, we hypothesized that response caution would increase with the number of alternatives, to reflect the decrease in prior probability predicted by the optimal-observer model (cf. Churchland et al., 2008).
Experiment 1: Similarity and number of alternatives interact
Experiment 1 was based on the prototypical multi-alternative case in RDM. Thus, the alternatives are presented as targets on a circle surrounding a moving-dot kinematogram. The alternatives are maximally spaced, as shown in Fig. 1. Participants were instructed to respond by moving a joystick in the target direction.
Method
Participants
A group of 10 students (8 female, age range 18–49 years) from the University of Amsterdam student pool participated for course credit. All had normal or corrected-to-normal vision.
RDM stimulus
To create the moving-dot kinematogram of Experiment 1 (and subsequent experiments) we used the Variable Coherence Random-Dot Motion (VCRDM) library for Psychtoolbox (Brainard, 1997).Footnote 3 The appearance of motion in VCRDM is created by controlling the locations of a subset of dots for three frames in a row. That is, when the second frame is drawn, the location of a subset of dots will be recomputed to align with the target direction. The location of the remaining dots is randomly assigned. The size of the subset—often referred to as the coherence level—is under the experimenter’s control. We set the coherence at 35%. Pilot studies indicated that this coherence level made the task sufficiently demanding for our participants, especially when choosing between seven or nine alternatives. Each dot consisted of 3 × 3 pixels, and the initial locations of each dot sequence were uniformly distributed in an aperture of 5-visual-degree diameter.
Design and procedure
Participants were instructed to indicate the apparent direction of motion of the moving-dot kinematogram. To do this, they could move a joystick in the direction of one of several alternatives, which were indicated by yellow circles. The locations of the alternatives were randomized over the full circle. The distance of each alternative from the center of the aperture was 5 visual degrees. There were either three, five, seven, or nine alternatives present, distributed around the circle in such a way that the angular distance between them was maximized (Fig. 1). We used odd numbers of alternatives to ensure that two alternatives were never diametrically opposed. This is important, because the flow of motion is sometimes perceived to be in the opposite direction (Anstis & Mackay, 1980), which would increase the error rates for even configurations of alternatives. The trial order was pseudorandomized such that no more than two consecutive trials had the same number of alternatives. After 32 practice trials (8 for each condition), the experiment was presented in eight blocks of 144 trials (1,152 trials in total). After each block, the participant could take a short break. The participants were instructed to respond as quickly as possible without making any errors. Feedback to their responses was provided by color coding the alternatives. If participants selected the target it turned green; if participants selected a foil, it turned red and the target turned green. Note that the participants did not receive feedback during a trial (that is, there was no cursor present in the display). Response times were defined as the duration between stimulus onset and the moment at which the joystick passed the imaginary circle on which the alternatives were aligned. The nearest alternative was considered as the choice the participant had made. At the beginning of each trial, a red fixation dot was presented together with the alternatives. After 500 ms, the RDM stimulus was presented, which remained on screen until the participant made a response. If the response was faster than 200 ms, a feedback screen appeared that stated “Te snel!” (too fast!).
Results and discussion
We excluded trials on which participants responded too quickly (the trials on which “too fast” feedback was provided; 0.11% of the trials, five trials in total). We first analyzed whether joystick responses differed between correct and incorrect responses. This was done to exclude the possibility that incorrect trials would not reflect errors in the decision-making process, but rather would reflect noise in the motor program required to execute the response. To do this, we first computed the response vector, which we defined as the line through the center of the aperture and the joystick coordinates at the time of response. We assumed that errors related to motor noise would show a larger angular distance between the response vector and the location of the alternative that was selected than would correct responses and errors related to the decision process, because the intended movement was toward a different alternative. The right panel of Fig. 6 shows that this was not the case. Using the cosine of the angular distance, we collapsed responses to the left and right of the selected alternative into one measure, with a cosine of 1 representing a response that was exactly toward the chosen alternative. Although the response vector for the incorrect responses was slightly more off than the response vector for the correct responses, it was clear that at least the majority of incorrect responses reflected errors in the decision process, and not in the motor execution process.
Behavioral data of Experiment 1. (Left) Mean response times (MRTs) as a function of the number of response alternatives, for Experiment 1. (Middle) Proportions of correct responses as a function of number of alternatives. Lines in these two panels represent linear model fits (see the text for details). (Right) Angular distance between the response vector and the location of the selected response alternative. The gray area indicates the distance at which another response alternative would have been closer. Error bars represent within-subjects standard errors of the means (Loftus & Masson, 1994)
Visual inspection of the response time data suggests that MRT increased linearly with the number of alternatives, which would not conform to Hick’s law (Fig. 6, left panel). To support this observation, we compared three regression models: a linear model and two log-linear models. The linear model (Model 1 in Table 1) predicted MRT as a function of number of alternatives (N) and response type (R, correct/incorrect). The log-linear models predicted MRT as a function of the logarithm of the number of alternatives and of response type. Whereas the second model included log N as a factor (Model 2 in Table 1), the third model included log (N + 1) (Model 3 in Table 1). This model was tested because sometimes Hick’s law is said to require an extra constant to account for uncertainty about the occurrence of the decision (in other words, the extra alternative that there is no stimulus; see, e.g., Hick, 1952). In addition, we included the type of response (correct or incorrect) and the interaction in the regression models. The models were fit to the data using least-squares fitting, and then the fits were compared on the basis of their maximum log likelihoods. The linear model had a higher log likelihood value than either of the log-linear models (Table 1). This supports the hypothesis that the data of Experiment 1 are better described by a linear model.
The results of Experiment 1 suggest that the effects of increasing the number of choice alternatives in the RDM task are at odds with the typical finding from multiple-choice experiments that the logarithm of the number of alternatives determines MRT. Previous research suggested that in some circumstances Hick’s law is not expected to apply (Kveraga, Boucher, & Hughes, 2002; Lawrence, St John, Abrams, & Snyder, 2008). However, we interpreted the results of Experiment 1 as an interaction between the effects of the number of alternatives and the similarity of the alternatives, which obscured the typical Hick’s law finding. Using the LBA model, we therefore aimed to disambiguate the effects of number and similarity.
LBA model of Experiment 1
Having established that the data were suited for modeling of the decision-making process, we now turned to the LBA model fit. To improve the estimate of the response time distribution of incorrect responses, we collapsed all trials in which an incorrect response was given. As a result, the LBA model consisted of only two accumulators: one for correct responses and one for incorrect responses. In addition, we Vincentized the data to obtain group estimates of the deciles used to fit the models (Vincent, 1912).Footnote 4 The models were fit to the data using SIMPLEX optimization routines (Nelder & Mead, 1965). For scaling purposes, we set the sum of the correct and incorrect drift rates to 1. To obtain the model that best described the data, we systematically varied which parameters were allowed to vary over the numbers of alternatives. In particular, each of the five model parameters was constrained over the numbers of alternatives, and these models were compared against a model in which all parameters were allowed to vary. Using the Bayesian information criterion (BIC), we assessed which of these models best balanced the fit to the data and the number of degrees of freedom.
Table 2 details how well each model accounted for the data by presenting BIC values and Schwarz weights (Wagenmakers & Farrell, 2004). Schwarz weights quantify the support for a particular model, given the data and the set of candidate models. Even when taking the additional parameters into account, the best model was the default model in which all parameters were allowed to vary. Importantly, the models in which drift rate (v), start point (A), or threshold (b) were constrained scored worse. The best LBA model fit is presented in Fig. 7. Inspecting the parameter values of this model shows that as the number of alternatives increases (and the similarity between the alternatives as well), the drift rate estimate for the correct responses decreases (Fig. 8, middle panel). In addition to drift rate changes, we found that response caution (i.e., criterion) in the LBA model conformed with the optimal-observer predictions. The best-fitting values for the decision criterion b show an increase with increasing N.
The best linear ballistic accumulator model explains the data well. The data are presented by defective cumulative distribution plots, which plot response probability against response time (RT) quantiles for correct and error responses separately. Black crosses, correct RTs; gray crosses, error RTs; circles, model predictions
Best-fitting linear ballistic accumulator model parameters as a function of the number of alternatives N, for Experiment 1. b, response criterion; A, upper bound of the start point distribution; v, mean drift rate; s, drift rate variance
Analysis of the parameters of the LBA model showed that the effects of similarity and number of alternatives can be disentangled using a descriptive model of decision-making. Such a model-based approach would be particularly useful if similarity and the number of alternatives were independently manipulated. In that case, one would be interested in the effects of both manipulations separately. Experiment 2 demonstrated that, also in this situation, the LBA model accounts for the separate effects due to similarity and the number of alternatives. We introduced two similarity conditions: one in which the average similarity between the alternatives increased with more alternatives, as in Experiment 1, and one in which the average similarity between the alternatives decreased with more alternatives.
Experiment 2: A different relation between similarity and number
Participants were asked to perform the RDM task in two conditions. The spaced condition was similar to Experiment 1. Here, either three, five, seven, or nine alternatives were equally spaced on the half circle (Fig. 9, left panel). In the clustered condition, there were nine possible stimulus locations—the same nine used in the N = 9 version of the spaced condition. The N = 3, N = 5, and N = 7 conditions were formed by using the central three, five, or seven locations from the N = 9 condition. As a consequence, the average distance between alternatives increased with every extra alternative. We hypothesized that in the clustered condition, the average similarity between alternatives would decrease with N.
Configurations of alternatives of the random-dot motion display used in Experiment 2. (Left) Spaced condition. (Right) Clustered condition
The manipulation of the average angular distance between alternatives led to two clear hypotheses: The effect of the number of alternatives on MRT would be sublinear in the clustered condition, in line with Hick’s law. This was because the average similarity between alternatives did not increase with more alternatives, as in the spaced condition and Experiment 1. Therefore, response time would not be higher due to the increased similarity, and the sublinear effect of the number of alternatives would not be negated by the angular distance manipulation. In addition, we predicted that responses in the spaced condition would replicate the findings of Experiment 1.
In terms of the changes of the LBA model parameters by the number of alternatives, we hypothesized that the decision criterion parameter (b) would increase with more alternatives, but that it would not differ between the spaced and clustered conditions. Following the optimal-observer logic, the decision criterion would only change with the number of alternatives, and not with the angular distance between the alternatives. On the other hand, we hypothesized that the drift rate parameter (v) would differ with both the number of alternatives and the angular distance condition. That is, increasing the number of alternatives as well as the different conditions would lead to changes in angle. Therefore, to account for the data, drift rate should be different for all conditions.
Method
Participants
A group of 5 students (3 female, age range 19–31 years) from the University of Amsterdam participated. All had normal or corrected-to-normal vision.
RDM stimulus
The stimulus was the same as in Experiment 1.
Design and procedure
The procedure was identical to that for Experiment 1. The design was also identical, except for the locations of the alternatives, which were fixed in the top half of the circle (Fig. 9). In the spaced condition, the alternatives were spaced maximally over half a circle. In the clustered condition, the alternatives were located at equal distances of \( \frac{1}{9}\pi \) from each other.
Results and discussion
We excluded trials on which participants responded too quickly (0.07% of the trials, three trials in total). Figure 10 presents the mean response times for each condition. Similar to Experiment 1, the data show an increase in MRT with more alternatives, and a decrease in accuracy. However, in contrast to Experiment 1, the increase is better described by a log-linear relation: We computed maximum log likelihoods for the three different regression models introduced in Experiment 1 and applied these to the spaced and clustered conditions separately. Table 3 shows that the data from both conditions are best described by the log-linear models, which is in accordance with Hick’s law.
(Left) Mean response times (MRTs) as a function of the number of response alternatives (N) from Experiment 2. (Middle) MRTs as a function of log N. (Right) Proportions of correct responses as a function of N. Error bars represent within-subjects standard errors (Loftus & Masson, 1994), and the lines represent log-linear model fits
LBA model of Experiment 2
Similar to Experiment 1, we fitted multiple LBA models to the data and assessed which model balanced the model fit and the degrees of freedom the best. To obtain stable representations of the response time distributions for correct and incorrect responses in each condition, we again Vincentized the data into deciles.
In addition to the default, unconstrained model (Model 1 in Table 4), we fitted models in which one of the parameters was constrained between the clustered and spaced condition (Models 2–6). Under the assumption that there would be no difference in motor response between these conditions, we additionally fit models in which T er was also constrained (Models 7–10). Finally, we fitted models in which either the two drift-rate-related parameters or the two criterion-related parameters were constrained (Models 11–12), as well as versions of those models with T er also constrained (Models 13–14).
The LBA model that best balanced the number of free parameters and the model fit was Model 14, of which the parameters are presented in Fig. 11. (The model fit is presented in Fig. 12.) As hypothesized, the best LBA model did not require the decision criterion to differ between the clustered and the spaced conditions, as the difference between these conditions only related to the similarity of the alternatives. This supports the view that the decision criterion value relates to the number of alternatives only. In contrast, the best model did require different drift rate values. This reflects that for fewer alternatives, the angular distance for the spaced condition was larger than the angular distance for the clustered condition, and that this difference decreased as the number of alternatives grew (see also Fig. 9). The model also shows that there is no reason to assume that different nondecision times were required for the clustered and spaced conditions, although the model without that assumption had a very close (but worse) BIC value.
Best-fitting linear ballistic accumulator model parameters as a function of the number of alternatives N, for Experiment 2. b, response criterion; A, upper bound of the start point distribution; v, mean drift rate; s, drift rate variance
Best-fitting linear ballistic accumulator model for Experiment 2. The data are presented as defective cumulative distribution plots, which plot response probability against response time (RT) quantiles for correct and error responses separately. Black crosses, correct RTs; gray crosses, error RTs; circles, model predictions
Discussion and conclusion
In two model analyses and two experiments, we studied how similarity and the number alternatives interact in the random-dot motion task. Using LBA model fits, we found that evidence accumulation for the correct choice decreases with angle, reflecting the increased difficulty associated with more similar alternatives. In addition, we found that more evidence for each alternative was required before a response was made. This reflected the decreased prior probability of all alternatives associated with an increase in alternatives. These results seem to be in agreement with previous findings (Churchland et al., 2008; van Maanen, Grasman, Forstmann, & Wagenmakers, 2012). For example, Churchland et al. reported data for a two-alternative RDM task with two angular distances. Responses in the 180-deg condition were faster than those in the 90-deg condition, as is predicted by our optimal-observer model.
Our results may be interpreted as arguing that the RDM paradigm is not applicable to the study of multiple-choice decision-making. We believe, however, that this conclusion is too strong. Rather, the present findings should be taken into account when interpreting experimental data in which the number of alternatives is manipulated, because the number of alternatives in RDM is confounded with the angular distance between the alternatives. One approach that could be taken concerning this confound would be to analyze the data using a specific process model of decision-making, such as the LBA model. Our LBA modeling exercise showed that the effects of similarity and number of alternatives are captured by different parameters of the model. Alternative models that may be used to analyze the data include the leaky competing accumulator model (LCA; Usher & McClelland, 2001; Usher, Olami, & McClelland, 2002) or a racing diffusion model (Leite & Ratcliff, 2010). These models make assumptions about the decision-making process similar to those of the LBA model, and are also suited for the modeling of multiple-choice data.
In fact, one prediction of the LCA model regarding the effect of multiple choices is that the threshold parameter increases with the number of alternatives. Usher et al. (2002) hypothesized that in order to maintain a fixed proportion of correct responses over time, the LCA threshold parameter would need to increase proportional to the logarithm of the number of alternatives. In the present article, this prediction has been experimentally verified, although in both experiments participants were not able to maintain a fixed (high) accuracy in responses, as anticipated by Usher et al.
Conclusion
Because the RDM task is a paradigm often used in the study of multiple-choice decision-making, we studied the interaction between similarity and number of alternatives in RDM. This interaction is a necessary consequence of the experimental paradigm, because adding alternatives necessarily leads to changes in the angular distance between the alternatives, and hence the similarity between alternatives. Using a model that describes optimal behavior in this task, we found that changes in similarity are represented by changes in the rate of the accumulation of evidence. In the optimal-observer model, this was reflected by changes in the likelihood of each alternative. The effect of the number of alternatives was located in the start-point values of the accumulation process, reflected by the prior probability of each alternative (Churchland et al., 2008). These findings were verified in two experiments and confirmed with a process model analysis using the LBA model. The normative changes from the optimal-observer model were confirmed by the LBA model that was fit to the data. In conclusion, our research shows that although the effects of number and similarity are confounded in the RDM task, they can still be studied in isolation with the aid of process models such as LBA.
Notes
An important assumption we make at this point is that there are no autocorrelations between the spikes at different time steps. This assumption seems justified, given that motion-sensitive cortical pyramidal cells encode for location and not for time.
A detailed derivation is provided as supplemental material.
The library can be downloaded from www.shadlen.org/Code/VCRDM.
Similar results were obtained for individual participants, although the model fits were poorer.
References
Anstis, S., & Mackay, D. (1980). The perception of apparent movement. Philosophical Transactions of the Royal Society B, 290, 153–168.
Ball, K., & Sekuler, R. (1982). A specific and enduring improvement in visual motion discrimination. Science, 218, 697–698. doi:10.1126/science.7134968
Baum, C., & Veeravalli, V. (1994). A sequential procedure for multihypothesis testing. IEEE Transactions on Information Theory, 40, 1994–2007.
Beck, J. M., Ma, W. J., Kiani, R., Hanks, T., Churchland, A. K., Roitman, J., . . . Pouget, A. (2008). Probabilistic population codes for Bayesian decision making. Neuron, 60, 1142–1152. doi:10.1016/j.neuron.2008.09.021
Bogacz, R., Brown, E., Moehlis, J., Holmes, P., & Cohen, J. D. (2006). The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced-choice tasks. Psychological Review, 113, 700–765. doi:10.1037/0033-295X.113.4.700
Brainard, D. H. (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. doi:10.1163/156856897X00357
Britten, K. H., Shadlen, M. N., Newsome, W. T., & Movshon, J. A. (1992). The analysis of visual motion: A comparison of neuronal and psychophysical performance. Journal of Neuroscience, 12, 4745–4765.
Brown, S. D., & Heathcote, A. (2008). The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178. doi:10.1016/j.cogpsych.2007.12.002
Brown, S. D., Steyvers, M., & Wagenmakers, E.-J. (2009). Observing evidence accumulation during multi-alternative decisions. Journal of Mathematical Psychology, 53, 453–462.
Churchland, A. K., Kiani, R., & Shadlen, M. N. (2008). Decision-making with multiple alternatives. Nature Neuroscience, 11, 693–702.
Ditterich, J. (2010). A comparison between mechanisms of multi-alternative perceptual decision making: Ability to explain human behavior, predictions for neurophysiology, and relationship with decision theory. Frontiers in Decision Neuroscience, 4, 184.
Dragalin, V., Tartakovsky, A., & Veeravalli, V. (1999). Multihypothesis sequential probability ratio tests: I. Asymptotic optimality. IEEE Transactions on Information Theory, 45, 2448–2461.
Forstmann, B. U., Anwander, A., Schäfer, A., Neumann, J., Brown, S., Wagenmakers, E.-J., . . . Turner R. (2010). Cortico–striatal connections predict control over speed and accuracy in perceptual decision making. Proceedings of the National Academy of Sciences, 107, 15916–15920. doi:10.1073/pnas.1004932107
Forstmann, B. U., Dutilh, G., Brown, S. D., Neumann, J., von Cramon, D. Y., Ridderinkhof, K. R., & Wagenmakers, E.-J. (2008). Striatum and pre-SMA facilitate decision-making under time pressure. Proceedings of the National Academy of Sciences, 105, 17538–17542. doi:10.1073/pnas.0805903105
Gold, J. I., & Shadlen, M. N. (2002). Banburismus and the brain: Decoding the relationship between sensory stimuli, decisions, and reward. Neuron, 36, 299–308. doi:10.1016/S0896-6273(02)00971-6
Hanks, T. D., Mazurek, M. E., Kiani, R., Hopp, E., & Shadlen, M. N. (2011). Elapsed decision time affects the weighting of prior probability in a perceptual decision task. Journal of Neuroscience, 31, 6339–6352. doi:10.1523/JNEUROSCI.5613-10.2011
Hawkins, G., Brown, S. D., Steyvers, M., & Wagenmakers, E.-J. (in press). Context effects in multi-alternative decision making: Empirical data and a Bayesian model. Cognitive Science.
Hick, W. E. (1952). On the rate of gain of information. Quarterly Journal of Experimental Psychology, 4, 11–26. doi:10.1080/17470215208416600
Ho, T. C., Brown, S., & Serences, J. T. (2009). Domain general mechanisms of perceptual decision making in human cortex. Journal of Neuroscience, 29, 8675–8687.
Hyman, R. (1953). Stimulus information as a determinant of reaction time. Journal of Experimental Psychology, 45, 188–196.
Jazayeri, M., & Movshon, J. A. (2006). Optimal representation of sensory information by neural populations. Nature Neuroscience, 9, 690–696. doi:10.1038/nn1691
Kveraga, K., Boucher, L., & Hughes, H. C. (2002). Saccades operate in violation of Hick’s law. Experimental Brain Research, 146, 307–314.
Lawrence, B. M., St John, A., Abrams, R. A., & Snyder, L. H. (2008). An anti-Hick’s effect in monkey and human saccade reaction times. Journal of Vision, 8(3), 26:1–7. doi:10.1167/8.3.26
Leite, F. P., & Ratcliff, R. (2010). Modeling reaction time and accuracy of multiple-alternative decisions. Attention, Perception, & Psychophysics, 72, 246–273. doi:10.3758/APP.72.1.246
Loftus, G. R., & Masson, M. E. J. (1994). Using confidence intervals in within-subject designs. Psychonomic Bulletin Review, 1, 476–490. doi:10.3758/BF03210951
Mulder, M. J., Bos, D., Weusten, J. M., van Belle, J., van Dijk, S. C., Simen, P., . . . Durston, S. (2010). Basic impairments in regulating the speed–accuracy tradeoff predict symptoms of attention-deficit/hyperactivity disorder.. Biological Psychiatry, 68, 1114–1119. doi:10.1016/j.biopsych.2010.07.031
Nelder, J., & Mead, R. (1965). A simplex method for function minimization. The Computer Journal, 7, 308–313.
Niwa, M., & Ditterich, J. (2008). Perceptual decisions between multiple directions of visual motion. Journal of Neuroscience, 28, 4435–4445. doi:10.1523/JNEUROSCI.5564-07.2008
Palmer, J., Huk, A. C., & Shadlen, M. N. (2005). The effect of stimulus strength on the speed and accuracy of a perceptual decision. Journal of Vision, 5(5), 1:376–404. doi:10.1167/5.5.1
Pilly, P. K., & Seitz, A. R. (2009). What a difference a parameter makes: A psychophysical comparison of random dot motion algorithms. Vision Research, 49, 1599–1612. doi:10.1016/j.visres.2009.03.019
Ratcliff, R. (1978). A theory of memory retrieval. Psychological Review, 85, 59–108. doi:10.1037/0033-295X.85.2.59
Roitman, J. D., & Shadlen, M. N. (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience, 22, 9475–9489.
Salzman, C. D., & Newsome, W. T. (1994). Neural mechanisms for forming a perceptual decision. Science, 264, 231–237.
Shadlen, M. N., & Newsome, W. T. (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology, 86, 1916–1936.
Simen, P., Contreras, D., Buck, C., Hu, P., Holmes, P., & Cohen, J. D. (2009). Reward rate optimization in two-alternative decision making: Empirical tests of theoretical predictions. Journal of Experimental Psychology: Human Perception and Performance, 35, 1865–1897. doi:10.1037/a0016926
Smith, P. L., & Vickers, D. (1988). The accumulator model of two-choice discrimination. Journal of Mathematical Psychology, 32, 135–168. doi:10.1016/0022-2496(88)90043-0
Swindale, N. (1998). Orientation tuning curves: Empirical description and estimation of parameters. Biological Cybernetics, 78, 45–56.
Teichner, W. H., & Krebs, M. J. (1974). Laws of visual choice reaction time. Psychological Review, 81, 75–98. doi:10.1037/h0035867
Usher, M., & McClelland, J. L. (2001). The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review, 108, 550–592. doi:10.1037/0033-295X.111.3.757
Usher, M., Olami, Z., & McClelland, J. (2002). Hick’s law in a stochastic race model with speed-accuracy tradeoff. Journal of Mathematical Psychology, 46, 704–715.
van Maanen, L., Brown, S. D., Eichele, T., Wagenmakers, E.-J., Ho, T., Serences, J. T., & Forstmann, B. U. (2011). Neural correlates of trial-to-trial fluctuations in response caution. Journal of Neuroscience, 31, 17488–17495. doi:10.1523/JNEUROSCI.2924-11.2011
van Maanen, L., Grasman, R. P. P. P., Forstmann, B. U., & Wagenmakers, E. J. (2012). Piéron’s law and optimal behavior in perceptual decision-making. Frontiers in Decision Neuroscience, 5, 143.
Vincent, S. B. (1912). The function of the vibrissae in the behavior of the white rat. Animal Behavior Monographs, 1(5).
Wagenmakers, E.-J., & Farrell, S. (2004). AIC model selection using Akaike weights. Psychonomic Bulletin Review, 11, 192–196. doi:10.3758/BF03206482
Wald, A. (1947). Sequential analysis. New York, NY: Wiley.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(PDF 76 kb)
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
van Maanen, L., Grasman, R.P.P.P., Forstmann, B.U. et al. Similarity and number of alternatives in the random-dot motion paradigm. Atten Percept Psychophys 74, 739–753 (2012). https://doi.org/10.3758/s13414-011-0267-7
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13414-011-0267-7