Abstract
People tend to slow down after they make an error. This phenomenon, generally referred to as post-error slowing, has been hypothesized to reflect perceptual distraction, time wasted on irrelevant processes, an a priori bias against the response made in error, increased variability in a priori bias, or an increase in response caution. Although the response caution interpretation has dominated the empirical literature, little research has attempted to test this interpretation in the context of a formal process model. Here, we used the drift diffusion model to isolate and identify the psychological processes responsible for post-error slowing. In a very large lexical decision data set, we found that post-error slowing was associated with an increase in response caution and—to a lesser extent—a change in response bias. In the present data set, we found no evidence that post-error slowing is caused by perceptual distraction or time wasted on irrelevant processes. These results support a response-monitoring account of post-error slowing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
“What does a man do after he makes an error?” This question is just as valid as when it was first articulated by Rabbitt and Rodgers (1977), over 30 years ago. One answer to this question is that, after making an erroneous decision, one slows down on the next decision—an empirical regularity known as post-error slowing (PES; Laming, 1968, 1979a, 1979b; Rabbitt, 1966, 1979; Rabbitt & Rodgers, 1977). However, this answer raises a new and more interesting question: Namely, why does one slow down after making an error? Various answers have been proposed, and one of the main goals of this article is to implement these answers in a formal model of decision making so as to compare their adequacy in a precise and quantitative fashion.
The competing explanations for PES, detailed in the next section, are (1) increased response caution, (2) an a priori bias away from the response that was just made in error, (3) an overall decrease in the across-trial variability of a priori bias, (4) distraction of attention, and (5) delayed startup due to irrelevant processes (e.g., overcoming disappointment). We propose that these five explanations map uniquely onto parameters in a drift diffusion model for response time (RT) and accuracy (Ratcliff, 1978; Ratcliff & McKoon, 2008). As we will explain below, this one-to-one mapping between psychological processes and model parameters allows for an informative diffusion model decomposition of PES and a rigorous assessment of the extent to which each explanation (or, indeed, any combination of them) holds true.
A major practical obstacle that we needed to overcome was that the drift diffusion model requires relatively many observations to produce informative parameter estimates; as a rule of thumb, the model requires at least 10 error RTs in each experimental condition. Because the interest here centered on trials that follow an error, this means that the model required at least 10 errors that immediately followed an error. With an error rate of 5% throughout, the minimum number of observations would already be 4,000. Thus, a reliable diffusion model decomposition of PES would require a relatively large data set (or a data set with many errors). Here we fit the model to a lexical decision data set featuring 39 participants who each completed 28,074 trials of speeded two-choice decisions (Keuleers, Brysbaert, & New, 2010).
In the next sections, we will briefly discuss the different explanations for PES and formalize these predictions in the context of the drift diffusion model. We then test the different explanations by fitting the model to the lexical decision data from Keuleers, Brysbaert, & New (2010).
Explanations for post-error slowing
Over the years, several explanations have been proposed to account for PES. The first explanation (i.e., increased response caution) is that an error prompts people to accumulate more information before they initiate a decision. The underlying idea is that people can adaptively change their response thresholds—becoming slightly less cautious after a correct response, and more cautious after an error—and thereby self-regulate to an optimal state of homeostasis characterized by fast responses and few errors (e.g., Botvinick, Braver, Barch, Carter, & Cohen, 2001; Brewer & Smith, 1989; Cohen, Botvinick, & Carter, 2000; Fitts, 1966; Rabbitt & Rodgers, 1977; Smith & Brewer, 1995; Vickers & Lee, 1998). This explanation is so appealing that it is often assumed to be correct without further testing. That is, PES is often interpreted as a direct measure of cognitive control. Conclusions about cognitive control are then based on associations between PES and physiological measures such as anterior cingulate activity (Li, Huang, Constable, & Sinha, 2006; Danielmeier, Eichele, Forstmann, Tittgemeyer, & Ullsperger, 2011), error-related negativity and positivity (Hajcak, McDonald, & Simons, 2003), or cortisol levels (Tops & Boksem, 2011). Alternatively, conclusions about cognitive control may be based on a comparison of PES between clinical groups (e.g., Shiels & Hawk, 2010).
The second explanation (i.e., a priori bias) is that people become negatively biased against the response option that was just executed in error (e.g., Laming, 1968, 1979b; Rabbitt & Rodgers, 1977). This implies that errors facilitate response alternations and hinder response repetitions, with respect to both response speed and probability of occurrence.
The third explanation (i.e., decreased variability in bias) is that, following an error, people more accurately control the timing of the onset of information accumulation. This idea, first promoted by Laming (1968, 1979a), is that in speeded RT tasks people often start to sample information from the display even before the stimulus is presented. This advance sampling of stimulus-unrelated information induces trial-to-trial variability in a priori bias. This variability may cause fast errors, and therefore a cautious participant would start the information accumulation process at stimulus onset, but not before.
The fourth explanation (i.e., distraction of attention) is that the occurrence of an error is an infrequent, surprising event that distracts participants during the processing of the subsequent stimulus (Notebaert et al., 2009). Thus, the error-induced distraction contaminates the process of evidence accumulation.
The fifth explanation (i.e., delayed startup) is that errors delay the start of evidence accumulation on the next trial; for instance, participants might need time after an error to reassess their own performance level and overcome disappointment (Rabbitt & Rodgers, 1977).
In the literature, the first explanation of PES (i.e., increased response caution) has always been the most dominant. Many studies that associate PES with cognitive control affirm this association simply by citing Rabbitt (1966). However, Rabbitt (1966, p. 272) concluded that his data “do not allow a choice between possible explanations.” Other studies have not tested the competing explanations in a rigorous and quantitative manner (but see White, Ratcliff, Vasey, & McKoon, 2010b). Here, we set out to test the five explanations above in the context of what is arguably the most popular and successful model for RTs and accuracy, the drift diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008).
A drift diffusion model decomposition of response times
In the analysis of speeded two-choice tasks, performance is usually summarized by mean RTs and proportions correct. Although concise, this summary ignores important aspects of the data and makes it difficult to draw conclusions about the underlying cognitive processes that drive performance (Wagenmakers, van der Maas, & Grasman, 2007). A more detailed and more informative analysis would take into account the entire RT distributions for both correct and error responses, in addition to proportions correct. These RT distributions can be analyzed with the help of formal models; here, we focus on the drift diffusion model.
The drift diffusion model has been successfully applied to a wide range of experimental tasks, including brightness discrimination, letter identification, lexical decision, recognition memory, signal detection, and the Implicit Association Test (e.g., Dutilh, Vandekerckhove, Tuerlinckx, & Wagenmakers, 2009; Klauer, Voss, Schmitz, & Teige-Mocigemba, 2007; Ratcliff, 1978; Ratcliff, Gomez, & McKoon, 2004; Ratcliff, Thapar, & McKoon, 2006, 2010; van Ravenzwaaij, van der Maas, & Wagenmakers, 2011; Wagenmakers, Ratcliff, Gomez, & McKoon, 2008). In these tasks and others, the model has been used to decompose the behavioral effects of phenomena such as practice (Dutilh et al., 2009; Dutilh, Krypotos, & Wagenmakers, 2011; Petrov, Horn, & Ratcliff, 2011), aging (Ratcliff, Thapar, & McKoon, 2001, 2006, 2010), psychological disorders (White, Ratcliff, Vasey, & McKoon, 2009, 2010a, 2010b), sleep deprivation (Ratcliff & Van Dongen, 2009), intelligence (Ratcliff, Schmiedek, & McKoon, 2008; Schmiedek, Oberauer, Wilhelm, Süß, & Wittmann, 2007; van Ravenzwaaij, Brown, & Wagenmakers, 2011), and so forth.
The success of the drift diffusion model is due to several factors. First, this model not only takes into account mean RTs, but considers entire RT distributions for correct and error responses; second, the drift diffusion model generally provides an excellent fit to observed data, with relatively few parameters left free to vary; third, the drift diffusion model accounts for many benchmark phenomena (Brown & Heathcote, 2008; but see Pratte, Rouder, Morey, & Feng, 2010); fourth, the model allows researchers to decompose observed performance into constituent cognitive processes of interest; finally, evidence accumulation in the drift diffusion model has been linked to the dynamics of neural firing rates, showing that diffusion-like processes can be instantiated in the brain (e.g., Gold & Shadlen, 2002, 2007). Additional advantages (and limitations) of a diffusion model analysis are discussed in more detail in Wagenmakers (2009).
Here, we briefly introduce the drift diffusion model as it applies to the lexical decision task, a task in which participants have to decide quickly whether a presented letter string is a word (e.g., party) or a nonword (e.g., drapa). The core of the model is the Wiener diffusion process, which describes how the relative evidence for one of two response alternatives accumulates over time. The meandering lines in Fig. 1 illustrate the continuous accumulation of noisy evidence following the presentation of a word stimulus. When the amount of diagnostic evidence for one of the response options reaches a predetermined response threshold (i.e., one of the horizontal boundaries in Fig. 1), the corresponding response is initiated. The darker gray line in Fig. 1 shows how the noise inherent in the accumulation process can sometimes cause the process to end up at the wrong (i.e., nonword) response boundary.
The drift diffusion model as it applies to the lexical decision task. A word stimulus has been presented (not shown), and two example sample paths represent the accumulations of evidence that result in one correct response (lighter line) and one error response (darker line). Repeated applications of the diffusion process yield histograms of both correct responses (upper histogram) and incorrect responses (lower histogram). As is evident from the histograms, the correct, upper, word boundary is reached more often than the incorrect, lower, nonword boundary. The total RT consists of the sum of a decision component, modeled by the noisy accumulation of evidence, and a nondecision component that represents the time needed for processes such as stimulus encoding and response execution
The standard version of the drift diffusion model decomposes RTs and proportions correct into seven different parameters:
-
1.
Mean drift rate (v). Drift rate quantifies the rate of information accumulation from the stimulus. This means that when the absolute value of drift rate is high, decisions are fast and accurate; thus, v relates to task difficulty or subject ability.
-
2.
Across-trial variability in drift rate (η). This parameter reflects the fact that drift rate may fluctuate from one trial to the next, according to a normal distribution with mean v and standard deviation η. The η parameter allows the drift diffusion model to account for data in which error responses are systematically slower than correct responses (Ratcliff, 1978).
-
3.
Boundary separation (a). Boundary separation quantifies response caution and modulates the speed–accuracy trade-off: At the price of an increase in RTs, participants can decrease their error rate by widening the boundary separation (e.g., Forstmann et al., 2008).
-
4.
Mean starting point (z). The starting point reflects the a priori bias of a participant for one or the other response. This parameter is usually manipulated via payoff or proportion manipulations (Edwards, 1965; Wagenmakers et al., 2008; but see Diederich & Busemeyer, 2006). Here, we report z as a proportion of boundary separation a, referred to as bias B.
-
5.
Across-trial variability in starting point (s z ). This parameter reflects the fact that starting point may fluctuate from one trial to the next, according to a uniform distribution with mean z and range s z . The parameter s z also allows the drift diffusion model to account for data in which error responses are systematically faster than correct responses (Laming, 1968; Ratcliff & Rouder, 1998). Analogous to the transformation of z to B, s z is often transformed to s B .
-
6.
Mean of the nondecision component of processing (T er). This parameter encompasses the time spent on common processes—that is, processes executed irrespective of the decision process. The drift diffusion model assumes that the observed RT is the sum of the nondecision component and the decision component (Luce, 1986):
$$ {\text{RT}} = {\text{DT}} + {{T}_{\text{er}}}, $$(1)where DT denotes decision time. Therefore, nondecision time T er does not affect response choice and acts solely to shift the entire RT distribution.
-
7.
Across-trial variability in the nondecision component of processing (s t ). This parameter reflects the fact that nondecision time may fluctuate from one trial to the next, according to a uniform distribution with mean T er and range s t . The parameter s t also allows the model to capture RT distributions that show a relatively shallow rise in the leading edge (Ratcliff & Tuerlinckx, 2002).
As noted above, one of the strengths of the drift diffusion model is that it allows us to decompose observed performance into several latent psychological processes. Such a decomposition relies on the validity of the mapping between model parameters and the postulated psychological processes. Fortunately, many experiments have attested to the specificity and reliability of the model parameters. For instance, Voss, Rothermund, and Voss (2004), Ratcliff and Rouder (1998), and Wagenmakers et al. (2008) showed that accuracy instructions increase boundary separation, easier stimuli have higher drift rates, and unequal reward rates or presentation proportions are associated with changes in starting point. Moreover, simulation studies have shown that the parameters of the diffusion model can be estimated reliably (e.g., Ratcliff & Tuerlinckx, 2002; Wagenmakers, van der Maas, & Molenaar, 2005). Finally, Ratcliff (2002) has shown that the model fits real data but fails to fit fake but plausible data.
From process to parameter: A drift diffusion model perspective on post-error slowing
Many recent applications of the drift diffusion model have been exploratory in nature; for instance, researchers have used the drift diffusion model to study the psychological processes that change with practice (Dutilh et al., 2011; Dutilh et al., 2009), sleep deprivation (Ratcliff & Van Dongen, 2009), hypoglycemia (Geddes et al., 2010), and dysphoria (White et al., 2009, 2010a), but this work has seldom been guided by strong prior expectations and theories. The situation is different in the case of PES, perhaps because explanations for PES have originated in part from a framework of sequential information processing (e.g., Laming, 1979a). Therefore, the competing explanations for PES—in terms of the cognitive processes that change after an error—can be mapped selectively to different parameters in the drift diffusion model, as is shown in Fig. 2.
Thus, the cognitive-process explanation of increased response caution maps onto an increase in boundary separation a; the explanation of a priori bias corresponds to a shift in bias B away from the boundary that was just reached in error; the explanation of decreased variability in bias translates to a decrease in across-trial variability s z ; the explanation of distraction of attention entails a decrease in mean drift rate v; and, finally, the explanation of delayed startup is associated with an increase in mean nondecision time T er. The unique links between processes and parameters mean that competing explanations for PES can be rigorously tested in any particular paradigm, as long as the drift diffusion model applies and the data set is sufficiently large. In the context of PES, the latter concern is particularly acute.
Method
The present data set was originally collected to validate a new measure for word frequency (i.e., SUBTLEX-NL; Keuleers, Brysbaert, & New, 2010). Each of 39 participants contributed 28,074 lexical decisions, for a grand total of 1,094,886 decisions. Half of the stimuli were uniquely presented words, and the other half were uniquely presented nonwords. The word stimuli were selected from the CELEX database (Baayen, Piepenbrock, & van Rijn, 1993), and the nonword stimuli were created with the Wuggy pseudoword generator (Keuleers & Brysbaert, 2010).
The experiment was presented in blocks of 500 trials with a self-paced break after every 100 trials. Each trial started with a 500-ms fixation period. The stimulus was then presented until the participant responded, up to a maximum of 2,000 ms. A new trial started 500 ms after the response. Participants received feedback about their accuracy after each block of 500 trials. Importantly, participants did not receive trial-by-trial feedback concerning errors. This means that any post-error effects were not contaminated by the possibly distracting presence of error feedback. More detailed descriptions of the experimental methods are presented in Keuleers, Brysbaert, & New (2010) and Keuleers, Diependaele, and Brysbaert (2010).
The enormous number of lexical decision trials in this data set featured a commensurate amount of errors; across all participants, 118,566 trials (i.e., 10.80%) contained errors. This abundance of errors allowed us to examine the explanations for PES across various conditions. Specifically, we were able to compare post-error effects separately for nonword and word stimuli of varying word frequencies. That is, we used word frequency (based on SUBTLEX) to divide all words into six equally large bins, the five cut points being 0.11, 0.48, 1.33, 3.73, and 14.16 occurrences per million.
Results and discussion
Below we first discuss the effects of errors on the observed performance—that is, on RTs and proportions correct. Next, we fit the drift diffusion model to the data and discuss the effects of errors on the latent psychological processes hypothesized to explain PES.Footnote 1
Post-error effects on observed data The different hypotheses about PES entail effects on RTs, effects on proportions correct, or a combination of the two. It would therefore be informative to show—both for post-error and postcorrect trials, as well as for different stimulus categories—entire distributions of RTs for correct and error responses, together with proportions correct. A convenient tool to paint this multivariate picture is the quantile probability plot (e.g., Ratcliff, 2002). Figure 3 shows a quantile probability plot for the data from Keuleers, Brysbaert, and New (2010), based on averaging RT quantiles and proportions across individual participants.
Post-error and word frequency effects on RT distributions and accuracy: Each pair of dots on the right half of the figure reflects the distribution of correct RTs in a condition, and its position on the x-axis defines the accuracy in this condition. Each correct-RT distribution on the right half has its incorrect-RT counterpart on the left half of the figure, at one minus the accuracy on the x-axis. Post-error trials are slower and somewhat more accurate than postcorrect trials. This pattern holds for all word stimuli, but it is more pronounced for low-frequency words (“freq 1”) than for high-frequency words (“freq 6”). In addition, the effect is more pronounced in the tail of the RT distribution
Figure 3 features two important factors in the design of this study—that is, post-error trials versus postcorrect trials (i.e., triangles vs. circles) and the word frequency of the current stimulus (including nonwords; different shades of gray). The plot is read as follows. Each column of points summarizes a single RT distribution by five quantiles (i.e., the .1, .3, .5, .7, and .9 quantiles; e.g., the .1 quantile is the RT value for which 10% of the RT distribution was faster; the .5 quantile is the median RT). Each column in the right half of the figure describes a correct-RT distribution for a particular condition; its position on the x-axis shows the corresponding proportion correct (e.g., x = .61 for the postcorrect, low-frequency “freq 1” words). This correct-RT distribution has an associated distribution of incorrect RTs, shown in the left half of the figure (e.g., x = 1 – .61 = .39 for the postcorrect, low-frequency “freq 1” words).
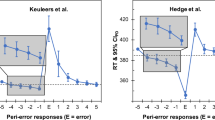
Figure 3 shows that word frequency benefits performance: High-frequency words are associated with low error rates and fast RT quantiles. More important for the present study, RT quantiles are slower after an error (triangles) than after a correct response (circles). The slowdown is smallest in the leading edge of the distribution (for correct responses, on average 3 ms for the .1 quantile) and biggest at the tail (on average 38 ms for the .9 quantile). These PES effects are more pronounced for low-frequency (Frequency Groups 1 and 2) than for high-frequency words. Figure 4 zooms in to the PES effect by presenting the data (and the model fit discussed later) as a delta plot (de Jong, Liang, & Lauber, 1994; Pratte et al., 2010; Speckman, Rouder, Morey, & Pratte, 2008). In a delta plot, the factor of interest—in this case, the PES effect—is shown as a function of response speed. Here, Fig. 4 shows the average PES effect (i.e., the PES effect across all experimental conditions, quantile-averaged across participants). The delta plot indicates that the PES effect is negligible for very fast responses and becomes more prominent when RTs are slow.
Delta plots of PES effect against response speed in postcorrect trials, separately for all word frequencies and nonwords. Solid circles represent the empirical data (error bars indicate standard errors), and lines with open circles represent predictions from the model. For both the empirical data and the model predictions, the effects were obtained by quantile-averaging the results across participants
In the following discussion, we will assess differences between conditions by quantifying the evidence in favor of or against the null hypothesis using a default Bayesian t test (Rouder, Speckman, Sun, Morey, & Iverson, 2009; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009; Wetzels et al., 2011). The resulting Bayes factor BF10 quantifies how much more (or less) likely the data are under the alternative hypothesis than under the null hypothesis. For instance, a BF10 of 2 indicates that the data are twice as likely under the alternative hypothesis than under the null hypothesis, whereas a BF10 of 1/2 indicates that the data are twice as likely under the null hypothesis than under the alternative hypothesis.
For the low-frequency words, accuracy is slightly higher following an error than following a correct response (BF10 = 51.8). For higher word frequencies, no change in accuracy was present (all Bayes factors BF10 < 1/2.61). The small decrease in post-error accuracy for nonwords (about 0.7%) is supported by a Bayes factor of 10.0.
Although the post-error effects in Fig. 3 are qualitatively consistent across different levels of word frequency, it is not unambiguously clear how these effects should be interpreted in terms of underlying psychological processes. The simultaneous increase in RTs and accuracy seems to support an explanation in terms of increased response caution. However, the observed results could also be produced by a combination of increased attention (i.e., drift rate v) and a delayed startup of processing (i.e., nondecision time T er). And, even if one were to ignore this alternative interpretation, it is by no means certain that the observed data would support a single psychological mechanism for PES. In order to address this issue and provide a comprehensive account of the data in terms of the underlying, possibly interacting psychological processes that cause PES, we now turn to a diffusion model decomposition.
Post-error effects on latent processes We fit the model to the individual data using the MATLAB package DMAT (Vandekerckhove & Tuerlinckx, 2007, 2008), which allows the user to estimate the model parameters using maximum likelihood. As noted above, the size of the present data set allowed us to examine several experimental conditions or factors. The primary factor was the Correctness of the Previous Trial, and secondary factors were Stimulus Type (i.e., Word vs. Nonword) on the Current Trial, Word Frequency on the Current Trial, and Stimulus Type on the Previous Trial.
For the secondary factors we used the BIC (Bayesian information criterion; Schwarz, 1978; Raftery, 1995) to eliminate excess parameters and select the most parsimonious model that still gave an acceptable fit to the data. This BIC-best model was then used to quantify the impact of the primary factor of interest; that is, the factor Post-error Versus Postcorrect was allowed to affect all of the diffusion model parameters.
In this BIC-best model, the different factors affected the model’s parameters as follows: Stimulus Type of the Current Trial was allowed to affect drift rate v and its variability η, as well as nondecision time T er. Word Frequency was allowed to affect drift rate v and T er. Stimulus Type of the Previous Trial was allowed to affect bias B and its variability s B . In support of the model selected to analyze the PES effect, Table 1 shows the BIC difference (averaged across participants) between the selected model described above and four alternative models. These alternatives implement restrictions on the selected model to test the necessity of including (1) the effect of word frequency on T er, (2) the stimulus type effect on η, (3) the previous stimulus’s effect on B and its variability s B , and (4) the word frequency effect on v. Table 1 shows that for the postcorrect trials, the alternative models all perform worse than the selected model. This indicates that the parameters excluded in each of the alternative models are essential to account for the data. For the post-error trials, the BIC recommends two alternative models over the selected model. However, the use of different models for the postcorrect and post-error conditions would hinder a direct comparison between them, and therefore we opted to analyze the data with the single model outlined above.
Figure 4, discussed earlier, compares the data against the model predictions. The solid dots represent the empirical data (i.e., the PES effect in all experimental conditions, quantile-averaged across participants), and the lines with open dots represent the predictions of the best-fitting model parameters. Overall, the fit is good, except perhaps for the .9 quantile; this might be due to the fact that this quantile is the most difficult to estimate reliably.
Figures 5 and 6 show the estimates for the diffusion model parameters, averaged over participants. The associated Figs. 7 and 8 present the differences in the model parameters for postcorrect versus post-error trials. The most obvious effect in Figs. 5 and 7 is the increase in boundary separation after an error, shown in the upper left panels of both figures. This increase in boundary separation indicates that, on average, participants became more cautious after committing an error. The Rouder et al. (2009) default Bayesian t test indicated that the data were about 180,000 times more likely under the alternative hypothesis of unequal boundary separation than under the null hypothesis of equal boundary separation; this is considered extreme evidence in favor of an effect.
The four main parameters of the diffusion model, shown separately for postcorrect and post-error trials. Bias B was estimated separately for postword and post-nonword conditions. Drift rate v and nondecision time T er were estimated separately for nonwords and for different categories of word frequency. The most prominent post-error effect is an increase in boundary separation. Error bars represent standard errors of the means
The three variability parameters of the diffusion model, shown separately for postcorrect and post-error trials. All variability parameters are slightly higher for post-error than for postcorrect trials, but the error bars show that these effects are unreliable. Error bars represent standard errors of the means
For each of the four main diffusion model parameters, box plots represent the distributions of the PES effect over participants. Comparisons with the dashed horizontal lines at zero suggest that PES effects express themselves only on boundary separation and a priori bias (after an erroneous nonword response). Boxes contain 50% of the values, and whiskers enclose 80% of the values
For each of the three variability parameters of the diffusion model, box plots represent the distributions of the PES effect over participants. Comparisons with the dashed horizontal lines at zero suggest that PES effects on the variability parameters are not reliable. Boxes contain 50% of the values, and whiskers enclose 80% of the values
The bottom left panels of Figs. 5 and 7 show the post-error effect on bias. After an error, participants shifted their a priori preference toward the “word” response, both when the erroneous response was “word” (BF10 = 11.2) and when it was “nonword” (BF10 > 8.51 × 107). In combination with the overall error-induced increase in boundary separation, this means that following an error, people became somewhat more careful to respond “word,” but even more careful to respond “nonword.” The reason for this asymmetry is currently unclear, and more empirical work will be needed to ascertain whether the asymmetry generalizes to other experimental designs.
The bottom left panel of Fig. 5 also shows a response repetition effect: Participants had a bias toward the response that was executed on the previous trial, regardless of whether that response had been correct (BF10 > 1.35 × 109 for the comparison of bias between postword responses and post-nonword responses) or incorrect (BF10 > 2.34 × 103 for the same comparison).
The right two panels of Figs. 5 and 7 show the post-error effects on drift rate and nondecision time. Neither drift rate (for all frequencies, BF10 < 1/3.06) nor nondecision time (for all frequencies, BF10 < 1/3.00) was affected by whether or not the response on the previous trial was incorrect. Drift rate did increase with word frequency, indicating that high-frequency words were easier to classify than low-frequency words (see also Ratcliff et al., 2004; Wagenmakers et al., 2008). Nondecision time was also affected by word frequency, indicating that processes such as stimulus encoding and response execution took less time for high-frequency words than they did for low-frequency words. This finding is conceptually consistent with that of Dutilh et al. (2011), who found that practice for specific lexical items reduced nondecision time.
Figure 6 shows the estimates for the variability parameters of the diffusion model, averaged over participants. The associated Fig. 8 presents the differences in the model parameters for postcorrect versus post-error trials. The figures suggest that none of the variability parameters are responsible for PES. However, we did find that the variability in drift η was larger for words than for nonwords, replicating the result from an earlier lexical decision study (Dutilh et al., 2009).
In sum, the diffusion model decomposition supports an explanation of PES in terms of increased response caution.
Concluding comments
“What does a man do after he makes an error?” Data from a 1,094,886-trial lexical decision task showed that people slow down after an error, and a diffusion model decomposition showed that this slowdown can be attributed almost exclusively to an increase in response caution. This result confirms the traditional explanation of PES in terms of self-regulation and cognitive control (e.g., Botvinick et al., 2001; Brewer & Smith, 1989; Cohen et al., 2000; Fitts, 1966; Hajcak et al., 2003; Li et al., 2006; Rabbitt & Rodgers, 1977; Shiels & Hawk, 2010; Smith & Brewer, 1995; Tops & Boksem, 2011; Verguts, Notebaert, Kunde, & Wühr, 2011; Vickers & Lee, 1998): That is, people adaptively change their response thresholds to a possibly nonstationary environment—by becoming more daring after each correct response and more cautious after each error, people reach an optimal state of homeostasis that is characterized by fast responses and few errors.
Although this explanation of PES has strong face validity, it is entirely possible that other explanations could also be correct in particular cases. Only by applying a formal process model can we evaluate the competing accounts of PES quantitatively. Our results are partially consistent with those of White et al. (2010b), who applied the drift diffusion model to data from a recognition memory task and found that participants with high trait anxiety responded more carefully after making an error (i.e., increased boundary separation a following an error). However, the data from White et al. (2010b) did not show a response caution effect for participants with low trait anxiety; in addition, their behavioral data did not show a PES effect, and, moreover, the diffusion model decomposition revealed that for both anxiety groups, errors were followed by an unexpected decrease in nondecision time and a decrease in discriminability (i.e., a drift rate difference between targets and lures). Therefore, we feel that our study presents a more compelling case in favor of the increased-response-caution explanation of PES.
The present study shows that the drift diffusion model can be used not only to theorize about the causes of PES, but also to decompose the behavioral aftereffects of an error into its constituent psychological processes. Such a decomposition is considerably more informative than the standard analysis of mean RTs and accuracy, and we believe that future studies of PES can benefit from taking a similar approach.
Notes
The analyses reported here concern the difference between postcorrect trials and post-error trials. Results based on the difference between pre-error and post-error trials yielded quantitatively and qualitatively similar results. The latter results can be found at the first author’s Web site.
References
Baayen, R. H., Piepenbrock, R., & van Rijn, H. (1993). The CELEX lexical database (CD-ROM). Philadelphia: Linguistic Data Consortium, University of Pennsylvania.
Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., & Cohen, J. D. (2001). Conflict monitoring and cognitive control. Psychological Review, 108, 624–652. doi:10.1037/0033-295X.108.3.624
Brewer, N., & Smith, G. A. (1989). Developmental changes in processing speed: Influence of speed–accuracy regulation. Journal of Experimental Psychology: General, 118, 298–310. doi:10.1037/0096-3445.118.3.298
Brown, S. D., & Heathcote, A. (2008). The simplest complete model of choice reaction time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178. doi:10.1016/j.cogpsych.2007.12.002
Cohen, J. D., Botvinick, M., & Carter, C. S. (2000). Anterior cingulate and prefrontal cortex: Who’s in control? Nature Neuroscience, 3, 421–423. doi:10.1038/74783
Danielmeier, C., Eichele, T., Forstmann, B. U., Tittgemeyer, M., & Ullsperger, M. (2011). Posterior medial frontal cortex activity predicts post-error adaptations in task-related visual and motor areas. Journal of Neuroscience, 31, 1780–1789. doi:10.1523/JNEUROSCI.4299-10.2011
de Jong, R., Liang, C.-C., & Lauber, E. (1994). Conditional and unconditional automaticity: A dual-process model of effects of spatial stimulus–response correspondence. Journal of Experimental Psychology: Human Perception and Performance, 20, 731–750. doi:10.1037/0096-1523.20.4.731
Diederich, A., & Busemeyer, J. R. (2006). Modeling the effects of payoff on response bias in a perceptual discrimination task: Bound-change, drift-rate-change, or two-stage-processing hypothesis. Perception & Psychophysics, 68, 194–207. doi:10.3758/BF03193669
Dutilh, G., Krypotos, A.-M., & Wagenmakers, E.-J. (2011). Task-related vs. stimulus-specific practice: A diffusion model account. Experimental Psychology. doi:10.1027/1618-3169/a000111
Dutilh, G., Vandekerckhove, J., Tuerlinckx, F., & Wagenmakers, E.-J. (2009). A diffusion model decomposition of the practice effect. Psychonomic Bulletin & Review, 16, 1026–1036. doi:10.3758/16.6.1026
Edwards, W. (1965). Optimal strategies for seeking information: Models for statistics, choice reaction times, and human information processing. Journal of Mathematical Psychology, 2, 312–329. doi:10.1016/0022-2496(65)90007-6
Fitts, P. M. (1966). Cognitive aspects of information processing: III. Set for speed versus accuracy. Journal of Experimental Psychology, 71, 849–857. doi:10.1037/h0023232
Forstmann, B. U., Dutilh, G., Brown, S. D., Neumann, J., von Cramon, D. Y., Ridderinkhof, K. R., & Wagenmakers, E.-J. (2008). Striatum and pre-SMA facilitate decision-making under time pressure. Proceedings of the National Academy of Sciences, 105, 17538–17542. doi:10.1073/pnas.0805903105
Geddes, J., Ratcliff, R., Allerhand, M., Childers, R., Wright, R. J., Frier, B. M., & Deary, I. J. (2010). Modeling the effects of hypoglycemia on a two-choice task in adult humans. Neuropsychology, 24, 652–660. doi:10.1037/a0020074
Gold, J. I., & Shadlen, M. N. (2002). Banburismus and the brain: Decoding the relationship between sensory stimuli, decisions, and reward. Neuron, 36, 299–308.
Gold, J. I., & Shadlen, M. N. (2007). The neural basis of decision making. Annual Review of Neuroscience, 30, 535–574. doi:10.1146/annurev.neuro.29.051605.113038
Hajcak, G., McDonald, N., & Simons, R. F. (2003). To err is autonomic: Error-related brain potentials, ANS activity, and post-error compensatory behavior. Psychophysiology, 40, 895–903. doi:10.1111/1469-8986.00107
Keuleers, E., & Brysbaert, M. (2010). Wuggy: A multilingual pseudoword generator. Behavior Research Methods, 42, 627–633. doi:10.3758/BRM.42.3.627
Keuleers, E., Brysbaert, M., & New, B. (2010). SUBTLEX-NL: A new measure for Dutch word frequency based on film subtitles. Behavior Research Methods, 42, 643–650. doi:10.3758/BRM.42.3.643
Keuleers, E., Diependaele, K., & Brysbaert, M. (2010). Practice effects in large-scale visual word recognition studies: A lexical decision study on 14,000 Dutch mono- and disyllabic words and nonwords. Frontiers in Psychology, 1, 174. doi:10.3389/fpsyg.2010.00174
Klauer, K. C., Voss, A., Schmitz, F., & Teige-Mocigemba, S. (2007). Process components of the Implicit Association Test: A diffusion-model analysis. Journal of Personality and Social Psychology, 93, 353–368. doi:10.1037/0022-3514.93.3.353
Laming, D. R. J. (1968). Information theory of choice-reaction times. London, U.K.: Academic Press.
Laming, D. (1979a). Autocorrelation of choice-reaction times. Acta Psychologica, 43, 381–412. doi:10.1016/0001-6918(79)90032-5
Laming, D. (1979b). Choice reaction performance following an error. Acta Psychologica, 43, 199–224. doi:10.1016/0001-6918(79)90026-X
Li, R. C., Huang, C., Constable, R. T., & Sinha, R. (2006). Imaging response inhibition in a stop-signal task: Neural correlates independent of signal monitoring and post-response processing. Journal of Neuroscience, 26, 186–192. doi:10.1523/JNEUROSCI.3741-05.2006
Luce, R. D. (1986). Response times: Their role in inferring mental organization. New York, NY: Oxford University Press, Clarendon Press.
Notebaert, W., Houtman, F., Van Opstal, F., Gevers, W., Fias, W., & Verguts, T. (2009). Post-error slowing: An orienting account. Cognition, 111, 275–279. doi:10.1016/j.cognition.2009.02.002
Petrov, A. A., Horn, N. M., & Ratcliff, R. (2011). Dissociable perceptual-learning mechanisms revealed by diffusion-model analysis. Psychonomic Bulletin & Review, 18, 490–497. doi:10.3758/s13423-011-0079-8
Pratte, M. S., Rouder, J. N., Morey, R. D., & Feng, C. (2010). Exploring the differences in distributional properties between Stroop and Simon effects using delta plots. Attention, Perception, & Psychophysics, 72, 2013–2025. doi:10.3758/APP.72.7.2013
Rabbitt, P. (1966). How old and young subjects monitor and control responses for accuracy and speed. Journal of Experimental Psychology, 71, 264–272.
Rabbitt, P. (1979). How old and young subjects monitor and control responses for accuracy and speed. British Journal of Psychology, 70, 305–311.
Rabbitt, P., & Rodgers, B. (1977). What does a man do after he makes an error? An analysis of response programming. Quarterly Journal of Experimental Psychology, 29, 727–743. doi:10.1080/14640747708400645
Raftery, A. E. (1995). Bayesian model selection in social research. In P. V. Marsden (Ed.), Sociological methodology 1995 (pp. 111–196). Cambridge, MA: Blackwell.
Ratcliff, R. (1978). A theory of memory retrieval. Psychological Review, 85, 59–108. doi:10.1037/0033-295X.85.2.59
Ratcliff, R. (2002). A diffusion model account of response time and accuracy in a brightness discrimination task: Fitting real data and failing to fit fake but plausible data. Psychonomic Bulletin & Review, 9, 278–291. doi:10.3758/BF03196283
Ratcliff, R., Gomez, P., & McKoon, G. (2004). A diffusion model account of the lexical decision task. Psychological Review, 111, 159–182. doi:10.1037/0033-295X.111.1.159
Ratcliff, R., & McKoon, G. (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20, 873–922. doi:10.1162/neco.2008.12-06-420
Ratcliff, R., & Rouder, J. N. (1998). Modeling response times for two-choice decisions. Psychological Science, 9, 347–356. doi:10.1111/1467-9280.00067
Ratcliff, R., Schmiedek, F., & McKoon, G. (2008). A diffusion model explanation of the worst performance rule for reaction time and IQ. Intelligence, 36, 10–17. doi:10.1016/j.intell.2006.12.002
Ratcliff, R., Thapar, A., & McKoon, G. (2001). The effects of aging on reaction time in a signal detection task. Psychology and Aging, 16, 323–341. doi:10.1037/0882-7974.16.2.323
Ratcliff, R., Thapar, A., & McKoon, G. (2006). Aging, practice, and perceptual tasks: A diffusion model analysis. Psychology and Aging, 21, 353–371. doi:10.1037/0882-7974.21.2.353
Ratcliff, R., Thapar, A., & McKoon, G. (2010). Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology, 60, 127–157. doi:10.1016/j.cogpsych.2009.09.001
Ratcliff, R., & Tuerlinckx, F. (2002). Estimating parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin & Review, 9, 438–481. doi:10.3758/BF03196302
Ratcliff, R., & Van Dongen, H. P. A. (2009). Sleep deprivation affects multiple distinct cognitive processes. Psychonomic Bulletin & Review, 16, 742–751. doi:10.3758/PBR.16.4.742
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16, 225–237. doi:10.3758/PBR.16.2.225
Schmiedek, F., Oberauer, K., Wilhelm, O., Süß, H.-M., & Wittmann, W. W. (2007). Individual differences in components of reaction time distributions and their relations to working memory and intelligence. Journal of Experimental Psychology: General, 136, 414–429. doi:10.1037/0096-3445.136.3.414
Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461–464.
Shiels, K., & Hawk, L. W., Jr. (2010). Self-regulation in ADHD: The role of error processing. Clinical Psychology Review, 951–961. doi:10.1016/j.cpr.2010.06.010
Smith, G. A., & Brewer, N. (1995). Slowness and age: Speed–accuracy mechanisms. Psychology and Aging, 10, 238–247. doi:10.1037/0882-7974.10.2.238
Speckman, P. L., Rouder, J. N., Morey, R. D., & Pratte, M. S. (2008). Delta plots and coherent distribution ordering. American Statistician, 62, 262–266. doi:10.1198/000313008X333493
Tops, M., & Boksem, M. A. S. (2011). Cortisol involvement in mechanisms of behavioral inhibition. Psychophysiology, 48, 723–732. doi:10.1111/j.1469-8986.2010.01131.x
Vandekerckhove, J., & Tuerlinckx, F. (2007). Fitting the Ratcliff diffusion model to experimental data. Psychonomic Bulletin & Review, 14, 1011–1026. doi:10.3758/BF03193087
Vandekerckhove, J., & Tuerlinckx, F. (2008). Diffusion model analysis with MATLAB: A DMAT primer. Behavior Research Methods, 40, 61–72. doi:10.3758/BRM.40.1.61
van Ravenzwaaij, D., Brown, S., & Wagenmakers, E.-J. (2011). An integrated perspective on the relation between response speed and intelligence. Cognition, 119, 381–393. doi:10.1016/j.cognition.2011.02.002
van Ravenzwaaij, D., van der Maas, H. L. J., & Wagenmakers, E.-J. (2011). Does the name–race Implicit Association Test measure racial prejudice? Experimental Psychology, 58, 271–277. doi:10.1027/1618-3169/a000093
Verguts, T., Notebaert, W., Kunde, W., & Wühr, P. (2011). Post-conflict slowing: Cognitive adaptation after conflict processing. Psychonomic Bulletin & Review, 18, 76–82. doi:10.3758/s13423-010-0016-2
Vickers, D., & Lee, M. D. (1998). Dynamic models of simple judgments: I. Properties of a self-regulating accumulator module. Nonlinear Dynamics, Psychology, and Life Sciences, 2, 169–194. doi:10.1023/A:1022371901259
Voss, A., Rothermund, K., & Voss, J. (2004). Interpreting the parameters of the diffusion model: An empirical validation. Memory & Cognition, 32, 1206–1220. doi:10.3758/BF03196893
Wagenmakers, E.-J. (2009). Methodological and empirical developments for the Ratcliff diffusion model of response times and accuracy. European Journal of Cognitive Psychology, 21, 641–671. doi:10.1080/09541440802205067
Wagenmakers, E.-J., Ratcliff, R., Gomez, P., & McKoon, G. (2008). A diffusion model account of criterion shifts in the lexical decision task. Journal of Memory and Language, 58, 140–159. doi:10.1016/j.jml.2007.04.006
Wagenmakers, E.-J., van der Maas, H. L. J., & Grasman, R. P. P. P. (2007). An EZ-diffusion model for response time and accuracy. Psychonomic Bulletin & Review, 14, 3–22. doi:10.3758/BF03194023
Wagenmakers, E.-J., van der Maas, H. L. J., & Molenaar, P. C. M. (2005). Catastrophe theory. In B. S. Everitt & D. C. Howell (Eds.), Encyclopedia of statistics in behavioral science (pp. 234–239). Chichester, U.K.: Wiley.
Wetzels, R., Matzke, D., Lee, M. D., Rouder, J. N., Iverson, G. J., & Wagenmakers, E.-J. (2011). Statistical evidence in experimental psychology: An empirical comparison using 855 t tests. Perspectives on Psychological Science, 6, 291–298. doi:10.1177/1745691611406923
Wetzels, R., Raaijmakers, J. G. W., Jakab, E., & Wagenmakers, E.-J. (2009). How to quantify support for and against the null hypothesis: A flexible WinBUGS implementation of a default Bayesian t test. Psychonomic Bulletin & Review, 16, 752–760. doi:10.3758/PBR.16.4.752
White, C., Ratcliff, R., Vasey, M., & McKoon, G. (2009). Dysphoria and memory for emotional material: A diffusion-model analysis. Cognition and Emotion, 23, 181–205. doi:10.1080/02699930801976770
White, C. N., Ratcliff, R., Vasey, M. W., & McKoon, G. (2010a). Anxiety enhances threat processing without competition among multiple inputs: A diffusion model analysis. Emotion, 10, 662–677. doi:10.1037/a0019474
White, C. N., Ratcliff, R., Vasey, M. W., & McKoon, G. (2010b). Using diffusion models to understand clinical disorders. Journal of Mathematical Psychology, 54, 39–52. doi:10.1016/j.jmp. 2010.01.004
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Dutilh, G., Vandekerckhove, J., Forstmann, B.U. et al. Testing theories of post-error slowing. Atten Percept Psychophys 74, 454–465 (2012). https://doi.org/10.3758/s13414-011-0243-2
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13414-011-0243-2