Abstract
Choice reaction time generally increases linearly with the logarithm of the number of potential stimulus–response alternatives, a regularity known as Hick’s law. Two apparent violations of this generalization, which have been reported for aimed eye movements (Kveraga, Boucher, & Hughes, Experimental Brain Research, 146, 307–314, 2002), and arm movements (Wright, Marino, Belovsky, & Chubb, Experimental Brain Research, 179, 475–496, 2007), occurred when the indicator stimulus was an abrupt change at the location that was the target of the to-be-made movement. We report two experiments that examined and rejected the hypothesis that these abrupt-onset indicator stimuli triggered a shift in exogenous attention and that this led to unusually small uncertainty effects. Each experiment compared this indicator stimulus with a single alternative: Experiment 1 tested an indicator stimulus at all locations other than the target; Experiment 2 tested a central pointer to the target. Neither alternative led to an uncertainty effect for pointing responses that was of the size typically observed for other responses using the same stimuli.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Hick’s law characterizes the uncertainty effect in choice reaction time tasks as an increase of response latency that is linear with the logarithm of the number of potential stimulus–response (S–R) alternativesFootnote 1 (Hick, 1952; Hyman, 1953). Although the size of this increase depends on the stimuli, the responses, and the level of practice, reaction times typically increase by as much as 100–150 ms for each doubling in the number of alternatives. For over 50 years, the accepted explanation of this uncertainty effect has implicated the S–R mapping process. Consistent with this explanation, it has generally been found that the size of the uncertainty effect increases for tasks with low S–R compatibility and that the effect is minimized for tasks with high S–R compatibility (Dassonville, Lewis, Foster, & Ashe, 1999; Teichner & Krebs, 1974).
Recently, several apparent violations of this generalization have been documented in which the latency to initiate certain types of movements is either independent of the number of possible S–R pairs or so small (several milliseconds for each doubling in the number of alternatives) as to seem almost negligible. Kveraga, Poucher, and Hughes (2002) showed such results for eye movements, and Wright, Marino, Belovsky, and Chubb (2007) showed them for aimed hand movements. These articles also reported data from conditions in which an identical stimulus arrangement led to a normal-sized uncertainty effect for spatially compatible keypress responses, a task that is functionally similar to the buttonpress tasks often studied in Hick’s law research.
This pattern of results presents a challenge for the standard interpretation that uncertainty effects are due to the S–R mapping process. If two S–R mappings are highly compatible and all that has changed is the response mode, it seems difficult within the framework of S–R compatibility to describe a principle that explains the change from an uncertainty effect close to zero to one that is large. Proponents of S–R compatibility as the primary determinant of the uncertainty effect (e.g., Lee, Keller, & Heinen, 2005) suggest that aimed eye or hand movements, such as those just described, involve an S–R mapping that is “direct” and thus has a negligible influence on latency. Although this explanation seems intuitively plausible, it is difficult to identify what makes the mappings in pointing tasks more direct than those in the buttonpress tasks, which the keypress tasks of Kveraga et al. (2002) and Wright et al. (2007) were intended to simulate. Buttonpress tasks pair an array of lights as the stimuli with an equal number of push-buttons for the responses. Each button is located directly below the single light for which it is the response. When a light flashes on, the participant responds by depressing the finger placed on the button directly below that light. The mapping here might thus be seen as straightforward or “direct”; however, this task has been found to produce uncertainty effects of well over 100 ms per doubling in the number of alternatives (Brainard, Irby, Fitts, & Alluisi, 1962; Hick, 1952; Hyman, 1953).
To add to the puzzle, Kveraga et al. (2002) and Wright et al. (2007) were not the first times that such dramatic changes in the size of the uncertainty effect had been observed to depend on the response modality. As Teichner and Krebs (1974) summarized in their meta-analysis, responding by naming stimuli that are digits or letters produces little or no uncertainty effect (Brainard et al., 1962; Mowbray, 1960). Interestingly, letters and digits appear to be special in this regard, for when a task involves naming familiar colors, animals, and faces, there is once again a substantial uncertainty effect (Morin, Konick, Troxell, & McPherson, 1965).
Another explanation, intended to reconcile the digit-naming data with the hypothesis that uncertainty effects arise from S–R processing, is that a mechanism in the digit-naming task bypasses the normal S–R processing stage altogether (Teichner & Krebs, 1974). Bypass mechanisms such as this have been called “privileged loops” by McLeod and Posner (1984). Kveraga et al. (2002) proposed that mechanisms in superior colliculus play a similar role in the case of eye movements. However, neither of these proposed privileged-loop mechanisms seems applicable as an explanation for the lack of an uncertainty effect for pointing responses. Of course, one might posit yet another, task-specific, privileged-loop mechanism for these pointing responses (but see Wright et al., 2007, where the reported data suggest that if such a privileged loop exists, it is not mediated by a mechanism in parietal cortex). However, each new class of response mode that fails to show an uncertainty effect lessens the appeal of accounts based on privileged-loop mechanisms. The main point of the present report is to explore an explanation for the apparent lack of an uncertainty effect when the responses are aimed hand or eye movements.
Attention mechanism hypothesis
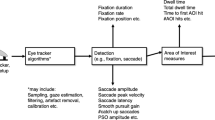
In contrast to most of the non-vocal-response tasks associated with Hick’s law, the experiments documenting the lack of an uncertainty effect for eye movements and aimed hand movements used as their indicator stimulus—that is, the stimulus indicating which response the participant was to make on a particular trial—an abrupt onset at the exact location that was also the target of the required eye movement or pointing response. This difference may be important, because transient signals can trigger exogenous shifts in attention, and as several authors have argued, such shifts of exogenous attention may automatically generate such movement plans as would be necessary to guide the hand or eyes to the location of the stimulus (for a review, see Umiltà, 2000). If an abrupt stimulus can lead to the automatic creation of a movement plan directed to its location, and that plan can simply be released, then this mechanism could bypass the bottleneck of S–R mapping. Figure 1 illustrates the privileged-loop mechanism that is consistent with this attention mechanism hypothesis. Experiment 1 will test this hypothesis using pointing responses; however, we feel that it might also apply to eye movement responses.
Model of motor mechanisms from perception to execution. Each stage in the model is executed in sequential order until control is passed to the next stage. The dotted line indicates how exogenous mechanisms might bypass the normal S–R mapping mechanism in a strict-stage motor execution model and go directly to motor planning
Note that the tasks to which our hypothesis might apply do not include the buttonpress task described earlier. In that task, the required response is not to move to the light, which is an abrupt-onset indicator stimulus, but to push a button on which a finger is pre-positioned. Although this button is spatially proximate to the light—typically located directly below and within 2 cm—its location does differ from that of the light, so an automatic response directed toward the stimulus would result in an error. Viewed this way, it is possible to see the attention mechanism hypothesis as a specific instantiation of the direct-mapping concept described previously.
As in the research of Wright et al. (2007), here we will study identical stimulus arrangements using two types of response. In addition, however, the present experiments will include two types of indicator stimulus. The stimulus arrangements consist of two or six, out of a possible eight, white outline circles. The two response types compare an aimed pointing movement, made by the arm to an indicated target location, with a keypress response—that is, a finger movement to press an indicated response key, with one key uniquely associated with each finger using a spatially compatible mapping.
The inclusion of the two types of indicator stimulus will provide an opportunity to test whether the lack of an uncertainty effect for pointing movements depends on whether the abrupt-onset indicator stimulus is or is not at the location of the movement target, while keeping the abrupt onset and the peripheral nature of the indicator stimulus the same. In the condition based on the methods used previously with aimed-movement responses, the indicator stimulus is a change of the interior of the stimulus circle associated with the correct response from the background gray to a white that matches the outline circle. In the pointing condition, this circle is the target of the correct response. In the keypress condition, each circle is consistently mapped to a single response key, and the associated key should be pressed when the stimulus circle fills in. Results from this “target-on” indicator stimulus condition will be compared with those from a second “distractors-on” condition, in which the indicator stimulus is the abrupt onset of changes at the distractor locations: That is, all stimulus circles other than the one indicating the correct response are filled. Therefore, in one condition the required response is indicated by an abrupt change at the location of the pointing-response target, whereas in the second condition the required response is indicated without any change at this location. Note that in the keypress condition, the indicator stimulus in both the target- and distractor-on conditions is spatially separated from the location of the required response in identical ways.
Experiment 1
Method
Participants
There were 10 participants (5 male, 5 female); all had vision correctible to 20/20 or better and were right-handed. They were paid $8/h supplemented with small, performance-based bonuses. The UCI Institutional Review Board approved the experiment.
Apparatus
A PC running a custom application written in C was used to present stimuli and record responses. Participants used a handheld, lightweight stylus to touch the target on the monitor—a Dell Model M991 CRT display, running at a 60-Hz refresh rate with a resolution of 1,024 x 768 pixels (see Fig. 1 of Wright et al., 2007, for a photograph showing the experimental setup). This monitor was mounted within a specially built desktop so that its surface was angled up from horizontal by 20°. An Optotrak Model 3020 recorded, with a 100-Hz sampling rate, the x-, y-, and z-coordinates of an infrared emitter mounted on the tip of the stylus. A disk with a small indentation, mounted on the surface of the monitor case 140 mm closer to the participant than the fixation point, served as the starting point for the stylus at the beginning of each trial.
Design
Each participant ran for five sessions, each lasting about 1 h. The first of these was treated as a practice day in which participants were exposed to all of the experimental manipulations.
This experiment had a fully within-subjects design. There were seven independent variables and either two or four dependent variables, depending on the response condition. In the keypress condition, the two dependent variables recorded were response latency—that is, the time from stimulus onset until a response key was pressed—and the particular response key that was pressed. In the pointing condition, the four dependent variables were (1) latency to initiate a movement—that is, the time from stimulus onset until the onset of a pointing movement was detected; (2) duration—that is, the time from movement onset until the end of the movement was detected; (3) end point error—that is, the distance between the movement and the center of the target circle; and (4) response error—which coded whether or not the movement ended outside the target circle, as well as several other error conditions that could occur.
There were seven independent variables. Three of these varied from trial to trial: (1) stimulus position (one of eight possible locations), (2) repetition (i.e., whether the stimulus/response for a trial matched that of the previous trial), and (3) cue onset delay. Two other variables were fixed within a block but varied across blocks within a test session: (4) number of possible targets (N = 2 or N = 6) and (5) stimulus arrangement. The last two independent variables, (6) response mode (keypress or pointing) and (7) type of indicator stimulus (target-on or distractor-on), were both fixed within all blocks of a test session but varied across test sessions, with one of the four combinations of these two variables occurring on each of the four test days. Their order was balanced across sets of participants using digram-balanced Latin squares.
Repetition was treated as an independent variable because studies have shown that participants are generally faster to respond when targets repeat (Kornblum, 1969). This is particularly an issue when, as in this experiment, the size of the set of possible targets varies. To appreciate the importance of taking this variable into account, consider that when there are two possible targets, repetitions are three times more likely to occur than when there are six possible targets.
Figure 2 shows the spatial arrangement of the eight possible indicator stimuli and pointing response targets used in this task, along with their relation to the starting position used for pointing responses. The subsets of these locations used in a block were constrained to include equal numbers of locations to the right and to the left of the vertical axis of symmetry. Due to this constraint, there are exactly 16 ways of selecting sets of either two or six locations. Each of these stimulus arrangements was used once in the 32 test blocks. A session was composed of 36 blocks: 4 practice blocks followed by the 32 test blocks, which alternated between N = 2 and N = 6 blocks. Each block consisted of 18 error-free trials with 2 catch trials included to help eliminate anticipatory movements.
Scale diagram showing the stimulus display and the starting point for pointing responses. The eight possible stimuli/response targets were 15-mm-diameter white circles on the gray background of the CRT display. They were located on a semicircle with a radius of 50 mm at angles of ±15°, ±45°, ±75°, and ±105° from vertical. The fixation mark was a cross made of 1-cm lines at the center of this circle. The starting point for pointing responses is denoted by the black dot on the case of the display, 140 mm below the fixation
Cue onset time varied from trial to trial and was randomly selected on each trial according to a truncated discrete approximation to an exponential distribution at time points separated by 16.67 ms, in the range from 100 ms before to 350 ms after the point in time when the stimulus would normally have been expected given the fixation sequence (see details below).
Procedures
Procedures for pointing sessions
Due to differences in height and position relative to the computer monitor across participants, each session began with a calibration procedure in which the Optotrak coordinates of the stylus were determined for perceived locations on the display screen. Each participant touched the stylus to the center of nine squares displayed in an array, each with known pixel values. From these data, a linear transformation was estimated that mapped the screen coordinates into the three-dimensional coordinate system of the Optotrak. At the end of this calibration process, the participants checked to be sure that the registration was accurate before beginning each block.
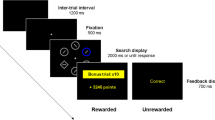
Each trial began with the screen blank except for a message to move the cursor to the starting location. After the stylus had remained within 3 mm of the starting location for 250 ms, this message disappeared, and a subset of two or six of the eight possible white circles (see Fig. 2) appeared, one at each of the possible target positions determined by the stimulus arrangement in use for the block. At this point, the fixation display sequence also began. The fixation cross blinked on for 500 ms and off for 500 ms for two cycles; this both directed visual attention to the fixation point and set up a temporal expectation of the target. The randomly selected stimulus onset time C was drawn from a distribution constructed so that the mean stimulus onset time coincided with the time T when the flashing fixation sequence would have begun its third cycle. If the stylus was lifted away from the starting location at any time before T – 150 ms, an error message was presented and the trial was restarted. If the stylus moved out of the starting area before C + 100 ms or, for a catch trial, any time up to T + 500 ms, the movement was labeled an anticipation error, an error message was displayed, and a new trial was randomly selected.
The factor Type of Indicator Stimulus had two conditions. In the target-on condition, the indicator stimulus was a change that occurred at the location of the target: The dark inside of one of the potential target circles was filled in to match the white outline of the circle. In this condition, the participant was instructed to move the stylus quickly to a point within that circle. In the distractor-on condition, the indicator stimulus was a change that occurred away from the target location: The target stimulus circle remained unchanged, while the dark inside of each of the nontarget distractors was filled in to match the white outline of the circle. The participant was instructed to move the stylus quickly to a point within the unchanged circle.
The instructions, like those of a discrete Fitts (1954) task, emphasized minimizing the total time to complete the movement and treated all movements ending within the target circle as correct, while all movements ending outside the target circle were labeled errors. The movement was determined to have begun when the stylus moved more than 3 mm in any direction from the starting location. The movement was determined to have ended when the stylus came within 2 mm of the surface of the display. (The calibration procedure estimated the curvature of the display surface, and this curvature was taken into account when determining the end of the movement.) Movement trajectory data were retained starting 500 ms before the target cue onset and ending 500 ms after the movement was determined to have ended.
Procedures for keypress sessions
The keypress task was indistinguishable from the pointing task in timing, stimulus arrangement, and presentation. Additionally, the feedback was identical for both bonuses and target scores, which are both fully described below. The primary difference in keypress task sessions was that, in response to the indicator stimulus, participants were to depress a key on a standard computer keyboard rather than use the stylus to respond with a single, aimed, pointing arm movement.
The keys used were on the home row: “A,” “S,” “D,” and “F” were used for the left-hand responses, and “J,” “K,” “L,” and “;” for the right-hand responses. At the start of each trial, the participant positioned the fingers of the two hands on or just above these keys. Because the extent of the movement required to press a key was minimal, movement trajectories were not collected, the responses were registered based solely on the activations of the keys, and the Optotrak calibration was not done.
The mapping of response fingers/keys onto the eight possible stimulus locations was fixed within and across participants. Because the combination of possible target locations used as stimuli varied from block to block, the finger/key combinations used to make responses also changed from block to block. In the N = 2 condition, in which only one finger on each hand was used to make responses, there was little tendency to be confused about the finger/key required to respond to the stimulus on any given trial. However, in the N = 6 condition, initially associating each stimulus in the set with the finger/key with which to respond sometimes posed a challenge. To help participants overcome this challenge, at the start of each block, the set of target locations for that block was displayed. Then, in turn, each target location was highlighted, and the letter on the keyboard associated with the key that was the response for that target was displayed until the appropriate key was pressed.
The instructions emphasized that all eight of the participant’s fingers should be on the appropriate response keys at the start of each trial, even in the N = 2 blocks. A human experimenter monitored the participant’s responses to ensure that these instructions were followed.
Feedback and bonuses in both session types
After each pointing or keypress response, a message was displayed giving the movement time in hundredths of a second. In addition, after a pointing response, a small marker was displayed at the location on the screen determined to be the movement endpoint. If the wrong key was pressed or if the pointing-movement endpoint was outside the target region, the message missed target was also displayed. This feedback stayed on the screen for 2 s. At the end of this period, the display was cleared and a new trial began.
After the last trial in each block, the display was cleared and a message was presented summarizing for the participant his/her performance and providing a score for the block. In addition to the score, this summary included the average total movement time, in hundredths of a second, the count of the number of errors—that is, trials on which the movement missed the target—and the count of the number of anticipation errors. The score was calculated as the sum of the average total movement time (in hundredths of a second; typically about 40 in the keypress task and 55 in the pointing task), three points for each missed target, and five points for each anticipation error. The participant received a bonus of $0.05 for each block in which the score was less than or equal to a target score for that block. The bonuses were designed to reward good performance. Four separate target scores were maintained for each participant, reflecting the four combinations of the two response conditions and the two levels of N. At the end of each block, the appropriate one of these scores was adjusted based on the average score for that block. Let T i be the target score for block i and S i the score for that block. T 1 was always set to 100, a value larger than the expected score for the first block of any condition. Subsequent target scores were computed according to a recursive formula.
Processing of movement trajectories
For the analyses of the trajectories, the raw trajectories were first fit using a smoothing spline, computed to maintain a tolerance of 0.5 mm between the measured and smoothed values, and temporally resampled to have 21 points. Thus, the interval between pairs of the resampled trajectory points corresponded to 5% of the duration of the original movement trajectory.
Results
Although there were seven factors in the experimental design, we have chosen to analyze the data by collapsing over three of these factors: cue onset delay, stimulus arrangement, and stimulus position. The primary purpose of including these three variables in the experiment was to minimize potential confounds by ensuring that their effects were balanced across the levels of the factors being analyzed. However, we did analyze the full design and found that although these three variables influenced the data in important ways, their effects never interacted with those factors analyzed here. The four independent variables used in the analyses reported were N (number of targets: two or six), repetition (repeat or no repeat of trial), response mode (keypress or pointing), and type of indicator stimulus (target-on or distractors-on). The dependent variable of primary interest was latency in both the keypress and pointing conditions. In addition, for completeness, the duration and the endpoint error for the pointing responses are also summarized.
Errors
Across participants, 4 trials in the keypress response condition (0.04%) and 58 trials in the pointing response condition (0.5%) were discarded and rerun within the same block because of problems recording the data: For instance, multiple keys were pressed “simultaneously” in the keypress condition, or the Optotrak was unable to see the stylus emitter in the pointing condition.
There were few anticipation errors—that is, movements made on a catch trial or movements that began within 100 ms of the stimulus onset on a normal trial; this happened on 13 trials (0.12%) in the keypress response condition and on 53 trials (0.47%) in the pointing response condition. This suggests that the inclusion of catch trials successfully induced the participants to wait for the cue stimulus before initiating a response. These trials were also detected as they happened and rerun within the same block.
Once the experiment was complete, separate analyses were done for the keypress and pointing conditions to identify trials with unusually long or short latencies relative to the distribution of each participant. To make the latency distributions more symmetric, this analysis was done after taking the log of the data. A latency was flagged as unusually short or long if it was more than three times the interquartile range away from the median. This analysis identified as having suspiciously short latencies 1 trial in the keypress condition and 28 trials (0.26%) in the pointing condition. In addition, this analysis identified as having suspiciously long latencies 19 trials (0.18%) in the keypress condition and 7 trials (0.06%) in the pointing condition. The data from these trials with suspiciously long or short latencies were not included in subsequent analyses. Because these trials could only be identified after the participant running was complete, they were not rerun.
In the pointing response condition, a trial was classified as an error when the movement ended outside the target circle; trials in the keypress response condition were classified as errors when an incorrect key was pressed. Overall, there was an average of 3.2% errors. However, a four-way analysis of variance on the error proportions after an arcsine transformation, with Response Mode, Repetition, Indicator Stimulus, and N as the factors, showed that the percentage of errors varied reliably across conditions. Table 1 summarizes the important aspects of this variation. The means involved in a significant three-way interaction involving response mode, indicator stimulus, and N, F(1, 11) = 8.121, p = .016, are shown in the left part of Table 1. Embedded within this three-way interaction is a strong two-way interaction between response mode and N, F(1, 11) = 23.685, p = .001. This can be seen looking at the differences across Ns in the bottom row of the table. For keypress responses (the first and second columns), the error rate increased as N increased, F(1, 11) = 19.138, p = .001; however, for pointing responses (the third and fourth columns), the error rate actually decreased significantly as N increased, F(1, 11) = 6.99, p = .023. The differences across Ns in the bottom row also provide a way to see the nature of the three-way interaction. For the keypress responses (the first and second columns), there was a two-way simple interaction between stimulus indicator and N, F(1, 11) = 18.818, p = .001: The effect of N was larger and statistically reliable only for the target-on condition, F(1, 11) = 25.699, p = .001 [F(1, 11) = 1.383, p > .25, for the distractors-on condition]. This two-way simple interaction was absent for the pointing responses, F(1, 11) = 0.018.
The rightmost two columns of Table 1 show the mean error percentages involved in the two-way interaction of repetition and N, F(1, 11) = 10.607, p = .008. For trials in which the stimulus and response were repeated, there was no reliable effect of N, F(1, 11) = 0.532. However, for trials that did not involve a repetition, the percentage of errors increased with N, F(1, 11) = 31.953, p = .001. All the other comparisons in the ANOVA produced p > .10.
Latency
The latency data are summarized in Fig. 3. The four panels break out the data by the four possible combinations of response mode and indicator stimulus. Each panel has two parts. The display in the left part of each panel shows the breakdown of latency by N and repetition, along with the associated 95% confidence intervals computed after removing the main effect of participants so as to better reflect the results of the repeated measures analyses of these data (Loftus & Masson, 1994). The display in the right part of each panel shows the uncertainty effect slope—that is, the increase in latency for each doubling in N, along with its 95% confidence interval. Note that the vertical scales are different on the right and left sides of each panel. The vertical scale used on the left differs between the panels on the top row, the pointing responses, and the panels on the bottom row, the keypress responses; however, the scale used on the right side of each panel is identical across all four panels.
Latency data for Experiment 1. Each panel shows data from one of the four combinations of response (keypress or pointing) and type of indicator (target-on or distractors-on). The four points on the left in each panel show the mean data broken out by N and repetition. The two data points on the right show, separately for repeat and nonrepeat trials, the uncertainty effect slope: that is, the increase in latency for each doubling in N. The error bars are 95% confidence intervals computed after the estimated main effect of participants was removed
An ANOVA on these data revealed that the differences between conditions are dominated by two significant three-way interactions: Response Mode x N x Repetition, F(1, 11) = 25.406, p = .000, and Response Mode x N x Type of Indicator Stimulus, F(1, 11) = 9.198, p = .011. Neither of the two remaining three-way interactions nor the four-way interaction was statistically significant; the strongest of these was the four-way interaction, F(1, 11) = 1.382, p = .265. Table 2 presents the data underlying the two significant three-way interactions. Because of its importance as a way of characterizing the uncertainty effect, the summary used here is the slope of the uncertainty effect.
The leftmost three columns of Table 2 show comparisons that explain the interaction of Response Mode x N x Indicator Stimulus, collapsing across repetition. The top-left 2 x 2 subtable contains estimates of the uncertainty effect slope for each of the four combinations of response mode and indicator stimulus. The clear pattern here is that the effect of increasing uncertainty is strong for the keypress responses and indistinguishable from 0 for the pointing responses. The differences in the third row of these two columns simply confirm that this response mode difference is reliable for both levels of indicator stimulus. The entries in the third column show how the size of the uncertainty effect depends on the type of indicator stimulus. The entries in the top two rows give this comparison separately for each level of response mode and show that the size of the uncertainty effect depends on the indicator stimulus for keypress responses and not for pointing responses. Stated in the terminology of ANOVA, these differences estimate the effect sizes for the 2 x 2 simple interaction of N and stimulus indicator at each level of response mode: for the keypress responses, F(1, 11) = 10.176, p = .009; for pointing responses, F(1, 11) = 0.179. The difference in these effect size estimates, shown in the third row of the third column, estimates the effect size of the three-way interaction reported above.
Columns four to six of Table 2 show comparisons that summarize the interaction of Response Mode x N x Repetition, collapsing across the types of indicator stimulus. The overall pattern here is virtually identical to that in the first three columns. Again there are strong uncertainty effects for keypress responses and negligible or small, but still statistically significant (in the case of nonrepetition trials), effects for pointing responses. The effect of repetition is also similar. The 2 x 2 simple interaction of N and repetition is statistically significant for the keypress responses, F(1, 11) = 50.098, p = .000, but not for pointing responses, F(1, 11) = 0.619.
The final column shows the average uncertainty effect for each level of response mode, collapsing over both the Indicator Stimulus and Repetition factors. The difference across the levels of response mode, in the third row, estimates the effect size of the significant two-way N x Response Mode interaction: F(1, 11) = 266.766, p = .000.
Duration
Duration data were collected only for the pointing condition, because the keypress responses were defined to be complete at the end of the latency interval. The mean duration was 369 ms (SE = 14). The duration data were analyzed using a 2 x 2 x 2 ANOVA with N, Repetition, and Indicator Stimulus as the three within-subjects factors. This analysis showed that the durations differed across conditions and that these differences were dominated by the significant two-way interaction of N x Repetition, F(1, 11) = 9.934, p = .009, and also reflect the marginally significant interaction of N x Indicator Stimulus, F(1, 11) = 4.639, p = .054. The three-way interaction and the remaining two-way interaction both had F(1, 11) < 1.
Collapsed across both indicator stimulus and repetition, there was a significant increase in duration going from N = 2 to N = 6 [6.1 ms; 95% confidence interval 4.0↔8.1 ms; F(1, 11) = 35.915, p = .000]. Consistent with the significant interaction of N x Indicator Stimulus, this increase was larger for the distractors-on condition (11.7 ms; 5.7↔17.7 ms) than for the target-on condition (0.5 ms; –5.6↔6.6 ms). Similarly, the size of the duration difference going from N = 2 to N = 6 also depended on whether a trial was a repetition (2.8 ms; 0.2↔5.3 ms) or not (9.4 ms; 5.9↔12.9 ms).
Endpoint error
The average distance between a target center and the point at which the movement ended on the display screen is the endpoint error. The average endpoint error was 3.05 mm (SE = 0.10). In an analysis conducted on these data, similar to that just described for the duration data, the only significant effect was due to repetition. Trials that were repetitions had smaller endpoint error (3.01 mm) than did those that were not (3.09 mm), F(1, 11) = 5.207, MSE = 1.25, p = .043. Among all the remaining main effects and interactions, the largest F(1, 11) = 1.119, p > .3, was for the effect of indicator stimulus.
Movement trajectories
Figure 4 gives two summaries of the movement trajectories. The panel on the left displays a scale representation of the average of the 48 time-normalized (see Method above) movement trajectories to each of the eight targets for a typical participant. The spacing of the 21 points along each trajectory represents 5% of the original movement duration. The dotted lines indicate 95% confidence intervals.
Trajectory analyses for Experiment 1. The left-hand panel shows average time-normalized movement trajectories from a representative participant. The intervals between successive points represent 5% of the movement duration. The light lines surrounding each trajectory represent 95% confidence intervals. The right-hand panel displays the results of an analysis that attempts to predict the target of a movement trajectory from the x- and y-positions and the movement direction at each of 21 points along the trajectory. Displayed are averages, across participants, of the adjusted proportions of trials (see text for details) falling into each of five error categories, as indicated by the inset legend. The N = 2 and N = 6 data are also displayed separately, as indicated by the inset legend
The panel on the right summarizes an analysis intended to explore the possibility that pointing movements may have been initiated before the participants had clearly formulated how they were to be carried out. To address this issue, a multivariate classification analysis (Krzanowski, 1988) was applied, separately, for each participant and for the data from each of the 21 time-normalized data points (as shown in right-hand panel of Fig. 4). At each time point, data triples, consisting of an x-position, a y-position, and the direction of movement in the xy-plane, were extracted from the 768 trajectories recorded for a participant. There were 48 observations for each combination of the eight targets and two levels of N. Of these, 24 were randomly selected from the movements directed toward each target (192 trials in all) to use as a “training” set. These were fit with eight multivariate normal distributions constructed using separate mean estimates for each target but covariance estimates that were pooled across the eight targets. Based on these fits, the optimal classifier was constructed that categorized the data from each trajectory into one of eight categories according to its movement target. This classifier was then used to predict the targets from a “test” data set consisting of the other 24 trials for each target at that level of N. The entire process was repeated for each participant, each level of N, and each of the 21 points along the time-normalized trajectories.
Comparing the predicted targets obtained from this analysis with the actual targets provides a way to assess how well the intended movement target could be distinguished at each point along the movement trajectory. The right-hand panel of Fig. 4 displays the results of this assessment averaged over the participants. For this figure, the data from each trial were grouped into one of five categories, depending on whether the prediction of the classification analysis was correct—that is, whether it matched the target—or, if not, how it differed from the actual target. Because the targets were organized along an arc, it was reasonable to group classification errors by the distance, in steps along this arc, between the predicted and the actual target, although this ignores whether a location was in the set of possible targets for that block of trials.
The proportion of errors in each of the resulting categories has been adjusted to reflect the number of opportunities for a trial to be classified into that category. To see how this adjustment worked, consider that there is only one target that counts as “correct.” However, for six of the eight targets, there are two ways of making one-step errors: The movement can be misclassified as being directed toward the target just clockwise or counterclockwise from the intended target. For the two most extreme targets, only a single one-step error is possible. Because each location was the target for an equal number of blocks, the observed proportion of trials falling into the one-step error category has been divided by 1.75. The conceptual advantage of this adjustment is that, if the initial portion of the movements were not directed at their targets, as the hypothesis underlying this analysis suggests, then the expected, adjusted proportion in each of the five categories would be the same, .125; this is the height of the horizontal reference line drawn across the figure.Footnote 2
As would be expected, at normalized time 0, the sample when the movement was first judged to have begun, the adjusted proportions are all close to chance. Similarly, at normalized time 1, the sample when the movement was judged to have ended, essentially all of the trials are judged to be correct. What is interesting is how quickly the classification of movements as correct increases. By 10% of the movement duration, roughly 37 ms into the movement (given the average movement time of 369 ms), the only error category that is above chance is the one-step errors, and the proportion of errors in this category has begun declining by 20% of the movement duration. That there should be some uncertainty, early in a movement, about the ultimate movement target is clear, looking at the average movement trajectories in the left panel of this figure. Although details of the trajectory shapes differ—they are more curved or less symmetric for some participants—the average trajectories for this participant are representative in the way that the movements to the extreme targets tend initially to be more similar, and those to the central targets diverge more quickly.
The data in the right-hand panel of this figure also address a second issue: If participants were keeping latency constant across N—that is, using a strategy that, for pointing movements, conceals an uncertainty effect—by initiating movements for N = 6 trials when they were less certain about the ultimate movement target, then that strategy should be revealed by this analysis. The solid points connected by the lines in this figure represent the data with N = 2. As indicated in the legend on the figure, a second plotting symbol, which does not necessarily fall on the lines, represents the data with N = 6. It is clear, just from looking at the figure, that there is very little, if any, difference between N = 2 and N = 6. That conclusion is supported by formal analyses showing that no effects involving N approach statistical significance, although the effects of normalized time, classification, and their interaction are all quite significant.
Discussion
Using a stimulus arrangement that remained constant, this experiment compared the uncertainty effect for the four combinations of two response modes and two types of indicator stimulus. The data in the target indicator condition replicate closely those reported by Wright et al. (2007). What is new here is the comparison between the target indicator and distractor indicator conditions. In both conditions, there was an abrupt-onset peripheral target. In the target indicator condition, which replicated previous research, that stimulus occurred uniquely at the actual location of the movement target for the pointing responses, and thus might have been expected to draw attention to that location. By contrast, in the distractor indicator condition, the abrupt-onset indicator stimulus occurred simultaneously at all of the distractor locations, and so would, if anything, have been expected to draw attention away from the movement target. For pointing movements, the uncertainty effect in both indicator stimulus conditions was, at most, quite small. When the response was a traditional keypress response, for which the location of the response was not the same as the location of the indicator stimulus in either condition, there was a large effect of uncertainty.
Taken together, these results suggest that the lack of an uncertainty effect previously observed for pointing movements does not depend on an abrupt stimulus onset at the location of the movement target. A straightforward explanation of this result is that, in those previously observed situations for which no uncertainty effect was observed, this absence did not result from the operation of an exogenous attentional mechanism.
One aspect of the data that might seem to be a concern is the existence of a statistically significant, if quite small (2.7 ms per doubling of N), uncertainty effect for nonrepetition trials. This result can be seen to derive particular importance from the perspective that repetition trials are special in that they may require less planning, because the previous movement plan can simply be repeated. However, as the right side of each panel in Fig. 3 shows, this result does little to actually undermine the conclusion given above. For, even excluding the repetition trials, the uncertainty is (non-significantly) smaller (and not statistically discernible from zero) in the distractor indicator condition (2.5 [–2.1↔7.0] ms per doubling of N) than in the target indicator condition (3.0 [0.5↔5.5]).
There were significant differences in the occurrence of errors across conditions. However, the pattern of these differences supports the conclusions reached on the basis of the latency data. The incidence of errors increased with N only for the keypress responses; for the pointing responses, there was actually a small, but statistically reliable, effect in the opposite direction.
As described in the Method section and discussed more fully in Wright et al. (2007), we believe that, for pointing responses, movement latency is the measure most directly analogous to the time measured for keypress responses. However, the presence of a significant duration increase with N in the distractor indicator condition raises the concern that participants might have begun to move either before having selected the movement target or without having prepared a specific movement plan to reach that target—in essence concealing an uncertainty effect on latencies by initiating a generic movement in the general direction of the targets, and then refining that movement in flight. Arguing against this concern, systematic differences in movement trajectories that accurately predict a movement’s target developed quickly and at the same rate for both N = 2 and N = 6. An alternative explanation of the observed increase in movement durations for N = 6 versus N = 2 is that they reflect a strategic adjustment in the speed–accuracy trade-off (Meyer, Smith, & Wright, 1982). Consistent with this interpretation is the fact that, unlike keypress responses, pointing responses yielded significantly fewer errors for N = 6 than for N = 2. Thus, it is at least plausible that participants perceived the movements to be more difficult when N = 6 and so slowed down their movements slightly, which made them more accurate.
If the conclusion we have drawn from this experiment is correct—that is, if the lack of an uncertainty effect previously observed for pointing movements does not depend on an abrupt stimulus onset at the location of the movement target—this provides indirect support for the alternative hypothesis that the dramatic size difference of the uncertainty effect between pointing and keypress responses, which was replicated here, should be attributed to differences in S–R compatibility. There is, however, one aspect of these data that does not accord well with this interpretation. For keypress responses, the switch from the target indicator to the distractor indicator condition caused an uncertainty effect increase of 21 ms per doubling of N, which is 27% of the uncertainty effect in the target indicator condition. This result might be taken as support for the S–R compatibility hypothesis, but only under the assumption that the target indicator leads to a more compatible mapping than do distractor indicators. Recall, however, that if the distractor indicators had any effect on pointing movements, it was to decrease the uncertainty effect. It is difficult to see why lower response-mapping compatibility for the distractor indicators should lead to an increased uncertainty effect for buttonpresses but not for pointing responses.
One way out of this apparent conundrum would be to posit that, for pointing movements, an abrupt onset involving all of the distractors is as compatible a stimulus as an abrupt onset at the target itself. Although this claim is perhaps counterintuitive, an analogous interpretation provides at least as plausible a way to save the attention mechanism hypothesis. It has been suggested that exogenous attention may be able to respond to an odd-man-out stimulus (Umiltà, 2000), a description that could be applied to the distractors-on indicator stimulus of Experiment 1. To explore the latter possibility, the next experiment used a central stimulus located at fixation.
Experiment 2
Like Experiment 1, Experiment 2 compared the uncertainty effects for the four combinations of the same two response modes and two types of indicator stimulus. The peripheral indicator stimulus in this experiment was the same as the target indicator stimulus of Experiment 1. To replace the distractors-on indicator stimulus, this experiment included a central indicator stimulus: a line at fixation pointing toward the location of the target stimulus. The question addressed by this experiment was then similar to that of Experiment 1—that is, whether the difference in indicator stimulus would lead to an uncertainty effect for the pointing responses more like that usually observed for keypress responses.
Experiments in attentional cuing have shown that pointers at fixation can direct endogenous attention toward a location but cannot direct exogenous attention (Umiltà, 2000). Thus, if in this second experiment the size of the uncertainty effect for pointing movements again does not depend on the indicator stimulus condition, this result would further strengthen the argument that it is not an exogenous attentional mechanism that has led to the anomalous lack of an uncertainty effect previously observed for experiments using aimed-movement responses.
Method
Participants
There were 8 participants (1 male, 7 female), each with 20/20 corrected vision, and all were right-handed. They were paid $8/h with bonuses. The UCI Institutional Review Board approved the experiment.
Apparatus, design, and procedures
The apparatus, design, and procedures were indistinguishable from those of Experiment 1, except for the factor Type of Indicator Stimulus. In Experiment 2, the type of indicator stimulus was either a peripheral or central indicator. The peripheral indicator was identical to that used in the target-change condition of Experiment 1, in which the dark inside of one of the potential target circles, located in the periphery, was filled in to match the white outline of the circle. The central indicator was a line, 2 cm long, with one end located at fixation in the center of the computer screen and the other oriented toward one of the potential target circles located in the periphery.
Results
Again, the analyses reported are based on four independent variables: N, number of targets (N = 2 or 6), repetition (repeat or no-repeat trials), response mode (keypress or pointing), and type of indicator stimulus (peripheral or central). The dependent variable of primary interest was latency in both the keypress and pointing conditions. In addition, for the pointing condition, duration and endpoint error were also analyzed. As in Experiment 1, these analyses collapsed the data over three other variables: stimulus configuration, target location, and cue onset delay, which were included as a way of decreasing their confounding effects. Including them in the analysis did not change the results.
Errors
Across participants, 85 trials in the keypress response condition (1.2%) and 43 trials in the pointing response condition (0.6%) were discarded and rerun within the same block because of problems recording the data: For instance, in the keypress condition, multiple keys were pressed “simultaneously” or a key was pressed that was not one of the possible responses, or in the pointing condition, the Optotrak was unable to see the stylus emitter.
There were few anticipation errors (i.e., movements made on a catch trial or that began within 100 ms of the stimulus onset on a normal trial): They occurred on 7 trials (0.1%) in the keypress response condition and on 47 trials (0.7%) in the pointing response condition, suggesting that, as in Experiment 1, including catch trials successfully induced the participants to wait for the cue stimulus before initiating a response. These trials were detected as they happened, discarded, and rerun within the same block.
Once the experiment was complete, separate analyses were done for the keypress and pointing conditions to identify trials with unusually long or short latencies relative to the distribution for each participant. To make the latency distributions more symmetric, this analysis was done after taking the log of the data. A latency was flagged as unusually short or long if it was more than more than three times the interquartile range away from the median. This analysis identified no trials having suspiciously short latencies in the keypress condition, and 8 trials (0.1%) in the pointing condition. In addition, this analysis identified 1 trial having a suspiciously long latency in the keypress condition and 6 trials (0.1%) in the pointing condition. The data from these trials with suspiciously long or short latencies were not included in subsequent analyses. Because these trials could only be identified after the participant running was complete, they were not rerun.
In the pointing response condition, a trial was classified as an error when the movement ended outside the target circle; trials in the keypress response condition were classified as errors when an incorrect key was pressed. Overall, there was an average error rate of 4.0% (SE = 0.1%). However, a four-way analysis of variance on the error proportions after an arcsine transformation, with Response Mode, Repetition, Indicator Stimulus, and N as the factors, showed that the proportion of errors varied reliably across conditions. This variation was dominated by a pair of two-way interactions, both involving the number of targets: N × Repetition, F(1, 7) = 15.950, p = .005, and N × Response Mode, F(1, 7) = 11.281, p = .012. The remaining interactions all had p > .2. Of the four main effects, two were statistically reliable: response mode, F(1, 7) = 6.925, p = .034, and N, F(1, 7) = 11.125, p = .012.
Consider first the interaction of N × Repetition. Consistent with previous results, for repetition trials, the increase in errors going from N = 2 to N = 6 was close to zero—0.4%, F(1, 7) = 0.006—but for nonrepetition trials, there was a statistically significant increase—2.1%, F(1, 7) = 31.996, p = .001. Consider next the N × Response Mode interaction. For the pointing movements, there was again a small decrease in errors associated with the increase in N. This –0.8% decrease was, however, not statistically reliable, F(1, 7) = 1.210, p = .308. However, for the keypress responses there was a statistically significant increase with N of 3.4%, F(7) = 25.304, p = .002.
Latency
The latency data are summarized in Fig. 5. This figure has the same organization as Fig. 3, which contained the analogous summary of the latency data from Experiment 1. Not only are the data displayed in the same way, but the overall pattern of results is remarkably similar. As was found in Experiment 1, two of the three-way interactions were reliable: Response Mode x N x Repetition, F(1, 7) = 11.116, p = .013, and Response Mode × N × Type of Indicator Stimulus, F(1, 7) = 23.784, p = .002. The four-way interaction and the final two three-way interactions were not reliable; among these terms, the closest to statistical significance was the three-way interaction of Indicator Stimulus × N × Repetition, F(1, 7) = 2.628, p = .149. So, as with Experiment 1, the key to understanding these interactions is that the effect of N and the interaction with it of indicator stimulus type were large for keypress responses but small or nonexistent for pointing responses. This is clear if the top two panels in Fig. 5 are compared with the bottom two panels. Reflecting this pattern, the remainder of the planned analysis focused on characterizing the effects of N, repetition, and type of indicator stimulus separately for the pointing and keypress conditions.
Latency data for Experiment 2. Each panel shows data from one of the four combinations of response (keypress or pointing) and type of indicator (peripheral or central). The four points on the left in each panel show the mean data broken out by N and repetition. The two data points on the right show, separately for repeat and nonrepeat trials, the uncertainty effect slope: that is, the increase in latency for each doubling in N. The error bars are 95% confidence intervals computed after the estimated main effect of participants was removed
Table 3 presents several summaries of the slopes characterizing the uncertainty effect, using the same organization as in Table 2. The leftmost three columns of Table 3 show estimates of the uncertainty effect slope for each of the four combinations of response mode and indicator stimulus. For the keypress responses, the estimates are about the size of the uncertainty effects that we have observed previously. The estimates are close to zero for the pointing responses. One difference between these results and Experiment 1 is that the uncertainty effect for pointing responses to the central indicator stimulus, although small (5.2 ms per doubling of N), is statistically discernible from zero. The cells in the third row of these two columns simply confirm that the response mode difference is reliable for both levels of indicator stimulus. The top two entries in the third column show that the size of the uncertainty effect depends strongly on the indicator stimulus for keypress responses, F(1, 7) = 35.629, p = .001, but not for pointing responses, F(1, 7) = 2.802, p = .138. The difference in these effect size estimates, shown in the third row of the third column, estimates the effect size of the three-way interaction reported above.
Columns four to six of Table 3 show comparisons that elaborate the interaction of Response Mode x N x Repetition, collapsing across types of indicator stimulus. As in Experiment 1, there is a strong effect of repetition on the size of the uncertainty effect for the keypress responses. For the pointing responses, there is again a small but significant uncertainty effect for the nonrepetition trials and a nonsignificant negative uncertainty effect for the repetition trials. The 2 × 2 simple interaction of N and repetition is statistically significant for both the keypress responses, F(1, 7) = 20.322, p = .003, and the pointing responses, F(1, 7) = 77.810, p = .000.
The final column shows the average, collapsing over both indicator stimulus and repetition, of the uncertainty effect for each level of response mode. The difference across the levels of response mode, in the third row, estimates the effect size of the significant two-way N x Response Mode interaction: F(1, 7) = 93.938, p = .000.
Duration
The mean duration for the pointing data was 348 ms (95% confidence interval 296↔302). These data were analyzed using a 2 × 2 × 2 ANOVA with N, Repetition, Indicator Stimulus as the three within-subjects factors. This showed that the increase going from N = 2 to N = 6, although small (5.8 ms [0.6↔11.0]), was statistically reliable, F(1, 7) = 6.994, p = .033. This main effect was modulated by the three-way interaction, F(1, 7) = 6.688, p = .036. One way to understand this interaction is to look at the effect of N for each of the four combinations of the Indicator Stimulus and Repetition factors. This approach shows that the effect of N was statistically reliable for trials that were not repetitions and had a central indicator stimulus (10 ms [5↔15]) and for trials that were repetitions and had a peripheral indicator stimulus (10 ms [2↔18]), but that there was not a reliable effect of N for trials that were not repetitions and had a peripheral indicator stimulus (4 ms [–11↔19]) or trials that were repetitions and had a central indicator stimulus (–1 ms [–5↔3]).
Endpoint error
The average endpoint error was 3.16 mm [2.83↔3.49]. An analysis was conducted for endpoint error similar to that done for the duration data. The only statistically reliable effect found was for the main effect of repetition, F(1, 7) = 10.665, p = .014; the average endpoint error dropped to 3.11 mm for repetition trials and increased to 3.21 mm for nonrepetition trials.
Movement trajectories
Figure 6 displays the results of the analysis designed to assess how well the intended movement target could be distinguished at each point along the movement trajectory. This figure, and the analysis that underlies it, is similar to that in the right-hand panel of Fig. 4, based on the data from Experiment 1. The results here are, if anything, more clear cut than those of Experiment 1. Other than the intended movement, the only target category that ever occurs at a level above chance is the one-step errors, and the proportion of errors in this category begins declining at 15% of the movement duration (roughly 50 ms).
Trajectory analyses for Experiment 2. Results of an analysis that attempts to predict the target of a movement trajectory from the x- and y-positions and the movement direction at each of 21 points along the trajectory. Displayed are averages, across participants, of the adjusted proportions of trials (see text for details) falling into each of five error categories, as indicated by the inset legend. The data are also shown separately for N = 2 and N = 6, as indicated by the inset legend
The data in this figure also address the issue of whether participants kept latency constant across Ns by initiating movements for N = 6 trials when they were less certain about the ultimate movement target. Just as in Experiment 1, there is no systematic separation between the solid points connected by the lines, which represent the data with N = 2, and the unconnected points, which represent the data with N = 6. This impression is supported by formal analyses showing that no effects involving N approach statistical significance, although the effects of normalized time, classification, and their interaction are all quite significant.
Discussion
Like Experiment 1, this experiment compared two response modes and two types of indicator stimulus using an identical stimulus arrangement. What is new here is the nature of the second type of indicator stimulus being compared. The peripheral indicator stimulus, which involved a change at the target location, was identical to the target indicator stimulus in Experiment 1. The central indicator stimulus, which was a line with one end at fixation that pointed to the target location, was new. This comparison is of interest because, unlike the peripheral indicator stimulus, a central indicator stimulus is thought only to recruit, if anything, endogenous attention.
The general pattern of results in Experiment 2 was remarkably similar to that in Experiment 1. For keypress responses, a large effect of uncertainty was observed whether the indicator stimulus was peripheral or central. What is more, the uncertainty effect size with the peripheral indicator stimulus, 75 ms per doubling of N, was quite similar to that observed for the analogous target indicator stimulus condition in Experiment 1: 79 ms per doubling of N. Also, as in Experiment 1, the nature of the indicator stimulus influenced the uncertainty effect size for the keypress responses. The switch from the peripheral to the central indicator stimulus led to a 43% increase in the size of the uncertainty effect: 32 ms per doubling of N. In contrast, pointing responses, with either type of indicator stimulus, elicited uncertainty effects that were much smaller: 3.3 ms per doubling of N. Although this estimate differed significantly from zero, its size was still less than 5% of that observed for keypress responses with either indicator stimulus.
Thus, the results from Experiment 2 reinforce the conclusion suggested by Experiment 1, that the large difference in the uncertainty effect observed for pointing movements versus keypress movements does not appear to be attributable to a confounding of the use of pointing movements and the use of abrupt-onset indicator stimuli at the location of the movement target. The explanation that the pointing–keypress difference resulted from this confounding seemed at least plausible, given theories of attention that have suggested that abrupt-onset peripheral stimuli recruit exogenous attention and that this may lead to the automatic generation of movement plans directed at the stimulus location.
Looking more closely at the pointing-response data does reveal one apparent difference between Experiments 1 and 2. For the nonrepetition trials—that is, trials on which the S–R combination differed from that of the previous trial—there was a statistically significant uncertainty effect in both indicator stimulus conditions: 10 ms per doubling of N [4↔16] for the central indicator stimulus, and 6 ms per doubling of N [4↔8] for the peripheral indicator stimulus. Although, the difference between these estimates was not statistically reliable, both differed reliably from the estimate for the repetition trials in the same indicator stimulus condition, 0 ms per doubling of N [–5↔5] for the central indicator stimulus and –3 ms per doubling of N [–8↔2] for the peripheral indicator stimulus. We will consider this difference further in the General Discussion.
The small increase in duration going from N = 2 to N = 6 complicates our interpretation of these data, and the pattern of its interaction with the Repetition and Indicator Stimulus factors is certainly puzzling. The concern is that the absence of a large uncertainty effect for pointing responses might have been achieved by having the onset of the indicator stimuli trigger a generic pointing movement that was then later refined. As in Experiment 1, two considerations argue against this interpretation. First, the small, if significant, effects on endpoint error involved the Repetition factor, not N, and in fact, endpoint error was actually slightly smaller for N = 6 than for N = 2. Second, the detailed trajectory analyses show that the target of each movement could be discriminated quite early in its trajectory and that this could be done equally well for movements in conditions in which N = 2 or 6.
General discussion
The two experiments reported in this article explored the attention mechanism hypothesis, an alternative to explanations based on either privileged loops or S–R compatibility, to account for the lack of the uncertainty effect sometimes observed in choice reaction time experiments. This hypothesis is specifically directed toward the lack of an uncertainty effect reported in two articles in which the response was a movement to a target location that was also the location of the stimulus that indicated the movement target, when the response was either a saccade (Kveraga et al., 2002) or an arm movement (Wright et al., 2007). That this hypothesis might be applicable in these two cases is suggested by a procedural difference between these studies and the majority of the previous research reporting an uncertainty effect (see, e.g., Teichner & Krebs, 1974).
The experiments reported here both used identical visual stimulus arrays and compared pointing and keypress responses. Each experiment also compared two types of what we call indicator stimuli, the stimulus that signals which of the N possible responses is required on a trial. Both experiments included the indicator stimulus condition used previously for aimed-movement responses—in which one of a set of outline circles, each marking a possible response, filled in to indicate the required response—and pitted it against a second indicator stimulus that differed across the experiments.
The two previous reports that failed to find a large uncertainty effect for aimed-movement responses differed from typical paradigms that have yielded Hick’s law in that they used an indicator stimulus that, like the target indicator stimulus in Experiment 1 and the peripheral indicator stimulus in Experiment 2, involved an abrupt onset at the movement target. As we outlined in the introduction, it is at least plausible that abrupt-onset indicator stimuli trigger an exogenous attention shift that is associated with the implicit preparation of a movement toward the stimulus location. The existence of such automatically generated motor programs could explain how the S–R mapping process, often posited as the source of the uncertainty effect, is bypassed in these tasks. In essence, then, the use of indicator stimuli that were coincident with the movement targets was confounded in the two previous articles with the requirement to make aimed-movement responses, either by pointing or saccades. The experiments reported here tested the attention mechanism hypothesis by eliminating this confound. This was done by comparing performance using the standard indicator stimulus, an abrupt onset at the target, with a second indicator stimulus that was similar but that would not be expected to trigger the automatic generation of movement plans to the appropriate target.
Experiment 1 pitted the standard indicator stimulus against an alternative that still retained abrupt onsets in the periphery; however, these abrupt onsets were at all of the distractor locations rather than at the target location. By eliminating the abrupt onset at the target location, this alternative indicator stimulus presumably also eliminated the implicit generation of movement plans to that target location. As summarized in Table 2, the results were unequivocal. Replicating the findings of Wright et al. (2007), the uncertainty effect estimates for keypress responses were over 50 times larger than those for the pointing responses in both indicator stimulus conditions. This result suggests that the small uncertainty effect for pointing movements does not result from the standard indicator stimulus, involving an abrupt onset at the target location. This interpretation is strengthened by the fact that the Indicator Stimulus factor had a large influence on the size of the uncertainty effect for keypress responses, but if there was an influence of this factor for the pointing responses, it was in the opposite direction from what the attention mechanism hypothesis would predict.
Experiment 2 addressed the additional suggestion that an “odd-man-out” indicator stimulus, such as that used as the alternative in Experiment 1, might still provide an adequate trigger directing exogenous attention to the target location. To explore this possibility, Experiment 2 compared the standard peripheral indicator stimulus with a line at fixation pointing in the direction of the target. In previous research, central stimuli like this have been associated with effects of endogenous but not of exogenous attention (Umiltà, 2000). As summarized in Table 3, the results in Experiment 2 were almost a copy of those from Experiment 1. Although in this case there was a small but statistically reliable uncertainty effect for pointing responses with the central indicator stimulus, this effect was not reliably larger than that observed for pointing responses with the peripheral indicator stimulus, and the uncertainty effect observed for keypress responses was at least 21 times larger, for either indicator stimulus type. Also, for the keypress responses, the uncertainty effect was 32 ms larger with the central indicator stimulus than with the standard.
Lawrence (2010) recently reported a finding using saccades as responses that is quite similar to our finding from Experiment 2. In past research using saccades as responses and a setup with indicator stimuli similar to the peripheral indicator in our Experiment 2, Lawrence and her colleagues (Lawrence & Gardella, 2009; Lawrence, St. John, Abrams, & Snyder, 2008) consistently found a statistically significant, negative uncertainty effect when N was increased from 2 to 6. Lawrence (2010) contrasted this condition with one in which the indicator stimulus was an arrow at fixation. As before, she found that, with the peripheral indicator stimulus that would be expected to trigger exogenous attention, there was a significant latency reduction of –8.6 ms per doubling of N. However, using the central arrow as an indicator stimulus, which would recruit attention through an endogenous mechanism, she found a significant latency increase of 9.5 ms per doubling of N.
Taken together, the two experiments reported here provide what we believe is compelling evidence against the attention mechanism hypothesis, and our argument is further strengthened by the results of Lawrence (2010). We found strong uncertainty effects for keypress responses and small, if any, uncertainty effects for pointing responses. This qualitative pattern of results was unaffected by two modifications to the indicator stimulus designed to eliminate triggers for an exogenous attentional mechanism that, by automatically generating a movement plan to the location of the movement target, might bypass the normal S–R mapping process for pointing movements.
If the attention mechanism hypothesis does not explain this pattern, what does? The two alternatives discussed in the introduction, S–R compatibility and privileged loops that bypass the S–R bottleneck, both remain plausible in light of the results reported here. Other than possibly eliminating a competitor, the results here have little to say for or against the privileged-loop hypothesis. In contrast, the results from these two experiments appear to in one case support and in the other argue against an explanation based solely on S–R compatibility. Both experiments included an indicator stimulus manipulation that might be expected to have reduced S–R compatibility. Consistent with this expectation, in both experiments this manipulation caused a marked increase in the uncertainty effect for the keypress responses. In Experiment 2, this manipulation was associated also with an increase in the uncertainty effect for the pointing movements. Although the difference across indicator stimulus conditions was not quite statistically significant, an outcome in this direction was consistent with what would be expected based on S–R compatibility. However, in Experiment 1, there was, if anything, a decrease in the uncertainty effect with this manipulation. This result is hard to reconcile with expectations based on S–R compatibility.
Despite this result, there would seem to be little doubt that S–R compatibility is an important factor that can influence the size of the uncertainty effect for choice responses, even when using an aimed movement as a response. What is puzzling is how the S–R mechanism can explain a difference in the uncertainty effect size as large as that observed here and elsewhere for the keypress and pointing tasks, when the S–R mapping in both tasks seems highly compatible.
Elaborating ideas initially proposed by Fitts (Fitts & Deininger, 1954; Fitts & Seeger, 1953), Kornblum, Hasbroucq, and Osman (1990) suggested that S–R compatibility should be understood in terms of two factors: (1) the dimensional overlap of the stimulus set and the response set, and (2) the specific mapping of the elements in the stimulus set onto the response set. Unfortunately, there is no objective, nonempirical method to evaluate the contribution of either of these factors. However, it seems clear that, at least for the target/peripheral indicator stimulus, the mapping used for both the keypress and pointing responses is maximally compatible. If correct, this implies that, if S–R compatibility differences are to explain the difference between keypress and pointing responses in the sizes of the uncertainty effect, that explanation must depend largely on the principle of dimensional overlap. However, there appear to be strong spatial homomorphisms between the stimulus and response sets for the sets of both keypress and pointing responses; this is important because such homomorphisms underlie the principle of dimensional overlap, as described by Kornblum et al.
One obvious difference between the keypress and pointing responses, from the perspective of dimensional overlap, appears to be that for the pointing responses the spatial frame of reference used to encode the stimuli and carry out the responses can be exactly the same, whereas keypress responses are made in a different plane, one that is both rotated and displaced from the plane in which the stimuli are presented. Evidence possibly supporting the importance of this difference for the uncertainty effect has been reported by Dassonville et al. (1999). They studied pointing responses made with a joystick using an indicator stimulus similar to the target indicator used here in Experiment 1, and they found a statistically significant uncertainty effect of 17 ms per doubling of N (Dassonville, personal communication).Footnote 3 Like both our pointing and keypress response conditions, these joystick responses would seem to have strong dimensional overlap and an optimal mapping between the stimulus and response sets. Consistent with this intuition, when Dassonville et al. tested either a condition that disrupted this optimal mapping (the movement target was the location one step counterclockwise from the indicator stimulus) or a condition with substantially less dimensional overlap (rather than a spatial indicator stimulus, a one- or two-letter string gave the compass heading of the target), they observed uncertainty effects that were larger by roughly a factor of 10. What we find most interesting, however, is that the joystick condition using the spatial indicator stimulus and a spatially consistent S–R mapping requires a pointing movement that, like the keypress responses we studied, must be made in a displaced frame of reference. However, although Dassonville et al. observed a significant uncertainty effect, its magnitude was less than one-quarter the uncertainty effect we and others have observed for keypress responses. This suggests to us that there may still be something that we do not understand about the difference in the uncertainty effect between pointing and keypress responses.
Another difference between keypress responses and both the pointing responses studied here and the joystick responses studied by Dassonville et al. (1999) is that, along with response selection, keypress movements also require effector selection. To produce a keypress response when there are N response options, the participant must not only determine the response that is appropriate but also the appropriate one of N fingers to make that response. By contrast, to produce a pointing response, irrespective of the number of response options or whether the response is made directly with the hand or indirectly using a joystick, the participant always uses the same effector to carry out the response. The role of effector selection as a factor that, in addition to response selection, influences the size of uncertainty effects is a question that awaits further investigation.
Notes
Typically in these tasks (although it is not necessary), there is a one-to-one mapping of stimuli onto responses, so their variation is confounded. We refer to these simply as the number of alternatives.
But note that a second implication of this adjustment is that the adjusted proportions at a time point no longer add to 1.
This estimate is based on nonrepeated trials only, and so is somewhat larger than the estimates we have been using to compare with those from the previous literature, many of which were obtained before a concern about the effect of repetitions on the uncertainty effect became widespread.
References
Brainard, R. W., Irby, T. S., Fitts, P. M., & Alluisi, E. A. (1962). Some variables influencing the rate of gain of information. Journal of Experimental Psychology, 63, 105–110. doi:10.1037/h0045304
Dassonville, P., Lewis, S. M., Foster, H. E., & Ashe, J. (1999). Choice and stimulus–response compatibility affect duration of response selection. Cognitive Brain Research, 7, 235–240. doi:10.1016/S0926-6410(98)00027-5
Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, 47, 381–391. doi:10.1037/h0055392
Fitts, P. M., & Deininger, R. L. (1954). S–R compatibility: Correspondence among paired elements within stimulus and response codes. Journal of Experimental Psychology, 48, 483–492. doi:10.1037/h0054967
Fitts, P. M., & Seeger, C. M. (1953). S–R compatibility: Spatial characteristics of stimulus and response codes. Journal of Experimental Psychology, 46, 199–210. doi:10.1037/h0062827
Hick, W. E. (1952). On the rate of gain of information. The Quarterly Journal of Experimental Psychology, 4, 11–26.
Hyman, R. (1953). Stimulus information as a determinant of reaction time. Journal of Experimental Psychology, 45, 188–196. doi:10.1037/h0056940
Kornblum, S. (1969). Sequential determinants of information processing in serial and discrete choice reaction time. Psychological Review, 76, 113–131. doi:10.1037/h0027245
Kornblum, S., Hasbroucq, T., & Osman, A. (1990). Dimensional overlap: Cognitive basis for stimulus–response compatibility—A model and taxonomy. Psychological Review, 97, 253–270. doi:10.1037/0033-295X.97.2.253
Krzanowski, W. J. (1988). Principles of multivariate analysis. Oxford: Oxford University Press.
Kveraga, K., Boucher, L., & Hughes, H. (2002). Saccades operate in violation of Hick’s law. Experimental Brain Research, 146, 307–314. doi:10.1007/s00221-002-1168-8
Lawrence, B. M. (2010). An anti-Hick’s effect for exogenous, but not endogenous, saccadic eye movements. Experimental Brain Research, 204, 115–118. doi:10.1007/s00221-010-2301-8
Lawrence, B. M., & Gardella, A. L. (2009). Saccades and reaches, behaving differently. Experimental Brain Research, 195, 413–418. doi:10.1007/s00221-009-1804-7
Lawrence, B. M., St. John, A., Abrams, R. A., & Snyder, L. H. (2008). An anti-Hick’s effect in monkey and human saccade reaction times. Journal of Vision, 8, 26:1–7. doi:10.1167/8.3.26
Lee, K., Keller, E., & Heinen, S. (2005). Properties of saccades generated as a choice response. Experimental Brain Research, 162, 278–286. doi:10.1007/s00221-004-2186-5
Loftus, G. R., & Masson, M. E. J. (1994). Using confidence intervals in within-subject designs. Psychonomic Bulletin & Review, 1, 476–490.
McLeod, P. D., & Posner, M. I. (1984). Privileged loops: From percept to act. In H. Bouma & D. G. Bouwhuis (Eds.), Attention and performance X: Control of language processes (pp. 55–66). Hillsdale, NJ: Erlbaum.
Meyer, D. E., Smith, J. E., & Wright, C. E. (1982). Models for the speed and accuracy of aimed movements. Psychological Review, 89, 449–482. doi:10.1037/0033-295X.89.5.449
Morin, R. E., Konick, A., Troxell, N., & McPherson, S. (1965). Information and reaction time for “naming” responses. Journal of Experimental Psychology, 70, 309–314. doi:10.1037/h0022206
Mowbray, G. H. (1960). Choice reaction times for skilled responses. The Quarterly Journal of Experimental Psychology, 12, 193–202. doi:10.1080/17470216008416726
Teichner, W. H., & Krebs, M. J. (1974). Laws of visual choice reaction time. Psychological Review, 81, 75–98. doi:10.1037/h0035867
Umiltà, C. (2000). Visuospatial attention. In F. Boller, J. Grafman, & G. Rizzolatti (Eds.), Handbook of neuropsychology, vol 1 (2nd ed.). Amsterdam: Elsevier Science.
Wright, C. E., Marino, V. M., Belovsky, S. A., & Chubb, C. (2007). Visually-guided, aimed movements can be unaffected by stimulus–response uncertainty. Experimental Brain Research, 179, 475–496. doi:10.1007/s00221-006-0805-z
Author Note
The authors thank Nina Macdonald, Paul Dassonville, and two anonymous reviewers for their comments on earlier versions of this article. C.C.’s involvement in this research was supported by NSF Grant BCS-0843897. Correspondence concerning this article should be sent to C. E. Wright, University of California, Irvine, CA 92697-5100 (e-mail: cewright@uci.edu).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Wright, C.E., Marino, V.F., Chubb, C. et al. Exploring attention-based explanations for some violations of Hick’s law for aimed movements. Atten Percept Psychophys 73, 854–871 (2011). https://doi.org/10.3758/s13414-010-0062-x
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13414-010-0062-x