Introduction

Magnitudes can be expressed in many distinct notations and formats, but irrespective of their representation or modality, they all appear to result in similar behavioral and neuronal responses (for a review and meta-analyses, see Cohen Kadosh, Lammertyn, & Izard, 2008). For instance, studies have reported similar behavioral results for magnitudes expressed as number of dots (Gebuis, Cohen Kadosh, de Haan, & Henik, 2008; Zhou et al., 2007), pitch (Rusconi, Kwan, Giordano, Umiltà, & Butterworth, 2006), time (Xuan, Zhang, He, & Chen, 2007), physical size or line length (Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003), and luminance (Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Cohen Kadosh & Henik, 2006). Concurrently, imaging studies have revealed support for similar processing mechanisms underlying distinct magnitudes, such as number, physical size, and line length (Fias et al., 2003) as well as luminance (Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Cohen Kadosh et al., 2005). Functional magnetic resonance imaging adaptation paradigms have revealed cross-notation adaptation for numbers and number words (Cohen Kadosh, Cohen Kadosh, Kaas, Henik, & Goebel, 2007), as well as for numbers and dots (Piazza, Pinel, Le Bihan, & Dehaene, 2007), and electroencephalography studies have demonstrated the time courses for the processing of distinct magnitudes to be highly comparable (Gebuis, Kenemans, de Haan, & van der Smagt, 2010; Libertus, Woldorff, & Brannon, 2007). The observation of similar behavioral and neuronal responses to distinct magnitudes served as a basis for the ATOM model, which states that magnitudes that have a similar (often spatial) metric are encoded by the same amodal magnitude system (Walsh, 2003). Similarly the triple code model (Dehaene, Piazza, Pinel, & Cohen, 2003) entails number encoding independently of its notation.

Notwithstanding the general level of consensus on an amodal magnitude system (Cohen Kadosh & Walsh, 2009), how stimuli that do not have an explicit spatial component are encoded remains controversial. Pinel, Piazza, Le Bihan and Dehaene (2004) manipulated number, physical size, and luminance within a single stimulus, and subjects were required to judge each dimension in separate blocks, a task often referred to as the numerical Stroop or congruency task (Algom, Dekel, & Pansky, 1996; Henik & Tzelgov, 1982). Pinel et al. (2004) demonstrated a congruency effect at the behavioral level only when subjects had to make numerical judgments but did not find a congruency effect in the imaging results, for either the numerical or the luminance judgment task. In contrast to these null results, two recent studies did show congruency effects between number and luminanceat the behavioral level (Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Cohen Kadosh & Henik, 2006), as well as the neuronal level (Cohen Kadosh, Cohen Kadosh, & Henik, 2008). The authors reasoned that the lack of an effect in the Pinel et al study was due to the manipulation of three distinct magnitudes in one stimulus, which probably resulted in the masking of the underlying interaction effects. The results of the studies of Cohen Kadosh and colleagues suggest that the amodal magnitude system is not limited to magnitudes with a spatial component. However, on closer inspection, their results appear contradictory: Faster responses were obtained for stimuli that were numerically larger and darker (Cohen Kadosh & Henik, 2006), but also for stimuli that were numerically larger and brighter (Cohen Kadosh et al., 2007; Pinel et al., 2004). These contrasting results are intriguing, especially when one considers the metaphor that is often used to describe our magnitude representations: the mental number line (Dehaene, 1992). In this metaphor, magnitudes from small to large are represented from left to right. This idea has gained support from different behavioral results, where small numbers appear to facilitate left-hand responses or responses to left-sided targets, whereas the opposite pattern occurs for large numbers (e.g. Dehaene, Bossini, & Gireaux, 1993; Fischer, Castel, Dodd, & Pratt, 2003; but for a different opinion see: Santens & Gevers, 2008; Gevers et al., 2010; Bonato, Priftis, Marenzi, & Zorzi, 2009). The number line is suggested to be “flexible,” since multiple associations between the same magnitudes (i.e., number and space) can exist (Cohen Kadosh & Walsh, 2009). For instance, when subjects imagine a clock instead of a ruler, opposite effects have been found (Bachtold, Baumuller, & Brugger, 1998). However, prerequisites for such number line “flexibility” to occur are the existence of more than one association between two magnitudes (e.g,. ruler and clock face) and explicit instructions to observers to imagine either of these associations. In the studies on number–luminance associations, these were not present. How, then, to reconcile the mental number line metaphor with these contradictory luminance–number congruency findings? Can large numbers be associated with both bright and dark stimuli? Or might a different, non-luminance-based explanation be more plausible for explaining the contradictory results obtained with luminance–number congruency paradigms?

In this study, we specifically focused on the origin of the number–luminance congruency effects. Apart from the prevalent hypothesis that luminance is associated with number, two alternative hypotheses for the interaction effects are plausible as well. Moreover, these can account for the contradictory findings introduced above.

The first hypothesis states that it is not luminance per se but (unsigned) luminance contrast (the brightness of the stimulus in relation to the brightness of the background) that explains the interaction effects. In the study in which numerically large and dark stimuli led to the fastest responses (Cohen Kadosh & Henik, 2006), a bright background was used, whereas in the study that revealed the fastest responses for numerically large and bright stimuli, a background darker than the stimuli was employed (Cohen Kadosh, Cohen Kadosh, & Henik, 2008). In essence, faster responses were always obtained for the stimuli that were numerically larger and had a larger luminance contrast or numerically smaller with a smaller luminance contrast. This idea was also proposed in a later manuscript by Cohen Kadosh, Lammertyn and Izard (2008, p. 135) and is consistent with a study by Durgin (2001) that revealed contrast adaptation affected numerosity processing of large numerosities in nonsymbolic notations (i.e., texture density). The second (more unorthodox) hypothesis stems from the idea that there might not be any magnitude association at all, yet subjects simply respond fastest to the most salient stimulus. The term “salient” here means the stimulus that directly draws attention due to its stimulus characteristic, be it size, position, color, or luminance (contrast). In the present experiment, the more salient stimulus is the stimulus with the largest luminance contrast.

Note that even though luminance contrast is the factor underlying the congruency effect in the luminance contrast, as well as the saliency, hypothesis, both hypotheses can lead to different outcomes, since the latter does not take into account the numerical magnitude of the stimulus. For example, when subjects have to respond to the numerically smaller stimulus, the luminance contrast hypothesis predicts faster responses for the numerically smaller number when it is brighter than for the stimulus presented simultaneously (e.g., 2 4; smaller number has a smaller luminance contrast), as compared with the reverse (e.g., 2 4; smaller number has a larger luminance contrast), whereas the saliency hypothesis would predict the opposite, since faster responses are predicted for the stimulus with a large luminance contrast (e.g., 2 4; smaller number is the most salient), as compared with a small luminance contrast (e.g., 2 4; smaller number is the least salient) (see also Fig. 1b).

Fig. 1
figure 1

The predicted outcomes for the three hypotheses in each of the six stimulus conditions. The four panels present the instruction conditions included in the experiment; respond to the stimulus that is numerically larger (a), numerically smaller (b), darker (c), or brighter (d). The six stimuli presented at the top of each panel are the three congruency conditions (congruent, neutral, incongruent) for stimuli brighter (a, b, c) or darker (d, e, f) than the background. The lower part of each panel shows the predicted results for the luminance, the luminance contrast, and the saliency hypotheses for the six stimuli. The brighter bars correspond to the stimuli brighter than the background (a, b, c) and the dark bars to the stimuli darker (d, e, f) than the background. Longer bars indicate slower responses

Full size image

In the experiments employed so far, the luminance contrast and the saliency hypothesis were confounded. Subjects were always requested to respond to the numerically larger stimulus. Under these task instructions, both the luminance contrast and the saliency hypotheses predict the same outcome (Fig. 1a reveals that the predictions for luminance and luminance contrast are the same for the “numerically larger” instruction whereas Fig. 1b reveals that this is not the case for the “numerically smaller” instruction).

In summary, there are (at least) three possible hypotheses about the number–luminance congruency task: (1) if number is associated with luminance, numerically larger stimuli should consistently be associated with either darker or brighter stimuli (note that in Fig. 1, the predictions for luminance congruency are presented only for the numerically larger and darker association; the predictions for the numerically larger and brighter association would reveal exactly the opposite pattern); (2) if number is associated with luminance contrast, numerically larger stimuli should consistently be associated with stimuli that have a larger luminance contrast; and (3) if the congruency effects are the result of saliency, the stimulus with the largest luminance contrast is always responded to mot quickly, irrespective of its numerical size.

To specifically test these three distinct hypotheses, we created a modified version of the number-luminance congruency task by adding two manipulations: a “contrast sign” manipulation and an “instruction” manipulation. For the contrast- sign manipulation, we used an intermediate gray background, instead of a black or white background. Consequently, on half of the trials, the stimuli were brighter than the background, and on half of the trials, the stimuli were darker than the background (Fig. 1). For the instruction manipulation, instead of two, we used four instruction conditions: respond to (1) the numerically larger, (2) the darker, (3) the numerically smaller, or (4) the brighter stimulus. The contrast sign and instruction manipulations were incorporated so as to be able to distinguish between the luminance, the luminance contrast, and the saliency hypotheses. Except for the condition in which subjects had to judge the numerically larger number, the conditions now predicted outcomes that allow differentiation between the three hypotheses (Fig. 1; bar graphs show the predicted outcomes for the three hypotheses in each of the four instruction conditions).

Method

Subjects

Twelve students (between 20 and 27 years of age; M = 23.26, SD = 2.52; 9 female, 3 male) from the University of Utrecht took part in the experiment. All the subjects were right-handed, native Dutch speakers and had normal or corrected-to-normal vision. For their participation, they received course credit.

Stimuli

All the stimuli were displayed on a 22-in> monitor using the Presentation software (Neurobehavioral Systems, Albany, CA). On each trial, the subjects were presented two Arabic numbers (height, 2° of visual angle), one presented on each side of the fixation cross. Manual responses were recorded using a response box.

Eight Arabic numbers (1 to 9, except for 5) and eight luminance levels (photometric values: 48, 63, 76, 95, 142, 172, 207, and 250 cd/m2) were used. The luminance levels were chosen such that they yielded four equal (Michelson) contrast steps with respect to the background (117 cd/m2) in either direction. Consequently, half of our stimuli were brighter and half were darker than the background, producing our contrast sign manipulation. Number and luminance values together constituted the three congruency conditions, resulting in the following pairs: (1) the numerically larger stimulus was darker, (2) both stimuli wer the same number but had distinct luminance levels or the reverse,or (3) the numerically larger stimulus was brighter.Footnote 1 These three congruency conditions were further divided over three number and three luminance distances, with the number distances being distance 1 (1–2, 3–4, 6–7, 8–9), distance 2 (1–3, 2–4, 6–8, 7–9), and distance 3 (1–4, 6–9) and the luminance distances being distance 1 (48–63, 76–95, 142–172, 207–250 cd/m2), distance 2 (48–76, 63–95, 142–207, 172–250 cd/m2), and distance 3 (48–95, 142–250 cd/m2).

Procedure

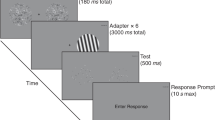
The paradigm consisted of two tasks: (1) a number comparison task, in which subjects had to respond to the numerical size of the stimulus, and (2) a luminance comparison task, in which subjects had to respond to the brightness of the stimulus. Both tasks consisted of two instruction conditions—our instruction manipulation. In the number comparison task, subjects had to respond to either the numerically larger or the numerically smaller stimulus, whereas in the luminance comparison task, subjects had to respond to either the darker or the brighter stimulus. Subjects made their judgment by pressing the button on the side corresponding with the target location (the stimuli were blocked for each instruction condition). The target was presented equally often on the left and right sides of fixation. Together, the experiment consisted of two comparison tasks (1,728 trials per comparison task) that consisted of two instruction conditions (864 trials per instruction condition) and two contrast sign conditions (432 trials per contrast sign condition), which again consisted of three congruency conditions (144 trials per congruency), which again consisted of three luminance distances (48 trials per distance), which again consisted of three number distances (16 trials per distance). The order of the four tasks was different for each of the 12 participants (12 out of the 24 possible combinations of task order were randomly chosen). Before the experimental trials started, the subjects received instructions and performed 15 practice trials. Each trial began with a fixation cross (250 ms), followed by the stimulus (which remained on the screen until the subject gave a manual response) and an intertrial interval (500 ms).

Analyses

For each subject, median reaction times for the correct responses and error rates were calculated. To investigate the presence of a congruency effect and its origin, we performed, for each comparison task separately, a repeated measures ANOVA with contrast sign manipulation (stimuli brighter or darker than the background), instruction manipulation (numerically larger/smaller stimuli; darker/brighter stimuli), and congruency (neutral, congruent, incongruent) as within-subjects variables. Thus we had a 2 × 2 × 3 factorial design for each comparison task.

Analyses of the interaction between the numerical distance of the magnitude dimension relevant to the task (e.g., luminance in the luminance judgment task) or the magnitude dimension irrelevant to the task (e.g., number in the luminance judgment task) and congruency are presented in the Supplemental Data available online.

Results

Reaction time results

The data for the number comparison tasks resemble the predicted outcomes for luminance contrast (see Fig. 2a and b). The repeated measures analyses revealed a significant main effect for congruency, F(2, 22) = 4.892, p = .017, partial η2 = .31; faster responses were obtained when the target stimulus was numerically larger and had a large luminance contrast (or numerically smaller with a small luminance contrast). The interaction between contrast sign and congruency, F(2, 22) = 20.690, p < .001, partial η2 = .65, was also significant. This interaction confirmed that luminance contrast interacted with numerical magnitude: Faster responses occurred for stimuli that were numerically larger (or smaller) and had a large (or small) luminance contrast.

Fig. 2
figure 2

The reaction time results of the number comparison tasks (a and b) and the luminance comparison tasks (c and d). The insets show the hypotheses related to our predictions (see Fig. 1). The inset with the darker silhouette shows the predictions in agreement with the results. The bright bars show the results for stimuli brighter than the background (conditions a, b, and c from Fig. 1), whereas the darker bars show the results for stimuli darker than the background (conditions d, e, and f from Fig. 1). By definition (see the text), C means “congruent” with the best-fitting hypothesis (see insets; i.e., the larger number is darker for the luminance hypothesis, the larger number has the largest unsigned contrast for the contrast hypothesis, etc.), N means “neutral,” and I means “incongruent.” In the number comparison tasks (a, b), the contrast sign manipulation clearly influenced the results, showing opposite congruency effects. This opposite effect was absent in the luminance comparison tasks (c, d), where it is clear that the luminance hypothesis fits our results best. In both the number and luminance comparison tasks, the instruction manipulation did not affect the results; the congruency effects are similar for the larger (a) and darker (b) conditions, when compared with the smaller (b) and brighter (d) instruction conditions, respectively. The error bars present the 95% confidence interval (Loftus & Masson, 1994)

Full size image

The data for the luminance comparison tasks revealed a pattern similar to that predicted by the luminance hypotheses. A significant main effect for congruency, F(2, 22) = 8.814, p = .002, partial η2 = .44, was obtained. This confirmed that number interacted with luminance processes. In addition, the main effect of contrast sign manipulation, F(1, 11) = 27.915, p < .001, partial η2 = .75, and the interaction between instruction and contrast sign manipulation, F(1,11) = 8.816, p = .013, partial η2 = .44, were significant.

Accuracy results

For the number comparison tasks, a main effect of congruency was present, F(2, 22) = 5.614, p = .011, partial η2 = .34, and contrast sign interacted with congruency, F(2, 22) = 21.745, p < .001, partial η2 = .66. These results mirror the reaction time data showing that the congruency effect was caused by the influence of luminance contrast on number processing. For the luminance comparison tasks, contrast sign interacted with instruction, F(1, 11) = 7.923, p = .017, partial η2 = .42, suggesting that the overall accuracy differed between the different task conditions. Together, the error results suggest that the reaction time results cannot be explained by a speed–accuracy trade-off.

Discussion

Previous studies (Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Cohen Kadosh & Henik, 2006; Pinel et al., 2004) generated conflicting results on the number–luminance congruency task. We hypothesized that these conflicting results can be explained in alternative ways. Instead of luminance information per se, luminance contrast or even saliency might have induced the congruency effects. To further disentangle the processes underlying number–luminance congruency effects, we expanded the number–luminance congruency paradigm with two extra manipulations—namely, contrast sign and instruction.

The results of the number comparison task revealed a congruency effect that was induced by either luminance contrast or saliency when subjects had to respond to the numerically larger stimulus, but when subjects had to respond to the numerically smaller stimulus, only luminance contrast could account for the congruency effects. Therefore, it appears plausible that the interaction effects obtained for both tasks were induced by luminance contrast, not saliency. Large luminance contrast stimuli were thus associated with numerically larger stimuli, and vice versa. For the luminance comparison task, number induced a congruency effect: Subjects associated darker stimuli consistently with numerically larger stimuli. Although the origin of the congruency effect was different for the luminance and number comparison tasks (luminance or luminance contrast, respectively), the interaction between congruency and (relevant or irrelevant) distance consistently revealed the same pattern (see the Supplementary results). In both tasks, the congruency effect decreased with increasing distance of the relevant dimension and increased with increasing distance of the irrelevant dimension. These results suggest that both magnitudes were not processed in a crude manner, but in a more refined one, which is compatible with the results from previous studies (Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Cohen Kadosh & Henik, 2006).

From our findings, we conclude that two distinct factors—namely, luminance contrast and luminance—interacted with number. Although seemingly contradictory, this result is easily explained by the differential strength of these interactions and the task conditions chosen. First, in the number comparison task, a luminance contrast, instead of a luminance effect, was apparent. This suggests that the mapping of luminance contrast onto number is stronger than the mapping of luminance onto number (assuming that luminance does map onto number). Therefore, the previously found luminance–number interactions (Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Cohen Kadosh & Henik, 2006) should be attributed to luminance contrast effects only. Second, our targets were brighter than the background on half of the trials and darker than the background on the other half (our contrast sign manipulation). Therefore, responding to luminance contrast (or saliency; be it explicitly or implicitly) in the luminance comparison task would lead to chance performance. In this case, a relatively small but significant interaction between number and luminance emerged. Note, however, that in this task, luminance was compared, not number. Therefore, from these results, it can be concluded only that number can be mapped onto luminance processes, not the reverse. The converse is true for the number comparison task. Here, it can be concluded only that luminance contrast can be mapped onto number processes.

Even though the number–luminance (contrast) interactions can be explained in terms of a mapping at the magnitude representation level, alternative explanations for congruency effects in (for instance) Stroop paradigms have been proposed as well (e.g., Kornblum, Hasbroucq, & Osman, 1990; Pansky & Algom, 2002). In addition to a mapping at the level of magnitude representations, a mapping at the intermediate conceptual (e.g. larger, smaller, brighter, darker) as well as the response level (left or right) could be distinguished as well. An increasing number of studies on numerical cognition have hinted at such a mapping at the intermediate conceptual representation level (e.g., Gevers, Lammertyn, Notebaert, Verguts, & Fias, 2006; Pansky & Algom, 2002; Santens & Gevers, 2008) and have excluded the possibility of a mapping at the response level (e.g., Gebuis, Herfs, Kenemans, de Haan, & van der Smagt, 2009; Gebuis et al., 2010). Therefore, although the present results cannot differentiate between these different explanations, an interaction at the intermediate conceptual level appears the most likely explanation for our results.

In summary, we demonstrate that luminance contrast can be mapped onto numbers and numbers onto levels of luminance. However, the latter was obtained only when luminance contrast or saliency was controlled for. Whether the interactions occur in the opposite direction as well (luminance interferes with number or number interferes with luminance contrast) remains an open question. Our results explain previous contradictory findings and give a valuable insight into possible factors that can induce number–luminance interferences. Those inclined to use the number–luminance congruency task in the future should pick their stimuli and task conditions in such a manner that multiple explanations, of which some are unrelated to magnitude, can be excluded.