The importance of reliable self-assessment of the quality of one’s own cognitive performance is widely acknowledged (Dunning, Heath, & Suls, 2004). One of the most studied inferential cues underlying self-assessment, or metacognitive monitoring, is fluency (for reviews, see Alter & Oppenheimer, 2009; Schwarz, 2004). Fluency is often a valid cue that shows an inverse relationship with both likelihood of success and metacognitive judgment (Benjamin & Bjork, 1996).

Response latency is an indicator of fluency that has been found to have both objective and subjective validity (Hertwig, Herzog, Schooler, & Reimer, 2008). For example, when the task involves knowledge questions, answers retrieved quickly have a greater chance of being correct than those provided after a long memory search (e.g., Robinson, Johnson, & Herndon, 1997). In such tasks, the more one relies on response latency, the better the reliability of one’s subjective judgment (Koriat & Ackerman, 2010). Yet since fluency is an inferential cue, it can also be misleading. For example, Kelley and Lindsay (1993) found that prior exposure to potential answers to general-knowledge questions increased the speed, frequency, and confidence with which respondents gave those answers on a test, regardless of whether those potential answers were correct (see also Koriat, 2008).

The present research extends the study of response latency as a cue for confidence within the domain of problem solving, which is generally understudied within the metacognitive literature. Several studies have manipulated fluency in problem-solving tasks by using hard-to-read fonts or requiring participants to furrow their brows, but these did not directly measure response latency or confidence per solution (e.g., Alter, Oppenheimer, Epley, & Eyre, 2007). Thompson, Prowse Turner, and Pennycook (2011) measured latency in studies informed by dual-process theories, which differentiate between fast and intuitive reasoning processes (System 1 or Type I) and lengthy, deliberate, and more thorough reasoning processes (System 2 or Type II) (Evans, 2009; Kahneman, 2002; Stanovich, 2009). They asked participants to judge the validity of premises (e.g., “The car has stalled. Therefore it ran out of gas”) by providing the first answer that came to mind and their feeling of rightness (FOR) about it. Participants then reconsidered their answer and provided final confidence ratings. Quick initial solutions were accompanied by higher FORs than those produced more slowly, which suggests that fluency was a cue for FOR. In this study, no direct comparison was made between the latency–accuracy and the latency–FOR associations or between the latency–accuracy and the latency–confidence associations at the same point in time. However, both FOR and ultimate accuracy were inversely related to reconsideration time.

Establishing the role of latency as an independent cue for confidence is challenging. When latency is inversely related to accuracy, an inverse latency–confidence relationship may stem from a strong confidence–accuracy association that is not mediated by latency, but by one or more other valid cues that underlie confidence. In an attempt to establish the role of latency as a cue for confidence in problem solutions, Topolinski and Reber (2010) used anagrams, algebraic equations, and remote associates and manipulated the delay until a proposed solution was presented (50–300 ms). Participants’ task was to decide whether the proposed solution was correct. Topolinski and Reber found that faster-appearing solutions were more frequently judged as being correct. This finding supports the role of latency as a cue for confidence, although not directly, since confidence was not elicited and the task did not allow a natural solving process.

The present study aimed to directly examine the independent sensitivity of confidence to response latency in problem-solving tasks. The tasks were chosen to generate variations in latency’s validity as a predictor of accuracy by using misleading (Experiment 1) and nonmisleading (Experiment 2) problems. To enhance the findings’ external validity, special attention was given to using only ecologically valid procedures, common in educational tests.

Experiment 1

Experiment 1 used misleading problems, of the type commonly used in the literature related to dual-process theories, to examine the independent sensitivity of confidence to response latency—for example: “A bat and a ball cost $1.10 in total. The bat costs $1 more than the ball. How much does the ball cost? ____cents” (Kahneman, 2002). The common initial intuition is 10, while the correct solution is 5, which can be easily verified. In such problems, although careful thinking may take longer, it should increase the chance of finding the correct solution. Thus, the relationship between response latency and accuracy should be weak, or even positive. However, if confidence is nevertheless inversely related to latency, as suggested by utilization of the fluency cue for confidence, this will be a pitfall: The quickly produced but often incorrect solutions are expected to be accompanied by high confidence, and effortful thought by low confidence. The predictive value of within-participant latency variability for accuracy and confidence was examined through mixed logistic and linear regressions (see Ackerman & Koriat, 2011; Jaeger, 2008).

To establish the independent nature of confidence, we examined whether the sensitivity of confidence to latency differs between more- and less-biasing testing scenarios. According to Stanovich (2009), for problems requiring critical thinking, an open-ended test format (OEtf) poses several challenges that can be eased by a multiple-choice test format (MCtf). In an OEtf, solvers must use macrolevel strategizing when deciding how to construe the problem. Inherent to this task is ambiguity about what features of the problem to rely upon. And even when the intuitive model is acknowledged to be wrong, constructing an alternative model of the problem is a major obstacle. The MCtf, in contrast, involves evaluation of a few given solution options. For respondents who have the knowledge and cognitive ability required to solve the problem (Frederick, 2005), the fact that the correct solution is readily present should hint at how to construe the problem, reduce ambiguity, and help in reconstructing the solution model when needed (Stanovich, 2009). Thus, we predicted that an MCtf would weaken the misleading force of the problems.

Method

Participants

Sixty-nine industrial engineering students at the Technion participated for course credit (44 % females). They were randomly assigned to the OEtf or MCtf.

Materials

The materials consisted of 12 short problems that were expected to elicit a particular misleading solution. One more problem was used for practice. The problems included the 3 problems used by Frederick (2005; the bat and ball, water lilies cover half a lake, and machines that produce widgets at a certain rate), the drinks version of Wason’s selection task (Beaman, 2002), the A-is-looking-at-B problem (Stanovich, 2009), and a conditional probability problem (Leron & Hazzan, 2009). The other problems were adapted from preparation booklets for the Graduate Management Admission Test (GMAT). Hebrew versions of the problems were used.

The problems were chosen through pretesting (N = 20) of 15 problems in an OEtf. For the chosen problems, at least 50 % (more than 80 % for 9 problems) provided one of the two expected solutions—the correct or the misleading solution—with not more than 80 % providing the correct solution. For each problem, a four-alternative MCtf version was then constructed using the two expected solutions and two other erroneous solutions provided by the pretest participants.

Procedure

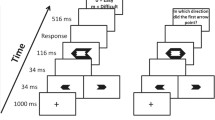
The experiment was conducted in a small computer lab in groups of 2–8 participants. The instruction booklet informed participants that there would be 13 problems of varying difficulty and detailed the procedure for each problem. Pressing a “Start” button on an empty screen brought up each problem. In the OEtf, respondents had to type the solution into a designated space; in the MCtf, they had to click the button associated with one of the four solution options. In both formats, units were displayed where relevant (e.g., currency units for the bat-and-ball problem). After entering their answer, participants pressed “Continue.” Response latency was measured from when participants pressed “Start” to when they pressed “Continue.” Pressing "Continue" exposed the question, “How confident are you that your answer is correct?” and a horizontal scale, along which an arrow could be dragged from 0 % to 100 %. After giving their rating, participants were asked whether they had encountered the problem before and whether their solution was meaningful or a wild guess. Pressing the “Next” button cleared the screen for the next problem.

The practice problem appeared first, and the rest were randomly ordered. The four solution options in the MCtf were randomized once for each problem and then appeared in the same order for all participants. The experiment took about 30 min to complete.

Results and discussion

Data for problems with which participants were familiar were dropped from the analysis. Participants who did not provide solutions, either correct or incorrect, to at least ten nonfamiliar problems were replaced. Over all the data, 11.3 % of the solutions in the OEtf and 5.0 % in the MCtf were reported to be wild guesses.

Because of the diversity in problem texts (13–46 words), we examined whether reading time underlay variability in response latencies. The correlation between word count and mean response time for a problem was not significant, p > .40.

Figure 1 presents the results of the regressions predicting accuracy and confidence by response latency for the two test formats. As can be seen, overall, solutions were provided more slowly and were less accurate under the OEtf than under the MCtf, both ps < .005, which supports our prediction that the MCtf would ease problem solving. However, confidence did not reflect these differences, resulting in a significant difference between the test formats in the extent of overconfidence, t(67) = 2.53, p = .01, d = 0.62.

Fig. 1
figure 1

Regression lines representing confidence predictions and the probability that solutions will be correct on the basis of response latency for the two test formats used in Experiment 1. The start and end points of the lines represent the means of the three solutions provided most quickly and most slowly per participant

Full size image

Latency as a predictor of accuracy

A mixed logistic regression (Proc Glimmix macro of SAS© 9.2) was used to examine the predictive value of latency (a continuous variable) for accuracy (a dichotomous variable) within participants. The thick lines in Fig. 1 represent the fitted regressions (N items = 797). As was predicted, latency was completely nonpredictive under the OEtf, t < 1. In contrast, as was expected, the MCtf attenuated the misleading nature of the problems. Under this test format, latency was predictive of accuracy, Exp(b) = −0.007, t(384.3) = 2.40, p < .05, with a significant interactive effect, t(702.5) = 2.12, p < .05, indicating a significant slope difference between the two formats.

Latency as a cue for confidence

To examine whether the confidence ratings reflected the found difference between the test formats, a mixed linear regression (Proc Mixed macro of SAS© 9.2) was used to predict confidence by latency (both are continuous variables) within participants. The thin lines in Fig. 1 show the regression lines. Response latency predicted confidence reliably for the OEtf, b = −.19, t(403) = 6.00, p < .0001, and the MCtf, b = −.25, t(389) = 9.31, p < .0001. Importantly, the interactive effect was not significant, t(772) = 1.46, p = .15, suggesting no significant slope difference between the test formats.Footnote 1

To control for the sensitivity of accuracy to latency, we added accuracy as an additional factor in the model. This yielded a similarly strong confidence–latency association, both ps < .0001, with no slope difference between the test formats, t < 1. Nevertheless, the main effect of accuracy was significant, t(706) = 8.86, p < .0001. This suggests that although higher confidence ratings were provided for the quick solutions than for the slower ones, confidence ratings were also higher for correct solutions than for incorrect ones. This finding suggests that other, reliable, cues beyond latency also guide confidence.

In sum, Experiment 1 examined the independent sensitivity of confidence to latency by generating comparable situations in which latency was either a valid or an invalid predictor of accuracy and by controlling for accuracy–confidence relationships. The results exposed a double dissociation between the latency–confidence and latency–accuracy relationships: Confidence was independently sensitive to latency, regardless of the latter’s predictive value. In contrast, confidence did not reflect the overall time and performance differences between the MCtf and OEtf.

Experiment 2

Experiment 2 further examined the latency–confidence relationship in an OEtf with nonmisleading problems. The chosen task was the compound remote associates (CRA) test, in which participants are presented with three words and must find a fourth which forms a compound word or a two-word phrase with each cue word separately (see Bowden & Jung-Beeman, 2003). As with the misleading problems used in Experiment 1, immediate associations for each word are expected to come up. However, an association that fits only one or two of the cue words does not satisfy the criterion. For example, for the triplet pine/crab/sauce the word pine might initially elicit pinecone rather than the correct pineapple. Recognition that the initial option does not fit should trigger a search for a better solution (Thompson et al., 2011). When an appropriate word is found, a strong “Aha!” experience is expected (Metcalfe & Wiebe, 1987). This insight experience should allow respondents to identify successful solutions and lead to a high confidence–accuracy correspondence. The question is whether the reliance of confidence on latency is attenuated in the presence of more reliable cues for success when the problems are nonmisleading.

Method

Participants

Twenty-eight undergraduate students were drawn from the same population as in Experiment 1.

Materials

These were 34 Hebrew CRA problems involving commonly used compound words and phrases. Pretesting (N = 56) ensured that all problems could be solved correctly. Two of the problems were used for demonstration, and two for self-practice.

Procedure

The experimental setting and procedure were the same as those in the OEtf condition of Experiment 1. The instructions detailed the procedure, explained what constituted a valid solution, and illustrated the procedure using two problems. The three words appeared side by side, with a space for the solution below them. After the demonstrations, the two practice problems appeared first, and the rest were randomly ordered for each participant.

Results and discussion

Over all the responses, fewer than 1 % of the answers were nonwords or “don’t know.” As was expected, there was high correspondence between confidence and accuracy (see Fig. 2a).

Fig. 2
figure 2

Experiment 2. a Regression lines representing confidence predictions and the probability that solutions will be correct on the basis of response latency. b Regression lines for correct and incorrect solutions. In both panels, the start and end points of the lines represent the means of the three solutions provided most quickly and most slowly per participant

Full size image

Latency as a predictor of accuracy

The thick line in Fig. 2a represents the fitted logistic regression function (N items = 831). As can be seen in the figure, overall, lengthy thinking did not greatly promote accuracy. Moreover, latency reliably predicted accuracy with a strong negative relationship, Exp(b) = −0.06, t(827.1) = 12.81, p < .0001.

Latency as a cue for confidence

The thin line in Fig. 2a shows the linear regression line for predicting confidence by latency. Latency was a highly reliable predictor of confidence, b = −0.80, t(812) = 28.6, p < .0001,Footnote 2 even more so than for accuracy (see t values). As in Experiment 1, to examine the independent latency–confidence relationship, a regression analysis was performed with answer accuracy as an additional factor. The strength of the latency–confidence relationship was attenuated but remained strong, b = −0.44, t(819) = 15.87, p < .0001. Nevertheless, the effect of accuracy was also significant, b = −45.58, t(820) = 23.67, p < .0001.

To further isolate the latency–confidence association, we broke down the data into correct and incorrect solutions. This essentially makes latency irrelevant as a predictor of accuracy within each problem set (see Fig. 2b). Latency predicted confidence reliably for both correct, b = −0.51, t(419) = 14.09, p < .0001, and incorrect, b = −0.41, t(391) = 10.58, p < .0001, solutions. Thus, confidence was independently sensitive to latency. The confidence gap in the middle latency range, in which both correct and incorrect solutions appear, supports the significant accuracy effect reported above. This gap suggests that other reliable cues also influenced confidence. However, the sensitivity of confidence to latency clearly weakened the differentiation between correct and incorrect solutions—in particular, in this middle range of latencies.

General discussion

This study extends previous studies that suggested that fluency affects metacognitive processes involved in problem solving (e.g., Alter et al., 2007; Thosmpon et al., 2011; Topolinski & Reber, 2010). Our aim was to dissociate the fluency–confidence relationship from the fluency–accuracy relationship, putting a special emphasis on ecologically valid procedures. Although there are many instantiations of fluency (see Alter & Oppenheimer, 2009), we used solving latency as the fluency indicator. This measure has the advantages of being objective, precise, and also subjectively valid, while allowing a natural answering process (Hertwig et al., 2008).

The two experiments involved three levels of validity for latency as a predictor of accuracy: no validity (OEtf) and moderate validity (MCtf) in Experiment 1 and high validity in Experiment 2. In both experiments, controlling for the latency–accuracy link exposed the independence of the latency–confidence association: Solutions produced quickly were persistently accompanied by higher confidence than were those that took longer to produce, regardless of the actual validity of latency. Interestingly, despite this insensitivity to latency’s validity, confidence differentiated well between correct and incorrect solutions. This finding suggests that other cues, which are reliable, are also active in informing confidence ratings. Future studies are called for to expose these cues.

In the present study, the results of Experiment 1 showed better predictive value for latency under the MCtf than under the OEtf. This finding supports Stanovich’s (2009) analysis, as described in the introduction. In Experiment 2, in contrast, the OEtf allowed latency to be highly reliable. Which test format, then, is better in this respect? Previous studies with other types of tasks have suggested that the OEtf (or free recall) allows better reliance on answering effort as a metacognitive cue than does the MCtf (or recognition). For example, Robinson et al. (1997) found that when answering knowledge questions, time–confidence and time–accuracy correlations were stronger under an OEtf (recall) than under an MCtf (recognition) (see also Kelley & Jacoby, 1996). They concluded that when people must generate an answer, the time it takes to produce it is highly diagnostic of accuracy. The present study suggests that test format per se is not the main differentiating factor. Given that confidence seems to be sensitive to latency regardless of the test format, the validity of latency as a predictor of accuracy in a particular task is the key feature that allows correspondence between confidence and accuracy in their sensitivity to latency. An interesting future research direction is to examine whether providing participants with feedback regarding the accuracy of answers (see Unkelbach, 2007) can help them adjust their confidence sensitivity to latency to its actual validity.

Over the three examined tasks, the success rate for slowly provided solutions was quite low despite all the problems being solvable by the target population. This finding is not surprising for researchers in the domain of dual-process theories (see Stanovich, 2009, for a review). With a focus on metacognition, the relatively low confidence accompanying those slowly provided solutions is of interest, since it raises questions regarding the regulation of problem solving. Why did the participants not try harder to improve their success rate? Were they satisfied with this low level of confidence or discouraged from investing further effort? Future investigation of this question may be inspired by theories of motivation (e.g., Zimmerman, 2008), regulation of study time (e.g., Metcalfe & Kornell, 2005; Nelson & Narens, 1990), and critical thinking (e.g., West, Toplak, & Stanovich, 2008). However, despite the discouraging unsuccessful lengthy processing, there is good news here: The relatively low confidence resulted in attenuated overconfidence. This is important even if this feeling is informed by the heuristic cue of fluency and is not based only on a genuine likelihood of success.

In sum, the present study helps explain why people tend to provide quick incorrect solutions without trying to improve them. The use of ecologically valid tasks was designed to help bridge theoretically oriented psychological studies with real-life practices and to guide test takers and educators on their way to improving the reliability of confidence judgments by acknowledging one of the commonly found pitfalls.