Until the beginning of 2020, the world has seen a steady and stationary growth in air traffic providing airlines with large profits. Thus, at the level of annual turnover in 2019, the largest airlines received significant revenues, namely, American Airlines—$ 47 billion, Lufthansa—$ 44 billion, Aeromexico—$ 43 billion, Delta Air Lines—$ 41 billion, Emirates Airlines—$ 24.5 billion, Aeroflot—677.9 billion rubles [1]. At the same time, airlines are forced to spend a lot of money on the purchase of fuel. The instability of the oil market, seasonal changes in prices for aviation fuel, geopolitical conditions, persistent inflation cause a stable growth of aviation fuel cost, which usually accounts for about a quarter of all operating costs. However, at present, this share can reach 43% [2]. So, in Russia since 2000 to 2006, the price of 1 ton of TS-1 aviation kerosene (used for subsonic jet aircraft) increased from 6 to 27 thousand rubles (in the prices of the corresponding years), in 2019, it was already about 47–48 thousand rubles/ton and in 2020—47–53 thousand rubles/ton.

The price of fuel made people think even more seriously in 2020, which brought an unprecedented challenge to passenger aviation—due to the COVID-19 pandemic international air traffic was significantly suspended, passenger traffic fell sharply, and all airlines were at a deep loss. They were forced to switch to a significant optimization of their costs, including aviation fuel.

Over the past decades, experts also warn about the upcoming problems with traditional energy resources, which are becoming decrease, and are skeptical about the remaining oil reserves, from which fuel is obtained today, including jet fuel for jet aircraft. According to various sources, humanity will face this problem directly in 20–30 years.

And finally, the third important reason for looking for alternative (non-oil) fuel options is related to environmental issues. Global warming on the planet makes the requirements for the content of harmful emissions that accompany the operation of all modern aircraft engines to be tightened. Obviously, there is no structural and technological perfection of traditional power plants of passenger aircraft, which use by-pass turbojet engines running on aviation kerosene, which will allow meeting the requirements put forward by the International Civil Aviation Organization (ICAO) for promising aircraft of the next decades (2025–2055). In accordance with these requirements, the level of target indicators assumes a 60–70% reduction in fuel consumption, a 50% reduction in CO2 emissions, 75–80%—in NOx, and a two-fold reduction in the noise level [3].

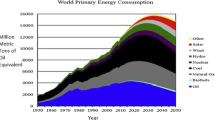
The task of increasing the aircraft fuel efficiency for economic, strategic, and environmental reasons through the introduction of new aircraft and engine models requires an annual improvement of 2% from 2020 to 2050. However, it is unlikely that such a goal can be achieved due to restricted technological and economic possibilities of aviation industry (Fig. 1).

Fig. 1.
figure 1

World consumption of aviation fuel taking into account the forecast up to 2050.

Full size image

For this triune reason (cost–resources–ecology) all over the world, multilateral research is being carried out and accelerated, related both to obtaining fuel from various alternative sources (biomass, synthetic oil, natural gas, hydrogen, and others), and to substantiating the possibility of their applications from the point of view of creating new effective power plants.

Figure 2 shows the energy capabilities of main energy sources available today. It does not show the most energy-intensive fuel—nuclear, with a specific energy consumption qm = 7.9×109 MJ/kg. However, the prospects for its use in aviation in the foreseeable future are hardly possible due to safety conditions. Since air transport today is the most massive carrier, therefore, the consideration of alternative, and therefore cheaper, affordable and safest fuel options for nature and humanity, is a major task for the whole world.

Fig. 2.
figure 2

Volumetric (qw) and mass (qm) energy intensity of various energy sources.

Full size image

In the direction of abandoning the “petroleum” fuel, researchers and developers of aviation technology pin great hopes on the use of cryogenic fuel (CF). The most striking representative of cryogenic fuel is liquid hydrogen (LH), the main advantage of which is determined by the high heat of combustion per unit mass (the specific mass consumption of hydrogen is about three times less than that of kerosene (see Fig. 2). Its use in space technology has made it possible to create such universal and so far unattainable rocket systems such as Saturn-5, Space Shuttle, and Energiya.

In gas turbine power plants, cryogenic fuels can also be used as a refrigerant—cooling the air upstream the compressor due to the cooling capacity of the fuel can also increase the engine efficiency.

Some studies on the possibility of using gas fuels in aviation began in the middle of the 20th century; in particular, these were the projects of the Lockheed Company on the use of hydrogen. In the late 1970s, the Tupolev Design Bureau began a large-scale assessment of the possibility of using cryogenic fuel. Under the leadership of General Designer A.A. Tupolev, a large program of bench and ground tests of the fuel system on LH was launched, aimed at testing the operability of new systems and ensuring the safe operation. With minimal costs, the production Tu-154 aircraft with NK-8-2 engines was converted into a Tu-155 flying laboratory, on which the second engine was replaced by the NK-88, which ran on hydrogen. The LH tank, the temperature of which should be below the boiling point (–253 °C), was located in the rear fuselage compartment continuously blown with air (or nitrogen). Since April 15, 1988, this aircraft has completed five flights. However, it was obvious that the high cost of obtaining LH at that time, the complexity of its storage both on board and on the ground at temperatures below –253 °C would create many problems. In addition, in terms of the volumetric heat of combustion, hydrogen is inferior to kerosene by almost eleven times (see Fig. 2), which leads to a significant increase in the volume of fuel tanks, and, as a consequence, the dimensions of the aircraft. An increase in aerodynamic resistance, like a snowball, will lead to an increase in fuel consumption, an increase in engine thrust, an increase in the mass of the aircraft, which will lead to an increase in the mass of the structure. Obviously, a smoother transition from kerosene was required in the beginning. Taking this into account, the Tu-155 was modified for flights using a more affordable and denser cryogenic fuel, namely, liquefied natural gas (LNG is a line of light hydrocarbons, ranging from CH4 methane to C5H12 pentane).

During transportation, LNG requires storage temperatures down to –162 °C, it is much cheaper not only for hydrogen, but also for kerosene, and its mass calorific value is 15% higher than that of kerosene. In addition, LNG is quite environmentally friendly, less fire hazardous than hydrogen, and by that time sufficient experience had already been accumulated in maintaining such a fuel in a safe state.

The first flights of the Tu-155 on LNG took place in January 1989. Almost 90 test flights were performed. All of them showed that fuel consumption in comparison with kerosene is reduced by almost 15% and such a “cryo aircraft”, in principle, can become economically more profitable.

The next step of the Tupolev Design Bureau in the direction of using LNG was the development of a technical proposal for the Tu-156 aircraft project. With the mass-geometric characteristics of the basic Tu-154 (length is 48 m, wingspan is 38 m, dry weight is 60 tons), it had to be equipped with three turbofan units NK-89 with a total thrust of 320 kN, capable of operating with two separate fuel systems: the existing standard one for kerosene and a new cryogenic one for LNG.

As already noted, one of the problems in creation of “cryogenic” aircraft is their fuel tanks (CFT), which require not only a significant volume, but also loaded with a sufficiently large internal pressure at ultra-low temperatures. For this reason, the shape of the CFT can be either spherical or cylindrical, which means that the traditional placement of such fuel in a thin wing becomes almost impossible. When designing the Tu-156, several options were considered for the placement of a CFT with LNG: under the wing, on the fuselage, inside the fuselage. Finally, an option was chosen that required minimal changes in the basic design and in which aerodynamics were not disturbed and serious alterations were not required to maintain the stability and controllability of the aircraft, namely, cylindrical CFTs were located in the rear passenger compartment (Fig. 3). This arrangement naturally led to a decrease in passenger capacity.

Fig. 3.
figure 3

Placement of CFT on Tu-156 aircraft.

Full size image

The collapse of the Soviet Union and the thesis put forward by the leadership of the new Russia that it does not need its own aircraft led to the complete closure of many promising projects, including the Tu-156, Yak-142, Energiya–Buran and others. But the revision of the positions and the reasons discussed above, more and more urgently require today substantiation of the possibility of using a specific alternative fuel, and, in essence, the choice of the very concept of transport aviation of the future. It is no coincidence that Raptor liquid-propellant rocket engines operating on liquid methane and oxygen are used on the largest Starship rocket for flights to the Moon and Mars with an unprecedented launch weight of 4850 tons.

Let us turn again to the experience of creating a LNG-powered passenger aircraft. On January 2, 1989, the first experimental Tu-204 took off (Fig. 4a). It should be noted that designers of the Tupolev Company approached the Tu-204 program not just as creating a new highly efficient passenger aircraft, but as a basic design, which for many years should have determined the appearance of a large number of modifications for various purposes, including its “cryogenic” version on LNG (Tu-206), as well as an even more promising aircraft already on liquefied hydrogen (Tu-216). In 1994, a survey of airlines was conducted to identify potential customers. The analysis of offers and applications received from airlines showed that there is a real demand for 60–70 Tu-206 aircraft. By 1997, according to the project, blow-off models were made, layout work was carried out, the concept design was completed and preparations for the implementation of the preliminary design were being completed. But the project did not go further than this.

The main data on the Tu-204-100 aircraft, designed for 210 passengers in an economy class and equipped with two PS-90 engines, as well as the Tu-206 aircraft with two PS-92 engines operating both on kerosene and LNG, are given in Table 1.

Table 1 .
Full size table

To accommodate cryogenic fuel in the Tu-206, it was supposed to use four tanks, which were located above the passenger compartment (Fig. 4b).

Fig. 4.
figure 4

Tu-204 (a) and its “cryogenic” brother Tu-206 with four CFTs (b).

Full size image

Let us consider the opportunities from a weight and economic point of view, which the transition to alternative fuel, in particular to LNG, can provide, using the Tu-206 aircraft project as an example. To solve this problem at the conceptual level, we first assess the weight efficiency of transition from the basic already existing aircraft design (in this case, the Tu-204) to a new one, which uses the alternative fuel. We will use an approach based on calculating the takeoff mass growth factors due to the initial change in mass when making changes in the functional parts of the aircraft. The origins of this approach were born and developed in works [4–9]. In the works of V.P. Gogolin [10–13], this approach has found a harmonious justification and refinement. Since this method is essentially based on sensitivity analysis using an analytical solution, therefore, further in this work we will use the introduced term “Sensitivity Factor of Mass” (CFM), which, according to the authors, is more general, since sensitivity analysis is widely used in design, in particular, in strength analysis [14].

According to this approach, the take-off mass of the aircraft m is represented in the form of four functional components

$$m = \sum\limits_{i = 1}^4 {{m_i}} = {m_{a.s}} + {m_{p.p}} + {m_{f{\text{.}}s}} + {m_{pl}},$$
(1)

where ma.s is the mass of the airframe structure (subsystem that implements the aerodynamic principle of flight: wing, fuselage, tail assembly, control system, landing gear); mp.p is the mass of the power plant (subsystem providing the thrust generation: engines, nacelles, pylons, thrust reverse devices, etc.); mf.s is the mass of the subsystem that provides supply to the power plant during a given flight time (fuel and devices for its placement and supply); mpl is the mass of the payload (a subsystem that includes masses associated with the purpose of the aircraft, in this case: commercial (payload) load—mcom, crew, payload equipment, equipment ensuring reliable and safe flight).

The first three terms on the right-hand side of equation (1) are directly dependent on m, and form the mass mdep = ma.s + mp.p + mf.s, and the fourth one is determined mainly by the design task of the aircraft (the mass mpl includes components not directly related to m, mpl = mindep). The use of relative masses \({\bar m_i} = {{{m_i}} \mathord{\left/ {\vphantom {{{m_i}} m}} \right. \kern-\nulldelimiterspace} m}\) makes it possible to obtain the well-known “equation for the existence of an aircraft”

$$m = {{{m_{pl}}} \mathord{\left/ {\vphantom {{{m_{pl}}} {\left( {1-{{\bar m}_{a{\rm{.}}s}}-{{\bar m}_{p.p}}-{{\bar m}_{f{\rm{.}}s}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-{{\bar m}_{a{\rm{.}}s}}-{{\bar m}_{p.p}}-{{\bar m}_{f{\rm{.}}s}}} \right)}} = {{{m_{pl}}} \mathord{\left/ {\vphantom {{{m_{pl}}} {\left( {1-{{\bar m}_{dep}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-{{\bar m}_{dep}}} \right)}}.$$
(2)

All elements of the right-hand side of Eq. (2) are weakly dependent on the mass of the aircraft m and are mainly determined by the requirements presented, which are implemented in the specific properties of the aircraft at the existing technical level. In this regard, it is obvious that Eq. (2) at the level of conceptual analysis is able to answer the question: what complex of properties can be implemented in a new project using other design solutions.

The transition to a new project from an already existing (basic) one will require partial changes in the masses of functional elements of the system, which will then develop into a general (final) change in the mass of the aircraft as a system formed by the interconnection of these elements. Thus, changes in the indicators of technical perfection of the basic design or the selected prototype through changes in \({\bar m_{a.s}}\), \({\bar m_{p.p}}\), \({\bar m_{f.s}}\) will lead to a change in the mass of the aircraft m, which can be considered as a continuous function of n variable parameters qj. Let us express the total mass differential in terms of these parameters, and taking into account the finite but small changes in qj, this transition can be represented in the form (3)

$$dm = \sum\limits_{j = 1}^n {\frac{{\partial m}}{{\partial {q_j}}}d} {q_j} \to \Delta m = \sum\limits_{j = 1}^n {\frac{{\partial m}}{{\partial {q_j}}}\Delta } {q_j}.$$
(3)

So, any changes of the design in the take-off mass can be assessed, in particular, due to the initial changes in the corresponding functional mass Δmi0 (i = 1–4, and the subscript “0” means the initial mass change):

$$\Delta m = \frac{{\partial m}}{{\partial {m_i}}}\Delta {m_{i0}} = {\mu _{mi}}\Delta {m_{i0}},$$
(4)

where μmi is the sensitivity factor of mass (SFM) of the aircraft, which is the ratio of the final increment m to the initial (local) change in mass Δmi0.

Further, without dwelling on the procedure for obtaining the SFM, but referring the reader to [13, Chapter 2] and using the same notation, we give the value of this coefficient for the case of the initial change in mass in the ith functional part of the aircraft

$${\mu _{mi}} = {1 \mathord{\left/ {\vphantom {1 {\left[ {{{{{\bar m}_{pl}} - \Delta {{\bar m}_{i0}} + \left( {{{\bar m}_{p.p}} + {{\bar m}_{a.s}}} \right){C_{xf}}} \mathord{\left/ {\vphantom {{{{\bar m}_{pl}} - \Delta {{\bar m}_{i0}} + \left( {{{\bar m}_{p.p}} + {{\bar m}_{a.s}}} \right){C_{xf}}} {{C_x}}}} \right. \kern-\nulldelimiterspace} {{C_x}}}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {{{{{\bar m}_{pl}} - \Delta {{\bar m}_{i0}} + \left( {{{\bar m}_{p.p}} + {{\bar m}_{a.s}}} \right){C_{xf}}} \mathord{\left/ {\vphantom {{{{\bar m}_{pl}} - \Delta {{\bar m}_{i0}} + \left( {{{\bar m}_{p.p}} + {{\bar m}_{a.s}}} \right){C_{xf}}} {{C_x}}}} \right. \kern-\nulldelimiterspace} {{C_x}}}} \right]}},$$
(5)

where Cxf and Cx are the aerodynamic drag coefficients of the fuselage and the entire aircraft; Δmi0 = Δmi0/m (to simplify the problem, this relative mass, which introduces small corrections, will not be considered in the future).

Based on the selected example, the following design assessment algorithm is proposed.

For the Tu-204 aircraft, the relative functional masses are determined and the SFM is calculated μmi = 2.43 (in formula (5) it was taken Cxf / Cx = 0.27).

During the transition from the basic Tu-204 aircraft to the new Tu-206, a conventional aircraft is introduced, which differs from the Tu-204 in the range Δl = 3600 – 4400 = –800 km and the mass of commercial cargo Δm = 25200 – 21000 = 4200 kg, which were laid down for the Tu-206. The conventional aircraft will have the same masses as the Tu-204: m, \({\bar m_{a.s}}\), \({\bar m_{p.p}}\). Other relative masses of the conventional aircraft will be \({\bar m_{f.s}}\) = (22.5 ×3600)/4400 /103 = 0.178 for the fuel system and \({\bar m_{pl}} = {\text{1}} - {\bar m_{a{\text{.}}s}} - {\bar m_{p.p}} - {\bar m_{f{\text{.}}s}} = 0.37\) for the payload.

The SFM of the conventional aircraft is calculated by Eq. (5): μm = 2.267.

Further, the transition to the Tu-206 project is carried out, taking into account the experience gained from the Tu-155 flying laboratory.

A part of aviation kerosene weighing mker = 5.5 t is remained in the plane.

The use of two types of fuel (kerosene and LNG) is carried out on the basis of the new combined PS92 engine or the modified PS90A engine with the assumed parameters obtained from proportional ratios with the base PS90A engine, which are accepted as similar to those for the NK-8-2U engines (Tu-154 aircraft) and NK-88 (Tu-155 aircraft):

—by specific fuel consumption \({k_{{c_p}}}\) = 0.065/0.0766;

—by the ratio of dry masses of engines km en = 2300/2100.

For LNG, four cylindrical tanks are used, located above the passenger cabin of the fuselage and covered by a spine firing. It is assumed that such a superstructure will lead to an increase in the aerodynamic drag coefficient Cx by 10–15%.

As a result of transition to LNG, there will be initial concomitant changes in the mass of functional components in the following positions.

The initial change in the mass of the power plant by increasing the mass of the new engine:

$$\Delta {m_{p.p.en0}} = {{103000 \times 0.0883 \times \left( {2300 - 2100} \right)} \mathord{\left/ {\vphantom {{103000 \times 0.0883 \times \left( {2300 - 2100} \right)} {2100}}} \right. \kern-\nulldelimiterspace} {2100}} = 866\;{\text{kg}}{\text{.}}$$

The initial change in the fuel mass due to new specific consumption:

$$\Delta {m_{fuel\,{c_p}0}} = {{103000 \times 0.1783 \times \left( {0.065--0.0766} \right)} \mathord{\left/ {\vphantom {{103000 \times 0.1783 \times \left( {0.065--0.0766} \right)} {0.0766}}} \right. \kern-\nulldelimiterspace} {0.0766}} = --2781{\text{ kg}}.$$

The initial change in the mass of the fuel and the mass of the propulsion system due to the increase in the aerodynamic drag:

$$\eqalign{ & \Delta {m_{fuel{C_x}0}} = 103000 \times 0.1783 \times 0.12 = 2204{\text{ kg}}; \cr & \Delta {m_{p.p.{C_x}}}_0 = 103000 \times 0.0883 \times 0.12 = 1091{\text{ kg}}. \cr} $$

We consider the initial changes in the mass of the fuel system (without fuel) due to the CFT for LNG.

To calculate the volume of tanks for LNG, we first determine the required mass and volume of fuel, taking its density ρLNG = 493 kg/m3.

$$\displaylines{ \Delta {m_{LNG}} = {m_{fuel}}--{m_{ker}} = 103000 \times 0.1783--5500 = 12865{\text{ kg}}; \cr {W_{LNG}} = {{12865} \mathord{\left/ {\vphantom {{12865} {493}}} \right. \kern-\nulldelimiterspace} {493}} = 26.1{\text{ }}{{\text{m}}^{\text{3}}}. \cr} $$

When designing the CFT, the requirements of the relevant Standards should be complied. Due to their lack for today for passenger aircraft using cryogenic fuel, we will use the State Standard GOST 56217-2014 developed for road transport, which sets out the requirements for the operation of cryogenic fuel systems with LNG. Considering that there will be different pressures during refueling and during operation in the CFT, it is necessary to provide for the coefficient of completeness of filling the fuel of such a tank kCFT. So, if the filling pressure is 0.1 MPa and the operating pressure is 1 MPa, then, in accordance with the GOST 56217-2014, kCFT = 0.85 and the volume of each of the four CFTs will be WCFT = 26.1 / 4 / kCFT = 7.7 m3.

Based on the length of the passenger cabin of the Tu-204 (30 m), the length of each CFT will be lCFT = 30/4 = 7.5 m. For cylindrical CFTs with the radius r, we use spherical bottoms with the radius R. To ensure the uniform strength of the CFT and increase its capacity, we will take R = 2r. In this case, the stagger of the bottom will be h = (2 – (3)0.5) r = 0.27r and the volume, which the bottom forms (spherical segment with radius R, height h, and base radius r), is

$${W_{bot}} = \pi {h^2}\left( {R--{h \mathord{\left/ {\vphantom {h 3}} \right. \kern-\nulldelimiterspace} 3}} \right) = \pi \;0.14{r^2}\left( {2r--0.09r} \right) = \pi 0.27{r^3}.$$
(6)

As a result, the volume of the tank can be represented as

$${W_{CFT}} = {W_{CFT{\text{ }}cyl}} + 2{W_{CFT{\text{ }}bot}} = \pi {r^2}\left( {{l_{CFT}}--0.54r} \right) = 7.7{\text{ }}{{\text{m}}^3}.$$
(7)

From the solution of this cubic equation, the radius of the CFT is determined r = 0.6 m.

The required tank wall thickness is determined from the operating conditions of the CFT for internal overpressure (p = 1 MPa)

$${\delta _{CFT}} = {{\eta pr} \mathord{\left/ {\vphantom {{\eta pr} \sigma }} \right. \kern-\nulldelimiterspace} \sigma } = 3 \times {10^6} \times 0.6/200 \times {10^6} = 0.009{\text{ m}}{\text{,}}$$
(8)

where η is the safety margin for vessels operating under excess pressure (η = 3); σ is the ultimate strength of the material, which is an aluminum alloy with σ = 200 MPa and density ρCFT = 2700 kg/m3.

The mass of all CFTs taking into account the areas of surfaces of four cylinders and eight bottoms (spherical segments Ssur bot = 2πrh ≈ 0.54πr2) covered with thermal insulation (polyurethane foam coating with a thickness of ;pc = 50 mm and a density of ρpc = 100 kg/m3) is

$$\Delta {m_{CFT0}} = 4\left[ {\left( {2\pi r\left( {{l_{CFT}}--2h} \right) + 2 \times 2\pi rh} \right)} \right]\left( {{\delta _{CFT}}{\rho _{CFT}} + {\delta _{pc}}{\rho _{pc}}} \right) = 2800{\text{ kg}}.$$
(9)

To take into account the mass of the spine firing, we assume that the height of the additional superstructure above the fuselage is hfairing = 2r = 1.2 m, then the additional surface area of the fuselage due to two lateral sides (see Fig. 4) is ΔSf = 2 × 1.2 × 30 = 72 m2.

Taking into account the specific mass of the side surface of the spine firing 24 kg/m2, the initial change in the design from the spine firing mass is

$$\Delta {m_{a.s.{\text{ }}fairing}}_0 = {\text{ }}72 \times 24{\text{ }} = 1728{\text{ kg}}.$$

The total sum of all the initial concomitant masses as a result of the use of LNG is the follows: Δmp.p.new en0 = 866 kg; Δmf.s Cp0 = –2781 kg; Δmfuel Cx0 = 2204 kg; Δmp.p Cx0 = 1092; Δmf.s CFT0 = 2800 kg; Δma.s fairings0 = 1728 kg; ΔmLNG0 = ΣΔmi0 = 3107 kg.

Further, using the SFM of the intermediate project, it is possible to determine the final change in take-off mass for a new aircraft:

$$\Delta {m_{new}} = {\mu _m}\Delta {m_{LNG}}_0 = 2.267 \times 3107 + 2800{\text{ }} = 9848{\text{ kg}}.$$

Thus, the takeoff mass of the new aircraft is

$${m_{new}} = m + \Delta {m_{new}} = 103000 + 9848 = 112848{\text{ kg}}.$$

So, the transition to an alternative type of fuel led to an increase in a take-off mass by 9.6% compared to the base model and, in this regard, it is obvious that the solution to the problem of the feasibility of this transition should be performed from an economic point of view. For this, the problem of minimizing costs for a given traffic is considered. To solve it, it is necessary to establish a relationship between the reduced operating costs and the mass of those parts that have changed. For analysis with obtaining real figures, we can find only the following costs: of the entire aircraft, of the engine and fuel, which we will bring to three components: the cost of an empty aircraft without engines, the cost of the engine and fuel. These functional parts will appear later.

It is more convenient to perform an economic assessment for an aircraft within one year operation. The annual reduced costs for the operation of the aircraft (Ra) are presented in the form

$${R_a} = C + {E_{st}}K,$$
(10)

where C is the cost of one year of operation; K is the annual deductions from capital investments; Est is the standardized coefficient of efficiency of capital investments considered as the annual share of payments for a bank loan.

The cost of one year of operation is recorded in the following form

$$C = {T_{fl}}A,$$
(11)

where Tfl is the flying time per year; A is the cost of one flight hour represented in the form of the following terms

$$A = {A_{dep{\text{.}}w.out - en}} + {A_{dep{\text{.}}en}} + {A_{main.w.out - en}} + {A_{main.en}} + {A_{fuel}} + {A_{wage}} + {V_{a.p}},$$
(12)

where Adep.w.out-en, Amain.w.out-en are the depreciation costs and maintenance of the aircraft without engines; Adep.en, Amain.en are the depreciation costs and maintenance of engines; Afuel is the fuel cost; Awage is the wages of the flight crew; Va.p. is the airport expenses.

The costs that we are interested in are associated with additional masses and, in this formulation of the problem, these are depreciation and fuel costs, and they can be written in the following form

$${A_{dep{\text{.}}w.out - en}} = {{{C_{w.out - en}}\left( {1 + {k_{rep{\text{.}}w.out - en}}{n_{rep{\text{.}}w.out - en}}} \right){k_{n{\text{.}}f{\text{.}}w.out - en}}} \mathord{\left/ {\vphantom {{{C_{w.out - en}}\left( {1 + {k_{rep{\text{.}}w.out - en}}{n_{rep{\text{.}}w.out - en}}} \right){k_{n{\text{.}}f{\text{.}}w.out - en}}} {{T_{w.out - en}};}}} \right. \kern-\nulldelimiterspace} {{T_{w.out - en}};}}$$
(13)
$${A_{dep.en}} = {{{C_{en}}\left( {1 + {k_{rep.en}}{n_{rep.en}}} \right){k_{n{\text{.}}f.en}}} \mathord{\left/ {\vphantom {{{C_{en}}\left( {1 + {k_{rep.en}}{n_{rep.en}}} \right){k_{n{\text{.}}f.en}}} {{T_{en}};}}} \right. \kern-\nulldelimiterspace} {{T_{en}};}}$$
(14)
$${A_{fuel}} = {{{C_{fuel}}{k_{n.f.fuel}}} \mathord{\left/ {\vphantom {{{C_{fuel}}{k_{n.f.fuel}}} {{t_{run}},}}} \right. \kern-\nulldelimiterspace} {{t_{run}},}}$$
(15)

where krep.w.out-en is the unit cost of capital repair of the aircraft without engine; krep.en is the unit cost of the engine capital repair; kn.f.w.out-en, kn.f.en, kn.f.fuel are the coefficients of the increase in the annual fuel consumption due to non-production flight time (training, aircraft trip, engine run); nrep.w.out-en, nrep.en are the amounts of annual repairs for the aircraft glider and engines; Cw.out-en is the cost of the aircraft without engines; Cen is the cost of the engine; Cfuel is the cost of fuel; Tw.out-en is the full service life of the aircraft without engine; Ten is the full service life of the engine.

Capital investments are determined by the amount spent on the purchase of an empty aircraft without engines (taking into account the cost of spare parts) Kw.out-en, engines (taking into account the costs not only for spare parts, but also for replacing engines due to different lifetimes of an engine and an empty aircraft without engines) Ken, as well as ground facilities Kground (they are assumed to be independent of the mass of aircraft parts), i.e.

$$K = {K_{w.out - en}} + {K_{en}} + {K_{ground}} = {C_{w.out - en}}{k_{s.p.w.out - en}} + {C_{en}}{k_{s.p.en}} + {K_{ground}}.$$
(16)

As a result, it is possible to obtain the dependence of the annual reduced costs for the aircraft operation on the cost of its constituent parts

$${R_a}\left( {{C_{w.out - en}},{C_{en}},{\text{ }}{C_{fuel}}} \right) = {\alpha _{w.out - en}}{C_{w.out - en}} + {\alpha _{en}}{C_{en}}{k_{s.p.en}} + {\alpha _{fuel}}{C_{fuel}} + F,$$
(17)

where F is the constant;

$${\alpha _{w.out - en}} = {{\left( {1 + {k_{rep.w.out - en}}{n_{rep.w.out - en}}} \right){k_{n.f.w.out - en}}{H_{fl}}} \mathord{\left/ {\vphantom {{\left( {1 + {k_{rep.w.out - en}}{n_{rep.w.out - en}}} \right){k_{n.f.w.out - en}}{H_{fl}}} {{T_{w.out - en}} + {E_{st}}{k_{s.p.w.out - en}}}}} \right. \kern-\nulldelimiterspace} {{T_{w.out - en}} + {E_{st}}{k_{s.p.w.out - en}}}};$$
$${\alpha _{en}} = {{\left( {1 + {k_{rep.en}}{n_{rep.en}}} \right){k_{n.f{\text{.}}en}}{H_{fl}}} \mathord{\left/ {\vphantom {{\left( {1 + {k_{rep.en}}{n_{rep.en}}} \right){k_{n.f{\text{.}}en}}{H_{fl}}} {{T_{en}} + {E_{st}}{k_{s{\text{.}}p{\text{.}}en}};}}} \right. \kern-\nulldelimiterspace} {{T_{en}} + {E_{st}}{k_{s{\text{.}}p{\text{.}}en}};}}$$
$${\alpha _{fuel}} = {{{k_{n.f.fuel}}{T_{fl}}} \mathord{\left/ {\vphantom {{{k_{n.f.fuel}}{T_{fl}}} {{t_{run}}.}}} \right. \kern-\nulldelimiterspace} {{t_{run}}.}}$$

The positive effect of the annual traffic can be assessed as follows

$$W = {{{k_l}{m_{com}}L{T_{fl}}} \mathord{\left/ {\vphantom {{{k_l}{m_{com}}L{T_{fl}}} {{t_{run}}}}} \right. \kern-\nulldelimiterspace} {{t_{run}}}},$$
(18)

where L is the distance of transportation; trun is the average time of one trip; kl is the average coefficient of the completeness of the aircraft loading.

The assessment of the economic efficiency of the use of LNG is carried out according to the scheme shown in Fig. 5, where E is the economic effect equal to the change in the reduced costs reversed in sign.

Fig. 5.
figure 5

Scheme for assessment the economic efficiency of the use of LNG.

Full size image

The previously calculated changes in the masses of functional parts should be transformed into three distinguished price groups:

$$\Delta {m_{en}} = {\mu _m}\left( {\Delta {m_{p.p{\text{ }}new.en0}} + \Delta {m_{p.p{C_x}0}}} \right) = 2.267 \times (866 + 1092) = 4441{\text{ kg;}}$$
$$\Delta {m_{w.out - en}} = {\mu _m}\left( {\Delta {m_{f{\text{.}}s.CFT0}} + \Delta {m_{a{\text{.}}s.fairing0}}} \right) = 2.267 \times 1728 + 2800 = 6717{\text{ kg}};$$
$$\Delta {m_{fuel}} = {\mu _m}\left( {\Delta {m_{f.s.{c_p}0}} + \Delta {m_{fuel\,{C_x}0}}} \right) = 2.267 \times ( - 2781 + 2204) = - 1309\;{\text{kg}}{\text{.}}$$

The expression for Δmfuel also can be used to estimate the fuel efficiency. Using expression (17), we able to calculate the difference between the reduced costs for new aircraft on LNG and the base one on the traditional fuel:

$$\Delta {R_a} = {R_{a Tu - 206}}--{R_{a{\text{ }}Tu - 204}} = {\alpha _{w.out - en}}\Delta {C_{w.out - en}} + {\alpha _{en}}\Delta {C_{en}}{k_{s{\text{.}}p\,en}} + {\alpha _{fuel}}\Delta {C_{fuel}}.$$
(19)

To transform men and mw.out-en to Cen and Cw.out-en, you can use an expression of the form

$${C_i} \sim {m_i}^{{k_e}},$$
(20)

where ke is the degree of elasticity of the relationship between the price and the mass. For simplicity, we take ke = 2/3, then ΔCi = 2/3(Ci /mi)Δmi.

To obtain ΔCfuel, you first need to determine the cost of jet fuel for a conventional aircraft Cker = mker cker. Then, for Tu-206, LNG costs are calculated, the final mass of which will be mfuel LNG = mfuel – Δmfuel, and the difference in fuel costs is

$$\Delta {C_{fuel}} = {m_{fuel}}{c_{ker}} - {m_{fuel\;LNG}}{c_{LNG}},$$
(21)

where cker and cLNG are the cost per unit mass of fuel.

To perform an economic calculation, we will take the following averaged parameter values: Tfl = 2000 h; kc = 0.58; nrep. w.out-en = 5; nrep. en = 1; krep. w.out-en = 0.125; krep. en = 0.25; kn.f.w.out-en = 1.05; kn.f.en = 1.07; kn.f.fuel = 1.13; ks.p.w.out-en = 1.05; ks.p.en = 1.46; Tw.out-en = 30000 h; Ten = 6000 h; Est = 0.12; trun = 5.14 h; cker = 51000 rub/t; cLNG ≈ 0.5cker, and we will also use data from the Internet to estimate the cost of a medium-haul aircraft: Cw.out-en ≈ 0.5Caircraft ≈ $23 mln; Cen /men = 3Cw.out-en /mw.out-en.

As a result, using expression (19) and all the necessary numerical values of the parameters, the annual economic effect getting from one Tu-206 aircraft compared to the Tu-204 is about 67.6 mln rubles. With today exchange rate ($1 = 70 rubles), this will be about $957 000. Thus, despite the increase in the weight of the new aircraft by 13%, there is an annual economic effect due to a decrease in LNG costs equal to 1.8% of the cost of the entire Tu-204 aircraft ($46 mln). Considering that the service life of a passenger aircraft is 20–30 years, this will provide airlines with significant cost savings, passengers—a decrease in ticket prices and a decrease in the environmental burden on the environment.

This methodology can be used to conceptually assess the use of any alternative fuel. Of course, the authors are aware that many factors were not taken into account, in particular, the rise in the cost of storage and delivery of cryogenic fuel. All these features can be easily entered into the calculation model, but this will require additional information.

In conclusion, let us go back to the prospects for using liquefied hydrogen. In the opinion of the authors, traditional schemes of long-haul aircraft are of little use in the case of using such “large-sized” fuel. In this regard, it is obvious that it is necessary to switch to the “Blended Wing Body” type layout scheme (Fig. 6), which is currently being intensively worked out in leading design organizations [15]. Such a scheme will be more efficient from an aerodynamic point of view and for the version with LNG, having lower mass consumption due to better aerodynamic quality, lack of fairing, etc.

Fig. 6
figure 6

.

Full size image

The approach based on the analysis of the sensitivity of the take-off mass of the aircraft allows us to conduct at the conceptual level similar studies on estimation of the aerodynamic scheme [16], but this requires, as already noted, a basic model of the aircraft.