INTRODUCTION

Ground level enhancement (GLE) events are caused by eruptions on the Sun that are accompanied by solar flares or coronal mass injections. Such processes often generate solar energetic particles (SEPs) (mainly protons) with energies of up to hundreds of MeV in the Sun and their emission into the interplanetary space. GLE events are extreme cases of SEPs where the proton energy can be more than 430 MeV (1 GW) [1].

The first GLE event of the new 25th solar activity cycle occurred on October 28, 2021, and was detected both on spacecraft and by ground-based stations of the World Neutron Monitor (NM) Network. These were mainly NMs that had an atmospheric cutoff rigidity of 1 GW or a geomagnetic cutoff rigidity close to it.

It should be noted that the new GLE event continued the series of low-amplitude events that began as early as the middle of the 24th cycle. However, the fair number of stations that recorded it with amplitudes above 1% (the mean threshold of fluctuation on a standard NM) allows us to analyze the event without simplifications. This requires data from a minimum number of stations with amplitudes above 2% [2]. This number is not strictly observed and depends on the amplitude of the increase at the NM. Based on the experience from analyzing many GLE events, the minimum number of NMs for a correct interpretation is around 20.

EVENT OF OCTOBER 28, 2021

The event lasted ~3 h and had a maximum amplitude of 6%. The highest amplitude was detected at Calgary and Fort Smith stations in North America. The neutron monitors in Apatity and Barentsburg (Svålbard) recorded amplitudes of 2–4%. The event (codenamed GLE73) originated from beta–gamma active region A2887 with coordinates S28W02, a flare of class X1.0, an X-ray emission maximum at 15:35 UT, and a type II/VI flare. The start of the event was first detected at the South Pole station at 15:55 UT. The GLE73 event increased the cosmic ray flux by 2–6% at polar NMs. Low-latitude stations did not detect this increase, but several mid-latitude stations whose asymptotic receiving cones were near the axis of anisotropy did. The first of these was the Calgary NM, located at a height of 1200 m. The data indicate the solar cosmic ray (SCR) spectrum was soft. The interplanetary and geomagnetic situation during the day of the GLE event was quiet, the Kp index was 1, the Dst index was near 0, and the solar wind speed and density were moderate. This means the configuration of the interplanetary magnetic field (IMF) generally corresponded to a typical Parker spiral.

The technique we created and used to determining parameters of the primary proton flux at the magnetosphere’s boundary requires that we calculate asymptotic cones (ACs) of reception for NMs with high accuracy and the model of the magnetosphere that most accurately describes the state of the Earth’s magnetosphere. We used Tsyganenko’s T-01 model [3], which works well in analyzing other GLE events. ACs were calculated for all stations in the 1 to 20 GW range of atmospheric cutoff rigidity. In our technique, there is no averaging or calculating of the effective penumbra rigidity, since the ACs of all stations are calculated in the abovementioned 1–20 GW range of rigidity with a constant step of 0.001 GW, and forbidden rigidities (values of particles that cannot penetrate from the interplanetary space to a given NM station) are marked in a special array and excluded from calculations when determining the response of this NM. This eliminates the error introduced by calculating the effective penumbra rigidity because this quantity depends on the type of the spectrum, which is not known before solving the inverse problem. Our map of asymptotic cones of reception for a series of stations is presented in Fig. 1. The station names start from the AC edge corresponding to 20 GW. The position of the axis of anisotropy is marked by plus signs; the lines of equal pitch angles are shown by black dots, and the corresponding values of the pitch angle are shown. The ACs were calculated for 17:00 UT using the T-01 magnetosphere model.

Fig. 1.
figure 1

Map of asymptotic receiving cones for some high-latitude stations at 17 UT: Thule (THUL), Inuvik (INUK), Fort Smith (FRSM), Calgary (CALG), Peawanuck (PWNK), Jang Bogo (JGBO), Nain (NAIN), SANAE (SNAE), South Pole (SOPO), Dome C (DOMC), Mawson (MWSN), Kerguelen (KERG), Apatity (APTY), Barentsburg (BRBG), Norilsk (NRLK), and Tixie Bay (TXBY). The plus signs denote the calculated axis of SCR anisotropy; the asterisks, the points of intersection of the celestial sphere and the IMF axis. Lines of equal pitch angles are shown by black dots; the numbers near them show the pitch angle.

Full size image

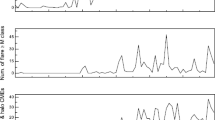
The growth profiles of the Calgary and Fort Smith NM stations during the GLE73 event (Fig. 2) are typical of a GLE: a rather sharp front and a slow decline, which is observed when the receiving cones of the stations are near the axis of anisotropy and acquire an anisotropic flux propagating along the axis of anisotropy with weak scattering and reaching the Earth first. The smooth growth shows that the station received a scattered particle flux whose density grew gradually and with a delay.

Fig. 2.
figure 2

Profiles of count growth at NM stations: (a) Apatity (APTY) and Barentsburg (BRBG); (b) Tixie Bay (TXBY) and Yakutsk (YKTK); (c) Calgary (CALG) and South Pole (SOPO); and (d) Fort Smith (FSMT) and Dome C (DOMC). Profiles of the Calgary, South Pole, and Dome C high-mountain stations are normalized to a barometric level of 1000 mb. Five-minute data are used.

Full size image

Some NMs are located in mountains. Due to the barometric effect, the amplitude of growth at these stations is considerably higher than when an NM is at sea level at the same geographic point. This is because the effective path lengths of galactic and solar cosmic rays in the atmosphere differ (~140 and ~100 g/cm2, respectively), and SCRs are absorbed more strongly by the atmosphere [4]. The magnitude of growth at different heights mut be adjusted to a common barometric level. Since most NMs are located near sea level, it is convenient to take 1000 mb as the base value. The adjustment to a common barometric level is done using two lengths of attenuation [5]. It is after barometric correction that the South Pole and Dome C NMs ceased to be among stations with the highest amplitude of growth, and Fort Smith and Peawanuck were the stations with the highest amplitude in the GLE73 event. These NMs can be used to solve the inverse problem only after performing all the described procedures.

Even though mid- and low-latitude NMs showed no increase in the SCR flux during the GLE73 event, some NMs with a zero increase must be in the list of the relevant stations. Such stations with a zero increase mark the upper limit of the energy spectrum of SCRs. Mid-latitude stations have an extended AC that covers more than 180° of longitude near the equator. Particles in the SCR flux above the cutoff threshold of such stations would raise the flux at them. We used Russian and European mid-latitude NMs with cutoff rigidities of 3–5 GW, e.g., Novosibirsk, Moscow, and Jungfrau. However, an excess of such stations is undesirable because the mean growth amplitude (mean in the number of used NMs) is reduced. The residue is reduced as well, and the minimum search becomes difficult. Hermanus, Potchefstroom, and other low-latitude stations we know could not exhibit an increase were therefore not used in solving the inverse problem. A total of 27 NM stations were selected for analysis, among which there were around 20 polar and near-polar stations.

The convergence of the solution depends on calculating the ACs that were used, so we are required to estimate the correspondence of the specified date and time, other parameters, and calculated ACs to the real position of the Earth in space. The hour of 17 UT corresponds to a turn of the prime meridian of Greenwich by 75° in the GSE coordinate system from the direction to the Sun. Apatity is located at ~35° E. The drift of protons with rigidities of 10–20 GW in the Earth’s magnetosphere is 40°–60°, depending on the state of the magnetosphere. As a result, the AC of Apatity in the range of 10–20 GW must be located in the 150°–170° range of longitudes. The interplanetary magnetic field under quiet conditions extends from the Sun to the Earth along a Parker spiral. At the Earth’s orbit, the angle between the tangent to this spiral and the direction to the Sun is 30°–60° to the West, depending on the speed of the solar wind. It is also known the ACs of Kerguelen and Apatity always intersect when the magnetosphere is not too disturbed. All of the above corresponds to the map in Fig. 1.

SOLVING THE INVERSE PROBLEM

Parameters of SCRs arriving at the magnetosphere’s boundary from interplanetary space are determined by solving the inverse problem with data from the ground-based NM network. In other words, characteristics of the SCR flux (the energy spectrum, pitch angle distribution, and direction of arrival) are chosen so that the increases (responses) calculated by these characteristics on the world NM network have minimal discrepancies with ones actually detected. The general way of solving the inverse problem was proposed for the first time in [6].

A key aspect of any way of solving the inverse problem is that the forms of the functional dependences specifying the relation between characteristics implicitly determine both the accuracy of the solution and the form of these dependences itself. For example, specifying the power form of the spectrum restricts possible solutions to only power dependences. When the real SCR spectrum has another form (e.g., exponential), any solution will have a large error that cannot be eliminated by optimizing the algorithm or choosing other parameters.

We must therefore specify the form of the dependences in the most general terms. This approach is used in our technique. SCR rigidity spectrum I(R) is specified in the form

$$I\left( R \right) = {{J}_{0}}{{R}^{{ - \gamma - \Delta \gamma \left( {R - 1} \right)}}},$$
(1)

where J0 is the SCR flux at R = 1, γ is the spectrum exponent, and Δγ is the spectrum correction.

This way of specifying the spectrum was proposed in [7] and has actively been used in our other works, e.g., [8]). It allows us to obtain different forms of the spectrum. The power spectrum is obtained when Δγ = 0. It has been determined empirically that for any reasonable value of R0, there exists a pair of values (γ, Δγ) such that functional dependence (1) on finite range of rigidity 1–20 GW coincides with the exponent gaving characteristic rigidity R0. Other values of the pair (γ, Δγ) specify a spectrum intermediate between the power and exponential forms.

The pitch angle distribution of SCRs can have different forms [9]. The simplest form of the pitch angle distribution (PAD) is Gaussian and was used in [6], where the computational capacities were modest. However, it does not always correspond to conditions of SCR propagation and scattering in interplanetary space. The PADs observed in the GLE events had a linear dependence [10], a dip at angles of ~90°, and an additional flux from the reverse (antisolar) direction. The last is possible when magnetic loop structures are extended from the Sun into interplanetary space, as was shown in [11, 12]. As when specifying the spectrum, it is important to create the most general form that can reflect the functional dependence at different values of the parameters, e.g., Gaussian, linear, bidirectional. The form we chose to specify the pitch angle distribution was

$$F\left( \theta \right) = {\text{exp}}\left( {\frac{{ - {\kern 1pt} {{\theta }^{2}}}}{c}} \right) \cdot \left[ {1 - a{\text{exp}}\left( {\frac{{ - {{{\left( {\theta - \frac{\pi }{2}} \right)}}^{2}}}}{b}} \right)} \right],$$
(2)

where θ is the pitch angle, c is the parameter determining the PAD width, and the factor in square brackets forms the PAD singularity at angles close to 90°. Analysis of expression (2) shows the possibilities of this form are much broader than the mere creation of a singularity at angles of ~90°. At the same time, the variety of PAD forms is obtained using only three parameters. Combinations of parameters (c, a, b) can yield a PAD with a linear form. At a = 0, expression (2) takes the form of a simple Gaussian. Values 1 > a > 0 and b \( \ll \) c result in a dip at pitch angles near 90°. At a < 0, a hump appears in the PAD near 90°. Both a displacement of the PAD maximum from 0° to any angle to 90° if a < 0 and a linear PAD at a > 0 are possible at b ≈ c. Expression (2) was used in seeking the solution to the inverse problem for a series of GLE events in [8, 11, 12].

Finally, the expression for calculating the response of the L-th NM has the form

$$\Delta {{N}_{L}} = \sum\limits_{R = 1}^{20} {I\left( R \right)F\left( {{{\theta }_{L}}\left( R \right)} \right)S\left( R \right){{A}_{L}}\left( R \right)dR} ,$$
(3)

where ΔN is the increase at the Lth NM station, S(R) is the tabulated specific collection function, and AL(R) is an array containing the list of admissible and forbidden rigidities for the Lth NM that forms when calculating the AC. Summation is done with the same rigidity step dR = 0.001 GW as in calculating the AC. The left-hand side of the expression is a function of six parameters (γ, Δγ, c, a, b, Ω, and Φ). Angles Ω and Φ determine the position of the axis of anisotropy. They are implicitly contained in (2) because the pitch angle is determined relative to a certain direction specified by angles Ω and Φ in the spherical coordinate system. The total residue throughout the NM network is expressed as

$$\begin{gathered} G\left( {{{\gamma }},{{\Delta \gamma }},c,a,b,{{\Theta }},{{\Phi }}} \right) \\ = \,\,\sum\limits_L {{{{\left( {{{\Delta }}{{N}_{L}}\left( {{{\gamma }},{{\Delta \gamma }},c,a,b,{{\Theta }},{{\Phi }}} \right) - {{\delta }}{{N}_{L}}} \right)}}^{2}}} , \\ \end{gathered} $$
(4)

where δNL is the increase actually measured at the Lth NM station. G expresses the sum of squared differences between the calculated NM response to the SCR flux specified by the parameters (γ, Δγ, c, a, b, Ω, Φ) and the real increase at the NM. The minimum of function G corresponds to the solution to the inverse problem.

Searching for the minimum of a multiparametric function is a complicated matter, but present-day computational capacities and new numerical means allow us to obtain a fairly stable solution to expression (4). Note that proceeding from the above preliminary analysis of the growth profiles, initial values of the parameters listed in the function G can be found not far from the minimum point. For example, the axis of anisotropy lies between the ACs of Inuvik and Peawanuck near Fort Smith and Calgary, which exhibited the maximum increase and a sharp leading front. This allows us to remain in the region of a stable solution, accelerates the search for the minimum of expression (4), and makes it easier to find.

SCR SPECTRA

The inverse problem is usually solved using 5-min NM data. The result is a sequence of spectra and other parameters of the SCR flux during the main GLE period. This sequence is determined with the same 5‑min step and describes the dynamics of SCR spectra over the GLE period. Even though the start of the increase was first recorded at 15:55 UT, the inverse problem can be solved only after 16:25 UT, when a sufficient number of NMs had recorded an amplitude of at least 2%. After 18:00 UT, the number of stations showing an amplitude high enough for solving the problem again became less than was needed.

Figure 3 presents the SCR spectra recalculated to the energy scale at certain points in time. Table 1 gives the numerical values of the parameters. The flux is determined in the units shown in the plot of the spectra; the second column presents characteristic energy E0 (GeV) or spectral exponent γ (values of E0 are in the column on the left; values of γ, on the right), and Ω and Φ are presented in degrees. Figure 4 shows the pitch angle distributions of SCRs.

Fig. 3.
figure 3

Energy spectra of SCRs for typical times in the (a) semilogarithmic and (b) double logarithmic scales. The lines in the left plot show the exponential dependence. The lines to the right show the power dependence.

Full size image
Table 1. Parameters of the SCR flux at different moments in time
Full size table
Fig. 4.
figure 4

(a) Pitch angle distributions of the SCR flux at 16:25, 16:30, and 16:40 UT in Cartesian coordinates and (b) the same PAD in polar coordinates. (c) Pitch angle distributions of SCRs at 16:40, 16:55, 17:05, and 17:45 UT in Cartesian coordinates and (d) the same PAD in polar coordinates. The PAD at 16:40 is shown for a comparison of scales.

Full size image

The spectrum at the beginning of the event (16:25 and 16:30 UT) had an exponential form. It then started to transition to the power form. This behavior corresponds to most GLE events processed in our technique [11]. The spectrum was still exponential at 16:40 UT, but considerably softer (characteristic energy E0 is lower). By the time we reach the maximum at 17:00 UT, the spectrum has become a power spectrum. Judging from the spectrum, the flux was halved at 16:30 UT. However, the PAD shows this happened only at small pitch angles (<40°). The reduction was negligible at large pitch angles. There is a simple explanation for this. When there is a brief flare on the Sun, particles moving with small pitch angles reach the Earth rapidly in a bunch and travel on, as is indicated by the drop in the flux density at small pitch angles. Particles scattered to large pitch angles drift more slowly along IMF lines and spread along them. The PAD also did not change shape appreciably after the first bunch passes. There is only a proportional increase in the flux at all angles with simultaneous softening of the spectrum.

The asterisks in Fig. 1 mark the intersection of the line along which the IMF vector lies and the celestial sphere (referred to as the IMF axis). For SCR protons propagating in the IMF, the direction of the magnetic field vector (from or to the Sun) is not important. What is important is the field line. We can see the IMF axis is quite far from the calculated axis of anisotropy. This is because the IMF was weak (only ~3 nT) during the second half of the day on October 28, as the ACE data show. Component Bx oscillated strongly from −2 to 2 nT with a change in sign. The value of Bz was positive most of the time, while By had consistently negative values. The longitude of the IMF axis shifted to −60° at positive Bx values, and to 60° at negative values. It is the position of the axis that is reflected on the map for 17 UT. The SCR flux is weakly sensitive to such rapid oscillations of the direction of the IMF vector. Calculations show the Larmor radius of a proton with a rigidity of 1 GW in a magnetic field of 3 nT is more than 1 million kilometers. This small IMF structure therefore has no effect on the motion of SCRs that have rigidities of one to several gigawatts.

GLE73 was generally an ordinary event. It was distinguished by neither its parameters nor the shapes of its profile. Other GLEs had low amplitudes throughout the 24th cycle, and GLE73 continued this series in the new 25th cycle.

The form of the PAD (at pitch angles <90°) was conspicuously linear for much of the event. A similar one was observed in the GLE70 event on December 13, 2006 [8] and in GLE71 (May 17, 2012), but it was very rare in events of 2000–2005 and earlier [11]. This could have been due to conditions at the source in the Sun at the instant of the flare, the weak interplanetary magnetic field, and its calmness. This feature of a PAD could be the subject of a separate study of the state of the IMF according to SCRs. Recall that the linear form of the PAD was not specified in solving the inverse problem. It appeared due to a special combination of the parameters (c, a, b) determining the general form of a PAD.

CONCLUSIONS

Results were presented from analyzing the first event of the 25th cycle in terms of solar cosmic rays (GLE73 of October 28, 2021). The energy spectra and other parameters of the solar cosmic ray flux beyond the Earth’s magnetosphere were obtained by solving the inverse problem through much of the event. GLE73 was an ordinary event. In the initial phase, the SCR spectrum had an exponential form. It then smoothly transitioned into a power spectrum. Characteristic energy E0 ≈ 0.6 GeV, and spectrum exponent γ ≈ 5.5. These are the most typical values of GLEs [11].