Analytical Description of the Dynamics of Planar Pulses Propagating in the Mode of Tunnel Ionization

Abstract

The method of moments is used to investigate the propagation of a planar pulse in the mode of tunnel ionization. A system of equations is obtained for the parameters of a signal and the conditions for its quasi-stable propagation are found according to Lyapunov.

INTRODUCTION

It is of interest to study the dynamics of intense pulses propagating in the mode of ionization for both fundamental research and application, since it is used in a variety of fields that include remote sensing of the atmosphere [1], control of lightning [2], supercontinuum generation [3], and generating terahertz radiation [4]. It is known that the solution to the nonlinear Schrödinger equation (NLSE) is stable only in one-dimensional case $D = 1$, which corresponds to purely spatial or temporal signals. The solutions are unstable at dimensionalities of D = 2 (which corresponds to beams or planar spatiotemporal pulses) and D = 3 (which corresponds to optical bullets) [5]. Several mechanisms have been proposed for stabilizing signals when D > 1: saturating nonlinearity [6], competing nonlinearities [7], higher-order diffraction or dispersion [8], gradient waveguide [9], and second-harmonic generation [10]. It was shown [11–18] that ionization can also stabilize a signal, due to the balance between self-focusing, diffraction, and plasma divergence. It is known that ionization shifts the pulse spectrum toward higher frequencies [19–21] due to the generation of free electrons. This results in a negative refractive index and thus a blue shift of the signal spectrum. This phenomenon is opposite to the familiar stimulated Raman self-scattering (SRS) [22–26].

The ionization of a dielectric by an intense light pulse can be described using the Keldysh formula [27]. There are two limiting modes, depending on the Keldysh parameter: multiphoton and tunneling ionization. It is of interest to analyze pulses propagating in the mode of tunneling ionization, since the region of the anomalous group velocity dispersion in most media belongs to the infrared transmission band [28]. The limit of tunneling ionization was studied in [28] mostly through experiments and numerical modeling, due to the mathematical difficulties in describing the contribution of the tunneling ionization to the signal dynamics. The Keldysh formula for the mode of tunneling ionization was approximated by a linear function in [19], and Talepbour et al. proposed using the power dependence of the rate of ionization on intensity for this purpose [29]. A drawback of these approaches is that the parameters of the approximate formulas for the rate of ionization have to be selected each time, depending on the considered range of intensity. In this work, we propose an approach to approximating the contribution from tunneling ionization that is free of the above shortcomings.

METHOD OF MOMENTS

In this work, we consider the dynamics of planar signals propagating in the mode of tunneling ionization using the method of moments [25, 30, 31]. The equations that describe the dynamics have the form

$$\begin{gathered} \frac{{\partial \psi }}{{\partial z}} + \frac{{i{{\beta }_{2}}}}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} - \frac{{{{\beta }_{3}}}}{6}\frac{{{{\partial }^{3}}\psi }}{{\partial {{\tau }^{3}}}} - i\gamma \psi {{\left| \psi \right|}^{2}} + \frac{\gamma }{\omega }\frac{\partial }{{\partial \tau }}\left( {\psi {{{\left| \psi \right|}}^{2}}} \right) \\ + \,\,i\gamma {{T}_{R}}\psi \frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }} + i\eta \psi \int\limits_{ - \infty }^\tau W d\tau {\kern 1pt} ' - \frac{{i\mu }}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{x}^{2}}}} = 0. \\ \end{gathered} $$

(1)

Here, ω is the central frequency of the signal; $k$ is the wavenumber at the central frequency; $z$ is the coordinate of signal propagation; $x$ is a transverse coordinate; $\tau = t - {z \mathord{\left/ {\vphantom {z {{{\vartheta }_{g}}}}} \right. \kern-0em} {{{\vartheta }_{g}}}}$ is the time spent in the co-moving coordinate system; ${{\vartheta }_{g}}$ is the group velocity at frequency ω; μ = 1/k; $\eta = {{s\omega {{\tau }_{c}}{{N}_{0}}} \mathord{\left/ {\vphantom {{s\omega {{\tau }_{c}}{{N}_{0}}} 2}} \right. \kern-0em} 2}$ is the parameter related to the electron plasma; $s = {{{{k}_{0}}\omega {{\tau }_{c}}} \mathord{\left/ {\vphantom {{{{k}_{0}}\omega {{\tau }_{c}}} {{{n}_{0}}{{N}_{c}}\left( {1 + {{\omega }^{2}}\tau _{c}^{2}} \right)}}} \right. \kern-0em} {{{n}_{0}}{{N}_{c}}\left( {1 + {{\omega }^{2}}\tau _{c}^{2}} \right)}}$ is the avalanche ionization cross section; ${{N}_{c}} = {{{{\varepsilon }_{0}}{{m}_{e}}{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}{{m}_{e}}{{\omega }^{2}}} {{{e}^{2}}}}} \right. \kern-0em} {{{e}^{2}}}}$ is the critical plasma density above which the plasma is not transparent; ${{\varepsilon }_{0}}$ is the susceptibility of a vacuum; ${{\tau }_{c}}$ is the period of electron collision; $e$ and $m$ are the elementary charge and electron mass, respectively; ${{N}_{0}}$ is the concentration of nonionized molecules; $W$is the degree of ionization, determined using the Keldysh formula in the limit of small Keldysh parameters (the mode of tunnel ionization); ${{\beta }_{2}}$ is the coefficient of group velocity dispersion (GVD); ${{\beta }_{3}}$ is a positive parameter that determines third-order dispersion; $\gamma$ is the coefficient of cubic nonlinearity; and ${{T}_{R}}$ characterizes the contribution from SRS. Coefficient ${{\beta }_{2}}$ is positive if the central frequency of the pulse lies in the region of the normal group velocity dispersion, and negative if it does not. The dependence of ionization $W$ on intensity I for a dielectric in the limit of tunneling ionization is determined using the Keldysh formula [27]

$$W = {{W}_{0}}{{\left( {\frac{{\left| \psi \right|}}{{{{B}_{T}}}}} \right)}^{{5{\text{/}}2}}}\exp \left( { - \frac{{{{B}_{T}}}}{{\left| \psi \right|}}} \right).$$

(2)

Here, ${{W}_{0}} = {{\sqrt \pi U_{i}^{{5{\text{/}}2}}{{m}^{{3{\text{/}}2}}}} \mathord{\left/ {\vphantom {{\sqrt \pi U_{i}^{{5{\text{/}}2}}{{m}^{{3{\text{/}}2}}}} {9\sqrt 8 {{\hbar }^{4}}{{N}_{0}}}}} \right. \kern-0em} {9\sqrt 8 {{\hbar }^{4}}{{N}_{0}}}},$ B_T = ${{\pi {{m}^{{1{\text{/}}2}}}U_{i}^{{3{\text{/}}2}}} \mathord{\left/ {\vphantom {{\pi {{m}^{{1{\text{/}}2}}}U_{i}^{{3{\text{/}}2}}} {2e\hbar }}} \right. \kern-0em} {2e\hbar }},$ $\hbar$ is the Planck constant, and ${{U}_{i}}$ is the ionization potential.

The dynamics of the parameters of a pulse was analyzed by the method of moments. We chose a trial solution in the form

$$\psi = B\exp \left[ { - \frac{1}{2}{{{\left( {\frac{\tau }{{{{\tau }_{p}}}}} \right)}}^{2}} - \frac{1}{2}{{{\left( {\frac{x}{a}} \right)}}^{2}} + i\left( {\phi - \frac{{C{{\tau }^{2}}}}{{2\tau _{p}^{2}}} - \frac{{\varepsilon {{x}^{2}}}}{{2{{a}^{2}}}}} \right)} \right],$$

(3)

where $B$ is the signal amplitude, ${{\tau }_{p}}$ is the length of the signal, $C$ is the parameter of frequency modulation, $\phi$ is the phase, $a$ is a parameter proportional to the width of a planar signal, and $\varepsilon$ describes the curvature of the wave surfaces. All parameters depend on coordinate $z.$ We define angular momentum as

$$E = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{2}}d\tau dx} } ,$$

(4)

$$\tau _{p}^{2} = \frac{2}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{\tau }^{2}}{{{\left| \psi \right|}}^{2}}d\tau } dx} ,$$

(5)

$${{a}^{2}} = \frac{2}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{x}^{2}}{{{\left| \psi \right|}}^{2}}d\tau } dx} ,$$

(6)

$$C = \frac{i}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\tau \left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial \tau }}} \right){{{\left| \psi \right|}}^{2}}d\tau } dx} ,$$

(7)

$$\varepsilon = \frac{i}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {x\left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial x}} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial x}}} \right){{{\left| \psi \right|}}^{2}}d\tau } dx} .$$

(8)

Using the method ${\text{of}}$ moments, we obtain the system of equations

$$E = {{B}^{2}}\pi {{\tau }_{p}}a = {\text{const}},$$

(9)

$$\frac{{d\nu }}{{dz}} = - \frac{C}{{{{L}_{d}}\nu }},$$

(10)

$$\frac{{d\rho }}{{dz}} = - \frac{\varepsilon }{{{{L}_{D}}\rho }},$$

(11)

$$\frac{{dC}}{{dz}} = - \frac{{\left( {1 + {{C}^{2}}} \right)}}{{{{L}_{d}}{{\nu }^{2}}}} + \frac{1}{{{{L}_{N}}\nu \rho }},$$

(12)

$$\frac{{d\varepsilon }}{{dz}} = - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}}\left( {1 + {{\varepsilon }^{2}}} \right) + \frac{1}{{{{L}_{N}}\nu \rho }} - \frac{{\exp \left( { - \sqrt {{{{{I}_{T}}\nu \rho } \mathord{\left/ {\vphantom {{{{I}_{T}}\nu \rho } {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} } \right)}}{{{{L}_{\eta }}{{\nu }^{{3{\text{/}}4}}}{{\rho }^{{7{\text{/}}4}}}}}.$$

(13)

In system (10)–(13), we introduced dimensionless parameters $\nu = {{{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{\tau }_{p}}} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}$ and $\rho = {a \mathord{\left/ {\vphantom {a {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}},$ where ${{\tau }_{0}}$ and ${{a}_{0}}$ are the initial values of the corresponding parameters. The characteristic lengths of dispersion, diffraction, nonlinearity, and ionization are expressed as ${{L}_{d}} = {{\tau _{0}^{2}} \mathord{\left/ {\vphantom {{\tau _{0}^{2}} {\left| {{{\beta }_{2}}} \right|}}} \right. \kern-0em} {\left| {{{\beta }_{2}}} \right|}},$ ${{L}_{D}} = {{a_{0}^{2}} \mathord{\left/ {\vphantom {{a_{0}^{2}} \mu }} \right. \kern-0em} \mu },$ ${{L}_{N}} = {{c{{n}_{0}}} \mathord{\left/ {\vphantom {{c{{n}_{0}}} {4\pi \gamma {{I}_{0}}}}} \right. \kern-0em} {4\pi \gamma {{I}_{0}}}},$ and ${{L}_{\eta }} = {{I_{T}^{{7{\text{/}}4}}} \mathord{\left/ {\vphantom {{I_{T}^{{7{\text{/}}4}}} {2\sqrt \pi \eta {{W}_{0}}{{\tau }_{0}}I_{0}^{{7{\text{/}}4}}}}} \right. \kern-0em} {2\sqrt \pi \eta {{W}_{0}}{{\tau }_{0}}I_{0}^{{7{\text{/}}4}}}},$ where we write ${{I}_{{0,T}}} = {{c{{n}_{0}}B_{{0,T}}^{2}} \mathord{\left/ {\vphantom {{c{{n}_{0}}B_{{0,T}}^{2}} {8\pi }}} \right. \kern-0em} {8\pi }}.$ In Eq. (13), we used the estimate ${{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} I}} \right. \kern-0em} I}\sim {{\left( {{{{{U}_{i}}} \mathord{\left/ {\vphantom {{{{U}_{i}}} {\hbar w}}} \right. \kern-0em} {\hbar w}}} \right)}^{2}} \gg 1$ and the key approximation $\exp \left( {{{{{B}_{T}}} \mathord{\left/ {\vphantom {{{{B}_{T}}} {\left| \psi \right|}}} \right. \kern-0em} {\left| \psi \right|}}} \right)\, \approx$ $\exp \left( {{{{{B}_{T}}} \mathord{\left/ {\vphantom {{{{B}_{T}}} {{{B}_{0}}}}} \right. \kern-0em} {{{B}_{0}}}}\, - \,\left( {{{{{B}_{T}}} \mathord{\left/ {\vphantom {{{{B}_{T}}} {2{{B}_{0}}}}} \right. \kern-0em} {2{{B}_{0}}}}} \right)\left( {{{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}\, + \,{{{{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{\tau }^{2}}} {\tau _{p}^{2}}}} \right. \kern-0em} {\tau _{p}^{2}}}} \right)} \right)$ to consider the ionization term, which allowed us to consider the contribution from tunneling ionization to the signal dynamics.

STATIONARY SOLUTION AND ITS STABILITY

To determine the parameters of the stationary state and conditions for its stability, we rewrite Eqs. (10)–(13) in the form

$$\frac{{d\nu }}{{d\xi }} = \frac{{{{P}_{\nu }}}}{{{{m}_{\nu }}}},$$

(14)

$$\frac{{d{{P}_{\nu }}}}{{d\xi }} = - \frac{{\partial U}}{{\partial \nu }},$$

(15)

$$\frac{{d\rho }}{{d\xi }} = \frac{{{{P}_{\rho }}}}{{{{m}_{\rho }}}},$$

(16)

$$\frac{{d{{P}_{\rho }}}}{{d\xi }} = - \frac{{\partial U}}{{\partial \rho }} + \tilde {F}.$$

(17)

Here, ${{P}_{\nu }} = {{{{m}_{\nu }}\partial \nu } \mathord{\left/ {\vphantom {{{{m}_{\nu }}\partial \nu } {\partial \xi }}} \right. \kern-0em} {\partial \xi }} = {{ - C} \mathord{\left/ {\vphantom {{ - C} \nu }} \right. \kern-0em} \nu },$ P_ρ = ${{{{m}_{\rho }}\partial \rho } \mathord{\left/ {\vphantom {{{{m}_{\rho }}\partial \rho } {\partial \xi }}} \right. \kern-0em} {\partial \xi }} = {{ - \varepsilon } \mathord{\left/ {\vphantom {{ - \varepsilon } \rho }} \right. \kern-0em} \rho },$ ${{m}_{\nu }} = 1,$ ${{m}_{\rho }} = {{{{L}_{D}}} \mathord{\left/ {\vphantom {{{{L}_{D}}} {{{L}_{d}}}}} \right. \kern-0em} {{{L}_{d}}}},$ and $\xi = {z \mathord{\left/ {\vphantom {z {{{L}_{d}}}}} \right. \kern-0em} {{{L}_{d}}}}.$ System (14)–(17) can be interpreted as a mechanical analogy describing the motion of a particle over a surface with coordinate axes $\nu$ and $\rho$ in potential field

$$U = \frac{1}{{2{{\nu }^{2}}}} + \frac{{{{L}_{d}}}}{{2{{L}_{D}}{{\rho }^{2}}}} - \frac{{{{L}_{d}}}}{{{{L}_{N}}\nu \rho }}.$$

(18)

In this case, the particle mass depends on the direction of motion. The role of an external force acting along coordinate $\rho$ is played by ionization term $\tilde {F} = {{{{L}_{d}}\exp ( - \sqrt {{{{{I}_{T}}\nu \rho } \mathord{\left/ {\vphantom {{{{I}_{T}}\nu \rho } {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} )} \mathord{\left/ {\vphantom {{{{L}_{d}}\exp ( - \sqrt {{{{{I}_{T}}\nu \rho } \mathord{\left/ {\vphantom {{{{I}_{T}}\nu \rho } {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} )} {{{L}_{\eta }}{{\nu }^{{3{\text{/}}4}}}{{\rho }^{{11{\text{/}}4}}}}}} \right. \kern-0em} {{{L}_{\eta }}{{\nu }^{{3{\text{/}}4}}}{{\rho }^{{11{\text{/}}4}}}}}.$ The stationary solution for this system of equations can be written as

$${{L}_{d}} = {{L}_{N}},$$

(19)

$$\frac{1}{{{{L}_{D}}}} = \frac{1}{{{{L}_{N}}}} - \frac{{\exp \left( { - \sqrt {{{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} } \right)}}{{{{L}_{\eta }}}}.$$

(20)

Equations (19) and (20) can be rewritten in the form

$${{\tau }_{0}} = \sqrt {\frac{{2\left| {{{\beta }_{2}}} \right|}}{{{{k}_{0}}{{n}_{2}}{{I}_{0}}}}} ,$$

(21)

$$\frac{1}{{{{a}_{0}}}} = \sqrt {{{k}_{0}}{{n}_{0}}\left( {\frac{{{{k}_{0}}{{n}_{2}}{{I}_{T}}}}{{2X}} - 2\sqrt \pi \eta {{W}_{0}}\sqrt {\frac{{2\left| {{{\beta }_{2}}} \right|}}{{{{k}_{0}}{{n}_{2}}{{I}_{T}}}}} \frac{{\exp ( - \sqrt X )}}{{{{X}^{{5{\text{/}}4}}}}}} \right)} .$$

(22)

Here, X = I_T/I₀, and we use the relation ${{8\pi \gamma } \mathord{\left/ {\vphantom {{8\pi \gamma } {c{{n}_{0}}}}} \right. \kern-0em} {c{{n}_{0}}}} \equiv {{k}_{0}}{{n}_{2}},$ where ${{n}_{2}}$ is the nonlinear refractive index of the medium. It follows from (21) and (22) that as the intensity of the signal grows, its length is reduced and its width rises. The radicand in Eq. (25) must be positive (a zero radicand corresponds to an infinite width of the signal). Using this condition, we obtain

$${{I}_{0}} < {{4{{I}_{T}}} \mathord{\left/ {\vphantom {{4{{I}_{T}}} {{{{\left( {\tilde {W}\left( {2{{A}^{2}}} \right)} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {\tilde {W}\left( {2{{A}^{2}}} \right)} \right)}}^{2}}}},$$

(23)

where $A = {{4\eta {{W}_{0}}\sqrt {2\pi \left| {{{\beta }_{2}}} \right|} } \mathord{\left/ {\vphantom {{4\eta {{W}_{0}}\sqrt {2\pi \left| {{{\beta }_{2}}} \right|} } {{{{\left( {{{k}_{0}}{{n}_{2}}{{I}_{T}}} \right)}}^{{3{\text{/}}2}}}}}} \right. \kern-0em} {{{{\left( {{{k}_{0}}{{n}_{2}}{{I}_{T}}} \right)}}^{{3{\text{/}}2}}}}}$ and $\tilde {W}\left( x \right)$ is the Lambert function [32].

Let us consider the stability of stationary solutions (21), (22) for system (14)–(17). We obtain four eigenvalues according to Lyapunov [33]:

$$\lambda = \pm \sqrt {\frac{{ - \left( {{{U}_{{,\nu \nu }}}{{m}_{2}} - d{{m}_{1}}} \right) \pm \sqrt {{{{\left( {{{U}_{{,\nu \nu }}}{{m}_{2}} - d{{m}_{1}}} \right)}}^{2}} - 4{{m}_{1}}{{m}_{2}}\left( {h{{U}_{{,\nu \rho }}} - d{{U}_{{,\nu \nu }}}} \right)} }}{{2{{m}_{1}}{{m}_{2}}}}} .$$

(24)

Here, the subscripts after the decimal point denote the derivative with respect to the respective variables $h = {{\tilde {F}}_{{,\nu }}} - {{U}_{{,\nu \rho }}},$ and $d = {{\tilde {F}}_{{,\rho }}} - {{U}_{{,\rho \rho }}}.$ The stationary solution will be stable if $\lambda$ has no positive real part. We can easily show that $\lambda$ will be purely imaginary if the conditions

$$h{{U}_{{,\nu \rho }}} - d{{U}_{{,\nu \nu }}} > 0,$$

(25)

$${{U}_{{,\nu \nu }}}{{m}_{2}} - d{{m}_{1}} > 0.$$

(26)

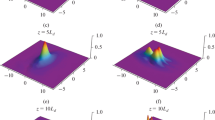
are met. The real part is zero, which means that the signal parameters will oscillate in the vicinity of stationary values under the action of weak perturbations. If we remove the ionization term $\left( {\tilde {F} = 0} \right),$ (25) and (26) can be written in the form of the minimum condition ${{U}_{{,\nu \nu }}}{{U}_{{,\rho \rho }}} - {{\left( {{{U}_{{,\nu \rho }}}} \right)}^{2}} > 0,$ ${{U}_{{,\nu \nu }}} > 0.$ As expected, the potential function in this case has no minimum. Figure 1a shows a view of potential surface $U$ with no ionization, while Fig. 1b shows corresponding vector field ${{F}_{\nu }},$ ${{F}_{\rho }}.$ If we allow for ionization, approximation (${{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}} \gg 1$), shows that conditions (25) and (26) are satisfied at any intensities. This result agrees with the conclusion reached for planar signals in [34], where a linear approximation of the Keldysh formula in the tunnel limit was used. It should be noted that when considering stability, we ignored the shift of the signal’s frequency. Allowing for this effect would bring the system out of equilibrium. However, since the shift in frequency is included in the system of equations for the signal parameters through higher dispersion $\left( {{{\beta }_{3}}} \right)$ and nonlinearity $\left( {{\gamma \mathord{\left/ {\vphantom {\gamma \omega }} \right. \kern-0em} \omega }} \right)$ [34], this instability at the initial stage of dynamics can be ignored. As was shown in [28, 35, 36], ionization-induced absorption also means the signal propagates in the mode of a light bullet at distances of several millimeters in a dielectric.

Let us examine the region of intensities that satisfies condition (23) as a function of the signal central wavelength. We take sapphire as a material. For sapphire (${{U}_{I}} = 7.3\,\,{\text{eV}},$ $~{{N}_{0}} = 2.36 \times {{10}^{{28}}}\,\,{{{\text{m}}}^{{ - 3}}},$ and ${{\tau }_{c}} = 1.59 \times {{10}^{{ - 15{\text{\;}}}}}\,\,{\text{s}}$ the approximate dependence of the refractive index on the wavelength in the mid-infrared range can be written as [37]

$${{n}_{0}} = 1.75\sqrt {1 + \frac{{1.73{{{\left( {\lambda [\mu {\text{m}}]} \right)}}^{2}}}}{{{{{\left( {\lambda [\mu {\text{m}}]} \right)}}^{2}} - {{{18}}^{2}}}}} ,$$

(27)

and the GVD coefficient is determined by the dependence

$${{\beta }_{2}} = \frac{{{{\lambda }^{3}}}}{{2\pi {{c}^{2}}}}\frac{{{{d}^{2}}{{n}_{0}}}}{{d{{\lambda }^{2}}}}.$$

(28)

Fig. 1.

(a) Potential field $U\left( {\nu ,\rho } \right),$ which determines the dynamics of relative length $\nu$ and width $\rho$ of a planar bullet (without ionization contribution ${{L}_{\eta }} = \infty$). (b) Corresponding field of forces whose projections are determined by the expressions ${{F}_{\nu }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \nu }}} \right. \kern-0em} {\partial \nu }}$ and ${{F}_{\rho }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \rho }}} \right. \kern-0em} {\partial \rho }}$.

The nonlinear refractive index is approximated by the relation [38]

$$\begin{gathered} {{n}_{2}} = n_{2}^{0} + {{N}_{1}}\exp \left( { - \frac{{\left( {\lambda - {{\lambda }_{0}}} \right)}}{{{{\lambda }_{1}}}}} \right) \\ + \,\,{{N}_{2}}\exp \left( { - \frac{{\left( {\lambda - {{\lambda }_{0}}} \right)}}{{{{\lambda }_{2}}}}} \right). \\ \end{gathered} $$

(29)

Here, $n_{2}^{0} = 2.5 \times {{10}^{{ - 16}}}\,\,{{{\text{c}}{{{\text{m}}}^{2}}} \mathord{\left/ {\vphantom {{{\text{c}}{{{\text{m}}}^{2}}} {\text{W}}}} \right. \kern-0em} {\text{W}}}{\kern 1pt} {\text{,}}$ N₁ = $2.3 \times {{10}^{{ - 16}}}\,\,{{{\text{c}}{{{\text{m}}}^{2}}} \mathord{\left/ {\vphantom {{{\text{c}}{{{\text{m}}}^{2}}} {\text{W}}}} \right. \kern-0em} {\text{W}}}{\text{,}}$ ${{\lambda }_{0}} = 266.0~\,\,{\text{nm}}{\text{,}}$ ${{\lambda }_{1}} = 46.6\,\,~{\text{nm}}{\text{,}}$ and ${{\lambda }_{2}} = 1086.3~\,\,{\text{nm}}{\text{.}}$ Substituting (27)–(29) into (23), we find the desired dependence (Fig. 2). For the region lying to the right of the dashed line, condition $\omega {{\tau }_{p}} > 10$ is satisfied, at which the slowly varying envelope approximation used is valid. With ${{I}_{0}} = 2.8 \times {{10}^{{13}}}\,\,{{\text{W}} \mathord{\left/ {\vphantom {{\text{W}} {{{{\text{m}}}^{2}}}}} \right. \kern-0em} {{{{\text{m}}}^{2}}}}$ and $\lambda = 5\,\,\mu {\text{m}},$ we find from (21) and (22) estimates of the planar pulse parameters: ${{\tau }_{0}} = 30\,\,{\text{fs}},$ and $a = 10\,\,\mu {\text{m}}.$

Fig. 2.

The solid line is described by the right-hand side of condition (23), which determines the upper limit of intensity for the existence of a stationary solution in sapphire. The region to the right of the dashed line, which determines the intensity according to formula (21) for ${{\tau }_{p}}\omega = 10,$ corresponds to the range of applicability of slowly varying envelopes $\left( {{{\tau }_{p}}\omega \geqslant 10} \right).$

Above, we found that conditions (25) and (26) for the stability of a planar bullet against perturbations of its length and width are satisfied at any intensity. This means that at minor deviations of a particle from its equilibrium position (we use a mechanical analogy), it is affected by restoring forces directed to the equilibrium point $\nu = 1,$ $\rho = 1.$ Analysis of the vector field with regard to ionization showed (see Fig. 3) that the restoring forces fall exponentially upon a drop in signal intensity (see the expression for the quantity $\tilde {F}$ describing the ionization contribution), and the restoring forces were such that the vector field resembled the vector field without ionization (Fig. 1) as early as intensity ${{I}_{0}} = 1.5 \times {{10}^{{13{\text{\;}}}}}\,\,{{\text{W}} \mathord{\left/ {\vphantom {{\text{W}} {{\text{c}}{{{\text{m}}}^{2}}}}} \right. \kern-0em} {{\text{c}}{{{\text{m}}}^{2}}}}$ (at a wavelength of $\lambda = 5\,\,\mu {\text{m}}$ (Fig. 3а). So even though the conditions of stability are formally satisfied at such intensity and the restoring forces are nonzero, small perturbations related to the effects that we have ignored will in fact quickly knock the system out of equilibrium. Analysis of the vector field suggests that the quasi-stability of a planar bullet at a wavelength of $\lambda = 5\,\,\mu {\text{m}}$ can be expected starting at an intensity of ${{I}_{0}} = 2 \times {{10}^{{13}}}\,\,{{\text{W}} \mathord{\left/ {\vphantom {{\text{W}} {{\text{c}}{{{\text{m}}}^{2}}}}} \right. \kern-0em} {{\text{c}}{{{\text{m}}}^{2}}}}.$ A similar situation was observed in studying the region of stability of three-dimensional light bullets [39]. In contrast to a planar bullet, the region of stability of a three-dimensional bullet is also limited in intensity from below. Here, we also analyzed the vector field and showed that the actual region of stability lies above the lower boundary of the formal window of stability due to absorption effects and terms of the next order of smallness.

Fig. 3.

Vector field ${{F}_{\nu }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \nu }}} \right. \kern-0em} {\partial \nu }},$ ${{F}_{\rho }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \rho + \tilde {F}}}} \right. \kern-0em} {\partial \rho + \tilde {F}}}$ (with regard to ionization) that determines the dynamics of a planar pulse with central wavelength $\lambda = 5\,\,\mu {\text{m}},$ propagating in sapphire with intensities of I₀ = (a) 1.5 × 10¹³, (b) 2 × 10¹³, (c) 2.3 × 10¹³, and (d) 2.8 × 10¹³ W/cm².

CONCLUSIONS

An analytical description was obtained for the propagation of planar pulses in the mode of mutual compensation for the effects of diffraction and ionization divergence on the one hand, and self-focusing on the other. The balance of the temporal dynamics was determined from the compensation for dispersive broadening by cubic nonlinearity. The dynamics of a planar signal in the mode of tunneling ionization was analyzed using the method of moments. Analytical expressions were obtained for the quasi-stationary length and width of a planar pulse. Conditions for quasi-stable propagation were found according to Lyapunov. It should be noted that allowing for the shift of frequency to the red region of the spectrum caused by stimulated Raman self-scattering, or to the blue region if ionization effects dominate, will slowly unbalance the system and create oscillations. Equilibrium will also be disturbed by the absorption of photons during ionization, which was ignored in this work. The equilibrium investigated in this work is therefore quasi-stable.