INTRODUCTION

In a tangentially magnetized ferrite film, the dipole spin waves (SWs) first described in a magnetostatic approximation in [1] can be excited and propagate with few losses. Despite the diversity of physical effects caused by SW propagation [2], the development and use of SW-based devices is limited in microwave technology. Reasons for this include the nonlinear dispersion dependences of SWs in free ferrite films and structures based on them. In order words, like the dependences of dispersion for acoustic waves in acoustic crystals, those of linear dispersion in a wide band of frequencies cannot be obtained for SWs. In a certain range of frequencies, however, a quasi-linear portion with a degree of linearity determined by structural parameters that satisfy the technical requirements for signal processing devices can form in the dispersion dependences of SWs for some ferrite structures. In this work, we study the possibility of linearizing dispersion dependences of SWs using metal planes placed at the ferrite film surfaces.

The simplest and most frequently used structure is obviously one with a metal screen above a ferrite film parallel to it with an air (or vacuum) gap of width w between the ferrite and the metal (such a structure without the upper metal screen would be similar to one shown in Fig. 1). Let a surface SW (SSW) with frequency ω0 = 2πf0 and wavenumber ky0 propagate in this metal‒dielectric‒ferrite structure in the direction of axis y. Experiments and calculations show [3, 4] that dispersion dependences f(ky) of the SSWs in this structure can have inflection points with \({{{{\partial }^{2}}\omega } \mathord{\left/ {\vphantom {{{{\partial }^{2}}\omega } {\partial k_{y}^{2}}}} \right. \kern-0em} {\partial k_{y}^{2}}}\) = ∂U/∂ky = 0, where U is the group velocity of SSWs.

Fig. 1.
figure 1

Geometry of the problem: (1) ideally conducting metal, (2) ferrite film, and (3) dielectric (or vacuum) gap.

Full size image

As was shown in [5], distance S traveled by the useful signal modulating SSWs with frequency f0 in such a structure along axis y with no distortions (the shape of the signal is preserved) is limited by the condition

$$\left| {{{{\left. {\frac{\pi }{U}\frac{{\partial U}}{{\partial \lambda }}} \right|}}_{{\lambda = {{\lambda }_{0}}}}}S} \right| \ll 1,$$
(1)

which includes modulus U of the vector of the group velocity of a modulated wave, modulated wavelength λ0 = 2π/ky0, and derivative ∂U/∂λ calculated at λ = λ0.

It is also convenient to write condition (1) in the form S \( \ll \) Scr, where critical distance Scr is calculated using the formula [6]

$${{S}_{{{\text{cr}}}}} = 2k_{y}^{{ - 2}}\left| {\frac{{{{{\left. {\frac{{\partial \omega }}{{\partial {{k}_{y}}}}} \right|}}_{{{{k}_{y}} = {{k}_{{y0}}}}}}}}{{{{{\left. {\frac{{{{\partial }^{2}}\omega }}{{\partial k_{y}^{2}}}} \right|}}_{{{{k}_{y}} = {{k}_{{y0}}}}}}}}} \right|\,\,{\text{or}}\,\,{{{{S}_{{{\text{cr}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{cr}}}}}} \lambda }} \right. \kern-0em} \lambda } = {{\left( {\pi {{k}_{y}}} \right)}^{{ - 1}}}\left| {\frac{{{{{\left. {\frac{{\partial \omega }}{{\partial {{k}_{y}}}}} \right|}}_{{{{k}_{y}} = {{k}_{{y0}}}}}}}}{{{{{\left. {\frac{{{{\partial }^{2}}\omega }}{{\partial k_{y}^{2}}}} \right|}}_{{{{k}_{y}} = {{k}_{{y0}}}}}}}}} \right|,$$
(2)

which includes the first and second derivatives of the dispersion dependence for the considered structure.

Note that to estimate the linearity of the dispersion dependence of a structure, it is convenient to calculate ratio Scr/λ instead of the absolute values of Scr. The former shows how many wavelengths λ can be traveled by a useful signal with its shape remaining virtually undistorted at different wavenumbers ky, and the corresponding values of carrier frequency f0 of the modulated wave. Formulas (1)–(3) can be used for waves of different natures in anisotropic media and structures.

It is obvious that if an SSW has frequency f0 and wavenumber ky0 corresponding to an inflection point where \({{{{\partial }^{2}}\omega } \mathord{\left/ {\vphantom {{{{\partial }^{2}}\omega } {\partial k_{y}^{2}}}} \right. \kern-0em} {\partial k_{y}^{2}}}\) = 0, we have (according to Eq. (2)) ratio Scr/λ0 → ∞ when this SSW is modulated by a useful signal. As was shown in [4], small intervals of wavenumbers with widths of 5–10 cm−1 and intervals of frequency with widths of 3–10 MHz form in the metal‒dielectric‒ferrite structure near such ky0 and f0 values. These intervals can be used in developing spin-wave devices to obtain the undistorted transmission of a useful signal.

It would seem that by changing the thickness of the dielectric in a metal‒dielectric‒ferrite structure, we can obtain denser localization of the inflection points and thereby increase the above intervals of wavenumber and frequency. The inflection points approach each other slightly upon a change in the thickness of the dielectric but then begin to separate [4]. As a result, ratio Scr/λ between them is ~12 at the closest approach of the inflection points, while it is Scr/λ → ∞ on the inflection points themselves. Intervals of wave number and frequency with ratios Scr/λ of more than 50 or 100 thus cannot be greatly increased in a metal‒dielectric‒ferrite structure.

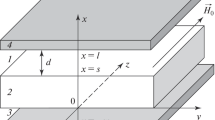
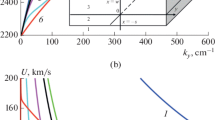
We may assume that in order to bring the inflection points closer, we must choose a structure that has a more complex dispersion equation and more than one variable parameter. In other words, we must investigate, e.g., the change in ratio Scr/λ in a metal‒dielectric‒ferrite‒dielectric‒metal (MDFDM) structure with variable thicknesses of both dielectric layers. The dispersion dependences of SSWs propagating in an MDFDM structure along axis y have been studied with [7–10] and without [11] a magnetostatic approximation. Based on our results, we can use MDFDM structures with parameters at which fairly wide quasi-linear intervals appear in the dispersion dependence of the SSWs. Let us consider the simplest MDFDM structure, in which a dielectric layer is missing and a metal screen is positioned directly on the ferrite surface, i.e., the MFDDM structure (Fig. 1). The dispersion dependences for such a structure calculated at H0 = 300 Oe, a film thickness of s = 10 µm, and a film magnetization of 4πM0 = 1750 G are presented in Fig. 2. The dependences of ratio Scr/λ on SSW wavenumber ky are givenin Fig. 3. The calculations in Figs. 2 and 3 were made without using a magnetostatic approximation based on the dispersion equation in [11].

Fig. 2.
figure 2

Dispersion dependences f(ky) of SSWs in an MFDM structure at dielectric thicknesses w of 5, 6, 8, 12, 20 µm, and ∞ (curves 1–6).

Full size image
Fig. 3.
figure 3

Dependences of ratio Scr/λ on wavenumber ky for an SSW in an MFDM structure at dielectric thicknesses w 5, 6, 8, 12, 20 µm, and ∞ (curves 1–6).

Full size image

It can be seen in Figs. 2 and 3 that the characteristics of the SSW change when the second metal surface approaches the ferrite film from below. At dielectric thickness w ≈ 6–9 μm, a quasi-linear interval appears in dispersion dependence f(ky) of the wave near low ky values. In this interval, the SSW has virtually constant group velocity U in the wider ranges of frequency and wavenumber than at other values of w (curves 2 and 3 in Fig. 2). This change in the f(ky) dependence is due to two points with Scr/λ → ∞ appearing quite close to each other when w ~ 6–9 µm (see curves 2 and 3 in Fig. 3). This allows us to increase wavenumber interval Δky and frequency interval Δf with Scr/λ > 100 to ~130 cm−1 and 130 MHz, respectively (i.e., to increase considerably these intervals relative to the MDF structure described in [4]).

It should be noted, however, that there is a small part of the dispersion dependence in intervals Δky and Δf (near the initial part of the SSW spectrum, where wavenumber ky ~ 2 cm−1 or less) in which the dispersion equation describing an SSW with no magnetostatic approximation has no solutions [11]. This must be considered when designing spin-wave electronic devices that use the MDFDM structure (the scale of the SSW dependences in Figs. 2 and 3 does not resolve these areas).

CONCLUSIONS

It was established that at certain parameters of the MDFDM structure, quasi-linear intervals appear in the dispersion dependence of an SSW. These intervals can ensure undistorted transmission of a useful signal by the SSW.