The use of modern high-tech lubricants is one of the key factors for reducing friction in the mating parts of triboassemblies and increasing the efficiency of tribosystems.

Continuous progress in the production of lubricants leads to complications in the development of mathematical models taking into account the thermal processes, the geometry of the reference node, and the totality of all acting loads.

The analysis of works [1–10] devoted to the effect of antifriction coatings on the thermal processes taking into account factors not previously taken into account shows the need to improve the existing calculation models, i.e., to take into account additional factors and changing the design of the base surface of a bearing bush to increase the duration of the hydrodynamic mode [11].

The purpose of this paper is to find the regularities for increasing the duration of the hydrodynamic mode of a radial plain bearing with an adapted supporting profile of the base surface covered by a polymer coating with an axial groove, taking into account the dependence of micropolar lubricant viscosity on the pressure and temperature.

FORMULATION OF THE PROBLEM

A model of the steady motion of a micropolar incompressible lubricant in the working gap of an infinite radial plain bearing is considered.

The shaft rotates with an angular velocity Ω, and the bearing bush is stationary. It is assumed that the space between the eccentrically located shaft and the bearing is completely filled with lubricant, and the bearing bush is coated with a polymer.

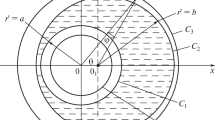
In the assumed arrangement of the polar coordinate system (Fig. 1), the equation of the shaft contour [12], the bearing bush under the coating with a noncircular profile of base surface, and the polymer coating that copies a noncircular bearing bush profile can be expressed by

$$r{\kern 1pt} ' = {{r}_{0}}\left( {1 + H} \right),\quad r{\kern 1pt} ' = {{r}_{1}} - a{\kern 1pt} '\sin \omega \theta ,\quad r{\kern 1pt} ' = {{r}_{1}}-\tilde {h} - a{\kern 1pt} '\sin \omega \theta .$$
(1)
Fig. 1.
figure 1

Calculation diagram of the tribocontact.

Full size image

Let us assume that the viscosity characteristics depend on the pressure according to the law

$$\mu {\kern 1pt} ' = {{\mu }_{0}}{{e}^{{\alpha '{\kern 1pt} p{\kern 1pt} ' - \beta {\kern 1pt} 'T{\kern 1pt} '}}},\quad \kappa {\kern 1pt} ' = {{\kappa }_{0}}{{e}^{{\alpha {\kern 1pt} '{\kern 1pt} p{\kern 1pt} ' - \beta {\kern 1pt} 'T{\kern 1pt} '}}},\quad \gamma {\kern 1pt} ' = {{\gamma }_{0}}{{e}^{{\alpha {\kern 1pt} '{\kern 1pt} p{\kern 1pt} ' - \beta {\kern 1pt} 'T{\kern 1pt} '}}}.$$
(2)

The initial basic equations taking into account Eq. (2) are dimensionless equations of motion of an incompressible fluid for a “thin layer” and a continuity equation with the corresponding boundary conditions

$$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{i}}}}{{\partial {{r}^{2}}}} + \frac{{N_{i}^{2}}}{{2{{N}_{1}}h}}\left( {2r - h} \right) = \frac{1}{{j{{e}^{{ - \alpha p - \beta T}}}}}\frac{{d{{p}_{i}}}}{{d\theta }},\quad {{\upsilon }_{i}} = \frac{1}{{2{{N}_{1}}h}}\left( {{{r}^{2}} - rh} \right),\quad \frac{{\partial {{u}_{i}}}}{{\partial r}} + \frac{{\partial {{{v}}_{i}}}}{{\partial \theta }} = 0. \\ {v} = 1,\quad u = - \eta \sin \theta ,\quad \upsilon = 0\quad {\text{at}}\quad r = 1 - \eta \cos \theta ; \\ {v} = 0,\quad u = 0,\quad \upsilon = 0\quad {\text{at}}\quad r = {{\eta }_{1}}\sin \omega \theta ,\quad {{\theta }_{1}} \leqslant \theta \leqslant {{\theta }_{2}}; \\ {v} = {v}{\kern 1pt} \text{*}{\kern 1pt} \left( \theta \right),\quad u = u{\kern 1pt} \text{*}{\kern 1pt} \left( \theta \right),\quad \upsilon = 0\quad {\text{at}}\quad r = {{\eta }_{2}} + {{\eta }_{1}}\sin \omega \theta , \\ 0 \leqslant \theta \leqslant {{\theta }_{1}}\quad {\text{and}}\quad {{\theta }_{2}} \leqslant \theta \leqslant 2\pi ; \\ \end{gathered} $$
(3)
$$p\left( 0 \right) = p\left( {{{\theta }_{1}}} \right) = p\left( {{{\theta }_{2}}} \right) = p\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}.$$
(4)

The pass to dimensionless quantities is carried out by the following relations

$$r{\kern 1pt} ' = {{r}_{1}}-\delta r,\quad \delta = {{r}_{1}} - {{r}_{0}},\quad r{\kern 1pt} ' = \left( {{{r}_{1}}-\tilde {h}} \right) - \delta r,$$
$$\delta = \left( {{{r}_{1}}-\tilde {h}} \right) - {{r}_{0}},\quad {{{v}}_{\theta }}_{{_{i}}} = \Omega {{r}_{0}}{{{v}}_{i}};\quad {{{v}}_{{r_{r}^{'}}}} = \Omega \delta u;$$
$$p{\kern 1pt} ' = p{\kern 1pt} \text{*}{\kern 1pt} p,\quad p{\kern 1pt} \text{*} = \frac{{\left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right)\Omega r_{0}^{2}}}{{2{{\delta }^{2}}}},\quad \upsilon {\kern 1pt} ' = \upsilon ,\quad \mu {\kern 1pt} ' = {{\mu }_{0}}\mu ,\quad \kappa {\kern 1pt} ' = {{\kappa }_{0}}\kappa ,\quad \gamma {\kern 1pt} ' = {{\gamma }_{0}}\gamma ,$$
(5)
$$T{\kern 1pt} ' = T{\kern 1pt} \text{*}{\kern 1pt} T,\quad \beta = T{\kern 1pt} \text{*}{\kern 1pt} \beta {\kern 1pt} ',\quad T{\kern 1pt} \text{*} = \frac{{\left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right){{\Omega }^{2}}r_{0}^{2}}}{{I\lambda }},$$
$${{N}^{2}} = \frac{{{{\kappa }_{0}}}}{{2{{\mu }_{0}} + {{\kappa }_{0}}}},\quad {{N}_{1}} = \frac{{2{{\mu }_{0}}{{l}^{2}}}}{{{{\delta }^{2}}{{\kappa }_{0}}}};\quad {{l}^{2}} = \frac{{{{\gamma }_{0}}}}{{4{{\mu }_{0}}}}.$$

Taking into account the boundary conditions, let us find the self-similar solution of problem Eq. (3) in the form

$${{v}_{i}} = \frac{{\partial {{\psi }_{i}}}}{{\partial r}} + {{V}_{i}}\left( {r,\theta } \right);\quad {{u}_{i}} = - \frac{{\partial {{\psi }_{i}}}}{{\partial \theta }} + {{U}_{i}}\left( {r,\theta } \right);$$
$$\begin{gathered} {{\psi }_{i}}\left( {r,\theta } \right) = \tilde {\psi }\left( {{{\xi }_{i}}} \right);\quad {{V}_{i}}\left( {r,\theta } \right) = {{{\tilde {v}}}_{i}}\left( {{{\xi }_{i}}} \right);\quad {{U}_{i}}\left( {r,\theta } \right) = - {{{\tilde {u}}}_{i}}\left( {{{\xi }_{i}}} \right) \cdot h{\kern 1pt} '\left( \theta \right); \\ {{\xi }_{2}} = \frac{r}{{h\left( \theta \right)}}\quad {\text{at}}\quad {{\theta }_{1}} \leqslant \theta \leqslant {{\theta }_{2}}; \\ \end{gathered} $$
(6)
$${{\xi }_{{1,3}}} = \frac{{r - {{\eta }_{2}}}}{{h\left( \theta \right) - {{\eta }_{2}}}}\quad {\text{at}}\quad 0 \leqslant \theta \leqslant {{\theta }_{1}}\quad {\text{and}}\quad {{\theta }_{2}} \leqslant \theta \leqslant 2\pi .$$

By substituting Eq. (6) into Eq. (3) and taking into account the boundary conditions Eq. (4), we obtain the following system of equations:

$$\begin{gathered} \tilde {\psi }_{i}^{{'''}} = {{a}_{i}};\quad \tilde {u}_{i}^{{''}} = {{b}_{i}} - \frac{{{{N}^{2}}}}{{2{{N}_{1}}}}\left( {2{{\xi }_{i}} - 1} \right);\quad {{{\tilde {u}}}_{i}}\left( {{{\xi }_{i}}} \right) + {{\xi }_{i}}{\tilde {v}}_{i}^{'}\left( {{{\xi }_{i}}} \right) = 0; \\ \frac{{d{{p}_{i}}}}{{d\theta }} = \frac{{{{b}_{i}}}}{{{{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}^{2}}}} + \frac{{{{a}_{i}}}}{{{{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}^{3}}}},\quad i = 1,3;\quad \frac{{d{{p}_{2}}}}{{d\theta }} = \frac{{{{b}_{2}}}}{{{{h}^{2}}\left( \theta \right)}} + \frac{{{{a}_{2}}}}{{{{h}^{3}}\left( \theta \right)}}. \\ \end{gathered} $$
(7)

System of equations (7) is solved under the following boundary conditions:

$${{\upsilon }_{i}}\left( 0 \right) = 0;\quad \tilde {\psi }_{i}^{'}\left( 0 \right) = 0,\quad \tilde {\psi }_{i}^{'}\left( 1 \right) = 0,\quad \tilde {u}_{i}^{'}\left( 1 \right) = - \eta \sin \theta ;\quad {\tilde {v}}_{i}^{'}\left( 1 \right) = 0;$$
$${{\upsilon }_{i}}\left( 1 \right) = 0;\quad {{\tilde {u}}_{i}}\left( 0 \right) = 0;\quad {{{\tilde {v}}}_{i}}\left( 0 \right) = 1;\quad \int\limits_0^1 {{{{\tilde {u}}}_{i}}} \left( {{{\xi }_{i}}} \right)d{{\xi }_{i}} = 0;$$
(8)
$$\int\limits_\theta ^{{{\xi }_{i}}} {{{{\tilde {u}}}_{i}}\left( {{{\xi }_{i}}} \right)} d{{\xi }_{i}} = 0;\quad p\left( \theta \right) = p\left( {{{\theta }_{1}}} \right) = p\left( {{{\theta }_{2}}} \right) = p\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}.$$

Taking into account boundary conditions (8) and integrating Eq. (7), we obtain as a result the expression

$$\tilde {\psi }_{i}^{'}\left( {{{\xi }_{i}}} \right) = {{a}_{i}}\frac{{{{\xi }_{i}}}}{2}\left( {{{\xi }_{i}} - 1} \right),\quad {{\tilde {u}}_{i}}\left( {{{\xi }_{i}}} \right) = {{b}_{i}}\frac{{\xi _{i}^{2}}}{2} - \frac{{{{N}^{2}}}}{{2{{N}_{1}}}}\left( {\frac{{\xi _{i}^{3}}}{3} - \frac{{\xi _{i}^{2}}}{2}} \right) - \left( {\frac{{{{N}^{2}}}}{{12{{N}_{1}}}} + \frac{{{{b}_{i}}}}{2} + 1} \right){{\xi }_{i}} + 1.$$

As follows from the equation \({{\tilde {u}}_{i}}\left( {{{\xi }_{i}}} \right) + {{\xi }_{i}}{\tilde {v}}_{i}^{'}\left( {{{\xi }_{i}}} \right) = 0\),

$${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = {\text{ }}6.$$
(9)

Based on the equality \(p\left( 0 \right) = p\left( {{{\theta }_{1}}} \right) = p\left( {{{\theta }_{2}}} \right) = p\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}\), we obtain

$${{a}_{1}} = - 6\left( {1 - {{\eta }_{2}}} \right)\left( {1 - \frac{{{{{\tilde {\eta }}}_{1}}}}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right);$$
$${{a}_{2}} = - 6\left( {1 + \left( {1 - \frac{{5{{\theta }_{1}}}}{{2\pi }}} \right)\left( {\frac{{{{\eta }_{1}}}}{{2\pi \omega }}\left( {\cos 2\pi \omega - \cos \omega {{\theta }_{1}}} \right) + \frac{\eta }{{2\pi }}\sin {{\theta }_{1}}} \right) - \frac{{\theta _{1}^{2}}}{{4{{\pi }^{2}}}}} \right),$$
(10)
$${{a}_{3}} = - 6\left( {1 - {{\eta }_{2}}} \right)\left( {1 + \left( {1 - \frac{{5{{\theta }_{2}}}}{{2\pi }}} \right)\left( {\frac{{{{{\tilde {\eta }}}_{1}}}}{{2\pi \omega }}\left( {\cos 2\pi \omega - \cos \omega \theta {}_{2}} \right) + \frac{{\tilde {\eta }}}{{2\pi }}\sin {{\theta }_{1}}} \right) - \frac{{\theta _{2}^{2}}}{{4{{\pi }^{2}}}}} \right),$$

where \({{\tilde {\eta }}_{1}} = \frac{{{{\eta }_{1}}}}{{1 - {{\eta }_{2}}}}\) and \(\tilde {\eta } = \frac{\eta }{{1 - {{\eta }_{2}}}}\).

The dimensionless hydrodynamic pressure in the lubricating layer is determined based on the equation

$$\begin{gathered} \frac{1}{{j{{\mu }_{i}}\left( \theta \right)}}\frac{{d{{p}_{i}}}}{{d\theta }} = \frac{{{{b}_{i}}}}{{{{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}^{2}}}} + \frac{{{{a}_{i}}}}{{{{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}^{3}}}},\quad i = 1,3; \\ \frac{1}{{j{{\mu }_{2}}\left( \theta \right)}}\frac{{d{{p}_{2}}}}{{d\theta }} = \frac{{{{b}_{2}}}}{{{{h}^{2}}\left( \theta \right)}} + \frac{{{{a}_{i}}}}{{{{h}^{3}}\left( \theta \right)}}. \\ \end{gathered} $$
(11)

Let us differentiate the expression \(\mu = {{e}^{{\alpha p - \beta T}}}\) with respect to θ. Taking into account the increase in the temperature

$$\frac{{dT{\kern 1pt} '}}{{d\theta }} = \frac{{dH{\kern 1pt} '}}{{d\theta }}\frac{1}{{{{C}_{p}}Q}} = - \frac{1}{{{{C}_{p}}}}\frac{{24{{\mu }_{0}}\mu \Omega {{r}_{0}}h\left( \theta \right)}}{{{{\delta }^{2}}{{a}_{i}}}}\int\limits_0^1 {{{{\left( {\frac{{\tilde {\psi }{\kern 1pt} '{\kern 1pt} '\left( \xi \right)}}{{{{h}^{2}}\left( \theta \right)}} + \frac{{\tilde {u}{\kern 1pt} '\left( \xi \right)}}{{{{h}^{2}}\left( \theta \right)}}} \right)}}^{2}}} d\xi ,$$

we can obtain

$$\frac{{d\mu }}{{d\theta }} = \mu \left( \theta \right)\left( {\alpha \frac{{dp}}{{d\theta }}--\beta \frac{{dT}}{{d\theta }}} \right) = \mu \left( \theta \right)\alpha \frac{{dp}}{{d\theta }} + \frac{{{{\mu }^{2}}\left( \theta \right)\beta 24{{\mu }_{0}}\Omega {{r}_{0}}h\left( \theta \right)}}{{T{\kern 1pt} \text{*}{\kern 1pt} {{C}_{p}}{{\delta }^{2}}{{a}_{i}}}} \cdot \int\limits_0^1 {{{{\left( {\frac{{\tilde {\psi }{\kern 1pt} '{\kern 1pt} '{\kern 1pt} \left( \xi \right)}}{{{{h}^{2}}\left( \theta \right)}} + \frac{{{\tilde {v}}{\kern 1pt} '{\kern 1pt} \left( \xi \right)}}{{{{h}^{2}}\left( \theta \right)}}} \right)}}^{2}}} d\xi .$$
(12)

By integrating these equations, we obtain

$$\begin{gathered} j{{\mu }_{i}}\left( \theta \right) = \frac{1}{{1 - \beta {{K}_{i}}\left[ {{{\Delta }_{1}}{{I}_{3}}\left( \theta \right) + {{\Delta }_{2}}{{I}_{2}}\left( \theta \right) + {{\Delta }_{3}}{{I}_{1}}\left( \theta \right)} \right] - \alpha \left[ {{{b}_{i}}{{I}_{2}}\left( \theta \right) + {{a}_{i}}{{I}_{3}}\left( \theta \right)} \right]}},\quad i = 1,3; \\ j{{\mu }_{2}}\left( \theta \right) = \frac{1}{{1 - \beta {{K}_{2}}\left[ {{{\Delta }_{1}}{{I}_{3}}\left( \theta \right) + {{\Delta }_{2}}{{I}_{2}}\left( \theta \right) + {{\Delta }_{3}}{{I}_{1}}\left( \theta \right)} \right] - \alpha \left[ {{{b}_{1}}{{I}_{2}}\left( \theta \right) + {{a}_{2}}{{I}_{3}}\left( \theta \right)} \right]}}, \\ \end{gathered} $$
(13)

where \({{K}_{i}} = \frac{{24{{\mu }_{0}}\Omega {{r}_{0}}}}{{T{\kern 1pt} \text{*}{\kern 1pt} {{C}_{p}}{{\delta }^{2}}{{a}_{i}}}}\); \({{\Delta }_{1}} = \int_0^1 {{{{\left( {\tilde {\psi }{\kern 1pt} '{\kern 1pt} '\left( {{{\xi }_{i}}} \right)} \right)}}^{2}}d{{\xi }_{i}}} = \frac{{a_{i}^{2}}}{{12}}\); \({{\Delta }_{2}} = 2\int_0^1 {\left( {\tilde {\psi }{\kern 1pt} '{\kern 1pt} '\left( {{{\xi }_{i}}} \right) \cdot {\tilde {v}}{\kern 1pt} '\left( {{{\xi }_{i}}} \right)} \right)} d{{\xi }_{i}}\) = \(\frac{1}{6}{{b}_{i}}{{a}_{i}} = {{a}_{i}}\); Δ3 = \(\int_0^1 {{{{\left( {{\tilde {v}}{\kern 1pt} '\left( {{{\xi }_{i}}} \right)} \right)}}^{2}}} d{{\xi }_{i}}\) = 4; \({{I}_{{{{K}_{i}}}}} = \int_0^\theta {\frac{{d\theta }}{{h_{i}^{K}\left( \theta \right)}}} \).

By solving Eq. (13) with respect to μ(θ), with an accuracy of \(O({{\eta }^{2}})\), \(O(\eta _{1}^{2})\), \(O(\eta _{2}^{2})\), \(O({{\tilde {\eta }}^{2}})\), \(O\left( {\eta {{\eta }_{1}}} \right)\), \(O\left( {\eta \tilde {\eta }} \right)\), \(O\left( {{{\eta }_{2}}\eta } \right)\), and \(O\left( {{{\eta }_{2}}\tilde {\eta }} \right)\) inclusive, we obtain the analytical expressions for the hydrodynamic pressure

$${{p}_{i}} = {{\mu }_{i}}\left( {{{b}_{i}}{{I}_{2}}\left( \theta \right) + {{a}_{i}}{{I}_{3}}\left( \theta \right)} \right) + \frac{{{{p}_{g}}}}{{{{p}_{a}}}}.$$

If the values of the hydrodynamic pressure and velocity are known, we can find the analytical expressions for the bearing capacity and friction force

$${{R}_{x}} = \frac{{6j\left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right)\Omega r_{0}^{3}}}{{2{{\delta }^{2}}}}$$
$$ \times \;\left[ {\int\limits_0^{{{\theta }_{1}}} {\left( {{{p}_{1}} - \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}} \right)\cos \theta d\theta + \int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} {\left( {{{p}_{2}} - \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}} \right)\cos \theta d\theta + \int\limits_{{{\theta }_{2}}}^{2\pi } {\left( {{{p}_{3}} - \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}} \right)\cos \theta d\theta } } } } \right];$$
$$\begin{gathered} {{R}_{y}} = \frac{{6j\left( {2{{\mu }_{0}} + {{\kappa }_{0}}} \right)\Omega r_{0}^{3}}}{{2{{\delta }^{2}}}} \\ \times \;\left[ {\int\limits_0^{{{\theta }_{1}}} {\left( {{{p}_{1}} - \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}} \right)\sin \theta d\theta + \int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} {\left( {{{p}_{2}} - \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}} \right)\sin \theta d\theta + \int\limits_{{{\theta }_{2}}}^{2\pi } {\left( {{{p}_{3}} - \frac{{{{p}_{g}}}}{{p{\kern 1pt} \text{*}}}} \right)\sin \theta d\theta } } } } \right]; \\ \end{gathered} $$
(15)
$${{L}_{{{\text{fr}}}}} = j{{\mu }_{0}}\Omega r_{0}^{3}\left( {1 + \left( {\alpha p - \beta T} \right) - \frac{{{{{\left( {\alpha p - \beta T} \right)}}^{2}}}}{2}} \right)\left[ {\int\limits_0^{{{\theta }_{1}}} {\left( {\frac{{\tilde {\psi }_{1}^{{''}}\left( 0 \right)}}{{{{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}^{2}}}} + \frac{{\tilde {u}_{1}^{'}\left( 0 \right)}}{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}} \right)d\theta } } \right.$$
$$ + \;\int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} {\left( {\frac{{\tilde {\psi }_{2}^{{''}}\left( 0 \right)}}{{{{h}^{2}}\left( \theta \right)}} + \frac{{\tilde {u}_{2}^{'}\left( 0 \right)}}{{h\left( \theta \right)}}} \right)d\theta } + \left. {\int\limits_{{{\theta }_{2}}}^{2\pi } {\left( {\frac{{\tilde {\psi }_{3}^{{''}}\left( 0 \right)}}{{{{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}^{2}}}} + \frac{{\tilde {u}_{3}^{'}\left( 0 \right)}}{{\left( {h\left( \theta \right) - {{\eta }_{2}}} \right)}}} \right)d\theta } } \right].$$

The numerical analysis of the obtained computational models at a speed of 1 m/s; θ2 – θ1 = 5.74°–22.92°; σ = 5–25 MPa; μ0 = 0.0707–0.0076 N s/m2; Ω = 100–2400 s–1; α = 0–1; Т = 25–100°С; δ = 0.05–0.07 × 10–3 m; r0 = 0.01995–0.04993 m; Pg = 0.2 MPa, made it possible to plot the curves of the friction coefficient (Fig. 2) when using a micropolar lubricant.

Fig. 2.
figure 2

Dependence of the friction coefficient in the bearing with a groove on the parameters characterizing (a) the lubricant viscosity and temperature or (b) the groove width.

Full size image

The numerical analysis of the expression that determines the magnitude of the vertical pressure component made it possible to plot the dependence of the accepted variable factors on this parameter (Fig. 3).

Fig. 3.
figure 3

Dependence of the pressure component in the bearing with an adapted profile and a groove on the groove width and working load: 1, σ = 14.1 MPa; 2, σ = 4.7 MPa.

Full size image

Thus, the bearings with a polymeric fluoroplastic-containing antifriction coating in the presence of an oil-supporting groove are able to operate both under the boundary and under the liquid friction.

EXPERIMENTAL

The experimental study consists of verification of the developed calculation model with an oil-containing groove and complex experimental studies with a new design of the base surface of a bearing bush, which is covered by an antifriction polymer coating with a groove.

The tribological experimental studies of radial bearings were carried out using a II 5018 modernized friction machine (Figs. 4, 5).

Fig. 4.
figure 4

Measurement of bulk temperature in the roller–shoe friction pair: 1, 2, thermocouples.

Full size image
Fig. 5.
figure 5

Pattern of the thermal imager to determine the bulk temperature in the roller-shoe friction pair with a fluoroplastic-containing composite polymer coating: 1, shoe holder; 2, prototype; 3, roller; 4, locknut; 5, thermocouple.

Full size image

The samples were made in the form of partial inserts from an annular blank at a central angle of 60°. The polymer coatings and grooves were applied to their surface at a coating depth of 0.55 mm. In addition, there were holes for thermocouples in the shoes (Fig. 4).

RESULTS

As a result of the theoretical study, it was found that the bearing capacity increases by about 12–14% and the friction coefficient decreases by 8–10% within the studied modes (Table 1).

Table 1. Theoretical results for the surface of a bearing bush with the fluorine-containing composite polymer coating
Full size table

During the experimental studies, the fields of rational application of the obtained models were determined. The stable hydrodynamic friction mode was obtained after a 2-minute run-in, while the load was increased stepwise five times up to 25 MPa (Table 2).

Table 2. Theoretical and experimental results for the surface of a bearing bush with the fluoroplastic-containing composite polymer coating
Full size table

DISCUSSION

The theoretical study established the needed section of a groove on the surface of the bearing bush for the bearing to reach the hydrodynamic lubrication mode at a given load.

Then, the calculation model that describes the flow of micropolar lubricant in the working gap was developed. When developing the model, the dependence of the lubricant viscosity on the pressure and temperature was taken into account. The obtained results allow us to find the main performance characteristics.

During the rotation of the trunnion in the groove, the circulation movement occurs in the studied structure, while the resulting force lifts the trunnion leading to the formation of a hydrodynamic wedge.

A new method to build computational models has been theoretically developed and experimentally confirmed, which makes it possible to expand significantly the scope in mechanical engineering, aircraft building, instrument making, etc., where it is needed to provide a hydrodynamic mode of lubrication.

PRIMARY RESULTS

(1) This study has demonstrated a significant expansion of the possibilities to use in practice the computational models for a bearing coated by a polymer with a groove and operating in the hydrodynamic lubrication mode, which makes it possible to determine the performance characteristics. (2) The calculation models take into account the use of additional lubrication with a polymer coating and a groove on the surface of the bearing bush. (3) The use of the studied radial plain bearings with a groove 3 mm wide substantially increases the load bearing capacity by 12–14% and decreases the friction coefficient by 8–10%. (4) The design of the bearing with a polymer coating and a groove 3 mm wide ensures stable trunnion floating, which has experimentally confirmed the correctness of the results of theoretical studies.

SPECIFICATION

\({{r}_{0}}\)

shaft radius;

\({{r}_{1}}\)

bearing brush radius;

\(\tilde {h}\)

groove height;

\(e\)

eccentricity;

\(\varepsilon \)

relative eccentricity;

\({{\mu }_{0}}\)

typical viscosity;

\(\mu {\kern 1pt} '\)

dynamic viscosity coefficient of lubricant;

\(p{\kern 1pt} '\)

hydrodynamic pressure in a lubricant layer;

\(\alpha {\kern 1pt} ',\;\beta {\kern 1pt} '\)

constant experimental coefficient;

\(T{\kern 1pt} '\)

temperature;

I

mechanical heat equivalent;

λ

lubricant heat conductivity;

\(\eta = \frac{l}{\delta }\)

structural parameter;

\({{\eta }_{2}} = \frac{{\tilde {h}}}{\delta }\)

structural parameter describing a groove;

θ1, θ2

corresponding angular coordinates of a groove;

\(u{\kern 1pt} \text{*}\left( \theta \right)\), \({v}{\kern 1pt} \text{*}\left( \theta \right)\)

known functions caused by the presence of a polymer coating on surface of the bearing bush, where Q is the lubricant consumption per unit time; Cр is the heat capacity at constant pressure; h(θ) is the thickness of the oil film.