Skip to main content
SpringerLink
Log in

Destruction of a perforated body in transverse shear

  • Reliability, Durability, and Wear Resistance of Machines and Constructions
  • Published:
Journal of Machinery Manufacture and Reliability Aims and scope Submit manuscript

Abstract

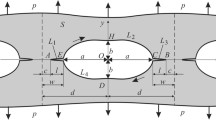
We consider the problem of doubly periodic system interaction of circular holes and straight cracks with end zones emanating from the surface of the circular holes designed collinear with the axes of abscises and ordinate in transverse shear. The solution to the problem of equilibrium of a perforated body under transverse shear cracks with connections in the end zone is reduced to solving two infinite algebraic systems and two nonlinear singular integral equations. From the solutions of these equations we find converging efforts in the binders of end zones. The condition of crack growth is formulated taking into account the criterion of maximum extraction binders.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Muskhelishvili, N.I., Nekotorye osnovnye zadachi matematicheskoi teorii uprugosti (Some Basic Problems of the Theory of Mathematical Elasticity), Moscow: Nauka, 1966.

    Google Scholar 

  2. Grigolyuk, E.I. and Fil’shtinskii, L.A., Perforirovannye plastiny i obolochki (Perforated Plates and Shells), Moscow: Nauka, 1970.

    MATH  Google Scholar 

  3. Panasyuk, V.V., Savruk, M.P., and Datsyshin, A.P., Raspredelenie napryazhenii okolo treshchin v plastinakh i obolochkakh (Stress Distribution Near Cracks in Plates and Shells), Kiev: Naukova dumka, 1976.

    Google Scholar 

  4. Il’yushin, A.A., Plastichnost’ (Plasticity), Moscow: Gostekhteoretizdat, 1948.

    Google Scholar 

  5. Birger, I.A., General Algorithms for Solving the Problems of Elasticity, Plasticity and Creeping Theory, in Uspekhi mekhaniki deformiruemykh sred (Progress of the Deformed Mediums Mechanics), Moscow: Nauka, 1975, pp. 51–73.

    Google Scholar 

  6. Gol’dshtein, R.V. and Perel’muter, M.N., Simulations of Cracks Resistance of Composite Materials, Vychislitel. Mekhan. Sploshn. Sred, 2009, vol. 2, no. 2, pp. 22–39.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Baku, Azerbaijan

    S. M. Guliyev

Authors
  1. S. M. Guliyev
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Original Russian Text © S.M. Guliyev, 2011, published in Problemy Mashinostroeniya i Nadezhnosti Mashin, 2011, No. 4, pp. 56–63.

About this article

Cite this article

Guliyev, S.M. Destruction of a perforated body in transverse shear. J. Mach. Manuf. Reliab. 40, 348–354 (2011). https://doi.org/10.3103/S105261881104008X

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S105261881104008X

Keywords

Search

Navigation