Time-Optimal Movement of Platform with Oscillators

Abstract—

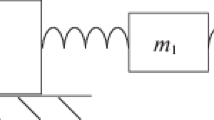
A system is considered that includes a rigid body moving along a horizontal straight line and carrying several linear oscillators. The only control action is an external limited force applied to the supporting body; there is no friction. The problem is solved for the time-optimal movement of the system to the required distance from a given equilibrium position to another similar state with oscillation damping. A control structure is proposed that satisfies the necessary conditions for optimality. The case of a platform with two oscillators is considered in detail, and the results of numerical experiments are presented.

APPENDIX

To prove Statement 3, it is necessary to prove that for each value of $T \in \left( {0,{{T}_{s}}} \right]$, the system of equations (4.5) has roots $0 < {{{{\tau }}}_{1}} < {{{{\tau }}}_{2}} < T$.

Since the case $T = {{T}_{s}}$ has already been mentioned in Statement 2, further we put $T < {{T}_{s}}$. Denoting the durations of control constancy intervals ${{\tau }} = {{{{\tau }}}_{1}}$, ${{\sigma }} = {{{{\tau }}}_{2}} - {{{{\tau }}}_{1}}$, ${{\delta }} = T - {{{{\tau }}}_{2}}$, we write the first equation (4.5) in the form

$$1 - 2\cos \delta + 2\cos \left( {\sigma + \delta } \right) - \cos \left( {\tau + \sigma + \delta } \right) = 0.$$

(A.1)

In Fig. 2, the time intervals ${{\tau }}$, ${{\sigma }}$, ${{\delta }}$ correspond to the angular measures of arcs ON₁, N₁N₂, N₂N₃. The point N₂ must lie beyond a circle with the boundary ${{{{\alpha }}}_{1}}$, otherwise it will not be possible to get from it to the ordinate axis at $u = 1$. Hence it follows ${{N}_{1}}{{N}_{2}} \geqslant {{N}_{1}}E$, i.e.,

$${{\sigma }} \geqslant 2{{\beta }}{\text{.}}$$

(A.2)

To solve system (4.5), it is enough to find such roots ${{\tau }}$, ${{\sigma }}$, ${{\delta }}$ of equation (A.1), which will satisfy it also when they are replaced by ${{\omega \tau }}$, ${{\omega \sigma }}$, ${{\omega \delta }}$. Let us consider such a change in scale by a factor of ${{\omega }}$ on the coordinate plane. Figure 10 shows the dependence of ${{2\beta }}$ on ${{\tau }}$ (4.8) in the form of a curve g, which is convex upward. On the same plane, we introduce the coordinates ${{\delta }}$, ${{\sigma }}$ and construct the lines given by Eqs. (A.1) for each fixed value of ${{\tau }}$. In Fig. 2 for a given value of ${{\tau }}$ (i.e., when the point N₁ is selected), the smallest value of ${{\sigma }} = 2{{\beta }}$ (at the point E) corresponds to the smallest value of ${{\delta }} = {{\tau }}$. Therefore, for a given ${{\tau }}$, equation (A.1) in Fig. 10 will describe a curve ${{{{\gamma }}}_{1}}$ coming from the point ${{E}_{1}}\left( {{{\tau }},2{{\beta }}\left( {{\tau }} \right)} \right) \in g$. If a numerical parameter $T = {{\tau }} + {{\sigma }} + {{\delta }}$ is assigned to each point of the curve ${{{{\gamma }}}_{1}}$, then the point ${{Z}_{1}}\left( {{{\tau }},2{{\pi }} - 2{{\tau }}} \right)$ will correspond to the value of $T = 2{{\pi }}$. Indeed, substituting $T = 2{{\pi }}$ into (3.10), we obtain ${\text{cos}}\,{{\delta }} = {\text{cos}}\left( {{{\sigma }} + {{\delta }}} \right)$, whence

$${{\sigma }} + 2{{\delta }} = 2{{\pi }}{\text{.}}$$

(A.3)

Fig. 10.

If we substitute $T = 2{{\pi }}$ in the first equation (4.5), then we get $\cos {{{{\tau }}}_{2}} = \cos {{{{\tau }}}_{1}}$, i.e., ${\text{cos}}\left( {{{\tau }} + {{\sigma }}} \right) = \cos {{\tau }}$, whence it follows ${{\sigma }} + 2{{\tau }} = 2{{\pi }}$. Thus, on the plane with the coordinates δ, ${{\sigma }}$, point ${{Z}_{1}}$ is located above the point ${{E}_{1}}$ and belongs to the line l with Eq. (A.3). On the arc ${{E}_{1}}{{Z}_{1}}$, the point with the parameter $T = 2{{\pi /}}\omega$ is denoted by ${{H}_{1}}$.

Differentiating (A.1) with respect to ${{\sigma }}$ (at ${{\tau }} = {\text{const}}$) and expressing $d{{\delta /}}d{{\sigma }}$ from this, we can show that the function ${{\delta }}\left( {{\sigma }} \right)$ on the interval ${{\sigma }} \in \left[ {2{{\beta }}\left( {{\tau }} \right),2{{\pi }} - 2{{\tau }}} \right]$ has a single extremum. At the same time, ${{d}^{2}}{{\delta /}}d{{{{\sigma }}}^{2}}$ < 0, as well as $d{{\delta /}}d{{\sigma }} \to - 1{\text{/}}2$ at $T \to 2{{\pi }}$, i.e., the points ${{E}_{1}}$ and ${{Z}_{1}}$ are connected by the curve ${{{{\gamma }}}_{1}}$ “convex to the right” and tangent to the straight line l at the point ${{Z}_{1}}$. The family of such curves (for each fixed ${{\tau }} \in \left( {0,{{\;\pi }}} \right)$), coming out of the points of the line g, depicts the set of solutions of Eq. (A.1) in the range of values ${{\tau }} + {{\sigma }} + {{\delta }} \leqslant 2{{\pi }}$.

We use these lines to graphically solve system (4.5) according to the following scheme. Having given a specific value of ${{\omega }}$, we determine the angle $\angle S$ from (4.9) and find the angular size ${{{{\tau }}}_{s}}$ of the arc OS, equal to the moment of switching control at point M in Fig. 3. For arbitrary ${{\tau }} \in (0,{{{{\tau }}}_{s}})$ we consider the corresponding curve ${{{{\gamma }}}_{1}}$ (in the form ${{E}_{1}}{{Z}_{1}}$), and for the value of ${{\omega \tau }}$, a similar curve ${{{{\gamma }}}_{2}}$ connecting the points ${{E}_{2}}\left( {{{\omega \tau }},2{{\beta }}\left( {{{\omega \tau }}} \right)} \right) \in g$ and ${{Z}_{2}}\left( {{{\omega \tau }},2{{\pi }} - 2{{\omega \tau }}} \right) \in l$ (Fig. 10). On the curve ${{{{\gamma }}}_{1}}$, we select the section ${{E}_{1}}{{H}_{1}}$ where, at the point ${{H}_{1}}$, the parameter $T = 2{{\pi /}}\omega$.

Let us show that under homothety with the center O and coefficient 1/ω (i.e., when the plane is compressed by a factor of ${{\omega }}$), the image ${{{{\gamma }}}_{3}}$ of the curve ${{{{\gamma }}}_{2}}$ intersects the arc ${{E}_{1}}{{H}_{1}}$ at its interior point. Indeed, a right-angled triangle ${{E}_{2}}{{Z}_{2}}{{D}_{2}}$ described around the curve ${{{{\gamma }}}_{2}}$ will transform in ${{E}_{3}}{{Z}_{3}}{{D}_{3}}$ (Fig. 10). The point ${{E}_{3}}$ will be below ${{E}_{1}}$ due to the convexity of the curve g (by Jensen’s inequality). The point ${{Z}_{3}}\left( {{{\tau }},\frac{{2{{\pi }}}}{{{\omega }}} - 2{{\tau }}} \right)$ will fall on the vertical ${{E}_{3}}{{E}_{1}}$, and above the point ${{E}_{1}}$, since $\frac{{2{{\pi }}}}{{{\omega }}} - 2{{\tau }} > 2{{\beta }}\left( {{\tau }} \right)$ (this follows from $\frac{{2{{\pi }}}}{{{\omega }}} = 2{{{{\tau }}}_{s}} + 2{{\beta }}({{\tau }_{s}})$ > 2τ + 2β(τ), since ${{{{\tau }}}_{s}} > {{\tau }}$ and the function ${{\varphi }}\left( {{\tau }} \right) = {{\tau }} + {{\beta }}\left( {{\tau }} \right)$ are steadily increasing). The image of a straight line l will pass through the point ${{Z}_{3}}$ in the form of a straight line ${{Z}_{3}}{{D}_{3}}$ with the equation ${{\sigma }} = \frac{{2{{\pi }}}}{{{\omega }}} - 2{{\delta }}$. The point ${{H}_{1}}$ lies above the straight line ${{Z}_{3}}{{D}_{3}}$, because its coordinates ${{{{\delta }}}_{h}}$, ${{{{\sigma }}}_{h}}$ satisfy the condition ${{{{\sigma }}}_{h}} > \frac{{2{{\pi }}}}{{{\omega }}} - 2{{{{\delta }}}_{h}}$. This follows from the relations ${{{{\sigma }}}_{h}} + {{{{\delta }}}_{h}} + {{{{\delta }}}_{h}} > {{{{\sigma }}}_{h}} + {{{{\delta }}}_{h}} + {{{{\tau }}}_{h}} = \frac{{2{{\pi }}}}{{{\omega }}}$ by virtue of ${{{{\delta }}}_{h}} > {{{{\tau }}}_{h}}$.

Since the vertical segment ${{Z}_{3}}{{E}_{3}}$ contains the point ${{E}_{1}}$ inside, and the inclined line ${{Z}_{3}}{{D}_{3}}$ intersects the arc ${{E}_{1}}{{H}_{1}}$, then the curve ${{{{\gamma }}}_{3}}$ (connecting ${{Z}_{3}}$ and ${{E}_{3}}$, located to the left of ${{Z}_{3}}{{D}_{3}}$) will intersect the arc ${{E}_{1}}{{H}_{1}}$ at some point ${{X}_{1}}$. Its coordinates ${{\delta }}$, ${{\sigma }}$ together with the selected value of ${{\tau }}$, are the solution of Eq. (3.10), as well as their multiple values ${{\omega \delta }}$, ${{\omega \sigma }}$, ${{\omega \tau }}$, since the homothetic point ${{X}_{2}}\left( {{{\omega \delta }},~{{\omega \sigma }}} \right)$ lies on the curve ${{{{\gamma }}}_{2}}$ with the parameter ${{\omega \tau }}$. Hence, for any $T \in \left( {0,{{T}_{s}}} \right]$, system (4.4), and (4.5) has a solution, which proves Statement 3.