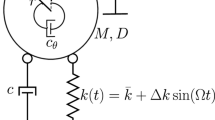Typical dielectric elastomer structures: dynamics and application in structural vibration control

Abstract

In recent years, dielectric elastomer (DE) structures have received great attention in various fields of engineering, such as artificial muscle, soft robot, resonator, and structural vibration control, due to its prominent advantages. In the present paper, the theoretical and experimental research into the dynamical behavior of DE structures and their application for vibration control is reviewed. In the theoretical research into dynamical behavior, from a mechanics viewpoint, DE structures are usually categorized into four types, i.e., spherical, rectangular, tubular, and circular. For each type of DE structure, the mathematical description is given and the dynamical behavior, such as the resonant property, jump, and bifurcation, is summarized. Moreover, the work on dynamical experiments is briefly outlined. In the application for vibration control, stack-type and tubular-type DE structures usually used as actuators are surveyed. The established control algorithms for the controlled systems using DE actuators are described. The challenges for the research into the dynamics of DE structure and its application for vibration control and some promising theories which may be applied for the research are pointed out.

中文概要

目 的

介电弹性体由于其卓越的优势受到工程界的广泛关注。本文主要综述典型介电弹性结构的动力学的理论和实验研究及其在振动控制中的应用,并指出其中存在的挑战及可能应用于研究的理论。

创新点

1. 综述四类典型介电弹性体结构的动力学数学模型和动力学行为,以及相应的动力学实验结果研究;2. 综述两类典型的介电弹性体结构在振动控制中的应用及相应的控制算法。

方 法

1. 从力学的角度出发,根据介电弹性体的结构形状,研究球形、矩形、管状及圆形介电弹性体结构的动力学模型数学描述及动力学行为;2. 实验分析介电弹性体结构的面内及离面动力学行为;3. 分析堆栈式和管状式介电弹性体结构在振动控制中的应用及控制算法。

结 论

1. 现有的介电弹性体结构动力学方面的理论研究局限于使用低阶模态,对高阶模态还未涉及;2. 现有施加在介电弹性体结构的机械力和电压都是时间的确定性函数,随机情形还属于空白;3. 对介电弹性体结构的随机最优控制,特别是以电压为控制项还未研究。

1 Introduction

A dielectric elastomer (DE) structure consists of a polymer film sandwiched between two compliant electrodes. By imposing a voltage on the compliant electrodes, the DE structure significantly reduces in thickness and expands in area. DE structure has several prominent advantages, such as light weight, low compliance, high stretch ability (more than 100%), short response time, high energy density, high efficiency over a broad range of frequencies, and chemical and biological compatibility (Pelrine et al., 2002; Ashley, 2003; O’Halloran et al., 2008; Zhao and Wang, 2014). Thus, DE structure has received extensive attention in many fields of engineering, such as artificial muscle, adaptive optical element, soft robot, programmable haptical surface, resonator, electromechanical transducer, and vibration control (Kovacs et al., 2009; Son and Goulbourne, 2009; Berardi, 2010; 2013; Brochu and Pei, 2010; McKay et al., 2010; Kaal and Herold, 2011).

The research into the static and dynamic responses of DE structure to mechanical stimulation constitutes the first and most important step in utilizing the advantages of DE structure. The quasi-static behavior and the stability of DE structure have been extensively investigated (Carpi et al., 2008). Recently, Zhou et al. (2014a) studied the electromechanical response of a DE tube actuator with and without boundary constraints to demonstrate an alternative to avoid electromechanical instability while achieving large actuation. Lu et al. (2015) investigated the electromechanical bifurcation and bulging propagation in a cylindrical DE tube and derived the bifurcation and phase coexistence conditions which were verified by experimentation. Xie et al. (2016) studied the bifurcation of ideal and non-ideal DE balloons under pressurized inflation and electric actuation. DE structure is mostly expected to work under dynamic excitation in many applications, e.g., pump, loudspeaker, and vibrotactile displays for mobile application. Thus, dynamical behavior, such as natural frequency and nonlinear response, was mostly investigated theoretically and experimentally (Fox and Goulbourne, 2008; Son and Goulbourne, 2010; Zhu et al., 2010a; 2010b; Liu et al., 2014; Sheng et al., 2014).

DE structure can be used to constitute actuator due to advantages such as large flexibility and short response time. Compared with piezoelectric actuator, DE actuator (DEA) can generate large deformation, and is suitable for application in vibration control, especially, for lightweight and large-span structures (Papaspiridis and Antoniadis, 2008; Sarban et al., 2009; Herold et al., 2011; Karsten et al., 2011; Kaal and Herold, 2015; Wahab and Rustighi, 2015). These structures often vibrate with large amplitudes even under small excitation. DEA is the ideal component for setting up control loop to alleviate unwanted vibration. Research into the application of DE structure for vibration control focused on the development of control algorithms, and feedforward and feedback control strategies have been proposed.

In this paper, existing theoretical work on the dynamical behavior of DE structure is classified into four types from a mechanics viewpoint. The mathematical description and dynamical behavior of each type of DE structure, such as the resonant property, jump, and bifurcation are summarized. The application of DE for structural vibration control and the control algorithm are reviewed. Some problems needed to be further studied and promising theories which may be applied are pointed out.

2 Dynamics of typical DE structures

2.1 Theoretical work

DE structures can be categorized into four types according to their shapes: spherical, rectangular, tubular, and circular.

2.1.1 Spherical DE structure

Zhu et al. (2010a) studied the nonlinear oscillation of a spherical DE balloon. Fig. 1 shows the balloon in its un-deformed and deformed states. In the un-deformed state, the radius and the thickness of the DE balloon are R and H, respectively. When the pressure inside the balloon exceeds the pressure outside by p and the two electrodes of the DE balloon are subject to a voltage Φ, the DE balloon deforms to radius r and the two electrodes gain charges +Q and −Q. The stretch of the membrane can be defined as

$$\lambda = {r \over R},$$

(1)

and the electric displacement in the membrane as

$$D = {Q \over {4\pi {r^2}}}{.}$$

(2)

Fig. 1

DE balloon deformation under pressure and volt-age. Reprinted from (Zhu et al., 2010a), Copyright 2010, with permission from John Wiley and Sons

The thermodynamics of the DE structure is characterized by the density of the Helmholtz free energy. By neglecting the effect of crosslinks on polarization, the energy density W is a sum of the elastic energy and the dielectric energy. By adopting the neo-Hookean model to describe the elasticity of the polymer for simplicity, the following expression can be obtained:

$$W(\lambda, D) = {\mu \over 2}(2{\lambda ^2} + {\lambda ^{ - 4}} - 3) + {{{D^2}} \over {2\varepsilon }},$$

(3)

where μ is the shear modulus and ε is the permittivity. Thermodynamics predicts that, for an arbitrary variation in the system, the variation of the free energy of the membrane should be equal to the work done by the voltage, pressure, and inertia, namely:

$$4\pi {R^2}H\delta W = \Phi \delta Q + 4\pi {r^2}p\delta r - 4\pi {r^2}H\;\rho {{{{\rm{d}}^2}r} \over {{\rm{d}}{t^2}}}\delta r,$$

(4)

where ρ is the density of the DE. Thus, the dynamical equation is

$${{{{\rm{d}}^2}\lambda } \over {{\rm{d}}{T^2}}} + g(\lambda, p, \Phi) = 0,$$

(5)

where T is dimensionless time.

By using Eq. (5), the state of equilibrium, small-amplitude oscillation around a state of equilibrium, nonlinear behavior under parametric excitation of time-varying pressure or voltage can be investigated. It is found that the natural frequency is tunable by varying the pressure or voltage. When the pressure is static but the voltage varies sinusoidally, the balloon resonates at multiple values of excitation frequency, leading to super-harmonic, harmonic, and sub-harmonic responses (but has not been observed in experiments so far). Furthermore, when the excitation frequency changes continuously, the oscillating amplitude of the balloon may jump at a certain value of excitation frequency. Fig. 2 shows these phenomena.

Fig. 2

Dynamic response of DE to static pressure and sinusoidal voltage: (a) resonance; (b) jump. Reprinted from (Zhu et al., 2010a), Copyright 2010, with permission from John Wiley and Sons

Mockensturm and Goulbourne (2006) studied the dynamical behavior of an inflated spherical DE membrane subject to an electric field. Saddle-node bifurcation occurs during inflation and deflation of the membrane. The bifurcation can be controlled by imposing a voltage. For a given mechanical pressure, the electrostatic pressure can be altered to move the bifurcation point either above or below the maintained mechanical pressure. Using a DE membrane enclosing a given amount of ideal gas as an actuator is not feasible since the imposed voltage may cause dielectric breakdown. As feasible actuator, the amount of gas enclosed in the DE membrane should be changeable.

Extending the work by Zhu et al. (2010a), Yong et al. (2011) studied the DE shell subject to a combination of pre-stress and voltage. They found that when the thickness of the shell increases, the system under constant voltage becomes more stable. The spherical DE shell may be destroyed as the mean voltage exceeds the critical mean voltage. In this analysis, the deformed DE shell keeps its spherical symmetry. However, it is noted that bifurcation instability may occur for a Mooney material subject to a voltage (Diaz-Calleja et al., 2009); a non-spherical shell can be found in the current configuration. Liang and Cai (2015) found a highly inhomogeneous electric field and stress/stretch distributions with a non-spherical shape and studied the stability analysis of a DE balloon in different equilibrium configurations. For a non-spherical configuration, the dynamical behavior will be more complicated.

2.1.2 Rectangular DE structure

Fig. 3 shows a DE membrane of dimensions L₁, L₂, and L₃ in an un-deformed state (Sheng et al., 2014). When the membrane is subject to forces P₁, P₂ and the two electrodes are subject to a voltage Ф, the membrane deforms to l₁, l₂, and l₃. Then, the stretches in the three main directions can be defined as λ _i =l _i /L _i (i=1, 2, 3). Due to the incompressibility, ${\lambda _3} = \lambda _1^{ - 1}\lambda _2^{ - 1}$. The free energy density of the DE can be expressed as a sum of electric density and elastic energy density, i.e.,

$$\begin{array}{*{20}c} {W = - {{\mu {J_{\rm{m}}}} \over 2}\ln \left({1 - {{\lambda _1^2 + \lambda _2^2 + \lambda _1^{ - 2}\lambda _2^{ - 2} - 3} \over {{J_{\rm{m}}}}}} \right)}\\ { + {\varepsilon \over 2}{{\left({{\Phi \over {{L_3}}}} \right)}^2}\lambda _1^2\lambda _2^2,\quad \quad \quad \quad } \end{array}$$

(6)

where J_m is a dimensionless parameter related to the limiting stretch. The Gent model is adopted to calculate the elastic energy for capturing the strain stiffening effect. The variation of the free energy of the membrane is equal to the work done by the voltage, forces P₁, P₂ and inertia force, and the damping forces which are linear functions of the deformation velocities in two in-plane biaxial directions. Thus, the dynamical equations can be obtained as follows:

$$\left\{ {\begin{array}{*{20}c} {{{L_1^2\rho } \over {3\mu }}{{{{\rm{d}}^2}{\lambda _1}} \over {{\rm{d}}{t^2}}} + {{{\lambda _1} - \lambda _1^{ - 3}\lambda _2^{ - 2}} \over {1 - {{\lambda _1^2 + \lambda _2^2 + \lambda _1^{ - 2}\lambda _2^{ - 2} - 3} \over {{J_{\rm{m}}}}}}}\quad \quad \quad \quad \quad }\\ {\quad - {\varepsilon \over \mu }{{\left({{\Phi \over {{L_3}}}} \right)}^2}{\lambda _1}\lambda _2^2 - {{{P_1}} \over {\mu {L_2}{L_3}}} + {1 \over 2}{{c{L_1}} \over {\mu {L_2}{L_3}}}{{{\rm{d}}{\lambda _1}} \over {{\rm{d}}t}} = 0,}\\ {{{L_2^2\rho } \over {3\mu }}{{{{\rm{d}}^2}{\lambda _2}} \over {{\rm{d}}{t^2}}} + {{{\lambda _2} - \lambda _1^{ - 2}\lambda _2^{ - 3}} \over {1 - {{\lambda _1^2 + \lambda _2^2 + \lambda _1^{ - 2}\lambda _2^{ - 2} - 3} \over {{J_{\rm{m}}}}}}}\quad \quad \quad \quad \quad }\\ {\quad - {\varepsilon \over \mu }{{\left({{\Phi \over {{L_3}}}} \right)}^2}\lambda _1^2{\lambda _2} - {{{P_2}} \over {\mu {L_2}{L_3}}} + {1 \over 2}{{c{L_2}} \over {\mu {L_1}{L_3}}}{{{\rm{d}}{\lambda _2}} \over {{\rm{d}}t}} = 0,} \end{array}} \right.$$

(7)

where c is the damping coefficient.

Fig. 3

DE membrane in the (a) un-deformed and (b) de-formed states. Reprinted from (Sheng et al., 2014), Copyight 2014, with permission from the IOP Publishing Ltd.

Sheng et al. (2014) studied the special case where lengths L₁=L₂ and the DE structure is isotropic and is subject to equal biaxial stresses, i.e., the two in-plane stretches are equal. The mechanical forces are static while the voltage varies sinusoidally. They found that the DE structure will undergo a nonlinear aperiodic-damped motion, and this in-plane dynamics of DE structure is highly nonlinear, with the output stretch being far from sinusoidal while the input voltage still being strictly regulated as sinusoidal. There will be a stability transition when taking the damping effect into account. The damping effect causes dynamic response to constant amplitude vibration and decreasing in amplitude. The higher the damping, the less time required to reach a stationary state.

Xu et al. (2012) considered the case where the DE structure deforms only under electric loading. Due to the homogeneity of the problem and the incompressibility of the material, the stretches in the three main directions are $1/\sqrt \lambda$, $1/\sqrt \lambda$, and λ, where λ is the stretch in the thickness direction. The potential energy consists of two parts: the elastic energy, for which the neo-Hookean model is used, and the electrostatic energy. The dynamical equation was derived using the Euler-Lagrange equation. They found that dynamic response enlarges the stable deformation interval of the DE structure, as shown in Fig. 4. Applying harmonic electric loading, resonance phenomena can be observed. Moreover, external damping, which is linear function of the deformation velocity in the thickness direction, was introduced. It was found that as the damping coefficient increases, the first-order resonant frequency increases, the maximal amplitude becomes smaller, and peaks of higher order modes are almost damped away. Furthermore, the first-order resonance frequency increases when the applied electric field decreases.

Fig. 4

Comparison between the vibration amplitude and the quasi-static compression. Reprinted from (Xu et al., 2012), Copyright 2012, with permission from AIP Publishing LLC

Zhang et al. (2014) studied a DE structure under a mechanical load and a voltage. P₂=0 and the width was unchanged, i.e., λ₁=λ, λ₂=1, and λ₃=1/λ. A rheological model was adopted to represent the viscoelasticity. It was modeled by two parallel units, one contained a spring and the other consisted of another spring and a dashpot. Following similar procedure to those in (Zhu et al., 2010a), the governing equations can be obtained. Besides the equation of the stretch in direction x with respect to λ, the stretch in direction x due to the dashpot also satisfies the first-order differential equation (Hong, 2011). The effects of viscoelasticity on static equilibrium and dynamic response subject to a static voltage and a sinusoidal mechanical load P are studied. It was found that the membrane resonates at multiple frequency values both with and without viscoelasticity. The viscoelasticity reduces the natural frequency and increases the mean stretch of vibration. Besides the viscoelasticity, the current leakage can also cause dissipation. Zhang et al. (2014) studied the situation where the power source was cut off. It was found that the natural frequency of the membrane may increase but the mean stretch reduces due to current leakage.

Li et al. (2012) investigated the electromechanical and dynamic analyses of a tunable DE resonator. Fig. 5a shows a DE membrane of thickness H, length L₁ in the 1-direction and L₂ in the 2-direction in an un-deformed state. The membrane is pre-stretched with the stretches λ_1p and λ_2p, and then attached to a rigid frame to maintain the pre-stretch, as illustrated in Fig. 5b. Two rigid mass bars with lumped mass m sandwich the DE membrane and divide it into two parts, marked as membrane A and membrane B. In the actuated state, the two electrodes of membrane A are subject to a voltage Ф_A, as depicted in Fig. 5c. Membranes A and B have deformed lengths L_1Aλ_1A and L_1Bλ_1B in the 1-direction, and L_2Aλ_2A and L_2Bλ_2B in the 2-direction, where λ_1A, λ_1B, λ_2A, and λ_2B denote the stretches. Here, the Gent model was adopted. The free energy densities of membranes A and B are of the form of Eq. (6). It is assumed that the stretches in the 2-direction for both membranes are the same. Balancing the force of the rigid bars sandwiching the membrane, the equation of motion is of the form:

$${{{{\rm{d}}^2}{\lambda _{1{\rm {A}}}}} \over {{\rm{d}}{t^2}}} + g({\lambda _{1{\rm {A}}}},{\lambda _{1{\rm {p}}}},{\lambda _{2{\rm {p}}}},{\Phi _{\rm{A}}}) = 0{.}$$

(8)

Fig. 5

DE membrane in the three states: (a) un-deformed state; (b) pre-stretched state; (c) actuated state. Reprinted from (Li et al., 2012), Copyright 2012, with permission from Elsevier

The function g(λ_1A, λ_1p, λ_2p, ϕ _A ) is different between with or without loss of tension. Here, loss of tension means that one of the tensile forces of the membrane becomes zero. Equilibrium state and oscillation about the equilibrium state subject to a static voltage were studied. The membrane resonates at multiple frequency values of excitation when a sinusoidal voltage is applied. The natural frequency can be tuned by static voltage and pre-stretches. Loss of tension, electromechanical instability, and electrical breakdown cause resonator failure. To avoid failure, it is essential to control the applied voltage within a safe range.

Zhou et al. (2014b) extended the work by Li et al. (2012) by considering the viscoelasticity of a DE membrane (Hong, 2011). The natural frequency of a purely elastic DE membrane resonator is changed solely by the applied voltage, while the natural frequency of a viscoelastic DE membrane resonator is time-dependent and affected by both the applied voltage and the inelastic deformation. In practice, the natural frequency needs to be tuned up and viscoelastic DE structure tends to be more suitable for application.

2.1.3 Tubular DE structure

Son and Goulbourne (2010) developed a numerical model to predict the dynamic response of tubular DE transducer. Fig. 6 shows a cylindrical elastic membrane modeling a tubular DE transducer. From the symmetry of the problem and the elastic membrane assumption, the state of stress is nearly constant throughout the thickness. Cylindrical polar coordinates (R, Θ, η) and (r, θ, z) at the mid-plane are employed in the un-deformed and deformed states, respectively. The deformations in the z-axis direction are entirely symmetric. It follows that the principal directions at any point in the deformed membrane coincide with the deformed coordinates (r, θ, z), and the meridian, latitudinal, and thickness stretch ratios are denoted as λ₁, λ₂, and λ₃, respectively:

$$\left\{ {\begin{array}{*{20}c} {r = r(\xi),\;\;\theta = \Theta, \;\;z = z(\xi),}\\ {{\lambda _1} = {{{\rm{d}}\xi } \over {{\rm{d}}\eta }},\;\;{\lambda _2} = {r \over R},\;\;{\lambda _3} = {h \over {{h_0}}},} \end{array}} \right.$$

(9)

where ξ and η are the meridian length of the cylindrical membrane in the deformed and un-deformed states, respectively; 2h₀ and 2h are the un-deformed and deformed thicknesses, respectively.

Fig. 6

(a) Schematic of a tubular DE structure; (b) An un-deformed cylindrical membrane; (c) Half of the un-deformed and deformed membrane. Reprinted from (Son and Goulbourne, 2010), Copyright 2010, with permission from Elsevier

Balancing the forces yields equations of motion in the meridian and radial directions as follows:

$$\left\{ {\begin{array}{*{20}c} {{{{\rm{d}}{N_1}} \over {{\rm{d}}\xi }} + {{{N_1}} \over r}{{{\rm{d}}r} \over {{\rm{d}}\xi }} - {{{N_2}} \over r}{{{\rm{d}}r} \over {{\rm{d}}\xi }} = 2{h_0}\rho R{{{{\rm{d}}^{2}}\xi } \over {{\rm{d}}{t^2}}},}\\ {P - {\kappa _1}{N_1} - {\kappa _2}{N_2} = 2{h_0}\rho R{{{{\rm{d}}^{2}}r} \over {{\rm{d}}{t^2}}},\quad \quad } \end{array}} \right.$$

(10)

where κ₁ and κ₂ are the principal curvatures, N₁ and N₂ are the in-plane stresses, the sum of elastic stress determined by an elastic strain energy function (Mooney-Rivlin function) and Maxwell stress:

$$\left\{ {\begin{array}{*{20}c} {{N_1} = 2{\lambda _3}{h_0}\left\{ {2\left({\lambda _2^2 - {1 \over {\lambda _1^2\lambda _2^2}}} \right)\left({{{\partial W} \over {\partial {I_1}}} + \lambda _1^2{{\partial W} \over {\partial {I_2}}}} \right)} \right.}\\ {\left. {\quad - {1 \over 2}\left[ {{\varepsilon _0}{\varepsilon _4}{{\left({{V \over {{h_0}{\lambda _3}}}} \right)}^2}} \right]} \right\},\quad \quad \quad \quad \quad \quad }\\ {{N_2} = 2{\lambda _3}{h_0}\left\{ {2\left({\lambda _1^2 - {1 \over {\lambda _1^2\lambda _2^2}}} \right)\left({{{\partial W} \over {\partial {I_1}}} + \lambda _2^2{{\partial W} \over {\partial {I_2}}}} \right)} \right.}\\ {\left. { - {1 \over 2}\left[ {{\varepsilon _0}{\varepsilon _4}{{\left({{V \over {{h_0}{\lambda _3}}}} \right)}^2}} \right]} \right\}{.}\quad \quad \quad \quad \quad } \end{array}} \right.$$

(11)

The Mooney-Rivlin function is W=C₁(I₁−3)+C₂(I₂−3), in which I₁ and I₂ are strain invariants and C₁ and C₂ are Mooney-Rivlin constants determined from uniaxial extension tests on rectangular samples supporting a uniformly distributed axial load. For simplification, it was assumed that the inertia effect in the meridian direction is negligible. To obtain the numerical solution for the dynamic response of a tubular DE transducer, a finite difference scheme (forward difference method) was employed.

The dynamic actuation and sensing response of tubular DE structure were investigated. Comparison between numerical and experimental results for the dynamic response of the DE transducer showed an overall error of 3%. This indicates that the dynamic model and solution approach based on the finite difference method are good for predicting the dynamic response of tubular DE structure.

2.1.4 Circular DE structure

Zhu et al. (2010b) studied the dynamical behavior of an inflated circular membrane. Fig. 7 illustrates the cross section of a DE membrane. In the stress-free state, the membrane is of circular shape with thickness H and radius A. The membrane is pre-stretched and attached to a rigid circular ring of radius a; particle R moves to a location of distance r from the center. The membrane is then inflated by time-varying pressure p(t) and voltage Ф(t). At time t, the membrane is assumed to deform into an axisymmetric shape, and particle R moves to a location with coordinates r and z. The two fields, r(R, t) and z(R, t), specify the time-dependent deformation of the membrane. The longitudinal stretch λ₁ and the latitudinal stretch λ₂ are defined as

$${\lambda _1} = \sqrt {{{\left({{{\partial r} \over {\partial R}}} \right)}^2} + {{\left({{{\partial z} \over {\partial R}}} \right)}^2}}, \;\;{\lambda _2} = {r \over R}{.}$$

(12)

Fig. 7

Cross section of a DE membrane in three states: (a) stress-free state; (b) pre-stretched state; (c) current state. Reprinted from (Zhu et al., 2010b), Copyright 2010, with permission from Elsevier

By using the principle of virtual work, the following equations can be obtained:

$$\left\{ {\begin{array}{*{20}c} { - {\partial \over {R\partial R}}\left({R{{\partial W({\lambda _1},{\lambda _2},\tilde D)} \over {\partial {\lambda _1}}}\sin \theta } \right) + {\lambda _1}{\lambda _2}{p \over H}\cos \theta }\\ { = \rho {{{\partial ^2}z} \over {\partial {t^2}}},\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{\partial \over {R\partial R}}\left({R{{\partial W({\lambda _1},{\lambda _2},\tilde D)} \over {\partial {\lambda _1}}}\cos \theta } \right) - {{\partial W({\lambda _1},{\lambda _2},\tilde D)} \over {R\partial {\lambda _2}}}}\\ { + {\lambda _1}{\lambda _2}{p \over H}\sin \theta = \rho {{{\partial ^2}r} \over {\partial {t^2}}},\quad \quad \quad \quad } \end{array}} \right.$$

(13)

where $W({\lambda _1},{\lambda _2},\tilde D)$ is the free energy density and it is the sum of the elastic energy with neo-Hookean model and the dielectric energy.

Instability of the equilibrium state, natural frequencies and vibration modes were investigated. When the pressure or voltage reaches a critical peak value, the fundamental natural frequency vanishes, and it takes an infinite time for the system to return to the equilibrium state, i.e., the equilibrium state becomes unstable. It was found that the natural frequencies of DE structure are tunable by varying the pre-stretch, pressure, or voltage. When it was driven by a sinusoidal voltage, the membrane resonated at multiple values of excitation frequency with different vibration modes. Super-harmonic, harmonic, and sub-harmonic responses were found. The multiple resonant peaks and out-of-plane vibration modes were consistent with experimental data (Fox and Goulbourne, 2008; 2009).

Chakravarty (2014) investigated the resonant frequencies of a pre-stretched circular DE membrane in air and in a vacuum. The Mooney-Rivlin hyper-elastic material model was adopted. The equation of motion of the out-of-plane deformation at arbitrary location on the membrane can be expressed in terms of a cylindrical coordinate system. Based on the required boundary and continuity conditions, the resonant frequency of vibration can be obtained. A finite element model was also developed. When the membrane vibrates in air, the surrounding air exerts force and opposes the movement. The added mass is the mass of the surrounding air that is required to accelerate the membrane, depending on the geometry of the membrane and the density of air. The resonant frequencies in air are less than those in a vacuum due to the added mass of air. The damping of air is low. It has a negligible effect on the frequency but reduces the amplitude of vibration.

The configuration of DE structure may be different from those mentioned in previous sections, and can be very complex, such as helical, stack, and folded (Carpi et al., 2005; 2007; Giousouf and Kovacs, 2013). The theoretical study of the dynamical behavior of DE structure with complex configuration is very difficult, so numerical method should be adopted. Park et al. (2012) developed a 3D nonlinear finite element formulation for DE structure. The mechanical and electrical governing equations are solved monolithically using an implicit time integrator, where the governing finite element equations are given for both static and dynamic responses. The formulation presented there forms the basis for computational tool that is needed to elucidate the electromechanical behavior and properties of DE structure for engineering applications. Furthermore, Park et al. (2013) presented a finite element formulation for DE structure that significantly alleviates the issue of volumetric locking due to its incompressible nature. The modified Q1P0 formulation of Simo et al. (1985) is proposed for electromechanical coupling.

Since there are some assumptions in the dynamical modeling of DE structure, more accurate models are needed to be proposed for considering effects such as viscoelasticity, damping, inhomogeneity, and current leakage. Nonlinear dynamical behavior including dynamical stability and dynamical failure should also be investigated.

2.2 Experimental studies

Several experiment studies on the in-plane and out-plane dynamical behaviors of DE structure have been conducted. The experimental system generally consists of a digital function generator for generating a signal with a particular waveform, a high-voltage supply for amplifying the signal created in LabVIEW, and a laser sensor for measuring the displacement of the membrane.

The in-plane dynamical deformation of a DE membrane under a pure-shear state at low frequency (1–15 Hz) was studied by Liu et al. (2014). A VHB4910 film was pre-stretched to improve its performance and then the specimen was mounted on a test chamber and the electrodes were applied. Fig. 8 shows the VHB film clamped to an adjustable stretching frame. They studied how the dynamical response was affected by peak voltage, frequency, pre-stretching, and signal waveform. It was found that the deformed equilibrium position of the membrane drifted severely during vibration, which may be due to the high viscoelasticity of the membrane and may lead to the issues in designing precise instruments. They also studied how these effects affected viscoelastic drifting. It is possible to achieve large displacement and small drift by balancing peak voltage and pre-stretching.

Fig. 8

(a) Sample preparation; (b) Experimental set-up used in dynamic electrical loading test. Reprinted from (Liu et al., 2014), Copyright 2014, with permission from IOP Publishing Ltd.

Iskandarani and Karimi (2013) modeled a DE sheet as a spring-mass-damper system. The developed set-up shown in Fig. 9 was used for finding material properties (Young’s modulus and damping constant) and for dynamic analysis. A DE sheet developed by Danfoss PolyPower A/S was used. An obvious inconsistency between the model and the system output was observed. This is due to the viscoelastic property inherent in any polymer. The design of the mechanical system is key, as the DE sheet has a low impact on the system dynamics. In this work, the error between experimental data and model simulation can be minimized by choosing the range of frequency within 0–20 Hz.

Fig. 9

Dynamic analysis experimental set-up of DEA. Reprinted from (Iskandarani and Karimi, 2013), Copyright 2012, with permission from Springer Science+Business Media

LVDT: linear variable differential transformer

Several tubular DE transducer samples made of VHB 4905 and silicone and an experimental set-up shown in Fig. 10 were developed by Son and Goulbourne (2010) to investigate the dynamical response by measuring capacitance and radial deformation. It was observed that silicone sensor had a larger dynamical sensing range than VHB sensor and the silicone actuators also showed a good actuation response. Within a limited frequency range, the VHB sensor showed poor dynamical response after 2.0 Hz and 13% radial strain under dynamical pressure, while the tubular silicone sensor showed good sensing response at higher frequencies up to 5.0 Hz and 8% radial strain. Tubular silicone actuator was assembled and dynamically actuated with a voltage signal (4.5 kV) at 0–30 Hz. It was concluded that tubular silicone transducer had a better dynamical sensing and actuation response in the frequency range in this experiment.

Fig. 10

Experimental set-up for dynamical response of tubular DE sensor and actuator. Reprinted from (Son and Goulbourne, 2010), Copyright 2010, with permission from Elsevier

The experiment made by York et al. (2010) focused on the hysteretic and rate-dependent material behavior. The experimental set-up and a sketch of the experimental set-up are shown in Fig. 11. Circular DEA designed for the out-of-plane mode was investigated under different combined electrical and mechanical loadings. The DEA used in the experiment was made of a silicone-based elastomer with a carbon-based electrode. Mechanical loading was accomplished using a linear electromagnetic actuator with an Aerotech Ensemble CP controller. Electrical loading was provided via a voltage amplifier. Force measurement was made by a load cell connected to a full bridge signal conditioning module. This experiment provided insight into the electrical dynamics and viscoelastic relaxation inherent in DEA. When the actuator was fixed at constant pre-deflection and cyclic voltage, hysteresis resulting from time-dependent charge and discharge behavior inherent to any resistor-capacitor circuit was observed at higher electrical loading rate. This hysteresis increased with increasing frequency and with increasing pre-deflection at sufficiently high rate. When the actuator was mechanically loaded and with constant voltage, hysteresis was observed even at a very slow loading rate. The hysteresis increased with an increase in loading rate. Relaxation experiment showed a large amount of viscous relaxation.

Fig. 11

DE experimental set-up (a) and a sketch of the experimental set-up (b). Reprinted from (York et al., 2010), Copyright 2010, with permission from IOP Publishing Ltd.

Fox and Goulbourne (2008) reported an experimental investigation into the out-of-plane dynamical deformations of an inflated and clamped circular DE membrane under a sinusoidal voltage signal and a harmonically varying mechanical input. A 3D high-speed optical device including a high-speed camera and grating projection was used to measure the membrane’s large deformation as it inflated. The DE membrane was made of VHB film. A completed specimen before and after inflation and experimental set-up is shown in Figs. 12 and 13, respectively. The response of the membrane departed from the classical dynamic response of continuum membrane structure. For an inflation volume of 60 ml, a resonance-type frequency was observed, whereby the deformed membrane appeared to be a mode shape that is reminiscent of the fourth mode shape of the classical drumhead problem. Higher voltage had a much more pronounced effect on the membrane’s response than smaller one.

Fig. 12

A completed specimen before and after inflation. Reprinted from (Fox and Goulbourne, 2008), Copyright 2008, with permission from Elsevier

Fig. 13

Experimental set-ups for dynamical electrical (a) and mechanical (b) loadings. Reprinted from (Fox and Goulbourne, 2008), Copyright 2008, with permission from Elsevier

Fox and Goulbourne (2009) further found that electrical excitation of resonance phenomena can be leveraged as a frequency-based displacement amplification scheme for actuation application. The electric field can be used to transform a smooth monolithic structure into specific symmetric surface pattern, which has significant implication for surface control problem. Chamber volume is an important system parameter when considering dynamic DE actuation, making the natural frequency a function not just of the internal pressure but also of the trapped volume.

The low-frequency response of rectangular DEA was studied by Sommer-Larsen et al. (2001) and Bauer and Paajanen (2006). Pelrine et al. (2000) investigated circular and linear actuators in a wide range of frequency, from 1 Hz up to 20 kHz. Heydt et al. (2006) conducted experiment on clamped partially inflated membrane to study the sound radiation property of DEA. To better understand the dynamical behavior of DE structure, more experimental studies on DE structure with complex configuration are needed.

3 Applications of DE structures in vibration control

A large number of different types of DEAs have been developed. The most notable ones include planar devices, rolls, tubes, stacks, diaphragms, extenders, and bimorph and unimorph benders (Pelrine et al., 1998; Carpi and Rossi, 2004; Pei et al., 2004; Schlaak et al., 2005; Carpi et al., 2007). According to the principle of operation, they can be classified into two different categories: expanding actuator working in planar direction and contractile actuator working in the thickness direction. In the following, two major types of DEAs used for active vibration control, i.e., stack-type contractile actuator and tubular-type expanding actuator, are described in detail.

3.1 Stack-type DEA

A stack-type DEA (SDEA) consists of multi-layer planar DEAs connected in series mechanically and in parallel electrically. The electrically activated thickness compression of each layer generates contraction of the whole device. Using this technology, the deflection in the vertical direction was increased only by applying low electrical voltage. Fig. 14 presents an example of the actuator and the corresponding parameters proposed by Karsten and Schlaak (2012). The vibration attenuation has been studied by several researchers (Herold et al., 2012; Karsten and Schlaak, 2012) using SDEA.

Fig. 14

(a) Investigated SDEA; (b) Actuator parameters. Reprinted from (Karsten and Schlaak, 2012), Copyright 2012, with permission from SPIE Publications

3.1.1 Adaptive absorber

The major drawback of traditional passive absorber is that the vibration attenuation occurs at only one frequency. If the resonant frequency of the device changes due to changes in temperature or aging, the passive absorber becomes ineffective and may potentially increase the vibration. Therefore, currently different kinds of adaptive absorbers with adjustable resonant frequency are investigated. It is known that the stiffness of the DE structure can be tuned by applying an electrical voltage (Pelrine and Kornbluh, 2008; Dubois et al., 2008). Thus, the SDEA can be used as an adaptive absorber. To determine the changeable dynamic stiffness of SDEA, the measurement set-up was built as shown in Fig. 15a, which is similar to the real application of an absorber. The SDEA was laid between two round stiff plates and fixed on the mini shaker. A mass of 100 g is mounted on the top plate. The transfer function for different applied voltages can be obtained using this set-up. Fig. 15b shows that increasing the applied voltage caused a reduction in the resonant frequency of the structure from 129 Hz in the initial state to 108 Hz, corresponding to a 16% shift. Thus, SDEA is a promising adaptive absorber applicable to the system with varying resonant frequency caused by, for example, the temperature variation.

Fig. 15

(a) Schematic measurement set-up for the determination of SDEA resonant frequency and mechanical stiffness (DESA in the figure is the same meaning as SDEA); (b) Transfer function for different offset voltages. Reprinted from (Karsten and Schlaak, 2012), Copyright 2012, with permission from SPIE Publications

3.1.2 Active suspension

Another possible application of SDEAs is the protection from vibration of lightweight sensitive equipment such as optic components. Karsten et al. (2011) built a simplified experimental set-up shown in Fig. 16a to analyze the feasibility of active suspension. In this set-up the sensitive electronic component is isolated from motor vibration through an active SDEA. Thereby, the sensor indicates disturbance on the electronic component and leads the signal to the controller, which activates the active SDEA. Thereon, the active SDEA produces a force against the vibration and eliminates the disturbance. An active proportional controller (p-controller) was designed. This type of controller is the simplest one. The recorded velocity signal was amplified and fed back to the actuator. The p-controller measuring the velocity is called a skyhook damper, which virtually increases the damping of the system and reduces the system response. The result of using the p-controller is shown in Fig. 16b. To design the feedback controller, the linear model of the actuator is determined based on experimental results using the least mean square estimation.

Fig. 16

(a) Experimental set-up for testing SDEA of control algorithms; (b) Results of using a p-controller. Reprinted from (Karsten et al., 2011), Copyright 2011, with permission from SPIE Publications

Stack DEA with compliant electrodes may yield an inhomogeneous strain distribution when connected to rigid boundary surfaces, leading to an overall loss of performance. To avoid such inhomogeneous strain distribution, a new stack DEA design with rigid but perforated electrodes was proposed by Herold et al. (2012). Since the electrodes are made of a solid metal, the electrical properties can be improved significantly compared to actuator with compliant electrodes, which typically show a relatively low conductivity. Thus, the resistive loss due to high current can be reduced, especially for dynamic applications at higher frequency. To show the potential of the new SDEA to efficiently reduce vibration, a truss structure is utilized, as shown in Fig. 17. The control strategy designed is the simplest p-control. Numerical results show that when the active vibration control is activated, a significant reduction in a certain frequency region is achieved.

Fig. 17

(a) Truss structure; (b) Actuator on truss structure. Reprinted from (Herold et al., 2012), Copyright 2012, with permission from SPIE Publications

Another development of the SDEA is a stack DEA mat, which contains several SDEAs. A photograph of the active mat is shown in Fig. 18. The entire mat is filled in with silicone used for manufacturing SDEAs. The developed active mat offers a low-cost approach for cancelation of active vibration. The proposed active mat can isolate sensitive devices with weights of up to 500 g (Karsten et al., 2013).

Fig. 18

Photograph of an active mat. Reprinted from (Karsten et al., 2013), Copyright 2013, with permission from SPIE Publications

3.2 Tubular-type DEA

To increase the actuation force for vibration control, a tubular-type DEA (TDEA) was manufactured by Danfoss PolyPower A/S (Sarban et al., 2009; 2010; Sarban and Jones, 2010; 2012; Jones and Sarban, 2012; 2013), as shown in Fig. 19. Fig. 19a shows a single sheet of PolyPower DE with a corrugated surface and an electrode on one side. For actuator fabrication a laminate of two sheets placed back to back was used. By rolling the DE laminate (Fig. 19b), the TDEA was built as shown in Fig. 19c. The corrugated design of the metallic electrodes reduces Ohmic loss in the electrodes and ensures the unidirectional expansion of the DE material, which results in an increase in force and stroke of the unidirectional actuator.

Fig. 19

PolyPower TDEA: (a) single sheet of DEA with corrugated surface and electrode; (b) rolling the DEA laminate to build a TDEA; (c) assembled TDEA. Re-printed from (Sarban and Jones, 2010), Copyright 2010, with permission from the authors

The force transmissibility of this type of actuator for both passive and active states of applied voltage is shown in Fig. 20 (Berardi, 2010). The transmissibility is defined as the complex ratio of the force measured at one end to the force at the other end of the actuator. The results show that the first resonance occurred at 72 Hz, which means the tested actuator should be used only for low-frequency control.

Fig. 20

Transmissibility of the TDEA for different applied voltages: (a) magnitude; (b) phase. Reprinted from (Berardi, 2010), Copyright 2010, with permission from Taylor & Francis Group

Several studies have been conducted for active vibration control using a TDEA.

3.2.1 Adaptive feedforward control

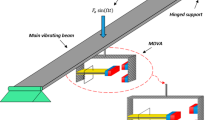
Sarban et al. (2009) built an experimental set-up for active vibration isolation using a TDEA, as shown in Fig. 21. The TDEA was mounted between a mass and a shaker with voltage input. The control objective was to reduce the movement of the mass. An adaptive feed-forward control strategy was used to achieve this. In this adaptive control scheme a reference signal is filtered by the feed-forward controller, which is a finite impulse response filter. The filter output is then fed back to the actuator to counteract the primary disturbance. The proposed controller provided large attenuation of the disturbance signal. Relatively good attenuation has been achieved under the condition of the reference and disturbance signals being in perfect coherence. However, in many applications, the disturbance and reference signals are not very coherent, which might reduce the performance of the anticipated active vibration control.

Fig. 21

Block diagram of active vibration isolation set-up. Reprinted from (Sarban et al., 2009), Copyright 2009, with permission from the authors

ADC/DAC: analog digital convertor/digital to analog con-vertor; LMS: least mean squares

Because of the nature of vibratory disturbance, there is a requirement for the actuator to be able to counteract both positive and negative structural movements. To allow the TDEA to counteract this movement, a bias electric field is applied to the actuator. This creates a biased initial position for the actuator, which allows the actuator to move in both positive and negative directions.

3.2.2 Active feedback control

An effort to control active feedback vibration using TDEAs has been made by Herold et al. (2011). An experimental test set-up was built to analyze the effectiveness of the active feedback control algorithms, as shown in Fig. 22a. The TDEA is clamped at one end and attached to a mass at the other end. The mass is suspended with two parallel flat springs, leading to the uniaxial guiding of the mass. The flat springs are made very flexible compared with the actuator’s stiffness in order not to influence the dynamic characteristics. The basic active feedback control strategy used is the p-control for increasing the damping of the structure. Therefore, the acceleration of the mass is integrated and fed back to the amplifier with a variable gain factor. The resonant peak could be significantly attenuated. However, the gain factor needs to be chosen carefully to achieve an optimal damping behavior. A more advanced control strategy is to realize active displacement feedback to virtually change the stiffness of the system and thus shift the eigen-frequency of the system (Kaal and Herold, 2011). Such system can be used as tuned absorber to attenuate harmonic disturbance with slowly varying excitation frequency.

Fig. 22

Experimental set-up for a single DOF structure (a) and a two DOF structure (b). Reprinted from (Herold et al., 2011), Copyright 2011, with permission from SPIE Publications

Herold et al. (2011) studied how to actively control a more complicated structure with two resonant frequencies. The experimental set-up is shown in Fig. 22b. Two parallel flexible beams are clamped at one end and loaded with two mass blocks. The parallel configuration of the beams guarantees a single degree-of-freedom (DOF) system for each mass. The mass m₁ is subject to broadband excitation and harmonic excitation. The proposed control strategy showed great effectiveness in reducing the vibration of the system.

Due to the underlying physical effect, DEA is generally nonlinear. Consequently, it automatically produces forces at high-order frequencies. This may cause harmful effect for the vibration control of structure with high modal density. A linearization method was proposed to minimize this parasitic effect (Kaal and Herold, 2011).

4 Conclusions and future development

In the present paper, existing theoretical and experiment studies on the dynamical behaviors of typical DE structures and the applications of DE structures for vibration control have been reviewed. It is worth mentioning that all existing theoretical work on the dynamics of DE structures was confined to using low-dimensional models. For spherical structure, only oscillation in the radial direction has been considered while for circular DE structure only the longitudinal and latitudinal oscillations have been considered. For rectangular and tubular structures, oscillation has been confined to the plane while the out-plane motion has been neglected. However, bifurcation instability may occur when a DE structure is subject to a voltage and other vibration modes may be triggered. Furthermore, asymmetry of practical DE structure induced by manufacture error may induce complex vibration, including multiple vibration modes. To accurately investigate the dynamical behavior of DE structure, the high-order modal expansion must be taken into account. High-order modal expansion can be substituted into the mathematical description of DE structure established by the virtual principle or Newton’s Law, and then a set of ordinary differential equations can be obtained.

Viscoelasticity and large deformation make the dynamical behavior of the DE structure more complicated. Moreover, in the existing work mechanical excitation and imposed voltage have been described by deterministic functions. In practice, however, DE structure may be subject to random disturbance. Thus, the random responses of DE structure should be further investigated. How does the mechanical excitation perturbed by random process influence the dynamical behavior of DE structure, and what about the imposed voltage with random component are needed to be studied. Considering all factors mentioned above, the dynamical behavior of DE structure comes down to the solution of a set of high-dimensional, strongly nonlinear, stochastic differential equations:

$$\ddot \lambda + g(\lambda, \dot \lambda, \xi, P,\Phi) = 0,$$

(14a)

$$\dot \xi = f(\lambda, \xi),$$

(14b)

where λ is a vector of the stretch ratios, P(t) and Φ(t) are random processes, and is related to the viscoelasticity. This issue focuses on the stochastic dynamic analysis of DE structure with given mechanical excitation and voltage and could be investigated through the theory of nonlinear stochastic dynamics (Zhu, 2006).

In the literature, DE structure has been adopted as actuator to implement vibration control. The control object, such as minimization of the responses of the main structure, can be obtained by elaborately designing the control term, i.e., the input voltage on the parallel electrodes. This subject, however, has not been covered by the existing literature. The controlled equations consist of the dynamical equations of the main structure with respect to the system state Y and and that of the DEA with respect to the stretch ratio vector λ. The designed quantity is the voltage imposed on the parallel electrodes. From an optimal control viewpoint, the optimization problem comes down to the search for an optimal function to optimize the given performance index:

$$J = E\left\{ {\int\nolimits_0^{{t_f}} {L(Y,\dot Y,\Phi, s){\rm{d}}s + {g_{\rm{f}}}\left[ {Y({t_{\rm{f}}}),\dot Y({t_{\rm{f}}})} \right]} } \right\},$$

(15)

where L is the cost function, g_f is the terminal cost, and t_f is the terminal time. This subject should be studied using the stochastic optimal control theory (Fleming and Rishel, 1975; Yong and Zhou, 1999; Zhu, 2006).