1 Introduction

The cable dome system originates from Fuller’s patent of 1962 (Fuller, 1975), in which he proposed a triangular cable net with compressive struts hinging on it. The first cable dome was designed by Geiger (Geiger et al., 1986) for the Seoul Olympics gymnastics and fencing halls in 1986, and cable domes have subsequently been widely used in many large-span structures. Currently, the largest is the Georgia dome designed for the Atlanta Olympics (Levy, 1994).

A traditional cable dome is composed of ridge cables, oblique cables, ring cables, and struts. In contrast to masts (Juozapaitis et al., 2008; Belevičius et al., 2013), an initial pre-stress in the cables and struts gives the cable dome rigidity, making it a structure with the ability to resist external loads (Wang et al., 2010). The roofing materials of cable domes can be divided into two categories: a flexible roof with tensioned membranes and a rigid roof with glass or thin steel plates. Up to now, most existing cable domes have been covered with tensioned membranes.

Tensioned membranes have the advantages of being lightweight and semi-transparent, and having strong span ability. However, the high cost, the large deformation, the low bearing capacity, the poor thermal insulation performance, and their poor anti-pollution performance make them unable to meet the demands of architecture today.

Meanwhile, traditional rigid roofing materials, such as glass panels and color steel plates, can meet those demands, and encourage the adaptation of cable domes. Cai et al. (2013) pointed out that a rigid roof lacks good in-plane stiffness. Therefore, substructures are needed to improve its span.

An improved scheme (Luo and Guo, 2012) was proposed for putting a single-layer reticulated shell on the top of struts, and this was successfully applied in Wuxi New District Science & Technology Communication Center (Guo et al., 2010a; 2010b). Vizotto (2010) proposed a computational model of free-form shell generation in the design of roof structures that relies on the optimized behavior of the membrane theory of thin shells; this offers a low cost, fast, and relatively easy design solution. Ario et al. (2013) designed a new emergency bridge called a MobilebridgeTM and obtained a shape-optimization structure for this new type of deployable bridge. Luo et al. (2012) put forward a new kind of structure with an orthogonal single-layer cable net added on the ridge cables to support a rigid roof, which was used in China for the Taiyuan Coal Trading Center.

Traditional on-site construction of a cable dome requires five steps: (1) assembly of a temporary tower in the center of the field and placing the inner tensile ring on it; (2) installation of connectors on the ridge cables, and then connecting the ridge cables with the inner tensile ring and the outer compressive ring; (3) lifting struts, radial cables, and ring cables to the designed location, and connecting them to the ridge cables; (4) establishing the pre-tension and forming the structure by tensioning the cables or supporting the struts; (5) installation of the membrane roof. However, this method is expensive and extends the construction period because of the installation of the temporary tower. In this case, lifting construction methods and developable construction methods could be applied on cable dome structures. Li et al. (2003) used an electro-hydraulic proportional control system to raise a 6075-t roof frame to the height of 26.5 m.

Based on the idea of supporting and lifting, Guo et al. (2010a; 2010b) proposed a new method called tower lifting and accumulative installation for cable domes. This method also contains five steps: (1) assembly of a temporary lifting tower in the center of the field; (2) installation of all the components in the center of the field and connection of the ridge cables with the outer compressive ring; (3) connection of the top part of the tower with the inner tensile ring by lifting cables and lifting the whole structure to the designed location; (4) establishment of the pre-tensions and forms of the structure by tensioning the cables or supporting the struts; (5) installation of the roof system. This method needs less time for working high above the ground, and makes construction less dangerous and more efficient.

Before tensioning, the cable-strut system is a mechanism; after tensioning it is a form with structural rigidity. During the construction process, the cable-strut system changes from a non-stress state in the beginning to a low-stress overhanging state and, finally, reaches a high-stress formed state. Thus, form-finding, which decides the initial pre-tension and shape of a cable dome, is necessary.

There has been extensive research on the form-finding of cable nets and tensegrity structures. Schek (1974) proposed the force-density method for the form-finding of tensile structures. Vassart and Motro (1999) expanded this method in symbolic forms to a search for new configurations. Hangai and Wu (1999) employed the analytical method of hybrid structures consisting cables and rigid roof. A dynamic relaxation method was proposed by Motro et al. (1987), and has been reliably applied to tensile structures (Barnes, 1999). Ohsaki and Kanno (2003) made the form-finding analysis of cable domes under nonlinear mathematical calculation into programming problems. Masic et al. (2005) and Zhang and Ohsaki (2006) put forward new methods using force density formulations.

Dong and Luo (2002) and Shen and Zhang (2002) proposed the nonlinear force method for the space truss with mobile mechanisms to solve the coupling problem of mechanism displacement with elastic deformation, and then put forward the nonlinear force method (NFM) (Luo and Shen, 2004). Luo (2010) from Southeast University put forward a new form-finding method based on the nonlinear dynamic finite element (NDFEM).

Among these methods, the dynamic relaxation method converts the static problem into a dynamic problem using a virtual mass and a viscous damping force. The structure is dispersed into virtual particles with virtual masses that are located at the spatial node position. Under an unbalanced force, these dispersed virtual particles move along the unbalanced force direction macroscopically to reduce the overall unbalanced force in the structure. During the iterative procedure, motion equations of single particles are built to find the result. However, the NDFEM needs to build nonlinear finite element motion equations for the whole structure to simulate the overall vibration. The NDFEM is stable in analysis, has good structural integrity when the total kinetic energy peaks, and is more efficient in many ways.

This paper addresses several key issues of rigid roof cable domes. A new structure called a tensile beam-cable dome (TBCD) is presented firstly, followed by the configuration features and mechanical characteristics of this structure. An efficient construction method, the integral tow-lifting method, is then presented to achieve installation and tensioning construction for this structure. A detailed introduction of NDFEM is introduced and tested in a six-meter scale model. Meanwhile, mechanism hinges on tensile beams are needed for the integral tow-lifting construction, making the whole structure a mechanism system, and the optimal distribution modes of those mechanism hinges are summarized in this paper.

2 Tensile beam-cable dome (TBCD)

2.1 Configurations of TBCD

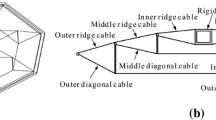
If the ridge cables of the traditional cable dome are replaced by hinged beams that can bear both tensile and flexural effects, then a new structure called a tensile beam-cable dome is created. TBCD consists of oblique cables, struts, ring cables, and tensile ridge beams. In addition, all the joints between tensile beams and other members are hinged, which is helpful in increasing the proportion of axial tensile stress during the construction process, and can improve the stability of whole structure. The details are shown in Fig. 1.

Fig. 1
figure 1

Components of tensile beam-cable dome

(a) Perspective view; (b) Section view. 1: outer tensile beam; 2: middle tensile beam; 3: inner tensile beam; 4: outer oblique cable; 5: outer strut; 6: inner oblique cable; 7: middle oblique cable; 8: middle strut; 9: inner tensile ring; 10: outer ring cable; 11: inner ring cable

Full size image

2.2 Distribution of TBCD

The hinges on tensile beams can be divided into two kinds: structure hinges and mechanism hinges. Structure hinges are set at the end of tensile beams and exist in normal use, while mechanism hinges are set at the middle of tensile beams and exist only during construction. Settings of hinges are flexible. According to the location of structure hinges and mechanism hinges, TBCD can be divided into four categories: Non-hinge TBCD (NTBCD), Single-hinge TBCD (STBCD), Double-hinge TBCD (DTBCD), and Three-hinge TBCD (TTBCD). The details are shown in Fig. 2 and Table 1.

Fig. 2
figure 2

Section view of TBCD

(a) Non-hinge TBCD; (b) Single-hinge TBCD; (c) Doublehinge TBCD; (d) Three-hinge TBCD

Full size image
Table 1 Classification of TBCD
Full size table

TTBCD has enough mechanism hinges to avoid large local bending stresses, whose mechanical characteristics are similar to traditional cable dome. However, under a rigid roof, large tension forces are needed to reduce the large local deformation that occurs at the location of the mechanism hinges. An ideal TBCD should have both large stiffness overall and small deformations locally. The locations of the tensile beam hinges set the mechanical characteristics of TBCD to some extent, and thus, the design and static tests (Xu et al., 2014) of hinge joints are important.

2.3 Advantages of TBCD

Traditional cable domes are made of cables and struts, their stiffness is formed by the building of pre-stress (Zhang et al., 2007). The level of pre-stress will not only affect the geometric configuration, but also determine the serviceability and load bearing capacity of traditional cable domes, which leads to a poor local stability (Kmet and Mojdis, 2013; 2015) during construction.

In contrast, due to the adding of tensile beams, TBCDs have enough bending stiffness to resist large local deformation. Thus, cable slack during the construction process consists of the initial state without stress, a low stress relaxation state during erection, and a high tensile stress state after the dome shape is formed. Furthermore, tensile beams can bear both tensile effects and flexural effects, which makes it easy for convergence and convenient to lay rigid roofing materials on. Thus, the TBCD has the advantages of both traditional cable domes and suspen-domes (Gao and Weng, 2004).

3 Integral tow-lifting construction technology for TBCD

The integral tow-lifting construction method includes assembly at a low altitude, tow-lifting at a moderate altitude, and tensioning to form at a high altitude. The key four steps are: 1) installing the outer compressive ring at the designed position, and then assembling the inner tensile ring, the hinged tensile beams, and the tow-lifting tool cables near the ground; 2) assembling oblique cables, ring cables, and struts at a low altitude followed by subsequent lifting and towing; 3) lifting the inner tensile ring and towing the outer tensile beams alternately by tool cables (towing cables and lifting cables) until the outer tensile beams are connected to the outer compressive ring; 4) finally, tensioning the outer oblique cables simultaneously to form the whole structure. The specific construction steps are shown in Fig. 3.

Fig. 3
figure 3

Integral tow-lifting construction process for TBCD

(a) Install inner tensile ring, tensile beams, and tool cables; (b) Install cables and struts; (c) Tow and lift alternately; (d) Connect tensile beams with the compressive ring; (e) Shorten the tensioning cables; (f) Tension the outer oblique cables and form the structure. 1: inner tensile ring; 2: tensile beam; 3: outer compressive ring; 4: lifting tool cable; 5: towing tool cable; 6: oblique cable; 7: ring cable; 8: compressive strut

Full size image

Integral tow-lifting construction technology uses the outer compressive rings as tow-lifting brackets. Furthermore, the small lifting force, the few working aloft, and the high efficiency of tensioning make this method convenient in use. However, it must emphasis that the tensile beam grid must maintain a “ω” shape during the whole process. That is vital for success.

In addition, in order to accomplish the assembly (tow-lifting and tensioning) processes on the construction site, we introduced tow-lifting and tensioning equipment, which is illustrated in Fig. 4.

Fig. 4
figure 4

The tow-lifting and tensioning equipment

Full size image

A set of tow-lifting and tensioning equipment is mainly made up of two hydraulic jacks, two steel strands, one tension frock, and two auxiliary connecting plates. During the tow-lifting and tensioning process, a set of equipment is set at the outer side of a cable. By tensioning the steel strands, the tensioning force built by hydraulic jacks is transferred to the outer compressive ring, and the cable head of the oblique cable or tool cable moves slowly towards the support. Finally, the cable head is connected with the connecting plate of the outer compressive ring, and the equipment is removed.

4 Nonlinear dynamic finite element method (NDFEM) for form-finding analysis

Due to the large displacement, mechanism deformation, and cable slackness during construction, a large difference in configuration occurs between the construction stages and the formed state of TBCD. The construction process is dynamic, but the whole system is in a static equilibrium state at a certain moment. Therefore, the whole construction process can be divided into several static cases.

4.1 Analytic logic and specific steps

The NDFEM method is used to determine the static equilibrium state of the tensile-beam and cable-strut systems during construction. By introducing a virtual inertia force and a viscous damping force, the equations of motion are established, which transform static problems into dynamic problems that are easy to solve. Furthermore, by iterative updating of the configuration of the tensile-beam and cable-strut systems, the dynamic equilibrium state gradually converges to the static equilibrium state. Thus, a tensile-beam and cable-strut system is in an unbalanced static state before the analysis, in a dynamic balanced state during the analysis, and reaches a static balanced state after convergence. The analysis includes the following steps: establishing an initial finite-element model; nonlinear dynamic finite element analysis and updating of the model when the total kinetic energy reaches its peak; dynamic analysis again until the configuration converges; and nonlinear static analysis of the converged model to verify the static equilibrium state. For TBCD, it is convenient for analysis that hinged tensile beams may be modeled by spar elements. The detailed process is shown in Fig. 5.

Fig. 5
figure 5

NDFEM form-finding process

Full size image

4.2 Key measures

There are two iteration grades in NDFEM form-finding analysis, the first grade is the dynamic equilibrium iteration, and the second is the model updating iteration.

The dynamic balance equation (Eq. (1)) adopts the Rayleigh damp matrix (Eq. (4)), in which the self-vibratory frequency and damping ratio can be set virtually. When the movement direction of the tensile-beam cable-strut system is known, the motion equation of Eq. (5) should be established to accelerate the efficiency of analysis, and in which the damping force is not considered.

$$M\ddot U + C\dot U + KU = F(t),$$
(1)
$$C = \alpha M + \beta K,$$
(2)
$$\alpha = {{2{\omega _i}{\omega _j}({\xi _i}{\omega _j} - {\xi _j}{\omega _i})} \over {\omega _j^2 - \omega _i^2}},$$
(3)
$$\beta = {{2({\xi _j}{\omega _j} - {\xi _i}{\omega _i})} \over {\omega _j^2 - \omega _i^2}},$$
(4)
$$M\ddot U + KU = F(t),$$
(5)

where U, \(\dot{U}\), and \(\ddot{U}\) are the displacement vector, speed vector, and acceleration vector, respectively; C is the Rayleigh damping matrix; F(t) is the load duration vector; K is the stiffness matrix; M is the mass matrix; α and β are Rayleigh damping coefficients; ω i and ω j are the self-resonant circular frequencies at step i and step j; ξ i and ξ j are the damping ratios that correspond to ω i and ω j , respectively. If ξ i =ξ j =ξ, Eqs. (3) and (4) can be simplified to Eqs. (6) and (7):

$$\alpha = {{2{\omega _i}{\omega _j}\xi } \over {{\omega _j} + {\omega _i}}},$$
(6)
$$\beta = {{2\xi } \over {{\omega _j} + {\omega _i}}}.$$
(7)

The parameters in the dynamic equilibrium iteration include: the maximum number of time steps for single dynamic analysis Nts, the maximum number of dynamic iterations for one single time step Nei, the initial time step size ΔT(1), the time step size adjustment coefficient Cts (Cts≥1), the convergence displacement value of the dynamic equilibrium iteration Uei, the convergence displacement Uci, and the allowable maximum number of iteration Nci. Subscript ‘ts’ means time size, ‘ei’ means equilibrium iteration, and ‘ci’ means convergence of iteration.

During the process of dynamic analysis, the displacement, the velocity, and the total kinetic energy are tracked in Eq. (8). The iterative analysis strategy is listed in Table 2 and Fig. 6.

$${E_k} = {1 \over 2}\dot U_k^{\rm{T}}M{\dot U_k},$$
(8)

where E k denotes the total kinetic energy of the kth time step in dynamic analysis, and denotes the velocity vector of the kth time step.

Fig. 6
figure 6

Peak value of total kinetic energy and its time step

Full size image
Table 2 Iterative analysis strategy
Full size table

5 Model experiment

5.1 Experimental model

To test the applicability of NDFEM in TBCD, an experiment with a three-hinge TBCD model was carried out. The experimental model is shown in Fig. 7. It was 6 m in span, eight pieces in radius, and three pieces in hoop (details in Table 3 and Fig. 8). A numerical model was built in ANSYS to verify the experimental results, whose parameters were the same as those of the experimental model, and the initial pre-tension of cables was built by adding an equivalent temperature difference.

Fig. 7
figure 7

Experimental model of three-hinge TBCD

1(a) 3D graph of numerical model (unit: mm); (b) Experimental model

Full size image
Fig. 8
figure 8

Model details and component numbers (unit: mm)

1: outer tensile beam; 2: middle tensile beam; 3: inner tensile beam; 4: outer oblique cable; 5: outer strut; 6: inner oblique cable; 7: middle oblique cable; 8: middle strut; 9: inner tensile ring; 10: outer ring cable; 11: inner ring cable

Full size image
Table 3 Parameters of components
Full size table

5.2 Test contents and method of the experiment

In the experiment, the key construction process had three steps: (1) setting up the temporary bracket in the center of the field, and installing the outer compressive ring at the designed position; (2) assembling the inner tensile ring, tensile beams, and cable-strut components in the non-stress state; and (3) shortening the outer tensile beams step by step until the whole structure formed. The tensioning process is divided into six stages. In each stage, lengths of the outer tensile beams are shortened by 20 mm. The detailed sequence is shown in Fig. 9.

Fig. 9
figure 9

Tensioning process of experimental model (unit: mm)

(a) Stage 1; (b) Stage 2; (c) Stage 3; (d) Stage 4; (e) Stage 5; (f) Stage 6

Full size image

The NDFEM is used to simulate this construction process. Figs. 10–12 show the average vertical displacement of the struts, the average relative deflection of the tensile beams, and the average axial force of the cables and beams, respectively. Table 4 lists the average internal force of the structure components in Stage 6. During construction, the largest difference of vertical displacement between the experimental and theoretical values is 24.3 mm, and appears in Stage 6 at the top side of the outer struts. The largest relative deflection difference of the tensile beams is 14 mm, and appears in Stage 1 at the location of middle mechanism hinges. The largest force difference is 931 kN, and appears in Stage 6. In Fig. 12, the errors between experimental values and theoretical values are within 12%. Thus, the NDFEM does ensure the accuracy of the construction simulation.

Fig. 10
figure 10

Average vertical displacement

Full size image
Fig. 11
figure 11

Average relative deflection

Full size image
Fig. 12
figure 12

Average axial force

Full size image
Table 4 Average internal forces in tensile beams and cables in Stage 6
Full size table

6 Mechanical characteristics and hinge distribution modes of TBCD

6.1 Mechanical characteristics of tensile beams

Due to the pre-tension and vertical loads, ridge beams bear tensioning and bending simultaneously, which is different from flexible cables. Schematic diagrams of components under different kinds of vertical loads are set out in Figs. 13 and 14.

Fig. 13
figure 13

Deformation of flexible cables (a), two-hinge tensile beams (b), and three-hinge tensile beams (c) under concentrated load

Full size image
Fig. 14
figure 14

Deformation of flexible cables (a), two-hinge tensile beams (b), and three-hinge tensile beams (c) under uniform load ( q denotes the uniformly distributed load)

Full size image

Under mid-span concentrated load, the flexible cable and three-hinge tensile beam are both axial tensile components. However, the two-hinge tensile beam is a kind of tensile-bending component, which makes it better to resist large deformations. The relation between load and displacement is shown as:

$${\Delta _1} = {\Delta _3} = {{FL} \over {4H}},$$
(9)
$${\Delta _2} = {{F{L^3}} \over {4H{L^2} + 192EI}},$$
(10)

where Δ n (n=1, 2, …, 10) means the local deformation shown in Figs. 13 and 14; E, I, F, H, and L denote the elastic modulus, the area moments of inertia, the mid-span concentrated load, the axial force, and the length of span, respectively. Thus, EI denotes the stiffness of components.

Under uniform load, the flexible cable is only a tensile component, but the three-hinge tensile beam and the two-hinge tensile beam bear tensioning and bending simultaneously. The deformations of mid-span and quarter-span are shown as follows.

The mid-span deformation of the flexible cable is

$$\sum {M = {1 \over 8}} q{L^2} - H{\Delta _4} = 0,\;\;{\Delta _4} = {{q{L^2}} \over {8H}}.$$
(11)

The mid-span deformation of the two-hinge tensile beam is

$$\matrix{{\sum M = {1 \over 8}q{L^2} - H{\Delta _6} - {{384EI{\Delta _6}} \over {40{L^2}}} = 0,} \cr {{\Delta _6} = {{5q{L^2}} \over {40H{L^2} + 384EI}}.} \cr } $$
(12)

The mid-span deformation of the three-hinge ridge beam is

$$\sum {M = {1 \over 8}} q{L^2} - H{\Delta _8} = 0,\;\;{\Delta _8} = {{q{L^2}} \over {8H}}.$$
(13)

The quarter-span deformation of the flexible cable is

$$\sum {M = {1 \over 2}} q{\left({{1 \over 4}L} \right)^2} - H\left({{\Delta _5} - {1 \over 2}{\Delta _3}} \right) = 0,\;\;{\Delta _5} = {{3q{L^2}} \over {32H}}.$$
(14)

The quarter-span deformation of the two-hinge tensile beam is

$$\matrix{{\sum {M = {3 \over {32}}q{L^2} - H{\Delta _7} - {{192EI{\Delta _7}} \over {19{L^2}}} = 0,} } \hfill \cr {\quad \;{\Delta _7} = {{5q{L^4}} \over {608H{L^2} + 6144EI}}.} \hfill \cr }$$
(15)

The quarter-span deformation of the three-hinge tensile beam is

$$\Delta = {\Delta _9} + {\Delta _{10}} = {{5q{L^4}} \over {160H{L^2} + 6144EI\cos \theta }} + {{q{L^2}} \over {16H}}.$$
(16)

The mechanism displacement is

$${\Delta _9} = {1 \over 2}{\Delta _8} = {{q{L^2}} \over {16H}}.$$

The bending deformation is

$$\matrix{{P{\Delta _{10}} + {{{\Delta _{10}} \times 384EI} \over {40{L^2}}} = {{q{L^2}} \over {32}},} \cr {{\Delta _{10}} = {{5q{L^4}} \over {160H{L^2} + 6144EI\;\cos \theta }}.} \cr }$$

It is clear that the mid-span deformations of both the flexible cable and the three-hinge tensile beam are consistent under these two load patterns, while the two-hinge tensile beam gives a relatively small value. In addition, due to the bending stiffness of tensile beams, the quarter-span deformations of both the two-hinge tensile beam and the three-hinge tensile beam are smaller than those of the flexible cable under uniform load. Furthermore, a larger pre-tension results in a smaller deformation, and thus, the out-of-plane stiffness of the tensile beam is proportional to its pre-tension. Therefore, tensile beams can, in some cases, reduce deformation. Initial pre-tension and location of mechanism hinges have a great influence on the deformation and stress state of tensile beams.

6.2 Distribution modes of mechanism hinges

When the integral tow-lifting construction method is adopted, the mechanism hinges should be set at the middle of the tensile beams to make the tensile beam grid a mechanism system. According to the locations of the mechanism hinges, TBCD has seven distribution modes of mechanism hinges. Their details are listed in Table 5 and Fig. 15.

Fig. 15
figure 15

Tensile-beam cable dome modes based on the distribution patterns of mechanism hinges

(a) Mode 1; (b) Mode 2; (c) Mode 3; (d) Mode 4; (e) Mode 5; (f) Mode 6; (g) Mode 7. The component numbers are the same as the ones in Fig. 8

Full size image
Table 5 Distribution modes of mechanism hinges
Full size table

6.3 Optimal distribution mode of mechanism hinges

6.3.1 Analysis models

To find the characteristics of TBCD during construction, eight analysis models are built: Models I–VII are the same as Modes 1–7 shown in Figs. 15, respectively; Model VIII is a traditional cable dome. These eight models are all of the Geiger system and have the same size and initial pre-tension; they are all 60 m in span, 6 m in height, and 20 m in altitude at the support, with 3 pieces in the hoop, and 12 pieces in the radial direction. They all have a 0.1 rise-span ratio. Fig. 16 and Tables 6 and 7 list the component lengths and numbers, the material parameters, and the component parameters, respectively.

Fig. 16
figure 16

Component lengths and numbers of numerical models (unit: mm)

1: outer ridge cable; 2: middle ridge cable; 3: inner ridge cable; 4: outer oblique cable; 5: outer strut; 6: inner oblique cable; 7: middle oblique cable; 8: middle strut; 9: inner tensile ring; 10: outer ring cable; 11: inner ring cable

Full size image
Table 6 Material parameters
Full size table
Table 7 Component specification, element type, and initial pre-tension
Full size table

6.3.2 Construction analysis

Based on integral tow-lifting construction technology and the NDFEM form-finding method, we set lifting cables, towing cables, and oblique cables, and take the outer compressive ring as support to simulate the whole tow-lifting and tensioning process in ANSYS. The analysis cases are presented in Table 8, where the symbol ‘+’ means the added value of outer oblique cables during construction when compared with formed state.

Table 8 Analysis cases during tow-lifting and tensioning
Full size table

According to the symmetry of the structures, eight sheets of towing cables, lifting cables, and oblique cables are used in each model. The no-damping motion Eq. (5) is used in the NDFEM form-finding analysis, and the parameters are set to: Nei=30, Nts=5, ΔT(1)=0.1 s, Cts=1.5, Uci=1 mm, Uei=0.005 mm, and Nci=100.

During the tow-lifting construction analysis, Model IV and Model VII were shown to be of bad shape and eventually collapsed. Mechanism-hinge distribution modes IV and VII are therefore not feasible. The static equilibrium configurations of the key cases are shown in Fig. 17. The force variation curves of the outer oblique cables, lifting cables, and towing cables are shown in Figs. 18–20, respectively. The tensile beams bear a tensile force from pre-tension and a bending moment from dead load simultaneously. Fig. 21 lists the local deformation of the mechanism hinges, and Fig. 22 lists the bending stresses of the tensile beams.

Fig. 17
figure 17

Configurations of key cases in static equilibrium

(a) Case 1; (b) Case 4; (c) Case 9; (d) Case 13; (e) Case 16

Full size image
Fig. 18
figure 18

Oblique cable force during construction in Cases 1–10 (a) and in Cases 11–16 (b)

Full size image
Fig. 19
figure 19

Lifting cable force during construction

Full size image
Fig. 20
figure 20

Towing cable force during construction

Full size image
Fig. 21
figure 21

Local deformation curve of mechanism hinges on outer (a), middle (b), and inner (c) tensile beams

Full size image
Fig. 22
figure 22

Bending stress curve of outer (a), middle (b), and inner (c) tensile beams

Full size image

The results are listed below.

  1. 1.

    Feasible modes should set hinges at the middle or inner tensile beams, such as Models I/II/III/V/VI. By contrast, Models IV and VII did not complete the construction analysis with a large out-of-plane deformation and large bending stress.

  2. 2.

    In the tow-lifting stage of Cases 1–9, the tensile-beam grid was in the “ω” shape, while cables and struts stayed hanging under the tensile-beam grid, the configurations were stable, and cable forces were relatively small.

  3. 3.

    During the adjusting stage of Cases 10–13, the tops of the outer and middle struts were above the outer compressive ring and the configurations changed from the hanging state to the stiffening state.

  4. 4.

    During the tensioning stage in Cases 14–16, the axial force of cables and tensile beams increased rapidly until the whole structure formed in Case 16.

  5. 5.

    In the whole process, large local deformations occurred at the hinges of tensile beams, while the bending stresses were relatively small.

  6. 6.

    Local deformations of the outer tensile beams were far less than those of the middle or inner tensile beams; therefore, the outer tensile beams have little influence on the overall configuration.

Furthermore, the maximum force of towing cables, lifting cables, and oblique cables are 55 kN, 23 kN, and 1578 kN, respectively. We utilized the construction equipment shown in Fig. 4 to finish this construction process. Considering safety in construction and the possibility of an unbalanced force between two jacks in one set of equipment, we set the minimum bearing capacity magnification as 2.0.

The specifications of jacks and steel strands are listed in Table 9, in which the tensile strength, the ultimate bearing capacity, the nominal load-bearing capacity, the elastic modulus, and the density of Φs15.24 steel strand are 1860 MPa, 260 kN, 130 kN, 2.0×1011 N/m2, and 7.85×103 kg/m3, respectively. We chose 130 kN as the bearing capacity of each steel strand.

Table 9 Specifications of jacks and steel strands
Full size table

6.3.3 Optimal distribution mode of mechanism hinges

By considering the influence of local deformation, the number of mechanism hinges, and the bending stress of tensile beams in sequence, the optimal distribution mode was selected from the feasible modes by an exclusive method.

At first, local deformations of outer tensile beams in Model I and Model VI were relatively small during construction, so that the mechanism hinges of the outer tensile beams may be deleted, and Model I/VI should be excluded. In addition, there were more mechanism hinges in Model II than in Model III or Model V, which will increase the complexity in construction and cost more. Thus, Model II should be excluded. Therefore, the mode with mechanism hinges set only on the inner tensile beams (Model III) and the one with mechanism hinges set only on the middle tensile beams (Model V) were equally optimal.

7 Conclusions

In this paper, a new structural system called the tensile beam-cable dome (TBCD) is presented. This structure exchanges the ridge cables of the traditional cable dome for hinged tensile beams. Due to the bending stiffness of these tensile beams, the tensile beam-cable dome provides enough out-of-plane stiffness and limited local deformation when compared with traditional cable domes, and the proper mechanism hinges can convert the tensile beam grid to a mechanism system during the construction process.

The integral tow-lifting construction technology for TBCD was applied. This method uses the outer compressive ring as tow-lifting brackets. The small lifting force, limited high-level work, and high efficiency of tensioning make this method convenient. Verified by a model experiment, this method could fulfill the configuration and force requirements, with the benefits of stability and high efficiency.

In addition, to simulate the large difference of configuration between different construction stages, the NDFEM for form-finding analysis was proposed. The whole construction process was divided into several static cases, and the dynamic process was transformed to static equilibrium states during the analysis.

By comparing the configurations of different numerical models during construction analysis, the feasible distribution modes of mechanism hinges were calculated and compared; the optimal modes will reduce both the complexity and the cost of the structure.

As a natural extension of this research, the study of tensile beam-cable domes can be extended and generalized for various categories of tensegrity structures, such as the Levy dome, the Kiewitt dome, the cable net, the cable truss, etc. This generality of the methods proposed in this paper needs to be verified by further work.