Effect of case drain pressure on slipper/swashplate pair within axial piston pump

Abstract

This paper pertains to case drain pressure limitation for axial piston swashplate pumps used in open-loop circuits. The critical case drain pressure for pumps of this type is considered from the oil film perspective of the slipper/swashplate pair: (1) height of the lubricating oil film, (2) supporting stiffness, and (3) location of the centroid of the equivalent hydrodynamic lifting force. A dynamic lubricating oil film simulation model is established to determine the critical case drain pressure for which the slipper cannot remain in a stable state. Based on the simulation results, the worst condition occurs at the point when the height of the lubricating oil film is the maximum, the supporting stiffness is the minimum, and the distance between the centroid of the equivalent hydrodynamic lifting force and the bottom center of the slipper is the maximum. The slipper is stable only when the difference between the case drain pressure and the suction pressure is within a reasonable range. Subsequently, a design criterion is put forward to specify the reasonable case drain pressure, and this is validated by experimental results.

中文概要

目 的

旨在探索壳体压力对滑靴副特性的影响, 期望给出特定泵结构和工况下极限壳体压力的确定准则, 提高滑靴运行的可靠性。

创新点

1. 基于滑靴平衡方程, 推导出滑靴支撑力等效半径与工况之间的关系;2. 得出离散油膜刚度计算公式;3. 给出评价准则, 确定极限壳体压力。

方 法

1. 基于滑靴副油膜模型分析不同进口压力和壳体压力对滑靴副油膜厚度、滑靴倾覆角度、油膜刚度和动压支撑力等效作用半径的影响;2. 以动压支撑力等效作用半径小于滑靴外径为评价标准确定泵极限壳体压力。

结 论

1. 给定泵结构和工况条件下, 油膜厚度和滑靴倾覆角度随着壳体压力的增大而增大;2. 壳体压力增大, 高低压过渡区支撑刚度降低, 等效动压支撑力作用点向滑靴外缘移动;3. 基于油膜模型提出的壳体压力确定准则可以有效的确定极限壳体压力。

1 Introduction

Axial piston swashplate pumps are widely used in fluid power circuits for high efficiency, power density, and structure compactness. During the past several decades, most of the available literature has been concerned about the optimization design (Ivantysyn, 2011; Kim, 2012), vibration and noise reduction (Kumar Seeniraj, 2009; Kumar Seeniraj et al., 2011), and variable control about the axial piston swashplate pumps (Grabbel and Ivantysynova, 2005; Kemmetmüller et al., 2010). Nowadays, much attention is paid to the refinement of preliminary design and microstructure innovation of friction pairs to improve pump performance and efficiency. The slipper is a very important component that carries the external clamping load from the piston and slides against the swashplate. It is common knowledge that partial abrasion happens during the delivery stroke as the oil film is much thinner compared with that during the suction stroke. Researchers at the Maha Fluid Power Research Center have developed a fully coupled fluid-structure thermal simulation model, i.e., CASPAR (calculation of swashplate type axial piston pump and motor), to predict pump efficiency, especially the performance of the friction pairs (Pelosi, 2012; Zecchi, 2013; Chacon, 2014; Wondergem, 2014). Schenk (2014) presented a coupled numerical model for the slipper/swashplate interface considering pressure deformation and thermal deflection, and investigated the impact of the hydrostatic and hydrodynamic deformation, respectively. The model was capable of calculating the lubricating gap height and power loss to find the optimal slipper design with the minimum power loss through an iterative optimization scheme. Unlike the complicated simulation model introduced by Maha Fluid Power Research Center, Manring (1998; 2001; 2013) presented the governing equations for more thorough analysis of the machine itself and guidelines for the design of axial piston pumps. He predicted the tipping phenomenon of the slipper, which resulted from the reciprocating inertia as well as the centrifugal inertia of slipper itself, neglecting the influence of the friction. Then he determined the physical contributors tending to separate the slipper from the swashplate. The worst tipping condition occurs at the top dead center based on the tipping criterion. The slipper-tipping phenomenon may be eliminated by increasing the charge pressure and the cylinder spring force. The case studies correlated well with design practices that are currently in use. Manring et al. (2014) further analyzed the speed limitations for the pump from physical aspects, i.e., cylinder tipping, piston chamber filling, and slipper tipping. Borghi et al. (2009a; 2009b) also adopted a stationary model to study the influence of pressure transition in the piston chamber, the swashplate angle, the radial clearance between the piston and the cylinder bore, and the retaining force point of application on the critical speed. The critical speed is small for high swashplate angle, high displacement, and low delivery pressure. In addition to slipper tipping, rigidity of the lubricating oil film of the slipper reflects the capacity of the slipper to resist the changes in external forces. Canbulut et al. (2004; 2009) used both experimental and neural network application for analyzing the effects of orifice diameters and radius ratios on the rigidity variations of the hydrostatic bearing system, and this type of neural network algorithm can be used to optimize other types of bearing systems. Nevertheless, the slipper is treated as an ideal hydrostatic bearing, neglecting the tilt.

In summary, much of these research work has been occupied with the very important subjects of slipper/swashplate friction pair, i.e., the lubricating oil film, the geometrical parameters, the retaining force, and the critical speed. However, these studies were based upon the assumption that the case drain pressure is smaller than the suction pressure, or even zero, so that the slipper remains in reasonable proximity with the swashplate. In reality, the reasonable proximity between the slipper and the swashplate is not guaranteed unless an appropriate case drain pressure is set for establishing this lubricating oil film.

In this study, the typical single-land slipper/swashplate interface, permissible suction pressure, and corresponding case drain pressure of the axial piston pumps in use are introduced. Based on the kinematic analysis and laminar flow assumption, a numerical model of the lubricating oil film between the slipper and swashplate is established, considering the case drain pressure. Then, to find the mechanism of slipper failure, the developed numerical model is used to study the effect of case drain pressure on the lubricating oil film. The characteristics of the slipper, which are sensitive to case drain pressure, are investigated, i.e., lubricating oil film thickness, tilting angle, supporting stiffness, and the centroid of the equivalent hydrodynamic lifting force. Subsequently, a design criterion for the case drain pressure is put forward to determine the critical case drain pressure of the given pump configuration and specified operating condition. Finally, the analytical results of this study are validated by experiment. Decomposition of the tested pumps shows that the numerical model is able to predict the critical case drain pressure with the proposed design criterion. Detailed information will be given in the following sections.

2 Numerical model of lubricating oil film between the slipper/swashplate

2.1 Slipper/Swashplate interface

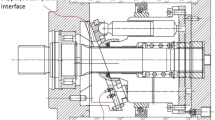
The slipper is borne by the swashplate with a pressurized pocket connected to the piston chamber, as shown in Fig. 1. Outside of the slipper pocket, a sealing land is always necessary to seal the high pressure against low case drain pressure during the delivery stroke. The pressure of the lubricating oil film is composed of hydrostatic pressure due to Poiseuille flow, hydrodynamic pressure due to Couette flow, and squeezing pressure due to slipper micromotion. Elastohydrodynamic pressure due to slipper and swashplate surface deformation is ignored in this study. The lifting force of the slipper/swashplate interface is dependent on not only the dimensions of the sealing surface but also the pressure in the pocket. However, little attention is paid to the characteristics of the lubricating oil film of the slipper/swashplate interface during the suction stroke, especially when the case drain pressure is larger than the suction pressure. The slipper rotates in an inclined position due to centrifugal and friction moments (Schenk, 2014). Reverse flow happens if the case drain pressure is higher than the suction pressure. In these cases, the slipper requires additional forces to be pressed on the swashplate.

Fig. 1

A free body diagram of the piston/slipper assembly

The symbols in Fig. 1 are explained in Sections 2 and 3

For normal operating conditions, the maximum permissible case drain pressure is a little higher than the inlet pressure, however, not being higher than several bars absolute. Researchers have examined the minimum inlet pressure, which depends on the speed and displacement of the axial piston unit, while nominal operating pressure is the maximum design pressure at which fatigue strength is ensured. However, there is no published criterion that restricts the value of the case drain pressure. In this study, only axial piston pumps used in open circuits are considered. The suction pressure and case drain pressure are listed in Table 1, which are available in the catalogs for each pump manufacturer. It is observed that the case drain pressures may be higher than the inlet pressures, and they do have maximum limits.

Table 1 Suction pressure and case drain pressure limitations of pumps in use

As one of the slipper performance indicators, supporting stiffness describes the capacity of the slipper to counteract the changing external clamping forces. The supporting stiffness is traditionally analyzed by neglecting the wedge-shaped distribution of the lubricating oil film due to oscillating clamping force and tilting moments. The slipper and the swashplate are parallel to each other. The damping orifices of piston and slipper, the oil pocket under the slipper, and the varying lubricating oil film constitute a hydrostatic bearing mechanism. If the external clamping force applied on the slipper increases, the height of the lubricating oil film decreases, with decrease in the leakage through the variable annular narrow clearance. Then, the pressure in the slipper pocket increases and the load-carrying capacity of the lubricating oil film increases, and vice versa. Therefore, the lubricating oil film works like a spring. The case drain pressure as pressure boundary is usually set to a constant value smaller than the suction pressure (zero by default), which is common in previous research, but this is not appropriate. Here is the reason. The lifting force F_l, which is derived in Appendix A, of the lubricating oil film of an ideal hydrostatic bearing can be expressed as

$$\matrix{{{F_{\rm{l}}} = {\rm{\pi }}{p_{\rm{L}}}R_{\rm{s}}^2 + {{3\mu {C_{{\rm{pb}}}}{C_{{\rm{sb}}}}{C_{{\rm{sp}}}}(R_{\rm{s}}^2 - r_{\rm{s}}^2)({p_{\rm{p}}} - {p_{\rm{L}}})} \over {{h^3}({C_{{\rm{pb}}}}{C_{{\rm{sb}}}} + {C_{{\rm{pb}}}}{C_{{\rm{sp}}}} + {C_{{\rm{sb}}}}{C_{{\rm{sp}}}})}},} \hfill \cr {{C_{pb}} = {{{\rm{\pi }}d_1^4} \over {128\mu {l_{\rm{1}}}}},\;{C_{sb}} = {{{\rm{\pi }}d_2^4} \over {128\mu {l_2}}},\;{C_{sp}} = {{{\rm{\pi }}{h^3}} \over {6\mu \ln ({R_{\rm{s}}}/{r_{\rm{s}}})}},} \hfill \cr }$$

(1)

where l₁, d₁, l₂, d₂ are the dimensions of piston orifice and slipper orifice; r_s and R_s are the inner radius and outer radius of the slipper sealing land, respectively; h is the average oil film thickness; μ is the oil viscosity; p_p is the instantaneous pressure in the piston chamber, which is smaller than the suction pressure p_s and larger than the delivery pressure p_d. During the suction stroke, p_p is determined by p_s and the loss factor c (Ivantysyn, 2011). p_L is the case drain pressure. According to Eq. (1), F_l is a function of the operation parameters p_s, p_L, and h, and the geometrical parameters d₁, l₁, d₂, l₂, r_s, and R_s.

The supporting stiffness J is defined as the variation of the lifting force divided by the variation of the lubricating oil film thickness, as shown in Eq. (2).

$$\matrix{{J = - {{{\rm{d}}{F_{\rm{l}}}} \over {{\rm{d}}h}} = {{a{h^2}({p_{\rm{p}}} - {p_{\rm{L}}})} \over {{{(b + c{h^3})}^2}}},} \hfill \cr {a = 1152{\rm{\pi (}}R_{\rm{s}}^2 - r_{\rm{s}}^2{\rm{)}}d_1^4d_2^4(d_1^4{l_2} + d_2^4{l_1}),} \hfill \cr {b = 6d_1^4d_2^4\ln ({R_{\rm{s}}}/{r_{\rm{s}}}),} \hfill \cr {c = 128(d_1^4{l_2} + d_2^4{l_1}).} \hfill \cr }$$

(2)

It can be concluded that the supporting stiffness is reduced due to the increase in case drain pressure for a given oil film thickness. The stability of the lubricating oil film is deteriorated to some extent. Therefore, the hydrostatic bearing mechanism may be destroyed when the supporting stiffness becomes inadequate to counteract the changing external force, especially during the suction stroke. Moreover, note that the supporting stiffness becomes negative if p_L is larger than p_p during the suction stroke. This condition will never happen in traditional analysis if p_L is set less than p_p, or even zero by default. For the case drain pressure being higher than the suction pressure under certain operating conditions in practice, it is inappropriate to use the traditional supporting stiffness to analyze the characteristics of the slipper, especially during the suction stroke, though in practice, the case drain pressure can be determined by laboratory tests. In this study, an apriori technique is presented for determining the range of case drain pressure that successfully keeps the slipper away from the swashplate within a permissible distance.

2.2 Kinematics model and lubricating oil film model

The force condition, the relevant kinematic parameters, and the key dimensions of the free body diagram of the piston/slipper assembly are shown in Fig. 1. OXYZ is the global Cartesian coordinate system. The macro motions of a slipper include the rotation about the main shaft, the reciprocating motion along the cylinder bore with the piston, and the sliding motion on the surface of the swashplate. Moreover, the slipper does rotate about its own axis due to the friction moment in the piston/slipper spherical joint (Borghi et al., 2009a; 2009b). To simplify the calculation, one local Cartesian coordinate system oxyz fixed with the center of the slipper socket is selected. The local Cartesian coordinate retains its x-axis always tangential to the trajectory of the slipper and the y-axis radially outward. The kinematic parameters of an arbitrary point (r, θ) under the slipper can be described by

$\begin{gathered} v_s = r_M \omega , \hfill \\ v_{sr} = v_s \cos \delta , \hfill \\ v_{s\theta } = \left\{ \begin{gathered} v_s \sin \delta , - \frac{\pi } {2} < \theta \leqslant \frac{\pi } {2}, \hfill \\ - v_s \sin \delta ,\frac{\pi } {2} < \theta \leqslant \frac{{3\pi }} {2}, \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $

(3)

where r_M is the equivalent radius of the arbitrary point (r, θ), ${r_{\rm{M}}} = \sqrt {{\rho ^2} + {r^2} + 2\rho r\cos \theta };\rho$ is the radial distance between the slipper center and the center of the oval trajectory, $\rho = {R_{\rm{c}}}\sqrt {{{\sin }^2}\varphi + {{(cos\varphi/cos\beta)}^2}}$; R_c is the piston pitch radius; φ is the angular position of the piston relative to the bottom dead center; β is the swashplate angle; v_s is the tangential velocity along the oval trajectory; v_sr and v_sθ are the radial velocity component and the circumferential velocity component, respectively; δ is the angle between v_s and the radius under the slipper radially outward; ω is the rotational velocity of the pump main shaft.

As mentioned above, the slipper rotates about its own axis due to the friction moment of the spherical joint. The spin angular velocity will be analyzed later in this section. In addition to the macro motion, the slipper microposition can be described by three variables, i.e., the average lubricating oil film thickness, the tilting angle, and the azimuth angle. The slipper remains in a dynamic balance state and the average lubricating oil film thickness, the titling angle, and the azimuth angle vary with the oscillating external forces and moments. The lubricating oil film between the slipper and the swashplate is regarded as laminar flow with micrometer-scale gap height, and there is no metal-to-metal contact.

The Reynolds equation can be obtained by the 2D Navier-Stokes equation and the continuity equation, which can be expressed as

$$\matrix{{{1 \over r}{\partial \over {\partial r}}\left({r{{{h^3}} \over \mu }{{\partial p} \over {\partial r}}} \right) + {1 \over {{r^2}}}{\partial \over {\partial \theta }}\left({{{{h^3}} \over \mu }{{\partial p} \over {\partial \theta }}} \right)} \hfill \cr { = 6{v_{{\rm{s}}r}}{{\partial h} \over {\partial r}} + 6\left({{{{v_{{\rm{s}}\theta }}} \over r} - {\omega _{\rm{z}}}} \right){{\partial h} \over {\partial \theta }} + 12{{\partial h} \over {\partial t}},} \hfill \cr}$$

(4)

where ω_z is spin velocity of the slipper, p is the pressure of an arbitrary point (r,θ), and the instantaneous lubricating oil film height h can be expressed by the function of three points h₁, h₂, and h₃ on the outer edge at an interval of 120°, assuming that the slipper and swashplate surfaces are ideally smooth and neglecting the deformation of the slipper and the swashplate.

$\begin{gathered} h(r,\theta ) = \frac{{\sqrt {1/3} }} {{R_s }}(h_2 - h_3 )r\sin \theta \hfill \\ + \frac{1} {{3R_s }}(2h_1 - h_2 - h_3 )r\cos \theta \hfill \\ + \frac{1} {3}(h_1 + h_2 + h_3 ). \hfill \\ \end{gathered} $

(5)

For the boundary conditions, the pressure at the inner radius r_s is equal to the pressure in the slipper pocket, and the pressure at the outer radius R_s is equal to the case drain pressure. Neglecting the complex flow field in the pump case due to the high-speed rotation of the cylinder and the piston/slipper assemblies, the pressure in the case can be taken as constant. Then, the pressure distribution within the lubricating oil film is obtained by solving the Reynolds equation using the finite volume method. The lifting force and the anti-overturning moments about the x- and y-axes can be obtained by integrating the pressure distribution under the slipper. The pressure in the slipper pocket is determined by the flow continuity equation. The fluid flows into this slipper pocket from the piston chamber via control orifices of the piston and slipper and then flows out of the pocket through a variable annular narrow clearance. Therefore, the pressure in the slipper pocket p_r is determined by

$$\matrix{{{{{C_1}{C_2}} \over {{C_1} + {C_2}}}({p_{\rm{p}}} - {p_{\rm{r}}}) = \int_{\theta = 0}^{\theta = 2{\rm{\pi }}} {\int_{z = 0}^{z = h} {{v_{\rm{r}}}{R_{\rm{s}}}{\rm{d}}z{\rm{d}}\theta}},} \hfill \cr {\quad \;\;{C_1} = {{{\rm{\pi }}d_1^4} \over {128\mu {l_1}}},\;\;{C_2} = {{{\rm{\pi }}d_2^4} \over {128\mu {l_2}}},} \hfill \cr }$$

(6)

where v_r is the radial flow velocity distribution along the z-axis, and can be expressed as

$${v_{\rm{r}}} = {1 \over {2\mu }}{{\partial p} \over {\partial r}}({z^2} - h \cdot z) + {v_{{\rm{s}}r}}{z \over h},$$

(7)

where z is the oil film thickness along the z-axis. To obtain the characteristics of the lubricating oil film, the equilibrium of forces and moments acting on the slipper should be obtained until a certain tolerance is reached. The slipper moves along its own axis and rotates about the x- and y-axes. Therefore, the equilibrium equations are

$$\left\{ \matrix{{m_{\rm{s}}}\ddot z = {F_{\rm{l}}} - {F_{{\rm{ps}}}} - {F_{\rm{r}}}, \hfill \cr {I_x}{{\ddot \delta }_x} = {M_{\rm{c}}} - \int\!\!\!\int {\;p{r^2}\cos \theta {\rm{d}}r{\rm{d}}\theta}, \hfill \cr {I_y}{{\ddot \delta }_y} = {M_{\rm{f}}} - \int\!\!\!\int {\;p{r^2}\sin \theta {\rm{d}}r{\rm{d}}\theta}, \hfill \cr {I_z}{{\ddot \delta }_z} = - {M_{{\rm{ps}}}} + \int\!\!\!\int {\;{\tau _{{\rm{s}}\theta }}{r^2}{\rm{d}}\theta {\rm{d}}r}, \hfill \cr} \right.$$

(8)

where m_s is the slipper mass; I _x , I _y , and I _y are moments of inertia of the slipper about the x-, y-, and z-axes; ${\ddot \delta _x},{\ddot \delta _y}$ and ${\ddot \delta _z}$ are angular accelerations along the x-, y-, and z-axes, respectively; M_c is the moment generated by the centrifugal force; M_f is the moment generated by the viscous friction force; M_ps is the friction moment of the spherical joint; τ_sθ is the circumferential frictional stress under the slipper sealing land. The lifting force of the lubricating oil film F_l is composed of the hydrostatic lifting force F_sl and the hydrodynamic lifting force F_dl. F_ps is the internal force between the piston and slipper, and F_ps is opposite to F_sp, which can be obtained from the axial equilibrium of the piston. F_r is the retaining force. Compared with other forces and moments, the inertial force and moments can be neglected. The spin angular velocity can be obtained by integrating the spin angular acceleration. The kinetic equation of the piston can be expressed as

$${m_{\rm{p}}}\ddot Z = - {F_{\rm{p}}} - {F_{\rm{f}}} + {F_{{\rm{sp}}}}\cos \beta,$$

(9)

where m_p is the piston mass, $\ddot Z$ is the acceleration of the piston along the Z-axis, F_p is the force generated by the pressure in the piston chamber, and F_f is the frictional force, which can be obtained from the piston/cylinder interface simulation model developed by our research group (Xu et al., 2013). For simplification, it is calculated in this study using the theoretical equation assuming that the piston is concentric with the cylinder bore and that the clearance between the piston and the cylinder is constant. F_f is composed of the frictional force generated by the relative motion of the piston with respect to the cylinder bore and the pressure drop between the piston chamber and the case.

$$\matrix{{{F_{\rm{f}}} = - 2\left[ {{{{v_1}} \over {{h_{\rm{p}}}}} + {{({p_{\rm{p}}} - {p_{\rm{L}}}){h_{\rm{p}}}} \over {2{l_{\rm{k}}}}}} \right]{\rm{\pi }}{r_{\rm{p}}}{l_{\rm{k}}},} \hfill \cr {\quad \;{l_{\rm{k}}} = {l_0} - {R_{\rm{c}}}\cos \varphi \tan \beta,} \hfill \cr }$$

(10)

where v₁ is the transitional velocity of the piston, h_p is the lubricating oil film thickness of the piston/cylinder friction pair, r_p is the piston radius, l_k is the instantaneous contact length between piston and cylinder bore at a given swashplate angle, and l_k equals l₀ when β=0.

The height of the lubricating oil film thickness is unknown in advance, so first-attempt values of h₁, h₂, h₃, h′₁, h′₂, and h′₃ are used, and the pressure distribution is determined from the Reynolds equation only when certain tolerance of the equilibrium of forces and moments acting on the slipper is reached. Finally, a simulation model is built based on the analysis above, and the nonlinear equations in the simulation model are solved by the successful adoption of Newton iterative method. The simulation procedure is shown in Fig. 2. Empirically, the variations of the pressure distribution and the micromotion of the slipper already show periodicity after four computing cycles. The simulation terminates if metal-to-metal contact occurs or if force/moment imbalance occurs.

Fig. 2

Simulation procedure

3 Characteristics of the lubricating oil film

The results of the numerical simulation model for the slipper/swashplate friction pair are presented. They are illustrated in terms of pressure and height distribution, average lubricating oil film thickness, slipper tilting angle, supporting stiffness, and location of the centroid of the hydrodynamic lifting force. The slipper considered is characterized by the geometrical parameters listed in Table 2. The nominal operating conditions are taken as the simulation parameters listed in Table 3. The pressure in the piston chamber has a smooth transition between the delivery pressure and the suction pressure. The overshoot and the undershoot of the pressure in the piston chamber are not considered and the hold-down force is considered a known quantity.

Table 2 Geometrical parameters of simulation

Table 3 Operating conditions of simulation

Taking the suction stroke for instance, the pressure and the thickness distribution of the oil film are shown in Fig. 3. With increasing case drain pressure, the pressure changes its distribution pattern. The hydrodynamic pressure is significant when the case drain pressure is small, and it is exactly the one that generates the anti-overturning moments. When the pressure in the piston chamber is smaller than the case drain pressure during the suction stroke, the fluid in the pump case, which is a combination of Poiseuille flow and Couette flow, flows backward into the slipper pocket, resulting in increase in the pressure in the slipper pocket. The pressure in the slipper pocket increases and so does the load-carrying force, resulting in increase in the height of the lubricating oil film. As mentioned above, the anti-overturning moments are a function of the height of the lubricating oil film. The higher the case drain pressure is, the larger the height of the lubricating oil film is, and the smaller the anti-overturning moments are. The height of the lubricating oil film thickness increases sharply, followed by breaking of the oil film, and the lubricating oil film is incapable of counteracting the frictional moment and the centrifugal moment. Therefore, reducing the thickness of the lubricating oil film and the tilting angle is very important to prevent the breaking of the lubricating oil film of the slipper/swashplate pair.

Fig. 3

Height and pressure distribution of lubricating oil film located at the suction stroke (φ=195°, p _s =0.8 bar)

3.1 Analysis of height of lubricating oil film and tilting angle of slipper

The oil film is wedge shaped and the microtilting state varies with the angular position and working parameters. The thickness difference of the three points reflects the tilting state of the slipper. Furthermore, the tilting angle and the average height of lubricating oil film can be obtained based on the thickness of the named three points. Figs. 4 and 5 show the comparison of the average height h_ave of lubricating oil film and the tilting angle α of the slipper, respectively, when the suction pressure is equal to 0.8 bar and the case drain pressures are 1.0 bar, 1.3 bar, and 1.4 bar (1 bar=100 kPa). As shown in Figs. 4 and 5, the pressure profile in the piston chamber during the delivery stroke is larger than that during the suction stroke, and it is assumed that the pressure changes smoothly and there is no pressure overshoot or undershoot in the transition region. It is concluded that the average height of the lubricating oil film increases with the increasing of case drain pressure, and so does the tilting angle of the slipper. During the delivery stroke, the average height of the lubricating oil film is lower than that during the suction stroke. As the case drain pressure is 0.5 bar higher than the suction pressure, there is a prominent increase in the thickness of the lubricating oil film during the suction stroke. Especially when the case drain pressure is 1.4 bar, the simulation failed in the transition region, because the thickness of the lubricating oil film becomes too large, which in turn implies the breaking of the oil film.

Fig. 4

Average height of the lubricating oil film ( p _s =0.8 bar)

Fig. 5

Slipper tilting angle ( p _s =0.8 bar)

During the suction stroke, the average height of the lubricating oil film increases at first and then decreases. This can be explained by the external clamping force acting on the slipper and the change rate of the height of lubricating oil film during the suction stroke. The external clamping force is composed of the force generated by the pressure in the piston chamber, the inertial force, the frictional force, and the retaining force. The inertial force and the frictional force change with respect to the angular position, while the retaining force remains constant and the hydraulic force only increases or decreases in the transition region. The change rate of the height of the lubricating oil film is positive when the external clamping force decreases, and the height of the lubricating oil film starts to increase. When the sum of the inertial force and the frictional force is maximum, the clamping force begins to increase and then the height of the lubricating oil film begins to decrease gradually. This means that the sum of the inertial force and the frictional force pulls the piston/slipper assembly away from the swashplate until their algebraic sum is the maximum at first, and then it helps in pushing the piston/slipper assembly against the swashplate in the suction stroke. Thus, under the combined action of the inertial force and the frictional force, the maximum height of the lubricating oil film is located at the point when the sum of the inertial force and the frictional force is the maximum, and the angular position is located at about 195° for the specified operating conditions in this study; the angular position may change under different pump configurations and operating conditions.

However, when the suction pressure increases, the phenomenon is improved as the height of the lubricating oil film and the tilting angle are within a reasonable range to retain the steady state of the slipper. The graphs of h_ave and α with respect to the angular position are shown, respectively, in Figs. 6 and 7 when the suction pressures equal 1.5 bar and 5 bar. For clarity, only one pressure profile with the suction pressure equal to 1.5 bar is shown in Figs. 6 and 7. Though the slipper can maintain a reasonable distance away from the swashplate, the slipper tilting angle is still too big. When the case drain pressure becomes lower or the suction pressure becomes higher, the average height of the lubricating oil film and the slipper tilting angle decrease obviously.

Fig. 6

Average height of the lubricating oil film

Fig. 7

Slipper tilting angle

3.2 Supporting stiffness

The reason why the simulation stops in the transition region from high delivery pressure to low suction pressure can be explained by the supporting stiffness. There are hydrostatic force, hydrodynamic force, and squeezing force under the slipper. Therefore, the supporting stiffness is a function of the height of the lubricating oil film, change rate of height of lubricating oil film, tilting angle of slipper, case drain pressure, and pressure in piston chamber. It can be calculated by the sum of the supporting stiffness of each grid under the slipper. The supporting stiffness is shown as

$$J = {1 \over {MN}}\sum {{{{\rm{d}}{F_{{\rm{1}}i}}} \over {{\rm{d}}{h_i}}}},$$

(11)

where M and N are numbers of units along the radial and circumferential directions, respectively; subscript i stands for the ith control unit. F_li=p _i A _i is the lifting force of an arbitrary unit, p _i is the pressure of the arbitrary volumetric control unit, A _i is the area of the arbitrary unit, and h _i is the height of the lubricating oil film of the arbitrary unit.

For simplicity in working with dimensionless values, the supporting stiffness in dimensionless form is used in this study. The dimensionless cell lifting load can be written as ${\overline F _{1i}} = {\overline p _i}{\overline A _i}$ where ${\overline p _i} = {p_i}/{p_{\rm{d}}}$ is the dimensionless pressure of an arbitrary unit, ${\overline A _i} = {A_i}/R_{\rm{s}}^2$ is the dimensionless area of the arbitrary unit, ${\overline h _i} = {h_i}/{R_{\rm{s}}}$ is the dimensionless oil film height of the arbitrary unit, and $\overline J = J/({p_{\rm{d}}}{R_{\rm{s}}})$ is the dimensionless supporting stiffness.

$$\bar J = {1 \over {MN}}\sum {{{{\rm{d}}{{\bar F}_{{\rm{1}}i}}} \over {{\rm{d}}{{\bar h}_i}}}}.$$

(12)

The supporting stiffness can retain a positive value due to the squeezing effect and the hydrodynamic effect, even if p_L is larger than the pressure in the piston chamber during the suction stroke. The supporting stiffnesses under different conditions are shown in Figs. 8 and 9. The actual supporting stiffness is a dynamic value over the pump operating cycle. As can be seen from Figs. 8 and 9, the supporting stiffness is positive if the case drain pressure remains in the reasonable numerical range. The supporting stiffness has little change during the delivery stroke under different case drain pressures for the reason that the slipper remains in a stable state as can be seen from the tilting angles shown in Figs. 5 and 7. In the transition region, the supporting stiffness changes evidently and there exists a minimum value in Figs. 8 and 9. Then, the supporting stiffness begins to increase with increasing clamping force due to the inertial force and the frictional force, as well as the decreasing height of the lubricating oil film. The supporting stiffness during the suction stroke decreases with the increase of the case drain pressure shown in Fig. 8, while the supporting stiffness is improved with the increase of suction pressure shown in Fig. 9.

Fig. 8

Supporting stiffness of the oil film ( p _s =0.8 bar)

Fig. 9

Supporting stiffness of the oil film

If the case drain pressure is 0.5 bar higher than the suction pressure, the minimum supporting stiffness decreases, which means the load-carrying capacity that counteracts the varying clamping force becomes weak. If the difference between the case drain pressure and the suction pressure is larger than 0.5 bar, the lubricating oil film cannot resist the change of the clamping force, resulting in the extremely large height of the lubricating oil film thickness, as shown in Fig. 4.

3.3 Location of the centroid of the hydrodynamic lifting force

From the analysis above, it is quite clear that the slipper cannot guarantee a good load-carrying capacity when the case drain pressure is 0.5 bar larger than the suction pressure. This unstable behavior can result in inadequate efficiency of the axial piston pump. As mentioned, the slipper is tilted due to tilting moments. The hydrostatic pressure is symmetrical about the x- and the y-axes and does not generate anti-overturning moments. Therefore, only the hydrodynamic pressure generates the anti-overturning moments. The geometrical location of the resultant hydrodynamic lifting force can be determined by finding its centroid. Here, a design criterion is put forward.

$$\left\{ \matrix{{F_{{\rm{dl}}}} > 0, \hfill \cr \sqrt {E_x^2 + E_y^2} {\rm{ = }}{E_{\rm{r}}} < {R_{\rm{s}}}, \hfill \cr} \right.$$

(13)

where E _x and E _y are the geometrical locations of centroid of hydrodynamic lifting force, E_r is the distance between centroid of hydrodynamic lifting force and slipper center. ${E_x} = - {M_{\rm{f}}}/{F_{{\rm{dl}}}},\quad {E_y} = - {M_{\rm{c}}}/{F_{{\rm{dl}}}}$ and ${F_{{\rm{dl}}}} = {m_{\rm{s}}}\ddot z - {F_{{\rm{ps}}}} - {F_{{\rm{sl}}}} - {F_{\rm{r}}}$.

A plane view of the centroid of the equivalent hydrodynamic lifting force is given in Figs. 10 and 11. It is obvious that the centroid of the hydrodynamic lifting force is located in the fourth quadrant, which is consistent with the position of the minimum oil film height shown in Fig. 3.

Fig. 10

Location of the centroid of the hydrodynamic lifting force ( p _s =0.8 bar)

Fig. 11

Location of the centroid of the hydrodynamic lifting force

The distance between the centroid of the hydrodynamic lifting force and the bottom center of the slipper is shown in Figs. 12 and 13. The centroid of the hydrodynamic lifting force is located near the bottom center of the slipper during the delivery stroke, and it moves out during the suction stroke. The maximum E_r is located at about 195°, where the clamping force is the smallest and the height of the lubricating oil film is the largest. As the case drain pressure increases, the centroid of the resultant hydrodynamic lifting force goes outward of the slipper sealing land. When the case drain pressure is 0.5 bar larger than the suction pressure, the centroid of the resultant hydrodynamic lifting force is located nearly at the edge of the slipper sealing land, especially for the low suction pressure, as shown in Fig. 12. If the difference between the case drain pressure and the suction pressure is more than 0.5 bar, the centroid of the resultant hydrodynamic lifting force is located out of the slipper sealing land. This phenomenon is impossible in practice, resulting in termination of the simulation. This unstable behavior is clearly due to the inability of the slipper to find an equilibrium position. Accordingly, such a harmful working condition should be avoided. The slipper can operate normally without severe tilting only when the centroid of the hydrodynamic lifting force is located within the outer radius of the slipper.

Fig. 12

Distance between the centroid of the hydrodynamic lifting force and the center of the slipper ( p _s =0.8 bar)

Fig. 13

Distance between the centroid of the hydrodynamic lifting force and the center of the slipper

4 Experiment verification

To evaluate the simulation results, the axial piston pump used in the simulation was tested under different case drain pressures on a standard test rig of pump. To eliminate the effect of other components, the test time should not be too long. As shown in Table 4, the whole test time was only 2 h for the pump under a certain case drain pressure, including the running in at the low delivery pressure of 30 bar. The rotational speed was set at 2200 r/min, and the swashplate angle was the maximum.

Table 4 Experimental parameters

A throttle valve was installed on the case drain pipe of the pump to adjust the case drain pressure. The case drain pressures were 1 atm (standard atmosphere), 1.3 bar, and 1.4 bar. Fig. 14 shows the wear conditions of the test decomposed pumps under the three case drain pressures. As shown in Fig. 14, the pump condition is rather good when the case drain pressure is 1 atm compared with that when the case drain pressure is 0.5 bar higher than the suction pressure after the same testing time. But, the retainer of the latter pump does have cracks on the distributed holes used to hold down the slipper, because the upper edge of the slipper destroys the integrity of the retaining plate, which means that the height of the lubricating oil film is large and the slipper tilt is severe. The retainer and the slipper suffered further wear and damage as the case drain pressure increased continuously. As the case drain pressure is set at 1.4 bar, the test had to terminate with a loud noise after a few testing steps. The pump was decomposed with broken retainer and severe abrasion of slippers.

Fig. 14

Decomposition of the test pumps

Therefore, the experimental results showed that the case drain pressure should be set within the allowable range to guarantee the normal working condition for the slipper, that is, the case drain pressure should be no more than 0.5 bar higher than the suction pressure and this result is consistent with simulation results.

5 Conclusions

In this study, a dynamic oil film simulation model is established to determine the critical case drain pressure for a given pump configuration and specified operating condition. Based on the simulation and experimental results, the following could be summarized.

• 1. With high suction pressure values, the average height of the lubricating oil film and the tilting angle of the slipper are small during suction stroke. The average height and tilting angle show increasing trend after the top dead center. Therefore, the hydrodynamic effect, which contributes to counteracting the overturning moments, is low in the transition region. This behavior is enhanced by low suction pressure and high case drain pressure.

• 2. Under low suction pressure and high case drain pressure, the slipper is characterized by an unstable behavior in the transition region, i.e., the supporting stiffness becomes very small and the centroid of the resultant hydrodynamic pressure moves to the edge of the slipper. If the difference between the case drain pressure and the suction pressure goes beyond the reasonable range, the slipper is unable to find an equilibrium position gradually.

• 3. The worst condition occurs at the point when the height of the lubricating oil film is the maximum, the supporting stiffness is the minimum, and the centroid of the resultant hydrodynamic lifting force is the farthest from the bottom center of the slipper. The proposed design criterion for the case drain pressure is effective in predicting the critical case drain pressure of the given pump configuration and specified operating condition. It is validated that the numerical model is able to predict the critical case drain pressure with the proposed design criterion by the decomposition of the tested pumps.

Appendix A

In this appendix, the detailed equations describing the lifting force and the supporting stiffness of the lubricating oil film are derived. The equations are developed considering the case drain pressure.

A1 Lifting force of the lubricating oil film

The oil flow through the piston orifice and slipper orifice is expressed as

$$\matrix{{{Q_1} = {{{C_{{\rm{pb}}}}{C_{{\rm{sb}}}}} \over {{C_{{\rm{pb}}}} + {C_{{\rm{sb}}}}}}({p_{\rm{p}}} - {p_{\rm{r}}}),} \hfill \cr {{C_{{\rm{pb}}}} = {{{\rm{\pi }}d_1^4} \over {128\mu {l_1}}},\;\;{C_{{\rm{sb}}}} = {{{\rm{\pi }}d_2^4} \over {128\mu {l_2}}}.} \hfill \cr}$$

(A1)

The oil flow through the variable annular damping is expressed as

$$\matrix{{{Q_2} = {C_{{\rm{sp}}}}({p_{\rm{r}}} - {p_{\rm{L}}}),} \hfill \cr {{C_{{\rm{sp}}}} = {{{\rm{\pi }}{h^3}} \over {6\mu \ln ({R_{\rm{s}}}/{r_{\rm{s}}})}}.} \hfill \cr }$$

(A2)

The oil flow through the piston orifice and the slipper orifice should be equal to the oil flow through the variable annular damping. So, p_r is determined by

$${p_{\rm{r}}} = {{{C_{{\rm{pb}}}}{C_{{\rm{sb}}}}{p_{\rm{p}}} + ({C_{{\rm{pb}}}} + {C_{{\rm{sb}}}}){C_{{\rm{sp}}}}{p_{\rm{L}}}} \over {{C_{{\rm{pb}}}}{C_{{\rm{sb}}}} + {C_{{\rm{pb}}}}{C_{{\rm{sp}}}} + {C_{{\rm{sb}}}}{C_{{\rm{sp}}}}}}.$$

(A3)

The pressure distribution p_oil under the slipper sealing land is expressed as

$${p_{{\rm{oil}}}} = {p_{\rm{L}}} + {{\ln ({R_{\rm{s}}}/r)} \over {\ln ({R_{\rm{s}}}/{r_{\rm{s}}})}}({p_{\rm{r}}} - {p_{\rm{L}}}).$$

(A4)

The lifting force of the lubricating oil film is expressed as

$\begin{gathered} F_1 = \pi p_r r_s^2 + \int_{r_s }^{R_s } {2\pi rp_{oil} } dr \hfill \\ = \pi p_r r_s^2 + \int_{r_s }^{R_s } {2\pi r} \left( {p_L + \frac{{\ln (R_s /r)}} {{\ln (R_s /r_s )}}(p_r - p_L )} \right)dr \hfill \\ = \pi p_L R_s^2 + \frac{{\pi (R_s^2 - r_s^2 )}} {{2\ln (R_s /r_s )}}(p_r - p_L ) \hfill \\ = \pi p_L R_s^2 + \frac{{3\mu C_{pb} C_{sb} C_{sp} (R_s^2 - r_s^2 )(p_p - p_L )}} {{h^3 (C_{pb} C_{sb} + C_{pb} C_{sb} + C_{sb} C_{sp} )}}. \hfill \\ \end{gathered} $

(A5)

A2 Supporting stiffness of the lubricating oil film

The supporting stiffness is characterized by the change in the lifting force generated by per unit of change of oil film thickness. Thus, the supporting stiffness is calculated by

$\begin{gathered} J = - \frac{{dF_1 }} {{dh}} \hfill \\ = - \frac{{d\left( {\pi p_L R_s^2 + \frac{{3\mu C_{pb} C_{sb} C_{sp} (R_s^2 - r_s^2 )(p_p - p_L )}} {{h^3 (C_{pb} C_{sb} + C_{pb} C_{sp} + C_{sb} C_{sp} )}}} \right)}} {{dh}} \hfill \\ = \frac{{1152\pi (R_s^2 - r_s^2 )d_1^4 d_2^4 (d_1^4 l_2 + d_2^4 l_1 )h^2 (p_p - p_L )}} {{[6d_1^4 d_2^4 \ln (R_s /r_s ) + 128(d_1^4 l_2 + d_2^4 l_1 )h^3 ]^2 }} \hfill \\ = \frac{{ah^2 (p_p - p_L )}} {{(b + ch^3 )^2 }}, \hfill \\ \end{gathered} $

(A6)

where

$$\matrix{{a = 1152{\rm{\pi }}(R_{\rm{s}}^2 - r_{\rm{s}}^2)d_1^4d_2^4(d_1^4{l_2} + d_2^4{l_1}),} \hfill \cr {b = 6d_1^4d_2^4\ln ({R_{\rm{s}}}/{r_{\rm{s}}}),} \hfill \cr {c = 128(d_1^4{l_2} + d_2^4{l_1}).} \hfill \cr }$$