1 Introduction

Water content is a basic parameter of the three-phase-system of soil and affects soil behavior notably in geotechnical engineering. Obviously, therefore, it is of great significance to be able to test the water content of soil efficiently. The time domain reflectometry (TDR) method has been widely used to measure water content in agriculture, hydraulic engineering, geotechnical engineering, etc., for its advantages of speed, reliability, and the possibility of automatic monitoring (Drnevich et al., 2001; Noborio, 2001; Imhoff et al., 2007; Cui et al., 2013; Chen, 2014).

The crucial point in calibrating soil water content using TDR technology is to establish the relationship between the dielectric constant and the water content, which is usually referred to as the calibration equation. At present there are mainly two approaches to set up the equation. One is the volumetric mixing model, which acquires the dielectric constant of a mixture by taking a weighted average of the dielectric constant of each component in the mixture according to their volumetric proportions. Since this theoretical model is usually based on some assumptions, it has limitations in practical use (Birchak et al., 1974; Dobson et al., 1985; Heimovaara et al., 1994; Chen et al., 2003). The other approach is to find a purely empirical equation to fit the experimental data points. Among these empirical equations, Topp’s equation is widely used (Topp et al., 1980). This equation shows that the relationship between apparent dielectric constant and volumetric water content is not sensitive to soil texture, soil bulk density, temperature, salt content, etc. Many studies found that this empirical equation had a high accuracy for inorganic soils but was inapplicable to organic soils, fine textural soils, and clay soils (Herkelrath et al., 1991; Jacobsen and Schjønning, 1993; Dirksen and Dasberg, 1993; Ponizovsky et al., 1999). There are also other types of empirical equations including a linear relationship between volumetric water content and the square root of the apparent dielectric constant (Hook and Livingston, 1996; Yu et al., 1997; Masbruch and Ferré, 2003). There are also equations considering the effect of soil density (Ledieu et al., 1986; Malicki et al., 1996). However, in geotechnical engineering, gravimetric water content is used more extensively. According to the theory of TDR, two physical quantities, dielectric constant and bulk electrical conductivity, of soil can be obtained through the TDR waveforms. The two parameters are used in an empirical relationship relating gravimetric water content and dry density. Siddiqui and Drnevich (1995) proposed a linear calibration equation to relate dielectric constant with gravimetric water content and dry density. Then the corresponding ‘two-step method’ was performed to obtain gravimetric water content and dry density from field measurements. Yu and Drnevich (2004) established a linear empirical calibration equation to relate bulk electrical conductivity to gravimetric water content and dry density. Using this equation with Siddiqui and Drnevich (1995)’s equation, only one TDR test is required to obtain the parameters of soil in situ. This method is called the ‘one-step method’. Since the relationship between soil bulk electrical conductivity and gravimetric water content is not linear (Abu-Hassanein et al., 1996; Zambrano, 2006), Jung (2011) proposed a ‘voltage normalization method’ and developed a calibration equation between the voltage drop parameter and the apparent dielectric constant to replace the bulk electrical conductivity equation in the ‘one-step method’. It is important that laboratory tests should be conducted to obtain the constants in the equations before using the ‘one-step method’ and the ‘two-step method’.

Generally, after calibration of the constants of the empirical equations, water content can be measured in the laboratory and in the field by the TDR method conveniently and efficiently with a high accuracy. But for the reasons listed below, there are some constraints on applying these calibration equations in field tests:

  1. 1.

    The ‘two-step method’ takes time and energy to obtain the measurements for the field test. In particular, when continuous testing at different depths is required, this method will be invalid since it is difficult to perform the second TDR test.

  2. 2.

    For both the ‘one-step method’ and the ‘two-step method’, the constants of the calibration equations are soil-dependent. As the soil is usually heterogeneous in the field and not of a single soil type, the calibration of each soil’s constants is difficult.

Hence, it is of great significance to propose a calibration equation that is applicable to various soils and correlates gravimetric water content with apparent dielectric constant directly in geotechnical practice. The object of this study is to establish such a calibration equation through analyzing TDR data points from laboratory tests and the literature.

2 A new empirical calibration equation

Herein, the soil-water-air three phase system of soil is described according to Hook and Livingston (1996) (Fig. 1). Solid particles are considered as an impervious layer with thickness ls and dielectric constant Ks that can have adsorbed moisture. Liquid and air phases are also treated as a liquid layer and an air layer with thicknesses lw and la, and dielectric constants Kw and K, respectively. X1 and X2 represent the positions of the probe inserted into the soil. The relationship between the volumes of each phase is:

$$l = {l_{\rm{a}}} + {l_{\rm{w}}} + {l_{\rm{s}}}{.}$$
(1)
Fig. 1
figure 1

Soil-water-air transmission line model (Reprinted from (Hook and Livingston, 1996), Copyright 1996, with permission from ACSESS)

Full size image

It is assumed that the total travel time of the TDR waveform through the tested soil sample is equal to the sum of the time in each phase, which can be given by

$$t = {t_{\rm{s}}} + {t_{\rm{w}}} + {t_{\rm{a}}},$$
(2)

where t, ts, tw, and ta represent the time of TDR waveform travel in the system, solid particles, water, and air, respectively.

Topp et al. (1980) showed that the velocity of an electromagnetic wave travelling through the medium could be described by an apparent dielectric constant Ka:

$$v = {c \over {\sqrt {{K_{\rm{a}}}} }},$$
(3)

where v is the velocity of electromagnetic wave that travels through the medium, and c is the velocity of an electromagnetic wave in free space (the apparent dielectric constant is also called the dielectric constant, so the two concepts are the same in this study).

The velocity of the TDR waveform in each phase can also be described by

$${v_i} = {{2{l_i}} \over {{t_i}}},$$
(4)

where i represents s, w, or a.

Combining Eqs. (2)–(4) leads to the equation:

$$l\sqrt {{K_{\rm{a}}}} = {l_{\rm{s}}}\sqrt {{K_{\rm{s}}}} + {l_{\rm{w}}}\sqrt {{K_{\rm{w}}}} + {l_{\rm{a}}}\sqrt K {.}$$
(5)

Define α as the value of the volume of the air phase compared to the volume of the solid phase, i.e.,

$$\alpha = {{{l_{\rm{a}}}} \over {{l_{\rm{s}}}}},$$
(6)

the gravimetric water content of soil can be expressed as

$$w = {{{l_{\rm{w}}}} \over {{G_{\rm{s}}}{l_{\rm{s}}}}},$$
(7)

where Gs is the specific gravity of the solids.

Combining Eq. (1) and Eqs. (5)–(7) leads to Eq. (8):

$$w = {{ - \sqrt K - {{\sqrt {{K_{\rm{s}}}} - \sqrt K } \over {1 + \alpha }} + \sqrt {{K_{\rm{a}}}} } \over {{G_{\rm{s}}}{{\sqrt {{K_{\rm{w}}}} } \over {1 + \alpha }} - {{{G_{\rm{s}}}} \over {1 + \alpha }}\sqrt {{K_{\rm{a}}}} }}{.}$$
(8)

As shown in Eq. (8), the relationship between gravimetric water content and apparent dielectric constant is influenced by the dielectric constant of each component, the value of α, etc. For most natural soils, the typical values of the dielectric constants of the solid phase Ks, air phase K, and liquid phase Kw are 3–5, 1, and 81, respectively. The value of the specific gravity of solids Gs is usually around 2.6–2.8. The parameters above can be regarded as constants. According to the definition of α, α is less than the void ratio, which varies between 0.4–1.5 (Chen Y., 2011). Then, the range of 1/(1+α) is limited between 0.4–0.71, which represents the degree of compaction of the soil. Therefore, it assumes that treating 1/(1+α) as constant will introduce negligible errors for soils of different types and compaction. From Eq. (8), the calibration equation between gravimetric water content and apparent dielectric constant has the form of

$$w = {{A + \sqrt {{K_{\rm{a}}}} } \over {B + C\sqrt {{K_{\rm{a}}}} }},$$
(9)

where A, B, and C are empirical constants. Values of them are obtained through regression analysis of real tests.

3 Data collection

To obtain the parameters in Eq. (9) through regression analysis, a total of 418 data points from TDR tests of 45 soil samples from our experiments and from the literature were collected.

3.1 Data from laboratory test

Three types of soils commonly used in engineering were used to conduct the laboratory tests: Fujian sand, Qiantang silt, and one clay soil. The properties of these soils, including the specific gravity of solids (Gs), liquid limit (LL), plasticity index (PI), grain-size distributions, and the classified types by the Unified Soil Classification System (USCS) are shown in Table 1.

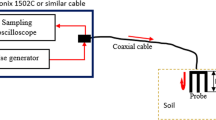
Table 1 Physical properties of soils in the laboratory tests
Full size table

The TDR tests were conducted with the Campbell Scientific TDR 100 apparatus and its PCTDR software. The TDR waveforms are analyzed to obtain the dielectric constant (Baker and Allmaras, 1990). The probe used here is the same as the one recommended by ASTM (2012a) with a height of 116 mm for the compact mold.

Before the test, the soil samples were oven dried, pulverized, sieved first, and mixed with tap water to approach the targeted water contents. After being placed in a room with a constant temperature around 20 °C in a sealed plastic bag for 24 h, the soil samples were then compacted in the mold according to ASTM (2012b) and a TDR test was performed. Finally the soil samples were oven dried to obtain the real gravimetric water content.

Through this method, the dielectric constant and the dry density of the sand, silt, and clay soil samples with seven, seven, and six different water contents, respectively, were obtained.

3.2 Data from the field test

Based on the pavement maintenance project of an airport in the west of China, TDR tests for soils of different depths at the pavement area and soil surface area were performed. Soil samples at targeted depths were taken by the dry drilling method. Part of the soil was sealed in plastic bags and tested by oven dry method while the rest was compacted in the mold for a TDR test. The properties of field soils are shown in Table 2.

Table 2 Physical properties of the field soils
Full size table

As the test condition in the field was complex and time was limited, twelve data points were obtained.

3.3 Data from the literature

Information from the literature on 39 soil samples and 386 TDR data points, including the values of dielectric constant, dry density, and gravimetric water content by the oven dry method, was used for re-analysis in this study. In this database, the number of samples for sandy soils, silt soils, and clay soils are 9, 8, and 22, respectively. The range of gravimetric water content is 0–0.55 g/g and dry density is 1.07–2.3 g/cm3. Temperature varies from 4 °C to 40 °C. Properties of soils from the literature are shown in Table 3.

Table 3 Properties of the soils from literatures
Full size table

According to their properties, the soils collected are classified into four types: sandy soils (S), silt soils (ML), low plasticity clay soils (CL) and high plasticity clay soils (CH). According to USCS, S soils include SW, SP, SM, SM-SC, and SM-SW soil types. CL soils include CL and CL-ML soil types. CH soils include CH and CH-CL soil types. The compaction energy levels used in Jung (2011) on ASTM Reference Soils (ASTM, 2010) were 360, 600, and 2700 kJ/m3 for compaction methods of reduced compaction (RC), standard compaction (SC), and modified compaction (MC), respectively (ASTM, 2007; 2009). Lin (1999) used the same compaction methods to conduct a compaction test for M1–M5 soils. The values of electrical conductivity used by Jung (2011) to perform a TDR test on ASTM Reference Soils (ASTM, 2010) are about 62 mS/m for tap water and 130 mS/m for saline water.

4 Results and discussion

4.1 Regression analysis

The data base collected above was used to obtain the parameters in Eq. (9) through regression analysis. As shown in Fig. 2 (p.245), ten points labeled with squares show great disparity, and these points were omitted during data fitting. At the same time, only the data points at 20 °C given by Drnevich et al. (2001) were adopted for the regression analysis. It should be pointed out that the subsequent statistical analysis covered the ten omitted scattered points. The results of regression analysis are shown in Fig. 2 and the empirical calibration equation is given in Eq. (10). The correlation coefficient R2 is 0.9019, showing a good correlation between the regression results and the data points.

$$w = {{ - 1{.}4637 + \sqrt {{K_{\rm{a}}}} } \over {22{.}1373 - 1{.}4606\sqrt {{K_{\rm{a}}}} }}{.}$$
(10)
Fig. 2
figure 2

Result of regression analysis by Eq. (10)

Full size image

Eq. (10) ignores the influence of soil type, dry density, compaction energy, pore fluid conductivity, temperature, etc. To quantify and evaluate the effect of these elements on the accuracy of Eq. (10), statistical quantitative evaluation indexes are adopted as follows: (1) errors (Δw) reflecting the difference between water contents calculated by Eq. (10) and by the oven dry method; (2) average errors (E); (3) standard errors (SE); (4) standard errors of estimate (SEE). E is used to evaluate the degree of deviation of the calculated result from the real value and SE indicates the discrete extent of E. SEE estimates the dispersion of the overall errors (Jung, 2011). The definitions of each parameter are shown as follows:

$$\Delta w = w - {w_{\rm{o}}},$$
(11)
$$E = {{\sum\nolimits_1^N {\vert \Delta w \vert } } \over N},$$
(12)
$${\rm{SE}} = \sqrt {{{\sum\nolimits_1^N {{{(\Delta w - E)}^2}} } \over N}},$$
(13)
$${\rm{SEE}} = \sqrt {{{\sum\nolimits_1^N {{{(\Delta w)}^2}} } \over {N - 2}}},$$
(14)

where wo is gravimetric water content obtained by the oven dry method and N is the number of data points.

4.2 Soil type effects

Error variations along with water content for different soil types are shown in Fig. 3. Values of E, SE, SEE, and the distribution of errors are shown in Table 4.

Fig. 3
figure 3

Errors of water content by Eq. (10) vs. gravimetric water content for different soil types

Full size image
Table 4 Errors for water content by Eq. (10) vs. different soil types
Full size table

As shown in Fig. 3, errors tend to increase with the increasing of water content. The reason is that the values of A, B, and C are assumed constant in the proposed Eq. (9) and obtained through regression analysis, which means the variation of water content with dry density is ignored.

As shown in Table 4, the values of statistic parameters for S, ML, and CL soils are small and the ratio of errors within ±0.03 g/g are large, which indicates that Eq. (10) has a good accuracy for these soils. But for CH soils, it shows a relatively poor result, which can be attributed to ignorance of the effect of bound water for soils with high clay contents. In general, errors of most data points of all soil types are within ±0.05 g/g.

4.3 Dry density effects

Errors varying with dry density are shown in Fig. 4. Values of E, SE, SEE, and the distribution of errors are shown in Table 5.

Fig. 4
figure 4

Errors of water content by Eq. (10) vs. dry density

Full size image
Table 5 Errors for water content by Eq. (10) vs. different dry densities
Full size table

As shown in Fig. 4, errors show a relatively obvious dependency on the change of dry density. With the increasing of dry density, errors gradually vary from negative to positive, meaning that Eq. (10) underestimates the result in cases of low dry density and overestimates the result in cases of high dry density. Note that errors are large for low dry density soils. The reason can also be attributed to the neglect of variation of A, B, and C.

As shown in Table 5, when dry density ranges around 1.3–2.3 g/cm3, the statistic parameters E and SEE are around 0.01–0.03 g/g and errors within ±0.05 g/g are at a high level, indicating that Eq. (10) has a good accuracy for a wide scope of dry density cases. However, for dry density of 1.0–1.3 g/cm3, it shows a poor result, which indicates that at this condition, the effect of dry density on the result of Eq. (10) cannot be ignored. Therefore, it is necessary to correct Eq. (10) to consider the effect of dry density.

In Eq. (9), parameters A, B, and C are assumed to be constants. Actually, they are variables and have a relationship with dry density, etc. Herein, values of A, B, and C are assumed to have a simple linear relation with dry density and then Eq. (9) becomes

$$w = {{\left({a{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{w}}}}} + b} \right) + \sqrt {{K_{\rm{a}}}} } \over {\left({c{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{w}}}}} + d} \right) + \left({f{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{w}}}}} + g} \right)\sqrt {{K_{\rm{a}}}} }},$$
(15)

where a, b, c, d, f, and g are modified constants, ρd is the dry density, and ρw is the density of water.

The data points collected in this research are used to make regression analysis of the parameters in Eq. (15). The result empirical calibration equation is given in Eq. (16). The value of R2 is 0.9413.

$$\begin{array}{*{20}c} {w = \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{{0{.}3039{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{w}}}}} - 2{.}1851 + \sqrt {{K_{\rm{a}}}} } \over {\left({18{.}0283{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{w}}}}} - 17{.}9531} \right) + \left({ - 0{.}6806{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{w}}}}} + 1{.}8351} \right)\sqrt {{K_{\rm{a}}}} }}{.}} \end{array}$$
(16)

Values of E, SE, SEE, and the distribution of errors after considering the effect of dry density by Eq. (16) are shown in Table 6.

Table 6 Errors for water content by Eq. (16) vs. different dry densities
Full size table

Through Table 6, statistic parameters of soil samples with 1.0–1.3 g/cm3 dry densities show obvious improvement. In reality, if information on dry density is available, Eq. (16) can offer a better accuracy.

Considering total density ρt, which is more available in geotechnical engineering practice, Eq. (16) can be combined with the following equation:

$${\rho _{\rm{d}}} = {{{\rho _{\rm{t}}}} \over {1 + w}}{.}$$
(17)

Combining Eq. (16) and Eq. (17), we can obtain the following equation:

$$w = {{ - {f_2} + \sqrt {f_2^2 - 4{f_1}{f_3}} } \over {2{f_1}}},$$
(18)

where

$$\begin{array}{*{20}c} {{f_1} = - 17{.}9531 + 1{.}8351\sqrt {{K_{\rm{a}}}},}\\ {{f_2} = 18{.}0283{\rho _{\rm{t}}} - 0{.}6806{\rho _{\rm{t}}}\sqrt {{K_{\rm{a}}}} + 0{.}8351\sqrt {{K_{\rm{a}}}} - 15{.}768,}\\ {{f_3} = - 0{.}3039{\rho _{\rm{t}}} - \sqrt {{K_{\rm{a}}}} + 2{.}1851{.}} \end{array}$$

Eq. (18) can offer the same accuracy as Eq. (16). As it is expressed in terms of total density, it can be more practical.

4.4 Compaction energy effects

For a unit soil with certain water content, when compacted with different compaction energy levels, the sample obtained will have different structures and compactness, which will influence the dielectric constant by the TDR test. For brevity, only comparisons of water content by Eq. (10) and the oven dry method for ASTM-CH soil are plotted in Fig. 5. Values of E, SE, SEE, and the distribution of errors for soil samples of ASTM Reference Soils and M1–M5 soils with three compaction energy levels are shown in Table 7.

Fig. 5
figure 5

Comparisons of water content by Eq. (10) and the oven dry method for ASTM-CH soil at different compaction energy levels

Full size image
Table 7 Errors for water content by Eq. (10) at different compaction energy levels
Full size table

Fig. 5 and Table 7 show that, with the compaction energy increasing, E and SEE have an increasing trend and the ratios of errors within ±0.03 g/g and ±0.05 g/g decrease correspondingly. This means that the errors of Eq. (10) increase with the increasing of compaction energy.

4.5 Pore fluid conductivity effects

Soils with different pore fluid conductivities will cause different energy losses under the TDR waveform, which will influence the value of their dielectric constants. Comparisons of water content by Eq. (10) and the oven dry method for ASTM-CH soil are shown in Fig. 6. Values of E, SE, SEE, and the distribution of errors for ASTM-CH soil with different pore fluid conductivity are shown in Table 8.

Fig. 6
figure 6

Comparisons of water content by Eq. (10) and the oven dry method for ASTM-CH soil at different pore fluid conductivities

Full size image
Table 8 Errors for water content by Eq. (10) at different pore fluid conductivities
Full size table

As shown in Fig. 6 and Table 8, with the pore fluid conductivity increasing, the statistical parameters E and SEE have an increasing trend and the ratio of errors within ±0.03 g/g and ±0.05 g/g decrease correspondingly, which indicates that errors of Eq. (10) increase with the increasing of pore fluid conductivity. Note that the parameters for soil with deionized water as pore fluid seem not to be in accordance with the conclusion above, which may be because the constants in Eq. (10) are obtained mainly from soil samples with tap water as the pore fluid. In addition, as the samples are small and the salinity is at a low level, the conclusions above need to be further discussed.

4.6 Temperature effects

Temperature has a different effect on the value of dielectric constant for different soil types (Wraith and Or, 1999; Robinson et al., 2003; Schanz et al., 2011). Pepin et al. (1995) and Persson and Berndtsson (1998) found that for sandy soils, dielectric constant decreases with the increasing of temperature. Drnevich et al. (2001) pointed out that due to a large content of clay particles, the dielectric constant of cohesive soils increases with the increasing of temperature.

Drnevich et al. (2001) performed TDR tests on cohesive and cohesionless soils with temperatures ranging from 4 °C to 40 °C. For brevity, only comparisons of water content by Eq. (10) and the oven dry method for Crosby Till soil are plotted in Fig. 7. Values of E, SE, SEE, and the distribution of errors for soil samples with different temperatures are shown in Table 9.

Fig. 7
figure 7

Comparisons of water content by Eq. (10) and the oven dry method for Crosby Till soil at different temperatures

Full size image
Table 9 Errors for water content by Eq. (10) at different temperatures
Full size table

As shown in Fig. 7 and Table 9, the statistical parameters E and SEE are relatively large, which is mainly due to the presence of some scattered data, specifically, the data points above 0.4 g/g with a low dry density. Errors trend to decrease with the increasing in temperature. When the temperature is within 4–30 °C, it has no significant influence on the result of Eq. (10). Drnevich et al. (2001) pointed out that the effect of temperatures from 5 °C to 20 °C can be ignored since their influence is small. ASTM (2012a) presents the equations used to modify the effect of temperature.

4.7 Comparison of Topp’s equation and ‘two-step method’ equation

Topp et al. (1980) proposed a widely used empirical calibration equation:

$$\begin{array}{*{20}c} {\theta = 4{.}3 \times {{10}^{ - 6}}K_{\rm{a}}^3 - 5{.}5 \times {{10}^{ - 4}}K_{\rm{a}}^2}\\ {\quad + 2{.}92 \times {{10}^{ - 2}}{K_{\rm{a}}} - 5{.}3 \times {{10}^{ - 2}},} \end{array}$$
(19)

where θ is the volumetric water content.

Gravimetric water content (w) and volumetric water content (θ) are related as follows:

$$w = {{{\rho _{\rm{w}}}} \over {{\rho _{\rm{d}}}}}\theta {.}$$
(20)

Combining Eqs. (19) and (20), the gravimetric water content calculated by Topp’s equation is obtained.

Siddiqui and Drnevich (1995) performed the ‘two-step method’ to test the water content and dry density of soil. The empirical calibration equation they developed is

$$\sqrt {{K_{\rm{a}}}} {{{\rho _{\rm{w}}}} \over {{\rho _{\rm{d}}}}} = {a_1} + {b_1}w,$$
(21)

where a1 and b1 are calibration constants.

Drnevich et al. (2005) pointed out that although calibration constants in Eq. (21) are soil-dependent, uniform calibration constants can be used within acceptable limits for engineering practice. Herein, the values of a1 and b1 are 1 and 8.5 for cohesionless soils and 0.95 and 8.8 for cohesive soils, respectively, as recommended by Drnevich et al. (2005).

Comparisons of water content calculated by Eq. (10), Topp’s equation, Eq. (21), and Eq. (16) are shown in Table 10.

Table 10 Comparison of water content obtained by Eq. (10), Topp’s equation, Eq. (21), and Eq. (16)
Full size table

As shown in Table 10, results calculated by Topp’s equation, Eq. (21), and Eq. (10) are very close. Compared with Topp’s equation which expresses water content in volumetric form and the ‘two-step method’ equation which considers the influence of dry density, the statistical parameters E and SEE of Eq. (10) are slightly larger than those in the two other methods. After being modified by considering the dry density effects, Eq. (16) has a better accuracy.

Through the analysis above, Eq. (10) shows a good accuracy for most of soil types and a slight influence by a wide range of dry densities, compaction energy levels, and pore fluid conductivity, at temperatures commonly encountered in engineering practice.

5 Conclusions

From the database including 45 kinds of soil samples and 418 data points, an empirical calibration equation has been developed to relate gravimetric water content directly with apparent dielectric constant. The main conclusions are as follows:

  1. 1.

    The accuracy of the new empirical calibration equation is within ±0.05 g/g for commonly encountered soils.

  2. 2.

    The new empirical calibration equation underestimates the result in low dry density and overestimates the result in high dry density. For dry density ranging between 1.3 and 2.3 g/cm3, the new empirical calibration equation shows a good accuracy.

  3. 3.

    Errors of the new empirical calibration equation tend to increase with the increasing of compaction energy and pore fluid conductivity. However, for the commonly encountered ranges of compaction energy and pore fluid conductivity, the new empirical calibration has a good accuracy.

  4. 4.

    Temperature has no sensible influence on the results from the new empirical calibration equation when it is used within 4–30 °C.

  5. 5.

    This empirical calibration equation can be used to measure water content by the TDR method conveniently and efficiently in engineering practice without calibration.