1 Introduction

Surface quality has a marked effect on the physical, chemical, and mechanical properties of a workpiece. Generally, the quality of the machined surface depends upon the positional accuracy of the tool tip relative to the part being machined, and this is affected by various errors caused by mechanical-geometric imperfections, mis-alignments, and wear of the linkages and elements of the machine tool structure (Okafor and Ertekin, 2000), etc. Most of these errors can be classified into three different types:

  1. 1.

    Errors due to geometric inaccuracies: manufacturing errors, assembly errors, etc.

  2. 2.

    Thermally induced errors: thermal expansion of the machine structure, etc.

  3. 3.

    Cutting force induced errors: stress deformation, etc.

Usually, geometric and spindle errors determine the basic inaccuracy of the machine tool (Ramesh et al., 2000). Most of the various geometric and spindle error components that are generated can be represented as the positioning error of each axis, straightness of each axis in perpendicular direction, pitch, yaw, and roll errors of each of the axes, and squareness error between the axes. These errors cause resultant positioning errors (Choi et al., 2003).

Rigid body kinematics and a homogeneous transformation matrix (HTM) are the most commonly used modelling techniques for machine error characterization. Slocum (1992) described the use of the HTM to model the relative position of a rigid body in 3D space with respect to a given coordinate system. Over the past decades, many researchers have developed the integrated errors model for multi-axis machine tools based on these modelling techniques. Choi et al. (2003) proposed a modified volumetric errors model for a three-axis machine tool, and predicted the roundness error of the machined surface. Both the geometric and spindle errors were integrated in the model. Abbaszadeh-Mir et al. (2002) presented an integrated errors model for a five-axis machine tool. Based on the error model, Bringmann and Knapp (2006) discussed the model-based calibration of a five-axis machine tool. Tian et al. (2014) proposed a general and systematic approach for geometric error modeling of machine tools due to the geometric errors arising from manufacturing and assembly. Zhong et al. (2015) presented a position geometric error modeling, identification, and compensation method for large five-axis machining center prototype.

In previous studies, models are mainly concerned with the mathematical expression of a machine tool’s integrated errors. Further study on the visualization of a 3D representation of a surface considering the geometric and spindle errors is relatively little reported, although the visualization of a 3D surface is an intuitive and powerful technique in surface characterization and comparison. There are some methods to generate the topography of a machined surface. In general, these can broadly be divided into two categories: (1) to reconstruct the 3D model of the surface with the measurement data captured from the actual machined surface (Bispink, 1992); (2) to predict the topography of the machined surface without the measurement data (Zhou, 2009). Compared with the first strategy, the focus of the prediction of surface topography is to study the surface generation mechanism which is quite different in different machining methods. Cheung and Lee (2000) proposed a method to predict the surface topography in ultra-precision diamond turning. Brandt et al. (2013) studied the surface generation process with consideration of the balance state in diamond machining. Yang and Liu (2015) developed a surface generation model which is used to predict the surface topography in peripheral milling with incorporating the cutting process parameters and several sources of machining error.

This paper proposes an approach for modeling and prediction of the surface generated in end turning process, which has taken into account the effects of the positioning errors between the tool tip and the part being machined. With the proposed method, the relationship between the machine errors and the topography of end turning surface is established. Further analysis of the effect of geometric and spindle errors on surface quality has been carried out. At the end of this paper, a simple approach to find the principal error component is proposed.

2 Volumetric errors model of lathe

The process of developing the integrated errors model mainly aims to obtain the relative displacement error between the cutting tool and the workpiece in the turning process. In general, a lathe consists of a bed, spindle, slide carriages, and a cutting tool. Practically, due to a variety of factors, such as manufacturing errors, assembly errors, temperature change, and stress deformation, the ideal relative position between different components cannot be achieved. Geometric and spindle errors are those errors that are extant in a machine on account of its basic design, the inaccuracies built-in during assembly and the components used on the machine. As such, they form one of the biggest sources of inaccuracy. In this paper, we mainly researched the effect of geometric and spindle errors.

The number of error elements varies depending on the number of axes of a particular machine. For a lathe as a two-axis machine tool, 19 error components are generally identified consisting of six error components along each axis and one squareness error (Table 1).

Table 1 Geometric error components of lathe
Full size table

Fig. 1 shows the topology of a lathe. According to the topology, six coordinate systems have been defined. The reference coordinate system (RCS) is established on the bed. The Z-slide carriage coordinate system (ZCS) is built on Z-slide carriage. The X-slide carriage coordinate system (XCS) is established on X-slide carriage. The spindle coordinate system (SCS) is set on the spindle. TCS is the cutting tool’s coordinate system. WCS is the coordinate system located on the workpiece. We define a tool branch, which locates the tool in RCS, and a workpiece branch, which locates the workpiece W in RCS. The integrated volumetric errors model can be divided into two sub-models. One is the tool branch which contains two slide carriages and a cutting tool. The other is the workpiece branch which consists of a spindle and a workpiece.

Fig. 1
figure 1

Structure (a) and topology (b) of lathe

Full size image

These branches can be regarded as a sequence of elements connected by joints that provide either rotational or translational motion. The relative location of these elements to other elements and to the reference frame can be obtained through HTM based on rigid body kinematics. To simplify the calculation, all the origins of coordinate systems are defined at the center of the workpiece except for TCS (Fig. 2, where ap is the depth of cut, Xm is the moving distance of the cutting tool in feed direction, and n is the spindle rotation speed).

Fig. 2
figure 2

Process of end turning

Full size image

2.1 Tool’s position in RCS

The tool branch is typically composed of two moving elements (namely Z-slide carriage and X-slide carriage), and a cutting tool. These two linear moving elements are designed to have only one degree of freedom in the z- and x-axis directions, respectively. However, all moving elements have six motion errors (three translational errors and three rotational errors) for geometric inaccuracy.

HTM \(T_{1}^{2}\) denotes the actual pose of the Z-slide carriage in frame RCS. With the consideration of the error components listed in Table 1, it can be formulated as

((1))

where δ x (z), δ y (z), and δ z (z) are the linear error motions of the linear z-axis along the x-, y-, and z-axis direction; ε x (z), ε y (z), and ε z (z) represent the rotational error motions of the linear z-axis about the x-, y-, and z-axis directions, respectively.

Meanwhile, the misalignments between the X-slide carriage and the Z-slide carriage cause a squareness error. As a result, there is a small angle between the moving direction of the X-slide carriage and the x-axis of ZCS, known as the squareness error η xz . Therefore, The HTM \(T_{2}^{3}\) from X-slide carriage to Z-slide carriage which represents the pose of the X-slide carriage in frame ZCS should take into account the effect of the squareness error η xz :

((2))

where δ x (x), δ y (x), and δ z (x) are translational errors; ε x (x), ε y (x), and ε z (x) are rotational errors when the X-slide carriage is moving in the x-axis direction; and R is the radius of workpiece.

The cutting tool is mounted on the X-slide carriage. The HTM \(T_{3}^{4}\) from cutting tool to X-slide carriage is a unit matrix I. As the origin of frame TCS is located on the tool tip, the coordinate of the tool tip in TCS can be expressed as pT=[0, 0, 0, 1]T. The tool tip’s position p′T in RCS can be obtained by successively multiplying the homogeneous transformation matrices from the reference coordinate system to the tool coordinate system:

$${p^{\prime}_T} = T_1^2T_2^3T_3^4{p_T}.$$
(3)

2.2 Workpiece’s position in RCS

In practice, the actual rotation center of the spindle will shift from the nominal rotation center. The HTM \(T_{1}^{5}\) from the SCS to the RCS can be represented as Eq. (4) with the assumption of small angle approximation.

((4))

where A(θ)=ε x (θ)sinθ−ε y (θ)cosθ and B(θ)=ε x (θ)cosθ+ ε y (θ)sinθ, and θ represents the rotation angle of the spindle.

Since the workpiece is fixed on the spindle, the HTM \(T_{5}^{6}\) from the workpiece to the spindle is a unit matrix I. Given that the nominal coordinate of the cutting point on machined surface in WCS is pW, and the error is ΔpW, then its actual coordinate p′W in RCS can be obtained by

$${p^{\prime}_{\rm{W}}} = T_1^5{\rm T}_5^6({p_{\rm{W}}} + \Delta {p_{\rm{W}}}).$$
(5)

2.3 Integrated volumetric errors model

In the turning process, the cutting tool tip coincides with the cutting point on the workpiece surface (Fig. 2). Therefore, the spatial relationship between the tool tip and the cutting point on the workpiece can be expressed as

$${p^{\prime}_{\rm{W}}} = {p^{\prime}_{\rm{T}}}.$$
(6)

Substituting Eqs. (3) and (5) into Eq. (6) gives the positioning errors of cutting point ΔpW as follows:

$$\Delta {p_{\rm{W}}} = {(T_5^6)^{ - 1}}{(T_1^5)^{ - 1}}T_1^2T_2^3T_3^4{p_{\rm{T}}} - {p_{\rm{W}}}.$$
(7)

Under ideal conditions, all the errors in Table 1 are equal to zero namely ΔpW=[0, 0, 0, 1]. In this case, the nominal cutting point coordinate pW in WCS can be easily obtained by Eq. (7):

$${p_{\rm{W}}} = {[(x - R)\cos \theta, \, - (x - R)\sin \theta, \, - z, \, 1]^{\rm{T}}}.$$
(8)

Substituting Eqs. (1), (2), (4), and (8) into Eq. (7), and neglecting the terms of higher than two, the actual tool positioning error versus workpiece which locates in the WCS can be obtained.

$$\left\{ \matrix{\Delta x = [{\delta _x}(x) + {\delta _z}(z)]\cos \theta + [(x - R){\varepsilon _z}(z) + {\delta _y}(x) \hfill \cr \quad \quad {\kern 1pt} + {\delta _y}(z)]\sin \theta - z[{\varepsilon _x}(\theta)\sin \theta - {\varepsilon _y}(\theta)\cos \theta ] \hfill \cr \quad \quad - {\delta _x}(\theta)\cos \theta - {\delta _y}(\theta)\sin \theta, \hfill \cr \Delta y = - [{\delta _x}(x) + {\delta _x}(z)]\sin \theta + [(x - R){\varepsilon _z}(z) + {\delta _y}(x) \hfill \cr \quad \quad {\kern 1pt} {\kern 1pt} + {\delta _y}(z)]\cos \theta - z[{\varepsilon _x}(\theta)\cos \theta + {\varepsilon _y}(\theta)\sin \theta ] \hfill \cr \quad \quad + {\delta _x}(\theta)\sin \theta - {\delta _y}(\theta)\cos \theta, \hfill \cr \Delta z = (x - R){\varepsilon _y}(\theta) - (x - R){\varepsilon _y}(z) + {\delta _z}(x) - x{\eta _{xz}} \hfill \cr \quad \quad + {\delta _z}(z) - {\delta _z}(\theta). \hfill \cr} \right.$$
(9)

When machining the end surface, the cutting tool does not move in the z direction. Thus, the errors related to the Z-slide carriage remain unchanged. Therefore, Eq. (9) can be rewritten as

$$\left\{ \matrix{\Delta x = [{\delta _x}(x) + {\delta _x}(z)]\cos \theta + [(x - R){\varepsilon _z}(z) + {\delta _y}(x) \hfill \cr \quad \quad + {\delta _y}(z)]\sin \theta - {\delta _x}(\theta)\cos \theta - {\delta _y}(\theta)\sin \theta, \hfill \cr \Delta y = - [{\delta _x}(x) + {\delta _x}(z)]\sin \theta + [(x - R){\varepsilon _z}(z) + {\delta _y}(x) \hfill \cr \quad \quad {\kern 1pt} {\kern 1pt} + {\delta _y}(z)]\cos \theta {\kern 1pt} + {\delta _x}(\theta)\sin \theta - {\delta _y}(\theta)\cos \theta, \hfill \cr \Delta z = (x - R){\varepsilon _y}(\theta) - (x - R){\varepsilon _y}(z) - x{\eta _{xz}} + {\delta _z}(z) - {\delta _z}(\theta), \hfill \cr} \right.$$
(10)

which describes the integrated volumetric errors in the end turning process.

3 End turning surface topography model

The actual turning surface is a synthetic result of machine errors, tool geometry, and cutting parameters. The mathematical model of the end turning surface should account for the combined impact of the three.

3.1 Ideal end turning surface topography model

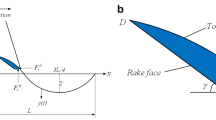
Under ideal conditions, the turning surface profile in the radial direction is depicted in Fig. 3. It is generated by repetition of the tool profile at intervals of feed per revolution (Cheung and Lee, 2000).

Fig. 3
figure 3

The ideal turning surface profile in the radial direction

Full size image

The height Rt between the peak and valley of the turning surface profile is given as

$${R_{\rm{t}}} = {R_0} - \sqrt {R_0^2 - {{(f{\rm{/}}2)}^2}},$$
(11)

where f is the feed per revolution, and R0 is the tool nose radius. As f(R0, Eq. (11) can be rewritten as

$${R_{\rm{t}}} \approx {{{f^2}} \over {8{R_0}}}.$$
(12)

After establishing the coordinate system as shown in Fig. 3, the height h(x) at any point of the tool tip profile can be expressed as

$$h(x) = {{{{(x - f/2)}^2}} \over {2{R_0}}}.$$
(13)

To predict the topography of the end turning surface, the surface has been divided into series of radial sections (Fig. 4). The number of radial sections N1 is given as

$${N_1} = \left\lceil {{{2{\rm{\pi }}} \over {\Delta \theta }}} \right\rceil,$$
(14)

where Δθ represents the angular resolution being adopted.

Fig. 4
figure 4

Tool trajectory under ideal conditions

Full size image

The number of spindle revolutions N2 during the turning process can be expressed as

$${N_2} = {R \over f}.$$
(15)

Therefore, the total discrete point number of the cutting tool locus can be defined as

$$N = {N_1}{N_2}.$$
(16)

As shown in Fig. 4, the tool moves in a spiral locus towards the center of the workpiece. The spiral locus can be expressed in polar coordinate as

((17))

which describes the locus of the cutting tool without errors.

3.2 Actual precision turning surface topography model

Actually, the geometric and spindle errors will lead to the distortion of the tool locus. The distortion in the z direction will significantly jeopardize the surface quality, but in the x and y directions it will have little influence. Additionally, the cutting tool does not move in the z direction. It follows that the machine errors related to Z-slide carriage remain unchanged. Therefore, the positional error of Z-slide carriage δ z (z) as a constant could be neglected. In this case, Eq. (11) can be reduced as

$$\Delta z = (x - R)[{\varepsilon _y}(\theta) - {\varepsilon _y}(z)] + {\delta _z}(x) - x{\eta _{xz}} - {\delta _z}(\theta).$$
(18)

In the local area of the turning surface, the roll error of spindle ε y (θ), the pitch error of the Z-slide carriage ε y (z), and the squareness error η xz have little change. They can be regarded as constants. Meanwhile, the displacement error of the workpiece in the vertical direction δ z (θ) usually can be simplified to a sine function changing with rotation angle (Cheung and Lee, 2000):

$${\delta _z}(\theta) = A\sin \left[ {2{\rm{\pi }}{f_{\rm{v}}}{{(i - 1)\Delta \theta } \over \omega } - \phi } \right],$$
(19)

where A is the amplitude of the displacement error, fv is the frequency, > is the initial phase, and ω is the spindle speed.

The straightness error of X-slide carriage δ z (x) is related to the slide carriage’s profile. Given that the straightness error of the X-slide carriage in the z direction is shown in Fig. 5.

Fig. 5
figure 5

Straightness error of the x -slide carriage in z direction δ z ( x )

Full size image

The curve shown in Fig. 5 is a spline curve which is generated by Matlab and used to simulate the straightness error of X-slide carriage. The tool tip position at the ith point of the tool locus can be represented as

$$\left\{ \matrix{x(i) = - r(i)\cos [\theta (i)] + \Delta x(i), \hfill \cr y(i) = r(i)\sin [\theta (i)] + \Delta y(i), \hfill \cr z(i) = - {a_{\rm{p}}} + \Delta z(i). \hfill \cr} \right.$$
(20)

The size of tool tip cannot be neglected with respect to the scale of surface morphology (Aramcharoen and Mativenga, 2009; Taha et al., 2010; Yusoff et al., 2010). The tool tip profile is shown in Fig. 3. It can be divided into a series of discrete points. Given that the discrete points number is N3. The spatial location of the jth tool tip discrete point when the tool cutting the ith point on the turning surface can be expressed in polar coordinates as

$$\left\{ \matrix{r(i,j) = R - (i - 1)f/{N_1} - (j - 1)f/{N_3}, \hfill \cr \theta (i,j) = - (i - 1)\Delta \theta, \hfill \cr z(i,j) = - {a_{\rm{p}}} + \Delta z(i) + {[(i - 1)f/{N_3} - 0.5f]^2}/{\rm{(}}2{R_0}). \hfill \cr} \right.$$
(21)

Its corresponding coordinates are given by

$$\left\{ \matrix{x(i,j) = - r(i,j)\cos [\theta (i)] + \Delta x(i), \hfill \cr y(i,j) = r(i,j)\sin [\theta (i)] + \Delta y(i), \hfill \cr z(i,j) = - {a_{\rm{p}}} + \Delta z(i) + {[(j - 1)f/{N_3} - 0.5f]^2}/{\rm{(}}2{R_0}), \hfill \cr} \right.$$
(22)

where i represents the cutting point on the end turning surface; and j represents the discrete point of the tool tip profile.

For the convenience of explanation, variables m and l are defined. m is the mth radial section, and l is the feed in radial direction. The relationship among i, m, and l is given as

$$i = m + (l - 1){N_1}.$$
(23)

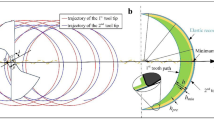
In practice, the volumetric errors Δz will lead to the trim between adjacent tool tip profile. As shown in Fig. 6, the lth tool tip profile in the mth radial section is partly cut by the (l−1)th and (l+1)th tool tip profile. The minimum edge profile below the intersecting points (Fig. 6) of each tool profile constitutes the surface profile. The surface roughness profile in radial direction of the workpiece can be constructed by trimming the lines above the points of intersection (Cheung and Lee, 2002). Given that p is a point of x-y plane, which is located on the mth radial section. z l −1, z l , and z l +1 represent the height of the (l−1)th, lth, and (l+1)th tool tip profile, respectively.

$${z_{l - 1}} = - {a_{\rm{p}}} + z[m + (l - 2){N_1}] + {{{{[(j - 1)f/{N_3} + f - 0.5f]}^2}} \over {2{R_0}}},$$
(24)
$${z_l} = - {a_{\rm{p}}} + z[m + (l - 1){N_1}] + {{[(j - 1)f/{N_3} - 0.5f]} \over {2{R_0}}},$$
(25)
$${z_{l + 1}} = - {a_{\rm{p}}} + z(m + l{N_1}) + {{{{[(j - 1)f/{N_3} - f - 0.5f]}^2}} \over {2{R_0}}}.$$
(26)
Fig. 6
figure 6

The trim between adjacent tool profile in radial direction

Full size image

As the actual height of point p is determined by the lowest tool tip profile, the actual height of the turning surface can be given as

$$z(i,j) = \min \{ {z_{l - 1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {z_l},{\kern 1pt} {\kern 1pt} {\kern 1pt} {z_{l + 1}}\}.$$
(27)

The end turning profile in the radial direction can be obtained by Eq. (27) (Fig. 7a). However, the interference will occur when the feed rate is small with respect to the volumetric errors, in which the surface formed at the preceding feed movement will be cut off by some succeeding tool movement (Fig. 7b). It can be seen that the surface profile formed per revolution is not only determined by the adjacent tool tip profile, but also by the other tool tip profile. For this reason, it is better to consider the effect of all tool profile when calculating the surface profile formed per revolution. Therefore, the actual coordinates of the point on the end turning surface are given by

$$\left\{ \matrix{x(i,j) = - \left[ {R - (i - 1){f \over {{N_1}}} - (j - 1){f \over {{N_3}}}} \right]\cos \theta + \Delta x(i), \hfill \cr y(i,j) = \left[ {R - (i - 1){f \over {{N_1}}} - (j - 1){f \over {{N_3}}}} \right]\sin \theta + \Delta y(i), \hfill \cr z(i,j) = \min \{ {z_{n - k}}\; \cdots \;{z_{n - 1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_{n + 1}}\; \cdots \;{z_{n + k}}\}. \hfill \cr} \right.$$
(28)
Fig. 7
figure 7

Simulated surface profile in the radial direction without (a) and with (b) tool interference

Full size image

These coordinates data are mapped on the surface elements of a cross lattice (Fig. 8). The surface elements are used to build the parametric surfacetopography in the end turning process, which are defined as

$$\left\{ \matrix{X = \left\lfloor {{{[{L_x}{\rm{/}}2 - r(i,j)\sin \theta + \Delta x(i)]} \over {{L_x}}}{n_x} + {1 \over 2}} \right\rfloor, \hfill \cr Y = \left\lfloor {{{[{L_y}{\rm{/}}2 + r(i,j)\sin \theta + \Delta y(i)]} \over {{L_y}}}{n_y} + {1 \over 2}} \right\rfloor, \hfill \cr Z = z(i,j), \hfill \cr} \right.$$
(29)

where n x and n y are the number of surface elements in the x and y directions; L x and L y are the length and the width of the simulated region, respectively.

Fig. 8
figure 8

Cross lattice used to build the parametric surface

Full size image

Thus, L x /n x and L y /n y are the intervals of the cross lattice in the x and y directions. They are much larger than the integrated errors in the x and y directions in the subsequent calculation process:

$${{{L_x}} \over {{n_x}}} \gg \Delta x(i),\,{{{L_y}} \over {{n_y}}} \gg \Delta y(i).$$
(30)

In this case, Eq. (30) can be reduced as

$$\left\{ \matrix{X = \left\lfloor {{{[{L_x}/2 - r(i,j)\sin \theta ]} \over {{L_x}}}{n_x} + {1 \over 2}} \right\rfloor, \hfill \cr Y = \left\lfloor {{{[{L_y}/2 + r(i,j)\sin \theta ]} \over {{L_y}}}{n_y} + {1 \over 2}} \right\rfloor, \hfill \cr Z = z(i,j). \hfill \cr} \right.$$
(31)

According to Eq. (31), real coding is adopted in the calculation of surface height data. After acquiring the height data of the points on the cross lattice, we can easily simulate the surface topography in end turning process by Matlab.

3.3 Prediction of surface roughness

A typical engineering surface consists of a range of spatial frequencies. The high frequency or short wavelength components are referred to as roughness, the medium frequencies as waviness and then there are low frequency components. As a standard procedure prior to areal roughness analysis, all the surface topography images are filtered. In this way, we identify and separate the functionally significant components of the surface in preparation for subsequent areal roughness analysis. A filter commonly used in surface filtering is the Gaussian filter given in ISO/CD 11562 (Krystek, 1996).

In this study, a low-pass Gaussian filter with cut-off wavelength of 0.8 mm is applied to separate the high frequency components. As shown in Fig. 9, the primary surface contains different scales of deviations. The filter adopted here can help us remove the long wavelength components, such as form errors and waviness.

Fig. 9
figure 9

Process of filtering

Full size image

After that, the surface roughness data is obtained. Generally, the arithmetic mean deviation (Sa), and the root mean square deviation (Sq) given in the work of Dong et al. (1994) are the simplest and most widely used amplitude parameters to evaluate areal roughness. It is assumed that sets {E MN } contains M×N filtered surface roughness heights over the simulated region. Then the predicted Sa and Sq are given as

$${S_{\rm{a}}} = {1 \over {MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\left\vert {E({x_i},{y_j})} \right\vert}},$$
(32)
$${S_{\rm{q}}} = \sqrt {{1 \over {MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left\vert {E({x_i},{y_j})} \right\vert}^2}}}},$$
(33)

where E(x i , y i ) is the predicted surface height on the filtered surface, M and N are the discrete points number in the x and y directions, respectively.

4 Simulation experiments and numerical analysis

4.1 Surface visualization

The visualization of a 3D representation of a surface is an intuitive but powerful and flexible technique in surface characterization and comparison. Without considering volumetric errors, the ideal turning surface topography has been simulated (Fig. 10).

Fig. 10
figure 10

Ideal turning surface

Full size image

It can be seen that the tool tip profile is perfectly marked on the turning surface when the tool moves with a spiral locus on the x-y plane to the center of the workpiece. However, the actual tool locus will deviate from the nominal position due to the machine errors.

To investigate the impact of the volumetric errors on the topography of the end turning surface, groups of experiments are conducted under various errors. The simulated conditions are listed in Table 2. Multiplying X-guide way straightness (Fig. 5) by different coefficients, a different carriage straightness error δ z (x) can be generated (Table 2). Simulated experiments in Cases a–d aim to analyze the effect of δ z (x), ε y (θ), ε y (z), and η xz on the end turning surface, respectively. The effect of spindle displacement error δ z (θ) with different amplitude and frequency combinations on the end turning surface is studied in Cases e–g. Case h simulates the topography of the end turning surface taking into account all the error components. These results are depicted in Fig. 11.

Fig. 11
figure 11figure 11

Simulated turning surface topography and surface radial profile in Case a–h ((a)–(h)) according to Table 2

Full size image
Table 2 Simulation plan under different error conditions
Full size table

Fig. 11a shows the effect of X-slide carriage straightness error δ z (x) on the surface topography. Note that the height of the surface profile in radial section becomes oscillating. Viewing from the surface profile, the tool path in the radial direction is nearly the same as the curve of the X-slide carriage straightness error shown in Fig. 5. Fig. 11b shows the effect of spindle roll error ε y (θ). It can be seen that the height of the surface increases as the radius decreases. It leads to a tilted surface profile in radialdirection. The effects of the carriage angular error ε y (z) and the squareness error η xz on the end turning surface are depicted in Figs. 11c and 11d, respectively. From Fig. 11c, it can be seen that the height of the surface decreases as the radius decreases. The topography shown in Fig. 11d is approximate to Fig. 11c. Both the tool path leans at a small angle in the clockwise direction.

Figs. 11e–11g show the effect of spindle displacement error δ z (θ) on the surface topography. Note that the topography distorts when the frequency changes. To explain this phenomenon, a ratio k is defined:

$$k = {{{f_{\rm{v}}}} \over {{f_{\rm{s}}}}} = {{{f_{\rm{v}}}} \over {n{\rm{/}}60}} = I + D,$$
(34)

where fv represents the frequency of δ z (θ); fs is spindle rotation frequency; I is 0 or a positive integer; and D is a decimal fraction in the range of [−0.5, 0.5].

The ratio k can be regarded as the number of spindle vibration cycles per revolution. Therefore, the integer I represents the completed vibration cycles. In Figs. 11e–11g, I=2. Thus, there are two ridges in Figs. 11e–11g. In Fig. 11e, D=0. This means that the spindle vibration completes an integer number of cycles per revolution, and makes the vibration equal in the same radial direction. This leads to the ridges stretching in a line. In other words, the fraction D makes the ridges distort. The sign of D determines the turning direction of these ridges. Lastly, surface under practical relevant condition concerning all volumetric errors is simulated as shown in Fig. 11h. From Fig. 11h, it can be seen that the simulated surface becomes rough compared with the ideal turning surface shown in Fig. 10.

4.2 Effect of geometric and spindle motion errors on surface roughness

To analyze the effect of geometric and spindle errors on the surface roughness, the Taguchi method is adopted in this study. In this experiment with six factors at five levels each, a standard L25 (56) orthogonal array is adopted in the study. Therefore, there are 25 simulations for a rotation rate of 1200 r/min, a tool nose radius of 1.554 mm, and a feed rate of 30 mm/min. Table 3 shows the results of the simulations, where no interaction among the six factors is assumed. Whereas Tables 4 and 5 show the average surface roughness for six factors under different levels evaluated by Sa and Sq, respectively. These results are plotted in Fig. 12.

Fig. 12
figure 12

Computation results of S a (a) and S q (b) for different factors

Full size image
Table 3 The 25 repetitions of the experiment
Full size table
Table 4 Response table for average surface roughness S a
Full size table
Table 5 Response table for average surface roughness S q
Full size table

From Fig. 12, it can be seen that the amplitude and the frequency of the spindle displacement error δ z (θ) have the greater impact on the end turning surface roughness compared to the other error components.

To investigate whether these factors’ effect on surface roughness was significant or could be ignored, an analysis of variance (ANOVA) is introduced. Tables 6 and 7 show the results of the variance analysis for Sa and Sq, respectively. This analysis was carried out for a level of significance of 5%, i.e., for a 95% level of confidence. In others words, only the value of P shown in the last column of Tables 6 and 7 is less than 0.05, the corresponding factor could be considered significant to the value of surface roughness. From the results shown in Tables 6 and 7, it can be seen that amplitude and frequency of spindle displacement error are more significant to the turning surface quality.

Table 6 Variance analysis for S a
Full size table
Table 7 Variance analysis for S q
Full size table

The amplitude and the frequency of spindle displacement error have the most significant effect on the surface roughness. Other error components, such as the straightness error of slide carriage δ z (x) and angular errors (ε y (θ), εy(z), and η xz ) have little effect on surface roughness. This could be explained in terms of range of surface roughness wave-length. From Figs. 11a–11e, it can be seen that these angular and straightness would lead to the deviations of surface profile in radial direction, which is a kind ofsurface form deviations. However, these long wavelength surface components have been removed from the primary surface data after filtering. That means the processed surface data for surface roughness analysis mainly contains surface roughness information. That’s why these angular and straightness errors are less significant to the value of surface roughness compared to the displacement error of the spindle, as these errors mainly change the surface form deviation.

4.3 Principal component analysis

Principal component analysis (PCA) is used to find the principal error component. As mutual coupling of all forms of volumetric errors, it is difficult using a rigorous mathematical method to find the principal error component which most affects surface quality. Here, a simple and effective approach is proposed. Assuming that there are three error sources which affect the surface quality, designated as errors A, B, and C. Firstly, the arithmetic roughness Sa is calculated based on the model presented in Section 3. Then the arithmetic roughness Sa1 without consideration of error A is calculated. The contribution of error A to the surface roughness Sa is defined as

$$c({\rm{A}}) = {{\left\vert {{S_{\rm{a}}} - {S_{{\rm{a1}}}}} \right\vert} \over {{S_{\rm{a}}}}}.$$
(35)

Similarly, c(B) and c(C) are given as

$$c({\rm{B}}) = {{\left\vert {{S_{\rm{a}}} - {S_{{\rm{a2}}}}} \right\vert} \over {{S_{\rm{a}}}}},\quad c({\rm{C}}) = {{\left\vert {{S_{\rm{a}}} - {S_{{\rm{a3}}}}} \right\vert} \over {{S_{\rm{a}}}}}.$$
(36)

By normalizing c(A), c(B), and c(C), impact factor values of errors A, B, and C are obtained, expressed as

$$D({\rm{A}}) = {{c({\rm{A}})} \over {c({\rm{A}}) + c({\rm{B}}) + c({\rm{C}})}}.$$
(37)

The larger the impact factor value, the greater the influence on the surface roughness.

Fig. 13 shows the contribution of different error components to the surface roughness for the Z-slide carriage pitch error ε y (z) of 0.0003 rad, the spindle roll error ε y (θ) of 0.0002 rad, the squareness error η xz of 0.0005 rad, and the coefficient multiplying by the X-slide carriage straightness error δ z (x) of 2. In this case, the X-slide carriage straightness error δ z (x) is found to be the principal component which plays a dominant role on the surface roughness.

Fig. 13
figure 13

Principal component analysis

Full size image

4.4 Applications of the model

The model can be used in these applications:

  1. 1.

    To analyze the impact of geometric and spindle errors on the quality of the end turning surface. Conventionally, a large number of cutting experiments need to be conducted to investigate the impact of these machine errors. Usually not only are these cutting experiments time consuming, but are also influenced by the experience of the operator. The model can overcome these shortcomings. It is relatively easy to predict the surface roughness under different conditions just by changing the input parameters of the model.

  2. 2.

    To find the principal error. The method of PCA shown in Section 4.3 is an effective tool to find the principal error component which plays a dominant role on the surface roughness. It is like a compass, giving the direction to improve the surface quality.

For ease of operation, a corresponding user interface has been developed (Fig. 14).

Fig. 14
figure 14

Corresponding user interface

Full size image

5 Conclusions

This paper proposes an approach for modeling and simulation of the surface generated in end turning process. The model incorporates the effects of the positioning errors between the tool tip and the part being machined. It provides the possibility to simulate the surface topography for given errors. Additionally, with the help of the simulated surface, the effects of geometric and spindle errors on the quality of the end turning surface have been analyzed. The results showed a clear dependency between the machine errors and the value of surface roughness. At the end of this paper, a simple approach to find the principal volumetric error components has been proposed.