Introduction

Thermal treatment in rocks produces cracks and alters the crack networks because of the different thermal expansion coefficients of grain minerals. Therefore, it leads to changes in the mechanical and petrophysical properties of rocks (Guéguen and Schubnel, 2003; Seibt and Kellner, 2003; Fortin et al., 2005; Abdulagatova et al., 2009; Fortin et al., 2011). The evolution of such properties can have either a positive or negative impact on different engineering applications. For example, improving the rock permeability is important for both enhanced oil recovery (Shafiei and Dusseault, 2013) and gas extraction from tight gas reservoirs (Zou et al., 2012). On the other hand, in underground coal gasification (UCG), the cavity zone may have an adverse effect on the stability of the surrounding rock and the gasification products may escape though pre-existing and newly created cracks and, thus, pollute underground water aquifers (Minchener, 2005; Yang et al., 2008; Kapusta et al., 2013). Similarly, in nuclear waste storage sites, temperature induces thermal cracking in the surrounding rocks and thus increases their permeability which may lead to nuclear waste leakage (McKinley et al., 2006; Monfared et al., 2011).

A wide range of studies has been carried out to understand the role of thermal loading on the mechanical properties of porous rocks. Wu et al. (2005) performed experiments on sandstone specimens being loaded under and after high temperature. Their results demonstrated that the values of the peak-strength, the elastic modulus, and the deformation modulus of the sandstone they studied decreased gradually showing a generally similar variation tendency. Ranjith et al. (2012) explored the mechanical response of sandstone and their results demonstrated that the compressive strength and the elastic modulus increased with increasing temperature up to 500 °C and then decreased for higher temperature values. Zuo et al. (2012) observed and studied the thermal cracking of sandstone under different temperatures with scanning electron microscope (SEM), and the experimental results indicated that the main mechanisms of the thermal cracking of sandstone were thermal expansion mismatch and thermal expansion anisotropy, and the critical temperature for the initiation and nucleation thermal cracking of sandstone was shown to be about 150 °C. These studies mainly aimed at the rock mechanics properties (strength and deformation parameters) after being subject to high temperature. Although the relationship between permeability and mechanical properties of rocks is of great importance (Brace et al., 1968; Luo et al., 2011), our knowledge is restricted in terms of how these quantities relate to rocks that have been previously subjected to high temperatures. This study focuses on the evolution of permeability (gas) due to deformation occurring in sandstone samples previously subjected to thermal treatment.

Experimental

Sandstone material and sample preparation

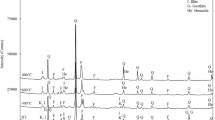
The test material was a sandstone collected from Jiangxi Province, China. It is composed of fine grains with a mean grain size of about 0.12 mm. From X­ray diffraction (XRD) analysis, the minerals in the sandstone specimens are mainly feldspar, quartz, kaolinite, and chlorite, and more detailed compositions of this rock are described in Fig. 1. A rock-drilling machine was used to core samples and a lathe was used to ensure samples’ smoothness and verticality. Sandstone samples with a diameter of 25 mm and a length of 50 mm were cored from a single block all at the same orientation (vertical to the bedding plane). Density, porosity, and P-wave velocity of the sandstone samples were measured before the thermal treatment and the results are presented in Table 1. In addition, the average permeability of the sandstone samples before the thermal treatment is about 5.823×10−16 m2. During thermal loading, samples stayed inside an electric furnace and they were heated at a rate of 10 °C/min (with a temperature control accuracy of ±1 °C). Samples remained inside the furnace for 4 h after having reached the desired temperature and then they were cooled to room temperature (while remaining inside the furnace). The low heating rate was applied to ensure that cracking resulted only due to temperature effects. Four temperature groups were used in the test, namely 20, 200, 400, and 600 °C. We originally used five groups, the highest of which was 800 °C, but the samples were seriously damaged after the heat treatment. Thus, we decided to omit this group. Fig. 2 shows photos of the sandstone samples after being heated at high temperatures. At room temperature the sandstone sample was gray, then at 200–600 °C the samples changed from gray to brownish red, and at 800 °C it was ochre. As shown in Fig. 2b, a large number of macroscopic cracks were produced by thermal stress in the sandstone samples after 800 °C, which made them unsuitable for use.

Fig. 1
figure 1

Mineral composition of sandstone (before heat treatment) derived from XRD

Full size image
Fig. 2
figure 2

Sandstone samples after heat treatment

(a) Available samples (20, 200, 400, and 600 °C); (b) Unavailable samples (800 °C)

Full size image
Table 1 Basic material parameters of tested sandstone samples
Full size table

Testing equipment and procedures

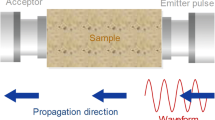
Triaxial compression experiments were carried out at a TAW-1000 electro-hydraulic servo controlled testing system, which enables gas permeability measurements under various confining pressure (Fig. 3). The radial and axial displacement transducer maximum ranges were 2 and 4 mm, respectively. Thus, the initial displacement was controlled as far as possible within 300 and 500 µm. During the experiments, the axial stress, axial and lateral strain of the tested sandstone samples were recorded simultaneously.

Fig. 3
figure 3

Sample assembly (a) and TAW-1000 electro-hydraulic servo controlled testing system (b)

Full size image

The sample was positioned between two steel end-plugs, each of which had a concentric hole at the center for fluid access to the upstream and downstream pore pressure system. The sample and steel end-plug were wrapped with black tape and tightened with heat-shrink pipe to isolate the pore pressure from the confining pressure. Then the axial and radial displacement transducers were installed, and the assembled sample was placed into the chamber on the lower cylinder of the load frame (Fig. 3a). Next the triaxial cell was lowered and filled with oil so that the confining pressure could be applied. During these experiments, we tested different confining pressures: Pc=0 MPa (uniaxial compression), 5, 10, and 20 MPa. In a triaxial compression test, the confining pressure was loaded to 1 MPa by displacement control at a rate of 20 mm/min. Then the loading method was changed to pressure control at a rate of 6 MPa/min to a desired confining pressure Pc, and then the axial stress (σ1) was increased incrementally at a rate of 0.06 mm/min while the radial stresses (σ2=σ3=Pc) remained constant, where σi (i=1, 2, 3) denote the three principal stresses.

For the measurement of rock permeability, two different experimental techniques were used: the steady-state flow (or permanent regime) method, and pulse test (or transient regime) technique. The choice of the one or the other method mainly depends on the range of permeability to be determined. In general, for materials with relatively high permeability (e.g., >10−16 m2), it is easy to reach the permanent flow regime, and the steady-state flow is preferred (Brace et al., 1968). In the case of the red sandstone samples used here, the initial permeability is relatively high, ranging from 10−16 to 10−15 m2. Thus, the steady-state flow method was chosen and the nitrogen was adopted for the penetrating fluid in this test. One end of the dry sample was connected to a nitrogen gas cylinder and 2.0 MPa pressure was applied to this end. The other end was open to atmospheric pressure. So a 2.0 MPa gas pressure gradient was imposed between these two ends and kept constant, which allowed the fluid to flow from one end of the sample towards the other. In the whole process of triaxial compression, 6–8 points of gas permeability were measured. When the gas valve was open, the gas flowed through the sample and then flowed into the transfer pipette (via previous water wetting). The transfer pipette had inhaled a small amount of water to form a blister in advance. Driven by the gas, the blister could move in the pipette. When the gas permeability was measured, the axial loading was suspended and the gas flow rate could be calculated by recording the distance (i.e., the fluid volume) the blister had moved in the pipette and the corresponding time.

For steady-state gas flow, the permeability was calculated according to Darcy’s law (Scheidegger, 1974) for compressive media:

$$K = {{2Q\mu L{P_0}} \over {A({P^2} - P_0^2)}},$$
(1)

where K is the sandstone permeability (m2), Q is the flow rate of the gas (m3/s), μ is the nitrogen dynamic viscosity (Pa·s) (1.83×10−5 Pa·s at 20 °C, 1×105 Pa), L is the length of the sample (m), A is the section of the sample (m2), P0 is the atmospheric pressure (Pa), and P is the injection pressure (Pa).

Results

Variations in rock properties after heat treatments

Density, porosity, and ultrasonic velocity are important rock properties and are often used to characterize porous materials. Density was calculated by measuring the weight and the volume (diameter and length) of the samples according to the methods recommended by the International Society of Rock Mechanics (ISRM) (Ulusay and Hudson, 2007). P-wave velocities were calculated by measuring the P-wave arrival times along the length of each sample using a Tektoninix digital phosphor oscilloscope 3012 and two P-wave transducers with a frequency of 0.5 MHz. Porosity was calculated by measuring the volume of the sample and the volume of the rock matrix using a core porosimeter. Table 1 shows the measured values of the above-mentioned properties of the sandstone samples before and after the thermal treatment (no mechanical loading). As shown in Table 1, the density and the P-wave velocity of this sandstone after heat treatment have smaller values than those before heat treatment; however, the porosity has an opposite tendency. In addition, the rates of variation of these three parameters increase with the increase of temperature. Variations in density, porosity, and P-wave velocity due to heat treatment temperature in sandstone (Tian et al., 2012) and other kinds of rocks (e.g., granite, marble, and limestone) were also studied by other researchers (Géraud et al., 1992; Chaki et al., 2008; Sengun, 2014) and their results came to similar conclusions with those above. It is likely that density decrease is caused by the volume expansion after the heat treatment, as was suggested by Wu et al. (2003) and Chen et al. (2005). The reason for changes in porosity and P-wave depending on heat treatment might be the change of the inner structure of the rock induced by thermally stress, as was measured by Géraud et al. (1992) using X-ray computerized tomography.

Stress strain relationship and mechanical parameters of the sandstone samples being subjected to different confining pressures after heat treatments

The stress-strain behavior of this sandstone under various confining pressures after heat treatment is shown in Fig. 4. It can be seen from the diagram that, when the sandstone samples are loaded under uniaxial compression (zero confining pressure, Fig. 4a): (1) for heat treatments from 20–200 °C, the strength increases and there is an abrupt stress drop after the peak stress; (2) the strength reduces, ductility increases and shows a slight yield stage before the peak stress from 200 °C to 600 °C; (3) the strength declines significantly (compared to the 200 °C case) after 600 °C. The mechanical behaviour of samples that were loaded under triaxial compression shows differences as compared to that of samples that were subjected to uniaxial compression (Figs. 4b, 4c, and 4d): the yield stage is remarkable before the peak stress, and the length of the yield stage is longer as the confining pressure rises.

Fig. 4
figure 4

Stress-strain relationship curves with different confining pressures after heat treatment

(a) Pc=0 MPa; (b) Pc=5 MPa; (c) Pc=10 MPa; (d) Pc=20 MPa; ε1: axial strain; ε3: radial strain

Full size image

Fig. 5 shows the strain values corresponding to the peak strength of sandstone samples being subjected to various confining pressures after different temperature treatments. In Fig. 5a, the peak strength for all tested confining pressures slightly increases from 20 to 200 °C, declines from 200 to 400 °C and declines rapidly from 400 to 600 °C. The equivalent strains decrease slightly from 20 to 200 °C and then increase from 200 to 600 °C.

Fig. 5
figure 5

5 Peak strength (a) and corresponding strain (b) of sandstone samples under different confining pressures after heat treatment

Full size image

From the analysis of the uniaxial and triaxial compression tests performed on the sandstone samples, we determined a series of mechanical parameters under various confining pressures after different temperature treatments (Table 2). In Table 2, the Young’s modulus E and Poisson’s ratio v were respectively calculated by Eqs. (2) and (3) (Timoshenko and Goodier, 1951), in which the stress and strain values used were corresponding to those values at the half peak stress of the stress-strain curves:

$$E = {{({\sigma _1} + {\sigma _3}){\sigma _1} - 2\sigma _3^2} \over {({\sigma _1} + {\sigma _3}){\varepsilon _1} - 2{\sigma _3}{\varepsilon _3}}},$$
(2)
$$\nu = {{{\sigma _1}{\varepsilon _3} - {\sigma _3}{\varepsilon _1}} \over {2{\sigma _3}{\varepsilon _3} - ({\sigma _1} + {\sigma _3}){\varepsilon _1}}}.$$
(3)
Table 2 Strength and deformation values of sandstone samples under triaxial compression tests
Full size table

Fig. 6 shows the Young’s modulus and Poisson’s ratio after different heat treatments. The results show that the Young’s modulus increases from 20 to 200 °C, then decreases from 200 to 600 °C, while the Poisson’s ratio does not show any particular trend with temperature. Mao et al. (2009) worked on limestone samples being subjected to a range of temperatures between room temperature and 800 °C, and showed that the relationship between the modulus of elasticity and temperature variation can be described by a cubic polynomial approximation, which is not in accordance with what we have observed for the equivalent case of sandstone samples. This discrepancy could be explained by the different mineralogical composition of the two rock types.

Fig. 6
figure 6

Young’s modulus (a) and Poisson’s ratio (b) after heat treatment at different temperatures

Full size image

Fig. 7 shows photographs of the fracture patterns of the sandstone samples after compression testing. The photographs demonstrate the following: (1) At room temperature, with increasing confining pressure, sandstone failure gradually changes from tensile to shear failure (orientation of the fractures). (2) Under uniaxial compression, within the range of 20–200 °C, the fractured pattern is shown as shear failure. The shear angle between the fracture surface and the axial direction of the sample is relatively small, and the sandstone shows axial splitting. In addition, with T>200 °C, the angle between the fracture surface and the axial direction increases. (3) The rock samples are less fragmented than those that have undergone heat treatment at 400–600 °C. From visual observations of the samples, it appears that both temperature and confining pressure should have some effect on the failure type of this sandstone. Such observation is also supported by Yin et al. (2012).

Fig. 7
figure 7

Fracture patterns of sandstone samples after compression tests

(a) Pc=0 MPa; (b) Pc=5 MPa; (c) Pc=10 MPa; (d) Pc=20 MPa

Full size image

Permeability changes and strain-volumetric curves

Martin (1993) proposed the crack strain model to calculate crack initiation strength, and soon afterward the model was expanded to a wide range of applications (Cai et al., 2004; Shang et al., 2015). In this study, the crack strain model was used to calculate the volumetric strain, and the crack volumetric strain to study the permeability evolution with crack strain, the expressions for which are as follows:

$$\varepsilon {\rm{v}} = {{\Delta V} \over V} = \varepsilon {\rm{axial}} + 2\varepsilon {\rm{lateral}},$$
(4)
$$\varepsilon {\rm{ve}} = {{\Delta V} \over {V{\rm{elastic}}}} = {{1 - 2\nu } \over E}({\sigma _1} + 2{\sigma _3}),$$
(5)
$$\varepsilon {\rm{vc}} = {\varepsilon _{\rm{v}}} - {\varepsilon _{{\rm{ve}}}},$$
(6)

where εv is the volumetric strain, εaxial is the axial strain, εlateral is the lateral strain, εve is the elastic volumetric strain, ΔV is the volume change, Velastic is the elastic volume, and εvc is the crack volumetric strain.

Fig. 8 shows the volumetric strain, crack volumetric strain, and permeability variation as a function of axial strain of the sandstone after heat treatment under 5 MPa confining pressure. A similar variation pattern is also observed in other confining pressure experiments (not shown herein). Fig. 8 demonstrates the following: (1) the maximum volumetric strain (contraction) decreases with temperatures from 20 to 200 °C and increases from 200 to 600 °C; (2) the permeability increases more rapidly during the deviatoric loading in higher temperature treatment samples (from 200 to 600 °C); (3) during the deviatoric loading, contraction takes place initially followed by dilation at the non-linear stage. This occurs in parallel with crack closure, stabilization, and growth as it is shown by the evolution of the calculated crack volumetric strain. Permeability shows an increasing trend.

Fig. 8
figure 8

Strain-volumetric and permeability curves of sandstone after heat treatment under 5 MPa confining pressure

(a) 20 °C; (b) 200 °C; (c) 400 °C; (d) 600 °C

Full size image

The permeability evolution with the stress-strain curve of the sandstone is presented in Fig. 9. According to the stress-strain behavior of a loaded rock sample, Takarli and Prince-Agbodjan (2008) defined these stages as follows: crack closure; linear elastic deformation; crack initiation and stable crack growth; crack damage and unstable crack growth; failure and post-peak behavior (Fig. 9). In this study, the definition was used to analyze the effect of heat treatment on the failure process taking place in sandstone samples. In the stress-strain diagram shown in Fig. 9, the crack closure threshold σcc is defined as zero calculated crack volumetric strain, the crack initiation threshold σci is marked as the point where the stress-strain curve departs from linearity, and the crack damage threshold σcd corresponds to the most-positive value of volumetric strain. These three stress levels represent important stages in the development of the macroscopic failure process of intact rock samples. From Fig. 9 the following can be seen: (1) During the initial stage of the deviatoric experiment (stage I, crack closure), the stress-stain response is non-linear. The rock sample gets compacted, and the crack volumetric strain decreases, which indicates that initial cracks close and the permeability of the rock decreases. (2) With increasing axial loading (stage II, linear elastic deformation), the rock continues to compact while the crack volumetric strain and permeability remain constant roughly. (3) As loading continues to increase (stage III, stable crack growth), the volumetric stress reaches a maximum value and the crack volumetric strain increases together with the permeability of the rock. This indicates that the microcrack population starts to increase. (4) Before the stress drop (stage IV, crack damage and unstable crack growth), compactant strain decreases, crack volumetric strain increases together with a significant rise in permeability, which might be linked to a higher number of microcracks. (5) As the axial loading reduces (stage V, failure and post-peak behavior), volumetric dilation in the rock sample begins. The crack volumetric strain reduces while the permeability of the rock soars, which is probably because of irregular macrofracture plane sliding.

Fig. 9
figure 9

Stress-strain relationship and permeability evolution after heat treatment

σci represents the crack initiation threshold when microfracturing begins; σf stands for the peak strength

Full size image

The data of the initial permeability under various confining pressures after heat treatment are presented in Fig. 10. Under the same confining pressure, it can be seen that: (1) from 20 to 200 °C the initial permeability decreases slightly as the temperature increases; (2) from 200 to 400 °C the initial permeability increases slowly as the temperature increases; (3) from 400 to 600 °C the initial permeability increases quickly as the temperature increases. Under the same treatment temperature: (1) the initial permeability generally decreases as the confining pressure increases, with the exception of 400 °C, which may be due to the randomness of the sandstone’s pore structure; (2) the variance in permeability values is smaller at 200 °C compared with that at 600 °C heat-treated samples.

Fig. 10
figure 10

Relationship between initial permeability and temperature after heat treatment

Full size image

Conclusions

In this paper we investigated the change in the mechanical properties and the evolution of the permeability characteristics in sandstone specimens being subjected to different confining pressures (Pc=0, 5, 10, and 20 MPa) after having undergone heat treatment at 20, 200, 400, and 600 °C. The following conclusions can be drawn:

  1. 1.

    At the temperature of 20–200 °C, the primary pore and cracks gradually closed, which improved the density degree and caused the strength and elastic modulus to increase and permeability to decrease. From 200 to 600 °C, the degradation effects of the temperature on sandstone became evident, the strength and elastic modulus decreased, and the strain corresponding to the peak stress and initial permeability increased significantly.

  2. 2.

    With the increase of the confining pressure, the degree of internal crack closure in the sandstone increased, which resulted in the reduction of the initial permeability; in addition, larger internal cracks occurred with the severely degraded sandstone samples, which had a greater effect on the closure with the increase of the confining pressure, and the initial permeability decreased more significantly.

  3. 3.

    Gas permeability of sandstone in a complete stress-strain process varied with the evolution of cracks in the samples. In general, the permeability decreased in the initial loading stage due to the crack closure, after which it remained stable in the elastic deformation stage, then gradually increased in the crack growth stage. Prior to the peak strength, the permeability was enhanced sharply by about one or two orders of magnitude.